O functie y=f(x) se numeste diferentiabila intr-un punct x 0 daca are o derivata definita in acel punct, i.e. dacă limita relaţiei există şi este finită.

Dacă funcția este diferențiabilă în fiecare punct al unui segment [a; b] sau intervalul (a; b), atunci se spune că este diferențiabilă pe segmentul [a; b] sau, respectiv, în intervalul (a; b).

Este valabilă următoarea teoremă, care stabilește o legătură între funcțiile diferențiabile și continue.

Teorema. Dacă funcția y=f(x) este diferențiabilă într-un anumit punct x 0 , atunci este continuă în acel punct.

Astfel, diferențiabilitatea unei funcții implică continuitatea acesteia.

Dovada. Daca atunci

unde b este o valoare infinitezimală, i.e. cantitate tinde spre zero la Ax>0. Dar apoi

Dy=f „(x 0) Dx+bDx=> Dy>0 pentru Dx>0, adică f(x) - f(x 0)>0 pentru x>x 0,

iar aceasta înseamnă că funcția f(x) este continuă în punctul x 0 . Q.E.D.

Astfel, în punctele de discontinuitate, funcția nu poate avea o derivată. Afirmația inversă nu este adevărată: există funcții continue care nu sunt diferențiabile în anumite puncte (adică nu au o derivată în aceste puncte).

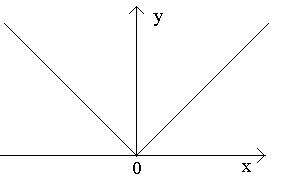
Luați în considerare punctele a, b, c din figură.

La punctul a, când Dx>0, relația nu are limită (deoarece limitele unilaterale sunt diferite pentru Dx>0-0 și Dx>0+0). Nu există o tangentă definită în punctul A pe grafic, dar există două tangente unilaterale diferite cu pante de 1 și 2 . Acest tip de punct se numește punct de colț.

În punctul b pentru Dx>0, raportul este o valoare infinit de mare constantă de semn. Funcția are o derivată infinită. În acest moment, graficul are o tangentă verticală. Tip punct - „punct de inflexiune” cu tangentă verticală.

În punctul c, derivatele unilaterale sunt cantități infinit de mari de semne diferite. În acest moment, graficul are două tangente verticale îmbinate. Tip - "cuspid" cu o tangentă verticală - un caz special al unui punct de colț.

1. Se consideră funcția y=|x|. Această funcție este continuă în punct

Să arătăm că nu are nicio derivată în acest moment.

f(0+Dx) = f(Dx) = |Dx|. Prin urmare, Dy = f(Dx) - f(0) = |Dx|

Dar apoi pentru Dx< 0 (т.е. при Дx стремящемся к 0 слева)

Și când Dx > 0

Astfel, relația pentru Dx> 0 are limite diferite la dreapta și la stânga, ceea ce înseamnă că relația nu are limită, i.e. derivata functiei y=|x| în punctul x= 0 nu există. Geometric, asta înseamnă că în punctul x= 0 această „curbă” nu are o tangentă definită (sunt două în acest punct).

2. Funcția este definită și continuă pe întreaga linie reală. Să aflăm dacă această funcție are o derivată la x= 0.

Prin urmare, funcția luată în considerare nu este diferențiabilă în punctul x= 0. Tangenta la curbă în acest punct formează un unghi p/2 cu axa x, adică. coincide cu axa y.

3 Definiţia derivatei unei funcţii într-un punct Fie definită funcţia f(x) într-o vecinătate a punctului x 0. DEFINIŢIE. Dacă există o limită (finită) a relației, atunci f (x) se numește punct diferențiabil x 0, iar limita însăși se numește derivată a funcției f (x) în punctul x 0 și se notează cu f „(x 0), adică notăm x \u003d x - x 0 este incrementul argumentului atunci când trecem de la punctul x 0 la punctul x și y \u003d f (x 0 + x) - f (x 0) ) este incrementul corespunzător al funcției.Atunci derivata funcției f (x) în punctul x 0 este limita raportului dintre incrementul funcției și incrementul argumentului care a determinat-o, când incrementul de argumentul tinde spre zero.

4 Exemplul 1. Să dăm exemple de calcul a derivatelor unor funcții elementare simple, pe baza definiției unei derivate. y = a x (0 0. Considerând că | x | 0 este un punct arbitrar, atunci 0. Avand in vedere ca | x | 0 este un punct arbitrar, apoi „>

0. Avand in vedere ca | x | 0 este un punct arbitrar, atunci Exemplul 4. y = sinx, x R. Luați x 0 R și calculați incrementul funcției în acest punct: Deci (sinx) = cosx, x R." title=" 5 Exemplul 3. Să luăm x 0 > 0. Considerând că | x | 0 este un punct arbitrar, atunci Exemplul 4. y = sinx, x R. Să luăm x 0 R și să calculăm incrementul funcției în acest punct: Deci (sinx) = cosx, x R." class="link_thumb"> 5 !} 5 Exemplul 3. Luați x 0 > 0. Având în vedere că | x | 0 este un punct arbitrar, atunci Exemplul 4. y = sinx, x R. Să luăm x 0 R și să calculăm incrementul funcției în acest punct: Deci (sinx) = cosx, x R. 0. Avand in vedere ca | x | 0 este un punct arbitrar, atunci Exemplul 4. y = sinx, x R. Luați x 0 R și calculați incrementul funcției în acest punct: Deci (sinx) = cosx, x R. "> 0. Având în vedere că | x | 0 - punct arbitrar, apoi Exemplul 4. y \u003d sinx, x R. Luați x 0 R și calculați incrementul funcției în acest punct: Deci (sinx) \u003d cosx, x R. "> 0. Având în vedere că | x | 0 este un punct arbitrar, atunci Exemplul 4. y = sinx, x R. Luați x 0 R și calculați incrementul funcției în acest punct: Deci (sinx) = cosx, x R." title=" 5 Exemplul 3. Să luăm x 0 > 0. Considerând că | x | 0 este un punct arbitrar, atunci Exemplul 4. y = sinx, x R. Să luăm x 0 R și să calculăm incrementul funcției în acest punct: Deci (sinx) = cosx, x R."> title="5 Exemplul 3. Luați x 0 > 0. Având în vedere că | x | 0 este un punct arbitrar, atunci Exemplul 4. y = sinx, x R. Să luăm x 0 R și să calculăm incrementul funcției în acest punct: Deci (sinx) = cosx, x R."> !}

6 TEOREMA. Dacă o funcție f(x) este diferențiabilă într-un punct x 0, atunci este continuă în acel punct. Dovada. Lasă-l să existe. Atunci de aici obținem că f (x) - f (x 0) \u003d f "(x 0) (x - x 0) + (x - x 0) α (x) pentru x x 0. Adică , f ( x) este continuă în punctul x 0. Continuitatea funcției diferențiabile (1)

7 NOTĂ. Continuitatea unei funcții într-un punct nu este o condiție suficientă pentru existența unei derivate în acest punct. Exemplul 5. f (x) \u003d x. Investigăm comportamentul lui f (x) în vecinătatea lui x 0 = 0. Aici și f (x) f (0) = 0 pentru x 0. Adică, funcția este continuă în punctul x 0 \u003d 0. Luați în considerare x y 0 Limita nu există, deoarece Deci, funcția f (x) \u003d x nu are o derivată în punctul x \u003d 0, deși este continuu in acest moment

8 Exemplu x y 0 la x 0. la x 0. I.e. f(x) este continuă la x = 0. Adică, f(x) nu are nicio derivată la x = 0 și, prin urmare, nu este diferențiabilă în acel punct. Investigăm comportamentul lui f (x) în vecinătatea punctului x = 0.

9 Fie că funcția y \u003d f (x) este diferențiabilă în punctul x 0. Apoi, conform (1), incrementul său în punctul x 0 poate fi scris ca y \u003d f (x 0 + x) - f (x 0) \u003d f ( x 0) x + o(x) la x. Diferenţialul funcţiei f (x 0) x - liniarul principal în raport cu partea x a incrementului funcţiei y \u003d f (x) în punctul x 0 se numeşte diferenţială a funcţiei în punctul x 0 cu incrementul x și se notează df (x 0; x) sau df (x 0 ) sau df sau dу. y \u003d f (x 0 + x) - f (x 0) \u003d df (x 0; x) + o (x) la x. DEFINIȚIE. Partea principală a incrementului, liniară în x. Un ordin infinitezimal mai mare decât x. Acum, incrementul funcției poate fi scris astfel:

10 NOTĂ. Incrementul x este adesea notat cu simbolul dx și se numește diferența variabilei independente. Astfel, diferența unei funcții într-un punct x 0 poate fi scrisă ca df (x 0) \u003d f "(x 0) dx. Dacă o funcție este diferențiabilă în fiecare punct al unui anumit interval, atunci diferența sa dy este o funcția lui x și dx: dy \u003d f "(x)dx. De aici, în special, se obține expresia pentru derivată, adică derivata poate fi considerată ca raportul dintre diferenţialul funcţiei şi diferenţialul variabilei independente.

11 Semnificația geometrică a derivatei și diferențialei Fie funcția y \u003d f (x) este definită în U (x 0) și diferențiabilă în punctul x 0. M0M0 M x0x0 x 0 + x y x y = f (x) y0y0 y 0 + y 0 L este secanta lui L 0 - tangente x y \u003d f (x 0 + x) - f (x 0) la x datorită continuității funcției. Tangenta la graficul funcției y \u003d f (x) în punctul M 0 este poziția limită a secantei L la x. y Dacă funcția este diferențiabilă în punctul x 0, atunci în ecuația secanta y / x f (x 0) la x și ecuația tangentei are forma y \u003d y 0 + f (x 0) (x - x 0) .

12 M0M0 M x0x0 x 0 + x dy = df(x 0; x) = f (x 0) x x y = f(x) f(x0)f(x0) f(x 0 + x) 0 x y F E EM = o (x) la x 0 L0L0 tg \u003d f (x 0) Dacă y / x la x, atunci linia dreaptă x \u003d x 0, rezultată din ecuația secantei, se numește tangentă verticală la graficul funcției de la punctul M 0. Din ecuația tangentei obținem y - y 0 \u003d f (x 0) (x - x 0) \u003d df (x 0) - creșterea ordonatei tangentei atunci când trecem de la punctul x 0 la punctul x . Normala graficului funcției în punctul M 0 este linia dreaptă perpendiculară pe tangenta care trece prin punctul M 0. Ecuația sa are forma y \u003d y 0 - 1 / f (x 0) (x - x) 0). L 1 - normal

13 Aplicații fizice ale derivatei și diferențialei Dacă S (t) este calea parcursă de un punct material în timpul t, atunci S "(t) este viteza instantanee a punctului material și dS \u003d S "(t) dt este distanța pe care punctul material ar parcurge-o într-o perioadă de timp de la t la t + dt, dacă s-ar deplasa cu o viteză egală cu viteza instantanee la momentul t. Dacă Q (t) este cantitatea de electricitate care curge prin secțiunea transversală a conductorului la momentul t, atunci Q "(t) \u003d I este puterea curentului. Dacă N (t) este cantitatea de substanță formată la momentul t în timpul unei reacții chimice, apoi N "(t) - viteza unei reacții chimice.

Dacă funcţia y = f(X) este diferențiabilă la un moment dat X = X 0, atunci este continuă în acest moment.

Astfel, în punctele de discontinuitate, funcția nu poate avea o derivată. Concluzia inversă este falsă, adică. din faptul că la un moment dat X = X 0 functie y = f(X) este continuă, nu rezultă că este diferențiabilă în acest punct. De exemplu, funcția y = |X| continuu pentru toti X (–< X < ), но в точке X= 0 nu are derivată. În acest moment, nu există nicio tangentă la grafic. Există o tangentă dreaptă și o tangentă stângă, dar nu se potrivesc.

21 Găsirea regulilor. producție sume

Regula 1 Dacă funcțiile y \u003d f (x) și y \u003d g (x) au o derivată în punctul x, atunci suma lor are și o derivată în punctul x, iar derivata sumei este egală cu suma lui derivatele:
(f (x) + 8 (x))" \u003d f (x) + (x).
În practică, această regulă este formulată într-un mod mai scurt: derivata sumei este egală cu suma derivatelor.
De exemplu,
Regula 2 Dacă funcția y \u003d f (x) are o derivată în punctul x, atunci funcția y \u003d kf (x) are o derivată în punctul x și:

În practică, această regulă este formulată într-un mod mai scurt: factorul constant poate fi scos din semnul derivatei. De exemplu,

Regula 3 Dacă funcțiile y \u003d f (x) și y \u003d g (x) au o derivată în punctul x, atunci produsul lor are și o derivată în punctul x și:

În practică, această regulă este formulată astfel: derivata produsului a două funcții este egală cu suma a doi termeni. Primul termen este produsul derivatei primei funcție și a celei de-a doua funcție, iar al doilea termen este produsul primei funcție și derivata celei de-a doua funcție.
De exemplu:
Regula 4 Dacă funcțiile y \u003d f (x) și y \u003d g (x) au o derivată atunci, iar câtul are o derivată în punctul x, în plus:

Tabelul derivatelor complexe

22 Diffir. funkt. la punct

Funcţie y=f(X) se numeste diferentiabila intr-un punct X 0 dacă incrementul său Δ y(X 0,Δ X) poate fi reprezentat ca

Δ y(X 0,Δ X)=AΔ X+o(Δ X).

Partea liniară principală AΔ X crește Δ y se numește diferența acestei funcții în punct X 0 corespunzător incrementului Δ X, și este notat cu simbolul dy(X 0,Δ X).

Pentru functia y=f(X) era diferențiabilă la punctul respectiv X 0, este necesar și suficient ca derivata f′( X 0), în timp ce egalitatea A=f′( X 0).

Expresia pentru diferential are forma

dy(X 0,dx)=f′( X 0)dx,

Unde dx=Δ X.

23 Prod. Diff. Funcții

Derivată a unei funcții complexe. Derivată a unei funcții definită parametric

Lăsa y - functie complexa X, adică y = f(u), u = g(X), sau

Dacă g(X) Și f(u) sunt funcții diferențiabile ale argumentelor lor, respectiv, la puncte XȘi u = g(X), atunci funcția complexă este și ea diferențiabilă la punct X si se gaseste prin formula

Derivată a unei funcții dată parametric.

24 Prod. și dif. De ordin superior

Să fie acum derivata de ordinul al treilea să fie definită într-o vecinătate a punctului și să fie diferențiabilă. Apoi

Dacă o funcție are o derivată parțială față de una dintre variabilele dintr-un domeniu D, atunci derivata numită, fiind ea însăși o funcție a lui , poate avea derivate parțiale față de aceeași variabilă sau de orice altă variabilă la un moment dat. Pentru funcția originală, aceste derivate vor fi derivate parțiale de ordinul doi (sau derivate parțiale secunde).

O derivată parțială de ordinul doi sau mai mare luată în raport cu diferite variabile se numește derivată parțială mixtă. De exemplu,

diferenţial de ordine n, Unde n > 1, a unei funcții la un moment dat se numește diferenţial în acest punct al diferenţialului de ordin (n - 1), acesta este

Pentru o funcție care depinde de o variabilă, a doua și a treia diferență arată astfel:

Din aceasta putem deriva forma generală a diferenţialului n-a ordine de la funcția:

25 Teoremele lui Fermat, Rolle, Langrage

v Teorema lui Fermat: Să fie definită o funcție și să atingă valorile maxime și minime ( MȘi m) în unele dintre . Dacă există o derivată în , atunci aceasta este în mod necesar egală cu 0.

Dovada: Există. Sunt posibile două cazuri:

1) , => , => .

2) , => , => .

Din 1) și 2) rezultă că

v Teorema lui Rolle (despre rădăcinile derivatei): Fie ca funcția să fie continuă și diferențiabilă și să ia aceleași valori la capetele segmentului: . Apoi există cel puțin un punct în , a cărui derivată este .

v Dovada: atinge continuu MȘi m. Atunci sunt posibile două cazuri:

2) cea mai mare valoare se realizează în intervalul conform teoremei lui Fermat.

v teorema lui Langrage (despre incremente finite): Fie funcția continuă pe și diferențiabilă pe . Atunci există cel puţin una dintre care este valabilă următoarea egalitate: .

Dovada: Să introducem funcția . (continuu pe și diferențiabil pe ).

Funcția satisface Teorema lui Rolle există pentru care: , , , .

Funcția este numită strict crescând pe dacă

Funcția este numită in scadere pe dacă

Funcția este numită strict în scădere pe dacă

Definiție: Derivata unei funcții într-un punct este limita la care tinde raportul dintre incrementul său în acel punct și incrementul corespunzător al argumentului atunci când acesta din urmă tinde spre zero:

Adică, dacă este definit în, atunci

Teorema 1:

Graficul unei funcții are o tangentă neverticală dacă și numai dacă există o valoare finită a derivatei acestei funcții la un punct dat.

Dovada:

Să fie o valoare f'()-finită, atunci

Să fie o tangentă non-verticală => există - finită.

Secanta tinde spre tangentă.

Teorema a fost demonstrată.

Ticket 2 Continuitatea unei funcții care are o derivată.

O funcție f (x) definită într-o vecinătate a unui punct a se numește continuă în acest punct dacă

Teorema: (o condiție necesară pentru existența unui derivat)

Dacă funcția are un punct finit, atunci este continuă în punctul respectiv.

Dovada:

Prin urmare - este continuă într-un punct.

Teorema a fost demonstrată.

cometariu : invers nu este adevărat, dacă o funcție este continuă într-un punct, atunci nu rezultă că are o derivată în acel punct.

Afirmație : dacă o funcție are o derivată dreaptă și stângă într-un punct, atunci este continuă atât la dreapta cât și la stânga.

Biletul 3

Derivată a sumei, produsului, coeficientului.

Derivată a funcției inverse.

Definiția unei funcții diferențiabile. Condiție necesară și suficientă pentru diferențiere.

Fie ca funcția să aibă o derivată într-un punct (final): .

Apoi, pentru suficient de mic, se poate scrie ca suma unei funcții, pe care o notăm prin, care tinde spre zero împreună cu:,

iar incrementul la un punct poate fi scris ca:

sau (1) ,

căci o expresie este înțeleasă ca o funcție astfel încât raportul său tinde spre zero împreună cu.

Explicaţie:

Definiție .

O functie se numeste diferentiabila intr-un punct daca incrementul ei poate fi reprezentat ca: (2),

unde A nu depinde de , ci depinde în general de .

Teorema 1:

Pentru ca o funcție să fie diferențiabilă într-un punct, este necesar și suficient ca ea să aibă o derivată finită în acel punct.

Dovada:

Suficiența stării dovedit mai sus: existența unei derivate finite a implicat posibilitatea reprezentării în forma (1), unde se poate stabili

Condiție de necesitate . Fie ca funcția să fie diferențiabilă într-un punct. Apoi din (2), presupunând, obținem.

Limita laturii drepte pentru există și este egală cu A:.

Aceasta înseamnă că există un derivat. Teorema a fost demonstrată.

Tichetul 6 Diferenţialul unei funcţii, semnificaţia ei geometrică.

Dacă funcţia f are un derivat f΄(x o ) la punct X o, atunci există o limită , unde Δ f=f(x o + Δ x)-f(x o ) ,, sau unde A=f΄(x o ) .

Definiție:

Funcţie f diferentiabil la un punct X o, dacă incrementul său poate fi reprezentat ca:

Unde AΔ x=df. (*)

Diferenţialul este partea liniară principală a incrementului funcţiei.

Dacă există o derivată finită f΄(x o ) la punct X o, apoi funcția f(x) este diferențiabilă în acest moment.

Este adevărat și invers: dacă funcția f diferentiabil la un punct X o, adică incrementul său poate fi reprezentat ca (*), atunci are o derivată în punct X o egal cu A:

Semnificația geometrică a diferenţialului:

AȘi B– puncte grafice f(x), corespunzătoare valorilor X oȘi (X o + Δ X) variabila independenta. ordonate punctuale AȘi B respectiv egale f(x o ) Și f(x o + Δ X). Increment de funcție Δ f=f(x o + Δ x)-f(x o ) la punct X o egală cu lungimea segmentului BDși poate fi reprezentat ca o sumă Δ f=BD=DC+CB, Unde DC=tgaΔ x=f΄(x o ) Δ XȘi α este unghiul dintre tangenta in punct A la grafic și direcția pozitivă a axei X. De aici este clar că DC este diferența funcției f la punct X o :

DC=df=f΄(x o ) Δ X.

Totodată, cota celui de-al doilea membru CB crește Δ f a luat în considerare dimensiunea. Această valoare, la Δ mare X, poate chiar mai mult decât termenul principal, dar este un ordin infinitezimal mai mare decât Δ X când Δ x→0.

PROPRIETĂȚI ALE FUNCȚIILOR CONTINUE PE UN INTERVAL

Să luăm în considerare câteva proprietăți ale funcțiilor continue pe un interval. Prezentăm aceste proprietăți fără dovezi.

Funcţie y = f(x) numit continuu pe segment [A, b], dacă este continuă în toate punctele interne ale acestui segment, și la capetele acestuia, i.e. la puncte AȘi b, este continuă la dreapta și, respectiv, la stânga.

Teorema 1. O funcție continuă pe segmentul [ A, b], cel puțin într-un punct al acestui segment ia cea mai mare valoare și cel puțin într-un punct - cea mai mică.

Teorema afirmă că dacă funcția y = f(x) continuu pe segmentul [ A, b], atunci există cel puțin un punct x 1 Î [ A, b] astfel încât valoarea funcției f(x)în acest moment va fi cea mai mare dintre toate valorile sale de pe acest segment: f(x1) ≥ f(x). În mod similar, există un astfel de punct x2, în care valoarea funcției va fi cea mai mică dintre toate valorile de pe segment: f(x 1) ≤ f(x).

Este clar că pot exista mai multe astfel de puncte, de exemplu, figura arată că funcția f(x) ia cea mai mică valoare în două puncte x2Și X 2 ".

cometariu. Afirmația teoremei poate deveni falsă dacă luăm în considerare valoarea funcției pe intervalul ( A, b). Într-adevăr, dacă luăm în considerare funcția y=x pe (0, 2), atunci este continuă pe acest interval, dar nu își atinge valorile maxime sau minime în el: atinge aceste valori la sfârșitul intervalului, dar capetele nu aparțin regiune.

De asemenea, teorema încetează să fie adevărată pentru funcțiile discontinue. Dă un exemplu.

Consecinţă. Dacă funcţia f(x) continuu pe [ A, b], atunci este mărginită pe acest interval.

Teorema 2. Lasă funcția y = f(x) continuu pe segmentul [ A, b] și ia valori ale diferitelor semne la capetele acestui segment, atunci există cel puțin un punct în interiorul segmentului x=C, unde funcția dispare: f(C)= 0, unde a< C< b

Această teoremă are o semnificație geometrică simplă: dacă punctele graficului unei funcții continue y = f(x), corespunzătoare capetelor segmentului [ A, b] se află pe părțile opuse ale axei Bou, atunci acest grafic cel puțin într-un punct al segmentului intersectează axa Bou. Este posibil ca funcțiile discontinue să nu aibă această proprietate.

Această teoremă admite următoarea generalizare.

Teorema 3 (teorema valorilor intermediare). Lasă funcția y = f(x) continuu pe segmentul [ A, b] Și f(a) = A, f(b) = B. Apoi pentru orice număr Cîntre AȘi B, există un astfel de punct în interiorul acestui segment CÎ [ A, b], Ce f(c) = C.

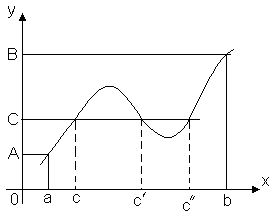
Această teoremă este evidentă din punct de vedere geometric. Luați în considerare graficul funcției y = f(x). Lăsa f(a) = A, f(b) = B. Apoi orice linie y=C, Unde C- orice număr între AȘi B, intersectează graficul funcției cel puțin într-un punct. Abscisa punctului de intersecție va fi acea valoare x=C, la care f(c) = C.

Astfel, o funcție continuă, care trece de la una dintre valorile sale la alta, trece în mod necesar prin toate valorile intermediare. În special:

Consecinţă. Dacă funcţia y = f(x) este continuă pe un anumit interval și ia valorile cele mai mari și cele mai mici, apoi pe acest interval ia, cel puțin o dată, orice valoare între cele mai mici și cele mai mari valori ale sale.

DERIVAT ȘI APLICAȚIILE EI. DEFINIȚIE DERIVATĂ

Să avem o funcție y=f(x), definite pe un anumit interval. Pentru fiecare valoare de argument X din acest interval funcţia y=f(x) are un anumit sens.

Luați în considerare două valori ale argumentului: initial X 0 și nou X.

Diferență x–x 0 este numit increment al argumentului x la punct X 0 și notat Δx. Prin urmare, ∆x = x – x 0 (incrementul argumentului poate fi pozitiv sau negativ). Din această egalitate rezultă că x=x 0 +Δx, adică valoarea inițială a variabilei a primit o anumită creștere. Apoi, dacă la punct X 0 valoarea funcției a fost f(x 0 ), apoi la noul punct X funcția va lua valoarea f(x) = f(x 0 +∆x).

Diferență a-a 0 = f(x) – f(x 0 ) numit creșterea funcției y = f(x) la punct X 0 și este notat cu simbolul Δy. Prin urmare,

Δy = f(x) – f(x 0 ) = f(x 0 +Δx) - f(x 0 ) .

(1)

De obicei, valoarea inițială a argumentului X 0 este considerat fix iar noua valoare X- variabil. Apoi y 0 = f(x 0 ) se dovedeşte a fi constantă şi y = f(x)- variabil. incremente ΔyȘi Δx vor fi și variabile și formula (1) arată că Dy este o funcție a variabilei Δx.

Compuneți raportul dintre incrementul funcției și incrementul argumentului

Să găsim limita acestei relații la Δx→0. Dacă această limită există, atunci se numește derivată a acestei funcții. f(x) la punct X 0 și notează f "(X 0). Asa de,

derivat această funcție y = f(x) la punct X 0 se numește limita raportului de creștere a funcției Δ y la incrementul argumentului Δ X când acesta din urmă tinde în mod arbitrar spre zero.

Rețineți că pentru aceeași funcție derivata în puncte diferite X poate lua valori diferite, de ex. derivata poate fi gândită ca o funcție a argumentului X. Aceasta functie este notata f "(X)

Derivatul este notat prin simboluri f "(X y", . Valoarea specifică a derivatului la x = a notat f "(A) sau y "| x=a.

Operația de găsire a derivatei unei funcții f(x) se numeste diferentierea acestei functii.

Pentru a găsi direct derivata prin definiție, puteți aplica următoarele regula generală:

Exemple.

SENSUL MECANIC AL DERIVATULUI

Din fizică se știe că legea mișcării uniforme are forma s = v t, Unde s- calea parcursă până la un moment dat t, v este viteza mișcării uniforme.

Cu toate acestea, din moment ce majoritatea mișcărilor care apar în natură sunt inegale, apoi, în general, viteza și, în consecință, distanța. s va depinde de timp t, adică va fi o funcție de timp.

Deci, lăsați punctul material să se miște în linie dreaptă într-o direcție conform legii s=s(t).

Observați un moment în timp t 0 . Până în acest punct, punctul a depășit poteca s=s(t 0 ). Să stabilim viteza v punct material la timp t 0 .

Pentru a face acest lucru, luați în considerare un alt moment în timp t 0 + Δ t. Ea corespunde distanței parcurse s =s(t 0 + Δ t). Apoi pentru intervalul de timp Δ t punctul a parcurs calea Δs =s(t 0 + Δ t)–Sf).

Să luăm în considerare relația. Se numește viteza medie în intervalul de timp Δ t. Viteza medie nu poate caracteriza cu exactitate viteza de mișcare a unui punct în acest moment t 0 (deoarece mișcarea este inegală). Pentru a exprima mai precis această viteză adevărată folosind viteza medie, trebuie să luați un interval de timp mai mic Δ t.

Deci, viteza de mișcare la un moment dat t 0 (viteza instantanee) este limita vitezei medii în intervalul de la t 0 la t 0 +Δ t când Δ t→0:

,

acestea. viteza de mișcare neuniformă este derivata distantei parcurse in raport cu timpul.

SENSUL GEOMETRIC AL DERIVATULUI

Să introducem mai întâi definiția unei tangente la o curbă într-un punct dat.

Să avem o curbă și un punct fix pe ea M 0(vezi figura) Luați în considerare un alt punct M aceasta curba si traseaza o secanta M 0 M. Dacă punct Mîncepe să se miște de-a lungul curbei și punctul M 0 rămâne staționar, secanta își schimbă poziția. Dacă, cu o aproximare nelimitată a punctului M curbă la punct M 0 pe orice parte, secanta tinde să ia poziția unei anumite linii drepte M 0 T, apoi linia dreaptă M 0 T se numeste tangenta la curba in punctul dat M 0.

Acea., tangentă la curba la un punct dat M 0 numită poziție limită a secantei M 0 M când punctul M tinde de-a lungul curbei către un punct M 0.

Luați în considerare acum funcția continuă y=f(x) iar curba corespunzătoare acestei funcţii. Pentru o oarecare valoare X Funcția 0 ia o valoare y0=f(x0). Aceste valori X 0 și y 0 pe curbă corespunde unui punct M0 (x 0; y 0). Să dăm un argument x0 increment Δ X. Noua valoare a argumentului corespunde valorii incrementate a funcției y 0 +Δ y=f(x 0 –Δ X). Primim un punct M(x 0+Δ X; y 0+Δ y). Să desenăm o secanta M 0 M si notam cu φ unghiul format de secanta cu directia pozitiva a axei Bou. Să facem o relație și să observăm că .

Dacă acum Δ X→0, deci, datorită continuității funcției Δ la→0 și, prin urmare, punctul M, deplasându-se de-a lungul curbei, se apropie la infinit de punct M 0. Apoi secanta M 0 M va tinde să ia poziția unei tangente la curbă în punct M 0, iar unghiul φ→α la Δ X→0, unde α reprezintă unghiul dintre tangentă și direcția pozitivă a axei Bou. Deoarece funcția tg φ depinde continuu de φ la φ≠π/2, atunci la φ→α tg φ → tg α și, prin urmare, panta tangentei va fi:

acestea. f"(x)= tgα .

Astfel, geometric y "(x 0) reprezintă panta tangentei la graficul acestei funcţii în punct x0, adică pentru o valoare dată a argumentului X, derivata este egala cu tangentei unghiului format de tangenta la graficul functiei f(x)în punctul corespunzător M0 (x; y) cu direcția pozitivă a axei Bou.

Exemplu. Aflați panta tangentei la curbă y = x 2 la punct M(-1; 1).

Am văzut deja că ( X 2)" = 2X. Dar panta tangentei la curbă este tg α = y„| x=-1 = - 2.

DIFERENȚIABILITATEA FUNCȚIILOR. CONTINUITATEA UNEI FUNCȚII DIFERENȚIABILE

Funcţie y=f(x) numit diferentiabil la un moment dat X 0 dacă are o anumită derivată în acest moment, i.e. dacă limita relaţiei există şi este finită.

Dacă o funcție este diferențiabilă în fiecare punct al unui segment [ A; b] sau interval ( A; b), apoi spun că asta diferentiabil pe segmentul [ A; b] sau, respectiv, în intervalul ( A; b).

Este valabilă următoarea teoremă, care stabilește o legătură între funcțiile diferențiabile și continue.

Teorema. Dacă funcţia y=f(x) diferentiabil la un moment dat x0, atunci este continuă în acest moment.

Astfel, diferențiabilitatea unei funcții implică continuitatea acesteia.

Dovada. Dacă , Acea

,

unde α este o valoare infinitezimală, i.e. cantitate care tinde spre zero la Δ X→0. Dar apoi

Δ y=f "(x0) Δ X+αΔ X=> Δ y→0 la Δ X→0, adică f(x) – f(x0)→0 la X→X 0 , ceea ce înseamnă că funcția f(x) continuu la un punct X 0 . Q.E.D.

Astfel, în punctele de discontinuitate, funcția nu poate avea o derivată. Afirmația inversă nu este adevărată: există funcții continue care nu sunt diferențiabile în anumite puncte (adică nu au o derivată în aceste puncte).

Luați în considerare punctele din figură a, b, c.

La punctul A la Δ X→0 relația nu are limită (deoarece limitele unilaterale sunt diferite pentru Δ X→0–0 și Δ X→0+0). La punctul A graficul nu are o tangentă definită, dar există două tangente unilaterale diferite cu pante La 1 și La 2. Acest tip de punct se numește punct de colț.

La punctul b la Δ X→0 raportul este de semn constant valoare infinit mare . Funcția are o derivată infinită. În acest moment, graficul are o tangentă verticală. Tip de punct - „punct de inflexiune” cu o tangentă verticală.

La punctul c derivatele unilaterale sunt cantități infinit de mari de semne diferite. În acest moment, graficul are două tangente verticale îmbinate. Tip - "cuspid" cu o tangentă verticală - un caz special al unui punct de colț.