§ 102. Vorabklärungen.

Im vorherigen Teil haben wir Brüche mit allen möglichen Nennern betrachtet und sie gewöhnliche Brüche genannt. Uns interessierte jeder Bruch, der bei der Messung oder Division entstand, egal welchen Nenner wir bekamen.

Jetzt werden wir aus der ganzen Menge von Brüchen Brüche mit Nennern auswählen: 10, 100, 1.000, 10.000 usw., d.h. solche Brüche, deren Nenner nur Zahlen sind, die durch Eins (1) gefolgt von Nullen (Eins oder mehrere). Solche Brüche werden genannt Dezimal.

Hier sind Beispiele für Dezimalzahlen:

Wir sind schon früher auf Dezimalbrüche gestoßen, haben aber keine besonderen Eigenschaften angegeben, die ihnen innewohnen. Jetzt werden wir zeigen, dass sie einige bemerkenswerte Eigenschaften haben, die alle Berechnungen mit Brüchen vereinfachen.

§ 103. Bild eines Dezimalbruchs ohne Nenner.

Dezimalbrüche werden normalerweise nicht wie gewöhnliche Brüche geschrieben, sondern gemäß den Regeln, nach denen ganze Zahlen geschrieben werden.

Um zu verstehen, wie man einen Dezimalbruch ohne Nenner schreibt, musst du dir merken, wie jede ganze Zahl im Dezimalsystem geschrieben wird. Wenn wir beispielsweise eine dreistellige Zahl nur mit der Zahl 2 schreiben, also der Zahl 222, dann hat jede dieser Zweien eine besondere Bedeutung, je nachdem, welche Stelle sie in der Zahl einnimmt. Die ersten beiden von rechts stehen für Einer, die Zweite für Zehner und die Dritte für Hunderter. Somit bezeichnet jede Ziffer links von jeder anderen Ziffer Einheiten, die zehnmal größer sind als die durch die vorherige Ziffer angegebenen. Wenn eine Ziffer fehlt, wird an ihrer Stelle eine Null geschrieben.

Bei einer ganzen Zahl steht also an erster Stelle rechts die Einer, an zweiter Stelle die Zehn usw.

Lassen Sie uns nun die Frage aufwerfen, welche Kategorie von Einheiten erhalten wird, wenn wir uns beispielsweise in der Nummer 222 befinden Rechts Seite werden wir eine weitere Nummer hinzufügen. Um diese Frage zu beantworten, müssen Sie berücksichtigen, dass die letzten beiden (die ersten von rechts) Einheiten bezeichnen.

Wenn wir also nach der Zwei, die Einheiten bezeichnet, nach einem kleinen Rückzug eine andere Zahl schreiben, zum Beispiel 3, dann wird sie Einheiten bezeichnen, zehnmal kleiner als die vorherigen, mit anderen Worten, es wird bedeuten Zehntel Einheiten; Das Ergebnis ist eine Zahl, die 222 ganze Einheiten und 3 Zehntel einer Einheit enthält.

Es ist üblich, ein Komma zwischen den ganzzahligen und gebrochenen Teilen der Zahl zu setzen, d.h. schreiben Sie so:

Wenn wir nach dem Tripel in dieser Zahl eine weitere Zahl hinzufügen, zum Beispiel 4, dann bedeutet dies 4 Hundertstel Bruchteile einer Einheit; Nummer sieht so aus:

und wird ausgesprochen: zweihundertzweiundzwanzig Punkt, vierunddreißig Hundertstel.

Eine neue Ziffer, zum Beispiel 5, die dieser Nummer zugeordnet wird, ergibt uns Tausendstel: 222,345 (zweihundertzweiundzwanzig Punkt, dreihundertfünfundvierzig Tausendstel).

Zur besseren Übersichtlichkeit kann die Anordnung in der Anzahl der Ganz- und Nachkommastellen in Form einer Tabelle dargestellt werden:

So haben wir erklärt, wie Dezimalbrüche ohne Nenner geschrieben werden. Lassen Sie uns einige dieser Brüche schreiben.

Um einen Bruch ohne Nenner 5/10 zu schreiben, müssen Sie berücksichtigen, dass er keine ganzen Zahlen hat und daher die Stelle der ganzen Zahlen mit Null besetzt sein muss, d. H. 5/10 = 0,5.

Der Bruch 2 9/100 ohne Nenner wird so geschrieben: 2,09, dh Null muss anstelle der Zehntel gesetzt werden. Würden wir diese 0 weglassen, kämen wir auf einen ganz anderen Bruch, nämlich 2,9, also zwei ganze Punkte und neun Zehntel.

Wenn Sie also Dezimalbrüche schreiben, müssen Sie die fehlenden Integer- und Bruchziffern mit Null bezeichnen:

0,325 - keine ganzen Zahlen,
0,012 - keine ganzen Zahlen und keine Zehntel,
1.208 - keine Hundertstel,
0,20406 - keine ganzen Zahlen, keine Hundertstel und keine Zehntausendstel.

Die Zahlen rechts vom Komma heißen Nachkommastellen.

Um Fehler beim Schreiben von Dezimalbrüchen zu vermeiden, müssen Sie daran denken, dass nach dem Dezimalkomma im Bild eines Dezimalbruchs so viele Ziffern stehen sollten, wie Nullen im Nenner stehen, wenn wir diesen Bruch mit einem Nenner schreiben, d.h.

0,1 \u003d 1 / 10 (der Nenner hat eine Null und eine Ziffer nach dem Dezimalkomma);

§ 104. Zuweisung von Nullen zu einem Dezimalbruch.

Im vorigen Absatz wurde beschrieben, wie Dezimalbrüche ohne Nenner dargestellt werden. Die Null ist beim Schreiben von Dezimalbrüchen von großer Bedeutung. Jeder reguläre Dezimalbruch hat eine Null anstelle von ganzen Zahlen, um anzuzeigen, dass ein solcher Bruch keine ganzen Zahlen hat. Wir schreiben jetzt mehrere verschiedene Dezimalzahlen mit den Zahlen: 0, 3 und 5.

0,35 - 0 ganze Zahlen, 35 Hundertstel,
0,035 - 0 ganze Zahlen, 35 Tausendstel,
0,305 - 0 ganze Zahlen, 305 Tausendstel,
0,0035 - 0 ganze Zahlen, 35 Zehntausendstel.

Lassen Sie uns nun herausfinden, was die Nullen bedeuten, die am Ende des Dezimalbruchs stehen, also rechts.

Wenn wir eine ganze Zahl nehmen, zum Beispiel 5, ein Komma dahinter setzen und dann eine Null nach dem Komma schreiben, dann bedeutet diese Null null Zehntel. Daher hat diese rechts zugeordnete Null keinen Einfluss auf den Wert der Zahl, d.h.

Nehmen wir nun die Zahl 6,1 und fügen rechts eine Null hinzu, wir erhalten 6,10, d.h. wir hatten 1/10 nach dem Komma, und es wurde 10/100, aber 10/100 sind gleich 1/10. Das heißt, der Wert der Zahl hat sich nicht geändert, und ab der Zuordnung rechts von Null haben sich nur die Art der Zahl und die Aussprache geändert (6.1 - sechs Komma ein Zehntel; 6.10 - sechs Komma zehn Hundertstel).

Durch ähnliche Argumentation können wir sicherstellen, dass das Zuweisen von Nullen rechts von einem Dezimalbruch seinen Wert nicht ändert. Daher können wir die folgenden Gleichungen schreiben:

1 = 1,0,
2,3 = 2,300,
6,7 = 6,70000 usw.

Wenn wir links vom Dezimalbruch Nullen zuweisen, haben sie keine Bedeutung. Wenn wir nämlich links von der Zahl 4,6 eine Null schreiben, nimmt die Zahl die Form 04,6 an. Wo ist Null? Es steht an der Stelle der Zehner, das heißt, es zeigt, dass es in dieser Zahl keine Zehner gibt, aber das ist auch ohne Null klar.

Es sollte jedoch beachtet werden, dass Dezimalbrüchen manchmal rechts Nullen zugeordnet sind. Beispielsweise gibt es vier Brüche: 0,32; 2,5; 13.1023; 5.238. Den Brüchen, die weniger Nachkommastellen haben, ordnen wir rechts Nullen zu: 0,3200; 2,5000; 13.1023; 5.2380.

Wofür ist das? Wenn wir rechts Nullen zuweisen, erhalten wir vier Nachkommastellen für jede Zahl, was bedeutet, dass jeder Bruch einen Nenner von 10.000 hat, und vor der Zuweisung von Nullen war der Nenner des ersten Bruchs 100, der zweite 10, der dritte 10 000 und die vierte 1 000. Also haben wir durch die Zuweisung von Nullen die Anzahl der Nachkommastellen unserer Brüche egalisiert, also auf einen gemeinsamen Nenner gebracht. Daher wird die Reduktion von Dezimalbrüchen auf einen gemeinsamen Nenner durchgeführt, indem diesen Brüchen Nullen zugewiesen werden.

Wenn andererseits ein Dezimalbruch rechts Nullen hat, können wir sie verwerfen, ohne seinen Wert zu ändern, zum Beispiel: 2,60 = 2,6; 3,150 = 3,15; 4.200 = 4,2.

Wie ist ein solches Weglassen von Nullen rechts vom Dezimalbruch zu verstehen? Es ist gleichbedeutend mit seiner Reduktion, und das sieht man, wenn wir diese Dezimalbrüche mit einem Nenner schreiben:

§ 105. Vergleich der Dezimalbrüche in der Größe.

Bei der Verwendung von Dezimalbrüchen ist es sehr wichtig, Brüche miteinander vergleichen zu können und die Frage beantworten zu können, welche davon gleich, welche größer und welche kleiner sind. Der Vergleich von Dezimalzahlen erfolgt anders als der Vergleich von ganzen Zahlen. Beispielsweise ist eine zweistellige Ganzzahl immer größer als eine einstellige Zahl, egal wie viele Einsen die einstellige Zahl enthält; Eine dreistellige Zahl ist mehr als eine zweistellige Zahl und noch mehr eine einstellige Zahl. Aber beim Vergleich von Dezimalbrüchen wäre es ein Fehler, alle Zeichen zu zählen, mit denen Brüche geschrieben werden.

Nehmen wir zwei Brüche: 3,5 und 2,5, und vergleichen Sie ihre Größe. Sie haben die gleichen Dezimalstellen, aber der erste Bruch hat 3 ganze Zahlen und der zweite hat 2. Der erste Bruch ist größer als der zweite, d.h.

Nehmen wir andere Brüche: 0,4 und 0,38. Um diese Brüche zu vergleichen, ist es sinnvoll, rechts vom ersten Bruch eine Null zuzuweisen. Dann vergleichen wir die Brüche 0,40 und 0,38. Jeder von ihnen hat zwei Nachkommastellen, was bedeutet, dass diese Brüche denselben Nenner 100 haben.

Wir brauchen nur ihre Zähler zu vergleichen, aber der Zähler 40 ist größer als 38. Also ist der erste Bruch größer als der zweite, d.h.

Der erste Bruch hat mehr Zehntel als der zweite, der zweite Bruch hat jedoch 8 Hundertstel mehr, aber sie sind weniger als ein Zehntel, weil 1/10 \u003d 10/100.

Vergleichen wir nun solche Brüche: 1,347 und 1,35. Wir weisen rechts vom zweiten Bruch eine Null zu und vergleichen die Dezimalbrüche: 1,347 und 1,350. Die ganzzahligen Teile sind gleich, also müssen Sie nur die Bruchteile vergleichen: 0,347 und 0,350. Der Nenner dieser Brüche ist gemeinsam, aber der Zähler des zweiten Bruchs ist größer als der Zähler des ersten, was bedeutet, dass der zweite Bruch größer als der erste ist, d. H. 1,35\u003e 1,347.

Vergleichen wir abschließend zwei weitere Brüche: 0,625 und 0,62473. Wir fügen dem ersten Bruch zwei Nullen hinzu, damit die Ziffern gleich sind, und vergleichen die resultierenden Brüche: 0,62500 und 0,62473. Ihre Nenner sind gleich, aber der Zähler des ersten Bruchs 62 500 ist größer als der Zähler des zweiten Bruchs 62 473. Daher ist der erste Bruch größer als der zweite, d. H. 0,625\u003e 0,62473.

Auf der Grundlage des Vorstehenden können wir die folgende Schlussfolgerung ziehen: von zwei Dezimalbrüchen ist der mit mehr ganzen Zahlen größer; wenn die ganzen Zahlen gleich sind, ist derjenige Bruch größer, in dem die Anzahl der Zehntel größer ist; wenn ganze Zahlen und Zehntel gleich sind, ist derjenige Bruch größer, in dem die Anzahl der Hundertstel größer ist usw.

§ 106. Erhöhung und Verringerung eines Dezimalbruchs um das 10-, 100-, 1000- usw.-fache.

Wir wissen bereits, dass das Hinzufügen von Nullen zu einer Dezimalzahl ihren Wert nicht beeinflusst. Als wir ganze Zahlen studierten, sahen wir, dass jede rechts zugeordnete Null die Zahl um das 10-fache erhöhte. Es ist nicht schwer zu verstehen, warum dies geschah. Wenn wir eine ganze Zahl nehmen, zum Beispiel 25, und rechts davon Null hinzufügen, dann erhöht sich die Zahl um das Zehnfache, die Zahl 250 ist zehnmal größer als 25. Wenn rechts die Null erschien, die Zahl 5, die früher Einheiten bezeichneten, fingen nun an, Zehner zu bezeichnen, und die Zahl 2, die früher für Zehner stand, steht jetzt für Hunderter. Dank des Erscheinens der Null wurden also die alten Ziffern durch neue ersetzt, sie wurden größer, sie rückten um eine Stelle nach links. Wenn es darum geht, einen Dezimalbruch beispielsweise um das 10-fache zu erhöhen, dann müssen wir auch die Ziffern um eine Stelle nach links verschieben, aber eine solche Verschiebung ist mit Null nicht zu erreichen. Ein Dezimalbruch besteht aus einem ganzzahligen Teil und einem Bruchteil, getrennt durch ein Komma. Links vom Dezimalpunkt steht die kleinste Ganzzahl, rechts die höchste Nachkommastelle. Betrachten Sie einen Bruch:

Wie können wir die Ziffern darin um mindestens eine Stelle verschieben, d.h. mit anderen Worten, wie können wir sie um das 10-fache erhöhen? Wenn wir das Komma um eine Stelle nach rechts verschieben, dann wirkt sich das zunächst auf das Schicksal der Fünf aus: Sie fällt aus dem Bereich der Bruchzahlen in den Bereich der ganzen Zahlen. Die Nummer hat dann folgende Form: 12345.678. Die Änderung geschah mit allen anderen Zahlen, und nicht nur mit der Fünf. Alle in der Nummer enthaltenen Zahlen begannen eine neue Rolle zu spielen, Folgendes geschah (siehe Tabelle):

Alle Ränge änderten ihren Namen, und alle Ränge stiegen sozusagen um einen Platz auf. Daraus erhöhte sich die Gesamtzahl um das 10-fache. Wenn Sie also das Komma um ein Zeichen nach rechts verschieben, erhöht sich die Zahl um das 10-fache.

Sehen wir uns einige weitere Beispiele an:

1) Nimm den Bruch 0,5 und schiebe das Komma um eine Stelle nach rechts; wir erhalten die Zahl 5, was 10 mal mehr als 0,5 ist, denn früher bedeutete die Fünf Zehntel einer Einheit, und jetzt bedeutet es ganze Einheiten.

2) Verschieben Sie das Komma in der Zahl 1.234 zwei Ziffern nach rechts; die Zahl wird 123,4. Diese Zahl ist 100-mal größer als die vorherige, da die Zahl 3 darin begann, Einheiten, die Zahl 2 - Zehner und die Zahl 1 - Hunderter zu bezeichnen.

Um also den Dezimalbruch um 10 zu erhöhen, müssen Sie das Komma darin um eine Stelle nach rechts verschieben; um es um das 100-fache zu erhöhen, müssen Sie das Komma um zwei Stellen nach rechts verschieben; um das 1.000-fache zu erhöhen - drei Ziffern nach rechts usw.

Wenn gleichzeitig nicht genügend Zeichen für die Nummer vorhanden sind, werden ihr rechts Nullen zugewiesen. Lassen Sie uns zum Beispiel den Bruch 1,5 um das 100-fache erhöhen, indem Sie das Komma um zwei Stellen verschieben; wir bekommen 150. Erhöhen wir den Bruch 0,6 um das 1.000-fache; wir bekommen 600.

bei Bedarf zurück Abnahme Dezimalbruch um 10, 100, 1.000 usw. Mal, dann müssen Sie das Komma darin um ein, zwei, drei usw. Zeichen nach links verschieben. Gegeben sei der Bruch 20,5; reduzieren wir es um das 10-fache; Dazu verschieben wir das Komma um ein Zeichen nach links, der Bruch hat die Form 2,05. Lassen Sie uns den Bruch 0,015 um das 100-fache reduzieren; wir erhalten 0,00015. Reduzieren wir die Zahl 334 um das Zehnfache; wir bekommen 33,4.

Brüche in der Form 0,8 geschrieben; 0,13; 2,856; 5.2; 0,04 heißt dezimal. Tatsächlich sind Dezimalbrüche eine vereinfachte Darstellung gewöhnlicher Brüche. Diese Notation ist für alle Brüche geeignet, deren Nenner 10, 100, 1000 usw. sind.

Betrachten Sie Beispiele (0,5 wird gelesen als null Komma fünf);

(0,15 wird gelesen als null Komma fünfzehn Hundertstel);

(5.3 wird gelesen als fünf Komma drei).

Beachten Sie, dass bei der Schreibweise eines Dezimalbruchs ein Komma den ganzzahligen Teil der Zahl vom Bruchteil trennt, der ganzzahlige Teil eines echten Bruchs ist 0. Die Schreibweise des Bruchteils eines Dezimalbruchs enthält so viele Ziffern wie dort sind Nullen im Nenner des entsprechenden gewöhnlichen Bruchs.

Betrachten Sie ein Beispiel, , , .

In einigen Fällen kann es notwendig sein, eine natürliche Zahl als Dezimalbruch zu betrachten, bei dem der Bruchteil gleich Null ist. Es ist üblich, das aufzuschreiben, 5 = 5,0; 245 = 245,0 und so weiter. Beachten Sie, dass in der Dezimalschreibweise einer natürlichen Zahl die Einheit der niedrigstwertigen Ziffer zehnmal kleiner ist als die Einheit der benachbarten höchstwertigen Ziffer. Dezimalbrüche haben die gleiche Eigenschaft. Daher kommt direkt nach dem Komma die zehnte Stelle, dann die hundertste Stelle, dann die tausendste Stelle und so weiter. Unten sind die Namen der Ziffern der Zahl 31,85431, die ersten beiden Spalten sind der ganzzahlige Teil, die restlichen Spalten sind der Bruchteil.

Dieser Bruch wird als einunddreißig Komma fünfundachtzigtausendvierhunderteinunddreißighunderttausendstel gelesen.

Dezimalstellen addieren und subtrahieren

Die erste Möglichkeit besteht darin, Dezimalzahlen in Commons umzuwandeln und sie zu addieren.

Wie Sie dem Beispiel entnehmen können, ist diese Methode sehr unpraktisch und es ist besser, die zweite Methode zu verwenden, die korrekter ist, ohne Dezimalbrüche in gewöhnliche Brüche umzuwandeln. So addieren Sie zwei Dezimalstellen:

• gleicht die Anzahl der Nachkommastellen in den Termen aus;
• schreiben Sie die Begriffe so untereinander, dass jede Ziffer des zweiten Begriffs unter der entsprechenden Ziffer des ersten Begriffs steht;
• addieren Sie die resultierenden Zahlen auf die gleiche Weise wie das Addieren natürlicher Zahlen;
• setzen Sie ein Komma unter die Kommas in den Bedingungen in der resultierenden Menge.

Betrachten Sie Beispiele:

• ausgleichen in der reduzierten und subtrahierten Anzahl der Nachkommastellen;
• schreibe den Subtrahend unter den Minuend, sodass jedes Bit des Subtrahend unter dem entsprechenden Bit des Minuend steht;
• subtrahieren wie natürliche Zahlen subtrahiert werden;
• setzen Sie ein Komma unter die Kommas im Minuend und subtrahend in der resultierenden Differenz.

Betrachten Sie Beispiele:

In den oben diskutierten Beispielen ist zu sehen, dass die Addition und Subtraktion von Dezimalbrüchen Bit für Bit durchgeführt wurde, also auf die gleiche Weise, wie wir ähnliche Operationen mit natürlichen Zahlen durchgeführt haben. Dies ist der Hauptvorteil der Dezimalschreibweise für Brüche.

Dezimale Multiplikation

Um einen Dezimalbruch mit 10, 100, 1000 usw. zu multiplizieren, muss das Komma in diesem Bruch jeweils nach rechts verschoben werden, um 1, 2, 3 usw., die Zahlen. Wenn also das Komma um 1, 2, 3 usw. nach rechts verschoben wird, erhöht sich der Bruch jeweils um 10, 100, 1000 usw. So multiplizieren Sie zwei Dezimalzahlen:

• multipliziere sie als natürliche Zahlen und ignoriere die Kommas;
• Trennen Sie im resultierenden Produkt so viele Ziffern mit einem Komma rechts, wie in beiden Faktoren zusammen nach den Kommas stehen.

Es gibt Fälle, in denen das Produkt weniger Ziffern enthält, als durch ein Komma getrennt werden müssen, die erforderliche Anzahl von Nullen wird links vor diesem Produkt hinzugefügt, und dann wird das Komma um die erforderliche Anzahl von Ziffern nach links verschoben.

Betrachten Sie Beispiele: 2 * 4 = 8, dann 0,2 * 0,4 = 0,08; 23 * 35 = 805, dann 0,023 * 0,35 = 0,00805.

Es gibt Fälle, in denen einer der Faktoren gleich 0,1 ist; 0,01; 0,001 usw., ist es bequemer, die folgende Regel zu verwenden.

• Um eine Dezimalzahl mit 0,1 zu multiplizieren; 0,01; 0,001 usw. muss das Komma in diesem Dezimalbruch jeweils um 1, 2, 3 usw. nach links verschoben werden.

Betrachten Sie Beispiele: 2,65 * 0,1 = 0,265; 457,6 * 0,01 = 4,576.

Die Multiplikationseigenschaften natürlicher Zahlen gelten auch für Dezimalbrüche.

• ab=ba- Kommutativgesetz der Multiplikation;
• (ab)c = a(bc)- assoziative Eigenschaft der Multiplikation;
• a (b + c) = ab + ac ist das Verteilungsgesetz der Multiplikation in Bezug auf die Addition.

Dezimalteilung

Das ist bekannt, wenn wir eine natürliche Zahl dividieren a zu einer natürlichen Zahl b bedeutet, eine solche natürliche Zahl zu finden c, was, wenn multipliziert mit b gibt Nummer a. Diese Regel bleibt wahr, wenn mindestens eine der Zahlen a, b, c ist eine Dezimalzahl.

Betrachten Sie ein Beispiel: Sie möchten 43,52 durch 17 Ecken teilen und das Komma ignorieren. In diesem Fall sollte das Komma im Privat unmittelbar vor der ersten Ziffer nach dem Dezimalpunkt im Dividenden verwendet werden.

Es gibt Fälle, in denen der Dividende kleiner als der Divisor ist, dann ist der ganzzahlige Teil des Quotienten gleich Null. Betrachten Sie ein Beispiel:

Schauen wir uns ein weiteres interessantes Beispiel an.

Der Divisionsprozess wird gestoppt, weil die Zahlen des Dividenden abgelaufen sind und der Rest keine Null erhalten hat. Es ist bekannt, dass sich ein Dezimalbruch nicht ändert, wenn ihm rechts beliebig viele Nullen zugeordnet werden. Dann wird klar, dass die Zahlen der Dividende nicht enden können.

Um einen Dezimalbruch durch 10, 100, 1000 usw. zu dividieren, ist es notwendig, das Komma in diesem Bruch um 1, 2, 3 usw. Zahlen nach links zu verschieben. Betrachten Sie ein Beispiel: 5,14: 10 = 0,514; 2: 100 = 0,02; 37,51: 1000 = 0,03751.

Wenn der Dividende und der Divisor gleichzeitig um 10, 100, 1000 usw. erhöht werden, ändert sich der Quotient nicht.

Betrachten wir ein Beispiel: 39,44: 1,6 = 24,65 Erhöhen wir den Dividenden und den Divisor um das 10-fache 394,4: 16 = 24,65 Es ist fair zu sagen, dass das Teilen eines Dezimalbruchs durch eine natürliche Zahl im zweiten Beispiel einfacher ist.

Um eine Dezimalzahl durch eine Dezimalzahl zu dividieren, müssen Sie:

• die Kommas im Dividenden und im Divisor um so viele Stellen nach rechts verschieben, wie sie nach dem Komma im Divisor enthalten sind;
• durch eine natürliche Zahl dividieren.

Betrachten Sie ein Beispiel: 23,6: 0,02 Beachten Sie, dass der Divisor zwei Dezimalstellen hat, also multiplizieren wir beide Zahlen mit 100, wir erhalten 2360: 2 = 1180, wir teilen das Ergebnis durch 100 und wir erhalten die Antwort 11,80 oder 23,6: 0, 02 = 11,8.

Dezimalvergleich

Es gibt zwei Möglichkeiten, Dezimalzahlen zu vergleichen. Methode eins: Sie müssen zwei Dezimalbrüche 4,321 und 4,32 vergleichen, die Anzahl der Dezimalstellen ausgleichen und Stück für Stück mit dem Vergleich beginnen, Zehntel mit Zehntel, Hundertstel mit Hundertstel usw. Als Ergebnis erhalten wir 4,321\u003e 4,320.

Die zweite Möglichkeit zum Vergleichen von Dezimalbrüchen erfolgt durch Multiplikation, multiplizieren Sie das obige Beispiel mit 1000 und vergleichen Sie 4321\u003e 4320. Welche Methode bequemer ist, wählt jeder für sich.

Als:

± dm … d 1 d 0 , d -1 d -2 …

wobei ± das Bruchzeichen ist: entweder + oder -,

, - Dezimalpunkt, der als Trennzeichen zwischen den ganzzahligen und gebrochenen Teilen der Zahl dient,

dk- Dezimalziffern.

Gleichzeitig hat die Reihenfolge der Ziffern vor dem Komma (links davon) ein Ende (wie min 1-pro Ziffer), und nach dem Komma (rechts) kann sie entweder endlich sein (optional , es dürfen überhaupt keine Ziffern nach dem Komma stehen) und unendlich.

Dezimalwert ± dm … d 1 d 0 , d -1 d -2 … ist eine reelle Zahl:

was gleich der Summe einer endlichen oder unendlichen Anzahl von Termen ist.

Die Darstellung reeller Zahlen durch Dezimalbrüche ist eine Verallgemeinerung der Notation ganzer Zahlen im dezimalen Zahlensystem. Die Dezimaldarstellung einer ganzen Zahl hat keine Nachkommastellen, und daher sieht diese Darstellung so aus:

± dm … d 1 d 0 ,

Und dies deckt sich mit der Aufzeichnung unserer Zahl im Dezimalzahlensystem.

Dezimal- Dies ist das Ergebnis der Division von 1 in 10, 100, 1000 und so weiter Teile. Diese Brüche sind für Berechnungen sehr praktisch, weil Sie basieren auf demselben Positionssystem, auf dem das Zählen und Notieren von ganzen Zahlen aufgebaut ist. Aus diesem Grund sind die Schreibweise und Regeln für Dezimalbrüche fast die gleichen wie für ganze Zahlen.

Beim Schreiben von Dezimalbrüchen müssen Sie den Nenner nicht markieren, er wird durch die Stelle bestimmt, die die entsprechende Zahl einnimmt. Schreiben Sie zuerst den ganzzahligen Teil der Zahl und setzen Sie dann rechts einen Dezimalpunkt. Die erste Ziffer nach dem Dezimalpunkt gibt die Anzahl der Zehntel an, die zweite die Anzahl der Hundertstel, die dritte die Anzahl der Tausendstel und so weiter. Die Zahlen nach dem Komma sind Nachkommastellen.

Zum Beispiel: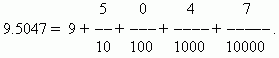

Einer der Vorteile von Dezimalbrüchen ist, dass sie sehr einfach auf die Form gewöhnlicher Brüche gebracht werden können: Die Zahl nach dem Komma (unsere ist 5047) ist Zähler; Nenner gleich n Grad 10, wo n- die Anzahl der Dezimalstellen (wir haben diese n=4):

Wenn der Dezimalbruch keinen ganzzahligen Teil enthält, setzen wir eine Null vor das Komma:

Eigenschaften von Dezimalbrüchen.

1. Dezimalzahl ändert sich nicht, wenn rechts Nullen hinzugefügt werden:

13.6 =13.6000.

2. Die Dezimalzahl ändert sich nicht, wenn die Nullen am Ende der Dezimalstelle entfernt werden:

0.00123000 = 0.00123.

Beachtung! Nullen, die NICHT am Ende einer Dezimalstelle stehen, dürfen nicht entfernt werden!

3. Der Dezimalbruch erhöht sich um 10, 100, 1000 und so weiter, wenn wir das Dezimalkomma jeweils auf 1-well, 2, 2 usw. nach rechts verschieben:

3,675 → 367,5 (der Bruch hat sich um das Hundertfache erhöht).

4. Der Dezimalbruch wird kleiner als zehn, einhundert, eintausend und so weiter, wenn wir das Dezimalkomma jeweils auf 1-gut, 2, 3 und so weiter nach links verschieben:

1536,78 → 1,53678 (der Bruch ist tausendmal kleiner geworden).

Arten von Dezimalzahlen.

Dezimalzahlen werden durch dividiert Finale, endlos und periodische Dezimalstellen.

Ende dezimal - dies ist ein Bruch mit einer endlichen Anzahl von Nachkommastellen (oder sie sind gar nicht vorhanden), d.h. sieht so aus:

Eine reelle Zahl kann nur dann als endlicher Dezimalbruch dargestellt werden, wenn diese Zahl rational ist und als irreduzibler Bruch geschrieben wird p/q Nenner q hat keine anderen Primteiler als 2 und 5.

Unendliche Dezimalzahl.

Enthält eine sich unendlich wiederholende Gruppe von angerufenen Ziffern Zeitraum. Der Punkt wird in Klammern geschrieben. Beispiel: 0,12345123451234512345… = 0.(12345).

Periodische Dezimalzahl- das ist so ein unendlicher Dezimalbruch, bei dem die Ziffernfolge nach dem Komma ab einer bestimmten Stelle eine sich periodisch wiederholende Zifferngruppe ist. Mit anderen Worten, periodischer Bruch ist eine Dezimalzahl, die so aussieht:

Ein solcher Bruch wird normalerweise kurz so geschrieben:

Zahlengruppe b 1 … b l, die wiederholt wird, ist Bruchteil Zeitraum, die Anzahl der Ziffern in dieser Gruppe ist Periodenlänge.

Wenn bei einem periodischen Bruch der Punkt unmittelbar nach dem Komma kommt, dann ist der Bruch rein periodisch. Wenn zwischen dem Komma und dem 1. Punkt Zahlen stehen, dann ist der Bruch gemischt periodisch, und eine Gruppe von Nachkommastellen bis zum 1. Punktzeichen - Bruch Vorperiode.

zum Beispiel, der Bruch 1,(23) = 1,2323… ist rein periodisch, und der Bruch 0,1(23)=0,12323… ist gemischt periodisch.

Die Haupteigenschaft periodischer Brüche, wodurch sie sich von der gesamten Menge der Dezimalbrüche unterscheiden, liegt in der Tatsache, dass periodische Brüche und nur sie rationale Zahlen darstellen. Genauer gesagt geschieht Folgendes:

Jede unendlich wiederkehrende Dezimalzahl repräsentiert eine rationale Zahl. Wenn umgekehrt eine rationale Zahl in einen unendlichen Dezimalbruch zerlegt wird, ist dieser Bruch periodisch.

In diesem Artikel werden wir verstehen, was ein Dezimalbruch ist, welche Merkmale und Eigenschaften er hat. Gehen! 🙂

Der Dezimalbruch ist ein Sonderfall der gewöhnlichen Brüche (bei denen der Nenner ein Vielfaches von 10 ist).

Definition

Dezimalzahlen sind Brüche, deren Nenner Zahlen sind, die aus einer Eins und einer bestimmten Anzahl darauf folgender Nullen bestehen. Das heißt, dies sind Brüche mit einem Nenner von 10, 100, 1000 usw. Ansonsten kann ein Dezimalbruch als Bruch mit einem Nenner von 10 oder einer der Zehnerpotenzen charakterisiert werden.

Bruchbeispiele:

, ,

Ein Dezimalbruch wird anders geschrieben als ein gewöhnlicher Bruch. Operationen mit diesen Brüchen unterscheiden sich auch von Operationen mit gewöhnlichen. Die Regeln für Operationen auf ihnen ähneln weitgehend den Regeln für Operationen auf ganzen Zahlen. Dies bestimmt insbesondere ihre Relevanz für die Lösung praktischer Probleme.

Darstellung eines Bruchs in Dezimalschreibweise

In der Dezimalschreibweise gibt es keinen Nenner, sie zeigt die Zahl des Zählers an. Im Allgemeinen werden Dezimalbrüche wie folgt geschrieben:

wobei X der ganzzahlige Teil des Bruchs ist, Y sein Bruchteil ist, "," das Dezimalkomma ist.

Für die korrekte Darstellung eines gewöhnlichen Bruchs als Dezimalzahl ist es erforderlich, dass er korrekt ist, dh mit einem hervorgehobenen ganzzahligen Teil (wenn möglich) und einem Zähler, der kleiner als der Nenner ist. Dann wird in Dezimalschreibweise der ganzzahlige Teil vor dem Dezimalpunkt (X) geschrieben und der Zähler des gewöhnlichen Bruchs wird nach dem Dezimalpunkt (Y) geschrieben.

Stellt der Zähler eine Zahl dar, deren Stellenzahl kleiner als die Anzahl der Nullen im Nenner ist, dann wird im Y-Teil die fehlende Stellenzahl in der Dezimalschreibweise mit Nullen vor den Zählerstellen aufgefüllt.

Beispiel:

Wenn der gewöhnliche Bruch kleiner als 1 ist, d.h. keinen ganzzahligen Teil hat, dann wird für X 0 dezimal geschrieben.

Im Bruchteil (Y) nach der letzten signifikanten Stelle (außer Null) kann eine beliebige Anzahl von Nullen eingegeben werden. Es hat keinen Einfluss auf den Wert des Bruchteils. Und umgekehrt: Alle Nullen am Ende des Nachkommateils des Dezimalbruchs können weggelassen werden.

Dezimalzahlen lesen

Teil X wird im allgemeinen Fall wie folgt gelesen: "X ganze Zahlen".

Der Y-Teil wird entsprechend der Zahl im Nenner gelesen. Für den Nenner 10 müssten Sie lauten: „Y Zehntel“, für den Nenner 100: „Y Hundertstel“, für den Nenner 1000: „Y Tausendstel“ und so weiter … 😉

Ein anderer Ansatz zum Lesen wird als korrekter angesehen, basierend auf dem Zählen der Anzahl der Ziffern des Bruchteils. Dazu müssen Sie verstehen, dass sich die Nachkommastellen in Bezug auf die Ziffern des ganzzahligen Teils des Bruchs spiegelbildlich befinden.

Namen zum richtigen Lesen sind in der Tabelle angegeben:

Auf dieser Grundlage sollte die Lesung auf der Entsprechung zum Namen der Kategorie der letzten Ziffer des Bruchteils basieren.

• 3.5 lautet "drei Komma fünf"
• 0,016 liest sich wie „null Komma sechzehn Tausendstel“

Einen beliebigen gewöhnlichen Bruch in eine Dezimalzahl umwandeln

Wenn der Nenner eines gewöhnlichen Bruchs 10 oder eine Zehnerpotenz ist, dann wird der Bruch wie oben beschrieben umgewandelt. In anderen Situationen sind zusätzliche Transformationen erforderlich.

Es gibt 2 Möglichkeiten zu übersetzen.

Der erste Weg der Übersetzung

Zähler und Nenner müssen mit einer solchen ganzen Zahl multipliziert werden, dass der Nenner 10 oder eine der Zehnerpotenzen ist. Und dann wird der Bruch in Dezimalschreibweise dargestellt.

Diese Methode ist für Brüche anwendbar, deren Nenner nur in 2 und 5 zerlegt wird. Also im vorherigen Beispiel . Wenn es andere Primfaktoren in der Erweiterung gibt (z. B. ), müssen Sie auf die 2. Methode zurückgreifen.

Die zweite Art der Übersetzung

Die zweite Methode besteht darin, den Zähler durch den Nenner in einer Spalte oder auf einem Taschenrechner zu dividieren. Der ganzzahlige Teil, falls vorhanden, wird nicht in die Transformation einbezogen.

Die lange Divisionsregel, die zu einem Dezimalbruch führt, wird unten beschrieben (siehe Dividieren von Dezimalzahlen).

Konvertieren Sie dezimal in normal

Dazu sollte der Bruchteil (rechts vom Komma) als Zähler geschrieben werden, und das Ergebnis des Lesens des Bruchteils sollte als entsprechende Zahl im Nenner geschrieben werden. Außerdem müssen Sie, wenn möglich, den resultierenden Bruchteil reduzieren.

Ende und unendliche Dezimalzahl

Der Dezimalbruch wird als endgültig bezeichnet, dessen Bruchteil aus einer endlichen Anzahl von Ziffern besteht.

Alle obigen Beispiele enthalten genau die letzten Dezimalbrüche. Allerdings kann nicht jeder gewöhnliche Bruch als letzte Dezimalzahl dargestellt werden. Wenn die 1. Übersetzungsmethode für einen bestimmten Bruch nicht anwendbar ist und die 2. Methode zeigt, dass die Division nicht abgeschlossen werden kann, kann nur ein unendlicher Dezimalbruch erhalten werden.

Es ist unmöglich, einen unendlichen Bruch in seiner vollen Form zu schreiben. In unvollständiger Form können solche Brüche dargestellt werden:

1. durch Reduzierung auf die gewünschte Anzahl von Dezimalstellen;
2. in Form eines periodischen Bruchs.

Als periodisch wird ein Bruch bezeichnet, bei dem nach dem Komma eine sich unendlich wiederholende Ziffernfolge unterschieden werden kann.

Die restlichen Brüche heißen nichtperiodisch. Bei nicht periodischen Brüchen ist nur die 1. Darstellungsart (Runden) erlaubt.

Ein Beispiel für einen periodischen Bruch: 0,8888888 ... Hier gibt es eine sich wiederholende Zahl 8, die sich offensichtlich endlos wiederholen wird, da es keinen Grund gibt, etwas anderes anzunehmen. Diese Nummer wird angerufen Bruchteil Zeitraum.

Periodische Fraktionen sind rein und gemischt. Ein Dezimalbruch ist rein, bei dem der Punkt unmittelbar nach dem Komma beginnt. Ein gemischter Bruch hat 1 oder mehr Stellen vor dem Komma.

54.33333 ... - periodischer reiner Dezimalbruch

2.5621212121 ... - periodischer gemischter Bruch

Beispiele für das Schreiben unendlicher Dezimalstellen:

Das 2. Beispiel zeigt, wie man einen Punkt in einem Periodenbruch richtig bildet.

Konvertieren von periodischen Dezimalzahlen in gewöhnliche

Um einen reinen periodischen Bruch in eine gewöhnliche Periode umzuwandeln, schreiben Sie ihn in den Zähler und schreiben Sie in den Nenner eine Zahl, die aus Neunen in einer Menge besteht, die der Anzahl der Ziffern in der Periode entspricht.

Eine gemischte wiederkehrende Dezimalzahl wird wie folgt übersetzt:

1. Sie müssen eine Zahl bilden, die aus der Zahl nach dem Dezimalpunkt vor dem Punkt und dem ersten Punkt besteht.
2. subtrahieren Sie von der resultierenden Zahl die Zahl nach dem Dezimalpunkt vor dem Punkt. Das Ergebnis ist der Zähler eines gewöhnlichen Bruchs;
3. Im Nenner müssen Sie eine Zahl eingeben, die aus der Anzahl der Neunen besteht, die der Anzahl der Ziffern des Zeitraums entsprechen, gefolgt von Nullen, deren Anzahl der Anzahl der Ziffern der Zahl nach dem Dezimalpunkt vor dem entspricht 1. Zeitraum.

Dezimalvergleich

Dezimalbrüche werden zunächst mit ihren ganzen Teilen verglichen. Der größere ist der Bruch, der den größeren ganzzahligen Teil hat.

Wenn die ganzzahligen Teile gleich sind, werden die Ziffern der entsprechenden Ziffern des Bruchteils verglichen, beginnend mit der ersten (ab den Zehnteln). Hier gilt das gleiche Prinzip: der größere der Brüche, der eine größere Zehntelreihe hat; wenn die Zehntelziffern gleich sind, werden die Hundertstelziffern verglichen und so weiter.

Soweit

, da bei gleichen ganzzahligen Teilen und gleichen Zehnteln im Bruchteil der 2. Bruch mehr Hundertstel hat.

Dezimalstellen addieren und subtrahieren

Dezimalzahlen werden wie ganze Zahlen addiert und subtrahiert, wobei die entsprechenden Ziffern untereinander geschrieben werden. Dazu müssen Sie Dezimalpunkte untereinander haben. Dann stimmen die Einheiten (Zehner usw.) des ganzzahligen Teils sowie die Zehntel (Hundertstel usw.) des Bruchteils überein. Die fehlenden Nachkommastellen werden mit Nullen aufgefüllt. Direkt Der Prozess der Addition und Subtraktion wird auf die gleiche Weise wie bei ganzen Zahlen durchgeführt.

Dezimale Multiplikation

Um Dezimalbrüche zu multiplizieren, müssen Sie sie untereinander schreiben, an der letzten Ziffer ausrichten und nicht auf die Position der Dezimalpunkte achten. Dann müssen Sie die Zahlen genauso multiplizieren wie beim Multiplizieren von ganzen Zahlen. Nachdem Sie das Ergebnis erhalten haben, sollten Sie die Anzahl der Nachkommastellen in beiden Brüchen neu berechnen und die Gesamtzahl der Nachkommastellen in der resultierenden Zahl mit einem Komma trennen. Wenn nicht genügend Ziffern vorhanden sind, werden sie durch Nullen ersetzt.

Multiplizieren und Dividieren von Dezimalzahlen mit 10 n

Diese Aktionen sind einfach und laufen darauf hinaus, den Dezimalpunkt zu verschieben. P Beim Multiplizieren wird das Komma um die Anzahl der Stellen nach rechts verschoben (der Bruch wird größer), die der Anzahl der Nullen in 10 n entspricht, wobei n eine beliebige ganzzahlige Potenz ist. Das heißt, eine bestimmte Anzahl von Ziffern wird vom Bruchteil auf die ganze Zahl übertragen. Beim Dividieren wird jeweils das Komma nach links verschoben (die Zahl wird kleiner) und ein Teil der Ziffern vom ganzzahligen Teil in den Bruchteil übertragen. Wenn nicht genügend Ziffern zum Übertragen vorhanden sind, werden die fehlenden Ziffern mit Nullen aufgefüllt.

Division einer Dezimalzahl und einer ganzen Zahl durch eine ganze Zahl und eine Dezimalzahl

Die Division einer Dezimalzahl durch eine ganze Zahl entspricht der Division zweier ganzer Zahlen. Außerdem muss nur die Position des Dezimalpunkts berücksichtigt werden: Beim Abbruch der Ziffer der Ziffer gefolgt von einem Komma muss nach der aktuellen Ziffer der generierten Antwort ein Komma gesetzt werden. Dann müssen Sie weiter dividieren, bis Sie Null erhalten. Wenn der Dividenden nicht genügend Vorzeichen für eine vollständige Division enthält, sollten Nullen als solche verwendet werden.

In ähnlicher Weise werden 2 ganze Zahlen in eine Spalte geteilt, wenn alle Ziffern des Dividenden abgerissen wurden und die vollständige Division noch nicht abgeschlossen ist. In diesem Fall wird nach dem Abbruch der letzten Ziffer des Dividenden ein Dezimalpunkt in die resultierende Antwort gesetzt und Nullen als abgerissene Ziffern verwendet. Jene. der Dividende wird hier tatsächlich als Dezimalbruch mit einem Null-Bruchteil dargestellt.

Um einen Dezimalbruch (oder eine ganze Zahl) durch eine Dezimalzahl zu dividieren, ist es notwendig, den Dividenden und den Divisor mit der Zahl 10 n zu multiplizieren, bei der die Anzahl der Nullen gleich der Anzahl der Nachkommastellen in der ist Divisor. Auf diese Weise werden sie das Dezimalkomma in dem Bruch los, durch den Sie dividieren möchten. Ferner ist der Teilungsprozess derselbe wie oben beschrieben.

Grafische Darstellung von Dezimalstellen

Grafisch werden Dezimalbrüche durch eine Koordinatenlinie dargestellt. Dazu werden einzelne Segmente zusätzlich in 10 gleiche Teile geteilt, so wie auf einem Lineal gleichzeitig Zentimeter und Millimeter aufgetragen werden. Dadurch wird sichergestellt, dass Dezimalstellen genau angezeigt werden und objektiv verglichen werden können.

Damit die Längsteilungen auf einzelnen Segmenten gleich sind, sollte man sorgfältig die Länge des einzelnen Segments selbst berücksichtigen. Es sollte so sein, dass die Bequemlichkeit einer zusätzlichen Unterteilung sichergestellt werden kann.

Brüche

Beachtung!
Es gibt zusätzliche
Material in Sondersektion 555.
Für diejenigen, die stark "nicht sehr ..."
Und für diejenigen, die "sehr viel...")

Brüche in der High School sind nicht sehr nervig. Vorerst. Bis Sie auf Exponenten mit rationalen Exponenten und Logarithmen stoßen. Und da…. Sie drücken, Sie drücken den Taschenrechner, und es zeigt die gesamte Anzeigetafel einiger Zahlen. Man muss mit dem Kopf denken, wie in der dritten Klasse.

Lasst uns endlich mit Brüchen umgehen! Nun, wie sehr kann man sich in ihnen verwirren!? Außerdem ist alles einfach und logisch. So, Was sind Brüche?

Arten von Brüchen. Transformationen.

Es gibt drei Arten von Brüchen.

1. Gemeinsame Brüche , Zum Beispiel:

Manchmal setzen sie anstelle einer horizontalen Linie einen Schrägstrich: 1/2, 3/4, 19/5, na ja, und so weiter. Hier werden wir oft diese Schreibweise verwenden. Die oberste Nummer wird angerufen Zähler, niedriger - Nenner. Wenn Sie diese Namen ständig verwechseln (es passiert ...), sagen Sie sich den Satz mit dem Ausdruck: " Zzzzz erinnern! Zzzzz Nenner - aus zzz u!" Schau, alles wird in Erinnerung bleiben.)

Ein Strich, der horizontal ist, der schräg ist, bedeutet Aufteilung obere Zahl (Zähler) bis untere Zahl (Nenner). Und alle! Anstelle eines Bindestrichs ist es durchaus möglich, ein Teilungszeichen zu setzen - zwei Punkte.

Wenn die Teilung vollständig möglich ist, muss sie durchgeführt werden. Anstelle des Bruchs "32/8" ist es also viel angenehmer, die Zahl "4" zu schreiben. Jene. 32 wird einfach durch 8 geteilt.

32/8 = 32: 8 = 4

Ich spreche nicht von der Fraktion "4/1". Das ist auch nur "4". Und wenn es sich nicht vollständig teilt, lassen wir es als Bruch. Manchmal muss man es umgekehrt machen. Machen Sie aus einer ganzen Zahl einen Bruch. Aber dazu später mehr.

2. Dezimalstellen , Zum Beispiel:

In dieser Form müssen die Antworten auf die Aufgaben "B" aufgeschrieben werden.

3. gemischte Zahlen , Zum Beispiel:

Gemischte Zahlen werden in der High School praktisch nicht verwendet. Um mit ihnen arbeiten zu können, müssen sie in gewöhnliche Brüche umgewandelt werden. Aber man muss auf jeden Fall wissen, wie es geht! Und dann wird eine solche Nummer im Puzzle auftauchen und hängen ... Von Grund auf neu. Aber wir erinnern uns an dieses Verfahren! Etwas niedriger.

Am vielseitigsten gemeinsame Brüche. Beginnen wir mit ihnen. Übrigens, wenn in dem Bruch alle möglichen Logarithmen, Sinus und andere Buchstaben stehen, ändert das nichts. In dem Sinne, dass alles Aktionen mit Bruchausdrücken unterscheiden sich nicht von Aktionen mit gewöhnlichen Brüchen!

Grundlegende Eigenschaft eines Bruchs.

So lass uns gehen! Zunächst werde ich Sie überraschen. Die ganze Vielfalt der Bruchtransformationen wird durch eine einzige Eigenschaft bereitgestellt! So heißt es Grundeigenschaft eines Bruchs. Erinnern: Wenn Zähler und Nenner eines Bruchs mit derselben Zahl multipliziert (dividiert) werden, ändert sich der Bruch nicht. Jene:

Es ist klar, dass Sie weiter schreiben können, bis Sie blau im Gesicht sind. Lassen Sie sich nicht von Sinus und Logarithmus verwirren, wir werden uns weiter damit befassen. Die Hauptsache zu verstehen ist, dass all diese verschiedenen Ausdrücke sind der gleiche Bruchteil . 2/3.

Und wir brauchen es, all diese Transformationen? Und wie! Jetzt werden Sie es selbst sehen. Lassen Sie uns zunächst die grundlegende Eigenschaft eines Bruchs für verwenden Abkürzungen für Brüche. Es scheint, dass die Sache elementar ist. Wir teilen Zähler und Nenner durch dieselbe Zahl und fertig! Es ist unmöglich, etwas falsch zu machen! Aber... der Mensch ist ein kreatives Wesen. Fehler kann man überall machen! Vor allem, wenn Sie nicht einen Bruch wie 5/10 kürzen müssen, sondern einen Bruchausdruck mit allen möglichen Buchstaben.

Wie Sie Brüche ohne unnötige Arbeit richtig und schnell kürzen, erfahren Sie im Sonderteil 555.

Ein normaler Schüler macht sich nicht die Mühe, Zähler und Nenner durch dieselbe Zahl (oder denselben Ausdruck) zu dividieren! Er streicht einfach alles gleich von oben und unten durch! Hier lauert ein typischer Fehler, ein Schnitzer, wenn man so will.

Zum Beispiel müssen Sie den Ausdruck vereinfachen:

Es gibt nichts zu überlegen, wir streichen den Buchstaben "a" von oben und die Zwei von unten! Wir bekommen:

Alles ist richtig. Aber du hast wirklich geteilt das Ganze Zähler u das Ganze Nenner "a". Wenn Sie es gewohnt sind, einfach durchzustreichen, dann können Sie in Eile das "a" im Ausdruck streichen

und wieder bekommen

Was kategorisch falsch wäre. Denn hier das Ganze Zähler auf "a" bereits nicht geteilt! Dieser Anteil kann nicht gekürzt werden. Übrigens ist eine solche Abkürzung, ähm ... eine ernsthafte Herausforderung für den Lehrer. Das wird nicht verziehen! Erinnern? Beim Reduzieren muss geteilt werden das Ganze Zähler u das Ganze Nenner!

Das Kürzen von Brüchen macht das Leben viel einfacher. Sie werden irgendwo einen Bruch bekommen, zum Beispiel 375/1000. Und wie kann man jetzt mit ihr arbeiten? Ohne Taschenrechner? Multiplizieren, sagen, addieren, quadrieren!? Und wenn Sie nicht zu faul sind, reduzieren Sie vorsichtig um fünf und sogar um fünf und sogar ... während es reduziert wird, kurz. Wir bekommen 3/8! Viel schöner, oder?

Die Grundeigenschaft eines Bruchs ermöglicht es Ihnen, gewöhnliche Brüche in Dezimalzahlen umzuwandeln und umgekehrt ohne Taschenrechner! Das ist wichtig für die Prüfung, oder?

Wie man Brüche von einer Form in eine andere umwandelt.

Mit Dezimalzahlen ist es einfach. Wie es gehört, so steht es geschrieben! Sagen wir 0,25. Es ist null Komma, fünfundzwanzig Hundertstel. Also schreiben wir: 25/100. Wir reduzieren (Teilen Sie Zähler und Nenner durch 25), wir erhalten den üblichen Bruch: 1/4. Alles. Es passiert, und nichts wird reduziert. Wie 0,3. Das sind drei Zehntel, d.h. 3/10.

Was ist, wenn ganze Zahlen ungleich Null sind? Nichts Schlimmes. Schreibe den ganzen Bruch auf ohne Kommas im Zähler und im Nenner - was gehört wird. Beispiel: 3.17. Das sind ganze drei, siebzehn Hundertstel. Wir schreiben 317 in den Zähler und 100 in den Nenner und erhalten 317/100. Nichts wird reduziert, das heißt alles. Das ist die Antwort. Elementar Watson! Aus all dem oben Gesagten eine nützliche Schlussfolgerung: Jeder Dezimalbruch kann in einen gewöhnlichen Bruch umgewandelt werden .

Aber die umgekehrte Umwandlung, gewöhnlich in dezimal, einige können nicht ohne Taschenrechner auskommen. Aber du musst! Wie werden Sie die Antwort auf die Prüfung aufschreiben!? Wir lesen und beherrschen diesen Prozess sorgfältig.

Was ist ein Dezimalbruch? Sie hat im Nenner stets ist 10 oder 100 oder 1000 oder 10000 wert und so weiter. Wenn dein üblicher Bruch einen solchen Nenner hat, gibt es kein Problem. Beispiel: 4/10 = 0,4. Oder 7/100 = 0,07. Oder 12/10 = 1,2. Und wenn sich in der Antwort auf die Aufgabe von Abschnitt "B" 1/2 herausstellte? Was werden wir als Antwort schreiben? Dezimalstellen sind erforderlich...

Wir erinnern Grundeigenschaft eines Bruchs ! Die Mathematik ermöglicht es Ihnen, Zähler und Nenner mit derselben Zahl zu multiplizieren. Übrigens für jeden! Außer Null natürlich. Nutzen wir diese Funktion zu unserem Vorteil! Womit kann der Nenner multipliziert werden, d.h. 2, sodass daraus 10 oder 100 oder 1000 werden (kleiner ist natürlich besser...)? 5, offensichtlich. Fühlen Sie sich frei, den Nenner zu multiplizieren (dies ist uns notwendig) mit 5. Dann muss aber auch der Zähler mit 5 multipliziert werden. Das ist schon Mathematik Forderungen! Wir erhalten 1/2 \u003d 1x5 / 2x5 \u003d 5/10 \u003d 0,5. Das ist alles.

Es kommen jedoch alle möglichen Nenner vor. Zum Beispiel wird der Bruch 3/16 fallen. Probieren Sie es aus, finden Sie heraus, womit Sie 16 multiplizieren müssen, um 100 oder 1000 zu erhalten ... Funktioniert nicht? Dann können Sie einfach 3 durch 16 teilen. Wenn Sie keinen Taschenrechner haben, müssen Sie in einer Ecke auf einem Blatt Papier dividieren, wie es in Grundschulklassen gelehrt wurde. Wir erhalten 0,1875.

Und es gibt einige sehr schlechte Nenner. Zum Beispiel kann der Bruch 1/3 nicht in eine gute Dezimalzahl umgewandelt werden. Sowohl auf einem Taschenrechner als auch auf einem Blatt Papier erhalten wir 0,3333333 ... Dies bedeutet, dass 1/3 in einen genauen Dezimalbruch umgewandelt wird übersetzt nicht. Genau wie 1/7, 5/6 und so weiter. Viele von ihnen sind nicht übersetzbar. Daher eine weitere nützliche Schlussfolgerung. Nicht jeder gewöhnliche Bruch lässt sich in eine Dezimalzahl umwandeln. !

Übrigens eine nützliche Information zur Selbstprüfung. In Abschnitt "B" als Antwort müssen Sie einen Dezimalbruch aufschreiben. Und Sie haben zum Beispiel 4/3. Dieser Bruch wird nicht in Dezimalzahlen umgewandelt. Das bedeutet, dass Sie irgendwo auf dem Weg einen Fehler gemacht haben! Komm zurück, überprüfe die Lösung.

Also mit aussortierten gewöhnlichen und dezimalen Brüchen. Es bleibt, sich mit gemischten Zahlen zu befassen. Um mit ihnen zu arbeiten, müssen sie alle in gewöhnliche Brüche umgewandelt werden. Wie kann man es machen? Du kannst einen Sechstklässler erwischen und ihn fragen. Aber nicht immer wird ein Sechstklässler zur Hand sein ... Wir werden es selbst tun müssen. Es ist nicht schwer. Multiplizieren Sie den Nenner des Bruchteils mit dem ganzzahligen Teil und addieren Sie den Zähler des Bruchteils. Dies ist der Zähler eines gemeinsamen Bruchs. Was ist mit dem Nenner? Der Nenner bleibt gleich. Klingt kompliziert, ist aber eigentlich ganz einfach. Sehen wir uns ein Beispiel an.

Geben Sie in dem Problem, das Sie mit Entsetzen gesehen haben, die Nummer ein:

Ruhig, ohne Panik verstehen wir. Der ganze Teil ist 1. Eins. Der Bruchteil ist 3/7. Daher ist der Nenner des Bruchteils 7. Dieser Nenner ist der Nenner des gewöhnlichen Bruchs. Wir zählen den Zähler. Wir multiplizieren 7 mit 1 (dem ganzzahligen Teil) und addieren 3 (den Zähler des Bruchteils). Wir erhalten 10. Dies ist der Zähler eines gewöhnlichen Bruchs. Das ist alles. Noch einfacher sieht es in mathematischer Notation aus:

Deutlich? Dann sichern Sie sich Ihren Erfolg! Wandle in gewöhnliche Brüche um. Sie sollten 10/7, 7/2, 23/10 und 21/4 erhalten.

Die umgekehrte Operation - Umwandlung eines unechten Bruchs in eine gemischte Zahl - wird in der High School selten benötigt. Nun, wenn... Und wenn Sie - nicht in der High School - können Sie in die Sonderabteilung 555 schauen. An der gleichen Stelle lernen Sie übrigens auch etwas über unechte Brüche.

Naja, fast alles. Sie haben sich an die Arten von Brüchen erinnert und verstanden als Konvertieren Sie sie von einem Typ in einen anderen. Bleibt die Frage: warum Tu es? Wo und wann kann man dieses tiefe Wissen anwenden?

Ich antworte. Jedes Beispiel selbst schlägt die notwendigen Maßnahmen vor. Wenn im Beispiel gewöhnliche Brüche, Dezimalzahlen und sogar gemischte Zahlen zu einem Haufen gemischt werden, übersetzen wir alles in gewöhnliche Brüche. Es kann immer getan werden. Nun, wenn so etwas wie 0,8 + 0,3 geschrieben wird, dann denken wir das, ohne Übersetzung. Warum brauchen wir zusätzliche Arbeit? Wir wählen die Lösung, die bequem ist uns !

Wenn die Aufgabe voller Dezimalbrüche ist, aber ähm ... irgendwelche bösen, gehen Sie zu gewöhnlichen, versuchen Sie es! Schau, alles wird gut. Zum Beispiel musst du die Zahl 0,125 quadrieren. Gar nicht so einfach, wenn man sich den Taschenrechner nicht abgewöhnt hat! Sie müssen nicht nur die Zahlen in einer Spalte multiplizieren, sondern auch überlegen, wo Sie das Komma einfügen! Das geht in meinen Augen definitiv nicht! Und wenn Sie zu einem gewöhnlichen Bruch gehen?

0,125 = 125/1000. Wir reduzieren um 5 (das ist für den Anfang). Wir bekommen 25/200. Noch einmal am 5. Wir bekommen 5/40. Oh, es schrumpft! Zurück zu 5! Wir bekommen 1/8. Einfach quadrieren (in Gedanken!) und 1/64 erhalten. Alles!

Fassen wir diese Lektion zusammen.

1. Es gibt drei Arten von Brüchen. Gewöhnliche, dezimale und gemischte Zahlen.

2. Dezimalzahlen und gemischte Zahlen stets können in gewöhnliche Brüche umgewandelt werden. Rückübersetzung nicht immer erhältlich.

3. Die Wahl des Bruchtyps für die Bearbeitung der Aufgabe hängt von dieser Aufgabe ab. Wenn es in einer Aufgabe verschiedene Arten von Brüchen gibt, ist es am zuverlässigsten, auf gewöhnliche Brüche umzusteigen.

Jetzt können Sie üben. Wandeln Sie zuerst diese Dezimalbrüche in gewöhnliche Brüche um:

3,8; 0,75; 0,15; 1,4; 0,725; 0,012

Sie sollten Antworten wie diese erhalten (in einem Durcheinander!):

Damit werden wir fertig. In dieser Lektion haben wir die wichtigsten Punkte zu Brüchen aufgefrischt. Es kommt jedoch vor, dass es nichts Besonderes zum Auffrischen gibt ...) Wenn jemand es ganz vergessen hat oder es noch nicht beherrscht ... Diese können zu einem speziellen Abschnitt 555 gehen. Dort sind alle Grundlagen ausführlich beschrieben. Viele plötzlich alles verstehen beginnen. Und sie lösen Brüche im Handumdrehen).

Wenn Ihnen diese Seite gefällt...

Übrigens habe ich noch ein paar interessantere Seiten für Sie.)

Sie können das Lösen von Beispielen üben und Ihr Niveau herausfinden. Testen mit sofortiger Verifizierung. Lernen - mit Interesse!)

Sie können sich mit Funktionen und Ableitungen vertraut machen.