Unterrichtsziele:

Kenntnisse, Fertigkeiten und Fähigkeiten zur effektiven Anwendung der verallgemeinerten Intervallmethode basierend auf der Eigenschaft kontinuierlicher Funktionen zu bilden;

Formulieren Sie einen Aktionsalgorithmus, der zu äquivalenten Transformationen führt;

Bringen Sie sich bei, es anzuwenden, wenn Sie Ungleichungen lösen;

Um den Transfer von Wissen, Fertigkeiten und Fähigkeiten auf neue Bedingungen durchzuführen.

Pädagogisch: Systematisierung, Konsolidierung, Verallgemeinerung von Wissen, Fertigkeiten und Fähigkeiten.

Pädagogisch: Aufklärung über die Notwendigkeit einer vollwertigen konsequenten Argumentation, Genauigkeit, Unabhängigkeit.

Entwickeln: die Entwicklung der mathematischen Logik, die Ausbildung eines mathematischen Denkstils (eine klare Zergliederung des Denkablaufs), kognitives Interesse.

1) Einführung, Festlegung des Ziels und der Ziele der Lektion - 2 min.

2) Kontrolle der Hausaufgaben - 2 min. (Frontalarbeit, Selbstbeherrschung).

3) Mathematische Begründung der Stufen der Lösung von Ungleichungen nach der Intervallmethode - 4 min (vorbereitete Schülerantworten).

4) Wiederholung der Eigenschaften von Ungleichungen - 2 min.

5) Vorbereitung auf das Aneignen (Studium) von neuem Unterrichtsmaterial durch Wiederholung und Aktualisierung des Grundwissens - 5 min. (Frontalarbeit, Antworten auf Fragen, Problemsituationen).

6) Verallgemeinerte Intervallmethode zum Lösen von Ungleichungen, erstes Verständnis - 13 min. (Kollektive Lösung von Ungleichungen nach der Methode der Intervalle: an der Tafel und in Heften).

7) Informationen zu den Hausaufgaben, Anweisungen zur Durchführung - 1 min.

8) Festigung des neuen Wissens - 15 min. (unabhängige Arbeit - Option 1).

9) Zusammenfassung der Lektion, Reflexion - 1 min.

1) Einführung, Festlegung des Ziels und der Ziele der Lektion. (Geschichte des Lehrers)

1) Die Notwendigkeit einer breiteren Anwendung der Intervallmethode in der Schule ergibt sich aus der Ideologie des gesamten Mathematikunterrichts. Der Punkt ist, dass die funktionale Linie (eine der wichtigsten beim Studium der Grundlagen der Mathematik) eine starke technologische Unterstützung erhält. Die Methode der Intervalle basiert auf so wichtigen Merkmalen der funktionalen Abhängigkeit wie Nullstellen einer Funktion, Intervalle mit konstantem Vorzeichen und Monotonie. Dann wird der funktionale Ursprung von Gleichungen und Ungleichungen sowie Methoden zu ihrer Lösung deutlicher. Die Kategorien der Stetigkeit einer Funktion, das Verhalten ihres Graphen in der Nähe von Punkten unendlicher Diskontinuität, Wurzelsätze, Vorzeichenkonstanz, Extrempunkte und ihre Typen werden sichtbarer. Und all dies ist organisch zu einem funktionellen Ganzen verbunden.

Andererseits ist auch die Geometrisierung der verwendeten Untersuchungsobjekte von unschätzbarem Wert, d.h. visuell, bildlich präsentieren alle verwendeten mathematischen Werkzeuge der funktionalen Abhängigkeit.

Die Grundprinzipien der Intervallmethode:

• funktionaler (allgemeiner) Ansatz;
• Vertrauen auf die Geometrisierung funktionaler Eigenschaften;
• Forschungsvisualisierung.

Dies führt zu den folgenden Vorteilen der Methode im Vergleich zu anderen, die bei der gleichen Art von Aufgaben verwendet werden: Einfachheit und Geschwindigkeit des Erreichens des Ziels; Sichtbarkeit (und die Fähigkeit zu kontrollieren oder zu überprüfen); Einsparung von Rechenressourcen und -zeit; Erfassungsbreite der Gesamtsituation, die Herausbildung und Entwicklung von Fähigkeiten des verallgemeinernden Denkens und Analysierens sowie die damit verbundene Fähigkeit, logische Schlussfolgerungen zu ziehen.

2) Überprüfung der Hausaufgaben.(Folie Nummer 4)

3) Eine Geschichte über die Methode der Intervalle zum Lösen von Ungleichungen. (Schüler antwortet).

Mathematische Begründung der Lösung von Ungleichungen nach der Methode der Intervalle.

1) Betrachten Sie die Ungleichungen: (x-2)(x-3)>0. (Folie Nummer 5)

Du kannst es so lösen: Das Produkt (Quotient) zweier Faktoren ist genau dann positiv, wenn beide Faktoren das gleiche Vorzeichen haben, also Ungleichheit entspricht der Kombination zweier Systeme: (Folie Nummer 6)

Aus dem ersten System erhalten wir x > 3, aus dem zweiten x< 2.

Die Lösung ist die Vereinigung der Lösungen der beiden Systeme.

Antworten:

Grafische Methode (Folie Nummer 7)

Eine andere Methode ist Intervallmethode(Folie Nummer 8).

Seine Idee ist wie folgt.

Markieren Sie auf der Reallinie die Nullstellen (Wurzeln) des Polynoms (x-2)(x-3) stehend

auf der linken Seite der Ungleichung, d.h. Nummer 2 und 3.

Wenn x > 3 (rechts von der größeren Wurzel), dann (x-2)(x-3) > 0, da jeder Faktor positiv ist.

Bewegt man sich entlang der Achse in negativer Richtung, so ändert der Faktor (x-3) beim Passieren des Punktes x=3 das Vorzeichen. Im Produkt (x-2) (x-3) erscheint ein negativer Faktor, als Ergebnis (x-2) (x-3)<0. При переходе через следующий корень появится еще один отрицательный множитель и произведение (х-2)(х-3)>0.

Jetzt ist es einfach, die Lösung der Ungleichung aufzuschreiben:

Fazit: Das Produkt kann nur beim Durchlaufen der Punkte x=2 und x=3 das Vorzeichen wechseln

und bewahrt daher das Vorzeichen auf jedem der erhaltenen Intervalle.

An diesem einfachen Beispiel ist die Idee der Intervallmethode leicht nachvollziehbar, zeigt aber keine nennenswerten Vorteile.

Die Rationalität der Intervallmethode, ihre Leistungsfähigkeit, betrachten wir im folgenden Beispiel (Folie Nr. 9, 10,11, 12))

2) Lösen Sie die Ungleichung (x-1)(x-2)(x-3)(x-4)(x-5)(x-6)(x-7)(x-8)(x-9) (x-10) > 0.

Um diese Ungleichung mit einer Menge von Systemen zu lösen, müsste man eine Menge von 512 Systemen mit 10 Ungleichungen in jedem System betrachten.

Verwenden wir die Intervallmethode. Wir markieren die Nullstellen des Polynoms auf der reellen Geraden. Auf dem Intervall x>10 ist das Polynom positiv, da jeder Faktor positiv ist. Beim Durchgang durch jede nächste Wurzel ändert das Polynom das Vorzeichen, da ein zusätzlicher negativer Faktor im Produkt erscheint. Jetzt ist es einfach, die Lösung der Ungleichung mit Vorzeichenwechsel zu schreiben.

Vorteile der Intervallmethode.

• Einfachheit und Schnelligkeit, um das Ziel zu erreichen;
• Sichtbarkeit (und die Fähigkeit zu kontrollieren oder zu überprüfen);
• eine deutliche Verringerung des Rechenaufwands und der Zeit;
• Umfang der Erfassung der Gesamtsituation;
• die Bildung und Entwicklung generalisierter Denk- und Analysefähigkeiten sowie der damit verbundenen Fähigkeiten, logische Schlussfolgerungen zu ziehen.

Kommentar. Es ist sehr praktisch, Ungleichungen zu lösen, deren linke Seite faktorisiert ist, da es nicht schwierig ist, Nullen (Wurzeln) zu finden.

Aufgabe: Lösen Sie die Ungleichung mit der Intervallmethode (x+3) 3 (x-4) 2 (x-5) > 0(Folie 13)

4) Wiederholung von Eigenschaften von Ungleichungen.

a) Frage: Welche Ungleichungen heißen äquivalent?

(Zwei Ungleichungen heißen äquivalent, wenn jede Lösung der ersten Ungleichung eine Lösung der zweiten ist und umgekehrt jede Lösung der zweiten eine Lösung der ersten ist).

Oder: Zwei Ungleichungen heißen äquivalent, wenn die Mengen ihrer Lösungen gleich sind.

Folie 14. Wiederholung der Eigenschaften von Ungleichungen.

Folie 15. Beantworten Sie die Frage und erklären Sie sie.

Sind Ungleichheiten gleich?

1) 4x-5<0 и 4х<5

2) -2x+5>0 und 2x-5<0

3) -3x 2 +5x-7>0 und 3x 2 -5x+7<0

4) (x+1) > 0 und (x 2 +5x+10)(x+1) > 0

5) Mündliche Frontalarbeit zur Vorbereitung auf die Aneignung (das Studium) von neuem Unterrichtsmaterial durch Wiederholung und Aktualisierung von Grundwissen.

Folie 16. Definition einer punktstetigen Funktion.

Folie 17. Eigenschaft stetiger Funktionen.

Folie 18. Lücken der Kontinuität finden.

Folie 19. Finden Sie den Fehler.

Folie 20. Lösen Sie die Ungleichung verbal,
mithilfe eines Diagramms.

Folie 21, 22. Ersetzen der Ungleichung durch eine äquivalente Bedingung.

Löse die Ungleichung

Diese Ungleichung ist äquivalent zur Bedingung f(x) < 0 zählen

Daher müssen wir alle Werte von x finden, für die die Bedingung f(x) < 0.

6) Verallgemeinerte Intervallmethode zum Lösen von Ungleichungen, erstes Verständnis - 10 min. (Kollektive Lösung von Ungleichungen nach der Methode der Intervalle: an der Tafel und in Heften).

Folie 23. Algorithmus. Verallgemeinerte Methode zur Lösung von Ungleichungen.

Lösung von Ungleichungen f(x)>0, f(x) > 0, f(x)<0, f(x)< 0 nach der Intervallmethode. (Planen)

Folie 24 und 25. Lösen der Ungleichung durch den Algorithmus. (Kommentare zu allen Punkten des Algorithmus).

Folie 26. Grafische Darstellung der Lösung dieser Ungleichung.

Folie 27. Lösen Sie die Ungleichung an der Tafel und in Heften .

Folie 28. Grafische Darstellung der Lösung dieser Ungleichung.

Folie 29. Lösen Sie die Ungleichung an der Tafel und in Heften

Folie 30. Grafische Darstellung der Lösung dieser Ungleichung.

Folie 31, 32. Lösen Sie die Ungleichung laut Bild

7) Informationen zu Hausaufgaben.(Löse nach der Intervallmethode Option Nummer 2)

8) Festigung neuer Kenntnisse (selbständiges Arbeiten, Option Nr. 1).

9) Zusammenfassung der Lektion, Selbstkontrolle bei vorgefertigten Lösungen (Folien 33, 34, 35), Wiederholung des Algorithmus der verallgemeinerten Methode der Intervalle und ihrer Anwendung.

10) Analyse der Aneignung des Stoffes und des Interesses der Studierenden am Thema. Diese Methode ist universell zum Lösen beliebiger Ungleichungen, einschließlich rational, mit einem Modul, irrational, exponentiell, logarithmisch, da die Intervallmethode die Lösung von Ungleichungen auf das Lösen von Gleichungen reduziert, den Definitionsbereich und den Wert der Funktion an einem Punkt findet keine Schwierigkeiten bereiten. Aber ich musste Beispiele von Ungleichungen geben, wo die Verwendung dieser Methode nicht gerechtfertigt ist, wo es vernünftiger ist, andere Methoden zur Lösung von Ungleichungen anzuwenden.

Präsentation „Anwendung der Kontinuität bei der Lösung von Ungleichungen“. (35 Folien)

Definition 4. Eine Funktion heißt auf einer Strecke stetig, wenn sie an jedem Punkt dieser Strecke stetig ist (am Punkt a ist sie rechts stetig, d. h. und am Punkt b ist sie links stetig, d. h.).

Alle elementaren Grundfunktionen sind in ihrem Definitionsbereich stetig.

Eigenschaften von Funktionen, die auf einem Segment stetig sind:

• 1) Wenn eine Funktion auf einem Segment stetig ist, dann ist sie auf diesem Segment beschränkt (das erste Weierstrass-Theorem).
• 2) Wenn eine Funktion auf einer Strecke stetig ist, dann erreicht sie auf dieser Strecke ihren Minimalwert und ihren Maximalwert (das zweite Weierstrass-Theorem) (siehe Abb. 2).
• 3) Wenn eine Funktion auf einem Segment stetig ist und an ihren Enden Werte mit unterschiedlichen Vorzeichen annimmt, dann gibt es mindestens einen Punkt innerhalb des Segments, so dass (Theorem von Bolzano-Cauchy).

Funktionshaltepunkte und ihre Klassifizierung

Funktionskontinuitätspunktsegment

Die Punkte, an denen die Stetigkeitsbedingung nicht erfüllt ist, heißen Unstetigkeitspunkte dieser Funktion. Ist eine Unstetigkeitsstelle einer Funktion, dann ist in ihr mindestens eine der drei Bedingungen für die Stetigkeit der Funktion aus den Definitionen 1, 2 nicht erfüllt, nämlich:

1) Die Funktion ist in der Nähe des Punktes definiert, aber nicht am Punkt selbst definiert. Die in Beispiel 2 a) betrachtete Funktion hat also an einer Stelle einen Bruch, da sie an dieser Stelle nicht definiert ist.

2) Die Funktion ist an einem Punkt und seiner Umgebung definiert, es gibt einseitige Grenzen und, aber sie sind einander nicht gleich: . Beispielsweise ist die Funktion aus Beispiel 2 b) an einem Punkt und seiner Umgebung definiert, aber da a.

3) Die Funktion ist am Punkt und seiner Umgebung definiert, es gibt einseitige Grenzen und sie sind einander gleich, aber nicht gleich dem Wert der Funktion am Punkt: . Zum Beispiel Funktion. Hier ist der Bruchpunkt: An dieser Stelle ist die Funktion definiert, es gibt einseitige Grenzen und einander gleich, aber, d.h.

Funktionshaltepunkte werden wie folgt klassifiziert.

Definition 5. Ein Punkt heißt Unstetigkeitspunkt erster Art einer Funktion, wenn es an diesem Punkt endliche Grenzwerte gibt, die aber einander nicht gleich sind: . Die Größe heißt dann Sprung der Funktion an der Stelle.

Bestimmung 6 . Ein Punkt wird als Punkt einer entfernbaren Unstetigkeit einer Funktion bezeichnet, wenn es an diesem Punkt endliche Grenzen gibt und sie einander gleich sind: , aber die Funktion selbst ist an dem Punkt nicht definiert, oder definiert, aber.

Definition 7. Ein Punkt heißt Unstetigkeitspunkt zweiter Art einer Funktion, wenn an diesem Punkt mindestens einer der einseitigen Grenzwerte (oder) nicht existiert oder gleich unendlich ist.

Beispiel 3. Haltepunkte der folgenden Funktionen finden und ihren Typ bestimmen: a) b)

Entscheidung. a) Die Funktion ist auf den Intervallen u definiert und stetig, da sie auf jedem dieser Intervalle durch stetige Elementarfunktionen gegeben ist. Daher können die Haltepunkte einer bestimmten Funktion nur diejenigen Punkte sein, an denen die Funktion ihre analytische Zuordnung ändert, d.h. Punkte i. Finden wir die einseitigen Grenzen der Funktion an dem Punkt:

Da einseitige Grenzen existieren und zwar endlich, aber nicht gleich sind, ist der Punkt ein Unstetigkeitspunkt erster Art. Funktionssprung:

Für einen Punkt finden wir.

Stetigkeit einer Funktion auf einem Intervall

Parametername	Bedeutung
Betreff des Artikels:	Stetigkeit einer Funktion auf einem Intervall
Rubrik (thematische Kategorie)	Mathematik

Definition. Eine Funktion heißt stetig auf einem Intervall, wenn sie an jedem Punkt dieses Intervalls stetig ist.

Wenn die Funktion definiert ist für X=a und worin f(X) = f(a),

dann sagen sie das f(X) am Punkt und rechts durchgehend. Ebenso, wenn f(X) = f(b), dann sagen wir das an der Stelle b diese Funktion durchgehend gelassen.

Definition. Die Funktion heißt normalerweise stetig auf dem Segment [ a, b], wenn es an jedem seiner Punkte stetig ist (am Punkt a durchgehend rechts, an einem Punkt b ist links durchgehend).

Höchster Wert Funktionen beim = f(x) auf dem Segment [ a, b f(x 1) das f(x) £ f(x 1) für alle X Î [ a, b].

Niedrigster Wert Funktionen beim = f(x) auf dem Segment [ a, b] ist es üblich, dies seinen Wert zu nennen f(x 2) das f(x) ³ f(x 2) für alle X Î [ a, b].

Auf einem Intervall stetige Funktionen haben eine Reihe wichtiger Eigenschaften, die durch die folgenden Sätze ausgedrückt werden.

Satz 3.3.1. Eine auf dem Segment stetige Funktion [ a, b], erreicht darauf seinen Minimalwert m und den größten Wert M, das heißt, es gibt solche Punkte x 1 und x 2 dieses Segments, die f(x 1) = m, f(x 2) = M.

Der Satz hat eine einfache geometrische Bedeutung (siehe Abb. 2).

Satz 3.3.2. Falls die Funktion beim = f(x) ist stetig auf dem Segment [ a, b] und nimmt an seinen Enden ungleiche Werte an f(a) = EIN, f(b) = B, A ¹ B, dann gibt es unabhängig von der Zahl C zwischen A und B einen Punkt mit Î [ a, b] so dass f(mit) = C.

Die geometrische Bedeutung des Theorems ist in Abb. 3 dargestellt. Jede gerade Linie beim= C, wobei A< C < B (или A >C > B), den Graphen der Funktion schneidet beim = f(x).

Folge. Wenn die Funktion auf einer Strecke stetig ist und an ihren Enden Werte unterschiedlichen Vorzeichens annimmt, dann gibt es auf dieser Strecke mindestens einen Punkt, an dem die Funktion verschwindet.

Die geometrische Bedeutung der Konsequenz ist in Abb.4 dargestellt.

Fragen zur Selbstkontrolle

1. Welche Funktion heißt an einem Punkt stetig?

2. Geben Sie eine weitere äquivalente Definition durch das Inkrement einer Funktion und Argumenten an.

3. Was kann man über Summe, Differenz, Produkt und Quotient zweier stetiger Funktionen sagen?

4. Für welche Werte des Arguments sind die gesamten rationalen und fraktional-rationalen Funktionen stetig?

5. Wann ist eine komplexe Funktion an einem Punkt stetig?

6. Was wird allgemein als Bruchpunkt von Funktionen bezeichnet?

7. Welche Punkte nennt man Unstetigkeitspunkte erster Art?

8. Welcher Wert wird normalerweise als Funktionssprung bezeichnet?

9. Erklären Sie die Begriffe „entfernbarer Haltepunkt“. Nenne Beispiele.

10. Welche Punkte nennt man Unstetigkeitspunkte zweiter Art? Nenne Beispiele.

11. Erklären Sie die Begriffe: ""Kontinuität auf dem Intervall"", ""Kontinuität auf der rechten Seite"", ""Kontinuität auf der linken Seite"", ""Kontinuität auf dem Segment"".

12. Definieren Sie die größten und kleinsten Werte von Funktionen.

13. Formulieren Sie einen Satz über die Kontinuitätsbeziehung auf einem Segment mit den größten und kleinsten Werten der Funktion. Erkläre es mit einem Bild.

14. Formulieren Sie einen Satz über den Zusammenhang zwischen der Stetigkeit von Funktionen auf einer Strecke und der Strecke von Funktionswerten. Veranschauliche seine geometrische Bedeutung in der Abbildung.

15. Geben Sie eine Konsequenz aus dem obigen Satz und seiner geometrischen Interpretation an.

VORTRAG №4

Vortragsthema: Ableitung der Funktion

Vorlesungsplan: Das Konzept eines Derivats, seine geometrische und physikalische Bedeutung. Grundregeln der Differenzierung. Ableitung einer komplexen Funktion. Einige Anwendungen des Derivats.

4.1. Das Konzept eines Derivats, seine geometrische und physikalische Bedeutung

Betrachten Sie die Funktion beim = f(x) angegeben im Intervall ] a, b[. Lassen XÎ ] a, b[ und X Î ] a, b[, dann das Funktionsinkrement an dem Punkt X 0 wird durch die Formel D ausgedrückt beim = f(x 0+D X) – f(x 0).

Definition. Die Ableitung der Funktion y = f(x) am Punkt X 0 wird normalerweise als Grenze des Verhältnisses des Inkrements dieser Funktion zum Inkrement des Arguments bezeichnet, wenn letzteres gegen Null geht:

f'(x 0) = oder ja"(x 0) =.

Die geometrische Bedeutung der Ableitung: Die Ableitung dieser Funktion an einem Punkt ist gleich der Tangente des Winkels zwischen der Ox-Achse und der Tangente an den Graphen dieser Funktion an dem entsprechenden Punkt (siehe Abb. 1):

f"(x 0) = tan a.

Definition. Wenn die Funktion f(x) ist auf dem Intervall [ ein, b], ist an jedem Punkt des Intervalls stetig ( ein, b), am Punkt a durchgehend rechts, an einem Punkt b linksstetig ist, dann sagen wir, dass die Funktion f(x) kontinuierlich auf dem Segment [ein, b].

Mit anderen Worten, die Funktion f(x) ist stetig auf dem Segment [ ein, b], wenn drei Bedingungen erfüllt sind:

1) "x 0 Î( ein, b): f(x) = f(x 0);

2) f(x) = f(a);

3) f(x) = f(b).

Für intervallstetige Funktionen betrachten wir einige Eigenschaften, die wir ohne Beweise in Form der folgenden Sätze formulieren.

Satz 1. Wenn die Funktion f(x) ist stetig auf dem Segment [ ein, b], dann erreicht er auf diesem Segment seinen kleinsten und seinen größten Wert.

Dieser Satz besagt (Abb. 1.15), dass auf dem Intervall [ ein, b] gibt es einen solchen Punkt x 1 das f(x 1) £ f(x) für alle x aus [ ein, b] und dass es einen Punkt gibt x 2 (x 2 О[ ein, b]) so dass " xÎ[ ein, b] (f(x 2) ³ f(x)).

Bedeutung f(x 1) ist die größte für die gegebene Funktion auf [ ein, b], a f(x 2) - die kleinste. Bezeichnen: f(x 1) = M, f(x 2) =m. Da für f(x) gilt die folgende Ungleichung: " xÎ[ ein, b] m£ f(x) £ M, dann erhalten wir aus Satz 1 das folgende Korollar.

Folge. Wenn die Funktion f(x) auf einem Segment stetig ist, dann ist es auf dieses Segment beschränkt.

Satz 2. Wenn die Funktion f(x) ist stetig auf dem Segment [ ein, b] und an den Segmentenden Werte unterschiedlicher Vorzeichen annimmt, dann gibt es einen solchen inneren Punkt x 0 Segment [ ein, b], in dem die Funktion zu 0 wird, d.h. $ x 0 Î ( ein, b) (f(x 0) = 0).

Dieser Satz besagt, dass der Graph einer Funktion y=f(x), kontinuierlich auf dem Segment [ ein, b], kreuzt die Achse Ochse mindestens einmal, wenn die Werte f(a) und f(b) haben entgegengesetzte Vorzeichen. Also (Abb. 1.16) f(a) > 0, f(b) < 0 и функция f(x) verschwindet punktuell x 1 , x 2 , x 3 .

Satz 3. Lassen Sie die Funktion f(x) ist stetig auf dem Segment [ ein, b], f(a) = EIN, f(b) = B und EIN¹ B. (Abb. 1.17). Dann für eine beliebige Zahl C, geschlossen zwischen den Zahlen EIN und B, gibt es einen solchen inneren Punkt x 0 Segment [ ein, b], was f(x 0) = C.

Folge. Wenn die Funktion f(x) ist stetig auf dem Segment [ ein, b], m- der kleinste Wert f(x), M- der größte Wert der Funktion f(x) auf dem Segment [ ein, b], dann nimmt die Funktion (mindestens einmal) einen beliebigen Wert an m zwischen m und M, und daher das Segment [ m, m] ist die Menge aller Werte der Funktion f(x) auf dem Segment [ ein, b].

Beachten Sie, dass, wenn die Funktion im Intervall kontinuierlich ist ( ein, b) oder hat im Intervall [ ein, b] des Unstetigkeitspunktes, dann gelten die Sätze 1, 2, 3 für eine solche Funktion nicht mehr.

Betrachten Sie abschließend den Satz über die Existenz einer Umkehrfunktion.

Erinnern Sie sich, dass ein Intervall ein Segment, ein Intervall oder ein endliches oder unendliches halbes Intervall ist.

Satz 4. Lassen f(x) ist im Intervall kontinuierlich X, erhöht (oder verringert) um X und hat eine Reihe von Werten Y. Dann zur Funktion y=f(x) gibt es eine Umkehrfunktion x= j(j) auf dem Intervall definiert Y, kontinuierlich und zunehmend (oder abnehmend) an Y mit vielen Bedeutungen X.

Kommentar. Lassen Sie die Funktion x= j(j) ist für die Funktion invers f(x). Da das Argument normalerweise mit bezeichnet wird x, und die Funktion durch j, dann schreiben wir die Umkehrfunktion als y=j(x).

Beispiel 1. Funktion y=x 2 (Abb. 1.8, a) am Set X= wenn es an allen inneren Punkten dieses Segments und an seinen Enden kontinuierlich ist, d.h. an Punkten a und b, ist rechts bzw. links stetig.

Satz 1. Eine auf dem Segment stetige Funktion [ a, b], mindestens an einem Punkt dieses Segments nimmt den größten Wert und mindestens an einem Punkt den kleinsten an.

Der Satz besagt, dass wenn die Funktion y = f(x) kontinuierlich auf dem Segment [ a, b], dann gibt es mindestens einen Punkt x 1 Î [ a, b] so dass der Wert der Funktion f(x) an diesem Punkt wird der größte aller seiner Werte in diesem Segment sein: f(x1) ≥ f(x). Ebenso gibt es einen solchen Punkt x2, in dem der Wert der Funktion der kleinste aller Werte auf dem Segment sein wird: f(x 1) ≤ f(x).

Es ist klar, dass es mehrere solcher Punkte geben kann, zum Beispiel zeigt die Figur, dass die Funktion f(x) nimmt an zwei Stellen den kleinsten Wert an x2 und x 2 ".

Kommentar. Die Aussage des Satzes kann falsch werden, wenn wir den Wert der Funktion auf dem Intervall ( a, b). In der Tat, wenn wir die Funktion betrachten y=x auf (0, 2), dann ist es in diesem Intervall kontinuierlich, erreicht aber nicht seine Maximal- oder Minimalwerte darin: Es erreicht diese Werte an den Enden des Intervalls, aber die Enden gehören nicht zu unserem Region.

Außerdem gilt der Satz nicht mehr für unstetige Funktionen. Gib ein Beispiel.

Folge. Wenn die Funktion f(x) kontinuierlich auf [ a, b], dann ist es auf dieses Segment beschränkt.

Satz 2. Lassen Sie die Funktion y = f(x) kontinuierlich auf dem Segment [ a, b] und an den Enden dieses Segments Werte mit unterschiedlichen Vorzeichen annimmt, dann befindet sich mindestens ein Punkt innerhalb des Segments x=C, wo die Funktion verschwindet: f(C)= 0, wobei a< C< b

Dieser Satz hat eine einfache geometrische Bedeutung: wenn die Punkte des Graphen eine stetige Funktion sind y = f(x), entsprechend den Enden des Segments [ a, b] liegen auf gegenüberliegenden Seiten der Achse Ochse, dann schneidet dieser Graph an mindestens einem Punkt des Segments die Achse Ochse. Diskontinuierliche Funktionen haben diese Eigenschaft möglicherweise nicht.

Dieser Satz lässt die folgende Verallgemeinerung zu.

Satz 3 (Satz über Zwischenwerte). Lassen Sie die Funktion y = f(x) kontinuierlich auf dem Segment [ a, b] und f(a) = A, f(b) = B. Dann für eine beliebige Zahl C zwischen EIN und B, gibt es einen solchen Punkt innerhalb dieses Segments CÎ [ a, b], was f(c) = C.

Dieser Satz ist geometrisch offensichtlich. Betrachten Sie den Graphen der Funktion y = f(x). Lassen f(a) = A, f(b) = B. Dann irgendeine Zeile y=C, wo C- eine beliebige Zahl dazwischen EIN und B, schneidet den Graphen der Funktion an mindestens einem Punkt. Die Abszisse des Schnittpunkts ist dieser Wert x=C, bei welchem f(c) = C.

Somit durchläuft eine kontinuierliche Funktion, die von einem ihrer Werte zu einem anderen übergeht, notwendigerweise alle Zwischenwerte. Insbesondere:

Folge. Wenn die Funktion y = f(x) in einem bestimmten Intervall kontinuierlich ist und den größten und den kleinsten Wert annimmt, dann nimmt es in diesem Intervall mindestens einmal einen beliebigen Wert zwischen seinem kleinsten und größten Wert an.

DERIVATE UND SEINE ANWENDUNGEN. DERIVATIVE DEFINITION

Lassen Sie uns eine Funktion haben y=f(x), in einem bestimmten Intervall definiert. Für jeden Argumentwert x aus diesem Intervall die Funktion y=f(x) hat eine bestimmte Bedeutung.

Betrachten Sie zwei Argumentwerte: initial x 0 und neu x.

Unterschied x–x 0 wird aufgerufen Inkrement von Argument x am Punkt x 0 und bezeichnet Δx. Auf diese Weise, ∆x = x – x 0 (Argumentinkrement kann entweder positiv oder negativ sein). Aus dieser Gleichheit folgt das x=x 0 +Δx, d.h. der Anfangswert der Variablen hat eine gewisse Erhöhung erhalten. Dann, wenn an der Stelle x 0 Funktionswert war f(x 0 ), dann am neuen Punkt x Die Funktion übernimmt den Wert f(x) = f(x 0 +∆x).

Unterschied y-y 0 = f(x) – f(x 0 ) namens Funktionsinkrement y = f(x) am Punkt x 0 und wird durch das Symbol gekennzeichnet Δy. Auf diese Weise,

Δy = f(x) – f(x 0 ) = f(x 0 +Δx) - f(x 0 ) .

(1)

Normalerweise der Anfangswert des Arguments x 0 gilt als fest und der neue Wert x- variabel. Dann j 0 = f(x 0 ) erweist sich als konstant und y = f(x)- variabel. Schritte Δy und Δx werden auch Variablen sein und Formel (1) zeigt dies Dy ist eine Funktion der Variablen Δx.

Bilden Sie das Verhältnis des Inkrements der Funktion zum Inkrement des Arguments

Lassen Sie uns den Grenzwert dieser Beziehung bei finden Δx→0. Wenn dieser Grenzwert existiert, wird er als Ableitung dieser Funktion bezeichnet. f(x) am Punkt x 0 und bezeichnen f "(x 0). So,

Derivat diese Funktion y = f(x) am Punkt x 0 wird die Grenze des Inkrementverhältnisses der Funktion Δ genannt j zum Inkrement des Arguments Δ x wenn letztere willkürlich gegen Null geht.

Beachten Sie, dass für dieselbe Funktion die Ableitung an verschiedenen Punkten erfolgt x kann unterschiedliche Werte annehmen, d.h. die Ableitung kann als Funktion des Arguments betrachtet werden x. Diese Funktion ist bezeichnet f "(x)

Die Ableitung wird durch die Symbole bezeichnet f "(x), y", . Der spezifische Wert des Derivats bei x = a bezeichnet f "(a) oder j "| x=a.

Die Operation zum Finden der Ableitung einer Funktion f(x) heißt die Differentiation dieser Funktion.

Um die Ableitung per Definition direkt zu finden, können Sie Folgendes anwenden Faustregel:

Beispiele.

MECHANISCHE BEDEUTUNG DES DERIVATS

Aus der Physik ist bekannt, dass das Gesetz der gleichförmigen Bewegung die Form hat s = v t, wo s- Bis zum Zeitpunkt zurückgelegter Weg t, v ist die Geschwindigkeit der gleichförmigen Bewegung.

Allerdings seit Die meisten in der Natur vorkommenden Bewegungen sind ungleichmäßig, dann im Allgemeinen die Geschwindigkeit und folglich die Entfernung s wird von der Zeit abhängen t, d.h. wird eine Funktion der Zeit sein.

Lassen Sie also den materiellen Punkt gemäß dem Gesetz in einer geraden Linie in eine Richtung bewegen s=s(t).

Notieren Sie sich einen Moment t 0 . An diesem Punkt hat der Punkt den Pfad passiert s=s(t 0 ). Lassen Sie uns die Geschwindigkeit bestimmen v materieller Zeitpunkt t 0 .

Betrachten Sie dazu einen anderen Zeitpunkt t 0 + Δ t. Sie entspricht der zurückgelegten Strecke s =s(t 0 + Δ t). Dann für das Zeitintervall Δ t der Punkt hat den Weg Δs zurückgelegt =s(t 0 + Δ t)–s(t).

Betrachten wir die Beziehung. Sie wird als Durchschnittsgeschwindigkeit im Zeitintervall Δ bezeichnet t. Die Durchschnittsgeschwindigkeit kann momentan die Bewegungsgeschwindigkeit eines Punktes nicht genau charakterisieren t 0 (weil die Bewegung ungleichmäßig ist). Um diese wahre Geschwindigkeit anhand der Durchschnittsgeschwindigkeit genauer auszudrücken, müssen Sie ein kleineres Zeitintervall Δ nehmen t.

Also die Geschwindigkeit der Bewegung zu einem bestimmten Zeitpunkt t 0 (Momentangeschwindigkeit) ist die Grenze der Durchschnittsgeschwindigkeit im Intervall von t 0 bis t 0 +Δ t wenn Δ t→0:

,

jene. Geschwindigkeit der ungleichmäßigen Bewegung ist die Ableitung der zurückgelegten Strecke nach der Zeit.

GEOMETRISCHE BEDEUTUNG DER DERIVATE

Führen wir zunächst die Definition einer Tangente an eine Kurve an einem gegebenen Punkt ein.

Angenommen, wir haben eine Kurve und einen Fixpunkt darauf M 0(siehe Abbildung) Betrachten Sie einen anderen Punkt M diese Kurve und zeichne eine Sekante M 0 M. Wenn Punkt M beginnt sich entlang der Kurve zu bewegen, und der Punkt M 0 stationär bleibt, ändert die Sekante ihre Position. Wenn, mit unbegrenzter Annäherung des Punktes M Kurve zu Punkt M 0 Auf jeder Seite neigt die Sekante dazu, die Position einer bestimmten geraden Linie einzunehmen M 0 T, dann die Gerade M 0 T heißt Tangente an die Kurve an dem gegebenen Punkt M 0.

Dass., Tangente auf die Kurve an einem bestimmten Punkt M 0 heißt Grenzlage der Sekante M 0 M wenn der Punkt M entlang der Kurve zu einem Punkt tendiert M 0.

Betrachten Sie nun die stetige Funktion y=f(x) und die dieser Funktion entsprechende Kurve. Für einen gewissen Wert X 0-Funktion nimmt einen Wert an y0=f(x0). Diese Werte x 0 und j 0 auf der Kurve entspricht einem Punkt M 0 (x 0; y 0). Lassen Sie uns ein Argument liefern x0 Erhöhung Δ X. Der neue Wert des Arguments entspricht dem inkrementierten Wert der Funktion j 0 +Δ y=f(x 0 –Δ x). Wir bekommen einen Punkt M(x 0+Δ x; ja 0+Δ y). Lassen Sie uns eine Sekante zeichnen M 0 M und bezeichnen mit φ den Winkel, den die Sekante mit der positiven Richtung der Achse bildet Ochse. Lassen Sie uns eine Beziehung herstellen und beachten Sie, dass .

Wenn jetzt Δ x→0 also wegen der Stetigkeit der Funktion Δ beim→0, und damit der Punkt M, das sich entlang der Kurve bewegt, nähert sich dem Punkt auf unbestimmte Zeit M 0. Dann die Sekante M 0 M neigt dazu, die Position einer Tangente an die Kurve an dem Punkt einzunehmen M 0, und der Winkel φ→α bei Δ x→0, wobei α den Winkel zwischen der Tangente und der positiven Richtung der Achse bezeichnet Ochse. Da die Funktion tg φ bei φ≠π/2 stetig von φ abhängt, ist bei φ→α tg φ → tg α und damit die Steigung der Tangente:

jene. f"(x)= tgα .

Also geometrisch y "(x 0) stellt die Steigung der Tangente an den Graphen dieser Funktion an dem Punkt dar x0, d.h. für einen gegebenen Wert des Arguments x, ist die Ableitung gleich der Tangente des Winkels, der durch die Tangente an den Graphen der Funktion gebildet wird f(x) an der entsprechenden Stelle M 0 (x; y) mit positiver Achsrichtung Ochse.

Beispiel. Finden Sie die Steigung der Tangente an die Kurve y = x 2 an Punkt M(-1; 1).

Das haben wir schon gesehen ( x 2)" = 2X. Aber die Steigung der Tangente an die Kurve ist tg α = j"| x=-1 = - 2.

DIFFERENZIERBARKEIT VON FUNKTIONEN. Kontinuität einer differenzierbaren Funktion

Funktion y=f(x) namens differenzierbar irgendwann x 0, wenn es an dieser Stelle eine bestimmte Ableitung hat, also wenn die Grenze der Relation existiert und endlich ist.

Wenn eine Funktion an jedem Punkt eines Segments differenzierbar ist [ a; b] oder Intervall ( a; b), dann sagen sie, dass es differenzierbar auf dem Segment [ a; b] bzw. im Intervall ( a; b).

Es gilt folgender Satz, der einen Zusammenhang zwischen differenzierbaren und stetigen Funktionen herstellt.

Satz. Wenn die Funktion y=f(x) irgendwann differenzierbar x0, dann ist sie an dieser Stelle stetig.

Die Differenzierbarkeit einer Funktion impliziert also ihre Stetigkeit.

Nachweisen. Wenn ein , dann

,

wobei α ein infinitesimaler Wert ist, d.h. Menge, die bei Δ gegen Null geht x→0. Aber dann

Δ j=f "(x0) Δ x+αΔ x=> Δ j→0 bei Δ x→0, d.h. f(x) – f(x0)→0 bei x→x 0 , was bedeutet, dass die Funktion f(x) kontinuierlich an Punkt x 0 . Q.E.D.

Daher kann die Funktion an Unstetigkeitspunkten keine Ableitung haben. Die umgekehrte Aussage ist nicht richtig: Es gibt stetige Funktionen, die an einigen Stellen nicht differenzierbar sind (d. h. an diesen Stellen keine Ableitung haben).

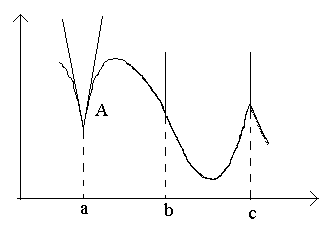
Betrachten Sie die Punkte in der Abbildung a, b, c.

Am Punkt a bei Δ x→0 hat die Beziehung keinen Grenzwert (weil die einseitigen Grenzwerte für Δ unterschiedlich sind x→0–0 und Δ x→0+0). Am Punkt EIN Der Graph hat keine definierte Tangente, aber es gibt zwei verschiedene einseitige Tangenten mit Steigungen zu 1 und zu 2. Diese Art von Punkt wird Eckpunkt genannt.

Am Punkt b bei Δ x→0 das Verhältnis ist von konstantem Vorzeichen unendlich großer Wert . Die Funktion hat eine unendliche Ableitung. An diesem Punkt hat der Graph eine vertikale Tangente. Punkttyp - "Wendepunkt" mit einer vertikalen Tangente.

Am Punkt c einseitige Ableitungen sind unendlich viele verschiedene Vorzeichen. An diesem Punkt hat der Graph zwei zusammengeführte vertikale Tangenten. Typ - "Spitze" mit einer vertikalen Tangente - ein Sonderfall eines Eckpunkts.