Das Prinzip der kleinsten Wirkung, das erstmals ausdrücklich von Jacobi formuliert wurde, ähnelt dem Prinzip von Hamilton, ist jedoch weniger allgemein und schwieriger zu beweisen. Dieses Prinzip gilt nur für den Fall, dass die Zusammenhänge und die Kraftfunktion zeitunabhängig sind und es daher ein Integral der lebendigen Kraft gibt.
Dieses Integral sieht so aus:
Das oben genannte Hamilton-Prinzip besagt, dass die Variation des Integrals

gleich Null ist, wenn die tatsächliche Bewegung in eine beliebige andere unendlich nahe Bewegung übergeht, die das System im selben Zeitintervall von derselben Anfangsposition zu derselben Endposition bringt.
Das Jacobi-Prinzip hingegen drückt eine Eigenschaft, Bewegung aus, die nicht von der Zeit abhängt. Jacobi betrachtet das Integral
Handlung definieren. Das von ihm aufgestellte Prinzip besagt, dass die Variation dieses Integrals Null ist, wenn wir die tatsächliche Bewegung des Systems mit jeder anderen unendlich nahen Bewegung vergleichen, die das System von derselben Anfangsposition zu derselben Endposition bringt. In diesem Fall achten wir nicht auf das aufgewendete Zeitintervall, sondern wir beobachten Gleichung (1), d. h. die Gleichung der Arbeitskraft mit dem gleichen Wert der Konstante h wie bei der tatsächlichen Bewegung.
Diese notwendige Extremumsbedingung führt allgemein gesprochen zum Minimum des Integrals (2), daher der Name des Prinzips der kleinsten Wirkung. Die Minimalbedingung scheint die natürlichste zu sein, da der Wert von T im Wesentlichen positiv ist und daher das Integral (2) notwendigerweise ein Minimum haben muss. Die Existenz eines Minimums kann nur dann streng bewiesen werden, wenn das Zeitintervall hinreichend klein ist. Der Beweis dieses Satzes findet sich in Darboux' bekanntem Kurs über die Theorie der Oberflächen. Wir werden sie hier jedoch nicht darstellen und uns auf die Ableitung der Bedingung beschränken
432. Beweis des Prinzips der kleinsten Wirkung.
Bei der eigentlichen Berechnung stoßen wir auf eine Schwierigkeit, die im Beweis des Satzes von Hamilton nicht vorhanden ist. Die Variable t bleibt nicht mehr unabhängig von Variationen; also die Variationen von q i und q. hängen mit der Variation von t durch eine komplexe Beziehung zusammen, die aus Gleichung (1) folgt. Der einfachste Weg, diese Schwierigkeit zu umgehen, besteht darin, die unabhängige Variable in eine zu ändern, deren Werte zwischen konstanten zeitunabhängigen Grenzen liegen. Sei k eine neue unabhängige Variable, deren Grenzen als unabhängig von t angenommen werden. Beim Bewegen des Systems sind die Parameter und t Funktionen dieser Variablen
Die gestrichenen Buchstaben q bezeichnen die zeitlichen Ableitungen der q-Parameter.
Da die Verbindungen als zeitunabhängig angenommen werden, sind die kartesischen Koordinaten x, y, z Funktionen von q, die keine Zeit enthalten. Daher sind ihre Ableitungen lineare homogene Funktionen von q und 7 eine homogene quadratische Form von q, deren Koeffizienten Funktionen von q sind. Wir haben
![]()
Um die zeitlichen Ableitungen von q zu unterscheiden, bezeichnen wir mit Klammern (q) die Ableitungen von q, in Bezug auf und in Übereinstimmung damit gesetzt
![]()
dann haben wir
![]()
und das Integral (2), ausgedrückt durch die neue unabhängige Variable A, nimmt die Form an;

Die Ableitung kann mit dem Living-Force-Theorem eliminiert werden. In der Tat wird das Integral der lebendigen Kraft sein
![]()
![]()
Indem wir diesen Ausdruck in die Formel für einsetzen, bringen wir das Integral (2) in die Form

Das die Aktion definierende Integral nahm somit die endgültige Form (3) an. Der Integrand ist die Quadratwurzel der quadratischen Form der Größen
Zeigen wir, dass die Differentialgleichungen der Extremale des Integrals (3) genau die Lagrange-Gleichungen sind. Die Extremalgleichungen, basierend auf den allgemeinen Formeln der Variationsrechnung, lauten:

Wir multiplizieren die Gleichungen mit 2 und führen partielle Differentiationen durch, wobei wir berücksichtigen, dass nicht enthält dann erhalten wir, wenn wir den Index nicht schreiben,
Dies sind die Extremalgleichungen, ausgedrückt durch die unabhängige Variable.Die Aufgabe besteht nun darin, auf die unabhängige Variable zurückzukommen
Da Г eine homogene Funktion zweiten Grades und eine homogene Funktion ersten Grades ist, haben wir
Andererseits kann man auf die Faktoren der Ableitungen in den Extremalgleichungen den Living-Force-Satz anwenden, der, wie wir oben gesehen haben, zur Substitution führt
![]()
Als Ergebnis aller Substitutionen werden die Extremalgleichungen auf die Form reduziert
![]()
![]()
Damit sind wir bei den Lagrange-Gleichungen angelangt.
433. Der Fall, wenn es keine treibenden Kräfte gibt.
Für den Fall, dass es keine treibenden Kräfte gibt, gibt es eine Gleichung für die Arbeitskraft, und wir haben sie

Die Bedingung, dass das Integral ein Minimum ist, ist in diesem Fall, dass der entsprechende Wert von -10 der kleinste sein muss. Wenn also keine treibenden Kräfte vorhanden sind, dann ist unter allen Bewegungen, in denen die lebendige Kraft denselben gegebenen Wert behält, die eigentliche Bewegung diejenige, die das System in kürzester Zeit von seiner Anfangsposition zu seiner Endposition bringt.
Wenn das System auf einen einzigen Punkt reduziert wird, der sich entlang einer festen Oberfläche bewegt, dann ist die tatsächliche Bewegung unter allen Bewegungen entlang der Oberfläche, die mit derselben Geschwindigkeit ausgeführt werden, eine solche Bewegung, bei der der Punkt von seiner Anfangsposition zur Endposition übergeht zum kürzesten
Zeitintervall. Mit anderen Worten, ein Punkt beschreibt auf der Oberfläche die kürzeste Linie zwischen seinen beiden Positionen, also eine geodätische Linie.
434. Bemerkung.
Das Prinzip der kleinsten Wirkung geht davon aus, dass das System mehrere Freiheitsgrade hat, denn wenn es nur einen Freiheitsgrad gäbe, dann würde eine Gleichung ausreichen, um die Bewegung zu bestimmen. Da die Bewegung in diesem Fall vollständig durch die Gleichung der lebendigen Kraft bestimmt werden kann, wird die tatsächliche Bewegung die einzige sein, die dieser Gleichung genügt, und daher mit keiner anderen Bewegung verglichen werden kann.

In haben wir kurz eines der bemerkenswertesten physikalischen Prinzipien - das Prinzip der kleinsten Wirkung - betrachtet und bei einem Beispiel angehalten, das ihm zu widersprechen schien. In diesem Artikel werden wir uns dieses Prinzip genauer ansehen und sehen, was in diesem Beispiel passiert.
Dieses Mal brauchen wir etwas mehr Mathematik. Ich werde jedoch erneut versuchen, den Hauptteil des Artikels auf elementarer Ebene darzustellen. Etwas strengere und komplexere Punkte werde ich farblich hervorheben, sie können unbeschadet des Hauptverständnisses des Artikels übersprungen werden.
Randbedingungen
Beginnen wir mit dem einfachsten Objekt – einer sich frei im Raum bewegenden Kugel, auf die keine Kräfte einwirken. Eine solche Kugel bewegt sich bekanntermaßen gleichmäßig und geradlinig. Nehmen wir der Einfachheit halber an, dass er sich entlang der Achse bewegt:
Um seine Bewegung genau zu beschreiben, werden in der Regel Anfangsbedingungen angegeben. Beispielsweise wird angegeben, dass sich der Ball zum Anfangszeitpunkt an dem Punkt mit der Koordinate befand und eine Geschwindigkeit hatte. Indem wir die Anfangsbedingungen in dieser Form festlegen, bestimmen wir eindeutig die weitere Bewegung des Balls - er bewegt sich mit konstanter Geschwindigkeit und seine Position zum Zeitpunkt der Zeit ist gleich der Anfangsposition plus der Geschwindigkeit multipliziert mit der verstrichenen Zeit : . Diese Art der Einstellung der Anfangsbedingungen ist sehr natürlich und intuitiv vertraut. Wir haben alle notwendigen Informationen über die Bewegung des Balls im Anfangsmoment gegeben, und dann wird seine Bewegung durch die Newtonschen Gesetze bestimmt.
Dies ist jedoch nicht die einzige Möglichkeit, die Bewegung des Balls zu spezifizieren. Eine andere Möglichkeit besteht darin, die Position des Balls zu zwei verschiedenen Zeiten und anzugeben. Jene. das einstellen:
1) zu dem Zeitpunkt, an dem sich der Ball an einem Punkt befand (mit Koordinate );
2) zu dem Zeitpunkt, an dem sich der Ball an einem Punkt befand (mit Koordinate ).
Der Ausdruck „war am Punkt“ bedeutet nicht, dass der Ball am Punkt ruhte. Im Moment könnte es durch die Spitze fliegen. Das bedeutet, dass seine Position zum Zeitpunkt mit dem Punkt zusammenfiel. Dasselbe gilt für den Punkt.
Diese beiden Bedingungen bestimmen auch eindeutig die Bewegung des Balls. Seine Bewegung ist leicht zu berechnen. Um beide Bedingungen zu erfüllen, muss die Geschwindigkeit des Balls offensichtlich sein. Die Position des Balls zum Zeitpunkt der Zeit ist wieder gleich der Ausgangsposition plus der Geschwindigkeit multipliziert mit der verstrichenen Zeit:
Beachten Sie, dass wir unter den Bedingungen des Problems die Anfangsgeschwindigkeit nicht einstellen mussten. Sie wurde eindeutig aus den Bedingungen 1) und 2) bestimmt.
Das Festlegen von Bedingungen auf die zweite Art sieht ungewöhnlich aus. Vielleicht ist es nicht klar, warum es notwendig sein kann, sie überhaupt in dieser Form zu setzen. Allerdings werden beim Prinzip der kleinsten Wirkung die Bedingungen in Form 1) und 2) verwendet und nicht in Form der Angabe von Anfangsposition und Anfangsgeschwindigkeit.
Flugbahn mit der geringsten Aktion
Lassen Sie uns nun ein wenig von der realen freien Bewegung der Kugel abschweifen und das folgende rein mathematische Problem betrachten. Nehmen wir an, wir haben einen Ball, den wir manuell beliebig bewegen können. In diesem Fall müssen wir die Bedingungen 1) und 2) erfüllen. Jene. in der Zeit zwischen und müssen wir es von Punkt zu Punkt bewegen. Dies kann auf ganz unterschiedliche Weise erfolgen. Jede solche Weise nennen wir die Flugbahn des Balls und sie kann als Funktion der Position des Balls von der Zeit beschrieben werden. Lassen Sie uns mehrere solcher Trajektorien in das Diagramm der Position des Balls über der Zeit einzeichnen:
Zum Beispiel können wir den Ball mit der gleichen Geschwindigkeit wie (grüne Flugbahn) bewegen. Oder wir können es die halbe Zeit am Punkt halten und es dann mit doppelter Geschwindigkeit zum Punkt bewegen (blauer Pfad). Sie können es zuerst in die entgegengesetzte Richtung bewegen und dann auf (brauner Pfad). Sie können es hin und her bewegen (roter Pfad). Im Allgemeinen können Sie es beliebig verschieben, solange die Bedingungen 1) und 2) erfüllt sind.
Für jede solche Trajektorie können wir eine Zahl abgleichen. In unserem Beispiel, d.h. wenn keine Kräfte auf den Ball einwirken, ist diese Zahl gleich der gesamten akkumulierten kinetischen Energie für die gesamte Zeit seiner Bewegung im Zeitintervall zwischen und und wird als Aktion bezeichnet.
In diesem Fall vermittelt das Wort "akkumulierte" kinetische Energie die Bedeutung nicht genau. In Wirklichkeit sammelt sich die kinetische Energie nirgendwo an, die Akkumulation wird nur verwendet, um die Aktion für die Flugbahn zu berechnen. In der Mathematik gibt es ein sehr gutes Konzept für eine solche Akkumulation - das Integral:Nehmen wir als Beispiel einen 1 kg schweren Ball, stellen einige Randbedingungen ein und berechnen die Aktion für zwei verschiedene Trajektorien. Lassen Sie den Punkt in einem Abstand von 1 Meter vom Punkt sein, und die Zeit ist 1 Sekunde von der Zeit entfernt. Jene. wir müssen die Kugel, die sich zum Anfangszeitpunkt auf dem Punkt befand, in einer Sekunde in einer Entfernung von 1 m entlang der Achse bewegen.Die Aktion wird normalerweise mit dem Buchstaben bezeichnet. Das Symbol bedeutet kinetische Energie. Dieses Integral bedeutet, dass die Aktion gleich der akkumulierten kinetischen Energie des Balls über das Zeitintervall von bis ist.
Im ersten Beispiel (grüne Flugbahn) haben wir den Ball gleichmäßig bewegt, d.h. mit der gleichen Geschwindigkeit, die natürlich gleich sein sollte: m / s. Die kinetische Energie des Balls zu jedem Zeitpunkt ist: = 1/2 J. In einer Sekunde wird 1/2 J kinetische Energie angesammelt. Jene. Aktion für eine solche Trajektorie ist: J s.
Lassen Sie uns jetzt den Ball nicht sofort von Punkt zu Punkt übertragen, sondern halten Sie ihn eine halbe Sekunde lang auf Punkt und übertragen Sie ihn dann für die verbleibende Zeit gleichmäßig auf Punkt . In der ersten halben Sekunde ruht der Ball und seine kinetische Energie ist Null. Daher ist der Wirkungsbeitrag dieses Teils der Trajektorie ebenfalls gleich Null. In der zweiten halben Sekunde bewegen wir den Ball mit doppelter Geschwindigkeit: m/s. Die kinetische Energie ist in diesem Fall gleich = 2 J. Der Beitrag dieses Zeitintervalls zur Aktion ist gleich 2 J multipliziert mit einer halben Sekunde, d.h. 1 Js. Daher ist die Gesamtaktion für eine solche Trajektorie gleich J s.
Ebenso entspricht jede andere Trajektorie mit den von uns gegebenen Randbedingungen 1) und 2) einer Zahl, die gleich der Wirkung für diese Trajektorie ist. Unter all diesen Trajektorien gibt es eine Trajektorie mit der geringsten Aktion. Es kann bewiesen werden, dass diese Trajektorie eine grüne Trajektorie ist, d.h. gleichmäßige Bewegung des Balls. Bei jeder anderen Flugbahn, egal wie knifflig sie ist, wird die Aktion größer als 1/2 sein.
In der Mathematik wird ein solcher Vergleich für jede Funktion einer bestimmten Zahl Funktional genannt. Nicht selten gibt es in Physik und Mathematik ähnliche Probleme wie bei uns, d.h. eine solche Funktion zu finden, für die der Wert einer bestimmten Funktion minimal ist. Eines der Probleme, das für die Entwicklung der Mathematik große historische Bedeutung hatte, ist beispielsweise das Problem der Bachistochrone. Jene. Die Kurve finden, entlang der die Kugel am schnellsten rollt. Auch hier kann jede Kurve durch die Funktion h(x) dargestellt werden, und jeder Funktion kann eine Zahl zugeordnet werden, in diesem Fall die Zeit, in der die Kugel rollt. Auch hier wird das Problem darauf reduziert, eine Funktion zu finden, für die der Wert der Funktion minimal ist. Der Zweig der Mathematik, der sich mit solchen Problemen befasst, heißt Variationsrechnung.
Prinzip der kleinsten Wirkung
In den oben diskutierten Beispielen haben wir zwei spezielle Trajektorien, die auf zwei verschiedene Arten erhalten werden.Die erste Flugbahn ergibt sich aus den Gesetzen der Physik und entspricht der realen Flugbahn einer freien Kugel, auf die keine Kräfte einwirken und für die die Randbedingungen in der Form 1) und 2) angegeben sind.
Die zweite Trajektorie ergibt sich aus dem mathematischen Problem, bei gegebenen Randbedingungen 1) und 2) eine Trajektorie zu finden, für die die Wirkung minimal ist.
Das Prinzip der kleinsten Wirkung besagt, dass diese beiden Pfade zusammenfallen müssen. Mit anderen Worten, wenn bekannt ist, dass sich der Ball so bewegt hat, dass die Randbedingungen 1) und 2) erfüllt sind, dann hat er sich notwendigerweise entlang einer Bahn bewegt, für die die Wirkung im Vergleich zu jeder anderen Bahn mit den gleichen Randbedingungen minimal ist .
Dies könnte als reiner Zufall gewertet werden. Sie kennen nie die Probleme, bei denen gleichmäßige Trajektorien und gerade Linien auftreten. Das Prinzip der kleinsten Wirkung erweist sich jedoch als ein sehr allgemeines Prinzip, das auch in anderen Situationen gilt, beispielsweise für die Bewegung einer Kugel in einem homogenen Gravitationsfeld. Dazu müssen Sie nur die kinetische Energie durch die Differenz zwischen kinetischer und potentieller Energie ersetzen. Diese Differenz wird als Lagrange-Funktion oder Lagrange-Funktion bezeichnet, und die Aktion wird nun gleich der gesamten akkumulierten Lagrange-Funktion. Tatsächlich enthält die Lagrange-Funktion alle notwendigen Informationen über die dynamischen Eigenschaften des Systems.
Wenn wir eine Kugel in einem gleichmäßigen Gravitationsfeld so abschießen, dass sie an einem Punkt vorbeifliegt und an einem Punkt ankommt, dann fliegt sie nach den Newtonschen Gesetzen entlang einer Parabel. Es ist diese Parabel, die mit den Trajektorien zusammenfällt, für die die Wirkung minimal sein wird.
Für einen Körper, der sich in einem Potentialfeld bewegt, beispielsweise im Gravitationsfeld der Erde, lautet die Lagrange-Funktion also: . Die kinetische Energie hängt von der Geschwindigkeit des Körpers ab und die potentielle Energie von seiner Position, d.h. Koordinaten . In der analytischen Mechanik wird der gesamte Koordinatensatz, der die Position des Systems bestimmt, normalerweise mit einem Buchstaben bezeichnet. Für eine frei im Gravitationsfeld bewegte Kugel bedeuten die Koordinaten , und .Um die Änderungsgeschwindigkeit einer Größe anzuzeigen, ist es in der Physik sehr üblich, einfach einen Punkt über diese Größe zu setzen. Sie bezeichnet beispielsweise die Änderungsrate der Koordinate , also die Geschwindigkeit des Körpers in Richtung . Unter Verwendung dieser Konventionen wird die Geschwindigkeit unseres Balls in der analytischen Mechanik als bezeichnet. Jene. bedeutet Geschwindigkeitskomponenten.
Da die Lagrange-Funktion von der Geschwindigkeit und den Koordinaten abhängt und auch explizit von der Zeit abhängen kann (explizit von der Zeit abhängt, was bedeutet, dass der Wert zu verschiedenen Zeiten unterschiedlich ist, für dieselben Geschwindigkeiten und Positionen des Balls), ist die Aktion in allgemein wird geschrieben als
Nicht immer minimal
Am Ende des vorherigen Teils haben wir uns jedoch ein Beispiel angesehen, bei dem das Prinzip der geringsten Aktion eindeutig nicht funktioniert. Dazu haben wir wieder eine freie Kugel genommen, auf die keine Kräfte wirken, und eine federnde Wand daneben gestellt.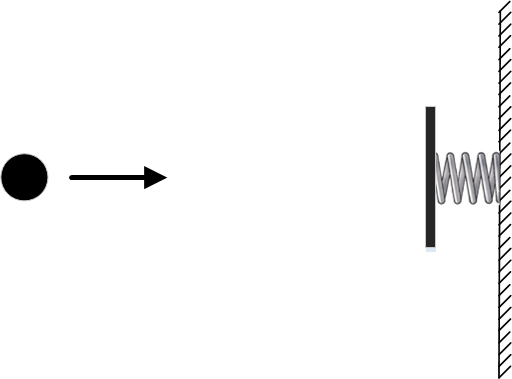
Wir setzen die Randbedingungen so, dass die Punkte und zusammenfallen. Jene. und zu dem Zeitpunkt und zu dem Zeitpunkt muss sich der Ball an der gleichen Stelle befinden. Eine der möglichen Flugbahnen wird der stillstehende Ball sein. Jene. das gesamte Zeitintervall zwischen und wird am Punkt stehen. Die kinetische und potentielle Energie sind in diesem Fall gleich Null, also ist die Aktion für eine solche Flugbahn auch gleich Null.
Genau genommen kann die potentielle Energie nicht gleich Null, sondern beliebig groß angenommen werden, da die Differenz der potentiellen Energie an verschiedenen Punkten im Raum wichtig ist. Eine Änderung des Wertes der potentiellen Energie wirkt sich jedoch nicht auf die Suche nach einer Flugbahn mit minimaler Wirkung aus. Es ist nur so, dass sich der Wert der Aktion für alle Trajektorien um die gleiche Zahl ändert und die Trajektorie mit der minimalen Aktion die Trajektorie mit der minimalen Aktion bleibt. Der Einfachheit halber wählen wir für unseren Ball die potentielle Energie gleich Null.Eine andere mögliche physikalische Flugbahn mit den gleichen Randbedingungen wird die Flugbahn sein, in der der Ball zuerst nach rechts fliegt und den Punkt zum Zeitpunkt passiert. Dann kollidiert er mit der Feder, drückt sie zusammen, die Feder richtet sich auf, drückt die Kugel zurück und sie fliegt wieder an der Spitze vorbei . Sie können die Geschwindigkeit des Balls so wählen, dass er, nachdem er von der Wand abgeprallt ist, genau in dem Moment über den Punkt geflogen ist . Die Wirkung auf eine solche Flugbahn ist im Wesentlichen gleich der akkumulierten kinetischen Energie während des Fluges zwischen dem Punkt und der Wand und zurück. Es wird einige Zeit geben, in der die Kugel die Feder zusammendrückt und ihre potentielle Energie ansteigt, und in dieser Zeit wird die potentielle Energie einen negativen Beitrag zur Aktion leisten. Aber ein solcher Zeitraum wird nicht sehr groß sein und wird die Wirkung nicht stark verringern.

Die Abbildung zeigt beide physikalisch möglichen Flugbahnen des Balls. Die grüne Flugbahn entspricht einem ruhenden Ball, während die blaue einem Ball entspricht, der von einer federnden Wand abprallt.
Allerdings hat nur eine davon einen minimalen Effekt, nämlich die erste! Die zweite Flugbahn hat mehr Aktion. Es stellt sich heraus, dass es bei diesem Problem zwei physikalisch mögliche Trajektorien gibt und nur eine mit minimaler Aktion. Jene. In diesem Fall funktioniert das Prinzip der kleinsten Wirkung nicht.
Stationäre Punkte
Um zu verstehen, was hier vor sich geht, schweifen wir vorerst vom Prinzip der kleinsten Wirkung ab und behandeln gewöhnliche Funktionen. Nehmen wir eine Funktion und zeichnen ihren Graphen:
Auf der Grafik habe ich vier besondere Punkte grün markiert. Was ist diesen Punkten gemeinsam? Stellen Sie sich vor, dass der Graph einer Funktion eine echte Rutsche ist, auf der eine Kugel rollen kann. Das Besondere an den vier gekennzeichneten Punkten ist, dass wenn Sie den Ball genau an diesem Punkt platzieren, er nirgendwo wegrollen wird. An allen anderen Punkten, z. B. Punkt E, kann er nicht stehen bleiben und beginnt nach unten zu rutschen. Solche Punkte heißen stationär. Das Finden solcher Punkte ist eine nützliche Aufgabe, da jedes Maximum oder Minimum einer Funktion, wenn es keine scharfen Brüche hat, notwendigerweise ein stationärer Punkt sein muss.
Klassifizieren wir diese Punkte genauer, dann ist Punkt A das absolute Minimum der Funktion, d.h. sein Wert ist kleiner als jeder andere Funktionswert. Punkt B ist weder Maximum noch Minimum und wird Sattelpunkt genannt. Punkt C heißt lokales Maximum, d.h. der Wert darin ist größer als in den Nachbarpunkten der Funktion. Und Punkt D ist ein lokales Minimum, d.h. der Wert darin ist kleiner als in den benachbarten Punkten der Funktion.
Der Zweig der Mathematik namens Analysis beschäftigt sich mit der Suche nach solchen Punkten. In anderer Weise wird sie manchmal auch als Infinitesimalanalyse bezeichnet, da sie mit infinitesimalen Mengen arbeiten kann. Aus Sicht der mathematischen Analyse haben stationäre Punkte eine besondere Eigenschaft, aufgrund derer sie gefunden werden. Um zu verstehen, was diese Eigenschaft ist, müssen wir verstehen, wie die Funktion in sehr kleinen Abständen von diesen Punkten aussieht. Dazu nehmen wir ein Mikroskop und schauen an unseren Punkten hinein. Die Abbildung zeigt, wie die Funktion in der Nähe verschiedener Punkte bei verschiedenen Vergrößerungen aussieht.

Es ist ersichtlich, dass bei sehr hoher Vergrößerung (d. h. bei sehr kleinen Abweichungen von x) die stationären Punkte genau gleich aussehen und sich stark von den nicht stationären Punkten unterscheiden. Es ist leicht zu verstehen, was dieser Unterschied ist - der Graph einer Funktion an einem stationären Punkt wird zu einer streng horizontalen Linie mit einer Zunahme und an einem nicht stationären Punkt zu einer geneigten Linie. Deshalb rollt die ortsfest installierte Kugel nicht.
Die Horizontalität einer Funktion an einem stationären Punkt kann auf andere Weise ausgedrückt werden: Eine Funktion an einem stationären Punkt ändert sich praktisch nicht bei einer sehr kleinen Änderung ihres Arguments, selbst im Vergleich zur Änderung des Arguments selbst. Die Funktion an einem instationären Punkt mit einer kleinen Änderung ändert sich proportional zur Änderung. Und je größer die Steigung der Funktion ist, desto mehr ändert sich die Funktion, wenn . Tatsächlich wird die Funktion mit zunehmender Funktion immer mehr wie eine Tangente an den Graphen an dem fraglichen Punkt.
In streng mathematischer Sprache bedeutet der Ausdruck "Funktion ändert sich an einem Punkt mit einer sehr kleinen Änderung praktisch nicht", dass das Verhältnis der Änderung der Funktion und der Änderung ihres Arguments gegen 0 tendiert, da es gegen 0 tendiert:$$display$$\lim_(∆x \to 0) \frac (∆y(x_0))(∆x) = \lim_(x \to 0) \frac (y(x_0+∆x)-y(x_0) )(∆x) = 0$$anzeige$$
Für einen nicht stationären Punkt tendiert dieses Verhältnis zu einer Zahl ungleich Null, die gleich dem Tangens der Steigung der Funktion an diesem Punkt ist. Dieselbe Zahl heißt Ableitung der Funktion an einem gegebenen Punkt. Die Ableitung einer Funktion zeigt, wie schnell sich eine Funktion bei einer kleinen Änderung ihres Arguments um einen bestimmten Punkt ändert. Stationäre Punkte sind also Punkte, an denen die Ableitung einer Funktion 0 ist.
Stationäre Bahnen
In Analogie zu stationären Punkten können wir das Konzept stationärer Trajektorien einführen. Denken Sie daran, dass wir für jede Trajektorie einen bestimmten Wert der Aktion haben, d.h. irgendeine Zahl. Dann kann es eine solche Trajektorie geben, dass sich für Trajektorien in ihrer Nähe mit denselben Randbedingungen die entsprechenden Werte der Aktion praktisch nicht von der Aktion für die stationärste Trajektorie unterscheiden. Eine solche Bahn heißt stationär. Mit anderen Worten, jede Trajektorie nahe der stationären Bahn hat einen Aktionswert, der sich nur geringfügig von der Aktion für diese stationäre Trajektorie unterscheidet.Wiederum hat „etwas anders“ in der mathematischen Sprache die folgende genaue Bedeutung. Nehmen wir an, wir haben ein Funktional für Funktionen mit den geforderten Randbedingungen 1) und 2), also und . Nehmen wir an, die Trajektorie sei stationär.Wir können jede andere Funktion so nehmen, dass sie an den Enden Nullwerte annimmt, d.h. = = 0. Nehmen Sie auch eine Variable , die wir immer kleiner machen werden. Aus diesen beiden Funktionen und einer Variablen können wir eine dritte Funktion zusammensetzen, die auch die Randbedingungen und erfüllt. Mit abnehmendem Wert nähert sich die der Funktion entsprechende Trajektorie zunehmend der Trajektorie .
In diesem Fall unterscheidet sich für stationäre Trajektorien für klein der Wert des Funktionals für die Trajektorien sehr wenig vom Wert des Funktionals für gerade im Vergleich zu . Jene.
$$display$$\lim_(ε \to 0) \frac (S(x"(t))-S(x(t)))ε=\lim_(ε \to 0) \frac (S(x( t)+εg(t))-S(x(t)))ε = 0$$anzeige$$
Außerdem sollte dies für jede Trajektorie gelten, die die Randbedingungen = = 0 erfüllt.Die Änderung des Funktionals bei einer kleinen Änderung der Funktion (genauer gesagt, der lineare Teil der Änderung des Funktionals, proportional zur Änderung der Funktion) wird als Variation des Funktionals bezeichnet und mit bezeichnet. Vom Begriff „Variation“ kommt der Name „Variationsrechnung“.
Für stationäre Trajektorien ist die Variation des Funktionals .
Die Methode zum Auffinden stationärer Funktionen (nicht nur für das Prinzip der kleinsten Wirkung, sondern auch für viele andere Probleme) wurde von zwei Mathematikern - Euler und Lagrange - gefunden. Es stellt sich heraus, dass eine stationäre Funktion, deren Funktion durch ein Integral wie das Aktionsintegral ausgedrückt wird, eine bestimmte Gleichung erfüllen muss, die jetzt als Euler-Lagrange-Gleichung bezeichnet wird.
Prinzip der stationären Aktion
Die Situation mit der minimalen Aktion für Trajektorien ist ähnlich der Situation mit dem Minimum für Funktionen. Damit eine Trajektorie die geringste Wirkung hat, muss es eine stationäre Trajektorie sein. Jedoch sind nicht alle stationären Trajektorien Trajektorien mit minimaler Aktion. Beispielsweise kann eine stationäre Trajektorie lokal eine minimale Wirkung haben. Jene. es wird weniger Wirkung haben als jede andere benachbarte Flugbahn. Irgendwo weit entfernt kann es jedoch andere Flugbahnen geben, für die die Wirkung noch geringer sein wird.Es stellt sich heraus, dass sich reale Körper nicht unbedingt mit der geringsten Aktion auf Bahnen bewegen müssen. Sie können sich entlang eines breiteren Satzes spezieller Trajektorien bewegen, nämlich stationärer Trajektorien. Jene. die reale Flugbahn des Körpers wird immer stationär sein. Daher wird das Prinzip der kleinsten Wirkung richtiger als Prinzip der stationären Wirkung bezeichnet. Nach etablierter Tradition wird es jedoch oft als Prinzip der geringsten Wirkung bezeichnet, was nicht nur die Minimalität, sondern auch die Stationarität von Trajektorien impliziert.
Jetzt können wir das Prinzip der stationären Wirkung in mathematischer Sprache schreiben, wie es normalerweise in Lehrbüchern geschrieben wird:.Wenn wir auf das Beispiel mit einem Ball und einer elastischen Wand zurückkommen, dann wird die Erklärung dieser Situation jetzt sehr einfach. Unter gegebenen Randbedingungen, dass der Ball sowohl zum Zeitpunkt als auch zum Zeitpunkt im Punkt sein muss, gibt es zwei stationäre Flugbahnen. Und der Ball kann sich tatsächlich auf jeder dieser Bahnen bewegen. Um explizit eine der Trajektorien auszuwählen, können Sie der Bewegung des Balls eine zusätzliche Bedingung auferlegen. Sagen Sie zum Beispiel, dass der Ball von der Wand abprallen soll. Dann wird die Trajektorie eindeutig bestimmt.Hier sind verallgemeinerte Koordinaten, d.h. eine Reihe von Variablen, die die Position des Systems eindeutig angeben.
- die Änderungsrate von verallgemeinerten Koordinaten.
- Lagrange-Funktion, die von den verallgemeinerten Koordinaten, ihren Geschwindigkeiten und möglicherweise der Zeit abhängt.
- eine Aktion, die von der spezifischen Trajektorie des Systems abhängt (d. h. von).Die realen Trajektorien des Systems sind stationär, d.h. für sie eine Variation der Aktion.
Aus dem Prinzip der kleinsten (genauer stationären) Wirkung ergeben sich einige bemerkenswerte Konsequenzen, die wir im nächsten Abschnitt diskutieren werden.
Als ich zum ersten Mal von diesem Prinzip erfuhr, hatte ich ein Gefühl von Mystik. Es scheint, dass die Natur auf mysteriöse Weise alle möglichen Wege der Systembewegung sortiert und die beste davon auswählt.
Heute möchte ich ein wenig über eines der bemerkenswertesten physikalischen Prinzipien sprechen – das Prinzip der geringsten Wirkung.
Hintergrund
Seit Galilei ist bekannt, dass sich Körper, auf die keine Kräfte wirken, geradlinig, also auf dem kürzesten Weg bewegen. Lichtstrahlen bewegen sich auch in geraden Linien.Auch reflektiertes Licht bewegt sich so, dass es auf dem kürzesten Weg von einem Punkt zum anderen gelangt. Im Bild ist der kürzeste Weg der grüne Weg, bei dem der Einfallswinkel gleich dem Reflexionswinkel ist. Jeder andere Pfad, wie der rote, wird länger sein.

Dies lässt sich leicht nachweisen, indem man einfach die Strahlengänge auf die gegenüberliegende Seite des Spiegels spiegelt. Sie sind im Bild gestrichelt dargestellt.

Es ist ersichtlich, dass der grüne Pfad ACB in eine gerade Linie ACB' übergeht. Und der rote Pfad verwandelt sich in eine unterbrochene Linie ADB ', die natürlich länger ist als die grüne.
Im Jahr 1662 schlug Pierre Fermat vor, dass die Lichtgeschwindigkeit in einer dichten Substanz wie Glas geringer ist als in Luft. Zuvor war die allgemein akzeptierte Version Descartes, wonach die Lichtgeschwindigkeit in Materie größer sein muss als in Luft, um das richtige Brechungsgesetz zu erhalten. Für Fermat erschien die Annahme, dass sich Licht in einem dichteren Medium schneller bewegen könnte als in einem dünneren, unnatürlich. Daher nahm er an, dass alles genau umgekehrt sei und bewies eine erstaunliche Sache - unter dieser Annahme wird Licht gebrochen, um sein Ziel in kürzester Zeit zu erreichen.

Auch in der Abbildung zeigt die grüne Farbe den Weg, den der Lichtstrahl tatsächlich zurücklegt. Der rot markierte Weg ist der kürzeste, aber nicht der schnellste, weil das Licht im Glas einen längeren Weg zurücklegen muss und seine Geschwindigkeit darin langsamer ist. Am schnellsten ist der tatsächliche Weg des Lichtstrahls.
All diese Tatsachen legten nahe, dass die Natur auf irgendeine rationale Weise handelt, Licht und Körper sich auf die optimalste Weise bewegen und so wenig Aufwand wie möglich aufwenden. Aber was diese Bemühungen waren und wie man sie berechnete, blieb ein Rätsel.
1744 führte Maupertuis den Begriff der „Wirkung“ ein und formulierte das Prinzip, wonach sich die wahre Flugbahn eines Teilchens von jeder anderen dadurch unterscheidet, dass die Wirkung dafür minimal ist. Maupertuis selbst konnte jedoch nicht klar definieren, was dieser Aktion gleichkommt. Eine rigorose mathematische Formulierung des Prinzips der kleinsten Wirkung wurde von anderen Mathematikern – Euler, Lagrange – entwickelt und schließlich von William Hamilton gegeben:

In mathematischer Sprache ist das Prinzip der kleinsten Wirkung recht kurz formuliert, aber nicht alle Leser verstehen die Bedeutung der verwendeten Notation. Ich möchte versuchen, dieses Prinzip klarer und einfacher zu erklären.
lockerer Körper
Stellen Sie sich also vor, Sie sitzen zu einem bestimmten Zeitpunkt in einem Auto und erhalten zu einem bestimmten Zeitpunkt eine einfache Aufgabe: Bis zu dem Zeitpunkt müssen Sie ein Auto zum Punkt fahren.
Kraftstoff für das Auto ist teuer und natürlich möchten Sie ihn so wenig wie möglich ausgeben. Ihr Auto wird mit den neuesten Supertechnologien hergestellt und kann so schnell beschleunigen oder verzögern, wie Sie möchten. Allerdings ist er so ausgelegt, dass er umso mehr Sprit verbraucht, je schneller er fährt. Außerdem ist der Kraftstoffverbrauch proportional zum Quadrat der Geschwindigkeit. Wenn Sie doppelt so schnell fahren, verbrauchen Sie in der gleichen Zeit viermal mehr Kraftstoff. Neben der Geschwindigkeit wird der Kraftstoffverbrauch natürlich auch von der Masse des Autos beeinflusst. Je schwerer unser Auto, desto mehr Kraftstoff verbraucht es. Der Kraftstoffverbrauch unseres Autos beträgt zu jedem Zeitpunkt , d.h. ist genau gleich der kinetischen Energie des Autos.
Wie also muss man fahren, um pünktlich ans Ziel zu kommen und möglichst wenig Sprit zu verbrauchen? Es ist klar, dass Sie in einer geraden Linie gehen müssen. Mit zunehmender Fahrstrecke wird genau nicht weniger Kraftstoff verbraucht. Und dann können Sie verschiedene Taktiken wählen. Sie können zum Beispiel schnell im Voraus an dem Punkt ankommen und sich einfach hinsetzen und warten, bis die Zeit gekommen ist. Die Fahrgeschwindigkeit und damit der Kraftstoffverbrauch zu jedem Zeitpunkt wird hoch sein, aber die Fahrzeit wird auch reduziert. Vielleicht ist der Gesamtkraftstoffverbrauch in diesem Fall nicht so groß. Oder Sie können gleichmäßig fahren, mit der gleichen Geschwindigkeit, so dass Sie ohne Eile genau im Moment ankommen. Oder ein Teil des Weges geht schnell und ein Teil langsamer. Was ist der beste Weg?
Es stellt sich heraus, dass die optimale und wirtschaftlichste Art des Fahrens darin besteht, mit konstanter Geschwindigkeit zu fahren, um genau zur festgelegten Zeit am Punkt zu sein. Jede andere Option verbraucht mehr Kraftstoff. An einigen Beispielen können Sie sich selbst davon überzeugen. Der Grund dafür ist, dass der Kraftstoffverbrauch mit dem Quadrat der Geschwindigkeit zunimmt. Wenn die Geschwindigkeit zunimmt, steigt daher der Kraftstoffverbrauch schneller als die Fahrzeit abnimmt, und der Gesamtkraftstoffverbrauch nimmt ebenfalls zu.
Wir haben also herausgefunden, dass, wenn ein Auto zu einem bestimmten Zeitpunkt Kraftstoff im Verhältnis zu seiner kinetischen Energie verbraucht, der wirtschaftlichste Weg, um genau zur festgelegten Zeit von Punkt zu Punkt zu gelangen, darin besteht, gleichmäßig und auf einer geraden Linie zu fahren, genau wie ein Körper bewegt sich ohne auf ihn einwirkende Kräfte. Jede andere Fahrweise führt zu einem höheren Gesamtkraftstoffverbrauch.
Im Bereich der Schwerkraft
Jetzt verbessern wir unser Auto ein wenig. Bringen wir Strahltriebwerke daran an, damit es frei in jede Richtung fliegen kann. Im Allgemeinen blieb das Design gleich, sodass der Kraftstoffverbrauch wieder streng proportional zur kinetischen Energie des Autos blieb. Wenn nun die Aufgabe gestellt wird, von einem Punkt zu einem Zeitpunkt abzufliegen und zu einem Zeitpunkt t anzukommen, dann wird der wirtschaftlichste Weg natürlich nach wie vor gleichmäßig und geradlinig fliegen, um genau zu dem Punkt anzukommen festgesetzte Zeit t. Dies entspricht wiederum der freien Bewegung des Körpers im dreidimensionalen Raum.
In das neueste Modell des Autos wurde jedoch ein ungewöhnliches Gerät eingebaut. Dieses Gerät ist in der Lage, Kraftstoff buchstäblich aus dem Nichts zu produzieren. Aber das Design ist so, dass je höher das Auto ist, desto mehr Kraftstoff produziert das Gerät zu einem bestimmten Zeitpunkt. Der Kraftstoffausstoß ist direkt proportional zur Höhe, auf der sich das Fahrzeug gerade befindet. Je schwerer das Auto ist, desto leistungsstärker ist das Gerät und desto mehr Kraftstoff wird produziert, und die Leistung ist direkt proportional zur Masse des Autos. Es stellte sich heraus, dass die Vorrichtung so beschaffen ist, dass die Kraftstoffabgabe genau gleich (wo ist die Beschleunigung im freien Fall) ist, d.h. potenzielle Energie des Autos.
Der Kraftstoffverbrauch zu jedem Zeitpunkt ist gleich der kinetischen Energie minus der potenziellen Energie des Autos (minus der potenziellen Energie, weil das installierte Fahrzeug Kraftstoff produziert und nicht verbraucht). Jetzt ist unsere Aufgabe die wirtschaftlichste Bewegung des Autos zwischen den Punkten und es wird schwieriger. Eine geradlinige gleichförmige Bewegung ist in diesem Fall nicht die effektivste. Es stellt sich heraus, dass es optimaler ist, ein wenig zu klettern, dort eine Weile zu verweilen, mehr Kraftstoff zu entwickeln und dann zum Punkt abzusteigen. Bei richtiger Flugbahn deckt der gesamte Treibstoffverbrauch durch Steigflug die zusätzlichen Treibstoffkosten für die Verlängerung der Flugbahn und die Erhöhung der Geschwindigkeit. Bei sorgfältiger Berechnung wäre es für ein Auto am wirtschaftlichsten, in einer Parabel zu fliegen, auf genau der gleichen Flugbahn und mit genau der gleichen Geschwindigkeit wie ein Stein im Schwerefeld der Erde.

Hier lohnt es sich, eine Erklärung abzugeben. Natürlich kann man einen Stein auf viele verschiedene Arten von einem Punkt aus so werfen, dass er den Punkt trifft. Aber Sie müssen es so werfen, dass es, nachdem es von einem Punkt nach dem anderen geflogen ist, genau zu dem Zeitpunkt auf einen Punkt trifft. Es ist diese Bewegung, die für unser Auto am wirtschaftlichsten ist.
Die Lagrange-Funktion und das Prinzip der kleinsten Wirkung
Nun können wir diese Analogie auf reale physische Körper übertragen. Ein Analogon der Intensität des Kraftstoffverbrauchs für Körper wird als Lagrange-Funktion oder Lagrange-Funktion (zu Ehren von Lagrange) bezeichnet und mit dem Buchstaben bezeichnet. Die Lagrange-Funktion zeigt, wie viel „Treibstoff“ der Körper zu einem bestimmten Zeitpunkt verbraucht. Für einen Körper, der sich in einem Potentialfeld bewegt, ist die Lagrange-Funktion gleich seiner kinetischen Energie minus seiner potentiellen Energie.Ein Analogon der Gesamtmenge an Kraftstoff, die für die gesamte Bewegungszeit verbraucht wird, d.h. der über die gesamte Bewegungszeit akkumulierte Wert der Lagrange-Funktion wird als "Aktion" bezeichnet.
Das Prinzip der kleinsten Wirkung besagt, dass sich der Körper so bewegt, dass die Wirkung (die von der Bewegungsbahn abhängt) minimal ist. In diesem Fall sollte man nicht vergessen, dass die Anfangs- und Endbedingungen gegeben sind, d.h. wo der Körper zu Zeit und zu Zeit ist.
Dabei muss sich der Körper nicht in einem einheitlichen Gravitationsfeld bewegen, das wir für unser Auto betrachtet haben. Sie können ganz unterschiedliche Situationen betrachten. Ein Körper kann an einem Gummiband schwingen, an einem Pendel schwingen oder um die Sonne fliegen, in all diesen Fällen bewegt er sich so, dass der "Gesamtverbrauch" minimiert wird, d.h. Handlung.
Wenn das System aus mehreren Körpern besteht, dann ist die Lagrange-Funktion eines solchen Systems gleich der gesamten kinetischen Energie aller Körper minus der gesamten potentiellen Energie aller Körper. Und wieder bewegen sich alle Körper gemeinsam, so dass die Wirkung des gesamten Systems während einer solchen Bewegung minimal ist.
Nicht so einfach
Tatsächlich habe ich ein wenig geschummelt, indem ich sagte, dass sich Körper immer so bewegen, dass die Aktion minimiert wird. Obwohl dies in sehr vielen Fällen zutrifft, kann man sich Situationen vorstellen, in denen die Aktion eindeutig nicht minimal ist.Nehmen wir zum Beispiel einen Ball und legen ihn in einen leeren Raum. In einiger Entfernung davon stellen wir eine elastische Wand auf. Nehmen wir an, wir möchten, dass der Ball nach einiger Zeit an der gleichen Stelle landet. Unter diesen gegebenen Bedingungen kann sich der Ball auf zwei verschiedene Arten bewegen. Erstens kann er einfach liegen bleiben. Zweitens können Sie es an die Wand schieben. Der Ball wird die Wand erreichen, von ihr abprallen und zurückkommen. Es ist klar, dass Sie es mit einer solchen Geschwindigkeit vorantreiben können, dass es genau zum richtigen Zeitpunkt zurückkehrt.

Beide Varianten der Bewegung des Balls sind möglich, aber die Wirkung im zweiten Fall wird größer sein, weil sich der Ball die ganze Zeit über mit einer kinetischen Energie ungleich Null bewegt.
Wie kann das Prinzip der kleinsten Wirkung gerettet werden, damit es in solchen Situationen gilt? Darüber sprechen wir in.
Sie gehorchen ihm, wobei dieses Prinzip eine der Schlüsselbestimmungen der modernen Physik ist. Die mit ihrer Hilfe erhaltenen Bewegungsgleichungen heißen Euler-Lagrange-Gleichungen.
Die erste Formulierung des Prinzips wurde 1999 von P. Maupertuis gegeben, der sofort auf seine universelle Natur hinwies und es für anwendbar auf Optik und Mechanik hielt. Aus diesem Prinzip leitete er die Gesetze der Reflexion und Brechung des Lichts ab.
Geschichte
Maupertuis kam zu diesem Prinzip aus dem Gefühl, dass die Perfektion des Universums eine gewisse Ökonomie in der Natur erfordert und jedem nutzlosen Energieaufwand entgegensteht. Die natürliche Bewegung muss so sein, dass eine gewisse Menge minimal wird. Es war nur notwendig, diesen Wert zu finden, was er weiterhin tat. Sie war das Produkt aus der Dauer (Zeit) der Bewegung innerhalb des Systems mal dem Betrag, den wir heute als kinetische Energie des Systems bezeichnen.
Euler (in „Reflexions sur quelques loix generales de la nature“, 1748) übernimmt das Prinzip der geringsten Aktion und nennt Aktion "Anstrengung". Sein Ausdruck in der Statik entspricht dem, was wir jetzt als potentielle Energie bezeichnen würden, so dass seine Aussage der kleinsten Wirkung in der Statik der Bedingung minimaler potentieller Energie für die Gleichgewichtskonfiguration entspricht.
In der klassischen Mechanik
Das Prinzip der kleinsten Wirkung dient als grundlegende und standardmäßige Grundlage für die Lagrange- und Hamilton-Formulierungen der Mechanik.
Betrachten wir zunächst die Konstruktion so Lagrangesche Mechanik. Am Beispiel eines physikalischen Systems mit einem Freiheitsgrad erinnern wir uns, dass eine Wirkung ein Funktional bezüglich (verallgemeinerter) Koordinaten (bei einem Freiheitsgrad - einer Koordinate) ist, das heißt, sie wird durch diese ausgedrückt dass jeder denkbaren Version der Funktion eine bestimmte Zahl zugeordnet ist - eine Aktion (in diesem Sinne können wir sagen, dass eine Aktion als Funktion eine Regel ist, die es ermöglicht, für jede gegebene Funktion eine genau definierte Zahl zu berechnen - auch Aktion genannt). Die Aktion sieht so aus:
wo ist der Lagrange des Systems in Abhängigkeit von der verallgemeinerten Koordinate , seiner ersten Ableitung in Bezug auf die Zeit und möglicherweise auch explizit in der Zeit . Wenn das System mehr Freiheitsgrade hat, hängt die Lagrange-Funktion von einer größeren Anzahl von verallgemeinerten Koordinaten und ihren ersten zeitlichen Ableitungen ab. Somit ist die Aktion ein Skalarfunktional, das von der Flugbahn des Körpers abhängt.
Die Tatsache, dass die Aktion ein Skalar ist, macht es einfach, sie in beliebigen verallgemeinerten Koordinaten zu schreiben, Hauptsache, die Position (Konfiguration) des Systems wird durch sie eindeutig charakterisiert (z. B. können diese anstelle von kartesischen Koordinaten polar sein Koordinaten, Abstände zwischen Punkten des Systems, Winkel oder deren Funktionen usw. d.).
Die Aktion kann für eine völlig beliebige Trajektorie berechnet werden, egal wie "wild" und "unnatürlich" sie auch sein mag. In der klassischen Mechanik gibt es jedoch unter allen möglichen Trajektorien nur eine, entlang der der Körper tatsächlich gehen wird. Das Prinzip der Stationarität der Wirkung gibt nur die Antwort auf die Frage, wie sich der Körper tatsächlich bewegen wird:
Das heißt, wenn die Lagrange-Funktion des Systems gegeben ist, können wir mit Hilfe der Variationsrechnung genau bestimmen, wie sich der Körper bewegen wird, indem wir zuerst die Bewegungsgleichungen - die Euler-Lagrange-Gleichungen - erhalten und sie dann lösen. Dies ermöglicht nicht nur eine ernsthafte Verallgemeinerung der Formulierung der Mechanik, sondern auch die Auswahl der bequemsten Koordinaten für jedes spezifische Problem, nicht auf kartesische beschränkt, was sehr nützlich sein kann, um die einfachsten und am leichtesten zu lösenden Gleichungen zu erhalten.
wo ist die Hamilton-Funktion des gegebenen Systems; - (verallgemeinerte) Koordinaten, - konjugierte (verallgemeinerte) Impulse, die zusammen zu jedem gegebenen Zeitpunkt den dynamischen Zustand des Systems charakterisieren und, da sie jeweils eine Funktion der Zeit sind, somit die Evolution (Bewegung) des Systems charakterisieren. Um in diesem Fall die Bewegungsgleichungen des Systems in Form von kanonischen Hamilton-Gleichungen zu erhalten, ist es notwendig, die so geschriebene Wirkung unabhängig für alle und zu variieren.
Es sei darauf hingewiesen, dass, wenn es im Prinzip möglich ist, das Bewegungsgesetz aus den Bedingungen des Problems zu finden, dies automatisch der Fall ist nicht bedeutet, dass es möglich ist, ein Funktional zu konstruieren, das während echter Bewegung einen stationären Wert annimmt. Ein Beispiel ist die gemeinsame Bewegung von elektrischen Ladungen und Monopolen – magnetischen Ladungen – in einem elektromagnetischen Feld. Ihre Bewegungsgleichungen lassen sich nicht aus dem Stationaritätsprinzip ableiten. In ähnlicher Weise haben einige Hamiltonsche Systeme Bewegungsgleichungen, die nicht aus diesem Prinzip folgen.
Beispiele
Triviale Beispiele helfen, die Verwendung des Funktionsprinzips durch die Euler-Lagrange-Gleichungen zu bewerten. Freies Teilchen (Masse m und Geschwindigkeit v) im euklidischen Raum bewegt sich geradlinig. Unter Verwendung der Euler-Lagrange-Gleichungen kann dies in Polarkoordinaten wie folgt dargestellt werden. Ohne Potential ist die Lagrange-Funktion einfach gleich der kinetischen Energie
in einem orthogonalen Koordinatensystem.
In Polarkoordinaten wird die kinetische Energie und damit die Lagrange-Funktion
Die Radial- und Winkelkomponenten der Gleichungen werden jeweils:
Lösen dieser beiden Gleichungen
Hier ist eine bedingte Aufzeichnung der unendlichen funktionalen Integration über alle Trajektorien x(t) und ist die Plancksche Konstante. Wir betonen, dass im Prinzip die Wirkung im Exponential selbst erscheint (oder erscheinen kann), beim Studium des Evolutionsoperators in der Quantenmechanik jedoch für Systeme, die ein exaktes klassisches (Nicht-Quanten-) Analogon haben, genau gleich ist die übliche klassische Handlung.
Die mathematische Analyse dieses Ausdrucks im klassischen Limes – für ausreichend große , also für sehr schnelle Oszillationen des imaginären Exponenten – zeigt, dass sich die allermeisten möglichen Trajektorien in diesem Integral im Limes (formal at ) gegenseitig aufheben. . Für fast jeden Pfad gibt es einen Pfad, auf dem der Phaseneinbruch genau entgegengesetzt ist, und sie summieren sich zu einem Beitrag von Null. Nur die Trajektorien, für die die Aktion nahe am Extremwert liegt (für die meisten Systeme - das Minimum), werden nicht reduziert. Dies ist eine rein mathematische Tatsache aus der Theorie der Funktionen einer komplexen Variablen; beispielsweise basiert darauf die stationäre Phasenmethode.
Infolgedessen bewegt sich das Teilchen in voller Übereinstimmung mit den Gesetzen der Quantenmechanik auf allen Bahnen gleichzeitig, aber unter normalen Bedingungen tragen nur nahezu stationäre (dh klassische) Bahnen zu den beobachteten Werten bei. Da die Quantenmechanik im Grenzbereich hoher Energien klassisch wird, können wir davon ausgehen, dass dies - quantenmechanische Herleitung des klassischen Wirkstationaritätsprinzips.
In der Quantenfeldtheorie
Auch in der Quantenfeldtheorie wird das Prinzip der Stationarität der Wirkung erfolgreich angewendet. Die Lagrange-Dichte beinhaltet hier die Operatoren der entsprechenden Quantenfelder. Obwohl es hier im Wesentlichen richtiger ist (mit Ausnahme des klassischen Grenzwertes und teilweise halbklassisch), nicht vom Prinzip der Stationarität der Wirkung zu sprechen, sondern von der Feynman-Integration über Trajektorien im Konfigurations- oder Phasenraum dieser Felder - unter Verwendung der Die gerade erwähnte Lagrange-Dichte.
Weitere Verallgemeinerungen
Allgemeiner wird unter einer Aktion ein Funktional verstanden, das eine Abbildung vom Konfigurationsraum auf die Menge der reellen Zahlen definiert und im Allgemeinen kein Integral sein muss, da zumindest nicht-lokale Aktionen prinzipiell möglich sind theoretisch. Außerdem ist ein Konfigurationsraum nicht notwendigerweise ein Funktionenraum, da er eine nicht-kommutative Geometrie haben kann.
2.2. Prinzip der kleinsten Wirkung
Im 18. Jahrhundert erfolgte eine weitere Akkumulation und Systematisierung wissenschaftlicher Ergebnisse, gekennzeichnet durch die Tendenz, einzelne wissenschaftliche Errungenschaften durch die systematische Anwendung mathematischer Analysemethoden auf das Studium physikalischer Phänomene zu einem streng geordneten, kohärenten Weltbild zusammenzufügen. Die Arbeit vieler brillanter Köpfe in dieser Richtung hat zur Schaffung der grundlegenden Theorie eines mechanistischen Forschungsprogramms geführt - der analytischen Mechanik, auf deren Grundlage verschiedene grundlegende Theorien geschaffen wurden, die eine bestimmte Klasse von Zusammenhängen beschreiben.
Phänomene: Hydrodynamik, Elastizitätstheorie, Aerodynamik usw. Eines der wichtigsten Ergebnisse der analytischen Mechanik ist das Prinzip der kleinsten Wirkung (Variationsprinzip), das für das Verständnis der Vorgänge in der Physik am Ende des 20. Jahrhunderts wichtig ist.
Die Wurzeln der Entstehung von Variationsprinzipien in der Wissenschaft reichen bis ins antike Griechenland zurück und sind mit dem Namen Heron aus Alexandria verbunden. Die Idee jedes Variationsprinzips besteht darin, einen bestimmten Wert zu variieren (zu ändern), der einen bestimmten Prozess charakterisiert, und aus allen möglichen Prozessen denjenigen auszuwählen, für den dieser Wert einen extremen (maximalen oder minimalen) Wert annimmt. Heron versuchte, die Gesetze der Lichtreflexion zu erklären, indem er den Wert variierte, der die Länge des Wegs charakterisiert, den ein Lichtstrahl von einer Quelle zu einem Beobachter zurücklegt, wenn er von einem Spiegel reflektiert wird. Er kam zu dem Schluss, dass ein Lichtstrahl von allen möglichen Wegen den kürzesten (von allen geometrisch möglichen) wählt.
Im 17. Jahrhundert, zweitausend Jahre später, machte der französische Mathematiker Fermat auf das Heronsche Prinzip aufmerksam, erweiterte es auf Medien mit unterschiedlichen Brechungsindizes und formulierte es daher zeitlich neu. Das Fermatsche Prinzip besagt, dass in einem Brechungsmedium, dessen Eigenschaften nicht von der Zeit abhängen, ein Lichtstrahl, der durch zwei Punkte geht, sich selbst einen Weg wählt, so dass die Zeit, die er braucht, um vom ersten zum zweiten Punkt zu gelangen, minimal ist. Das Heronsche Prinzip erweist sich als Spezialfall des Fermatschen Prinzips für Medien mit konstantem Brechungsindex.
Fermats Prinzip zog die Aufmerksamkeit der Zeitgenossen auf sich. Einerseits war er der beste Beweis für das „Ökonomieprinzip“ in der Natur, für den rationalen göttlichen Plan, der sich in der Struktur der Welt verwirklicht, andererseits widersprach er Newtons Korpuskulartheorie des Lichts. Nach Newton stellte sich heraus, dass in dichteren Medien die Lichtgeschwindigkeit größer sein sollte, während aus dem Fermatschen Prinzip folgte, dass in solchen Medien die Lichtgeschwindigkeit kleiner wird.
1740 analysierte der Mathematiker Pierre Louis Moreau de Maupertuis kritisch Fermats Prinzip und folgte dem theologischen
logische Motive über Perfektion und das sparsamste Gerät des Universums, proklamierten in der Arbeit „Über die verschiedenen Naturgesetze, die unvereinbar schienen“ das Prinzip der geringsten Wirkung. Maupertuis gab Fermats kürzeste Zeit auf und führte ein neues Konzept ein – Action. Die Wirkung ist gleich dem Produkt aus dem Impuls des Körpers (Impuls Р = mV) und dem vom Körper zurückgelegten Weg. Die Zeit hat keinen Vorteil gegenüber dem Raum und umgekehrt. Daher wählt das Licht nicht den kürzesten Weg und nicht die kürzeste Zeit, um es zu reisen, sondern laut Maupertuis „wählt den Weg, der eine realere Ökonomie ergibt: Der Weg, dem es folgt, ist der Weg, auf dem die Größe der Aktion ist minimal.“ Das Prinzip der kleinsten Wirkung wurde in den Arbeiten von Euler und Lagrange weiterentwickelt; er war die Grundlage, auf der Lagrange ein neues Gebiet der mathematischen Analyse entwickelte – die Variationsrechnung. Dieses Prinzip wurde in den Arbeiten von Hamilton weiter verallgemeinert und vervollständigt. In einer verallgemeinerten Form verwendet das Prinzip der kleinsten Wirkung das Aktionskonzept, das nicht in Bezug auf den Impuls, sondern in Bezug auf die Lagrange-Funktion ausgedrückt wird. Für den Fall, dass sich ein Teilchen in einem Potentialfeld bewegt, kann die Lagrange-Funktion als Differenz der Kinetik dargestellt werden ![]() und potentielle Energie:
und potentielle Energie:
(Das Konzept „Energie“ wird in Kapitel 3 dieses Abschnitts ausführlich behandelt.)
Das Produkt wird als Elementaraktion bezeichnet. Die Gesamtaktion ist die Summe aller Werte über das gesamte betrachtete Zeitintervall, also die Gesamtaktion A:

Die Bewegungsgleichungen eines Teilchens erhält man nach dem Prinzip der kleinsten Wirkung, wonach die reale Bewegung so erfolgt, dass die Wirkung extrem ausfällt, d. h. ihre Variation gegen 0 geht:
![]()
Das Lagrange-Hamilton-Variationsprinzip erlaubt leicht eine Erweiterung auf Systeme, die aus Nicht-
wie viele (viele) Teilchen. Die Bewegung solcher Systeme wird normalerweise in einem abstrakten Raum (eine bequeme mathematische Technik) mit einer großen Anzahl von Dimensionen betrachtet. Angenommen, für N Punkte wird ein abstrakter Raum mit 3N Koordinaten von N Teilchen eingeführt, der ein System bildet, das als Konfigurationsraum bezeichnet wird. Die Abfolge verschiedener Zustände des Systems wird in diesem Konfigurationsraum durch eine Kurve repräsentiert – eine Trajektorie. Betrachtet man alle möglichen Wege, die zwei gegebene Punkte dieses 3N-dimensionalen Raums verbinden, kann man sich vergewissern, dass die wirkliche Bewegung des Systems nach dem Prinzip der geringsten Wirkung erfolgt: unter allen möglichen Bahnen ist diejenige, für die die Wirkung extrem ist, vorbei das gesamte Zeitintervall der Bewegung wird realisiert.
Bei der Minimierung der Wirkung in der klassischen Mechanik erhält man die Euler-Lagrange-Gleichungen, deren Zusammenhang mit den Newtonschen Gesetzen bekannt ist. Die Euler-Lagrange-Gleichungen für die Lagrangefunktion des klassischen elektromagnetischen Feldes entpuppen sich als Maxwellsche Gleichungen. Wir sehen also, dass die Verwendung der Lagrange-Funktion und des Prinzips der kleinsten Wirkung es einem ermöglicht, die Teilchendynamik einzustellen. Die Lagrange-Funktion hat jedoch noch ein weiteres wichtiges Merkmal, das den Lagrange-Formalismus zum Hauptformalismus bei der Lösung fast aller Probleme der modernen Physik gemacht hat. Tatsache ist, dass zusammen mit der Newtonschen Mechanik in der Physik bereits im 19. Jahrhundert für einige physikalische Größen Erhaltungssätze formuliert wurden: der Energieerhaltungssatz, der Impulserhaltungssatz, der Drehimpulserhaltungssatz, das Gesetz der Erhaltung der elektrischen Ladung. Die Zahl der Erhaltungssätze im Zusammenhang mit der Entwicklung der Quanten- und Elementarteilchenphysik in unserem Jahrhundert ist noch größer geworden. Es stellt sich die Frage, wie man eine gemeinsame Basis finden kann, um sowohl die Bewegungsgleichungen (z. B. die Newtonschen Gesetze oder die Maxwellschen Gleichungen) als auch die zeitlich erhaltenen Größen zu schreiben. Es stellte sich heraus, dass eine solche Grundlage die Verwendung des Lagrange-Formalismus ist, da sich herausstellt, dass der Lagrange einer bestimmten Theorie invariant (unverändert) in Bezug auf Transformationen ist, die dem spezifischen abstrakten Raum entsprechen, der in dieser Theorie betrachtet wird, was zur Erhaltung führt Rechtsvorschriften. Diese Merkmale des Lagrange
führte nicht zu der Zweckmäßigkeit, physikalische Theorien in der Sprache der Lagrangianer zu formulieren. Die Erkenntnis dieses Umstandes kam der Physik durch das Aufkommen von Einsteins Relativitätstheorie.
| " |
