Nachweisen

Lassen ABC" ist ein beliebiges Dreieck. Lassen Sie uns über die Spitze gehen B gerade Linie parallel zu gerader Linie AC (Eine solche Gerade heißt Euklidische Gerade). Markieren Sie einen Punkt darauf D damit die Punkte EIN und D liegen auf gegenüberliegenden Seiten einer geraden Linie BC.Winkel DBC und ACB gleich wie innen liegendes Kreuz, gebildet durch eine Sekante BC mit parallelen Linien AC und BD. Also die Summe der Winkel eines Dreiecks an den Eckpunkten B und Mit gleich dem Winkel ABD.Die Summe aller drei Winkel eines Dreiecks ist gleich der Summe der Winkel ABD und BAK. Da diese Winkel innenseitig einseitig parallel sind AC und BD bei Sekante AB, dann ist ihre Summe 180°. Der Satz ist bewiesen.

Konsequenzen

Aus dem Satz folgt, dass jedes Dreieck zwei spitze Winkel hat. In der Tat, indem wir den Widerspruchsbeweis anwenden, nehmen wir an, dass das Dreieck nur einen spitzen Winkel oder überhaupt keinen spitzen Winkel hat. Dann hat dieses Dreieck mindestens zwei Winkel, die jeweils mindestens 90° groß sind. Die Summe dieser Winkel beträgt nicht weniger als 180°. Das ist aber unmöglich, da die Summe aller Winkel eines Dreiecks 180° beträgt. Q.E.D.

Verallgemeinerung zur Simplextheorie

Wo ist der Winkel zwischen den Flächen i und j des Simplex.

Anmerkungen

• Auf einer Kugel übersteigt die Summe der Winkel eines Dreiecks immer 180°, die Differenz wird als Kugelexzess bezeichnet und ist proportional zur Fläche des Dreiecks.
• In der Lobatschewski-Ebene ist die Summe der Winkel eines Dreiecks immer kleiner als 180°. Der Unterschied ist auch proportional zur Fläche des Dreiecks.

siehe auch

Wikimedia-Stiftung. 2010 .

• Taylor
• Untere Schwanenbrücke

Sehen Sie, was der "Satz über die Summe der Winkel eines Dreiecks" in anderen Wörterbüchern ist:

Polygonwinkelsummensatz- Eigenschaft von Polygonen in der euklidischen Geometrie: Die Summe der Winkel n eines Polygons ist 180°(n 2). Inhalt 1 Beweis 2 Bemerkung ... Wikipedia

Satz des Pythagoras- Der Satz des Pythagoras ist einer der grundlegenden Sätze der euklidischen Geometrie, der die Beziehung zwischen den Seiten eines rechtwinkligen Dreiecks festlegt. Inhalt 1 ... Wikipedia

Fläche eines Dreiecks

Satz des Pythagoras- Der Satz des Pythagoras ist einer der grundlegenden Sätze der euklidischen Geometrie, der die Beziehung zwischen den Seiten eines rechtwinkligen Dreiecks festlegt. Inhalt 1 Aussagen 2 Beweise ... Wikipedia

Kosinussatz- Der Kosinussatz ist eine Verallgemeinerung des Satzes des Pythagoras. Das Quadrat einer Seite eines Dreiecks ist gleich der Summe der Quadrate seiner beiden anderen Seiten, ohne das Produkt dieser Seiten mit dem Kosinus des Winkels zwischen ihnen zu verdoppeln. Für ein flaches Dreieck mit den Seiten a, b, c und dem Winkel α ... ... Wikipedia

Dreieck- Dieser Begriff hat andere Bedeutungen, siehe Dreieck (Bedeutungen). Ein Dreieck (im euklidischen Raum) ist eine geometrische Figur, die aus drei Liniensegmenten besteht, die drei nichtlineare Punkte verbinden. Drei Punkte, ... ... Wikipedia

Zeichen der Gleichheit von Dreiecken- Standardnotation Dreieck ist das einfachste Polygon mit 3 Ecken (Winkel) und 3 Seiten; ein Teil einer Ebene, der von drei Punkten begrenzt wird, die nicht auf derselben geraden Linie liegen, und drei Liniensegmenten, die diese Punkte paarweise verbinden. Die Eckpunkte eines Dreiecks ... Wikipedia

Euklid- Altgriechischer Mathematiker. Arbeitete im 3. Jahrhundert in Alexandria. BC e. Das Hauptwerk „Anfänge“ (15 Bücher), das die Grundlagen der antiken Mathematik, der elementaren Geometrie, der Zahlenlehre, der allgemeinen Beziehungslehre und einer Methode zur Flächen- und Volumenbestimmung enthält, … … Enzyklopädisches Wörterbuch

EUKLID- (gestorben zwischen 275 und 270 v. Chr.) Altgriechischer Mathematiker. Informationen über Zeit und Ort seiner Geburt haben uns nicht erreicht, aber es ist bekannt, dass Euklid in Alexandria lebte und die Blütezeit seiner Tätigkeit auf die Regierungszeit von Ptolemaios I. in Ägypten fällt ... ... Großes enzyklopädisches Wörterbuch

NICHT-EUKLIDISCHE GEOMETRIE- Geometrie ähnlich der Geometrie von Euklid, indem sie die Bewegung von Figuren definiert, sich aber von der euklidischen Geometrie dadurch unterscheidet, dass eines ihrer fünf Postulate (zweites oder fünftes) durch ihre Negation ersetzt wird. Leugnung eines der euklidischen Postulate ... ... Collier Enzyklopädie

Ziele und Ziele:

Lehrreich:

• Wissen über das Dreieck wiederholen und verallgemeinern;
• beweise den Dreieckssummensatz;
• überprüfen Sie praktisch die Richtigkeit der Formulierung des Theorems;
• lernen, das erworbene Wissen bei der Lösung von Problemen anzuwenden.

Entwicklung:

• Entwicklung von geometrischem Denken, Interesse am Fach, kognitiver und kreativer Aktivität der Schüler, mathematischer Sprache, Fähigkeit zum selbstständigen Erwerb von Wissen.

Lehrreich:

• die persönlichen Qualitäten der Schüler zu entwickeln, wie z. B. Zielstrebigkeit, Ausdauer, Genauigkeit, Teamfähigkeit.

Ausrüstung: Multimedia-Beamer, Dreiecke aus farbigem Papier, Unterrichtsmaterial „Mathematik zum Anfassen“, Computer, Leinwand.

Vorbereitungsphase: Der Lehrer gibt dem Schüler die Aufgabe, einen historischen Hintergrund zum Satz "Die Summe der Winkel eines Dreiecks" vorzubereiten.

Unterrichtsart: neues Material lernen.

Während des Unterrichts

I. Organisatorischer Moment

Grüße. Psychologische Einstellung von Studenten zur Arbeit.

II. Sich warm laufen

Wir sind der geometrischen Figur „Dreieck“ in früheren Lektionen begegnet. Wiederholen wir, was wir über das Dreieck wissen?

Die Schüler arbeiten in Gruppen. Sie erhalten die Möglichkeit, miteinander zu kommunizieren, um jeweils eigenständig den Erkenntnisprozess aufzubauen.

Was ist passiert? Jede Gruppe macht ihre Vorschläge und der Lehrer schreibt sie an die Tafel. Die Ergebnisse werden diskutiert:

Bild 1

III. Wir formulieren die Unterrichtsaufgabe

Wir wissen also schon viel über das Dreieck. Aber nicht alles. Jeder von euch hat Dreiecke und Winkelmesser auf seinem Schreibtisch. Was meinen Sie, welche Aufgabe können wir formulieren?

Die Schüler formulieren die Aufgabe der Lektion - die Summe der Winkel eines Dreiecks zu finden.

IV. Erklärung des neuen Materials

Praktischer Teil(trägt zur Aktualisierung von Wissen und Fähigkeiten zur Selbsterkenntnis bei.) Messen Sie die Winkel mit einem Winkelmesser und berechnen Sie ihre Summe. Notieren Sie die Ergebnisse in einem Notizbuch (hören Sie die erhaltenen Antworten an). Wir stellen fest, dass die Summe der Winkel bei allen unterschiedlich ausgefallen ist (das kann passieren, weil der Winkelmesser ungenau angesetzt, die Berechnung nachlässig durchgeführt wurde etc.).

Falten Sie entlang der gepunkteten Linien und finden Sie heraus, was die Summe der Winkel des Dreiecks sonst noch ist:

a)
Figur 2

b)
Figur 3

in)
Figur 4

G)
Abbildung 5

e)
Abbildung 6

Nach Abschluss der praktischen Arbeit formulieren die Studierenden die Antwort: Die Winkelsumme eines Dreiecks ist gleich dem Gradmaß des erweiterten Winkels, also 180°.

Lehrer: In der Mathematik erlaubt die praktische Arbeit nur eine Aussage, die aber bewiesen werden muss. Eine Aussage, deren Gültigkeit durch Beweis belegt ist, heißt Theorem. Welchen Satz können wir formulieren und beweisen?

Studenten: Die Summe der Winkel eines Dreiecks beträgt 180 Grad.

Geschichte Referenz: Die Eigenschaft der Winkelsumme eines Dreiecks wurde im alten Ägypten festgestellt. Der Beweis, der in modernen Lehrbüchern gegeben wird, findet sich in Proclus 'Kommentaren zu Euklids Elementen. Proklos behauptet, dass dieser Beweis (Abb. 8) von den Pythagoräern (5. Jahrhundert v. Chr.) entdeckt wurde. Im ersten Buch der Elemente führt Euklid einen weiteren Beweis des Satzes über die Winkelsumme eines Dreiecks an, der mit Hilfe einer Zeichnung leicht verständlich ist (Abb. 7):

Abbildung 7

Abbildung 8

Zeichnungen werden über einen Projektor auf dem Bildschirm angezeigt.

Der Lehrer bietet an, den Satz mit Hilfe von Zeichnungen zu beweisen.

Anschließend erfolgt der Beweis mit dem CMD „Live Mathematics“. Der Lehrer am Computer projiziert den Beweis des Theorems.

Dreieckswinkelsummensatz: „Die Winkelsumme eines Dreiecks ist 180°“

Abbildung 9

Nachweisen:

a)

Abbildung 10

b)

Abbildung 11

in)

Abbildung 12

Die Schüler im Heft halten den Beweis des Satzes kurz fest:

Satz: Die Winkelsumme eines Dreiecks beträgt 180°.

Abbildung 13

Gegeben:ΔABC

Beweisen: A + B + C = 180°.

Nachweisen:

Was bewiesen werden musste.

V.Phys. Minute.

VI. Erklärung des neuen Materials (Fortsetzung)

Die Konsequenz des Satzes über die Summe der Winkel eines Dreiecks wird von den Schülern selbst hergeleitet, dies trägt zur Entwicklung der Fähigkeit bei, einen eigenen Standpunkt zu formulieren, auszudrücken und zu argumentieren:

In jedem Dreieck sind entweder alle Winkel spitz oder zwei spitze Winkel und der dritte stumpf oder rechts.

Wenn alle Winkel in einem Dreieck spitz sind, dann heißt es spitzwinklig.

Wenn einer der Winkel eines Dreiecks stumpf ist, dann heißt es stumpf.

Wenn einer der Winkel eines Dreiecks recht ist, dann heißt es rechteckig.

Der Dreieckssummensatz erlaubt es uns, Dreiecke nicht nur nach Seiten, sondern auch nach Winkeln zu klassifizieren. (Im Zuge der Einführung in die Dreiecksarten wird eine Tabelle ausgefüllt)

Tabelle 1

Dreiecksansicht	Gleichschenklig	Gleichseitig	Vielseitig
Rechteckig
stumpf
spitzwinklig

VII. Konsolidierung des studierten Materials.

1. Probleme mündlich lösen:

(Die Zeichnungen werden über den Projektor auf dem Bildschirm angezeigt.)

(grundlegende Zusammenfassung)

Visuelle Geometrie Klasse 7. Referenzauszug Nr. 4 Die Summe der Winkel eines Dreiecks.

Großer französischer Wissenschaftler des 17. Jahrhunderts Blaise Paskal Schon als Kind bastelte er gerne an geometrischen Formen. Er war mit dem Winkelmesser vertraut und wusste, wie man Winkel misst. Der junge Forscher bemerkte, dass für alle Dreiecke die Summe der drei Winkel gleich ist - 180 °. "Wie kannst du es beweisen? dachte Paskal. "Schließlich kann man nicht die Summe der Winkel aller Dreiecke überprüfen - es gibt unendlich viele davon." Dann schnitt er mit einer Schere zwei Ecken des Dreiecks ab und befestigte sie an der dritten Ecke. Es stellte sich ein entwickelter Winkel heraus, der, wie Sie wissen, gleich 180 ° ist. Es war seine erste eigene Entdeckung. Das weitere Schicksal des Jungen war bereits vorbestimmt.

In diesem Thema lernen Sie fünf Merkmale der Gleichheit rechtwinkliger Dreiecke und die vielleicht beliebteste Eigenschaft eines rechtwinkligen Dreiecks mit 30° kennen. Es hört sich so an: Das Bein, das einem Winkel von 30 ° gegenüberliegt, entspricht der halben Hypotenuse. Wenn wir ein gleichseitiges Dreieck durch eine Höhe teilen, erhalten wir sofort einen Beweis für diese Eigenschaft.

SATZ. Die Winkelsumme eines Dreiecks beträgt 180°. Um dies zu beweisen, ziehen wir eine Linie durch den Scheitelpunkt parallel zur Basis. Die dunklen Winkel sind gleich und die grauen Winkel sind gleich, da sie auf parallelen Linien liegen. Die dunkle Ecke, die graue Ecke und die Ecke am Scheitel bilden eine gerade Ecke, ihre Summe beträgt 180°. Aus dem Satz folgt, dass die Winkel eines gleichseitigen Dreiecks jeweils 60° betragen und dass die Summe der spitzen Winkel eines rechtwinkligen Dreiecks 90° beträgt.

äußere Ecke Dreieck heißt der Winkel, der an den Winkel des Dreiecks angrenzt. Daher werden manchmal die Winkel des Dreiecks selbst als Innenwinkel bezeichnet.

THEOREM über den Außenwinkel eines Dreiecks. Der Außenwinkel eines Dreiecks ist gleich der Summe zweier nicht benachbarter Innenwinkel. Tatsächlich vervollständigen eine äußere Ecke und zwei nicht daran angrenzende innere Ecken die gefüllte Ecke bis zu 180°. Aus dem Satz folgt, dass ein Außenwinkel größer ist als jeder nicht benachbarte Innenwinkel.

THEOREM über die Beziehungen zwischen Seiten und Winkeln eines Dreiecks. In einem Dreieck liegt die größere Seite dem größeren Winkel gegenüber und die größere Seite dem größeren Winkel. Daraus folgt: 1) Das Bein ist kleiner als die Hypotenuse. 2) Die Senkrechte ist kleiner als die Steigung.

Abstand von Punkt zu Linie . Da die Senkrechte kleiner ist als jede Schräge, die von demselben Punkt gezogen wird, wird ihre Länge als Abstand vom Punkt zur Linie genommen.

Dreiecksungleichung . Die Länge jeder Seite eines Dreiecks ist kleiner als die Summe seiner beiden anderen Seiten, d.h. a< b + с , b< а + с , mit< а + b . Folge. Die Länge der Polylinie ist größer als das Segment, das ihre Enden verbindet.

ZEICHEN DER GLEICHHEIT
RECHTECKIGE DREIECKE

Auf zwei Beinen. Sind zwei Schenkel eines rechtwinkligen Dreiecks jeweils gleich zwei Schenkeln eines anderen Dreiecks, so sind solche Dreiecke kongruent.

Entlang des Beins und des angrenzenden spitzen Winkels. Sind der Schenkel und der daran angrenzende spitze Winkel eines rechtwinkligen Dreiecks jeweils gleich dem Schenkel und der daran angrenzende spitze Winkel eines anderen Dreiecks, so sind solche Dreiecke kongruent.

Entlang des Beines und gegenüberliegender spitzer Winkel. Wenn der Schenkel und der gegenüberliegende spitze Winkel eines rechtwinkligen Dreiecks jeweils gleich dem Schenkel und dem gegenüberliegenden spitzen Winkel eines anderen Dreiecks sind, dann sind solche Dreiecke kongruent.

Durch Hypotenuse und spitzen Winkel. Wenn die Hypotenuse und der spitze Winkel eines rechtwinkligen Dreiecks jeweils gleich der Hypotenuse und dem spitzen Winkel eines anderen Dreiecks sind, dann sind solche Dreiecke kongruent.

Der Beweis dieser Kriterien reduziert sich sofort auf eines der Kriterien für die Gleichheit von Dreiecken.

Nach Bein und Hypotenuse. Wenn Bein und Hypotenuse eines rechtwinkligen Dreiecks jeweils gleich Bein und Hypotenuse eines anderen rechtwinkligen Dreiecks sind, dann sind solche Dreiecke kongruent.

Nachweisen. Wir wenden Dreiecke mit gleichen Beinen an. Wir erhalten ein gleichschenkliges Dreieck. Seine von oben gezeichnete Höhe ist auch der Median. Dann sind die zweiten Schenkel der Dreiecke gleich, und die Dreiecke sind auf drei Seiten gleich.

SATZ auf der Eigenschaft eines gegenüber liegenden Beins einen Winkel von 30°. Das dem 30°-Winkel gegenüberliegende Bein entspricht der Hälfte der Hypotenuse. Man beweist es, indem man das Dreieck zu einem gleichseitigen ergänzt.

THEOREM über die Eigenschaft von Winkelhalbierenden. Jeder Punkt auf der Winkelhalbierenden ist von seinen Seiten gleich weit entfernt. Wenn ein Punkt von den Seiten eines Winkels gleich weit entfernt ist, dann liegt er auf der Winkelhalbierenden. Bewiesen, indem man zwei Senkrechte zu den Seiten des Winkels zeichnet und rechtwinklige Dreiecke betrachtet.

Zweiter großer Punkt . Die Winkelhalbierenden eines Dreiecks schneiden sich in einem Punkt.

Abstand zwischen parallelen Linien. SATZ. Alle Punkte zweier paralleler Geraden sind von der anderen Geraden gleich weit entfernt. Die Definition des Abstands zwischen parallelen Geraden folgt aus dem Satz.

Definition. Der Abstand zwischen zwei parallelen Linien ist der Abstand von einem beliebigen Punkt auf einer der parallelen Linien zur anderen Linie.

Detaillierte Beweise der Theoreme

Dies ist das Referenz-Abstract Nr. 4 in Geometrie in Klasse 7. Wählen Sie die nächsten Schritte:

Dreieck . Spitze, stumpfe und rechtwinklige Dreiecke.

Die Beine und die Hypotenuse. Gleichschenkliges und gleichseitiges Dreieck.

Die Summe der Winkel eines Dreiecks.

Die äußere Ecke des Dreiecks. Zeichen der Gleichheit von Dreiecken.

Wunderbare Linien und Punkte in einem Dreieck: Höhen, Seitenhalbierende,

Winkelhalbierende, Median e Senkrechte, Orthozentrum,

Schwerpunkt, Mittelpunkt des umschriebenen Kreises, Mittelpunkt des einbeschriebenen Kreises.

Satz des Pythagoras. Das Seitenverhältnis eines beliebigen Dreiecks.

Dreieck ist ein Polygon mit drei Seiten (oder drei Ecken). Die Seiten eines Dreiecks werden oft mit kleinen Buchstaben bezeichnet, die den Großbuchstaben entsprechen, die gegenüberliegende Ecken bezeichnen.

Wenn alle drei Winkel spitz sind ( Abb. 20), dann dies spitzwinkliges Dreieck . Wenn eine der Ecken stimmt(C, Abb.21), das ist rechtwinkliges Dreieck; Seitenein, beinen rechten Winkel bilden, nennt man Beine; Seitecgegenüber dem rechten Winkel heißt Hypotenuse. Wenn einer von stumpfe Winkel ( B, Abb.22), das ist Stumpfes Dreieck.


Dreieck ABC (Abb. 23) - gleichschenklig, Wenn zwei seine Seiten sind gleicha= c); diese gleichen Seiten heißen seitlich, wird der Dritte angerufen Basis Dreieck. Dreieck ABC (Abb. 24) - gleichseitig, Wenn alles seine Seiten sind gleicha = b = c). Im Allgemeinen ( a ≠ b ≠ c) wir haben skaliert Dreieck .

Grundlegende Eigenschaften von Dreiecken. In jedem Dreieck:

1. Der größeren Seite steht ein größerer Winkel gegenüber und umgekehrt.

2. Gleichen Winkeln liegen gleiche Seiten gegenüber und umgekehrt.

Insbesondere alle Winkel in gleichseitig Dreieck sind gleich.

3. Die Summe der Winkel eines Dreiecks ist 180 º .

Aus den letzten beiden Eigenschaften folgt, dass jeder Winkel gleichseitig ist

Dreieck ist 60 º.

4. Fortsetzung einer der Seiten des Dreiecks (AC, Abb. 25), wir bekommen extern

Winkel BCD . Der Außenwinkel eines Dreiecks ist gleich der Summe der Innenwinkel,

nicht damit verwandt :BCD=A+B.

5. Irgendein Seite eines Dreiecks ist kleiner als die Summe der beiden anderen Seiten und mehr

ihre Unterschiede (a < b + c, a > b – c;b < a + c, b > a – c;c < a + b,c > a – b).

Zeichen der Gleichheit von Dreiecken.

Dreiecke sind kongruent, wenn sie jeweils gleich sind:

a ) zwei Seiten und der Winkel zwischen ihnen;

b ) zwei Ecken und die daran angrenzende Seite;

c) drei Seiten.

Zeichen der Gleichheit rechtwinkliger Dreiecke.

Zwei rechteckig Dreiecke sind kongruent, wenn eine der folgenden Bedingungen zutrifft:

1) ihre Beine sind gleich;

2) das Bein und die Hypotenuse eines Dreiecks sind gleich dem Bein und der Hypotenuse des anderen;

3) die Hypotenuse und der spitze Winkel eines Dreiecks sind gleich der Hypotenuse und dem spitzen Winkel des anderen;

4) das Bein und der angrenzende spitze Winkel eines Dreiecks sind gleich dem Bein und dem angrenzenden spitzen Winkel des anderen;

5) das Bein und der gegenüberliegende spitze Winkel eines Dreiecks sind gleich dem Bein und gegenüber dem spitzen Winkel des anderen.

Wunderbare Linien und Punkte in einem Dreieck.

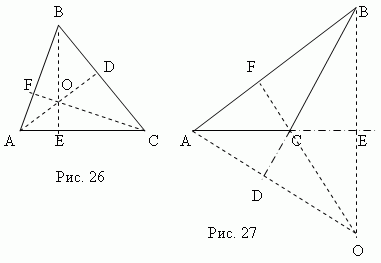
Höhe Dreieck istaufrecht,von jedem Scheitelpunkt auf die gegenüberliegende Seite fallen gelassen ( oder seine Fortsetzung). Diese Seite heißtdie Basis des Dreiecks . Die drei Höhen eines Dreiecks schneiden sich immeran einer Stellenamens Orthozentrum Dreieck. Das Orthozentrum eines spitzen Dreiecks (PunktÖ , Abb. 26) befindet sich innerhalb des Dreiecks undOrthozentrum eines stumpfen Dreiecks (PunktÖ , Abb.27) – draußen; Der Orthomittelpunkt eines rechtwinkligen Dreiecks fällt mit der Spitze des rechten Winkels zusammen.

Median - Das Liniensegment , die jeden Eckpunkt eines Dreiecks mit dem Mittelpunkt der gegenüberliegenden Seite verbindet. Drei Seitenhalbierende eines Dreiecks (AD , BE , CF , Abb.28) schneiden sich in einem Punkt Ö , die immer innerhalb des Dreiecks liegt und sein sein Schwerpunkt. Dieser Punkt teilt jeden Median 2:1 von oben.

Bisektor - Das halbierendes Segment Ecke von oben nach oben Schnittpunkt mit der Gegenseite. Drei Winkelhalbierende eines Dreiecks (AD , BE , CF , Abb.29) schneiden sich in einem Punkt Oh, immer in einem Dreieck liegen und Sein eingeschriebener Kreismittelpunkt(siehe Abschnitt „Beschriftetund umschriebene Polygone).

Die Winkelhalbierende teilt die gegenüberliegende Seite in Teile, die proportional zu den angrenzenden Seiten sind ; zum Beispiel in Abb. 29 AE : CE = AB : BC .

Mittlere Senkrechte ist eine vom Mittelwert gezogene Senkrechte Segmentpunkte (Seiten). Drei senkrechte Winkelhalbierende des Dreiecks ABC(KO , MO , NO , Abb.30 ) schneiden sich in einem Punkt O, das ist Center umschriebener Kreis (Punkte K , M , N die Mittelpunkte der Seiten eines Dreiecks ABC).

In einem spitzwinkligen Dreieck liegt dieser Punkt innerhalb des Dreiecks; in stumpf - draußen; im Rechteck - in der Mitte der Hypotenuse. Orthozentrum, Schwerpunkt, Mittelpunkt des umschriebenen Kreises und Mittelpunkt des einbeschriebenen Kreises fallen nur in einem gleichseitigen Dreieck zusammen.

Satz des Pythagoras. In einem rechtwinkligen Dreieck das Quadrat der LängeDie Hypotenuse ist gleich der Summe der Quadrate der Beinlängen.

Der Beweis des Satzes von Pythagoras folgt offensichtlich aus Abb.31. Betrachten Sie ein rechtwinkliges Dreieck ABC mit Beinen ein, b und Hypotenuse c.

Lass uns ein Quadrat bauen AKMB unter Verwendung der Hypotenuse AB als Seite. DannVerlängern Sie die Seiten eines rechtwinkligen Dreiecks ABC also um ein quadrat zu bekommen CDEF , dessen Seite gleich ista+b.Nun ist klar, dass die Fläche ein Quadrat ist CDEF ist ( a+b) 2 . Andererseits diese die Fläche ist gleich der Summe Bereiche vier rechtwinklige dreiecke und Quadrat AKMB , das heißt

c 2 + 4 (ab / 2) = c 2 + 2 ab,

von hier,

c 2 + 2 ab= (a+b) 2 ,

und schließlich haben wir:

c 2 =a 2 +b 2 .

Das Seitenverhältnis eines beliebigen Dreiecks.

Im allgemeinen Fall (für ein beliebiges Dreieck) gilt:

c 2 =a 2 +b 2 – 2ab· cos c,

wo C - Winkel zwischen den Seitena und b .

>>Geometrie: Die Summe der Winkel eines Dreiecks. Komplette Lektionen

THEMA DER UNTERRICHTSSTUNDE: Die Summe der Winkel eines Dreiecks.

Unterrichtsziele:

• Vertiefung und Überprüfung der Kenntnisse der Studierenden zum Thema: „Winkelsumme eines Dreiecks“;
• Beweis der Eigenschaften der Winkel eines Dreiecks;
• Die Verwendung dieser Eigenschaft bei der Lösung der einfachsten Probleme;
• Die Verwendung von historischem Material für die Entwicklung der kognitiven Aktivität von Schülern;
• Vermittlung der Fähigkeit zur Genauigkeit bei der Erstellung von Zeichnungen.

Unterrichtsziele:

• Überprüfen Sie die Fähigkeit der Schüler, Probleme zu lösen.

Unterrichtsplan:

1. Dreieck;
2. Satz über die Winkelsumme eines Dreiecks;
3. Aufgabenbeispiel.

Dreieck.

Datei:O.gif Dreieck- das einfachste Polygon mit 3 Ecken (Ecken) und 3 Seiten; ein Teil einer Ebene, die von drei Punkten und drei Liniensegmenten begrenzt wird, die diese Punkte paarweise verbinden.
Drei Punkte im Raum, die nicht auf einer Geraden liegen, entsprechen genau einer Ebene.
Jedes Polygon kann in Dreiecke unterteilt werden - dieser Vorgang wird aufgerufen Triangulation.
Es gibt einen Abschnitt der Mathematik, der ausschließlich dem Studium der Muster von Dreiecken gewidmet ist - Trigonometrie.

Satz über die Summe der Winkel eines Dreiecks.

File:T.gif Der Dreieckswinkelsummensatz ist ein klassischer Satz der euklidischen Geometrie, der besagt, dass die Winkelsumme eines Dreiecks 180° beträgt.

Nachweisen" :

Sei Δ ABC gegeben. Lassen Sie uns eine Linie parallel zu (AC) durch den Scheitelpunkt B ziehen und den Punkt D darauf markieren, so dass die Punkte A und D auf gegenüberliegenden Seiten der Linie BC liegen. Dann sind der Winkel (DBC) und der Winkel (ACB) gleich als innere Kreuze, die auf den parallelen Linien BD und AC und der Sekante (BC) liegen. Dann ist die Summe der Winkel des Dreiecks an den Eckpunkten B und C gleich dem Winkel (ABD). Aber der Winkel (ABD) und der Winkel (BAC) an der Spitze A des Dreiecks ABC sind einseitig innenliegend mit parallelen Linien BD und AC und einer Sekante (AB), und ihre Summe ist 180°. Die Summe der Winkel eines Dreiecks beträgt also 180°. Der Satz ist bewiesen.

Konsequenzen.

Der Außenwinkel eines Dreiecks ist gleich der Summe der beiden Winkel des Dreiecks, die ihm nicht benachbart sind.

Nachweisen:

Sei Δ ABC gegeben. Der Punkt D liegt auf der Geraden AC, so dass A zwischen C und D liegt. Dann liegt BAD außerhalb des Winkels des Dreiecks an der Spitze A und A + BAD = 180°. Aber A + B + C = 180°, also B + C = 180° – A. Also BAD = B + C. Die Folgerung ist bewiesen.

Konsequenzen.

Ein Außenwinkel eines Dreiecks ist größer als jeder Winkel des Dreiecks, der nicht daran angrenzt.

Aufgabe.

Der Außenwinkel eines Dreiecks ist der Winkel, der an einen beliebigen Winkel dieses Dreiecks angrenzt. Beweisen Sie, dass ein Außenwinkel eines Dreiecks gleich der Summe zweier nicht benachbarter Winkel des Dreiecks ist.
(Abb.1)

Entscheidung:

Sei Δ ABC ∠DAC extern (Abb.1). Dann ist ∠DAC=180°-∠BAC (nach der Eigenschaft benachbarter Winkel), nach dem Satz über die Winkelsumme eines Dreiecks ∠B+∠C =180°-∠BAC. Aus diesen Gleichungen erhalten wir ∠DAC=∠B+∠C

Interessante Tatsache:

Die Summe der Winkel eines Dreiecks :

In der Geometrie von Lobatschewski ist die Summe der Winkel eines Dreiecks immer kleiner als 180. In der Geometrie von Euklid ist sie immer gleich 180. In der Riemannschen Geometrie ist die Summe der Winkel eines Dreiecks immer größer als 180.

Aus der Geschichte der Mathematik:

Euklid (III. Jahrhundert v. Chr.) Gibt in dem Werk „Anfänge“ die folgende Definition an: „Parallel sind gerade Linien, die in derselben Ebene liegen und sich auf beiden Seiten nicht treffen, da sie sich in beide Richtungen auf unbestimmte Zeit erstrecken“ .
Posidonius (1. Jahrhundert v. Chr.) "Zwei gerade Linien, die in derselben Ebene liegen und den gleichen Abstand voneinander haben"
Der antike griechische Wissenschaftler Pappus (III. Jahrhundert v. Chr.) Führte das Symbol paralleler Linien ein - Zeichen =. Später verwendete der englische Ökonom Ricardo (1720-1823) dieses Symbol als Gleichheitszeichen.
Erst im 18. Jahrhundert begannen sie, das Symbol paralleler Linien zu verwenden - das Zeichen ||.
Die Live-Verbindung zwischen den Generationen wird keinen Moment unterbrochen, jeden Tag lernen wir die gesammelten Erfahrungen unserer Vorfahren kennen. Die alten Griechen zogen auf der Grundlage von Beobachtungen und praktischen Erfahrungen Schlussfolgerungen, äußerten Hypothesen und versuchten dann bei Treffen von Wissenschaftlern - Symposien (wörtlich "Fest") - diese Hypothesen zu untermauern und zu beweisen. Damals wurde die Aussage gemacht: "Wahrheit wird in einem Streit geboren."

Fragen:

1. Was ist ein Dreieck?
2. Was besagt der Dreieckssummensatz?
3. Wie groß ist der Außenwinkel des Dreiecks?