फ़ंक्शन y=f(x) को किसी बिंदु x 0 पर अवकलनीय कहा जाता है यदि इस बिंदु पर इसका एक निश्चित व्युत्पन्न है, अर्थात। यदि रिश्ते की सीमा मौजूद है और सीमित है।

यदि कोई फलन किसी निश्चित खंड के प्रत्येक बिंदु पर अवकलनीय है [ए; b] या अंतराल (a; b), तो हम कहते हैं कि यह अंतराल [a; बी] या, क्रमशः, अंतराल में (ए; बी)।

निम्नलिखित प्रमेय मान्य है, जो अवकलनीय और सतत कार्यों के बीच संबंध स्थापित करता है।

प्रमेय. यदि फ़ंक्शन y=f(x) किसी बिंदु x 0 पर अवकलनीय है, तो यह इस बिंदु पर निरंतर है।

इस प्रकार, किसी फ़ंक्शन की भिन्नता से उसकी निरंतरता का अनुसरण होता है।

सबूत. तो अगर

जहाँ b एक अतिसूक्ष्म मात्रा है, अर्थात Dx>0 होने पर एक मात्रा शून्य की ओर प्रवृत्त होती है। परन्तु फिर

Dy=f "(x 0) Dx+bDx=> Dy>0 पर Dx>0, यानी f(x) - f(x 0)>0 पर x>x 0,

और इसका मतलब यह है कि फ़ंक्शन f(x) बिंदु x 0 पर निरंतर है। क्यू.ई.डी.

इस प्रकार, फ़ंक्शन में असंततता बिंदुओं पर व्युत्पन्न नहीं हो सकता है। इसका विपरीत सत्य नहीं है: ऐसे निरंतर कार्य हैं जो कुछ बिंदुओं पर भिन्न नहीं होते हैं (अर्थात, इन बिंदुओं पर कोई व्युत्पन्न नहीं होता है)।

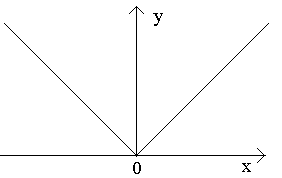
आइए चित्र में बिंदु a, b, c को देखें।

Dx>0 के लिए बिंदु a पर, अनुपात की कोई सीमा नहीं है (क्योंकि Dx>0-0 और Dx>0+0 के लिए एक तरफा सीमाएं अलग-अलग हैं)। ग्राफ़ के बिंदु A पर कोई विशिष्ट स्पर्शरेखा नहीं है, लेकिन 1 और 2 की ढलान वाली दो अलग-अलग एक-तरफ़ा स्पर्शरेखाएँ हैं। इस प्रकार के बिंदु को कोना बिंदु कहा जाता है।

Dx>0 के लिए बिंदु b पर, अनुपात स्थिर चिह्न का और असीम रूप से बड़ा है। फ़ंक्शन में अनंत व्युत्पन्न हैं। इस बिंदु पर ग्राफ़ में एक ऊर्ध्वाधर स्पर्शरेखा है। बिंदु प्रकार - ऊर्ध्वाधर स्पर्शरेखा के साथ "विभक्ति बिंदु"।

बिंदु c पर, एक तरफा व्युत्पन्न विभिन्न संकेतों की असीम रूप से बड़ी मात्रा में होते हैं। इस बिंदु पर ग्राफ़ में दो विलयित ऊर्ध्वाधर स्पर्शरेखाएँ हैं। प्रकार - एक ऊर्ध्वाधर स्पर्शरेखा के साथ "वापसी बिंदु" - एक कोने बिंदु का एक विशेष मामला।

1. फ़ंक्शन y=|x| पर विचार करें। यह फ़ंक्शन बिंदु पर निरंतर है

आइए हम दिखाते हैं कि इस बिंदु पर इसका कोई व्युत्पन्न नहीं है।

f(0+Dx) = f(Dx) = |Dx| इसलिए, Дy = f(Дx) - f(0) = |Дx|

लेकिन फिर Dx पर< 0 (т.е. при Дx стремящемся к 0 слева)

और जब Dx > 0

इस प्रकार, दाएँ और बाएँ पर Dx> 0 के अनुपात की अलग-अलग सीमाएँ हैं, जिसका अर्थ है कि अनुपात की कोई सीमा नहीं है, अर्थात। फ़ंक्शन y=|x| का व्युत्पन्न बिंदु x= 0 पर मौजूद नहीं है। ज्यामितीय रूप से, इसका मतलब है कि बिंदु x = 0 पर इस "वक्र" की कोई विशिष्ट स्पर्शरेखा नहीं है (इस बिंदु पर दो हैं)।

2. फ़ंक्शन संपूर्ण संख्या रेखा पर परिभाषित और निरंतर है। आइए जानें कि क्या इस फ़ंक्शन का x= 0 पर कोई व्युत्पन्न है।

नतीजतन, विचाराधीन फ़ंक्शन बिंदु x = 0 पर भिन्न नहीं है। इस बिंदु पर वक्र की स्पर्शरेखा भुज अक्ष के साथ एक कोण p/2 बनाती है, अर्थात। ओए अक्ष के साथ मेल खाता है।

3 किसी बिंदु पर किसी फ़ंक्शन के व्युत्पन्न की परिभाषा मान लें कि फ़ंक्शन f(x) को बिंदु x 0 के किसी पड़ोस में परिभाषित किया गया है। परिभाषा। यदि संबंध की कोई (परिमित) सीमा है तो f(x) को अवकलनीय बिंदु x 0 कहा जाता है, और सीमा को स्वयं बिंदु x 0 पर फ़ंक्शन f(x) का व्युत्पन्न कहा जाता है और इसे f द्वारा दर्शाया जाता है। (x 0), अर्थात, मान लीजिए कि बिंदु x 0 से बिंदु x पर जाने पर x = x – x 0 तर्क की वृद्धि है, और y = f(x 0 + x) – f(x 0) है फ़ंक्शन की संगत वृद्धि। फिर बिंदु x 0 पर फ़ंक्शन f(x) का व्युत्पन्न फ़ंक्शन की वृद्धि और तर्क वृद्धि के अनुपात की सीमा है जो इसे उत्पन्न करती है, जब तर्क वृद्धि शून्य हो जाती है।

4 उदाहरण 1. आइए हम व्युत्पन्न की परिभाषा के आधार पर कुछ सरल प्राथमिक कार्यों के व्युत्पन्न की गणना के उदाहरण दें। y = a x (0 0. यह मानते हुए कि | x | 0 एक मनमाना बिंदु है, तो 0.मान लीजिए कि | एक्स | 0 एक मनमाना बिंदु है, तो">

0.मान लीजिए कि | एक्स | 0 एक मनमाना बिंदु है, तो उदाहरण 4. y = synx, x R. x 0 R लें और इस बिंदु पर फ़ंक्शन की वृद्धि की गणना करें: तो (sinx) = cosx, x R.' title=' 5 उदाहरण 3. आइए x 0 > 0 लें। यह मानते हुए कि | x | 0 एक मनमाना बिंदु है, तो उदाहरण 4. y = synx, x R। x 0 R लें और इस बिंदु पर फ़ंक्शन की वृद्धि की गणना करें: तो ( सिनएक्स) = कॉसएक्स, एक्स आर।" class="link_thumb"> 5 !} 5 उदाहरण 3. x 0 > 0 लें। यह मानते हुए | एक्स | 0 एक मनमाना बिंदु है, तो उदाहरण 4. y = synx, x R. x 0 R लें और इस बिंदु पर फ़ंक्शन की वृद्धि की गणना करें: तो (sinx) = cosx, x R। 0.मान लीजिए कि | एक्स | 0 एक मनमाना बिंदु है, तो उदाहरण 4. y = synx, x R. x 0 R लें और इस बिंदु पर फ़ंक्शन की वृद्धि की गणना करें: तो (sinx) = cosx, x R.'> 0. यह मानते हुए कि | x | 0 - मनमाना बिंदु, फिर उदाहरण 4. y = synx, x R. x 0 R लें और इस बिंदु पर फ़ंक्शन की वृद्धि की गणना करें: तो (sinx) = cosx, x R.'> 0. यह मानते हुए कि | एक्स | 0 एक मनमाना बिंदु है, तो उदाहरण 4. y = synx, x R. x 0 R लें और इस बिंदु पर फ़ंक्शन की वृद्धि की गणना करें: तो (sinx) = cosx, x R.' title=' 5 उदाहरण 3. आइए x 0 > 0 लें। यह मानते हुए कि | x | 0 एक मनमाना बिंदु है, तो उदाहरण 4. y = synx, x R। x 0 R लें और इस बिंदु पर फ़ंक्शन की वृद्धि की गणना करें: तो ( सिनएक्स) = कॉसएक्स, एक्स आर।"> title="5 उदाहरण 3. x 0 > 0 लें। यह मानते हुए | एक्स | 0 एक मनमाना बिंदु है, तो उदाहरण 4. y = synx, x R. x 0 R लें और इस बिंदु पर फ़ंक्शन की वृद्धि की गणना करें: तो (sinx) = cosx, x R।"> !}

6 प्रमेय. यदि कोई फ़ंक्शन f(x) किसी बिंदु x 0 पर अवकलनीय है, तो यह उस बिंदु पर निरंतर है। सबूत। अस्तित्व में रहने दें, फिर यहां से हमें यह मिलता है कि x x 0 के लिए f (x) – f (x 0) = f "(x 0) (x – x 0) + (x – x 0)α(x) f( x) बिंदु x 0 पर सतत है। अवकलनीय फलन की निरंतरता (1)

7 नोट. किसी बिंदु पर किसी फ़ंक्शन की निरंतरता उस बिंदु पर व्युत्पन्न के अस्तित्व के लिए पर्याप्त शर्त नहीं है। उदाहरण 5. एफ(एक्स) = एक्स. आइए x 0 = 0 के आसपास f (x) के व्यवहार का अध्ययन करें। यहां x 0 पर f (x) f (0) = 0 है। यानी फ़ंक्शन बिंदु x 0 = 0 पर निरंतर है। x y 0 पर विचार करें, सीमा मौजूद नहीं है, इसलिए, फ़ंक्शन f (x) = x का बिंदु x = 0 पर कोई व्युत्पन्न नहीं है, हालांकि यह इस पर निरंतर है बिंदु

8 उदाहरण x y 0 at x 0. at x 0. अर्थात f(x) बिंदु x = 0 पर सतत है। अर्थात, f(x) का बिंदु x = 0 पर कोई अवकलज नहीं है और इसलिए, इस बिंदु पर अवकलनीय नहीं है। आइए बिंदु x = 0 के आसपास f (x) के व्यवहार का अध्ययन करें।

9 मान लीजिए फलन y = f(x) बिंदु x 0 पर अवकलनीय है। फिर, (1) के अनुसार, बिंदु x 0 पर इसकी वृद्धि को y = f(x 0 + x) – f(x) के रूप में लिखा जा सकता है 0) = एफ ( एक्स 0) एक्स + ओ(एक्स) एक्स पर। फ़ंक्शन f (x 0) x का अंतर, बिंदु x 0 पर फ़ंक्शन y = f(x) की वृद्धि के x भाग के सापेक्ष मुख्य रैखिक है, जिसे बिंदु x 0 पर फ़ंक्शन का अंतर कहा जाता है वृद्धि x और इसे df(x 0 ; x) या df(x 0 ) या df या dу दर्शाया जाता है। y = f(x 0 + x) – f(x 0) = df(x 0; x) + o(x) x पर। परिभाषा। वेतन वृद्धि का मुख्य भाग, x के संबंध में रैखिक। x से उच्च कोटि का एक अतिसूक्ष्म। अब फ़ंक्शन इंक्रीमेंट को इस प्रकार लिखा जा सकता है:

10 नोट. वृद्धि x को अक्सर प्रतीक dx द्वारा दर्शाया जाता है और इसे स्वतंत्र चर का अंतर कहा जाता है। इस प्रकार, बिंदु x 0 पर किसी फ़ंक्शन का अंतर df(x 0) = f "(x 0) dx के रूप में लिखा जा सकता है। यदि कोई फ़ंक्शन एक निश्चित अंतराल के प्रत्येक बिंदु पर भिन्न है, तो इसका अंतर dy है x और dx का एक फलन: dy = f "(x)dx. यहां से, विशेष रूप से, हम व्युत्पन्न के लिए एक अभिव्यक्ति प्राप्त करते हैं। अर्थात्, व्युत्पन्न को किसी फ़ंक्शन के अंतर और स्वतंत्र चर के अंतर के अनुपात के रूप में माना जा सकता है।

11 व्युत्पन्न और अंतर का ज्यामितीय अर्थ मान लें कि फ़ंक्शन y = f(x) को U(x 0) में परिभाषित किया गया है और बिंदु x 0 पर अवकलनीय है। М0М0 М x0x0 x 0 + x y x y = f(x) y0y0 y 0 + y 0 L - छेदक L 0 - स्पर्शरेखा x y = f(x 0 + x) - f(x 0) फ़ंक्शन की निरंतरता के कारण x पर। बिंदु M 0 पर फलन y = f(x) के ग्राफ की स्पर्शरेखा, x पर छेदक L की सीमित स्थिति है। y यदि फलन बिंदु x 0 पर अवकलनीय है, तो छेदक समीकरण y/ x f (x 0) में x और स्पर्श रेखा समीकरण का रूप y = y 0 + f (x 0) (x – x 0) होता है।

12 М0М0 М x0x0 x 0 + x dy = df(x 0; x) = f (x 0) x x y = f(x) f(x0)f(x0) f(x 0 + x) 0 x y F E EM = o (x) x 0 के लिए स्पर्श रेखा समीकरण से हमें y - y 0 = f (x 0) (x - x 0) = df (x 0) प्राप्त होता है - बिंदु x 0 से बिंदु x पर जाने पर स्पर्श रेखा की कोटि में वृद्धि। बिंदु M 0 पर किसी फ़ंक्शन के ग्राफ़ का अभिलंब बिंदु M 0 से गुजरने वाली स्पर्श रेखा पर लंबवत एक सीधी रेखा है। इसके समीकरण का रूप y = y 0 – 1/f (x 0) (x – x 0) है। एल 1 – सामान्य

13 व्युत्पन्न और अंतर के भौतिक अनुप्रयोग यदि S(t) समय t में किसी भौतिक बिंदु द्वारा तय किया गया पथ है, तो S "(t) सामग्री बिंदु की तात्कालिक गति है, और dS = S "(t)dt है वह दूरी जो भौतिक बिंदु t से t + dt तक की समयावधि के दौरान तय करेगा, यदि वह उस समय t पर तात्कालिक गति के बराबर गति से आगे बढ़ रहा हो। यदि Q(t) समय t पर कंडक्टर के क्रॉस सेक्शन के माध्यम से बहने वाली बिजली की मात्रा है, तो Q "(t) = I वर्तमान ताकत है। यदि N(t) समय t के दौरान बनने वाले पदार्थ की मात्रा है एक रासायनिक प्रतिक्रिया, फिर एन "(टी) - रासायनिक प्रतिक्रिया की दर।

यदि फ़ंक्शन य = एफ(एक्स) कुछ बिंदु पर भिन्न है एक्स = एक्स 0, तो यह इस बिंदु पर निरंतर है।

इस प्रकार, फ़ंक्शन में असंततता बिंदुओं पर व्युत्पन्न नहीं हो सकता है। विपरीत निष्कर्ष गलत है, अर्थात इस तथ्य से कि किसी बिंदु पर एक्स = एक्स 0 फ़ंक्शन य = एफ(एक्स) निरंतर है इसका मतलब यह नहीं है कि यह इस बिंदु पर भिन्न है। उदाहरण के लिए, फ़ंक्शन य = |एक्स| सभी के लिए निरंतर एक्स (–< एक्स < ), но в точке एक्स= 0 का कोई व्युत्पन्न नहीं है. इस बिंदु पर ग्राफ़ की कोई स्पर्शरेखा नहीं है। एक दायां स्पर्शरेखा और एक बायां स्पर्शरेखा है, लेकिन वे संपाती नहीं हैं।

21 नियम ढूँढना उत्पादन मात्रा

नियम 1।यदि फ़ंक्शन y = f(x) और y = g(x) का बिंदु x पर व्युत्पन्न है, तो उनके योग का भी बिंदु x पर व्युत्पन्न है, और योग का व्युत्पन्न व्युत्पन्न के योग के बराबर है:
(f(x) + 8(x))" =f (x)+ (x).
व्यवहार में, यह नियम अधिक संक्षेप में तैयार किया गया है: किसी योग का व्युत्पन्न उसके व्युत्पन्नों के योग के बराबर होता है।
उदाहरण के लिए,
नियम 2.यदि फ़ंक्शन y = f(x) का व्युत्पन्न बिंदु x पर है, तो फ़ंक्शन y = kf(x) का भी बिंदु x पर व्युत्पन्न है, और:

व्यवहार में, यह नियम अधिक संक्षेप में तैयार किया गया है: स्थिर कारक को व्युत्पन्न के चिह्न से बाहर निकाला जा सकता है। उदाहरण के लिए,

नियम 3.यदि फ़ंक्शन y=f(x) और y =g(x) का बिंदु x पर व्युत्पन्न है, तो उनके उत्पाद का भी बिंदु x पर व्युत्पन्न है, और:

व्यवहार में, यह नियम निम्नानुसार तैयार किया गया है: दो कार्यों के उत्पाद का व्युत्पन्न दो पदों के योग के बराबर है। पहला पद पहले फ़ंक्शन और दूसरे फ़ंक्शन के व्युत्पन्न का उत्पाद है, और दूसरा पद पहले फ़ंक्शन का उत्पाद और दूसरे फ़ंक्शन का व्युत्पन्न है।
उदाहरण के लिए:
नियम 4.यदि फ़ंक्शन y = f(x) और y=g(x) का व्युत्पन्न है तो भागफल का बिंदु x पर व्युत्पन्न है, और:

जटिल व्युत्पन्नों की तालिका

22 अंतर. कार्यात्मक बिंदु पर

समारोह य=एफ(एक्स) को बिंदु पर अवकलनीय कहा जाता है एक्स 0 यदि इसकी वृद्धि Δ है य(एक्स 0,Δ एक्स) के रूप में दर्शाया जा सकता है

Δ य(एक्स 0,Δ एक्स)=एΔ एक्स+हे(Δ एक्स).

मुख्य रैखिक भाग एΔ एक्सवेतन वृद्धि Δ यबिंदु पर इस फ़ंक्शन का अंतर कहा जाता है एक्स 0, वृद्धि के अनुरूप Δ एक्स, और प्रतीक द्वारा दर्शाया गया है डीवाई(एक्स 0,Δ एक्स).

समारोह के लिए य=एफ(एक्स) बिंदु पर अवकलनीय था एक्स 0, व्युत्पन्न के अस्तित्व के लिए यह आवश्यक और पर्याप्त है एफ′( एक्स 0), और समानता सत्य है ए=एफ′( एक्स 0).

अंतर के लिए अभिव्यक्ति का रूप है

डीवाई(एक्स 0,डीएक्स)=एफ′( एक्स 0)डीएक्स,

कहाँ डीएक्स=Δ एक्स.

23 उत्पाद. जटिल समारोह

एक जटिल फ़ंक्शन का व्युत्पन्न. पैरामीट्रिक रूप से निर्दिष्ट फ़ंक्शन का व्युत्पन्न

होने देना य - जटिल कार्य एक्स, अर्थात। य = एफ(यू), यू = जी(एक्स), या

अगर जी(एक्स) और एफ(यू) - बिंदुओं पर क्रमशः उनके तर्कों के भिन्न-भिन्न कार्य एक्सऔर यू = जी(एक्स), तब जटिल फलन भी बिंदु पर अवकलनीय होता है एक्स और सूत्र द्वारा पाया जाता है

पैरामीट्रिक रूप से दिए गए फ़ंक्शन का व्युत्पन्न।

24 उत्पादन और अंतर। उच्चतम आदेश

अब मान लीजिए कि वें क्रम का अवकलज बिंदु के एक निश्चित पड़ोस में परिभाषित किया गया है और अवकलनीय है। तब

यदि किसी फ़ंक्शन में किसी डोमेन डी में किसी एक चर के संबंध में आंशिक व्युत्पन्न है, तो उक्त व्युत्पन्न, स्वयं एक फ़ंक्शन होने के नाते, किसी बिंदु पर उसी या किसी अन्य चर के संबंध में आंशिक व्युत्पन्न हो सकता है। मूल फ़ंक्शन के लिए, ये डेरिवेटिव दूसरे क्रम के आंशिक डेरिवेटिव (या दूसरे आंशिक डेरिवेटिव) होंगे।

विभिन्न चरों के संबंध में लिए गए दूसरे या उच्च क्रम के आंशिक व्युत्पन्न को मिश्रित आंशिक व्युत्पन्न कहा जाता है। उदाहरण के लिए,

आदेश में अंतर एन, कहाँ एन > 1किसी फ़ंक्शन के किसी बिंदु पर ऑर्डर अंतर के इस बिंदु पर अंतर कहा जाता है (एन - 1), वह है

एक फ़ंक्शन के लिए जो एक चर पर निर्भर करता है, दूसरा और तीसरा अंतर इस तरह दिखता है:

यहां से हम अंतर का एक सामान्य दृष्टिकोण प्राप्त कर सकते हैं एनफ़ंक्शन से वां क्रम:

25 फ़र्मेट, रोले, लैंग्रेंज के प्रमेय

वी फ़र्मेट का प्रमेय:फ़ंक्शन को परिभाषित होने दें और उसके अधिकतम और न्यूनतम मान तक पहुंचने दें ( एमऔर एम) कुछ में . यदि इसमें कोई व्युत्पन्न है, तो यह आवश्यक रूप से 0 के बराबर है।

प्रमाण: मौजूद है. दो संभावित मामले हैं:

1) , => , => .

2) , => , => .

1) और 2) से यह इस प्रकार है

वी रोले का प्रमेय (व्युत्पन्न की जड़ों के बारे में):फ़ंक्शन को निरंतर चालू और अवकलनीय रहने दें और खंड के अंत में समान मान लें: . फिर वहां से कम से कम एक बिंदु है, जिस पर व्युत्पन्न है।

v प्रमाण: निरंतर पहुँचता है एमऔर एम. तब दो स्थितियाँ संभव हैं:

2) फ़र्मेट के प्रमेय के अनुसार अंतराल के भीतर सबसे बड़ा मूल्य प्राप्त किया जाता है।

वी लैंग्रेज़ का प्रमेय (अंतिम वेतन वृद्धि के बारे में):फ़ंक्शन को निरंतर चालू और अवकलनीय रहने दें। फिर इनमें से कम से कम एक तो है, जिसके लिए निम्नलिखित समानता है:।

प्रमाण: आइए फ़ंक्शन का परिचय दें। (निरंतर पर और अवकलनीय पर)।

रोले के प्रमेय को संतुष्ट करने वाला एक फ़ंक्शन मौजूद है, जिसके लिए: , , , ।

· फ़ंक्शन को कॉल किया जाता है सख्ती से बढ़ रहा हैअगर पर

· फ़ंक्शन को कॉल किया जाता है घटतेअगर पर

· फ़ंक्शन को कॉल किया जाता है सख्ती से घट रही हैअगर पर

परिभाषा: किसी बिंदु पर किसी फ़ंक्शन का व्युत्पन्न वह सीमा है जिस तक उस बिंदु पर इसकी वृद्धि का अनुपात तर्क की संबंधित वृद्धि के साथ तब होता है जब बाद वाला शून्य हो जाता है:

अर्थात यदि परिभाषित किया जाए तो

प्रमेय 1:

किसी फ़ंक्शन के ग्राफ़ में एक गैर-ऊर्ध्वाधर स्पर्शरेखा होती है यदि और केवल तभी जब किसी दिए गए बिंदु पर उस फ़ंक्शन के व्युत्पन्न का एक सीमित मान हो।

सबूत:

मान लीजिए कि एक मान f'()-परिमित है

मान लीजिए कि एक गैर-ऊर्ध्वाधर स्पर्शरेखा है => एक परिमित है।

सेकेंट स्पर्शरेखा की ओर प्रवृत्त होता है।

प्रमेय सिद्ध हो चुका है।

टिकट 2 व्युत्पन्न वाले फ़ंक्शन की निरंतरता।

किसी बिंदु a के किसी पड़ोस में परिभाषित फ़ंक्शन f (x) को इस बिंदु पर निरंतर कहा जाता है

प्रमेय: (व्युत्पन्न के अस्तित्व के लिए एक आवश्यक शर्त)

यदि कोई फलन किसी बिंदु पर परिमित है, तो वह उस बिंदु पर सतत नहीं है।

सबूत:

इसलिए, यह एक बिंदु पर निरंतर है।

प्रमेय सिद्ध हो चुका है।

टिप्पणी : विपरीत कथन सत्य नहीं है; यदि कोई फ़ंक्शन किसी बिंदु पर निरंतर है, तो इसका मतलब यह नहीं है कि उस बिंदु पर इसका व्युत्पन्न है।

कथन : यदि किसी फ़ंक्शन में एक बिंदु पर दाएं और बाएं व्युत्पन्न हैं, तो यह दाएं और बाएं दोनों पर निरंतर है।

टिकट 3

किसी योग, उत्पाद, भागफल का व्युत्पन्न।

व्युत्क्रम फलन का व्युत्पन्न.

एक अवकलनीय फलन की परिभाषा. भिन्नता के लिए आवश्यक एवं पर्याप्त शर्त।

मान लीजिए कि फ़ंक्शन का एक बिंदु (परिमित) पर व्युत्पन्न है: .

फिर, पर्याप्त रूप से छोटे लोगों के लिए, हम इसे एक योग और कुछ फ़ंक्शन के रूप में लिख सकते हैं, जिसे हम निरूपित करते हैं, जो एक साथ शून्य हो जाता है:,

और एक बिंदु पर वृद्धि को इस प्रकार लिखा जा सकता है:

या (1) ,

आख़िरकार, अभिव्यक्ति को एक फ़ंक्शन के रूप में समझा जाता है जैसे कि इसका अनुपात शून्य हो जाता है।

स्पष्टीकरण:

परिभाषा .

किसी फ़ंक्शन को एक बिंदु पर अवकलनीय कहा जाता है यदि इसकी वृद्धि को इस प्रकार दर्शाया जा सकता है: (2),

जहां A निर्भर नहीं करता है, लेकिन आम तौर पर निर्भर करता है।

प्रमेय 1:

किसी फ़ंक्शन के किसी बिंदु पर अवकलनीय होने के लिए, यह आवश्यक और पर्याप्त है कि उस बिंदु पर इसका एक परिमित व्युत्पन्न हो।

सबूत:

शर्त की पर्याप्तता ऊपर सिद्ध किया गया था: एक परिमित व्युत्पन्न के अस्तित्व से यह फॉर्म (1) में प्रतिनिधित्व की संभावना का पालन करता है, जहां हम रख सकते हैं।

आवश्यकता शर्त . मान लीजिए कि फलन एक बिंदु पर अवकलनीय है। फिर (2) से, यह मानते हुए, हम प्राप्त करते हैं।

दाईं ओर की सीमा मौजूद है और A: के बराबर है।

इसका मतलब है कि एक व्युत्पन्न है. प्रमेय सिद्ध हो चुका है।

टिकट 6 किसी फ़ंक्शन का अंतर, इसका ज्यामितीय अर्थ।

यदि फ़ंक्शन एफएक व्युत्पन्न है f΄(x हे ) बिंदु पर एक्स हे, तो वहां एक सीमा है जहां Δ एफ=एफ(एक्स हे + Δ एक्स)-एफ(एक्स हे ) ,,या जहां A=f΄(x हे ) .

परिभाषा:

समारोह एफबिंदु पर भिन्न एक्स हे, यदि इसकी वृद्धि को इस प्रकार दर्शाया जा सकता है:

कहाँ एΔ एक्स=डीएफ. (*)

अंतर फ़ंक्शन की वृद्धि का मुख्य रैखिक भाग है।

यदि कोई परिमित व्युत्पन्न है f΄(x हे ) बिंदु पर एक्स हे, फिर फ़ंक्शन एफ(एक्स)इस बिंदु पर भिन्न है।

इसका विपरीत भी सत्य है: यदि फलन एफबिंदु पर भिन्न एक्स हे, अर्थात। इसकी वृद्धि को फॉर्म (*) में दर्शाया जा सकता है, फिर इसमें बिंदु पर व्युत्पन्न होता है एक्स हे, के बराबर ए:

अंतर का ज्यामितीय अर्थ:

एऔर बी- ग्राफ अंक एफ(एक्स), मूल्यों के अनुरूप एक्स हेऔर (एक्स हे + Δ एक्स)स्वतंत्र चर। अंकों का क्रम एऔर बीक्रमशः बराबर एफ(एक्स हे ) और एफ(एक्स हे + Δ एक्स). फ़ंक्शन वृद्धि Δ एफ=एफ(एक्स हे + Δ एक्स)-एफ(एक्स हे ) बिंदु पर एक्स हेखंड की लंबाई के बराबर बी.डीऔर योग Δ के रूप में दर्शाया जा सकता है एफ=बीडी=डीसी+सीबी, कहाँ डीसी=tgαΔ x=f΄(x हे ) Δ एक्सऔर α बिंदु पर स्पर्शरेखा के बीच का कोण है एग्राफ़ और अक्ष की सकारात्मक दिशा के लिए एक्स. इससे यह स्पष्ट है कि डीसीएक विभेदक कार्य है एफबिंदु पर एक्स हे :

DC=df=f΄(x हे ) Δ एक्स.

वहीं, दूसरे सदस्य की हिस्सेदारी सी.बी.वेतन वृद्धि Δ एफमूल्य का हिसाब रखें. यह मान, बड़े पैमाने पर Δ एक्स, शायद मुख्य पद से भी बड़ा, लेकिन यह Δ से उच्च क्रम का एक अतिसूक्ष्म है एक्स, जब Δ x→0.

एक साक्षात्कार पर निरंतर कार्यों के गुण

आइए एक अंतराल पर निरंतर चलने वाले कार्यों के कुछ गुणों पर विचार करें। हम इन संपत्तियों को बिना सबूत के पेश करते हैं।

समारोह वाई = एफ(एक्स)बुलाया खंड पर निरंतर [ए, बी], यदि यह इस खंड के सभी आंतरिक बिंदुओं और इसके सिरों पर निरंतर है, अर्थात। बिंदुओं पर एऔर बी, क्रमशः दाएं और बाएं पर निरंतर है।

प्रमेय 1.अंतराल पर निरंतर एक फ़ंक्शन [ ए, बी], इस खंड के कम से कम एक बिंदु पर सबसे बड़ा मान होता है और कम से कम एक बिंदु पर सबसे छोटा।

प्रमेय बताता है कि यदि कोई फ़ंक्शन वाई = एफ(एक्स)अंतराल पर निरंतर है [ ए, बी], तो कम से कम एक बिंदु है एक्स 1 Î [ ए, बी] जैसे कि फ़ंक्शन का मान एफ(एक्स)इस बिंदु पर इस खंड पर इसके सभी मूल्य सबसे बड़े होंगे: एफ(एक्स 1) ≥ एफ(एक्स). इसी तरह एक बिंदु ऐसा भी है एक्स 2, जिसमें फ़ंक्शन मान सेगमेंट के सभी मानों में से सबसे छोटा होगा: एफ(एक्स 1) ≤ एफ(एक्स).

यह स्पष्ट है कि ऐसे कई बिंदु हो सकते हैं; उदाहरण के लिए, चित्र दिखाता है कि फ़ंक्शन एफ(एक्स)दो बिंदुओं पर सबसे छोटा मान लेता है एक्स 2और एक्स 2 ".

टिप्पणी. यदि हम अंतराल पर फ़ंक्शन के मान पर विचार करते हैं तो प्रमेय का कथन गलत हो सकता है ( ए, बी). दरअसल, अगर हम फ़ंक्शन पर विचार करें वाई = एक्स(0, 2) पर, यह इस अंतराल पर निरंतर है, लेकिन इसमें सबसे बड़े या सबसे छोटे मूल्यों तक नहीं पहुंचता है: यह अंतराल के अंत में इन मूल्यों तक पहुंचता है, लेकिन छोर संबंधित नहीं होते हैं हमारे डोमेन के लिए.

साथ ही, असंतत कार्यों के लिए प्रमेय सत्य नहीं रह जाता है। एक उदाहरण दें।

परिणाम।यदि फ़ंक्शन एफ(एक्स)निरंतर है [ ए, बी], तो यह इस खंड पर सीमित है।

प्रमेय 2.कार्य करने दो वाई = एफ(एक्स)अंतराल पर निरंतर है [ ए, बी] और इस खंड के अंत में विभिन्न चिह्नों का मान लेता है, तो खंड के अंदर कम से कम एक बिंदु होता है एक्स = सी, जिसमें फ़ंक्शन शून्य हो जाता है: एफ(सी)= 0, जहां ए< C< b

इस प्रमेय का एक सरल ज्यामितीय अर्थ है: यदि किसी सतत फलन के ग्राफ के बिंदु वाई = एफ(एक्स), खंड के सिरों के अनुरूप [ ए, बी] अक्ष के विपरीत दिशा में स्थित हों बैल, तो यह ग्राफ़ खंड के कम से कम एक बिंदु पर अक्ष को प्रतिच्छेद करता है बैल. असंतत कार्यों में यह गुण नहीं हो सकता है।

यह प्रमेय निम्नलिखित सामान्यीकरण को स्वीकार करता है।

प्रमेय 3 (मध्यवर्ती मूल्य प्रमेय)।कार्य करने दो वाई = एफ(एक्स)अंतराल पर निरंतर है [ ए, बी] और एफ(ए) = ए, एफ(बी) = बी. फिर किसी भी संख्या के लिए सी, के बीच निष्कर्ष निकाला गया एऔर बी, इस खंड के अंदर एक ऐसा बिंदु है सीÎ [ ए, बी], क्या एफ(सी) = सी.

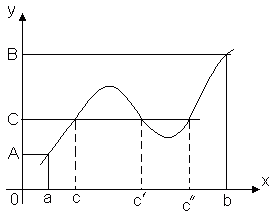
यह प्रमेय ज्यामितीय रूप से स्पष्ट है। फ़ंक्शन के ग्राफ़ पर विचार करें वाई = एफ(एक्स). होने देना एफ(ए) = ए, एफ(बी) = बी. फिर कोई भी सीधी रेखा वाई = सी, कहाँ सी- बीच में कोई भी संख्या एऔर बी, फ़ंक्शन के ग्राफ़ को कम से कम एक बिंदु पर प्रतिच्छेद करेगा। प्रतिच्छेदन बिंदु का भुज वह मान होगा एक्स = सी, जिस पर एफ(सी) = सी.

इस प्रकार, एक सतत फलन, एक मान से दूसरे मान की ओर बढ़ते हुए, आवश्यक रूप से सभी मध्यवर्ती मानों से होकर गुजरता है। विशेष रूप से:

परिणाम।यदि फ़ंक्शन वाई = एफ(एक्स)एक निश्चित अंतराल पर निरंतर होता है और सबसे बड़े और सबसे छोटे मान लेता है, फिर इस अंतराल पर यह कम से कम एक बार अपने सबसे छोटे और सबसे बड़े मानों के बीच मौजूद किसी भी मान को लेता है।

व्युत्पन्न और उसके अनुप्रयोग. व्युत्पन्न की परिभाषा

आइये कुछ कार्य करें y=f(x),कुछ अंतराल पर परिभाषित. प्रत्येक तर्क मान के लिए एक्सइस अंतराल से फ़ंक्शन y=f(x)एक निश्चित अर्थ है.

दो तर्क मानों पर विचार करें: प्रारंभिक एक्स 0 और नया एक्स.

अंतर एक्स–एक्स 0 कहा जाता है तर्क x को बढ़ाकरबिंदु पर एक्स 0 और दर्शाया गया है Δx. इस प्रकार, Δx = x – x 0 (तर्क वृद्धि या तो सकारात्मक या नकारात्मक हो सकती है)। इस समानता से यह निष्कर्ष निकलता है एक्स=एक्स 0 +Δx, अर्थात। वेरिएबल के प्रारंभिक मूल्य में कुछ वृद्धि हुई है। फिर, यदि बिंदु पर एक्स 0 फ़ंक्शन मान था एफ(एक्स 0 ), फिर एक नये बिंदु पर एक्सफ़ंक्शन मान लेगा एफ(एक्स) = एफ(एक्स 0 +Δx).

अंतर Y y 0 = एफ(एक्स) – एफ(एक्स 0 ) बुलाया कार्य वृद्धि वाई = एफ(एक्स)बिंदु पर एक्स 0 और प्रतीक द्वारा दर्शाया गया है Δय. इस प्रकार,

Δy = f(x) – f(x 0 ) = एफ(एक्स 0 +Δx) - f(x 0 ) .

(1)

आमतौर पर तर्क का प्रारंभिक मूल्य एक्स 0 को निश्चित माना जाता है, और नया मान एक्स- चर। तब य 0 = एफ(एक्स 0 ) स्थिर हो जाता है, और वाई = एफ(एक्स)- चर। वेतन वृद्धि Δयऔर Δxचर भी होंगे और सूत्र (1) यह दर्शाता है डीवाईएक वेरिएबल का एक फ़ंक्शन है Δx.

आइए फ़ंक्शन की वृद्धि और तर्क की वृद्धि का अनुपात बनाएं

आइए इस अनुपात की सीमा ज्ञात करें Δx→0. यदि यह सीमा मौजूद है, तो इसे इस फ़ंक्शन का व्युत्पन्न कहा जाता है एफ(एक्स)बिंदु पर एक्स 0 और निरूपित करें एफ "(एक्स 0). इसलिए,

यौगिकयह फ़ंक्शन वाई = एफ(एक्स)बिंदु पर एक्स 0 को फ़ंक्शन वृद्धि अनुपात की सीमा कहा जाता है Δ यतर्क वृद्धि के लिए Δ एक्स, जब उत्तरार्द्ध मनमाने ढंग से शून्य हो जाता है।

ध्यान दें कि एक ही फ़ंक्शन के लिए विभिन्न बिंदुओं पर व्युत्पन्न एक्सअलग-अलग मान ले सकते हैं, यानी व्युत्पन्न को तर्क का एक कार्य माना जा सकता है एक्स. यह फ़ंक्शन निर्दिष्ट है एफ "(एक्स)

व्युत्पन्न को प्रतीकों द्वारा दर्शाया जाता है एफ "(एक्स),वाई", । व्युत्पन्न का विशिष्ट मूल्य एक्स = एद्वारा चिह्नित एफ "(ए) या य "| एक्स=ए.

किसी फ़ंक्शन का व्युत्पन्न खोजने की प्रक्रिया एफ(एक्स)इस फ़ंक्शन का विभेदन कहा जाता है।

परिभाषा के अनुसार सीधे व्युत्पन्न खोजने के लिए, आप निम्नलिखित का उपयोग कर सकते हैं: अंगूठे का नियम:

उदाहरण।

व्युत्पन्न का यांत्रिक अर्थ

भौतिकी से ज्ञात होता है कि एकसमान गति के नियम का क्या रूप है एस = वी टी, कहाँ एस- पथ समय के क्षण तक चला गया टी, वी– एकसमान गति की गति.

हालाँकि, क्योंकि प्रकृति में होने वाली अधिकांश गतिविधियाँ असमान होती हैं, फिर सामान्यतः गति, और, परिणामस्वरूप, दूरी एससमय पर निर्भर करेगा टी, अर्थात। समय का एक कार्य होगा.

तो, एक भौतिक बिंदु को कानून के अनुसार एक दिशा में एक सीधी रेखा में चलने दें s=s(t).

आइए समय में एक निश्चित बिंदु को चिह्नित करें टी 0 . इस बिंदु पर बिंदु रास्ता पार कर चुका है s=s(t 0 ). आइए गति निर्धारित करें वीसमय के एक क्षण में भौतिक बिंदु टी 0 .

ऐसा करने के लिए, आइए किसी अन्य समय बिंदु पर विचार करें टी 0 + Δ टी. यह यात्रा पथ से मेल खाता है =एस(टी 0 + Δ टी). फिर समय की अवधि में Δ टीबिंदु ने पथ Δs की यात्रा की है =एस(टी 0 + Δ टी)–अनुसूचित जनजाति)।

आइए दृष्टिकोण पर विचार करें. इसे समय अंतराल Δ में औसत गति कहा जाता है टी. औसत गति इस समय किसी बिंदु की गति की गति को सटीक रूप से चित्रित नहीं कर सकती है टी 0 (क्योंकि गति असमान है)। औसत गति का उपयोग करके इस वास्तविक गति को अधिक सटीक रूप से व्यक्त करने के लिए, आपको कम समय Δ लेने की आवश्यकता है टी.

तो, समय में एक निश्चित क्षण में गति की गति टी 0 (तात्कालिक गति) से अंतराल में औसत गति की सीमा है टी 0 से टी 0 +Δ टी, जब Δ टी→0:

,

वे। असमान गतियह समय के संबंध में तय की गई दूरी का व्युत्पन्न है।

व्युत्पन्न का ज्यामितीय अर्थ

आइए सबसे पहले किसी दिए गए बिंदु पर वक्र की स्पर्शरेखा की परिभाषा का परिचय दें।

आइए हमारे पास एक वक्र और उस पर एक निश्चित बिंदु है म 0(आंकड़ा देखें) एक और बिंदु पर विचार करें एमइस वक्र और एक छेदक रेखा खींचिए म0 म. अगर बात एमवक्र और बिंदु के अनुदिश चलना शुरू कर देता है म 0गतिहीन रहता है, तब सेकेंट अपनी स्थिति बदल देता है। यदि, बिंदु के असीमित सन्निकटन के साथ एमएक वक्र के अनुदिश एक बिंदु तक म 0किसी भी तरफ छेदक एक निश्चित सीधी रेखा की स्थिति पर कब्जा कर लेता है एम 0 टी, फिर सीधे एम 0 टीकिसी दिए गए बिंदु पर वक्र की स्पर्श रेखा कहलाती है म 0.

वह।, स्पर्शरेखाकिसी दिए गए बिंदु पर वक्र के लिए म 0सेकेंट की सीमा स्थिति कहलाती है म0 मजब बिंदु एमवक्र के अनुदिश एक बिंदु की ओर बढ़ता है म 0.

आइए अब सतत फलन पर विचार करें y=f(x)और इस फ़ंक्शन के अनुरूप वक्र। कुछ कीमत पर एक्स 0 फ़ंक्शन मान लेता है आप 0 =एफ(एक्स 0).ये मूल्य एक्स 0 और यवक्र पर 0 एक बिंदु से मेल खाता है म 0 (x 0 ; य 0).चलिए तर्क देते हैं एक्स 0वृद्धि Δ एक्स. तर्क का नया मान फ़ंक्शन के बढ़े हुए मान से मेल खाता है य 0 +Δ y=f(x 0 –Δ एक्स). हमें बात समझ में आ गई एम(एक्स 0+Δ एक्स; य 0+Δ य).आइए एक सेकेंट बनाएं म0 मऔर अक्ष की धनात्मक दिशा के साथ छेदक द्वारा बने कोण को φ से निरूपित करें बैल. आइए एक रिश्ता बनाएं और उस पर ध्यान दें।

यदि अब Δ एक्स→0, तो फ़ंक्शन Δ की निरंतरता के कारण पर→0, और इसलिए बात एम, एक वक्र के साथ चलते हुए, बिना किसी सीमा के बिंदु तक पहुंचता है म 0. फिर सेकेंट म0 मबिंदु पर वक्र की स्पर्शरेखा की स्थिति लेने की प्रवृत्ति होगी म 0, और कोण φ→α Δ पर एक्स→0, जहां α स्पर्शरेखा और अक्ष की सकारात्मक दिशा के बीच के कोण को दर्शाता है बैल. चूंकि फ़ंक्शन tan φ लगातार φ≠π/2 के लिए φ पर निर्भर करता है, तो φ→α tan φ → tan α के लिए और, इसलिए, स्पर्शरेखा का ढलान होगा:

वे। एफ "(एक्स)= टीजी α .

इस प्रकार, ज्यामितीय रूप से वाई "(एक्स 0)बिंदु पर इस फ़ंक्शन के ग्राफ़ के स्पर्शरेखा के ढलान का प्रतिनिधित्व करता है एक्स 0, अर्थात। किसी दिए गए तर्क मान के लिए एक्स, व्युत्पन्न फ़ंक्शन के ग्राफ़ के स्पर्शरेखा द्वारा गठित कोण के स्पर्शरेखा के बराबर है एफ(एक्स)उचित बिंदु पर एम 0 (एक्स; वाई)सकारात्मक अक्ष दिशा के साथ बैल।

उदाहरण।वक्र की स्पर्श रेखा का ढलान ज्ञात कीजिए वाई = एक्स 2 बिंदु पर एम(-1; 1).

हम पहले ही देख चुके हैं कि ( एक्स 2)" = 2एक्स. लेकिन वक्र की स्पर्श रेखा का कोणीय गुणांक tan α = है य"| x=-1 = – 2.

कार्यों की भिन्नता. भिन्न-भिन्न प्रकार्य की निरंतरता

समारोह y=f(x)बुलाया विभेदककिन्हीं बिंदुओं पर एक्स 0 यदि इस बिंदु पर इसका एक निश्चित व्युत्पन्न है, अर्थात। यदि रिश्ते की सीमा मौजूद है और सीमित है।

यदि कोई फलन किसी निश्चित खंड के प्रत्येक बिंदु पर अवकलनीय है [ ए; बी] या अंतराल ( ए; बी), फिर वे कहते हैं कि वह विभेदकखंड पर [ ए; बी] या, क्रमशः, अंतराल में ( ए; बी).

निम्नलिखित प्रमेय मान्य है, जो अवकलनीय और सतत कार्यों के बीच संबंध स्थापित करता है।

प्रमेय.यदि फ़ंक्शन y=f(x)किसी बिंदु पर भिन्न एक्स 0, तो यह इस बिंदु पर निरंतर है।

इस प्रकार, किसी फ़ंक्शन की भिन्नता से उसकी निरंतरता का अनुसरण होता है।

सबूत. अगर , वह

,

जहां α एक अतिसूक्ष्म मात्रा है, अर्थात एक मात्रा Δ के रूप में शून्य की ओर प्रवृत्त होती है एक्स→0. परन्तु फिर

Δ य=एफ "(एक्स 0) Δ एक्स+αΔ एक्स=> Δ य→0 पर Δ एक्स→0, यानी एफ(एक्स) – एफ(एक्स 0)→0 पर एक्स→एक्स 0 , जिसका अर्थ है कि फ़ंक्शन एफ(एक्स)एक बिंदु पर निरंतर एक्स 0 . क्यू.ई.डी.

इस प्रकार, फ़ंक्शन में असंततता बिंदुओं पर व्युत्पन्न नहीं हो सकता है। इसका विपरीत सत्य नहीं है: ऐसे निरंतर कार्य हैं जो कुछ बिंदुओं पर भिन्न नहीं होते हैं (अर्थात, इन बिंदुओं पर कोई व्युत्पन्न नहीं होता है)।

चित्र के बिंदुओं पर विचार करें ए, बी, सी.

बिंदु पर एΔ पर एक्स→0 अनुपात की कोई सीमा नहीं है (क्योंकि Δ के लिए एक तरफा सीमाएँ भिन्न हैं एक्स→0–0 और Δ एक्स→0+0). बिंदु पर एग्राफ़ में कोई परिभाषित स्पर्शरेखा नहीं है, लेकिन ढलानों के साथ दो अलग-अलग एक-तरफ़ा स्पर्शरेखाएँ हैं को 1 और को 2. इस प्रकार के बिंदु को कोना बिंदु कहा जाता है।

बिंदु पर बीΔ पर एक्स→0 अनुपात अनंत रूप से बड़ी मात्रा का एक स्थिर चिह्न है। फ़ंक्शन में अनंत व्युत्पन्न हैं। इस बिंदु पर ग्राफ़ में एक ऊर्ध्वाधर स्पर्शरेखा है। बिंदु प्रकार - ऊर्ध्वाधर स्पर्शरेखा का "विभक्ति बिंदु"।

बिंदु पर सीएकतरफ़ा व्युत्पन्न विभिन्न संकेतों की असीम रूप से बड़ी मात्रा में होते हैं। इस बिंदु पर ग्राफ़ में दो विलयित ऊर्ध्वाधर स्पर्शरेखाएँ हैं। प्रकार - एक ऊर्ध्वाधर स्पर्शरेखा के साथ "वापसी बिंदु" - एक कोने बिंदु का एक विशेष मामला।