អត្ថបទនេះបន្តប្រធានបទនៃសមីការបន្ទាត់ត្រង់នៅលើយន្តហោះ៖ ពិចារណាប្រភេទនៃសមីការដូចជាសមីការទូទៅនៃបន្ទាត់ត្រង់។ ចូរកំណត់ទ្រឹស្តីបទមួយ ហើយផ្តល់ភស្តុតាងរបស់វា។ ចូរយើងស្វែងយល់ថាតើសមីការទូទៅមិនពេញលេញនៃបន្ទាត់ត្រង់គឺជាអ្វី និងរបៀបធ្វើការផ្លាស់ប្តូរពីសមីការទូទៅទៅប្រភេទសមីការផ្សេងទៀតនៃបន្ទាត់ត្រង់។ យើងនឹងបង្រួបបង្រួមទ្រឹស្ដីទាំងមូលជាមួយនឹងការបង្ហាញ និងដោះស្រាយបញ្ហាជាក់ស្តែង។

Yandex.RTB R-A-339285-1

អនុញ្ញាតឱ្យប្រព័ន្ធកូអរដោនេរាងចតុកោណ O x y ត្រូវបានផ្តល់ឱ្យនៅលើយន្តហោះ។

ទ្រឹស្តីបទ ១

សមីការណាមួយនៃសញ្ញាបត្រទីមួយដែលមានទម្រង់ A x + B y + C \u003d 0 ដែល A, B, C គឺជាចំនួនពិតមួយចំនួន (A និង B មិនស្មើនឹងសូន្យក្នុងពេលតែមួយ) កំណត់បន្ទាត់ត្រង់នៅក្នុង ប្រព័ន្ធសំរបសំរួលរាងចតុកោណនៅលើយន្តហោះ។ នៅក្នុងវេនបន្ទាត់ណាមួយនៅក្នុងប្រព័ន្ធកូអរដោនេចតុកោណនៅលើយន្តហោះត្រូវបានកំណត់ដោយសមីការដែលមានទម្រង់ A x + B y + C = 0 សម្រាប់សំណុំជាក់លាក់នៃតម្លៃ A, B, C ។

ភស្តុតាង

ទ្រឹស្តីបទនេះមានពីរចំណុច យើងនឹងបញ្ជាក់អំពីពួកវានីមួយៗ។

1. ចូរយើងបង្ហាញថាសមីការ A x + B y + C = 0 កំណត់បន្ទាត់នៅលើយន្តហោះ។

សូម​ឲ្យ​មាន​ចំណុច​មួយ​ចំនួន M 0 (x 0 , y 0) ដែល​កូអរដោនេ​ត្រូវ​គ្នា​នឹង​សមីការ A x + B y + C = 0 ។ ដូចនេះ៖ A x 0 + B y 0 + C = 0 ។ ដកពីផ្នែកខាងឆ្វេង និងខាងស្តាំនៃសមីការ A x + B y + C \u003d 0 ផ្នែកខាងឆ្វេង និងខាងស្តាំនៃសមីការ A x 0 + B y 0 + C \u003d 0 យើងទទួលបានសមីការថ្មីដែលមើលទៅដូចជា A (x − x 0) + B (y − y 0) = 0 ។ វាស្មើនឹង A x + B y + C = 0 ។

សមីការលទ្ធផល A (x − x 0) + B (y − y 0) = 0 គឺជាលក្ខខណ្ឌចាំបាច់ និងគ្រប់គ្រាន់សម្រាប់កាត់កែងនៃវ៉ិចទ័រ n → = (A, B) និង M 0 M → = (x − x 0, y - y 0) ។ ដូច្នេះ​សំណុំ​នៃ​ចំណុច M (x, y) កំណត់​ក្នុង​ប្រព័ន្ធ​កូអរដោណេ​ចតុកោណ​ជា​បន្ទាត់​ត្រង់​កាត់​កែង​ទៅ​ទិស​នៃ​វ៉ិចទ័រ n → = (A, B) ។ យើងអាចសន្មត់ថាវាមិនដូច្នោះទេ ប៉ុន្តែបន្ទាប់មកវ៉ិចទ័រ n → = (A, B) និង M 0 M → = (x − x 0, y - y 0) នឹងមិនកាត់កែងទេ ហើយសមភាព A (x − x 0) + B (y - y 0) = 0 មិនពិតទេ។

ដូច្នេះសមីការ A (x - x 0) + B (y - y 0) \u003d 0 កំណត់បន្ទាត់ជាក់លាក់មួយនៅក្នុងប្រព័ន្ធកូអរដោណេចតុកោណនៅលើយន្តហោះ ហើយដូច្នេះសមីការសមមូល A x + B y + C \u003d 0 កំណត់បន្ទាត់ដូចគ្នា។ ដូច្នេះ យើង​បាន​បង្ហាញ​ពី​ផ្នែក​ដំបូង​នៃ​ទ្រឹស្តីបទ។

1. អនុញ្ញាតឱ្យយើងបង្ហាញថាបន្ទាត់ត្រង់ណាមួយនៅក្នុងប្រព័ន្ធកូអរដោណេចតុកោណនៅលើយន្តហោះអាចត្រូវបានផ្តល់ដោយសមីការនៃដឺក្រេទីមួយ A x + B y + C = 0 ។

ចូរកំណត់បន្ទាត់ត្រង់ a នៅក្នុងប្រព័ន្ធកូអរដោណេចតុកោណនៅលើយន្តហោះ។ ចំណុច M 0 (x 0 , y 0) ដែលតាមរយៈបន្ទាត់នេះឆ្លងកាត់ ក៏ដូចជាវ៉ិចទ័រធម្មតានៃបន្ទាត់នេះ n → = (A , B) ។

អនុញ្ញាតឱ្យមានចំណុចមួយចំនួន M (x , y) - ចំណុចអណ្តែតនៃបន្ទាត់។ ក្នុងករណីនេះ វ៉ិចទ័រ n → = (A , B) និង M 0 M → = (x − x 0 , y - y 0) កាត់កែងទៅគ្នាទៅវិញទៅមក ហើយផលិតផលមាត្រដ្ឋានរបស់វាគឺសូន្យ៖

n → , M 0 M → = A (x − x 0) + B (y − y 0) = 0

ចូរយើងសរសេរសមីការ A x + B y - A x 0 - B y 0 = 0 កំណត់ C: C = - A x 0 - B y 0 ហើយចុងក្រោយទទួលបានសមីការ A x + B y + C = 0 ។

ដូច្នេះ យើង​បាន​ធ្វើ​ការ​បញ្ជាក់​ផ្នែក​ទីពីរ​នៃ​ទ្រឹស្តីបទ ហើយ​យើង​បាន​បង្ហាញ​ទ្រឹស្តីបទ​ទាំងមូល។

និយមន័យ ១

សមីការដែលមើលទៅដូច A x + B y + C = 0 - នេះ​គឺជា សមីការទូទៅនៃបន្ទាត់ត្រង់នៅលើយន្តហោះនៅក្នុងប្រព័ន្ធកូអរដោណេចតុកោណអូ x y ។

ដោយផ្អែកលើទ្រឹស្តីបទដែលបានបញ្ជាក់ យើងអាចសន្និដ្ឋានបានថា បន្ទាត់ត្រង់មួយដែលបានផ្តល់ឱ្យនៅលើយន្តហោះនៅក្នុងប្រព័ន្ធកូអរដោណេចតុកោណថេរ និងសមីការទូទៅរបស់វាត្រូវបានភ្ជាប់គ្នាដោយ inextricably ។ នៅក្នុងពាក្យផ្សេងទៀត បន្ទាត់ដើមត្រូវគ្នាទៅនឹងសមីការទូទៅរបស់វា; សមីការទូទៅនៃបន្ទាត់ត្រង់ត្រូវគ្នាទៅនឹងបន្ទាត់ត្រង់ដែលបានផ្តល់ឱ្យ។

វាក៏ធ្វើតាមពីភស្តុតាងនៃទ្រឹស្តីបទដែលថាមេគុណ A និង B សម្រាប់អថេរ x និង y គឺជាកូអរដោនេនៃវ៉ិចទ័រធម្មតានៃបន្ទាត់ត្រង់ដែលត្រូវបានផ្តល់ដោយសមីការទូទៅនៃបន្ទាត់ត្រង់ A x + B y + C = 0 ។

ពិចារណាឧទាហរណ៍ជាក់លាក់នៃសមីការទូទៅនៃបន្ទាត់ត្រង់មួយ។

អនុញ្ញាតឱ្យសមីការ 2 x + 3 y − 2 = 0 ត្រូវបានផ្តល់ឱ្យ ដែលត្រូវនឹងបន្ទាត់ត្រង់នៅក្នុងប្រព័ន្ធកូអរដោនេចតុកោណដែលបានផ្តល់ឱ្យ។ វ៉ិចទ័រធម្មតានៃបន្ទាត់នេះគឺជាវ៉ិចទ័រ n → = (2 , 3) ​​​​។ គូរបន្ទាត់ត្រង់ដែលបានផ្តល់ឱ្យក្នុងគំនូរ។

ខាងក្រោមនេះក៏អាចប្រកែកបានដែរ៖ បន្ទាត់ត្រង់ដែលយើងឃើញក្នុងគំនូរត្រូវបានកំណត់ដោយសមីការទូទៅ 2 x + 3 y - 2 = 0 ចាប់តាំងពីកូអរដោនេនៃចំណុចទាំងអស់នៃបន្ទាត់ត្រង់ដែលបានផ្តល់ឱ្យត្រូវគ្នាទៅនឹងសមីការនេះ។

យើងអាចទទួលបានសមីការ λ · A x + λ · B y + λ · C = 0 ដោយគុណភាគីទាំងពីរនៃសមីការបន្ទាត់ត្រង់ទូទៅដោយចំនួនមិនសូន្យ λ ។ សមីការលទ្ធផលគឺស្មើនឹងសមីការទូទៅដើម ដូច្នេះវានឹងពណ៌នាអំពីបន្ទាត់ដូចគ្នានៅក្នុងយន្តហោះ។

និយមន័យ ២

បំពេញសមីការទូទៅនៃបន្ទាត់ត្រង់- សមីការទូទៅនៃបន្ទាត់ A x + B y + C \u003d 0 ដែលលេខ A, B, C គឺមិនមែនសូន្យ។ បើមិនដូច្នោះទេសមីការគឺ មិនពេញលេញ.

ចូរយើងវិភាគការប្រែប្រួលទាំងអស់នៃសមីការទូទៅមិនពេញលេញនៃបន្ទាត់ត្រង់។

1. នៅពេល A \u003d 0, B ≠ 0, C ≠ 0 សមីការទូទៅក្លាយជា B y + C \u003d 0 ។ សមីការទូទៅមិនពេញលេញបែបនេះកំណត់បន្ទាត់ត្រង់នៅក្នុងប្រព័ន្ធកូអរដោណេចតុកោណ O x y ដែលស្របទៅនឹងអ័ក្ស O x ចាប់តាំងពីសម្រាប់តម្លៃពិតនៃ x អថេរ y នឹងយកតម្លៃ - គ. ម្យ៉ាងវិញទៀត សមីការទូទៅនៃបន្ទាត់ A x + B y + C \u003d 0 នៅពេល A \u003d 0, B ≠ 0 កំណត់ទីតាំងនៃចំនុច (x, y) ដែលកូអរដោនេគឺស្មើនឹងលេខដូចគ្នា - គ.
2. ប្រសិនបើ A \u003d 0, B ≠ 0, C \u003d 0 សមីការទូទៅក្លាយជា y \u003d 0 ។ សមីការមិនពេញលេញបែបនេះកំណត់អ័ក្ស x O x ។
3. នៅពេល A ≠ 0, B \u003d 0, C ≠ 0 យើងទទួលបានសមីការទូទៅមិនពេញលេញ A x + C \u003d 0 ដោយកំណត់បន្ទាត់ត្រង់ស្របទៅនឹងអ័ក្ស y ។
4. អនុញ្ញាតឱ្យ A ≠ 0, B \u003d 0, C \u003d 0 បន្ទាប់មកសមីការទូទៅមិនពេញលេញនឹងយកទម្រង់ x \u003d 0 ហើយនេះគឺជាសមីការនៃបន្ទាត់កូអរដោនេ O y ។
5. ទីបំផុតនៅពេលដែល A ≠ 0, B ≠ 0, C \u003d 0 សមីការទូទៅមិនពេញលេញទទួលបានទម្រង់ A x + B y \u003d 0 ។ ហើយសមីការនេះពិពណ៌នាអំពីបន្ទាត់ត្រង់ដែលឆ្លងកាត់ប្រភពដើម។ ជាការពិតណាស់ លេខគូ (0 , 0) ត្រូវគ្នានឹងសមភាព A x + B y = 0 ចាប់តាំងពី A · 0 + B · 0 = 0 ។

អនុញ្ញាតឱ្យយើងបង្ហាញក្រាហ្វិកប្រភេទខាងលើទាំងអស់នៃសមីការទូទៅមិនពេញលេញនៃបន្ទាត់ត្រង់មួយ។

ឧទាហរណ៍ ១

វាត្រូវបានគេដឹងថាបន្ទាត់ត្រង់ដែលបានផ្តល់ឱ្យគឺស្របទៅនឹងអ័ក្ស y ហើយឆ្លងកាត់ចំណុច 2 7 , - 11 ។ វាចាំបាច់ក្នុងការសរសេរសមីការទូទៅនៃបន្ទាត់ត្រង់ដែលបានផ្តល់ឱ្យ។

ដំណោះស្រាយ

បន្ទាត់ត្រង់ស្របទៅនឹងអ័ក្ស y ត្រូវបានផ្តល់ដោយសមីការនៃទម្រង់ A x + C \u003d 0 ដែលក្នុងនោះ A ≠ 0 ។ លក្ខខណ្ឌក៏បញ្ជាក់ពីកូអរដោនេនៃចំណុចដែលបន្ទាត់ឆ្លងកាត់ ហើយកូអរដោនេនៃចំណុចនេះត្រូវគ្នាទៅនឹងលក្ខខណ្ឌនៃសមីការទូទៅមិនពេញលេញ A x + C = 0 , i.e. សមភាពគឺត្រឹមត្រូវ៖

A 2 7 + C = 0

វាអាចទៅរួចដើម្បីកំណត់ C ពីវាដោយផ្តល់ឱ្យ A តម្លៃដែលមិនមែនជាសូន្យឧទាហរណ៍ A = 7 ។ ក្នុងករណីនេះយើងទទួលបាន៖ 7 2 7 + C \u003d 0 ⇔ C \u003d - 2 ។ យើងស្គាល់មេគុណ A និង C ជំនួសវាទៅក្នុងសមីការ A x + C = 0 ហើយទទួលបានសមីការដែលត្រូវការនៃបន្ទាត់៖ 7 x − 2 = 0

ចម្លើយ៖ 7 x − 2 = 0

ឧទាហរណ៍ ២

គំនូរបង្ហាញពីបន្ទាត់ត្រង់មួយ វាចាំបាច់ក្នុងការសរសេរសមីការរបស់វា។

ដំណោះស្រាយ

គំនូរដែលបានផ្តល់ឱ្យអនុញ្ញាតឱ្យយើងងាយស្រួលយកទិន្នន័យដំបូងសម្រាប់ដោះស្រាយបញ្ហា។ យើង​ឃើញ​ក្នុង​គំនូរ​ថា​បន្ទាត់​ដែល​បាន​ផ្តល់​ឲ្យ​ស្រប​នឹង​អ័ក្ស​ O x ហើយ​កាត់​តាម​ចំណុច (0 , 3) ​​​។

បន្ទាត់ត្រង់ដែលស្របទៅនឹង abscissa ត្រូវបានកំណត់ដោយសមីការទូទៅមិនពេញលេញ B y + С = 0 ។ ស្វែងរកតម្លៃនៃ B និង C ។ កូអរដោនេនៃចំណុច (0, 3) ចាប់តាំងពីបន្ទាត់ត្រង់ដែលបានផ្តល់ឱ្យឆ្លងកាត់វានឹងបំពេញសមីការនៃបន្ទាត់ត្រង់ B y + С = 0 បន្ទាប់មកសមភាពមានសុពលភាព: В · 3 + С = 0 ។ ចូរកំណត់ B ទៅតម្លៃមួយចំនួនក្រៅពីសូន្យ។ ចូរនិយាយថា B \u003d 1 ក្នុងករណីនេះពីសមភាព B · 3 + C \u003d 0 យើងអាចរកឃើញ C: C \u003d - 3 ។ ដោយប្រើតម្លៃដែលស្គាល់នៃ B និង C យើងទទួលបានសមីការដែលត្រូវការនៃបន្ទាត់ត្រង់: y - 3 = 0 ។

ចម្លើយ៖ y − 3 = 0 ។

សមីការទូទៅនៃបន្ទាត់ត្រង់ឆ្លងកាត់ចំណុចដែលបានផ្តល់ឱ្យនៃយន្តហោះ

អនុញ្ញាតឱ្យបន្ទាត់ដែលបានផ្តល់ឱ្យឆ្លងកាត់ចំណុច M 0 (x 0, y 0) បន្ទាប់មកកូអរដោនេរបស់វាត្រូវគ្នាទៅនឹងសមីការទូទៅនៃបន្ទាត់ i.e. សមភាពគឺពិត៖ A x 0 + B y 0 + C = 0 ។ ដកផ្នែកខាងឆ្វេង និងខាងស្តាំនៃសមីការនេះចេញពីផ្នែកខាងឆ្វេង និងខាងស្តាំនៃសមីការពេញលេញទូទៅនៃបន្ទាត់ត្រង់។ យើងទទួលបាន៖ A (x − x 0) + B (y - y 0) + C \u003d 0 សមីការនេះគឺស្មើនឹងសញ្ញាទូទៅដើម ឆ្លងកាត់ចំនុច M 0 (x 0, y 0) ហើយមាន វ៉ិចទ័រធម្មតា n → \u003d (A, B) ។

លទ្ធផលដែលយើងទទួលបានធ្វើឱ្យវាអាចសរសេរសមីការទូទៅនៃបន្ទាត់ត្រង់សម្រាប់កូអរដោនេនៃវ៉ិចទ័រធម្មតានៃបន្ទាត់ត្រង់ និងកូអរដោនេនៃចំណុចជាក់លាក់នៃបន្ទាត់ត្រង់នេះ។

ឧទាហរណ៍ ៣

ផ្តល់ចំណុច M 0 (- 3, 4) ដែលបន្ទាត់ឆ្លងកាត់ និងវ៉ិចទ័រធម្មតានៃបន្ទាត់នេះ n → = (1 , − 2) ។ វាចាំបាច់ក្នុងការសរសេរសមីការនៃបន្ទាត់ត្រង់ដែលបានផ្តល់ឱ្យ។

ដំណោះស្រាយ

លក្ខខណ្ឌដំបូងអនុញ្ញាតឱ្យយើងទទួលបានទិន្នន័យចាំបាច់សម្រាប់ការចងក្រងសមីការ៖ A \u003d 1, B \u003d - 2, x 0 \u003d - 3, y 0 \u003d ៤. បន្ទាប់មក៖

A (x − x 0) + B (y − y 0) = 0 ⇔ 1 (x − (− 3)) - 2 y (y − 4) = 0 ⇔ ⇔ x − 2 y + 22 = 0

បញ្ហាអាចត្រូវបានដោះស្រាយខុសគ្នា។ សមីការទូទៅនៃបន្ទាត់ត្រង់មានទម្រង់ A x + B y + C = 0 ។ វ៉ិចទ័រធម្មតាដែលបានផ្តល់ឱ្យអនុញ្ញាតឱ្យអ្នកទទួលបានតម្លៃនៃមេគុណ A និង B បន្ទាប់មក៖

A x + B y + C = 0 ⇔ 1 x − 2 y + C = 0 ⇔ x − 2 y + C = 0

ឥឡូវនេះ ចូរយើងស្វែងរកតម្លៃនៃ C ដោយប្រើចំណុច M 0 (- 3, 4) ដែលបានផ្តល់ឱ្យដោយលក្ខខណ្ឌនៃបញ្ហាដែលតាមរយៈបន្ទាត់ឆ្លងកាត់។ កូអរដោនេនៃចំណុចនេះត្រូវគ្នាទៅនឹងសមីការ x − 2 · y + C = 0 , i.e. - 3 - 2 4 + C \u003d 0 ។ ដូច្នេះ C = 11 ។ សមីការបន្ទាត់ត្រង់ដែលត្រូវការមានទម្រង់៖ x − 2 · y + 11 = 0 ។

ចម្លើយ៖ x − 2 y + 11 = 0 ។

ឧទាហរណ៍ 4

ដែលបានផ្តល់ឱ្យបន្ទាត់ 2 3 x - y - 1 2 = 0 និងចំណុច M 0 ដេកលើបន្ទាត់នេះ។ មានតែ abscissa នៃចំណុចនេះត្រូវបានគេដឹងហើយវាស្មើនឹង - 3 ។ វាចាំបាច់ដើម្បីកំណត់ការចាត់តាំងនៃចំណុចដែលបានផ្តល់ឱ្យ។

ដំណោះស្រាយ

ចូរ​កំណត់​ការ​កំណត់​កូអរដោនេ​នៃ​ចំណុច M 0 ជា x 0 និង y 0 ។ ទិន្នន័យដំបូងបង្ហាញថា x 0 \u003d - 3 ។ ដោយសារចំនុចនេះជាកម្មសិទ្ធិរបស់បន្ទាត់មួយ នោះកូអរដោនេរបស់វាត្រូវគ្នាទៅនឹងសមីការទូទៅនៃបន្ទាត់នេះ។ បន្ទាប់មកសមភាពខាងក្រោមនឹងក្លាយជាការពិត៖

2 3 x 0 − y 0 − 1 2 = 0

កំណត់ y 0 : 2 3 ( − 3 ) - y 0 − 1 2 = 0 ⇔ − 5 2 − y 0 = 0 ⇔ y 0 = − 5 2

ចម្លើយ៖ - 5 2

ការផ្លាស់ប្តូរពីសមីការទូទៅនៃបន្ទាត់ត្រង់ទៅប្រភេទផ្សេងទៀតនៃសមីការនៃបន្ទាត់ត្រង់មួយ និងច្រាសមកវិញ

ដូចដែលយើងដឹងមានប្រភេទជាច្រើននៃសមីការនៃបន្ទាត់ត្រង់ដូចគ្នានៅក្នុងយន្តហោះ។ ជម្រើសនៃប្រភេទនៃសមីការអាស្រ័យលើលក្ខខណ្ឌនៃបញ្ហា; វាអាចទៅរួចក្នុងការជ្រើសរើសមួយដែលងាយស្រួលជាងសម្រាប់ដំណោះស្រាយរបស់វា។ នេះគឺជាកន្លែងដែលជំនាញនៃការបំប្លែងសមីការនៃប្រភេទមួយទៅជាសមីការនៃប្រភេទមួយផ្សេងទៀតគឺមានប្រយោជន៍ណាស់។

ជាដំបូង សូមពិចារណាពីការផ្លាស់ប្តូរពីសមីការទូទៅនៃទម្រង់ A x + B y + C = 0 ទៅសមីការ Canonical x − x 1 a x = y − y 1 a y ។

ប្រសិនបើ A ≠ 0 នោះយើងផ្ទេរពាក្យ B y ទៅខាងស្តាំនៃសមីការទូទៅ។ នៅផ្នែកខាងឆ្វេងយើងយក A ចេញពីតង្កៀប។ ជាលទ្ធផលយើងទទួលបាន៖ A x + C A = − B y ។

សមភាពនេះអាចសរសេរជាសមាមាត្រ៖ x + C A - B = y A ។

ប្រសិនបើ B ≠ 0 យើងទុកតែពាក្យ A x នៅផ្នែកខាងឆ្វេងនៃសមីការទូទៅ យើងផ្ទេរអ្នកផ្សេងទៀតទៅខាងស្តាំ យើងទទួលបាន៖ A x \u003d - B y - C ។ យើងដក - B ចេញពីតង្កៀបបន្ទាប់មក៖ A x \u003d - B y + C B ។

ចូរសរសេរឡើងវិញនូវសមភាពជាសមាមាត្រ៖ x − B = y + C B A ។

ជាការពិតណាស់ មិនចាំបាច់ទន្ទេញរូបមន្តលទ្ធផលនោះទេ។ វាគ្រប់គ្រាន់ដើម្បីដឹងពីក្បួនដោះស្រាយនៃសកម្មភាពកំឡុងពេលផ្លាស់ប្តូរពីសមីការទូទៅទៅ Canonical មួយ។

ឧទាហរណ៍ ៥

សមីការទូទៅនៃបន្ទាត់ 3 y - 4 = 0 ត្រូវបានផ្តល់ឱ្យ។ វាត្រូវតែបំប្លែងទៅជាសមីការ Canonical។

ដំណោះស្រាយ

យើងសរសេរសមីការដើមជា 3 y - 4 = 0 ។ បន្ទាប់​មក យើង​ធ្វើ​តាម​ក្បួន​ដោះស្រាយ៖ ពាក្យ 0 x នៅ​ខាង​ឆ្វេង។ ហើយនៅផ្នែកខាងស្តាំយើងយកចេញ - 3 ចេញពីតង្កៀប; យើងទទួលបាន៖ 0 x = − 3 y − 4 3 ។

ចូរសរសេរសមភាពលទ្ធផលជាសមាមាត្រ៖ x − 3 = y − 4 3 0 ។ ដូច្នេះហើយ យើងបានទទួលសមីការនៃទម្រង់ Canonical ។

ចម្លើយ៖ x − 3 = y − 4 3 0.

ដើម្បីបំប្លែងសមីការទូទៅនៃបន្ទាត់ត្រង់ទៅជាប៉ារ៉ាម៉ែត ទីមួយ ការផ្លាស់ប្តូរទៅជាទម្រង់ Canonical ត្រូវបានអនុវត្ត ហើយបន្ទាប់មកការផ្លាស់ប្តូរពីសមីការ Canonical នៃបន្ទាត់ត្រង់ទៅជាសមីការប៉ារ៉ាម៉ែត្រ។

ឧទាហរណ៍ ៦

បន្ទាត់ត្រង់ត្រូវបានផ្តល់ដោយសមីការ 2 x − 5 y − 1 = 0 ។ សរសេរសមីការប៉ារ៉ាម៉ែត្រនៃបន្ទាត់នេះ។

ដំណោះស្រាយ

ចូរធ្វើការផ្លាស់ប្តូរពីសមីការទូទៅទៅ Canonical មួយ៖

2 x − 5 y − 1 = 0 ⇔ 2 x = 5 y + 1 ⇔ 2 x = 5 y + 1 5 ⇔ x 5 = y + 1 5 2

ឥឡូវនេះ ចូរយើងយកផ្នែកទាំងពីរនៃសមីការ Canonical លទ្ធផលស្មើនឹង λ បន្ទាប់មក៖

x 5 = λ y + 1 5 2 = λ ⇔ x = 5 λ y = − 1 5 + 2 λ , λ ∈ R

ចម្លើយ៖x = 5 λ y = − 1 5 + 2 λ , λ ∈ R

សមីការទូទៅអាចបំប្លែងទៅជាសមីការបន្ទាត់ត្រង់ដែលមានជម្រាល y = k x + b ប៉ុន្តែនៅពេល B ≠ 0 ប៉ុណ្ណោះ។ សម្រាប់ការផ្លាស់ប្តូរនៅខាងឆ្វេងយើងទុកពាក្យ B y នៅសល់ត្រូវបានផ្ទេរទៅខាងស្តាំ។ យើងទទួលបាន៖ B y = - A x - C ។ ចូរបែងចែកផ្នែកទាំងពីរនៃសមភាពលទ្ធផលដោយ B ដែលខុសពីសូន្យ៖ y = - A B x - C B ។

ឧទាហរណ៍ ៧

សមីការទូទៅនៃបន្ទាត់ត្រង់មួយត្រូវបានផ្តល់ឱ្យ៖ 2 x + 7 y = 0 ។ អ្នកត្រូវបំប្លែងសមីការនោះទៅជាសមីការជម្រាល។

ដំណោះស្រាយ

ចូរយើងអនុវត្តសកម្មភាពចាំបាច់យោងទៅតាមក្បួនដោះស្រាយ៖

2 x + 7 y = 0 ⇔ 7 y − 2 x ⇔ y = − 2 7 x

ចម្លើយ៖ y = − 2 7 x ។

ពីសមីការទូទៅនៃបន្ទាត់ត្រង់មួយ វាគ្រប់គ្រាន់ដើម្បីគ្រាន់តែទទួលបានសមីការនៅក្នុងផ្នែកនៃទម្រង់ x a + y b = 1 ។ ដើម្បីធ្វើការផ្លាស់ប្តូរបែបនេះ យើងផ្ទេរលេខ C ទៅផ្នែកខាងស្តាំនៃសមភាពចែកផ្នែកទាំងពីរនៃសមភាពលទ្ធផលដោយ - С ហើយចុងក្រោយផ្ទេរមេគុណសម្រាប់អថេរ x និង y ទៅភាគបែង៖

A x + B y + C = 0 ⇔ A x + B y = - C ⇔ ⇔ A - C x + B - C y = 1 ⇔ x - C A + y - C B = 1

ឧទាហរណ៍ ៨

វាចាំបាច់ក្នុងការបំប្លែងសមីការទូទៅនៃបន្ទាត់ត្រង់ x − 7 y + 1 2 = 0 ទៅជាសមីការនៃបន្ទាត់ត្រង់ជាចម្រៀក។

ដំណោះស្រាយ

ចូររំកិល 1 2 ទៅខាងស្តាំ៖ x − 7 y + 1 2 = 0 ⇔ x − 7 y = − 1 2 ។

ចែកដោយ −1/2 ទាំងសងខាងនៃសមីការ៖ x − 7 y = − 1 2 ⇔ 1 − 1 2 x − 7 − 1 2 y = 1 ។

ចម្លើយ៖ x − 1 2 + y 1 14 = 1 ។

ជាទូទៅការផ្លាស់ប្តូរបញ្ច្រាសក៏មានភាពងាយស្រួលផងដែរ: ពីប្រភេទសមីការផ្សេងទៀតទៅទូទៅ។

សមីការនៃបន្ទាត់ត្រង់នៅក្នុងផ្នែក និងសមីការដែលមានជម្រាលអាចត្រូវបានបម្លែងយ៉ាងងាយស្រួលទៅជាទូទៅមួយដោយគ្រាន់តែប្រមូលពាក្យទាំងអស់នៅផ្នែកខាងឆ្វេងនៃសមីការ៖

x a + y b ⇔ 1 a x + 1 b y − 1 = 0 ⇔ A x + B y + C = 0 y = k x + b ⇔ y - k x - b = 0 ⇔ A x + B y + C = 0

សមីការ Canonical ត្រូវបានបំប្លែងទៅជា ទូទៅ តាមគ្រោងការណ៍ខាងក្រោម៖

x − x 1 a x = y − y 1 a y ⇔ a y (x − x 1) = a x (y − y 1) ⇔ ⇔ a y x − a x y − a y x 1 + a x y 1 = 0 ⇔ A x + B y + C = 0

ដើម្បីឆ្លងពីប៉ារ៉ាម៉ែត្រ ការផ្លាស់ប្តូរទៅជា Canonical ត្រូវបានអនុវត្តដំបូង ហើយបន្ទាប់មកទៅទូទៅមួយ៖

x = x 1 + a x λ y = y 1 + a y λ ⇔ x − x 1 a x = y − y 1 a y ⇔ A x + B y + C = 0

ឧទាហរណ៍ ៩

សមីការប៉ារ៉ាម៉ែត្រនៃបន្ទាត់ត្រង់ x = - 1 + 2 · λ y = 4 ត្រូវបានផ្តល់ឱ្យ។ វាចាំបាច់ក្នុងការសរសេរសមីការទូទៅនៃបន្ទាត់នេះ។

ដំណោះស្រាយ

ចូរយើងធ្វើការផ្លាស់ប្តូរពីសមីការប៉ារ៉ាម៉ែត្រទៅជា Canonical៖

x = − 1 + 2 λ y = 4 ⇔ x = − 1 + 2 λ y = 4 + 0 λ ⇔ λ = x + 1 2 λ = y − 4 0 ⇔ x + 1 2 = y − 4 0

ចូរផ្លាស់ទីពី Canonical ទៅទូទៅ៖

x + 1 2 = y − 4 0 ⇔ 0 (x + 1) = 2 (y − 4) ⇔ y − 4 = 0

ចម្លើយ៖ y − 4 = 0

ឧទាហរណ៍ 10

សមីការនៃបន្ទាត់ត្រង់នៅក្នុងផ្នែក x 3 + y 1 2 = 1 ត្រូវបានផ្តល់ឱ្យ។ វាចាំបាច់ដើម្បីអនុវត្តការផ្លាស់ប្តូរទៅជាទម្រង់ទូទៅនៃសមីការ។

ដំណោះស្រាយ៖

ចូរយើងសរសេរសមីការឡើងវិញក្នុងទម្រង់ដែលត្រូវការ៖

x 3 + y 1 2 = 1 ⇔ 1 3 x + 2 y − 1 = 0

ចម្លើយ៖ 1 3 x + 2 y − 1 = 0 ។

គូរសមីការទូទៅនៃបន្ទាត់ត្រង់

ខាងលើ យើងបាននិយាយថាសមីការទូទៅអាចត្រូវបានសរសេរជាមួយនឹងកូអរដោណេដែលគេស្គាល់នៃវ៉ិចទ័រធម្មតា និងកូអរដោនេនៃចំណុចដែលបន្ទាត់ឆ្លងកាត់។ បន្ទាត់ត្រង់បែបនេះត្រូវបានកំណត់ដោយសមីការ A (x - x 0) + B (y - y 0) = 0 ។ នៅកន្លែងដដែលយើងបានវិភាគឧទាហរណ៍ដែលត្រូវគ្នា។

ឥឡូវនេះសូមក្រឡេកមើលឧទាហរណ៍ស្មុគ្រស្មាញបន្ថែមទៀតដែលក្នុងនោះដំបូងវាចាំបាច់ដើម្បីកំណត់កូអរដោនេនៃវ៉ិចទ័រធម្មតា។

ឧទាហរណ៍ 11

ផ្តល់បន្ទាត់ស្របទៅនឹងបន្ទាត់ 2 x − 3 y + 3 3 = 0 ។ គេស្គាល់ផងដែរគឺចំណុច M 0 (4 , 1) ដែលបន្ទាត់ដែលបានផ្តល់ឱ្យឆ្លងកាត់។ វាចាំបាច់ក្នុងការសរសេរសមីការនៃបន្ទាត់ត្រង់ដែលបានផ្តល់ឱ្យ។

ដំណោះស្រាយ

លក្ខខណ្ឌដំបូងប្រាប់យើងថាបន្ទាត់គឺស្របគ្នា បន្ទាប់មកជាវ៉ិចទ័រធម្មតានៃបន្ទាត់ដែលសមីការត្រូវសរសេរ យើងយកវ៉ិចទ័រផ្ទាល់នៃបន្ទាត់ n → = (2, − 3): 2 x − 3 y + 3 3 = 0 ។ ឥឡូវនេះយើងដឹងពីទិន្នន័យចាំបាច់ទាំងអស់ដើម្បីសរសេរសមីការទូទៅនៃបន្ទាត់ត្រង់មួយ៖

A (x − x 0) + B (y − y 0) = 0 ⇔ 2 (x − 4) − 3 (y − 1) = 0 ⇔ 2 x − 3 y − 5 = 0

ចម្លើយ៖ 2 x − 3 y − 5 = 0 ។

ឧទាហរណ៍ 12

បន្ទាត់​ដែល​បាន​ផ្តល់​ឱ្យ​កាត់​តាម​ដើម​កាត់​កែង​ទៅ​នឹង​បន្ទាត់ x − 2 3 = y + 4 5 ។ វាចាំបាច់ក្នុងការសរសេរសមីការទូទៅនៃបន្ទាត់ត្រង់ដែលបានផ្តល់ឱ្យ។

ដំណោះស្រាយ

វ៉ិចទ័រធម្មតានៃបន្ទាត់ដែលបានផ្តល់ឱ្យនឹងជាវ៉ិចទ័រដឹកនាំនៃបន្ទាត់ x − 2 3 = y + 4 5 ។

បន្ទាប់មក n → = (3, 5) ។ បន្ទាត់ត្រង់ឆ្លងកាត់ប្រភពដើម i.e. តាមរយៈចំណុច O (0, 0) ។ ចូរយើងចងក្រងសមីការទូទៅនៃបន្ទាត់ត្រង់មួយ៖

A (x − x 0) + B (y − y 0) = 0 ⇔ 3 (x − 0) + 5 (y − 0) = 0 ⇔ 3 x + 5 y = 0

ចម្លើយ៖ 3 x + 5 y = 0 ។

ប្រសិនបើអ្នកសម្គាល់ឃើញមានកំហុសនៅក្នុងអត្ថបទ សូមបន្លិចវា ហើយចុច Ctrl+Enter

ក្នុង​ករណី​ជា​ច្រើន ការ​គូស​ប្លង់​អនុគមន៍​គឺ​ងាយ​ស្រួល​ជាង​ប្រសិន​បើ​អ្នក​គូស​ប្លង់ asymtotes នៃ​ខ្សែ​កោង​ដំបូង។

និយមន័យ 1. Asymptotes ត្រូវបានគេហៅថាបន្ទាត់បែបនេះ ដែលក្រាហ្វនៃអនុគមន៍ខិតជិតដូចការចង់បាន នៅពេលដែលអថេរមានទំនោរទៅបូកនឹងភាពគ្មានកំណត់ ឬដកគ្មានដែនកំណត់។

និយមន័យ 2. បន្ទាត់ត្រង់ត្រូវបានគេហៅថា asymptote នៃក្រាហ្វនៃអនុគមន៍ ប្រសិនបើចម្ងាយពីចំណុចអថេរ មក្រាហ្វនៃអនុគមន៍រហូតដល់បន្ទាត់នេះមានទំនោរទៅសូន្យ ដោយសារចំនុចផ្លាស់ទីទៅឆ្ងាយដោយគ្មានកំណត់ មពីប្រភពដើមនៃកូអរដោនេតាមបណ្តោយសាខាណាមួយនៃក្រាហ្វនៃអនុគមន៍។

មាន asymptotes បីប្រភេទ៖ បញ្ឈរ ផ្ដេក និង oblique ។

រោគសញ្ញាបញ្ឈរ

និយមន័យ. ត្រង់ x = កគឺ asymptote បញ្ឈរនៃក្រាហ្វនៃមុខងារ ប្រសិនបើចំណុច x = កគឺ ចំណុចបំបែកនៃប្រភេទទីពីរសម្រាប់លក្ខណៈពិសេសនេះ។

វាធ្វើតាមនិយមន័យថាបន្ទាត់ x = កគឺជា asymptote បញ្ឈរនៃក្រាហ្វនៃអនុគមន៍ f(x) ប្រសិនបើយ៉ាងហោចណាស់លក្ខខណ្ឌមួយក្នុងចំណោមលក្ខខណ្ឌខាងក្រោមត្រូវបានបំពេញ៖

ទន្ទឹមនឹងនេះមុខងារ f(x) ប្រហែលជាមិនត្រូវបានកំណត់ទាល់តែសោះ រៀងគ្នាសម្រាប់ x ≥ កនិង x ≤ ក .

មតិយោបល់៖

ឧទាហរណ៍ ១ក្រាហ្វមុខងារ y=ln xមាន asymptote បញ្ឈរ x= 0 (ឧ. ស្របគ្នានឹងអ័ក្ស អូ) នៅលើព្រំដែននៃដែននិយមន័យ ចាប់តាំងពីដែនកំណត់នៃអនុគមន៍នៅពេលដែល x ទំនោរទៅសូន្យនៅខាងស្តាំគឺស្មើនឹងដកគ្មានដែនកំណត់៖

(រូបភាពខាងលើ) ។

ដោយខ្លួនឯង ហើយបន្ទាប់មកមើលដំណោះស្រាយ

ឧទាហរណ៍ ២ស្វែងរក asymtotes នៃក្រាហ្វនៃអនុគមន៍។

ឧទាហរណ៍ ៣ស្វែងរក asymtotes នៃក្រាហ្វនៃមុខងារមួយ។

asymtotes ផ្ដេក

ប្រសិនបើ (ដែនកំណត់នៃអនុគមន៍នៅពេលដែលអាគុយម៉ង់មានទំនោរទៅបូកឬដកអគ្មានកំណត់គឺស្មើនឹងតម្លៃមួយចំនួន ខ) បន្ទាប់មក y = ខ – asymptote ផ្ដេក កោង y = f(x ។

ឧទាហរណ៍ ៥ក្រាហ្វមុខងារ

នៅ ក> 1 មាន asymptote ផ្ដេកខាងឆ្វេង y= 0 (ឧ. ស្របគ្នានឹងអ័ក្ស គោ), ចាប់តាំងពីដែនកំណត់នៃអនុគមន៍នៅពេលដែល "x" ទំនោរទៅដកគ្មានដែនកំណត់គឺស្មើនឹងសូន្យ:

ខ្សែកោងមិនមាន asymptote ផ្ដេកត្រឹមត្រូវទេ ដោយសារដែនកំណត់នៃអនុគមន៍ដែល x ទំនោរទៅបូកនឹងភាពគ្មានកំណត់គឺស្មើនឹងភាពគ្មានកំណត់៖

រោគសញ្ញា Oblique

asymptotes បញ្ឈរ និងផ្ដេកដែលយើងបានពិចារណាខាងលើគឺស្របទៅនឹងអ័ក្សកូអរដោនេ ដូច្នេះដើម្បីបង្កើតវា យើងត្រូវការតែចំនួនជាក់លាក់មួយប៉ុណ្ណោះ - ចំណុចនៅលើអ័ក្ស abscissa ឬ ordinate ដែល asymptote ឆ្លងកាត់។ ច្រើនទៀតគឺត្រូវការសម្រាប់ asymptote oblique - ជម្រាល kដែលបង្ហាញពីមុំទំនោរនៃបន្ទាត់ត្រង់ និងស្ទាក់ចាប់ ខដែលបង្ហាញពីចំនួនបន្ទាត់ខាងលើ ឬខាងក្រោមប្រភពដើម។ អ្នកទាំងឡាយណាដែលមិនមានពេលវេលាដើម្បីបំភ្លេចធរណីមាត្រវិភាគ ហើយពីវា - សមីការនៃបន្ទាត់ត្រង់នឹងសម្គាល់ថាសម្រាប់ asymptote oblique ពួកគេរកឃើញ សមីការជម្រាល. អត្ថិភាពនៃ asymptote oblique ត្រូវបានកំណត់ដោយទ្រឹស្តីបទខាងក្រោម ដោយឈរលើមូលដ្ឋាននៃមេគុណដែលទើបតែដាក់ឈ្មោះត្រូវបានរកឃើញ។

ទ្រឹស្តីបទ។ដើម្បីធ្វើខ្សែកោង y = f(x) មាន asymptote y = kx + ខ វាចាំបាច់ និងគ្រប់គ្រាន់ដែលមានដែនកំណត់កំណត់ kនិង ខនៃអនុគមន៍ដែលកំពុងពិចារណាដូចដែលអថេរមានទំនោរទៅ xបូក​នឹង​ភាព​គ្មាន​កំណត់ និង​ដក​គ្មាន​កំណត់៖

(1)

(2)

លេខ​នេះ​បាន​រក​ឃើញ kនិង ខនិងជាមេគុណនៃ asymptote oblique ។

ក្នុងករណីទី 1 (នៅពេល x ទំនោរទៅបូកនឹងភាពគ្មានទីបញ្ចប់) ការ asymptote oblique ខាងស្តាំត្រូវបានទទួល ហើយនៅក្នុងទីពីរ (នៅពេលដែល x ទំនោរទៅដក infinity) asymptote ខាងឆ្វេងត្រូវបានទទួល។ asymptote oblique ត្រឹមត្រូវត្រូវបានបង្ហាញនៅក្នុងរូបភព។ ពី​ខាងក្រោម។

នៅពេលស្វែងរកសមីការនៃ oblique asymptote វាចាំបាច់ត្រូវគិតគូរពីទំនោរនៃ x ទៅទាំងបូក infinity និង minus infinity ។ សម្រាប់មុខងារមួយចំនួន ឧទាហរណ៍ សម្រាប់ប្រភាគប្រភាគ ដែនកំណត់ទាំងនេះស្របគ្នា ប៉ុន្តែសម្រាប់មុខងារជាច្រើន ដែនកំណត់ទាំងនេះគឺខុសគ្នា ហើយមានតែមួយក្នុងចំណោមពួកវាប៉ុណ្ណោះដែលអាចមាន។

ប្រសិនបើដែនកំណត់ស្របគ្នានឹង x ទំនោរទៅបូកនឹងភាពគ្មានកំណត់ និងដកអគ្មានកំណត់ នោះបន្ទាត់ត្រង់ y = kx + ខ គឺជា asymptote ជ្រុងពីរនៃខ្សែកោង។

ប្រសិនបើយ៉ាងហោចណាស់មួយនៃដែនកំណត់កំណត់ asymptote y = kx + ខ មិនមានទេ បន្ទាប់មកក្រាហ្វនៃមុខងារមិនមាន asymptote oblique (ប៉ុន្តែអាចមានបញ្ឈរមួយ)។

វាងាយស្រួលមើលថា asymptote ផ្ដេក y = ខគឺជាករណីពិសេសនៃ oblique y = kx + ខនៅ k = 0 .

ដូច្នេះ ប្រសិនបើខ្សែកោងមាន asymptote ផ្ដេកក្នុងទិសដៅណាមួយ នោះមិនមាន asymptote oblique នៅក្នុងទិសដៅនោះទេ ហើយច្រាសមកវិញ។

ឧទាហរណ៍ ៦ស្វែងរក asymtotes នៃក្រាហ្វនៃមុខងារមួយ។

ដំណោះស្រាយ។ មុខងារត្រូវបានកំណត់នៅលើបន្ទាត់លេខទាំងមូល លើកលែងតែ x= 0, i.e.

ដូច្នេះនៅចំណុចបំបែក x= 0 ខ្សែកោងអាចមាន asymptote បញ្ឈរ។ ជាការពិត ដែនកំណត់នៃអនុគមន៍ដែល x មានទំនោរទៅសូន្យពីខាងឆ្វេងគឺបូកនឹងភាពគ្មានទីបញ្ចប់៖

អាស្រ័យហេតុនេះ x= 0 គឺជា asymptote បញ្ឈរនៃក្រាហ្វនៃមុខងារនេះ។

ក្រាហ្វនៃអនុគមន៍នេះមិនមាន asymptote ផ្តេកទេ ចាប់តាំងពីដែនកំណត់នៃអនុគមន៍ នៅពេលដែល x ទំនោរទៅបូកគ្មានដែនកំណត់ គឺស្មើនឹងបូកគ្មានដែនកំណត់៖

ចូរយើងស្វែងយល់ពីវត្តមានរបស់ asymptote oblique៖

មានដែនកំណត់កំណត់ k= 2 និង ខ= 0 ។ ត្រង់ y = 2xគឺ​ជា​គំនូស​តាង​ពីរ​ជ្រុង​នៃ​ក្រាហ្វ​នៃ​អនុគមន៍​នេះ (រូប​ក្នុង​ឧទាហរណ៍)។

ឧទាហរណ៍ ៧ស្វែងរក asymtotes នៃក្រាហ្វនៃមុខងារមួយ។

ដំណោះស្រាយ។ មុខងារមានចំណុចបំបែកមួយ។ x= −1 ។ អនុញ្ញាតឱ្យយើងគណនាដែនកំណត់ម្ខាង និងកំណត់ប្រភេទនៃភាពមិនដំណើរការ៖

សេចក្តីសន្និដ្ឋាន៖ x= −1 គឺជាចំណុចដាច់នៃប្រភេទទីពីរ ដូច្នេះបន្ទាត់ x= −1 គឺជា asymptote បញ្ឈរនៃក្រាហ្វនៃអនុគមន៍នេះ។

កំពុងរកមើល asymtotes oblique ។ ដោយសារមុខងារនេះគឺប្រភាគសមហេតុផល ដែនកំណត់សម្រាប់ និងសម្រាប់នឹងស្របគ្នា។ ដូច្នេះ យើងរកឃើញមេគុណសម្រាប់ជំនួសបន្ទាត់ត្រង់មួយ - asymptote oblique ចូលទៅក្នុងសមីការ៖

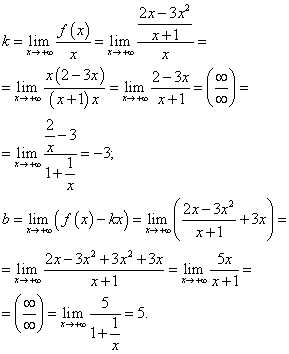
ការជំនួសមេគុណដែលបានរកឃើញទៅក្នុងសមីការនៃបន្ទាត់ត្រង់ជាមួយនឹងជម្រាលមួយ យើងទទួលបានសមីការនៃ asymptote oblique៖

y = −3x + 5 .

នៅក្នុងរូបភាព ក្រាហ្វនៃមុខងារត្រូវបានសម្គាល់ជាពណ៌ប៊ឺហ្គូឌី ហើយ asymtotes មានពណ៌ខ្មៅ។

ឧទាហរណ៍ ៨ស្វែងរក asymtotes នៃក្រាហ្វនៃមុខងារមួយ។

ដំណោះស្រាយ។ ដោយសារមុខងារនេះបន្ត ក្រាហ្វរបស់វាមិនមានសញ្ញាបញ្ឈរទេ។ យើងកំពុងស្វែងរករោគសញ្ញា oblique៖

.

ដូច្នេះក្រាហ្វនៃមុខងារនេះមាន asymptote y= 0 នៅ និងមិនមាន asymptote នៅ .

ឧទាហរណ៍ ៩ស្វែងរក asymtotes នៃក្រាហ្វនៃមុខងារមួយ។

ដំណោះស្រាយ។ ជាដំបូង យើងស្វែងរកសញ្ញាសម្គាល់បញ្ឈរ។ ដើម្បីធ្វើដូចនេះយើងរកឃើញដែននៃមុខងារ។ មុខងារត្រូវបានកំណត់នៅពេលដែលវិសមភាពរក្សា និង . សញ្ញាអថេរ xផ្គូផ្គងសញ្ញា។ ដូច្នេះ សូម​ពិចារណា​អំពី​វិសមភាព​សមមូល។ ពីនេះយើងទទួលបានវិសាលភាពនៃមុខងារ៖ . asymptote បញ្ឈរអាចស្ថិតនៅលើព្រំដែននៃដែននៃអនុគមន៍ប៉ុណ្ណោះ។ ប៉ុន្តែ x= 0 មិនអាចជា asymptote បញ្ឈរបានទេ ព្រោះមុខងារត្រូវបានកំណត់សម្រាប់ x = 0 .

ពិចារណាដែនកំណត់ខាងស្តាំនៅ (ដែនកំណត់ដៃឆ្វេងមិនមានទេ)៖

.

ចំណុច x= 2 គឺជាចំណុចដាច់នៃប្រភេទទីពីរ ដូច្នេះបន្ទាត់ x= 2 - asymptote បញ្ឈរនៃក្រាហ្វនៃមុខងារនេះ។

យើងកំពុងស្វែងរករោគសញ្ញា oblique៖

ដូច្នេះ y = x+ 1 - asymptote oblique នៃក្រាហ្វនៃមុខងារនេះនៅ . យើងកំពុងស្វែងរក asymptote oblique សម្រាប់៖

ដូច្នេះ y = −x − 1 - oblique asymptote នៅ។

ឧទាហរណ៍ 10ស្វែងរក asymtotes នៃក្រាហ្វនៃមុខងារមួយ។

ដំណោះស្រាយ។ មុខងារមានវិសាលភាព . ចាប់តាំងពី asymptote បញ្ឈរនៃក្រាហ្វនៃអនុគមន៍នេះអាចស្ថិតនៅលើព្រំដែននៃដែននៃនិយមន័យ នោះយើងនឹងរកឃើញដែនកំណត់ម្ខាងនៃអនុគមន៍នៅ។

លក្ខណៈសម្បត្តិនៃបន្ទាត់ត្រង់នៅក្នុងធរណីមាត្រ Euclidean ។

មាន​បន្ទាត់​ជា​ច្រើន​ដែល​មិន​ចេះ​ចប់​ដែល​អាច​គូស​តាម​ចំណុច​ណា​មួយ​បាន។

តាម​រយៈ​ចំណុច​មិន​ស្រប​គ្នា​ពីរ​ណា​មួយ មាន​តែ​បន្ទាត់​ត្រង់​មួយ។

បន្ទាត់មិនស្របគ្នាពីរនៅក្នុងយន្តហោះ ប្រសព្វគ្នានៅចំណុចតែមួយ ឬជា

ប៉ារ៉ាឡែល (ធ្វើតាមពីមួយមុន) ។

នៅក្នុងលំហបីវិមាត្រ មានជម្រើសបីសម្រាប់ទីតាំងដែលទាក់ទងនៃបន្ទាត់ពីរ៖

• បន្ទាត់ប្រសព្វ;

• បន្ទាត់ត្រង់គឺស្របគ្នា;

• បន្ទាត់ត្រង់ប្រសព្វ។

ត្រង់ បន្ទាត់- ខ្សែកោងពិជគណិតនៃលំដាប់ទីមួយ៖ នៅក្នុងប្រព័ន្ធសំរបសំរួល Cartesian បន្ទាត់ត្រង់

ត្រូវបានផ្តល់ឱ្យនៅលើយន្តហោះដោយសមីការនៃដឺក្រេទីមួយ (សមីការលីនេអ៊ែរ) ។

សមីការទូទៅនៃបន្ទាត់ត្រង់។

និយមន័យ. បន្ទាត់ណាមួយនៅក្នុងយន្តហោះអាចត្រូវបានផ្តល់ដោយសមីការលំដាប់ទីមួយ

Ah + Wu + C = 0,

និងថេរ ក, ខមិនស្មើនឹងសូន្យក្នុងពេលតែមួយ។ សមីការលំដាប់ទីមួយនេះត្រូវបានគេហៅថា ទូទៅ

សមីការបន្ទាត់ត្រង់។អាស្រ័យលើតម្លៃនៃថេរ ក, ខនិង ពីករណីពិសេសខាងក្រោមអាចធ្វើទៅបាន៖

. C = 0, A ≠ 0, B ≠ 0- បន្ទាត់ឆ្លងកាត់ប្រភពដើម

. A = 0, B ≠0, C ≠0 (ដោយ + C = 0)- បន្ទាត់ត្រង់ស្របទៅនឹងអ័ក្ស អូ

. B = 0, A ≠ 0, C ≠ 0 ( Ax + C = 0)- បន្ទាត់ត្រង់ស្របទៅនឹងអ័ក្ស អូ

. B = C = 0, A ≠ 0- បន្ទាត់ស្របគ្នានឹងអ័ក្ស អូ

. A = C = 0, B ≠ 0- បន្ទាត់ស្របគ្នានឹងអ័ក្ស អូ

សមីការ​នៃ​បន្ទាត់​ត្រង់​អាច​ត្រូវ​បាន​តំណាង​ក្នុង​ទម្រង់​ផ្សេង​គ្នា​អាស្រ័យ​លើ​ការ​ផ្តល់​ឱ្យ

លក្ខខណ្ឌដំបូង។

សមីការនៃបន្ទាត់ត្រង់ដោយចំណុចមួយ និងវ៉ិចទ័រធម្មតា។

និយមន័យ. នៅក្នុងប្រព័ន្ធកូអរដោណេចតុកោណ Cartesian វ៉ិចទ័រដែលមានសមាសធាតុ (A, B)

កាត់កែងទៅនឹងបន្ទាត់ដែលផ្តល់ដោយសមីការ

Ah + Wu + C = 0 ។

ឧទាហរណ៍. ស្វែងរកសមីការនៃបន្ទាត់ត្រង់ឆ្លងកាត់ចំណុចមួយ។ A(1, 2)កាត់កែងទៅនឹងវ៉ិចទ័រ (3, -1).

ដំណោះស្រាយ. ចូរសរសេរនៅ A \u003d 3 និង B \u003d -1 សមីការនៃបន្ទាត់ត្រង់៖ 3x - y + C \u003d 0 ។ ដើម្បីរកមេគុណ C

យើងជំនួសកូអរដោនេនៃចំណុច A ទៅក្នុងកន្សោមលទ្ធផល។ យើងទទួលបាន៖ 3 - 2 + C \u003d 0 ដូច្នេះ

គ = -១. សរុប៖ សមីការដែលចង់បាន៖ 3x - y - 1 \u003d 0 ។

សមីការនៃបន្ទាត់ត្រង់ឆ្លងកាត់ពីរចំណុច។

សូម​ឱ្យ​ពិន្ទុ​ពីរ​ត្រូវ​បាន​ផ្តល់​ឱ្យ​ក្នុង​លំហ M 1 (x 1 , y 1 , z 1)និង M2 (x 2, y 2, z 2),បន្ទាប់មក សមីការបន្ទាត់ត្រង់,

ឆ្លងកាត់ចំណុចទាំងនេះ៖

ប្រសិនបើភាគបែងណាមួយស្មើនឹងសូន្យនោះ ភាគបែងដែលត្រូវគ្នាគួរតែត្រូវបានកំណត់ឱ្យស្មើសូន្យ។ នៅ​លើ

យន្តហោះ សមីការនៃបន្ទាត់ត្រង់ដែលសរសេរខាងលើត្រូវបានធ្វើឱ្យសាមញ្ញ៖

ប្រសិនបើ x 1 ≠ x 2និង x = x ១, ប្រសិនបើ x 1 = x 2 .

ប្រភាគ = គបានហៅ កត្តាជម្រាល ត្រង់.

ឧទាហរណ៍. រកសមីការនៃបន្ទាត់ត្រង់ឆ្លងកាត់ចំនុច A(1,2) និង B(3,4)។

ដំណោះស្រាយ. អនុវត្តរូបមន្តខាងលើយើងទទួលបាន៖

សមីការនៃបន្ទាត់ត្រង់ដោយចំណុចមួយ និងជម្រាលមួយ។

ប្រសិនបើសមីការទូទៅនៃបន្ទាត់ត្រង់ Ah + Wu + C = 0នាំយកទៅទម្រង់:

និងកំណត់ បន្ទាប់មកសមីការលទ្ធផលត្រូវបានគេហៅថា

សមីការនៃបន្ទាត់ត្រង់ជាមួយជម្រាល k ។

សមីការនៃបន្ទាត់ត្រង់លើចំណុចមួយ និងវ៉ិចទ័រដឹកនាំ។

ដោយភាពស្រដៀងគ្នាជាមួយនឹងចំណុចដែលពិចារណាសមីការនៃបន្ទាត់ត្រង់តាមរយៈវ៉ិចទ័រធម្មតា អ្នកអាចបញ្ចូលកិច្ចការ

បន្ទាត់ត្រង់ឆ្លងកាត់ចំណុចមួយ និងវ៉ិចទ័រទិសដៅនៃបន្ទាត់ត្រង់មួយ។

និយមន័យ. រាល់វ៉ិចទ័រដែលមិនមែនជាសូន្យ (α 1 , α 2)សមាសធាតុដែលបំពេញលក្ខខណ្ឌ

Aα 1 + Bα 2 = 0បានហៅ វ៉ិចទ័រទិសដៅនៃបន្ទាត់ត្រង់។

Ah + Wu + C = 0 ។

ឧទាហរណ៍. រកសមីការនៃបន្ទាត់ត្រង់ជាមួយវ៉ិចទ័រទិសដៅ (1, -1) ហើយឆ្លងកាត់ចំណុច A(1, 2) ។

ដំណោះស្រាយ. យើងនឹងរកមើលសមីការនៃបន្ទាត់ត្រង់ដែលចង់បានក្នុងទម្រង់៖ អ័ក្ស + ដោយ + C = 0 ។យោងតាមនិយមន័យ

មេគុណត្រូវតែបំពេញលក្ខខណ្ឌ៖

1 * A + (-1) * B = 0, i.e. ក = ខ។

បន្ទាប់មកសមីការនៃបន្ទាត់ត្រង់មានទម្រង់៖ អ័ក្ស + Ay + C = 0,ឬ x + y + C / A = 0 ។

នៅ x=1, y=2យើង​ទទួល​បាន គ/ក = -៣, i.e. សមីការដែលចង់បាន៖

x + y − 3 = 0

សមីការនៃបន្ទាត់ត្រង់នៅក្នុងផ្នែក។

ប្រសិនបើនៅក្នុងសមីការទូទៅនៃបន្ទាត់ត្រង់ Ah + Wu + C = 0 C≠0 បន្ទាប់មកបែងចែកដោយ -C យើងទទួលបាន៖

ឬ កន្លែងណា

អត្ថន័យធរណីមាត្រនៃមេគុណគឺ មេគុណ a គឺជាកូអរដោនេនៃចំនុចប្រសព្វ

ត្រង់ជាមួយអ័ក្ស អូក ខ- កូអរដោនេនៃចំនុចប្រសព្វនៃបន្ទាត់ជាមួយអ័ក្ស អូ.

ឧទាហរណ៍. សមីការទូទៅនៃបន្ទាត់ត្រង់ត្រូវបានផ្តល់ឱ្យ x − y + 1 = 0 ។ស្វែងរកសមីការនៃបន្ទាត់ត្រង់នេះនៅក្នុងផ្នែក។

C \u003d 1, , a \u003d -1, b \u003d ១.

សមីការធម្មតានៃបន្ទាត់ត្រង់។

ប្រសិនបើភាគីទាំងពីរនៃសមីការ Ah + Wu + C = 0ចែកដោយលេខ ដែលត្រូវបានគេហៅថា

កត្តាធ្វើឱ្យធម្មតា។បន្ទាប់មកយើងទទួលបាន

xcosφ + ysinφ - p = 0 -សមីការធម្មតានៃបន្ទាត់ត្រង់.

សញ្ញា ± នៃកត្តាធម្មតាត្រូវតែត្រូវបានជ្រើសរើសដូច្នេះ μ * គ< 0.

រ- ប្រវែងកាត់កាត់ពីដើមទៅបន្ទាត់

ក φ - មុំបង្កើតដោយកាត់កែងនេះជាមួយនឹងទិសដៅវិជ្ជមាននៃអ័ក្ស អូ។

ឧទាហរណ៍. ផ្តល់សមីការទូទៅនៃបន្ទាត់ត្រង់ 12x − 5y − 65 = 0. តម្រូវឱ្យសរសេរសមីការប្រភេទផ្សេងៗ

បន្ទាត់ត្រង់នេះ។

សមីការនៃបន្ទាត់ត្រង់នេះនៅក្នុងផ្នែក:

សមីការនៃបន្ទាត់នេះជាមួយនឹងជម្រាល: (ចែកនឹង 5)

សមីការនៃបន្ទាត់ត្រង់:

cos φ = 12/13; sin φ= −5/13; p=5 ។

វាគួរតែត្រូវបានកត់សម្គាល់ថាមិនមែនគ្រប់បន្ទាត់ត្រង់អាចត្រូវបានតំណាងដោយសមីការនៅក្នុងផ្នែកទេឧទាហរណ៍បន្ទាត់ត្រង់។

ស្របទៅនឹងអ័ក្ស ឬឆ្លងកាត់ប្រភពដើម។

មុំរវាងបន្ទាត់នៅលើយន្តហោះ។

និយមន័យ. ប្រសិនបើបន្ទាត់ពីរត្រូវបានផ្តល់ឱ្យ y \u003d k 1 x + b 1, y \u003d k 2 x + b 2បន្ទាប់មកមុំស្រួចរវាងបន្ទាត់ទាំងនេះ

នឹងត្រូវបានកំណត់ថាជា

បន្ទាត់ពីរគឺស្របគ្នាប្រសិនបើ k 1 = k 2. បន្ទាត់ពីរគឺកាត់កែង

ប្រសិនបើ k 1 \u003d -1 / k 2 .

ទ្រឹស្តីបទ.

ផ្ទាល់ Ah + Wu + C = 0និង A 1 x + B 1 y + C 1 \u003d 0គឺស្របគ្នានៅពេលដែលមេគុណមានសមាមាត្រ

A 1 \u003d λA, B 1 \u003d λB. ប្រសិនបើផងដែរ។ С 1 \u003d λСបន្ទាប់មកបន្ទាត់ស្របគ្នា។ សំរបសំរួលនៃចំនុចប្រសព្វនៃបន្ទាត់ពីរ

ត្រូវបានរកឃើញជាដំណោះស្រាយចំពោះប្រព័ន្ធសមីការនៃបន្ទាត់ទាំងនេះ។

សមីការនៃបន្ទាត់ដែលឆ្លងកាត់ចំណុចដែលបានផ្តល់ឱ្យគឺកាត់កែងទៅនឹងបន្ទាត់ដែលបានផ្តល់ឱ្យ។

និយមន័យ. បន្ទាត់ឆ្លងកាត់ចំណុចមួយ។ M 1 (x 1, y 1)និងកាត់កែងទៅបន្ទាត់ y = kx + b

តំណាងដោយសមីការ៖

ចម្ងាយពីចំណុចមួយទៅបន្ទាត់មួយ។

ទ្រឹស្តីបទ. ប្រសិនបើចំណុចមួយត្រូវបានផ្តល់ឱ្យ M(x 0, y 0),បន្ទាប់មកចម្ងាយទៅបន្ទាត់ Ah + Wu + C = 0បានកំណត់ថា:

ភស្តុតាង. សូមឱ្យចំណុច M 1 (x 1, y 1)- មូលដ្ឋាននៃកាត់កែងបានធ្លាក់ចុះពីចំណុច មសម្រាប់ការផ្តល់ឱ្យ

ផ្ទាល់។ បន្ទាប់មកចម្ងាយរវាងចំណុច មនិង ម ១:

(1)

កូអរដោនេ x ១និង ១អាចត្រូវបានរកឃើញជាដំណោះស្រាយចំពោះប្រព័ន្ធសមីការ៖

សមីការទីពីរនៃប្រព័ន្ធគឺជាសមីការនៃបន្ទាត់ត្រង់ឆ្លងកាត់ចំណុចដែលបានផ្តល់ឱ្យ M 0 កាត់កែង

បន្ទាត់ដែលបានផ្តល់ឱ្យ។ ប្រសិនបើយើងបំប្លែងសមីការទីមួយនៃប្រព័ន្ធទៅជាទម្រង់៖

A(x − x 0) + B(y - y 0) + Ax 0 + ដោយ 0 + C = 0,

បន្ទាប់មក ដំណោះស្រាយ យើងទទួលបាន៖

ការជំនួសកន្សោមទាំងនេះទៅជាសមីការ (១) យើងរកឃើញ៖

ទ្រឹស្តីបទត្រូវបានបញ្ជាក់។

សមីការ

Ah+Wu+C=0

(កន្លែងណា A, B, Cអាចមានតម្លៃណាមួយ ដរាបណាមេគុណ ក, ខមិនមែនសូន្យទាំងពីរក្នុងពេលតែមួយ) តំណាង បន្ទាត់ត្រង់. បន្ទាត់ត្រង់ណាមួយអាចត្រូវបានតំណាងដោយសមីការនៃប្រភេទនេះ។ ដូច្នេះវាត្រូវបានគេហៅថា សមីការទូទៅនៃបន្ទាត់ត្រង់.

ប្រសិនបើ ក ប៉ុន្តែ X ស្របទៅនឹងអ័ក្ស x.

ប្រសិនបើ ក អេ=0 នោះគឺសមីការមិនមាន នៅបន្ទាប់មកវាតំណាងឱ្យបន្ទាត់ ស្របទៅនឹងអ័ក្ស OY.

កុកឡា អេមិនស្មើនឹងសូន្យ នោះសមីការទូទៅនៃបន្ទាត់ត្រង់អាចជា ដោះស្រាយទាក់ទងនឹងការតែងតាំងនៅ បន្ទាប់មកវាត្រូវបានបម្លែងទៅជាទម្រង់

(កន្លែងណា a=-A/B; b=-C/B).

ដូចគ្នានេះដែរនៅពេលដែល ប៉ុន្តែខុសពីសូន្យ សមីការទូទៅនៃបន្ទាត់ត្រង់អាចត្រូវបានដោះស្រាយដោយគោរព X.

ប្រសិនបើ ក ពី=0 នោះគឺសមីការទូទៅនៃបន្ទាត់ត្រង់មិនមានពាក្យទំនេរទេ បន្ទាប់មកវាតំណាងឱ្យបន្ទាត់ត្រង់ឆ្លងកាត់ប្រភពដើម

5.

សមីការនៃបន្ទាត់ឆ្លងកាត់ចំណុចដែលបានផ្តល់ឱ្យ ក(x 1 , y 1) ក្នុងទិសដៅដែលបានកំណត់ដោយជម្រាល k,

y - y 1 = k(x - x 1). (1)

សមីការនេះកំណត់ខ្មៅដៃនៃបន្ទាត់ឆ្លងកាត់ចំណុចមួយ។ ក(x 1 , y 1) ដែលត្រូវបានគេហៅថាកណ្តាលនៃធ្នឹម។

. សមីការនៃបន្ទាត់ត្រង់ឆ្លងកាត់ចំណុចពីរ៖ ក(x 1 , y 1) និង ខ(x 2 , y២) សរសេរដូចនេះ៖

ចំណោទនៃបន្ទាត់ត្រង់មួយឆ្លងកាត់ចំនុចដែលបានផ្តល់ឱ្យពីរត្រូវបានកំណត់ដោយរូបមន្ត

7 សមីការនៃបន្ទាត់ត្រង់នៅក្នុងផ្នែក

ប្រសិនបើនៅក្នុងសមីការទូទៅនៃបន្ទាត់ បន្ទាប់មកបែងចែក (1) ដោយ យើងទទួលបានសមីការនៃបន្ទាត់នៅក្នុងផ្នែក

កន្លែងណា , ។ បន្ទាត់កាត់អ័ក្សនៅចំណុច អ័ក្សនៅចំណុច។

រូបមន្ត ៨៖ មុំរវាងបន្ទាត់នៅលើយន្តហោះ

នៅ គោលដៅ α រវាងបន្ទាត់ត្រង់ពីរដែលផ្តល់ដោយសមីការ៖ y=k 1 x+b 1 (ជួរទីមួយ) និង y=k 2 x+b 2 (ជួរទីពីរ) អាចត្រូវបានគណនាដោយរូបមន្ត (មុំត្រូវបានវាស់ពីបន្ទាត់ទី 1 ដល់ទី 2 ។ ច្រាសទ្រនិចនាឡិកា ):

tg(α)=(k 2 -k 1 )/(1+k 1 k 2 )

9 ការរៀបចំគ្នាទៅវិញទៅមកនៃបន្ទាត់ត្រង់ពីរនៅលើយន្តហោះមួយ។.

អនុញ្ញាតឱ្យទាំងពីរឥឡូវនេះ សមីការបន្ទាត់ត្រង់ត្រូវបានសរសេរជាទម្រង់ទូទៅ។

ទ្រឹស្តីបទ។ អនុញ្ញាតឱ្យ

- ទូទៅ សមីការបន្ទាត់ត្រង់ពីរ សំរបសំរួលយន្តហោះ Oxy ។ បន្ទាប់មក

1) បើអញ្ចឹង ត្រង់និងការប្រកួត;

2) ប្រសិនបើបន្ទាប់មកបន្ទាត់និង

ប៉ារ៉ាឡែល;

3) បើអញ្ចឹង ត្រង់ប្រសព្វ។

ភស្តុតាង។ លក្ខខណ្ឌគឺស្មើនឹងភាពជាប់គ្នានៃធម្មតា។ វ៉ិចទ័រទិន្នន័យផ្ទាល់៖

ដូច្នេះប្រសិនបើ ត្រង់ប្រសព្វ។

ប្រសិនបើ , បន្ទាប់មក , , និង សមីការ ត្រង់យកទម្រង់៖

ឬ , i.e. ត្រង់ការប្រកួត។ ចំណាំថាមេគុណសមាមាត្រ បើមិនដូច្នេះទេ មេគុណនៃចំនួនសរុប សមីការនឹងសូន្យ ដែលវាមិនអាចទៅរួចទេ។

ប្រសិនបើ ត្រង់មិនស្របគ្នា និងមិនប្រសព្វគ្នា នោះករណីនៅតែមាន ពោលគឺឧ។ ត្រង់គឺស្របគ្នា។

ទ្រឹស្តីបទត្រូវបានបញ្ជាក់។

ដើម្បីកំណត់ចម្ងាយពីចំណុចមួយទៅបន្ទាត់មួយ អ្នកត្រូវដឹងពីសមីការនៃបន្ទាត់ និងកូអរដោនេនៃចំនុចនៅក្នុងប្រព័ន្ធកូអរដោណេ Cartesian ។ ចម្ងាយពីចំណុចមួយទៅបន្ទាត់គឺកាត់កែងពីចំណុចនោះទៅបន្ទាត់។

ការណែនាំ

សមីការទូទៅនៃបន្ទាត់ត្រង់នៅក្នុងកូអរដោណេ Cartesian គឺ Ax+By+C=0 ដែល A, B និង C គឺជាលេខដែលគេស្គាល់។ សូម​ឲ្យ​ចំណុច O មាន​កូអរដោនេ (x1, y1) ក្នុង​ប្រព័ន្ធ​កូអរដោណេ Cartesian ។

ក្នុងករណីនេះ គម្លាតនៃចំណុចនេះពីបន្ទាត់ត្រង់គឺ δ=(Ax1+By1+C)/sqrt((A^2)+(B^2)) ប្រសិនបើ C<0, и δ=(Ax1+By1+C)/(-sqrt((A^2)+(B^2))), если C>0.

ចម្ងាយពីចំណុចមួយទៅបន្ទាត់ត្រង់គឺជាគម្លាតដាច់ខាតនៃចំណុចពីបន្ទាត់ត្រង់មួយ នោះគឺ r=|(Ax1+By1+C)/sqrt((A^2)+(B^2))| បើ គ<0, и δ=|(Ax1+By1+C)/(-sqrt((A^2)+(B^2)))|, если C>0.

ឥឡូវ​សូម​ឱ្យ​ចំណុច​ដែល​មាន​កូអរដោណេ (x1, y1, z1) ត្រូវ​បាន​ផ្តល់​ឱ្យ​ក្នុង​ចន្លោះ​បី​វិមាត្រ។ បន្ទាត់ត្រង់អាចត្រូវបានកំណត់តាមប៉ារ៉ាម៉ែត្រ ដោយប្រព័ន្ធនៃសមីការបី៖ x = x0+ta, y = y0+tb, z = z0+tc ដែល t ជាចំនួនពិត។ ចម្ងាយពីចំណុចមួយទៅបន្ទាត់មួយអាចត្រូវបានរកឃើញថាជាចម្ងាយអប្បបរមាពីចំណុចនេះទៅចំណុចបំពាននៅលើបន្ទាត់។ មេគុណ t នៃចំណុចនេះគឺ tmin=(a(x1-x0)+b(y1-y0)+c(z1-z0))/((a^2)+(b^2)+(c^2) )

ចម្ងាយពីចំណុច (x1, y1) ទៅបន្ទាត់ត្រង់ក៏អាចគណនាបានដែរ ប្រសិនបើបន្ទាត់ត្រង់ត្រូវបានផ្តល់ដោយសមីការដែលមានជម្រាល៖ y = kx+b ។ បន្ទាប់មកសមីការនៃបន្ទាត់ត្រង់ដែលកាត់កែងនឹងមើលទៅដូច៖ y = (-1/k)x+a ។ បន្ទាប់មកអ្នកត្រូវយកទៅពិចារណាថាបន្ទាត់នេះត្រូវតែឆ្លងកាត់ចំណុច (x1, y1) ។ ពីទីនេះលេខ a ត្រូវបានរកឃើញ។ បន្ទាប់ពីការបំលែង ចម្ងាយរវាងចំណុច និងបន្ទាត់ក៏ត្រូវបានរកឃើញផងដែរ។

31 . មូលដ្ឋានលើយន្តហោះ និងក្នុងលំហ

និយមន័យ។ មូលដ្ឋានលើយន្តហោះវ៉ិចទ័រឯករាជ្យលីនេអ៊ែរទាំងពីរត្រូវបានគេហៅថា។

វ៉ិចទ័រមិនជាប់គ្នាទាំងពីរបង្កើតជាមូលដ្ឋានមួយ។ អនុញ្ញាតឱ្យ កវ៉ិចទ័រណាមួយនៅលើយន្តហោះ និងវ៉ិចទ័រ ខនិង គបង្កើតជាមូលដ្ឋាន។ ដោយសារវ៉ិចទ័រទាំងបីគឺអាស្រ័យទៅលើយន្តហោះ វ៉ិចទ័រ កត្រូវបានបង្ហាញជាលីនេអ៊ែរនៅក្នុងលក្ខខណ្ឌនៃវ៉ិចទ័រមូលដ្ឋាន ពោលគឺទំនាក់ទំនង

និយមន័យ។ មូលដ្ឋាននៅក្នុងលំហវ៉ិចទ័រឯករាជ្យលីនេអ៊ែរទាំងបីត្រូវបានគេហៅថា។ វ៉ិចទ័រដែលមិនមែនជា coplanar ទាំងបីបង្កើតជាមូលដ្ឋានមួយ។ ដូចនៅក្នុងករណីនៃយន្តហោះវាត្រូវបានបង្កើតឡើងថាវ៉ិចទ័រណាមួយ។ ក decompose ទៅជាវ៉ិចទ័រ ខ, គនិង ឃ

និយមន័យទូទៅ (ដើម្បីធ្វើឱ្យវាច្បាស់ដល់មនុស្សគ្រប់គ្នា) មូលដ្ឋាននៅលើយន្តហោះមួយ (ក្នុងលំហ) គឺជាគូដែលបានបញ្ជាទិញ (បីដង) នៃវ៉ិចទ័រដែលមិនមែនជាកូឡែណឺរ (មិនមែនកូបឡាណា) ។ វ៉ិចទ័រណាមួយអាចត្រូវបានពង្រីកដោយឡែកក្នុងលក្ខខណ្ឌនៃមូលដ្ឋាន។ មេគុណពង្រីកត្រូវបានគេហៅថាកូអរដោនេនៃវ៉ិចទ័រនេះដោយគោរពតាមមូលដ្ឋានដែលបានផ្តល់ឱ្យ។ វ៉ិចទ័រ​បង្កើត​បាន​មូលដ្ឋាន​នៅ​ក្នុង​លំហ​កូអរដោណេ Cartesian Oxyz ។