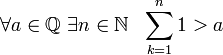ជាប្រវត្តិសាស្ត្រទីមួយ ចំនួនគត់$N$ ជាលទ្ធផលនៃការគណនាឡើងវិញនៃ farts ។ សំណុំនៃលេខទាំងនេះគឺគ្មានកំណត់ ហើយបង្កើតជាស៊េរីធម្មជាតិ $N=\(1, 2, 3, ..., n, ...\)$ ។ នៅក្នុងសំណុំនេះ ប្រតិបត្តិការនៃការបូក និងគុណគឺអាចធ្វើទៅបាន។ ដើម្បីអនុវត្តប្រតិបត្តិការដកលេខថ្មីត្រូវបានទាមទារ ដែលនាំទៅដល់ការលេចចេញនូវសំណុំចំនួនគត់៖ $Z$។ $Z=N_+\cup N_- \cup \(0\)$ ។ ដូច្នេះនៅក្នុងសំណុំនៃចំនួនគត់ ប្រតិបត្តិការនៃការបូក គុណ ដក តែងតែត្រូវបានអនុវត្ត។
លេខសនិទាន
តម្រូវការដើម្បីអនុវត្តការបែងចែកបាននាំឱ្យមានសំណុំនៃលេខសនិទាន $Q$ ។ $Q=\(\frac(m)(n), m\in Z, n\in N\)$។
និយមន័យ។ចំនួនសនិទានភាពពីរគឺស្មើគ្នា៖ $\frac(m_1)(n_1)=\frac(m_2)(n_2)$ - ប្រសិនបើ $m_1\cdot n_2=n_1\cdot m_2$ ។ នេះមានន័យថារាល់ ចំនួនសមហេតុផលអាចត្រូវបានតំណាងដោយឡែកពីគ្នាជាប្រភាគដែលមិនអាចកាត់ថ្លៃបាន $\frac(m)(n)$ ។ $gcd(m, n)=1$ ។
លក្ខណៈសម្បត្តិនៃសំណុំនៃលេខសនិទាន
1. ជាលទ្ធផល ប្រតិបត្តិការនព្វន្ធលើសពីចំនួនសនិទានកម្ម (បូក គុណ ដក ចែក លើកលែងតែចែកដោយសូន្យ) លេខសនិទានត្រូវបានទទួល។
2. សំណុំនៃលេខសនិទានភាពត្រូវបានតម្រៀប នោះគឺសម្រាប់គូនៃលេខសនិទាន $a$ និង $b$ ឬ $a
3. សំណុំនៃលេខសនិទានភាពគឺក្រាស់ នោះគឺសម្រាប់គូនៃលេខសនិទានណាមួយ $a$ និង $b$ មានលេខសនិទាន $c$ ដូចនោះ $a លេខសនិទានភាពវិជ្ជមានណាមួយអាចតែងតែត្រូវបានតំណាងជាប្រភាគទសភាគ៖ មិនកំណត់ ឬតាមកាលកំណត់។ ឧទាហរណ៍៖ $\frac(3)(5)=0.6$, $\frac(1)(3)=0.333...=0,(3)$ ។ $\frac(m)(n)=a_0,a_1a_1...a_kb_1b_2b_3...b_nb_1b_2b_3...b_n...$ ។ $b_1b_2b_3...b_n...$ - ត្រូវបានគេហៅថារយៈពេលនៃប្រភាគទសភាគ ដែលមិនមែនទាំងអស់ $b_i=0$ ទេ។ ចំណាំថាប្រភាគកំណត់អាចត្រូវបានសរសេរជាប្រភាគតាមកាលកំណត់គ្មានកំណត់ជាមួយនឹងសូន្យនៅក្នុងរយៈពេល។ $\frac(m)(n)=a_0,a_1a_1...a_k000000...$, $a_k\ne0$។ ទោះយ៉ាងណាក៏ដោយ ការតំណាងមួយទៀតនៃលេខសនិទានភាពជាប្រភាគទសភាគគឺជារឿងធម្មតាជាង៖ $\frac(m)(n)=a_0,a_1a_1...(a_k-1)999...$ ។ លេខសនិទានអវិជ្ជមាន $-\frac(m)(n)$ ត្រូវបានសរសេរជាការពង្រីកទសភាគនៃចំនួនសនិទាននៃទម្រង់ $\frac(m)(n)$ ដែលយកដោយសញ្ញាផ្ទុយ។ លេខ $0$ តំណាងឱ្យ $0,000...$។ ដូច្នេះ លេខសនិទានភាពណាមួយគឺតែងតែតំណាងឱ្យជាប្រភាគតាមកាលកំណត់ទសភាគគ្មានកំណត់ ដែលមិនមាន $0$ ក្នុងរយៈពេល លើកលែងតែលេខ $0$ ខ្លួនវាផ្ទាល់។ ទិដ្ឋភាពនេះគឺតែមួយគត់។ សំណុំនៃលេខសនិទានភាពត្រូវបានបិទនៅក្រោមប្រតិបត្តិការនព្វន្ធចំនួនបួន។ ទោះយ៉ាងណាក៏ដោយ នៅក្នុងសំណុំនៃលេខសនិទានភាព ដំណោះស្រាយនៃសមីការសាមញ្ញបំផុតនៃទម្រង់ $x^2-n=0$ មិនតែងតែកើតឡើងនោះទេ។ ដូច្នេះ ចាំបាច់ត្រូវណែនាំលេខថ្មី។ ចូរយើងបង្ហាញថាក្នុងចំណោមលេខសនិទានភាព គ្មានលេខដែលការ៉េស្មើនឹងបីទេ។ ភស្តុតាងត្រូវបានអនុវត្តដោយវិធីសាស្រ្តនៃការផ្ទុយ។ ឧបមាថាមានលេខសនិទាន $\frac(m)(n)$ ដែលការេរបស់វាមានបី៖ $\left(\frac(m)(n)\right)^2=3\;\;\;( 1 )$។ $\frac(m^2)(n^2)=3$, $m^2=3n^2។\;\;\;(2)$ ផ្នែកខាងស្តាំនៃសមភាព (2) ត្រូវបានបែងចែកដោយ 3។ ដូច្នេះ $m^2$ ក៏ត្រូវបានបែងចែកដោយ 3 ដូច្នេះ $m$ ត្រូវបានបែងចែកដោយ 3 ដែលមានន័យថា $m=3k$។ ជំនួសសមីការ (២) យើងទទួលបាន៖ $3k^2=n^2.\;\;\;(3)$ ផ្នែកខាងឆ្វេងនៃ $(3)$ ត្រូវបានបែងចែកដោយ $3$ ដូច្នេះផ្នែកខាងស្តាំក៏បែងចែកដោយ $3 ។ ហេតុនេះ $n^2$ ត្រូវបានបែងចែកដោយ $3$ ដូច្នេះហើយ $n$ ក៏ត្រូវបានបែងចែកដោយ $3$ មកពីណា $n=3p$។ ជាលទ្ធផល យើងទទួលបាន៖ $\frac(m)(n)=\frac(3k)(3p)$, i.e. ប្រភាគ $\frac(m)(n)$ ប្រែទៅជាអាចកាត់បន្ថយបាន ដែលផ្ទុយនឹងការសន្មត់ . នេះមានន័យថាក្នុងចំណោមលេខសនិទានភាពមិនមានលេខបែបនេះទេ ការេដែលស្មើនឹងបី។ ប៉ុន្តែមានលេខដែលការ៉េគឺបី។ វាអាចត្រូវបានតំណាងថាជាប្រភាគគ្មានកំណត់។ ហើយយើងទទួលបានលេខប្រភេទថ្មី។ ចូរហៅពួកគេថាមិនសមហេតុផល។ និយមន័យ។ចំនួនមិនសមហេតុផល គឺជាប្រភាគដែលមិនកំណត់កាលកំណត់។ សំណុំនៃប្រភាគដែលមិនកំណត់កាលកំណត់ទាំងអស់ត្រូវបានគេហៅថា សំណុំនៃចំនួនមិនសមហេតុផល ហើយត្រូវបានតំណាងដោយ $I$ ។ ការរួបរួមនៃសំណុំលេខសនិទាន $Q$ និងលេខមិនសមហេតុផល $I$ ផ្តល់ឱ្យសំណុំនៃចំនួនពិត $R$: $Q\cup I=R$ ។ ដូច្នេះ ចំនួនពិតណាមួយអាចត្រូវបានតំណាងជាប្រភាគទសភាគគ្មានកំណត់៖ តាមកាលកំណត់ក្នុងករណីចំនួនសនិទាន និងមិនមែនតាមកាលកំណត់ក្នុងករណីចំនួនមិនសមហេតុផល។ សម្រាប់ចំនួនពិត $a=a_0,a_1a_2a_3\ldots a_n\ldots$, $b=b_0,b_1b_2b_3\ldots b_n\ldots$ ការប្រៀបធៀបមានដូចខាងក្រោម៖ 1) អនុញ្ញាតឱ្យ $a$ និង $b$ ទាំងពីរវិជ្ជមាន៖ $a>0$, $b>0$ បន្ទាប់មក៖ $a=b$ ប្រសិនបើសម្រាប់ $k$ $a_k=b_k$; $a>b$ ប្រសិនបើ $\មាន s$ $\forall k 2) អនុញ្ញាតឱ្យ $a>0$, $b<0$, или иначе: $b<0 3) អនុញ្ញាតឱ្យ $a$ និង $b$ ទាំងពីរអវិជ្ជមាន៖ $a<0$, $b<0$, тогда: $a=b$ ប្រសិនបើសម្រាប់ $-a=-b$; មានចំនួននៃលក្ខណៈខុសគ្នា - ប្រតិបត្តិការដកឫសការ៉េជាញឹកញាប់នាំឱ្យពួកគេ (ហើយមិនត្រឹមតែប៉ុណ្ណោះ យើងមិនទាន់ដឹងវានៅឡើយទេ)។ ដូច្នេះ យើងត្រូវស្វែងយល់ពីលេខថ្មីឲ្យបានលម្អិតបន្ថែមទៀត។ ប៉ុន្តែជាដំបូង ចូរយើងព្យាយាមរៀបចំប្រព័ន្ធចំណេះដឹងរបស់យើងអំពី "ចាស់" ពោលគឺ សនិទានភាព លេខ។ 1. និមិត្តសញ្ញាមួយចំនួននៃភាសាគណិតវិទ្យា
ទាំងនេះគឺជាចំនួនសរុប ប្រភាគទូទៅ ប្រភាគទសភាគ។ សម្រាប់លេខទាំងអស់នេះ អ្នកអាចប្រើសញ្ញាណដូចគ្នា ដែលយើងនឹងពិភាក្សាឥឡូវនេះ។ 5 = 5.00000... = 5,(0). ដូចគ្នានឹងលេខ 8.377: 8.377 = 8.377000... = 8.377(0) ។ ដើម្បីធ្វើឱ្យអ្វីគ្រប់យ៉ាងស្អាត ពួកគេនិយាយដូចនេះ៖ 8.377 គឺជាប្រភាគទសភាគកំណត់ ហើយ 8.377000 ... គឺជាប្រភាគទសភាគគ្មានកំណត់។ ជាទូទៅ លេខសនិទានភាពណាមួយអាចត្រូវបានសរសេរជាប្រភាគទសភាគគ្មានកំណត់។ មតិយោបល់។
ការសន្និដ្ឋាននេះគឺងាយស្រួលសម្រាប់ទ្រឹស្តី ប៉ុន្តែមិនងាយស្រួលសម្រាប់ការអនុវត្តនោះទេ។ យ៉ាងណាមិញ ប្រសិនបើប្រភាគទសភាគចុងក្រោយ 8.377 ត្រូវបានផ្តល់ឱ្យ នោះហេតុអ្វីបានជាចាំបាច់ត្រូវសរសេរវាក្នុងទម្រង់ 8.377 (0)? ដូច្នេះ គេតែងតែនិយាយដូចនេះ៖ លេខសនិទានភាពណាមួយអាចត្រូវបានសរសេរជាប្រភាគទសភាគកំណត់ ឬជាប្រភាគទសភាគគ្មានកំណត់។ សំណុំនៃលេខសនិទានភាពត្រូវបានតាង និងអាចសរសេរដូចខាងក្រោមៈ វាប្រែថាធាតុផ្សេងគ្នាអាចតំណាងឱ្យប្រភាគដូចគ្នា ឧទាហរណ៍ និង , (ប្រភាគទាំងអស់ដែលអាចទទួលបានពីគ្នាទៅវិញទៅមកដោយការគុណ ឬចែកដោយចំនួនធម្មជាតិដូចគ្នាតំណាងឱ្យចំនួនសនិទានដូចគ្នា)។ ដោយសារដោយការបែងចែកភាគយក និងភាគបែងនៃប្រភាគដោយចែកចែកទូទៅធំបំផុតរបស់ពួកគេ មនុស្សម្នាក់អាចទទួលបានតំណាងដែលមិនអាចកាត់ថ្លៃបានតែមួយគត់នៃចំនួនសនិទាន នោះគេអាចនិយាយអំពីសំណុំរបស់ពួកគេជាសំណុំ មិនអាចកាត់ថ្លៃបាន។ប្រភាគដែលមានចំនួនគត់ coprime និងភាគបែងធម្មជាតិ៖ នេះគឺជាផ្នែកចែកទូទៅដ៏ធំបំផុតនៃលេខ និង . សំណុំនៃលេខសនិទានភាពគឺជាការទូទៅធម្មជាតិនៃសំណុំចំនួនគត់។ វាងាយស្រួលមើលថា ប្រសិនបើលេខសមហេតុផលមានភាគបែង នោះវាគឺជាចំនួនគត់។ សំណុំនៃលេខសនិទានភាពគឺនៅគ្រប់ទីកន្លែងដែលក្រាស់នៅលើអ័ក្សលេខ៖ រវាងលេខសនិទានភាពពីរផ្សេងគ្នា យ៉ាងហោចណាស់មានលេខសនិទានមួយ (ហេតុដូច្នេះហើយ សំណុំលេខសនិទានគ្មានកំណត់)។ ទោះយ៉ាងណាក៏ដោយ វាប្រែថា សំណុំនៃលេខសនិទានភាពមានលេខដែលអាចរាប់បាន (នោះគឺធាតុទាំងអស់របស់វាអាចត្រូវបានប្តូរលេខ)។ ចំណាំ ដោយវិធីនេះ សូម្បីតែជនជាតិក្រិចបុរាណក៏ជឿជាក់លើអត្ថិភាពនៃលេខដែលមិនអាចត្រូវបានតំណាងជាប្រភាគ (ឧទាហរណ៍ ពួកគេបានបង្ហាញថាមិនមានលេខសនិទានទេដែលការ៉េគឺ 2) ទ្រព្យសម្បត្តិ លក្ខណៈសម្បត្តិមូលដ្ឋាន សំណុំនៃលេខសនិទានកម្មបំពេញលក្ខណៈសម្បត្តិមូលដ្ឋានដប់ប្រាំមួយដែលអាចទទួលបានយ៉ាងងាយស្រួលពីលក្ខណៈសម្បត្តិនៃចំនួនគត់។ លក្ខណៈសម្បត្តិបន្ថែម លក្ខណៈសម្បត្តិផ្សេងទៀតទាំងអស់ដែលមាននៅក្នុងលេខសនិទាន មិនត្រូវបានជ្រើសរើសជាលក្ខណៈមូលដ្ឋានទេ ពីព្រោះជាទូទៅ ពួកវាលែងផ្អែកលើលក្ខណៈសម្បត្តិនៃចំនួនគត់ដោយផ្ទាល់ទៀតហើយ ប៉ុន្តែអាចបញ្ជាក់បានដោយផ្អែកលើលក្ខណៈសម្បត្តិមូលដ្ឋានដែលបានផ្តល់ឱ្យ ឬដោយផ្ទាល់តាមនិយមន័យនៃ វត្ថុគណិតវិទ្យាមួយចំនួន។ មានទ្រព្យសម្បត្តិបន្ថែមបែបនេះច្រើន។ វាសមហេតុផលនៅទីនេះដើម្បីដកស្រង់ពួកគេមួយចំនួន។ 25..កំណត់ J នៃចំនួនមិនសមហេតុផល ឧទាហរណ៍នៃចំនួនមិនសមហេតុផល: សំណុំនៃលេខមិនសមហេតុផលត្រូវបានបង្ហាញដោយអក្សរធំជាភាសាអង់គ្លេស [ai] - "ខ្ញុំ" ។ ក្នុងចំណោមសំណុំលេខ លេខមិនសមហេតុផលកាន់កាប់កន្លែងពិសេស។ ពួកគេមិនត្រូវបានរាប់បញ្ចូលក្នុងលេខសមហេតុផលទេ។ លេខមិនសមហេតុផល(មិនដូចសនិទានទេ) មិនអាចតំណាងជាប្រភាគ a/b ដែល a ∈ Z (a ជារបស់ចំនួនគត់) b∈N (b ជារបស់លេខធម្មជាតិ)។ 26. សំណុំ R នៃចំនួនពិត ចំនួនពិត មកពីវិគីភីឌាជាសព្វវចនាធិប្បាយដោយឥតគិតថ្លៃ លោតទៅ៖ រុករក, ស្វែងរក ពិត, ឬ ចំនួនពិត- អរូបីគណិតវិទ្យាដែលកើតចេញពីតម្រូវការវាស់វែងធរណីមាត្រ និងបរិមាណរូបវន្តនៃពិភពលោកជុំវិញ ព្រមទាំងអនុវត្តប្រតិបត្តិការដូចជា ស្រង់ឫស គណនាលោការីត ដោះស្រាយសមីការពិជគណិត។ ជួរលេខ ប្រសិនបើលេខធម្មជាតិបានកើតឡើងនៅក្នុងដំណើរការនៃការរាប់ចំនួនសមហេតុផល - ពីតម្រូវការដើម្បីធ្វើប្រតិបត្តិការជាមួយផ្នែកទាំងមូល នោះចំនួនពិតត្រូវបានបម្រុងទុកសម្រាប់ការវាស់បរិមាណបន្ត។ ដូច្នេះ ការពង្រីកភាគហ៊ុននៃលេខដែលកំពុងពិចារណាបាននាំឱ្យមានសំណុំនៃចំនួនពិត ដែលបន្ថែមពីលើលេខសនិទាន ក៏រួមបញ្ចូលធាតុផ្សេងទៀតដែលហៅថា លេខមិនសមហេតុផល. គំនិតនៃចំនួនពិតអាចត្រូវបានគេមើលឃើញដោយប្រើ បន្ទាត់លេខ. ប្រសិនបើអ្នកជ្រើសរើសទិសដៅនៅលើបន្ទាត់ត្រង់ ចំណុចចាប់ផ្តើម និងឯកតានៃប្រវែងសម្រាប់វាស់ផ្នែក នោះចំនួនពិតនីមួយៗអាចត្រូវបានផ្សារភ្ជាប់ជាមួយនឹងចំណុចជាក់លាក់មួយនៅលើបន្ទាត់ត្រង់នេះ ហើយផ្ទុយទៅវិញ ចំនុចនីមួយៗនឹងតំណាងឱ្យមួយចំនួន ហើយលើសពីនេះទៅទៀត មួយគត់ លេខពិត។ ដោយសារតែការឆ្លើយឆ្លងនេះ ពាក្យបន្ទាត់លេខជាធម្មតាត្រូវបានគេប្រើជាសទិសន័យសម្រាប់សំណុំនៃចំនួនពិត។ គោលគំនិតនៃចំនួនពិតបានមកជាផ្លូវវែងឆ្ងាយនៃការក្លាយជា។ សូម្បីតែនៅប្រទេសក្រិចបុរាណក៏ដោយ នៅក្នុងសាលា Pythagoras ដែលដាក់លេខទាំងមូល និងទំនាក់ទំនងរបស់ពួកគេជាមូលដ្ឋានសម្រាប់អ្វីៗទាំងអស់ អត្ថិភាពនៃ បរិមាណដែលមិនអាចគណនាបាន។(ភាពមិនស៊ីសង្វាក់គ្នានៃជ្រុងម្ខាង និងអង្កត់ទ្រូងនៃការ៉េ) ពោលគឺនៅក្នុងវាក្យស័ព្ទទំនើប លេខដែលមិនសមហេតុផល។ បន្ទាប់ពីរឿងនេះ Eudoxus នៃ Cnidus បានព្យាយាមបង្កើតទ្រឹស្តីទូទៅនៃចំនួនដែលរួមបញ្ចូលបរិមាណដែលមិនអាចគណនាបាន។ បន្ទាប់ពីនោះមក អស់រយៈពេលជាងពីរពាន់ឆ្នាំ គ្មាននរណាម្នាក់មានអារម្មណ៍ថាត្រូវការនិយមន័យច្បាស់លាស់នៃគោលគំនិតនៃចំនួនពិតប្រាកដនោះទេ ទោះបីជាមានការពង្រីកបន្តិចម្តងៗនៃគំនិតនេះក៏ដោយ។ មានតែនៅក្នុងពាក់កណ្តាលទីពីរនៃសតវត្សទី 19 នៅពេលដែលការអភិវឌ្ឍន៍នៃការវិភាគគណិតវិទ្យាទាមទារឱ្យមានការរៀបចំឡើងវិញនូវមូលដ្ឋានគ្រឹះរបស់វានៅកម្រិតថ្មីនៃភាពតឹងរ៉ឹងខ្ពស់ ទ្រឹស្តីដ៏តឹងរឹងនៃចំនួនពិតត្រូវបានបង្កើតឡើងនៅក្នុងស្នាដៃរបស់ K. Weierstrass, R. Dedekind , G. Cantor, E. Heine, S. Mere ។ តាមទស្សនៈនៃគណិតវិទ្យាសម័យទំនើប សំណុំនៃចំនួនពិតគឺជាវាលលំដាប់បន្ត។ និយមន័យនេះ ឬប្រព័ន្ធសមមូលនៃ axioms កំណត់យ៉ាងជាក់លាក់នូវគោលគំនិតនៃចំនួនពិតក្នុងន័យថាមានតែមួយប៉ុណ្ណោះ រហូតដល់ isomorphism វាលលំដាប់បន្ត។ សំណុំនៃចំនួនពិតមានសញ្ញាសម្គាល់ស្តង់ដារ - រ("bold R") ឬ (eng. ក្តារខៀនដិត"R") ពីឡាតាំង។ ពិត- ត្រឹមត្រូវ។ 27. ប្រព័ន្ធលេខ កំណត់ចំណាំ- វិធីសាស្រ្តនិមិត្តសញ្ញានៃការសរសេរលេខ តំណាងឱ្យលេខដោយប្រើតួអក្សរសរសេរ។ កំណត់សម្គាល់៖ ប្រព័ន្ធលេខត្រូវបានបែងចែកទៅជា ទីតាំង, មិនមែនទីតាំងនិង លាយ.លេខមិនសមហេតុផល
លេខពិត
ការប្រៀបធៀបចំនួនពិត
ជាឧទាហរណ៍ សូមពិចារណាចំនួនគត់ 5 ប្រភាគទូទៅ និងទសភាគ 8.377។ ចំនួនគត់ 5 អាចត្រូវបានសរសេរជាទសភាគគ្មានកំណត់៖ 5.0000... ទសភាគ 8.377 ក៏អាចសរសេរជាចំនួនគ្មានកំណត់ផងដែរ។ ប្រភាគទសភាគ: 8.377000... សម្រាប់លេខ ចូរយើងប្រើវិធី "ចែកមុំ"៖
ដូចដែលអ្នកអាចឃើញដោយចាប់ផ្តើមពីខ្ទង់ទីពីរបន្ទាប់ពីចំនុចទសភាគក្រុមនៃលេខដូចគ្នាត្រូវបានធ្វើម្តងទៀត: 18, 18, 18, ... ។ ដូចនេះ = 0.3181818... ។ សរុបមក វាត្រូវបានសរសេរដូចនេះ៖ ០.៣ (១៨)។ ក្រុមលេខដែលកើតឡើងដដែលៗបន្ទាប់ពីចំនុចទសភាគត្រូវបានគេហៅថារយៈពេលមួយ ហើយប្រភាគទសភាគខ្លួនវាត្រូវបានគេហៅថាប្រភាគទសភាគគ្មានកំណត់។
ប្រភាគតាមកាលកំណត់ទសភាគគ្មានកំណត់។ ដើម្បីធ្វើដូចនេះសរសេរលេខ 0 ក្នុងរយៈពេល:
ដូច្នេះ លេខ 5 និងលេខ និងលេខ 8.377 ត្រូវបានសរសេរជាប្រភាគទសភាគគ្មានកំណត់។![]()