ដំណោះស្រាយក្រាហ្វិកនៃសមីការ
សួស្តីឆ្នាំ ២០០៩
សេចក្តីផ្តើម
តម្រូវការដើម្បីដោះស្រាយសមីការបួនជ្រុងនៅសម័យបុរាណគឺបណ្តាលមកពីតម្រូវការក្នុងការដោះស្រាយបញ្ហាទាក់ទងនឹងការស្វែងរកតំបន់នៃដី និងផែនដីនៃធម្មជាតិយោធា ក៏ដូចជាការអភិវឌ្ឍន៍តារាសាស្ត្រ និងគណិតវិទ្យាខ្លួនឯង។ ជនជាតិបាប៊ីឡូនបានដឹងពីរបៀបដោះស្រាយសមីការបួនជ្រុងប្រហែលឆ្នាំ 2000 មុនគ។ ច្បាប់សម្រាប់ការដោះស្រាយសមីការទាំងនេះដែលមានចែងនៅក្នុងអត្ថបទរបស់បាប៊ីឡូន គឺស្របគ្នានឹងសមីការសម័យទំនើប ប៉ុន្តែគេមិនដឹងថាតើជនជាតិបាប៊ីឡូនចូលមកក្បួននេះដោយរបៀបណានោះទេ។
រូបមន្តសម្រាប់ដោះស្រាយសមីការការ៉េនៅអឺរ៉ុបត្រូវបានបង្កើតឡើងជាលើកដំបូងក្នុងសៀវភៅ Abacus ដែលសរសេរក្នុងឆ្នាំ ១២០២ ដោយគណិតវិទូជនជាតិអ៊ីតាលី Leonardo Fibonacci។ សៀវភៅរបស់គាត់បានរួមចំណែកដល់ការរីករាលដាលនៃចំណេះដឹងពិជគណិតមិនត្រឹមតែនៅក្នុងប្រទេសអ៊ីតាលីប៉ុណ្ណោះទេ ប៉ុន្តែថែមទាំងនៅក្នុងប្រទេសអាល្លឺម៉ង់ បារាំង និងបណ្តាប្រទេសអឺរ៉ុបផ្សេងទៀតផងដែរ។
ប៉ុន្តែច្បាប់ទូទៅសម្រាប់ការដោះស្រាយសមីការបួនជ្រុង ជាមួយនឹងការបន្សំដែលអាចធ្វើបានទាំងអស់នៃមេគុណ b និង c ត្រូវបានបង្កើតឡើងនៅក្នុងទ្វីបអឺរ៉ុបតែនៅក្នុងឆ្នាំ 1544 ដោយ M. Stiefel ។
នៅឆ្នាំ 1591 ហ្វ្រង់ស្វ័រវៀត បានណែនាំរូបមន្តសម្រាប់ដោះស្រាយសមីការការ៉េ។
ប្រភេទមួយចំនួននៃសមីការការ៉េអាចត្រូវបានដោះស្រាយនៅក្នុងបាប៊ីឡូនបុរាណ។
Diophantus នៃ Alexandria និង អេកលីដ, អាល់-ឃវ៉ារីសមីនិង Omar Khayyamដោះស្រាយសមីការតាមធរណីមាត្រ និងក្រាហ្វិក។
នៅថ្នាក់ទី 7 យើងបានសិក្សាមុខងារ y \u003d C, y=kx, y =kx+ ម, y =x 2,y = -x 2, នៅថ្នាក់ទី ៨ - y = √x, y =|x|, y=ពូថៅ2 + bx+ គ, y =k/ x. នៅក្នុងសៀវភៅសិក្សាពិជគណិតថ្នាក់ទី៩ ខ្ញុំបានឃើញមុខងារដែលខ្ញុំមិនទាន់ស្គាល់៖ y=x 3, y=x 4,y=x 2n, y=x- 2n, y= 3√x, (x– ក) 2 + (y -ខ) 2 = r 2 និងអ្នកដទៃ។ មានច្បាប់សម្រាប់បង្កើតក្រាហ្វនៃមុខងារទាំងនេះ។ ខ្ញុំឆ្ងល់ថាតើមានមុខងារផ្សេងទៀតដែលគោរពច្បាប់ទាំងនេះដែរឬទេ?
ការងាររបស់ខ្ញុំគឺសិក្សាក្រាហ្វនៃមុខងារ និងដោះស្រាយសមីការក្រាហ្វិក។
1. តើមុខងារអ្វីខ្លះ
ក្រាហ្វនៃអនុគមន៍គឺជាសំណុំនៃចំណុចទាំងអស់នៃប្លង់កូអរដោនេ អេស៊ីសស៊ីស ដែលស្មើនឹងតម្លៃនៃអាគុយម៉ង់ ហើយការចាត់តាំងគឺស្មើនឹងតម្លៃដែលត្រូវគ្នានៃអនុគមន៍។
អនុគមន៍លីនេអ៊ែរត្រូវបានផ្តល់ដោយសមីការ y=kx+ ខកន្លែងណា kនិង ខ- លេខមួយចំនួន។ ក្រាហ្វនៃមុខងារនេះគឺជាបន្ទាត់ត្រង់។
អនុគមន៍សមាមាត្របញ្ច្រាស y=k/ xដែលជាកន្លែងដែល k ¹ 0. ក្រាហ្វនៃអនុគមន៍នេះត្រូវបានគេហៅថាអ៊ីពែបូឡា។
មុខងារ (x– ក) 2 + (y -ខ) 2 = r2 កន្លែងណា ក, ខនិង r- លេខមួយចំនួន។ ក្រាហ្វនៃអនុគមន៍នេះគឺជារង្វង់នៃកាំ r ដែលស្ថិតនៅកណ្តាលចំណុច A ( ក, ខ).
មុខងារបួនជ្រុង y= ពូថៅ2 + bx+ គកន្លែងណា ក,ខ, ជាមួយ- លេខមួយចំនួននិង ក¹ 0. ក្រាហ្វនៃអនុគមន៍នេះគឺជាប៉ារ៉ាបូឡា។
សមីការ នៅ2 (ក– x) = x2 (ក+ x) . ក្រាហ្វនៃសមីការនេះនឹងជាខ្សែកោងដែលហៅថា ស្ត្រូហ្វីត។
/>សមីការ (x2 + y2 ) 2 = ក(x2 – y2 ) . ក្រាហ្វនៃសមីការនេះត្រូវបានគេហៅថា Bernoulli lemniscate ។
សមីការ។ ក្រាហ្វនៃសមីការនេះត្រូវបានគេហៅថា astroid ។
ខ្សែកោង (x2 y2 - 2 ក x)2 =4 ក2 (x2 +y2 ) . ខ្សែកោងនេះត្រូវបានគេហៅថា cardioid ។
មុខងារ៖ y=x 3 - ប៉ារ៉ាបូឡាគូប, y=x 4, y = 1/x 2.
2. គំនិតនៃសមីការ ដំណោះស្រាយក្រាហ្វិករបស់វា។
សមីការគឺជាកន្សោមដែលមានអថេរ។
ដោះស្រាយសមីការ- នេះមានន័យថាស្វែងរកឫសគល់របស់វាទាំងអស់ ឬបង្ហាញថាវាមិនមាន។
ឫសគល់នៃសមីការគឺជាលេខដែលនៅពេលជំនួសទៅក្នុងសមីការ បង្កើតសមភាពលេខត្រឹមត្រូវ។
ការដោះស្រាយសមីការក្រាហ្វិកអនុញ្ញាតឱ្យអ្នកស្វែងរកតម្លៃពិតប្រាកដ ឬប្រហាក់ប្រហែលនៃឫស អនុញ្ញាតឱ្យអ្នកស្វែងរកចំនួនឫសនៃសមីការ។
នៅពេលគូរក្រាហ្វ និងការដោះស្រាយសមីការ លក្ខណៈសម្បត្តិនៃអនុគមន៍មួយត្រូវបានប្រើប្រាស់ ដូច្នេះវិធីសាស្ត្រនេះត្រូវបានគេហៅថាជាក្រាហ្វិកមុខងារ។
ដើម្បីដោះស្រាយសមីការ យើងបែងចែកវាជាពីរផ្នែក ណែនាំមុខងារពីរ បង្កើតក្រាហ្វរបស់ពួកគេ ស្វែងរកកូអរដោនេនៃចំនុចប្រសព្វនៃក្រាហ្វ។ abscissas នៃចំនុចទាំងនេះគឺជាឫសគល់នៃសមីការ។
3. ក្បួនដោះស្រាយសម្រាប់បង្កើតក្រាហ្វនៃអនុគមន៍មួយ។
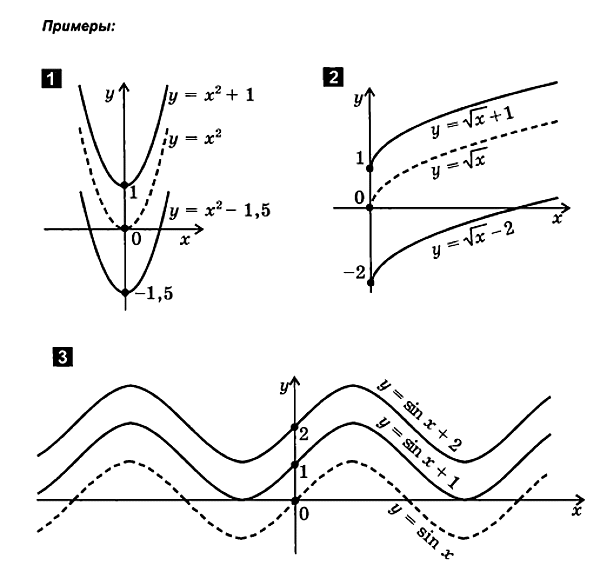
ដឹងពីក្រាហ្វនៃមុខងារ y=f(x) អ្នកអាចគ្រោងមុខងារ y=f(x+ ម) ,y=f(x)+ លីត្រនិង y=f(x+ ម)+ លីត្រ. ក្រាហ្វទាំងអស់នេះត្រូវបានទទួលពីក្រាហ្វនៃអនុគមន៍ y=f(x) ដោយប្រើការបំប្លែងការបកប្រែប៉ារ៉ាឡែល៖ បើក │ ម│ មាត្រដ្ឋានឯកតាទៅខាងស្តាំឬខាងឆ្វេងតាមអ័ក្ស x និងនៅលើ │ លីត្រ│ មាត្រដ្ឋានឯកតាឡើងលើឬចុះតាមអ័ក្ស y.
4. ដំណោះស្រាយក្រាហ្វិកនៃសមីការការ៉េ
ដោយប្រើឧទាហរណ៍នៃអនុគមន៍ quadratic យើងនឹងពិចារណាដំណោះស្រាយក្រាហ្វិកនៃសមីការការ៉េ។ ក្រាហ្វនៃអនុគមន៍ quadratic គឺប៉ារ៉ាបូឡា។
តើជនជាតិក្រិចបុរាណដឹងអ្វីខ្លះអំពីប៉ារ៉ាបូឡា?
និមិត្តសញ្ញាគណិតវិទ្យាសម័យទំនើបមានដើមកំណើតនៅសតវត្សទី 16 ។
គណិតវិទូក្រិកបុរាណមិនមានវិធីសាស្ត្រកូអរដោណេ ឬគោលគំនិតនៃអនុគមន៍ទេ។ ទោះជាយ៉ាងណាក៏ដោយលក្ខណៈសម្បត្តិរបស់ប៉ារ៉ាបូឡាត្រូវបានសិក្សាដោយពួកគេយ៉ាងលំអិត។ ការច្នៃប្រឌិតរបស់គណិតវិទូបុរាណគឺពិតជាអស្ចារ្យណាស់ ព្រោះពួកគេអាចប្រើតែគំនូរ និងការពិពណ៌នាដោយពាក្យសំដីនៃភាពអាស្រ័យ។
ភាគច្រើនបានរុករកយ៉ាងពេញលេញនូវប៉ារ៉ាបូឡា អ៊ីពែបូឡា និងពងក្រពើ Apollonius នៃ Pergaដែលរស់នៅក្នុងសតវត្សទី 3 មុនគ។ គាត់ក៏បានផ្តល់ឈ្មោះដល់ខ្សែកោងទាំងនេះ និងចង្អុលបង្ហាញនូវលក្ខខណ្ឌអ្វីដែលចំនុចដែលស្ថិតនៅលើខ្សែកោងជាក់លាក់ណាមួយពេញចិត្ត (បន្ទាប់ពីទាំងអស់ វាមិនមានរូបមន្តទេ!)
មានក្បួនដោះស្រាយសម្រាប់បង្កើតប៉ារ៉ាបូឡា៖
ស្វែងរកកូអរដោនេនៃចំនុចកំពូលនៃប៉ារ៉ាបូឡា A (x0; y0)៖ X=- ខ/2 ក;
y0=aho2+in0+s;
រកអ័ក្សស៊ីមេទ្រីនៃប៉ារ៉ាបូឡា (បន្ទាត់ត្រង់ x=x0);
PAGE_BREAK--
ការចងក្រងតារាងតម្លៃសម្រាប់ចំណុចត្រួតពិនិត្យអគារ;
យើងសាងសង់ចំណុចដែលទទួលបាន និងបង្កើតចំណុចស៊ីមេទ្រីទៅនឹងពួកវាដោយគោរពតាមអ័ក្សស៊ីមេទ្រី។
1. ចូរយើងបង្កើតប៉ារ៉ាបូឡាតាមក្បួនដោះស្រាយ y= x2 – 2 x– 3 . Abscissas នៃចំនុចប្រសព្វជាមួយអ័ក្ស xនិងជាឫសគល់នៃសមីការការ៉េ x2 – 2 x– 3 = 0.
មានវិធីប្រាំយ៉ាងដើម្បីដោះស្រាយសមីការនេះតាមក្រាហ្វិក។
2. ចូរបំបែកសមីការជាពីរមុខងារ៖ y= x2 និង y= 2 x+ 3
3. ចូរបំបែកសមីការជាពីរមុខងារ៖ y= x2 –3 និង y=2 x. ឫសនៃសមីការគឺជា abscissas នៃចំនុចប្រសព្វនៃ parabola ជាមួយបន្ទាត់។
4. បំប្លែងសមីការ x2 – 2 x– 3 = 0 ដោយជ្រើសរើសការ៉េពេញលើមុខងារ៖ y= (x–1) 2 និង y=4. ឫសនៃសមីការគឺជា abscissas នៃចំនុចប្រសព្វនៃ parabola ជាមួយបន្ទាត់។
5. យើងបែងចែកពាក្យតាមពាក្យទាំងពីរផ្នែកនៃសមីការ x2 – 2 x– 3 = 0 នៅលើ x, យើងទទួលបាន x– 2 – 3/ x= 0 ចូរបែងចែកសមីការនេះជាមុខងារពីរ៖ y= x– 2, y= 3/ x. ឫសគល់នៃសមីការគឺ abscissas នៃចំនុចប្រសព្វនៃបន្ទាត់ និងអ៊ីពែបូឡា។
5. ដំណោះស្រាយក្រាហ្វិកនៃសមីការដឺក្រេន
ឧទាហរណ៍ ១ដោះស្រាយសមីការ x5 = 3 – 2 x.
y= x5 , y= 3 – 2 x.
ចម្លើយ៖ x = ១.
ឧទាហរណ៍ ២ដោះស្រាយសមីការ 3 √ x= 10 – x.
ឫសគល់នៃសមីការនេះគឺជា abscissa នៃចំនុចប្រសព្វនៃក្រាហ្វនៃមុខងារពីរ៖ y= 3 √ x, y= 10 – x.
ចម្លើយ៖ x=8 ។
សេចក្តីសន្និដ្ឋាន
ពិចារណាក្រាហ្វិកមុខងារ៖ y=ពូថៅ2 + bx+ គ, y =k/ x, y = √x, y =|x|, y=x 3, y=x 4,y= 3√x, ខ្ញុំបានកត់សម្គាល់ឃើញថាក្រាហ្វទាំងអស់នេះត្រូវបានបង្កើតឡើងស្របតាមច្បាប់នៃការបកប្រែប៉ារ៉ាឡែលទាក់ទងទៅនឹងអ័ក្ស xនិង y.
ដោយប្រើឧទាហរណ៍នៃការដោះស្រាយសមីការ quadratic យើងអាចសន្និដ្ឋានថាវិធីសាស្ត្រក្រាហ្វិចក៏អាចអនុវត្តបានចំពោះសមីការដឺក្រេ n ។
វិធីសាស្រ្តក្រាហ្វិកសម្រាប់ការដោះស្រាយសមីការគឺស្រស់ស្អាត និងអាចយល់បាន ប៉ុន្តែពួកគេមិនផ្តល់ការធានា 100% នៃការដោះស្រាយសមីការណាមួយឡើយ។ abscissas នៃចំនុចប្រសព្វនៃក្រាហ្វអាចប្រហាក់ប្រហែល។
នៅថ្នាក់ទី 9 និងនៅក្នុងថ្នាក់ជាន់ខ្ពស់ខ្ញុំនឹងនៅតែស្គាល់មុខងារផ្សេងទៀត។ ខ្ញុំចាប់អារម្មណ៍ចង់ដឹងថាតើមុខងារទាំងនោះគោរពតាមច្បាប់នៃការបកប្រែប៉ារ៉ាឡែលនៅពេលគូរក្រាហ្វិករបស់ពួកគេ។
នៅឆ្នាំក្រោយ ខ្ញុំក៏ចង់ពិចារណាពីបញ្ហានៃដំណោះស្រាយក្រាហ្វិកនៃប្រព័ន្ធសមីការ និងវិសមភាព។
អក្សរសាស្ត្រ
1. ពិជគណិត។ ថ្នាក់ទី 7 ។ ផ្នែកទី 1. សៀវភៅសិក្សាសម្រាប់ស្ថាប័នអប់រំ / A.G. Mordkovich ។ ទីក្រុងម៉ូស្គូ: Mnemosyne, 2007 ។
2. ពិជគណិត។ ថ្នាក់ទី ៨ ។ ផ្នែកទី 1. សៀវភៅសិក្សាសម្រាប់ស្ថាប័នអប់រំ / A.G. Mordkovich ។ ទីក្រុងម៉ូស្គូ: Mnemosyne, 2007 ។
3. ពិជគណិត។ ថ្នាក់ទី 9 ផ្នែកទី 1. សៀវភៅសិក្សាសម្រាប់ស្ថាប័នអប់រំ / A.G. Mordkovich ។ ទីក្រុងម៉ូស្គូ: Mnemosyne, 2007 ។
4. Glazer G.I. ប្រវត្តិគណិតវិទ្យានៅសាលា។ ថ្នាក់ VII-VIII ។ - អិមៈ ការត្រាស់ដឹង ឆ្នាំ១៩៨២។
5. ទិនានុប្បវត្តិគណិតវិទ្យា№5 2009; លេខ 8 2007; លេខ 23 2008 ។
6. ដំណោះស្រាយក្រាហ្វិកនៃសមីការ គេហទំព័រអ៊ីនធឺណិត៖ Tol WIKI; stimul.biz/en; wiki.iot.ru/images; berdsk.edu; pege 3–6.htm ។
ការងារស្រាវជ្រាវរបស់និស្សិតលើប្រធានបទ៖
"ការអនុវត្តមុខងារលីនេអ៊ែរក្នុងការដោះស្រាយបញ្ហា"
"កម្មវិធីនៃក្រាហ្វអនុគមន៍លីនេអ៊ែរដើម្បីដោះស្រាយបញ្ហា"
MKOU "អនុវិទ្យាល័យ Bogucharskaya លេខ 1"
ការងារស្រាវជ្រាវគណិតវិទ្យា។
ប្រធានបទ៖ "ការអនុវត្តក្រាហ្វនៃមុខងារលីនេអ៊ែរ ដើម្បីដោះស្រាយបញ្ហា"
7 ថ្នាក់ "ខ"
ក្បាល: Fomenko Olga Mikhailovna
ទីក្រុង Boguchar
១.សេចក្តីផ្តើម………………………………………………………………… ២
2. ផ្នែកសំខាន់…………………………………………………………… 3-11
2.1 បច្ចេកទេសដោះស្រាយបញ្ហាអត្ថបទដោយប្រើក្រាហ្វមុខងារលីនេអ៊ែរ
2.2 ការដោះស្រាយបញ្ហាអត្ថបទសម្រាប់ចលនាដោយប្រើក្រាហ្វ
៣.សេចក្តីសន្និដ្ឋាន………………………………………………………………… ១១
៤.អក្សរសិល្ប៍…………………………………………………………………….១២
ការណែនាំ
"ថ្នាក់ពិជគណិត.7" ពិចារណាលើកិច្ចការដែលយោងទៅតាមកាលវិភាគដែលបានផ្តល់ឱ្យវាចាំបាច់ដើម្បីឆ្លើយសំណួរមួយចំនួន។
ឧទាហរណ៍:
№332 អ្នករស់នៅរដូវក្តៅបានចេញពីផ្ទះដោយឡានទៅភូមិ។ គាត់បើកឡានមុនគេនៅលើផ្លូវហាយវ៉េ ហើយបន្ទាប់មកនៅលើផ្លូវជនបទ ដោយបន្ថយល្បឿនដូចគាត់ធ្វើអ៊ីចឹង។ កាលវិភាគនៃចលនារបស់អ្នករស់នៅរដូវក្តៅត្រូវបានបង្ហាញក្នុងរូប។ ឆ្លើយសំនួរ:
ក) តើអ្នករស់នៅរដូវក្តៅបានបើកបរតាមបណ្តោយផ្លូវហាយវេរយៈពេលប៉ុន្មាន ហើយតើគាត់បានបើកបរប៉ុន្មានគីឡូម៉ែត្រ។ តើអ្វីទៅជាល្បឿននៃរថយន្តនៅលើផ្នែកនៃផ្លូវនេះ;
ខ) តើអ្នករស់នៅរដូវក្តៅបានបើកបរលើផ្លូវប្រទេសរយៈពេលប៉ុន្មាន ហើយតើគាត់បានបើកបរប៉ុន្មានគីឡូម៉ែត្រ។ តើអ្វីជាល្បឿននៃរថយន្តនៅក្នុងផ្នែកនេះ;
គ) តើអ្នករស់នៅរដូវក្តៅបានធ្វើដំណើរពីផ្ទះទៅភូមិរយៈពេលប៉ុន្មាន?
នៅក្នុងវគ្គនៃការស្វែងរកសម្ភារៈលើប្រធានបទនេះនៅក្នុងអក្សរសិល្ប៍ និងអ៊ីនធឺណិត ខ្ញុំបានរកឃើញដោយខ្លួនឯងថា ដំណើរការ និងដំណើរការរាងកាយ និងសង្គម និងសេដ្ឋកិច្ចជាច្រើនស្ថិតនៅក្នុងទំនាក់ទំនងលីនេអ៊ែរនៅក្នុងពិភពលោក ប៉ុន្តែខ្ញុំបានដោះស្រាយលើចលនានេះ ដូចជា ដែលស្គាល់ និងពេញនិយមបំផុតក្នុងចំណោមពួកយើងទាំងអស់គ្នា។ នៅក្នុងគម្រោង ខ្ញុំបានពិពណ៌នាអំពីបញ្ហាពាក្យ និងរបៀបដោះស្រាយវាដោយប្រើក្រាហ្វមុខងារលីនេអ៊ែរ។
សម្មតិកម្ម៖ដោយមានជំនួយពីក្រាហ្វ អ្នកមិនត្រឹមតែអាចទទួលបានការបង្ហាញដែលមើលឃើញអំពីលក្ខណៈសម្បត្តិនៃមុខងារមួយប៉ុណ្ណោះទេ ស្គាល់លក្ខណៈសម្បត្តិនៃមុខងារលីនេអ៊ែរ និងទម្រង់ជាក់លាក់របស់វា សមាមាត្រដោយផ្ទាល់ ប៉ុន្តែក៏អាចដោះស្រាយបញ្ហាពាក្យផងដែរ។
គោលបំណងនៃការស្រាវជ្រាវរបស់ខ្ញុំគឺជាការសិក្សាអំពីការប្រើប្រាស់ក្រាហ្វនៃមុខងារលីនេអ៊ែរក្នុងការដោះស្រាយបញ្ហាអត្ថបទសម្រាប់ចលនា។ ដើម្បីសម្រេចបាននូវគោលដៅទាំងនេះ សូមធ្វើដូចខាងក្រោម ភារកិច្ច:
ដើម្បីសិក្សាវិធីសាស្រ្តក្នុងការដោះស្រាយបញ្ហាអត្ថបទសម្រាប់ចលនាដោយប្រើក្រាហ្វមុខងារលីនេអ៊ែរ;
រៀនពីរបៀបដោះស្រាយបញ្ហាចលនាដោយប្រើវិធីនេះ;
ធ្វើការសន្និដ្ឋានប្រៀបធៀបអំពីគុណសម្បត្តិ និងគុណវិបត្តិនៃការដោះស្រាយបញ្ហាដោយប្រើក្រាហ្វមុខងារលីនេអ៊ែរ។
កម្មវត្ថុនៃការសិក្សា៖ក្រាហ្វមុខងារលីនេអ៊ែរ។
វិធីសាស្រ្តស្រាវជ្រាវ៖
ទ្រឹស្តី (ការសិក្សានិងការវិភាគ), ការស្វែងរកប្រព័ន្ធ, ការអនុវត្តជាក់ស្តែង។
ផ្នែកដ៏សំខាន់។
នៅក្នុងការស្រាវជ្រាវរបស់ខ្ញុំ ខ្ញុំបានសម្រេចចិត្តព្យាយាមផ្តល់ការបកស្រាយក្រាហ្វិកនៃកិច្ចការសម្រាប់ចលនាដែលបង្ហាញនៅក្នុងសៀវភៅសិក្សារបស់យើង បន្ទាប់មកតាមកាលវិភាគ ឆ្លើយសំណួរនៃកិច្ចការ។ សម្រាប់ដំណោះស្រាយបែបនេះ ខ្ញុំបានយកភារកិច្ចជាមួយនឹងចលនាឯកសណ្ឋាន rectilinear នៅលើផ្នែកមួយនៃផ្លូវ។ វាបានប្រែក្លាយថាបញ្ហាជាច្រើនត្រូវបានដោះស្រាយតាមរបៀបនេះច្រើនជាងវិធីធម្មតាដោយប្រើសមីការ។ គុណវិបត្តិតែមួយគត់នៃបច្ចេកទេសនេះគឺថា ដើម្បីទទួលបានចម្លើយត្រឹមត្រូវចំពោះសំណួរនៃបញ្ហា មនុស្សម្នាក់ត្រូវតែអាចជ្រើសរើសមាត្រដ្ឋាននៃឯកតារង្វាស់បានត្រឹមត្រូវនៅលើអ័ក្សកូអរដោនេ។ តួនាទីដ៏ធំមួយនៅក្នុងជម្រើសត្រឹមត្រូវនៃមាត្រដ្ឋាននេះត្រូវបានលេងដោយបទពិសោធន៍នៃការដោះស្រាយ។ ដូច្នេះ ដើម្បីស្ទាត់ជំនាញសិល្បៈនៃការដោះស្រាយបញ្ហាដោយប្រើក្រាហ្វ ខ្ញុំត្រូវពិចារណាវាជាចំនួនច្រើន។
កំណត់ប្រព័ន្ធកូអរដោនេ sOt ជាមួយអ័ក្ស abscissa Ot និងអ័ក្ស ordinate Os ។ ដើម្បីធ្វើដូចនេះយោងទៅតាមលក្ខខណ្ឌនៃបញ្ហាវាចាំបាច់ត្រូវជ្រើសរើសប្រភពដើម: ការចាប់ផ្តើមនៃចលនារបស់វត្ថុឬពីវត្ថុជាច្រើនដែលបានចាប់ផ្តើមផ្លាស់ទីមុនឬធ្វើដំណើរឆ្ងាយជាងត្រូវបានជ្រើសរើស។ នៅលើអ័ក្ស abscissa សម្គាល់ចន្លោះពេលនៅក្នុងឯកតារង្វាស់របស់វា ហើយនៅលើអ័ក្សកំណត់ សម្គាល់ចម្ងាយក្នុងមាត្រដ្ឋានដែលបានជ្រើសរើសនៃឯកតារង្វាស់របស់វា។
ចំនុចនៅលើយន្តហោះកូអរដោណេត្រូវតែត្រូវបានសម្គាល់ដោយយោងទៅតាមមាត្រដ្ឋាននៃកិច្ចការ ហើយបន្ទាត់ត្រូវតែគូសយ៉ាងត្រឹមត្រូវ។ ភាពត្រឹមត្រូវនៃដំណោះស្រាយនៃបញ្ហាគឺអាស្រ័យលើនេះ។ ដូច្នេះវាមានសារៈសំខាន់ខ្លាំងណាស់ក្នុងការជ្រើសរើសមាត្រដ្ឋាននៃការបែងចែកនៅលើអ័ក្សកូអរដោនេដោយជោគជ័យ៖ វាត្រូវតែត្រូវបានជ្រើសរើសតាមរបៀបដែលកូអរដោនេនៃចំណុចត្រូវបានកំណត់កាន់តែត្រឹមត្រូវ ហើយប្រសិនបើអាចធ្វើទៅបាន មានទីតាំងនៅចំណុច nodal ពោលគឺឧ។ នៅចំនុចប្រសព្វនៃការបែងចែកអ័ក្សកូអរដោនេ។ ពេលខ្លះវាមានប្រយោជន៍ក្នុងការយកផ្នែកឯកតានៅលើអ័ក្ស abscissa ចំនួនកោសិកាដែលជាពហុគុណនៃលក្ខខណ្ឌនៃបញ្ហាទាក់ទងនឹងពេលវេលា និងនៅលើអ័ក្សកំណត់ - ចំនួនកោសិកាដែលជាពហុគុណនៃលក្ខខណ្ឌ។ នៃបញ្ហាទាក់ទងនឹងចម្ងាយ។ ឧទាហរណ៍ 12 នាទីក្នុងពេលវេលាតម្រូវឱ្យជ្រើសរើសចំនួនក្រឡាក្នុងពហុគុណនៃ 5 ពីព្រោះ 12 នាទីគឺមួយភាគប្រាំនៃមួយម៉ោង។
ការដោះស្រាយបញ្ហាអត្ថបទសម្រាប់ចលនាដោយប្រើក្រាហ្វ
ចម្លើយ៖ ៩ គ.ម.

ដំណោះស្រាយដោយប្រើសមីការ៖
x/12 ម៉ោង។ - ពេលវេលាពី A ដល់ B
x/18 ម៉ោង។ - ពេលវេលាត្រឡប់មកវិញ
ចម្លើយ៖ ៩ គ.ម
កិច្ចការទី 2. (លេខ 156 នៅក្នុងសៀវភៅសិក្សារបស់ Yu.N. Makarychev "ពិជគណិត 7") ។
រថយន្ត២គ្រឿងបើកធ្លាក់ផ្លូវក្នុងល្បឿនលឿនដូចគ្នា ។ ប្រសិនបើទីមួយបង្កើនល្បឿន 10 គីឡូម៉ែត្រក្នុងមួយម៉ោង ហើយទីពីរបន្ថយវា 10 គីឡូម៉ែត្រក្នុងមួយម៉ោង នោះទីមួយនឹងគ្របដណ្តប់បានច្រើនក្នុងរយៈពេល 2 ម៉ោង ដូចលើកទីពីរក្នុងរយៈពេល 3 ម៉ោង។ តើរថយន្តបើកលឿនប៉ុណ្ណា?
ដំណោះស្រាយដោយប្រើសមីការ៖
អនុញ្ញាតឱ្យ x គីឡូម៉ែត្រក្នុងមួយម៉ោងជាល្បឿននៃរថយន្ត;
(x+10) និង (x-10) រៀងគ្នាល្បឿនបន្ទាប់ពីបង្កើននិងបន្ថយ;
2(x+10)=3(x-10)
ចម្លើយ៖ ៥០ គីឡូម៉ែត្រក្នុងមួយម៉ោង
ដោះស្រាយជាមួយក្រាហ្វអនុគមន៍លីនេអ៊ែរ៖

1. ចូរកំណត់ប្លង់កូអរដោនេ sOt ជាមួយអ័ក្ស abscissa Оt ដែលយើងសម្គាល់ចន្លោះពេលនៃចលនា និងអ័ក្សកំណត់ Os ដែលយើងសម្គាល់ចម្ងាយដែលធ្វើដំណើរដោយយានជំនិះ
2. ចូរយើងដាក់ការបែងចែកនៅលើមាត្រដ្ឋានតាមបណ្តោយអ័ក្ស abscissa - មួយម៉ោងក្នុង 5 កោសិកា (ក្នុង 1 កោសិកា - 12 នាទី); យើងអនុវត្តការបែងចែកតាមអ័ក្ស y ប៉ុន្តែមិនបញ្ជាក់មាត្រដ្ឋានទេ។
3. ចូរយើងបង្កើតបន្ទាត់នៃចលនានៃឡានទីមួយ I: ការចាប់ផ្តើមនៃចលនានៅចំណុចមួយ c
4. ចូរយើងបង្កើតបន្ទាត់នៃចលនារបស់ម៉ាស៊ីនទីពីរ II: ការចាប់ផ្តើមនៃចលនានៅចំណុចជាមួយនឹងកូអរដោនេ (0; 0) ។ បន្ទាប់យើងសម្គាល់ចំណុចបំពាន (3; s 1) នៅលើយន្តហោះ ពីព្រោះ រថយន្តដែលមានល្បឿនថ្មីនេះបានធ្វើដំណើរលើផ្លូវអស់រយៈពេល៣ម៉ោង។
4. ចូរកំណត់ល្បឿននៃរថយន្ត v មុនពេលការផ្លាស់ប្តូររបស់វា។ ចូរយើងបង្ហាញពីភាពខុសគ្នានៃលំដាប់នៃចំនុចដែលស្ថិតនៅលើបន្ទាត់ជាមួយ abscissa 1 ដោយសញ្ញា ∆s ។ យោងតាមលក្ខខណ្ឌផ្នែកនេះត្រូវគ្នានឹងប្រវែង (10 + 10) គីឡូម៉ែត្រព្រោះ ក្នុងមួយក្នុងចំណោមពួកគេល្បឿនបានថយចុះ ហើយក្នុងមួយទៀតល្បឿនបានកើនឡើង ១០ គីឡូម៉ែត្រក្នុងមួយម៉ោង។ នេះមានន័យថាបន្ទាត់នៃចលនារបស់រថយន្តមុនពេលផ្លាស់ប្តូរល្បឿនគួរតែស្មើគ្នាពីបន្ទាត់ I និង II ហើយមានទីតាំងនៅលើយន្តហោះសម្របសម្រួលរវាងពួកគេ .. យោងតាមកាលវិភាគ Δs \u003d 2cl ។ ត្រូវគ្នានឹង 20 គីឡូម៉ែត្រ v = 5 កោសិកា ដូច្នេះយើងដោះស្រាយសមាមាត្រ v = 50 គីឡូម៉ែត្រក្នុងមួយម៉ោង។
ចម្លើយ៖ ៥០ គីឡូម៉ែត្រក្នុងមួយម៉ោង។
កិច្ចការទី 3
ដោះស្រាយជាមួយក្រាហ្វអនុគមន៍លីនេអ៊ែរ៖
ចំណុចយោងគឺចំណត M

សម្គាល់ចំណុច N (0; 162) ។
ចម្លើយ៖ ២ ម៉ោង ២០ នាទី។
ដំណោះស្រាយដោយប្រើសមីការ៖
162 -45(x+0.75)-36x=0
162-45x − 33.75 −36x = 0
៨១x=១២៨.២៥
2) ![]()
ចម្លើយ៖ ២ ម៉ោង ២០ នាទី។
កិច្ចការទី 4 ។
អ្នកជិះកង់ចាកចេញពីចំណុច A. ស្របពេលជាមួយគ្នានោះ អ្នកជិះម៉ូតូក្នុងល្បឿន១៦គ. អ្នកជិះកង់បានធ្វើដំណើរក្នុងល្បឿន ១២ គីឡូម៉ែត្រក្នុងមួយម៉ោង។ តើអ្នកជិះម៉ូតូវ៉ាអ្នកជិះកង់នៅចម្ងាយប៉ុន្មានពីចំណុច A?
ដោះស្រាយជាមួយក្រាហ្វអនុគមន៍លីនេអ៊ែរ៖
1. ចូរកំណត់ប្លង់កូអរដោនេ sOt ជាមួយអ័ក្ស abscissa Ot ដែលយើងសម្គាល់ចន្លោះពេលនៃចលនា និងអ័ក្ស y Os ដែលយើងនឹងសម្គាល់ចម្ងាយដែលធ្វើដំណើរដោយអ្នកបើកបរម៉ូតូ និងអ្នកជិះកង់
2. ចូរយើងគូរការបែងចែកនៅលើមាត្រដ្ឋានមួយ: តាមបណ្តោយអ័ក្ស y - ក្នុង 2 ក្រឡា 8 គីឡូម៉ែត្រ; នៅតាមបណ្តោយ abscissa - ក្នុង 2 កោសិកា - 1 ម៉ោង។
3. ចូរយើងកសាងបន្ទាត់នៃចលនារបស់អ្នកបើកបរម៉ូតូ II: យើងសម្គាល់ការចាប់ផ្តើមនៃចលនារបស់គាត់នៅប្រភពដើមនៃកូអរដោនេ B (0; 0) ។ អ្នកបើកបរម៉ូតូបានបើកបរក្នុងល្បឿន ១៦ គីឡូម៉ែត្រក្នុងមួយម៉ោង ដែលមានន័យថា ផ្លូវត្រង់ទី II ត្រូវឆ្លងកាត់ចំណុចកូអរដោណេ (១; ១៦) ។

4. ចូរយើងបង្កើតចលនាសម្រាប់អ្នកជិះកង់ I: ការចាប់ផ្តើមរបស់វានឹងមាននៅចំណុច A (0; 20) ពីព្រោះ ចំណុច B មានចំងាយ២០គីឡូម៉ែត្រពីចំណុច A ហើយគាត់បានចាកចេញស្របពេលជាមួយអ្នកជិះម៉ូតូ ។ អ្នកជិះកង់បានធ្វើដំណើរក្នុងល្បឿន 12 គីឡូម៉ែត្រក្នុងមួយម៉ោង ដែលមានន័យថាខ្សែដែលខ្ញុំត្រូវឆ្លងកាត់ចំណុចដែលមានកូអរដោនេ (1; 32) ។
5. ស្វែងរក P (5; 80) - ចំណុចប្រសព្វនៃបន្ទាត់ I និង II ដែលឆ្លុះបញ្ចាំងពីចលនារបស់អ្នកជិះកង់ និងអ្នកជិះកង់៖ ការចាត់តាំងរបស់វានឹងបង្ហាញចំងាយពីចំណុច B ដែលអ្នកបើកបរម៉ូតូនឹងចាប់អ្នកជិះកង់។ .
P(5; 80) |=s = 80, |=80 - 20 = 60(km) - ចំងាយពីចំណុច A ដែលអ្នកបើកបរម៉ូតូនឹងតាមទាន់អ្នកជិះកង់។
ចម្លើយ៖ ៦០ គីឡូម៉ែត្រ។
ដំណោះស្រាយដោយប្រើសមីការ៖
ទុក x km ជាចំងាយពីចំណុច A ដល់ចំណុចប្រជុំ
x / 12 ពេលជិះកង់
(x +20) / 16 ពេលអ្នកជិះម៉ូតូ
x /12=(x +20)/16
១៦x=១២x+២៤០
៤x=២៤០
x=60
ចម្លើយ៖ ៦០ គីឡូម៉ែត្រ
កិច្ចការទី 5 ។
ចម្ងាយរវាងទីក្រុងត្រូវបានគ្របដណ្តប់ដោយអ្នកជិះកង់ក្នុងរយៈពេល 2 ម៉ោង ហើយអ្នកជិះកង់ក្នុងរយៈពេល 5 ម៉ោង ។ ល្បឿនរបស់អ្នកជិះកង់គឺ 18 គីឡូម៉ែត្រក្នុងមួយម៉ោង តិចជាងល្បឿនរបស់អ្នកជិះម៉ូតូ។ ស្វែងរកល្បឿនរបស់អ្នកជិះកង់ និងអ្នកជិះម៉ូតូ និងចម្ងាយរវាងទីក្រុង។
ដោះស្រាយជាមួយក្រាហ្វអនុគមន៍លីនេអ៊ែរ៖

1. កំណត់ប្លង់កូអរដោនេ sOt ជាមួយអ័ក្ស abscissa Ot ដែលយើងសម្គាល់ចន្លោះពេលនៃចលនា និងអ័ក្ស y Os ដែលយើងសម្គាល់ចម្ងាយ។
2. ចូរយើងដាក់ការបែងចែកតាមអ័ក្ស abscissa ក្នុងក្រឡា 2 សម្រាប់រយៈពេល 1 ម៉ោង ចូរទុកចម្ងាយដោយមិនបែងចែកតាមអ័ក្សតម្រៀប។
3. ចូរគូរបន្ទាត់នៃចលនា I របស់អ្នកជិះកង់ក្នុងរយៈពេល 5 ម៉ោង និងបន្ទាត់នៃចលនារបស់អ្នកជិះកង់ II ក្នុងរយៈពេល 2 ម៉ោង។ ចុងបញ្ចប់នៃបន្ទាត់ទាំងពីរត្រូវតែមានការតម្រៀបដូចគ្នា។
4. ចូរគូរផ្នែកជាមួយ abscissa 1 រវាងបន្ទាត់ I និង II ។ ប្រវែងនៃផ្នែកនេះឆ្លុះបញ្ចាំងពីចម្ងាយស្មើនឹង 18 គីឡូម៉ែត្រ។ ពីគំនូរយើងទទួលបានក្រឡា 3 ស្មើនឹង 18 គីឡូម៉ែត្រដែលមានន័យថាមាន 6 គីឡូម៉ែត្រក្នុង 1 ក្រឡា។
5. បន្ទាប់មកយោងទៅតាមកាលវិភាគយើងកំណត់ល្បឿនរបស់អ្នកជិះកង់គឺ 12 គីឡូម៉ែត្រក្នុងមួយម៉ោងល្បឿនរបស់អ្នកជិះកង់គឺ 30 គីឡូម៉ែត្រក្នុងមួយម៉ោងចម្ងាយរវាងទីក្រុងគឺ 60 គីឡូម៉ែត្រ។
ដំណោះស្រាយដោយប្រើសមីការ៖
សូមឱ្យ x គីឡូម៉ែត្រក្នុងមួយម៉ោងជាល្បឿនរបស់អ្នកជិះកង់ បន្ទាប់មក (x +18) គីឡូម៉ែត្រក្នុងមួយម៉ោង ជាល្បឿនរបស់អ្នកជិះកង់
2(x+18)=5x
2x +36=5x
x=12
2) 12+18=30(km/h) ល្បឿនអ្នកជិះ
3) (គីឡូម៉ែត្រ) ចម្ងាយរវាងទីក្រុង
ចម្លើយ៖ ១២ គីឡូម៉ែត្រ / ម៉ោង; 30 គីឡូម៉ែត្រ / ម៉ោង; ៦០ គ.ម
ចម្លើយ៖ ៦០ គីឡូម៉ែត្រ។
កិច្ចការទី 6 ។
ទូកធ្វើដំណើរចម្ងាយ ៣០ គីឡូម៉ែត្រក្នុងរយៈពេល ៣ ម៉ោង ២០ នាទីតាមដងទន្លេ និង ២៨ គីឡូម៉ែត្រទល់នឹងចរន្តក្នុងរយៈពេល ៤ ម៉ោង។ តើទូកនឹងគ្របដណ្តប់បឹងប៉ុន្មានក្នុងរយៈពេល 1,5 ម៉ោង?
ដោះស្រាយជាមួយក្រាហ្វអនុគមន៍លីនេអ៊ែរ៖
1. កំណត់ប្លង់កូអរដោនេ sOt ជាមួយអ័ក្ស abscissa Ot ដែលយើងសម្គាល់ចន្លោះពេលនៃចលនា និងអ័ក្ស y Os ដែលយើងសម្គាល់ចម្ងាយដែលធ្វើដំណើរដោយទូក
2. ចូរយើងគូរការបែងចែកនៅលើមាត្រដ្ឋានមួយ: តាមបណ្តោយអ័ក្ស y - ក្នុងក្រឡាពីរ 4 គីឡូម៉ែត្រ; តាមអ័ក្ស abscissa - ក្នុង 6 កោសិកា - 1 ម៉ោង (ក្នុង 1 កោសិកា - 10 នាទី) ដោយសារតែ យោងតាមលក្ខខណ្ឌនៃបញ្ហា ពេលវេលាត្រូវបានផ្តល់ជានាទី។
3. ចូរយើងបង្កើតបន្ទាត់នៃចលនារបស់ទូកតាមដងទន្លេ I: ការចាប់ផ្តើមនៃបន្ទាត់នឹងស្ថិតនៅត្រង់ចំនុចដែលមានកូអរដោណេ (0; 0) ។ ទូកបើកចម្ងាយ ៣០ គីឡូម៉ែត្រក្នុងរយៈពេល ៣ ម៉ោង ២០ នាទី ដែលមានន័យថា ខ្សែត្រូវឆ្លងកាត់ចំណុចដោយកូអរដោណេ (; ៣០) ពីព្រោះ 3h 20 នាទី។ = ម៉ោង

4. ចូរយើងកសាងខ្សែបន្ទាត់នៃចលនារបស់ទូកទល់នឹងចរន្តនៃទន្លេ II: យើងយកការចាប់ផ្តើមនៃចលនានៅចំណុចមួយជាមួយនឹងកូអរដោនេ (0; 0) ។ ទូកបើកចម្ងាយ 28 គីឡូម៉ែត្រក្នុងរយៈពេល 4 ម៉ោងដែលមានន័យថាខ្សែនៃចលនាត្រូវតែឆ្លងកាត់ចំណុចដែលមានកូអរដោនេ (4; 28) ។
5. ចូរយើងកសាងបន្ទាត់នៃចលនារបស់ទូកនៅលើបឹង៖ យើងនឹងយកការចាប់ផ្តើមនៃចលនានៅចំណុចជាមួយនឹងកូអរដោនេ (0; 0) ។ ខ្សែបន្ទាត់នៃចលនារបស់ទូកនឹងត្រូវស្ថិតនៅស្មើៗគ្នារវាងបន្ទាត់នៃចលនារបស់ទូកតាមដងទន្លេ។ នេះមានន័យថាយើងត្រូវបែងចែកផ្នែកដែលមានចំណុចទាំងអស់ជាមួយ abscissa 1 រវាងបន្ទាត់នៃចលនាតាមបណ្តោយទន្លេនៅពាក់កណ្តាលនិងសម្គាល់កណ្តាលរបស់វា។ ចាប់ពី (0; 0) តាមរយៈចំណុចសម្គាល់នេះ យើងនឹងគូរកាំរស្មី ដែលនឹងក្លាយជាបន្ទាត់នៃចលនានៅតាមបណ្តោយបឹង។
6. យោងតាមលក្ខខណ្ឌនៃបញ្ហា វាចាំបាច់ក្នុងការស្វែងរកចម្ងាយដែលធ្វើដំណើរដោយទូកនៅលើបឹងក្នុងរយៈពេល 1,5 ម៉ោង ដែលមានន័យថាយើងត្រូវកំណត់នៅលើបន្ទាត់នេះ តម្រៀបនៃចំណុចជាមួយ abscissa t \u003d 1.5, | \u003d s \u003d 12, | \u003d 12 គីឡូម៉ែត្រ 1,5 ម៉ោង។
ចម្លើយ៖ ១២ គ.ម.
ដំណោះស្រាយដោយប្រើប្រព័ន្ធសមីការ៖
សូមឱ្យ x គីឡូម៉ែត្រក្នុងមួយម៉ោងជាល្បឿននៃបឹង និង y គីឡូម៉ែត្រក្នុងមួយម៉ោងជាល្បឿននៃទន្លេ
ចម្លើយ៖ ១២ គ.ម.
កិច្ចការទី 7 ។
ទូកធ្វើដំណើរតាមដងទន្លេក្នុងចម្ងាយ ៣៤ គីឡូម៉ែត្រក្នុងពេលដូចគ្នា ២៦ គីឡូម៉ែត្រធៀបនឹងចរន្តទឹក។ ល្បឿនផ្ទាល់ខ្លួនរបស់ទូកគឺ ១៥ គីឡូម៉ែត្រក្នុងមួយម៉ោង។ ស្វែងរកល្បឿននៃទន្លេ។
ដោះស្រាយជាមួយក្រាហ្វអនុគមន៍លីនេអ៊ែរ៖
1. កំណត់ប្លង់កូអរដោនេ sOt ជាមួយអ័ក្ស abscissa Ot ដែលយើងសម្គាល់ចន្លោះពេលនៃចលនា និងអ័ក្ស y Os ដែលយើងសម្គាល់ចម្ងាយដែលធ្វើដំណើរដោយទូក។
2. ចូរយើងគូរការបែងចែកនៅលើមាត្រដ្ឋានមួយ: តាមបណ្តោយអ័ក្ស y - ក្នុង 1 ក្រឡា 1 គីឡូម៉ែត្រ; នៅលើអ័ក្ស abscissa យើងទុកពេលវេលាដោយគ្មានការបែងចែក។
3. ចូរសង់ខ្សែបន្ទាត់ I នៃចលនារបស់ទូកតាមដងទន្លេពី 0 គីឡូម៉ែត្រទៅចំណុច 34 គីឡូម៉ែត្រ៖ ការចាប់ផ្តើមនៃខ្សែនឹងស្ថិតនៅត្រង់ចំនុចដែលមានកូអរដោណេ (0; 0) កូអរដោនេទីពីរនឹងជា (x 34).
4. ចូរយើងកសាងខ្សែបន្ទាត់ II នៃចលនារបស់ទូកទល់នឹងចរន្តទឹកទន្លេពី 0 គីឡូម៉ែត្រទៅចំណុច 26 គីឡូម៉ែត្រ៖ ការចាប់ផ្តើមនៃខ្សែនឹងស្ថិតនៅចំណុចដែលមានកូអរដោណេ (0; 0) កូអរដោនេទីពីរនឹង ( x; 26).
5. គូរកាំរស្មី III ពីប្រភពដើម (0; 0) តាមរយៈពាក់កណ្តាលនៃផ្នែកដែលបំពានដែលមានចំណុចទាំងអស់ដែលមាន abscissa ដូចគ្នារវាងបន្ទាត់ពីរនៃចលនា I និង II ។ ធ្នឹមនេះនឹងឆ្លុះបញ្ចាំងពីចលនាផ្ទាល់ខ្លួនរបស់ទូក ដូចជា ល្បឿនផ្ទាល់ខ្លួនរបស់ទូក គឺជាមធ្យមនព្វន្ធនៃល្បឿន 2 ទឹកឡើងលើ និងចុះទឹកទន្លេ។ នៅលើធ្នឹមលទ្ធផលយើងរកឃើញចំណុចមួយដែលមានលំដាប់នៃ 15 ពីព្រោះ ល្បឿនផ្ទាល់ខ្លួនរបស់ទូកគឺ ១៥ គីឡូម៉ែត្រក្នុងមួយម៉ោង។ abscissa នៃចំណុចដែលបានរកឃើញនឹងត្រូវគ្នាទៅនឹងការបែងចែក 1 ម៉ោង។
6. ដើម្បីស្វែងរកល្បឿននៃទន្លេវាគ្រប់គ្រាន់ដើម្បីស្វែងរកប្រវែងនៃចម្រៀកជាមួយ abscissa 1 ពីបន្ទាត់ III ដល់បន្ទាត់ II ។ ល្បឿននៃទន្លេគឺ 2 គីឡូម៉ែត្រក្នុងមួយម៉ោង។
ចម្លើយ៖ ២ គីឡូម៉ែត្រ / ម៉ោង។
ដំណោះស្រាយដោយប្រើសមីការ៖
ល្បឿនទន្លេ x គីឡូម៉ែត្រ / ម៉ោង។
34 / (15 + x) \u003d 26 / (15-x) ការដោះស្រាយសមាមាត្រ យើងទទួលបាន៖
ចម្លើយ៖ ២ គីឡូម៉ែត្រ / ម៉ោង។
សេចក្តីសន្និដ្ឋាន។
គុណសម្បត្តិ៖
ភារកិច្ចអាចត្រូវបានសរសេរយ៉ាងខ្លី;
គុណវិបត្តិ៖
អក្សរសាស្ត្រ។
1. Makarychev Yu. N., Mindyuk N.G., Neshkov K. I., Suvorova S. B., Algebra: សៀវភៅសិក្សាសម្រាប់ថ្នាក់ទី 7 នៃស្ថាប័នអប់រំ "Prosveshchenie", M., 2000 ។
2.Bulynin V. , ការប្រើប្រាស់វិធីសាស្រ្តក្រាហ្វិកក្នុងការដោះស្រាយបញ្ហាអត្ថបទ កាសែតអប់រំនិងវិធីសាស្រ្ត "គណិតវិទ្យា", លេខ 14, 2005 ។
3. Zvavich L.I. ឯកសារ Didactic លើពិជគណិតសម្រាប់ថ្នាក់ទី 7 ។
មើលខ្លឹមសារឯកសារ
"ពាក្យ"
នៅមេរៀនពិជគណិតថ្នាក់ទី៧ ខ្ញុំបានស្គាល់ប្រធានបទ “មុខងារលីនេអ៊ែរ។ ការរៀបចំក្រាហ្វនៃអនុគមន៍លីនេអ៊ែរទៅវិញទៅមក។ ខ្ញុំបានរៀនពីរបៀបបង្កើតក្រាហ្វនៃអនុគមន៍លីនេអ៊ែរ រៀនលក្ខណៈសម្បត្តិរបស់វា រៀនពីរបៀបកំណត់ទីតាំងដែលទាក់ទងនៃក្រាហ្វដោយប្រើរូបមន្តដែលបានផ្តល់ឱ្យ។ ខ្ញុំបានកត់សម្គាល់ឃើញថានៅក្នុងសៀវភៅសិក្សាដោយ Yu.N. Makarychev
"ថ្នាក់ពិជគណិត.7" ពិចារណាលើកិច្ចការដែលយោងទៅតាមកាលវិភាគដែលបានផ្តល់ឱ្យវាចាំបាច់ដើម្បីឆ្លើយសំណួរមួយចំនួន។ ឧទាហរណ៍នៃកិច្ចការបែបនេះត្រូវបានបង្ហាញនៅលើស្លាយ។
យោងតាមកាលវិភាគដែលបានផ្តល់ឱ្យវាអាចត្រូវបានកំណត់ថា
ហើយខ្ញុំមានសំណួរមួយ តើវាអាចទៅរួចទេក្នុងការដោះស្រាយបញ្ហាសម្រាប់ចលនាមិនមែនដោយសកម្មភាព ឬការប្រើសមីការ ប៉ុន្តែត្រូវប្រើក្រាហ្វិកនៃមុខងារលីនេអ៊ែរសម្រាប់រឿងនេះ?
សម្មតិកម្ម គោលដៅ និងគោលបំណងត្រូវបានបង្ហាញនៅលើស្លាយ
នៅក្នុងការស្រាវជ្រាវរបស់ខ្ញុំ ខ្ញុំបានសម្រេចចិត្តព្យាយាមផ្តល់ការបកស្រាយក្រាហ្វិកនៃកិច្ចការសម្រាប់ចលនាដែលបង្ហាញនៅក្នុងសៀវភៅសិក្សារបស់យើង បន្ទាប់មកតាមកាលវិភាគ ឆ្លើយសំណួរនៃកិច្ចការ។ សម្រាប់ដំណោះស្រាយបែបនេះ ខ្ញុំបានយកភារកិច្ចជាមួយនឹងចលនាឯកសណ្ឋាន rectilinear នៅលើផ្នែកមួយនៃផ្លូវ។
វាបានប្រែក្លាយថាបញ្ហាជាច្រើនត្រូវបានដោះស្រាយតាមរបៀបនេះ។ គុណវិបត្តិតែមួយគត់នៃបច្ចេកទេសនេះគឺថា ដើម្បីទទួលបានចម្លើយត្រឹមត្រូវចំពោះសំណួរនៃបញ្ហា មនុស្សម្នាក់ត្រូវតែអាចជ្រើសរើសមាត្រដ្ឋាននៃឯកតារង្វាស់បានត្រឹមត្រូវនៅលើអ័ក្សកូអរដោនេ។ តួនាទីដ៏ធំមួយនៅក្នុងជម្រើសត្រឹមត្រូវនៃមាត្រដ្ឋាននេះត្រូវបានលេងដោយបទពិសោធន៍នៃការដោះស្រាយ។ ដូច្នេះ ដើម្បីស្ទាត់ជំនាញសិល្បៈនៃការដោះស្រាយបញ្ហាដោយប្រើក្រាហ្វ ខ្ញុំត្រូវពិចារណាវាជាចំនួនច្រើន។
បច្ចេកទេសសម្រាប់ដោះស្រាយបញ្ហាអត្ថបទដោយប្រើក្រាហ្វមុខងារលីនេអ៊ែរ។
ដើម្បីដោះស្រាយបញ្ហាអត្ថបទដោយប្រើក្រាហ្វមុខងារលីនេអ៊ែរ អ្នកត្រូវ៖
កំណត់ប្រព័ន្ធកូអរដោណេ ដើម្បីធ្វើការនេះ យោងទៅតាមលក្ខខណ្ឌនៃបញ្ហា ចាំបាច់ត្រូវជ្រើសរើសប្រភពដើម៖ ការចាប់ផ្តើមនៃចលនារបស់វត្ថុ ឬពីវត្ថុជាច្រើន វត្ថុដែលចាប់ផ្តើមផ្លាស់ទីមុន ឬធ្វើដំណើរឆ្ងាយជាងគឺត្រូវបានជ្រើសរើស។ . នៅលើអ័ក្ស abscissa សម្គាល់ចន្លោះពេលនៅក្នុងឯកតារង្វាស់របស់វា ហើយនៅលើអ័ក្សកំណត់ សម្គាល់ចម្ងាយក្នុងមាត្រដ្ឋានដែលបានជ្រើសរើសនៃឯកតារង្វាស់របស់វា។
គូរបន្ទាត់នៃចលនានៃវត្ថុនីមួយៗដែលបានបញ្ជាក់នៅក្នុងសេចក្តីថ្លែងការណ៍បញ្ហាតាមរយៈកូអរដោនេនៃចំនុចត្រង់យ៉ាងហោចណាស់ពីរ។ ជាធម្មតាល្បឿននៃវត្ថុមួយផ្តល់ព័ត៌មានអំពីការឆ្លងកាត់ចម្ងាយក្នុងមួយឯកតានៃពេលវេលាចាប់ពីការចាប់ផ្តើមនៃចលនារបស់វា។ ប្រសិនបើវត្ថុចាប់ផ្តើមផ្លាស់ទីនៅពេលក្រោយ នោះចំណុចចាប់ផ្តើមនៃចលនារបស់វាត្រូវបានផ្លាស់ប្តូរដោយចំនួនឯកតាដែលបានផ្តល់ឱ្យទៅខាងស្តាំនៃប្រភពដើមតាមអ័ក្ស x ។ ប្រសិនបើវត្ថុចាប់ផ្តើមផ្លាស់ទីពីកន្លែងដាច់ស្រយាលពីចំណុចយោងដោយចម្ងាយជាក់លាក់មួយ នោះចំនុចនៃការចាប់ផ្តើមនៃចលនារបស់វាត្រូវបានផ្លាស់ទីលំនៅទៅខាងលើតាមអ័ក្ស y ។
ចំណុចប្រជុំនៃវត្ថុជាច្រើននៅលើយន្តហោះកូអរដោណេត្រូវបានបង្ហាញដោយចំណុចប្រសព្វនៃបន្ទាត់ដែលពណ៌នាអំពីចលនារបស់ពួកគេ ដែលមានន័យថា កូអរដោនេនៃចំណុចនេះផ្តល់ព័ត៌មានអំពីពេលវេលានៃការប្រជុំ និងចម្ងាយនៃកន្លែងប្រជុំពីប្រភពដើម។
ភាពខុសគ្នានៃល្បឿននៃចលនារបស់វត្ថុពីរត្រូវបានកំណត់ដោយប្រវែងនៃផ្នែកដែលមានចំណុចទាំងអស់ជាមួយ abscissa 1 ដែលស្ថិតនៅចន្លោះបន្ទាត់នៃចលនានៃវត្ថុទាំងនេះ។
ចំនុចនៅលើយន្តហោះកូអរដោណេត្រូវតែត្រូវបានសម្គាល់ដោយយោងទៅតាមមាត្រដ្ឋាននៃកិច្ចការ ហើយបន្ទាត់ត្រូវតែគូសយ៉ាងត្រឹមត្រូវ។ ភាពត្រឹមត្រូវនៃដំណោះស្រាយនៃបញ្ហាគឺអាស្រ័យលើនេះ។
បញ្ហា 1. (លេខ 673 នៅក្នុងសៀវភៅសិក្សារបស់ Yu.N. Makarychev "ពិជគណិត 7") ។
អ្នកជិះកង់បានធ្វើដំណើរតាមផ្លូវ AB ក្នុងល្បឿន ១២ គីឡូម៉ែត្រក្នុងមួយម៉ោង។ ត្រលប់មកវិញគាត់បានអភិវឌ្ឍល្បឿន 18 គីឡូម៉ែត្រក្នុងមួយម៉ោងហើយចំណាយពេល 15 នាទីតិចជាងនៅលើផ្លូវត្រឡប់មកវិញជាងនៅតាមផ្លូវពី A ទៅ B ។ ប៉ុន្មានគីឡូម៉ែត្រពី A ទៅ B ។
ដំណោះស្រាយដោយប្រើសមីការ៖
ទុក x km ជាចំងាយពី A ដល់ B ។
x/12 ម៉ោង។ - ពេលវេលាពី A ដល់ B
x/18 ម៉ោង។ - ពេលវេលាត្រឡប់មកវិញ
ដោយសារគាត់ចំណាយពេល 15 នាទីតិចជាងក្នុងដំណើរត្រឡប់មកវិញ យើងនឹងសរសេរសមីការ
ចម្លើយ៖ ៩ គ.ម
ដោះស្រាយជាមួយក្រាហ្វអនុគមន៍លីនេអ៊ែរ៖
1. យើងកំណត់ប្លង់កូអរដោនេ sOtc ជាមួយអ័ក្ស abscissa Оt ដែលយើងសម្គាល់ចន្លោះពេលនៃចលនា និងអ័ក្សកំណត់ Os ដែលយើងសម្គាល់ចម្ងាយ។
2. ចូរយើងគូរការបែងចែកនៅលើមាត្រដ្ឋានមួយ: តាមអ័ក្ស y - ក្នុងក្រឡាមួយ 3 គីឡូម៉ែត្រ; តាមអ័ក្ស abscissa - មួយម៉ោងក្នុង 4 កោសិកា (ក្នុង 1 កោសិកា - 15 នាទី) ។
3. ចូរយើងបង្កើតបន្ទាត់នៃចលនានៅទីនោះ៖ សម្គាល់ការចាប់ផ្តើមនៃចលនាដោយចំនុច (0; 0)។ អ្នកជិះកង់បានធ្វើដំណើរក្នុងល្បឿន ១២ គីឡូម៉ែត្រក្នុងមួយម៉ោង ដែលមានន័យថា ផ្លូវត្រង់ត្រូវឆ្លងកាត់ចំណុច (១; ១២)។
4. ចូរយើងបង្កើតបន្ទាត់នៃចលនាត្រឡប់មកវិញ៖ សម្គាល់ចុងបញ្ចប់នៃបន្ទាត់ដោយចំនុច (; 0) ពីព្រោះ អ្នកជិះកង់បានចំណាយពេលតិចជាង ១៥ នាទីក្នុងការធ្វើដំណើរត្រឡប់មកវិញ។ គាត់បានបើកបរក្នុងល្បឿន 18 គីឡូម៉ែត្រក្នុងមួយម៉ោង ដែលមានន័យថាចំណុចបន្ទាប់នៃខ្សែមានកូអរដោណេ (;18) ។
5. ចំណាំ (; 9) - ចំណុចប្រសព្វនៃបន្ទាត់៖ លំដាប់របស់វានឹងបង្ហាញចម្ងាយ៖ s = 9
ចម្លើយ៖ ៩ គ.ម.
កិច្ចការទី 2 (លេខ 757 នៅក្នុងសៀវភៅសិក្សារបស់ Yu.N. Makarychev "Algebra 7")
ចម្ងាយរវាងផែ M និង N គឺ 162 គីឡូម៉ែត្រ។ កប៉ាល់ម៉ូតូមួយគ្រឿងបានចេញពីផែ M ក្នុងល្បឿន ៤៥ គីឡូម៉ែត្រក្នុងមួយម៉ោង។ បន្ទាប់ពី 45 នាទី កប៉ាល់ម៉ូតូមួយផ្សេងទៀតបានចាកចេញពីផែ N ឆ្ពោះទៅរកគាត់ដែលមានល្បឿន 36 គីឡូម៉ែត្រក្នុងមួយម៉ោង។ តើក្នុងរយៈពេលប៉ុន្មានម៉ោងបន្ទាប់ពីការចាកចេញនៃកប៉ាល់ទីមួយពួកគេនឹងជួបគ្នា?
ដំណោះស្រាយដោយប្រើសមីការ៖
សូមឱ្យមានការប្រជុំក្នុងរយៈពេល x ម៉ោង។
162 -45(x+0.75)-36x=0
162-45x − 33.75 −36x = 0
៨១x=១២៨.២៥
2) ![]()
ចម្លើយ៖ ២ ម៉ោង ២០ នាទី។
ដោះស្រាយជាមួយក្រាហ្វអនុគមន៍លីនេអ៊ែរ៖
1. កំណត់ប្លង់កូអរដោនេ sOt ជាមួយអ័ក្ស abscissa Ot ដែលយើងសម្គាល់ចន្លោះពេលនៃចលនា និងអ័ក្ស y Os ដែលនៅលើនោះ។
ចំណាំចម្ងាយពីផែ M ដល់ផែ N ស្មើនឹង ១៦២ គីឡូម៉ែត្រ។ ការចាប់ផ្ដើម
ចំណុចយោងគឺចំណត M
2. ចូរយើងគូរការបែងចែកនៅលើមាត្រដ្ឋានមួយ: តាមបណ្តោយអ័ក្ស y - ក្នុងក្រឡាពីរ 18 គីឡូម៉ែត្រ; តាមអ័ក្ស abscissa - មួយម៉ោងក្នុង 6 កោសិកា (ក្នុង 1 កោសិកា - 10 នាទី) ចាប់តាំងពី លក្ខខណ្ឌការងារបញ្ជាក់ពេលវេលាជានាទី។
សម្គាល់ចំណុច N (0; 162) ។
3. ចូរយើងបង្កើតបន្ទាត់នៃចលនានៃកប៉ាល់ទីមួយ I: ការចាប់ផ្តើមនៃចលនារបស់វានឹងស្ថិតនៅត្រង់ចំនុចដែលមានកូអរដោណេ (0; 0)។ កប៉ាល់ទីមួយបានបើកក្នុងល្បឿន 45 គីឡូម៉ែត្រក្នុងមួយម៉ោងដែលមានន័យថាបន្ទាត់ត្រង់ត្រូវតែឆ្លងកាត់ចំណុចដែលមានកូអរដោនេ (1; 45) ។
4. ចូរយើងបង្កើតបន្ទាត់នៃចលនានៃកប៉ាល់ទី II : ការចាប់ផ្តើមនៃចលនានឹងស្ថិតនៅចំណុច c
កូអរដោនេ (; 162), ចាប់តាំងពីគាត់បានចាកចេញពីចំណុច N, 162 គីឡូម៉ែត្រពី M, 45 នាទី។ យឺតជាងលើកទីមួយ និង 45 នាទី។ \u003d ម៉ោង កប៉ាល់ទីពីរបានបើកក្នុងល្បឿន 36 គីឡូម៉ែត្រក្នុងមួយម៉ោង ដែលមានន័យថាបន្ទាត់ត្រង់ត្រូវតែឆ្លងកាត់ចំណុច (; 126) ចាប់តាំងពីកប៉ាល់ទីពីរបានចាកចេញក្នុងទិសដៅនៃចំណុច M: 162 - 36 \ u003d 126 (km) ។
5. ចំនុចប្រសព្វនៃបន្ទាត់ I និង II គឺចំនុច A (; 108) ។ abscissa នៃចំណុចបង្ហាញពីពេលវេលាបន្ទាប់ពីនោះបន្ទាប់ពីការចាកចេញនៃកប៉ាល់ទីមួយពួកគេបានជួបគ្នា: t =, |=h = 2h20min ។ - ពេលវេលានៃការជួបប្រជុំគ្នានៃនាវាពីរបន្ទាប់ពីការចាកចេញនៃនាវាទីមួយ។
ចម្លើយ៖ ២ ម៉ោង ២០ នាទី។
សេចក្តីសន្និដ្ឋាន។
នៅចុងបញ្ចប់នៃការសិក្សា ខ្ញុំអាចកំណត់ពីគុណសម្បត្តិ និងគុណវិបត្តិនៃការដោះស្រាយបញ្ហាតាមក្រាហ្វិក។
គុណសម្បត្តិ៖
ភារកិច្ចអាចត្រូវបានសរសេរយ៉ាងខ្លី;
វាងាយស្រួលណាស់ក្នុងការធ្វើការជាមួយលេខតូច។
គុណវិបត្តិ៖
វាពិបាកក្នុងការធ្វើការជាមួយលេខធំ។
មើលមាតិកាបទបង្ហាញ
"គម្រោង"

កម្រិតដំបូង
ដោះស្រាយសមីការ វិសមភាព ប្រព័ន្ធដោយប្រើក្រាហ្វមុខងារ។ មគ្គុទ្ទេសក៍មើលឃើញ (2019)
កិច្ចការជាច្រើនដែលយើងធ្លាប់ប្រើក្នុងការគណនាពិជគណិតសុទ្ធអាចដោះស្រាយបានកាន់តែងាយស្រួល និងលឿនជាងមុន ការប្រើក្រាហ្វមុខងារនឹងជួយយើងក្នុងរឿងនេះ។ អ្នកនិយាយថា "យ៉ាងម៉េច?" ដើម្បីគូរអ្វីមួយ ហើយត្រូវគូរអ្វី? ជឿខ្ញុំ ពេលខ្លះវាកាន់តែងាយស្រួល និងងាយស្រួលជាង។ តើយើងនឹងចាប់ផ្តើមទេ? តោះចាប់ផ្តើមជាមួយសមីការ!
ដំណោះស្រាយក្រាហ្វិកនៃសមីការ
ដំណោះស្រាយក្រាហ្វិកនៃសមីការលីនេអ៊ែរ
ដូចដែលអ្នកបានដឹងរួចមកហើយ ក្រាហ្វនៃសមីការលីនេអ៊ែរ គឺជាបន្ទាត់ត្រង់ ដូច្នេះឈ្មោះនៃប្រភេទនេះ។ សមីការលីនេអ៊ែរគឺពិតជាងាយស្រួលក្នុងការដោះស្រាយពិជគណិត - យើងផ្ទេរការមិនស្គាល់ទាំងអស់ទៅផ្នែកម្ខាងនៃសមីការ អ្វីគ្រប់យ៉ាងដែលយើងដឹង - ទៅមួយទៀត ហើយ voila! យើងបានរកឃើញឫស។ ឥឡូវនេះខ្ញុំនឹងបង្ហាញអ្នកពីរបៀបធ្វើវា វិធីក្រាហ្វិក។
ដូច្នេះអ្នកមានសមីការ៖
តើត្រូវដោះស្រាយដោយរបៀបណា?
ជម្រើសទី 1ហើយរឿងធម្មតាបំផុតគឺការផ្លាស់ទីអ្នកមិនស្គាល់ទៅម្ខាង ហើយអ្នកស្គាល់ទៅម្ខាងទៀត យើងទទួលបាន៖
ហើយឥឡូវនេះយើងកំពុងសាងសង់។ តើអ្នកទទួលបានអ្វីខ្លះ?
តើអ្នកគិតថាអ្វីជាឫសគល់នៃសមីការរបស់យើង? ត្រឹមត្រូវហើយ កូអរដោនេនៃចំណុចប្រសព្វនៃក្រាហ្វ៖

ចម្លើយរបស់យើងគឺ
នោះជាប្រាជ្ញាទាំងមូលនៃដំណោះស្រាយក្រាហ្វិក។ ដូចដែលអ្នកអាចពិនិត្យបានយ៉ាងងាយស្រួល ឫសនៃសមីការរបស់យើងគឺជាលេខ!
ដូចដែលខ្ញុំបាននិយាយខាងលើ នេះគឺជាជម្រើសទូទៅបំផុត នៅជិតដំណោះស្រាយពិជគណិត ប៉ុន្តែអ្នកអាចដោះស្រាយវាតាមវិធីមួយផ្សេងទៀត។ ដើម្បីពិចារណាដំណោះស្រាយជំនួស ចូរយើងត្រឡប់ទៅសមីការរបស់យើងវិញ៖
លើកនេះ យើងនឹងមិនផ្លាស់ទីអ្វីពីម្ខាងទៅម្ខាងទេ ប៉ុន្តែនឹងបង្កើតក្រាហ្វដោយផ្ទាល់ ដូចដែលពួកគេឥឡូវនេះ៖
សាងសង់? មើល!

តើលើកនេះមានដំណោះស្រាយអ្វី? ត្រឹមត្រូវហើយ។ ដូចគ្នាដែរគឺជាកូអរដោនេនៃចំនុចប្រសព្វនៃក្រាហ្វ៖

ហើយម្តងទៀត ចម្លើយរបស់យើងគឺ។
ដូចដែលអ្នកអាចឃើញជាមួយនឹងសមីការលីនេអ៊ែរ អ្វីគ្រប់យ៉ាងគឺសាមញ្ញបំផុត។ វាដល់ពេលដែលត្រូវពិចារណាអ្វីមួយដែលកាន់តែស្មុគស្មាញ... ឧទាហរណ៍៖ ដំណោះស្រាយក្រាហ្វិកនៃសមីការការ៉េ។
ដំណោះស្រាយក្រាហ្វិកនៃសមីការការ៉េ
ដូច្នេះឥឡូវនេះ ចូរចាប់ផ្តើមដោះស្រាយសមីការការ៉េ។ ឧបមាថាអ្នកត្រូវស្វែងរកឫសគល់នៃសមីការនេះ៖
ជាការពិតណាស់ ឥឡូវនេះ អ្នកអាចចាប់ផ្តើមរាប់តាមរយៈការរើសអើង ឬយោងទៅតាមទ្រឹស្តីបទ Vieta ប៉ុន្តែសរសៃប្រសាទជាច្រើនមានកំហុសនៅពេលគុណ ឬ ការ៉េ ជាពិសេសប្រសិនបើឧទាហរណ៍មានលេខធំ ហើយដូចដែលអ្នកដឹង អ្នកនឹងមិនមាន calculator on the exam... អាស្រ័យហេតុនេះ ចូរយើងព្យាយាមបន្ធូរអារម្មណ៍បន្តិច ហើយគូរខណៈពេលកំពុងដោះស្រាយសមីការនេះ។
តាមក្រាហ្វិក ដំណោះស្រាយចំពោះសមីការនេះអាចត្រូវបានរកឃើញតាមវិធីផ្សេងៗ។ ពិចារណាជម្រើសផ្សេងៗ ហើយអ្នកខ្លួនឯងនឹងជ្រើសរើសមួយណាដែលអ្នកចូលចិត្តជាងគេ។
វិធីសាស្រ្ត 1. ដោយផ្ទាល់
យើងគ្រាន់តែបង្កើតប៉ារ៉ាបូឡាតាមសមីការនេះ៖
ដើម្បីឱ្យវាឆាប់រហ័ស ខ្ញុំនឹងប្រាប់អ្នកនូវគន្លឹះមួយចំនួន៖ វាងាយស្រួលក្នុងការចាប់ផ្តើមការសាងសង់ដោយកំណត់ចំនុចកំពូលនៃប៉ារ៉ាបូឡា។រូបមន្តខាងក្រោមនឹងជួយកំណត់កូអរដោនេនៃចំនុចកំពូលនៃប៉ារ៉ាបូឡា៖
អ្នកនិយាយថា "ឈប់! រូបមន្តសម្រាប់គឺស្រដៀងទៅនឹងរូបមន្តសម្រាប់ស្វែងរកអ្នករើសអើង "បាទ វាគឺហើយនេះគឺជាគុណវិបត្តិដ៏ធំនៃ "ដោយផ្ទាល់" ការសាងសង់ប៉ារ៉ាបូឡាដើម្បីស្វែងរកឫសរបស់វា។ ទោះយ៉ាងណាក៏ដោយ ចូររាប់ដល់ទីបញ្ចប់ ហើយបន្ទាប់មកខ្ញុំនឹងបង្ហាញអ្នកពីរបៀបធ្វើឱ្យវាកាន់តែងាយស្រួល (ច្រើន!)!
តើអ្នកបានរាប់ទេ? តើកូអរដោនេនៃចំនុចកំពូលនៃប៉ារ៉ាបូឡាមានអ្វីខ្លះ? តោះស្វែងយល់ទាំងអស់គ្នា៖
ពិតជាចម្លើយដូចគ្នា? ល្អណាស់! ហើយឥឡូវនេះយើងបានដឹងពីកូអរដោនេនៃ vertex រួចហើយ ហើយដើម្បីបង្កើត parabola យើងត្រូវការច្រើនជាងនេះទៀត ... ពិន្ទុ។ តើអ្នកគិតយ៉ាងណាដែរ តើយើងត្រូវការពិន្ទុអប្បបរមាប៉ុន្មាន? ត្រឹមត្រូវ។
អ្នកដឹងថាប៉ារ៉ាបូឡាមានភាពស៊ីមេទ្រីអំពីចំនុចកំពូលរបស់វា ឧទាហរណ៍៖

ដូច្នោះហើយ យើងត្រូវការចំណុចពីរបន្ថែមទៀតនៅតាមបណ្តោយផ្នែកខាងឆ្វេង ឬខាងស្តាំនៃប៉ារ៉ាបូឡា ហើយនៅពេលអនាគត យើងនឹងឆ្លុះបញ្ចាំងពីចំណុចទាំងនេះដោយស៊ីមេទ្រីនៅផ្នែកម្ខាងទៀត៖

យើងត្រលប់ទៅប៉ារ៉ាបូឡារបស់យើង។ សម្រាប់ករណីរបស់យើង ចំណុច។ យើងត្រូវការចំណុចពីរទៀតរៀងខ្លួន តើយើងអាចយកចំណុចវិជ្ជមានបានទេ ប៉ុន្តែតើយើងអាចយកចំណុចអវិជ្ជមានបានទេ? តើអ្វីជាចំណុចល្អបំផុតសម្រាប់អ្នក? វាកាន់តែងាយស្រួលសម្រាប់ខ្ញុំក្នុងការធ្វើការជាមួយវិជ្ជមាន ដូច្នេះខ្ញុំនឹងគណនាជាមួយ និង។
ឥឡូវនេះយើងមានបីពិន្ទុ ហើយយើងអាចបង្កើតប៉ារ៉ាបូឡារបស់យើងបានយ៉ាងងាយស្រួលដោយឆ្លុះបញ្ចាំងពីរចំណុចចុងក្រោយអំពីកំពូលរបស់វា៖

តើអ្នកគិតថាអ្វីជាដំណោះស្រាយចំពោះសមីការ? នោះហើយជាសិទ្ធិ ចំណុចដែល នោះគឺ និង។ ដោយសារតែ។
ហើយបើយើងនិយាយអ៊ីចឹងបានន័យថាក៏ត្រូវតែស្មើដែរឬ។
គ្រាន់តែ? យើងបានបញ្ចប់ការដោះស្រាយសមីការជាមួយអ្នកតាមវិធីក្រាហ្វិកដ៏ស្មុគស្មាញ ឬនឹងមានច្រើនទៀត!
ជាការពិតណាស់ អ្នកអាចពិនិត្យមើលចម្លើយរបស់យើងតាមពិជគណិត - អ្នកអាចគណនាឫសតាមរយៈទ្រឹស្តីបទ Vieta ឬ Discriminant ។ តើអ្នកទទួលបានអ្វីខ្លះ? ដូចគ្នា? អ្នកឃើញ! ឥឡូវនេះសូមមើលដំណោះស្រាយក្រាហ្វិកដ៏សាមញ្ញមួយ ខ្ញុំប្រាកដថាអ្នកនឹងចូលចិត្តវាខ្លាំងណាស់!
វិធីសាស្រ្ត 2. បំបែកទៅជាមុខងារជាច្រើន។
ចូរយើងយកអ្វីគ្រប់យ៉ាងផងដែរ សមីការរបស់យើង៖ ប៉ុន្តែយើងសរសេរវាតាមរបៀបខុសគ្នាបន្តិចគឺ៖
តើយើងអាចសរសេរដូចនេះបានទេ? យើងអាចធ្វើបាន ចាប់តាំងពីការបំប្លែងគឺស្មើនឹង។ តោះមើលបន្ថែមទៀត។
ចូរយើងបង្កើតមុខងារពីរដាច់ដោយឡែកពីគ្នា៖
- - ក្រាហ្វគឺជាប៉ារ៉ាបូឡាដ៏សាមញ្ញ ដែលអ្នកអាចបង្កើតបានយ៉ាងងាយស្រួល ទោះបីជាមិនកំណត់ចំនុចកំពូលដោយប្រើរូបមន្ត និងបង្កើតតារាងដើម្បីកំណត់ចំណុចផ្សេងទៀត។
- - ក្រាហ្វគឺជាបន្ទាត់ត្រង់ ដែលអ្នកអាចបង្កើតបានយ៉ាងងាយស្រួលដោយការប៉ាន់ប្រមាណតម្លៃ និងនៅក្នុងក្បាលរបស់អ្នកដោយមិនចាំបាច់ងាកទៅរកម៉ាស៊ីនគិតលេខ។
សាងសង់? ប្រៀបធៀបជាមួយអ្វីដែលខ្ញុំទទួលបាន៖

តើអ្នកគិតថានៅក្នុង ករណីនេះតើឫសគល់នៃសមីការ? ត្រឹមត្រូវ! សំរបសំរួលដោយ ដែលត្រូវបានទទួលដោយការឆ្លងកាត់ក្រាហ្វពីរ ហើយនោះគឺ៖

ដូច្នោះហើយដំណោះស្រាយចំពោះសមីការនេះគឺ៖
តើអ្នកនិយាយអ្វី? យល់ស្រប វិធីសាស្រ្តដំណោះស្រាយនេះគឺងាយស្រួលជាងវិធីមុន ហើយថែមទាំងងាយស្រួលជាងការស្វែងរកឫសគល់តាមរយៈអ្នករើសអើងទៅទៀត! បើដូច្នេះមែន សូមសាកល្បងវិធីនេះ ដើម្បីដោះស្រាយសមីការខាងក្រោម៖
តើអ្នកទទួលបានអ្វីខ្លះ? ចូរប្រៀបធៀបតារាងរបស់យើង៖

ក្រាហ្វបង្ហាញថាចម្លើយគឺ៖
តើអ្នកបានគ្រប់គ្រងទេ? ល្អណាស់! ឥឡូវនេះ សូមក្រឡេកមើលសមីការដែលមានភាពស្មុគស្មាញបន្តិច ពោលគឺដំណោះស្រាយនៃសមីការចម្រុះ ពោលគឺសមីការដែលមានមុខងារនៃប្រភេទផ្សេងៗគ្នា។
ដំណោះស្រាយក្រាហ្វិកនៃសមីការចម្រុះ
ឥឡូវយើងព្យាយាមដោះស្រាយដូចខាងក្រោម៖
ជាការពិតណាស់ អ្នកអាចនាំយកអ្វីគ្រប់យ៉ាងទៅជាភាគបែងរួម ស្វែងរកឫសគល់នៃសមីការលទ្ធផល ដោយមិនភ្លេចគិតគូរពី ODZ ប៉ុន្តែម្តងទៀត យើងនឹងព្យាយាមដោះស្រាយវាតាមក្រាហ្វិក ដូចដែលយើងបានធ្វើនៅក្នុងករណីមុនទាំងអស់។
លើកនេះសូមរៀបចំក្រាហ្វទាំងពីរខាងក្រោម៖
- - ក្រាហ្វគឺជាអ៊ីពែបូឡា
- - ក្រាហ្វគឺជាបន្ទាត់ត្រង់ដែលអ្នកអាចបង្កើតបានយ៉ាងងាយស្រួលដោយការប៉ាន់ប្រមាណតម្លៃនិងនៅក្នុងក្បាលរបស់អ្នកដោយមិនចាំបាច់ងាកទៅរកម៉ាស៊ីនគិតលេខ។
យល់? ឥឡូវនេះចាប់ផ្តើមសាងសង់។
នេះជាអ្វីដែលបានកើតឡើងចំពោះខ្ញុំ៖

ក្រឡេកមើលរូបភាពនេះ តើអ្វីជាឫសគល់នៃសមីការរបស់យើង?
នោះហើយជាសិទ្ធិ។ នេះជាការបញ្ជាក់៖

ព្យាយាមដោតឫសរបស់យើងទៅក្នុងសមីការ។ បានកើតឡើង?
ត្រឹមត្រូវហើយ! យល់ស្រប ការដោះស្រាយសមីការបែបនេះជាក្រាហ្វិកគឺជាសេចក្តីរីករាយ!
ព្យាយាមដោះស្រាយសមីការដោយខ្លួនឯងតាមក្រាហ្វិក៖
ខ្ញុំផ្តល់ឱ្យអ្នកនូវតម្រុយមួយ៖ ផ្លាស់ទីផ្នែកនៃសមីការទៅខាងស្តាំដើម្បីឱ្យភាគីទាំងពីរមានមុខងារសាមញ្ញបំផុតក្នុងការសាងសង់។ មានតម្រុយទេ? ចាត់វិធានការ!
ឥឡូវនេះសូមមើលអ្វីដែលអ្នកទទួលបាន៖
រៀងគ្នា៖
- - ប៉ារ៉ាបូឡាគូប។
- - បន្ទាត់ត្រង់ធម្មតា។
អញ្ចឹងយើងកំពុងសាងសង់៖

ដូចដែលអ្នកបានសរសេរទុកជាយូរមក ឫសគល់នៃសមីការនេះគឺ - ។
ដោយបានដោះស្រាយឧទាហរណ៍មួយចំនួនធំបែបនេះ ខ្ញុំប្រាកដថាអ្នកបានដឹងពីរបៀបដែលអ្នកអាចដោះស្រាយសមីការក្រាហ្វិកយ៉ាងងាយស្រួល និងរហ័ស។ វាដល់ពេលដែលត្រូវរកវិធីដោះស្រាយប្រព័ន្ធតាមវិធីនេះ។
ដំណោះស្រាយក្រាហ្វិកនៃប្រព័ន្ធ
ដំណោះស្រាយក្រាហ្វិកនៃប្រព័ន្ធគឺសំខាន់មិនខុសពីដំណោះស្រាយក្រាហ្វិកនៃសមីការទេ។ យើងក៏នឹងបង្កើតក្រាហ្វពីរផងដែរ ហើយចំនុចប្រសព្វរបស់ពួកគេនឹងក្លាយជាឫសគល់នៃប្រព័ន្ធនេះ។ ក្រាហ្វមួយគឺជាសមីការមួយ ក្រាហ្វទីពីរគឺជាសមីការមួយទៀត។ អ្វីគ្រប់យ៉ាងគឺសាមញ្ញបំផុត!
ចូរចាប់ផ្តើមជាមួយនឹងសាមញ្ញបំផុត - ប្រព័ន្ធដោះស្រាយសមីការលីនេអ៊ែរ។
ប្រព័ន្ធដោះស្រាយសមីការលីនេអ៊ែរ
ឧបមាថាយើងមានប្រព័ន្ធដូចខាងក្រោមៈ
ដើម្បីចាប់ផ្តើមយើងនឹងផ្លាស់ប្តូរវាតាមរបៀបដែលនៅខាងឆ្វេងមានអ្វីគ្រប់យ៉ាងដែលត្រូវបានភ្ជាប់ជាមួយហើយនៅខាងស្តាំ - អ្វីដែលភ្ជាប់ជាមួយ។ ម្យ៉ាងវិញទៀត យើងសរសេរសមីការទាំងនេះជាមុខងារក្នុងទម្រង់ធម្មតាសម្រាប់យើង៖
ហើយឥឡូវនេះ យើងគ្រាន់តែបង្កើតបន្ទាត់ត្រង់ពីរ។ តើអ្វីជាដំណោះស្រាយនៅក្នុងករណីរបស់យើង? ត្រឹមត្រូវ! ចំនុចប្រសព្វរបស់ពួកគេ! ហើយនៅទីនេះអ្នកត្រូវប្រុងប្រយ័ត្នខ្លាំងណាស់! គិតថាហេតុអ្វី? ខ្ញុំនឹងផ្តល់ឱ្យអ្នកនូវតម្រុយមួយ៖ យើងកំពុងដោះស្រាយជាមួយប្រព័ន្ធមួយ៖ ប្រព័ន្ធមានទាំងពីរ ហើយ... ទទួលបានព័ត៌មានជំនួយទេ?
ត្រឹមត្រូវហើយ! ពេលដោះស្រាយប្រព័ន្ធ យើងត្រូវមើលកូអរដោណេទាំងពីរ ហើយមិនត្រឹមតែប៉ុណ្ណោះ ដូចជាពេលដោះស្រាយសមីការ! ចំណុចសំខាន់មួយទៀតគឺត្រូវសរសេរវាឱ្យត្រឹមត្រូវ ហើយកុំច្រឡំថាយើងមានតម្លៃនៅឯណា ហើយតម្លៃនៅឯណា! ថត? ឥឡូវនេះយើងប្រៀបធៀបអ្វីគ្រប់យ៉ាងតាមលំដាប់លំដោយ:

ហើយចម្លើយ៖ អាយ។ ធ្វើការពិនិត្យ - ជំនួសឫសដែលបានរកឃើញទៅក្នុងប្រព័ន្ធ ហើយត្រូវប្រាកដថាយើងបានដោះស្រាយវាត្រឹមត្រូវតាមក្រាហ្វិក?
ប្រព័ន្ធដោះស្រាយសមីការមិនលីនេអ៊ែរ
ប៉ុន្តែចុះយ៉ាងណាបើជំនួសឱ្យបន្ទាត់ត្រង់មួយ យើងមានសមីការបួនជ្រុង? វាមិនអីទេ! អ្នកគ្រាន់តែសង់ប៉ារ៉ាបូឡាជំនួសឱ្យបន្ទាត់ត្រង់! កុំជឿ? ព្យាយាមដោះស្រាយប្រព័ន្ធដូចខាងក្រោមៈ
តើអ្វីជាជំហានបន្ទាប់របស់យើង? ត្រឹមត្រូវហើយ សរសេរវាចុះ ដើម្បីឱ្យវាងាយស្រួលសម្រាប់យើងក្នុងការបង្កើតក្រាហ្វ៖
ហើយឥឡូវនេះវាជារឿងតូចតាច - ខ្ញុំបានសាងសង់វាយ៉ាងឆាប់រហ័ស ហើយនេះគឺជាដំណោះស្រាយសម្រាប់អ្នក! អគារ៖

តើក្រាហ្វិកដូចគ្នាទេ? ឥឡូវសម្គាល់ដំណោះស្រាយរបស់ប្រព័ន្ធក្នុងរូបភាព ហើយសរសេរចម្លើយដែលបានបង្ហាញឱ្យបានត្រឹមត្រូវ!
ខ្ញុំបានធ្វើអ្វីគ្រប់យ៉ាង? ប្រៀបធៀបជាមួយកំណត់ចំណាំរបស់ខ្ញុំ៖

ត្រឹមត្រូវហើយ? ល្អណាស់! អ្នកបានចុចលើកិច្ចការដូចជាគ្រាប់ហើយ! ហើយប្រសិនបើដូច្នេះ ចូរផ្តល់ឱ្យអ្នកនូវប្រព័ន្ធដ៏ស្មុគស្មាញមួយបន្ថែមទៀត៖
ពួកយើងកំពុងធ្វើអ្វីហ្នឹង? ត្រឹមត្រូវ! យើងសរសេរប្រព័ន្ធដើម្បីឱ្យវាងាយស្រួលក្នុងការសាងសង់៖
ខ្ញុំនឹងផ្តល់តម្រុយបន្តិចបន្តួច ព្រោះប្រព័ន្ធមើលទៅស្មុគស្មាញណាស់! នៅពេលសាងសង់ក្រាហ្វសូមបង្កើតវា "ច្រើនទៀត" ហើយសំខាន់បំផុតកុំភ្ញាក់ផ្អើលចំពោះចំនួនចំនុចប្រសព្វ។
អញ្ចឹងតោះទៅ! ដកដង្ហើមចេញ? ឥឡូវនេះចាប់ផ្តើមសាងសង់!
អញ្ចឹងម៉េចដែរ? ស្អាត? តើអ្នកទទួលបានចំណុចប្រសព្វប៉ុន្មាន? ខ្ញុំមានបី! ចូរប្រៀបធៀបក្រាហ្វរបស់យើង៖

វិធីដូចគ្នា? ឥឡូវនេះសរសេរដោយប្រុងប្រយ័ត្ននូវដំណោះស្រាយទាំងអស់នៃប្រព័ន្ធរបស់យើង៖
ឥឡូវមើលប្រព័ន្ធម្តងទៀត៖
តើអ្នកអាចស្រមៃថាអ្នកបានដោះស្រាយវាក្នុងរយៈពេលត្រឹមតែ 15 នាទីទេ? យល់ស្រប គណិតវិទ្យានៅតែសាមញ្ញ ជាពិសេសពេលមើលកន្សោម អ្នកមិនខ្លាចធ្វើខុសទេ តែអ្នកយកវាទៅសម្រេចចិត្ត! អ្នកជាមនុស្សធំ!
ដំណោះស្រាយក្រាហ្វិកនៃវិសមភាព
ដំណោះស្រាយក្រាហ្វិកនៃវិសមភាពលីនេអ៊ែរ
បន្ទាប់ពីឧទាហរណ៍ចុងក្រោយនេះ អ្នកត្រូវបំពេញភារកិច្ចហើយ! ឥឡូវដកដង្ហើមចេញ - បើប្រៀបធៀបទៅនឹងផ្នែកមុន ៗ នេះនឹងងាយស្រួលណាស់!
យើងចាប់ផ្តើមដូចធម្មតា ជាមួយនឹងដំណោះស្រាយក្រាហ្វិកនៃវិសមភាពលីនេអ៊ែរ។ ឧទាហរណ៍មួយនេះ៖
ដើម្បីចាប់ផ្តើម យើងនឹងអនុវត្តការបំប្លែងដ៏សាមញ្ញបំផុត - យើងនឹងបើកតង្កៀបនៃការ៉េដ៏ល្អឥតខ្ចោះ ហើយផ្តល់ពាក្យស្រដៀងគ្នានេះ៖
វិសមភាពមិនមានភាពតឹងរ៉ឹងទេ ដូច្នេះហើយ - មិនត្រូវបានរាប់បញ្ចូលក្នុងចន្លោះពេលនោះទេ ហើយដំណោះស្រាយនឹងជាចំណុចទាំងអស់ដែលនៅខាងស្ដាំ ចាប់តាំងពីច្រើន ច្រើនទៀត ហើយដូច្នេះនៅលើ៖

ចម្លើយ៖
អស់ហើយ! យ៉ាងងាយស្រួល? តោះដោះស្រាយវិសមភាពសាមញ្ញជាមួយអថេរពីរ៖
ចូរយើងគូរមុខងារមួយនៅក្នុងប្រព័ន្ធកូអរដោណេ។

តើអ្នកមានតារាងបែបនេះទេ? ហើយឥឡូវនេះយើងពិនិត្យមើលដោយប្រុងប្រយ័ត្ននូវអ្វីដែលយើងមាននៅក្នុងវិសមភាព? តូចជាង? ដូច្នេះ យើងគូរលើអ្វីៗទាំងអស់ដែលនៅខាងឆ្វេងនៃបន្ទាត់ត្រង់របស់យើង។ ចុះបើមានទៀត? នោះហើយជាត្រឹមត្រូវ បន្ទាប់មកពួកគេនឹងលាបពណ៌លើអ្វីគ្រប់យ៉ាងដែលនៅខាងស្ដាំនៃបន្ទាត់ត្រង់របស់យើង។ អ្វីគ្រប់យ៉ាងគឺសាមញ្ញ។

ដំណោះស្រាយទាំងអស់ចំពោះវិសមភាពនេះគឺមានស្រមោលពណ៌ទឹកក្រូច។ នោះហើយជាវា វិសមភាពអថេរពីរត្រូវបានដោះស្រាយ។ នេះមានន័យថា កូអរដោណេ និងចំណុចណាមួយពីតំបន់ដែលមានស្រមោល គឺជាដំណោះស្រាយ។
ដំណោះស្រាយក្រាហ្វិកនៃវិសមភាពការ៉េ
ឥឡូវនេះយើងនឹងដោះស្រាយជាមួយនឹងវិធីដោះស្រាយក្រាហ្វិកវិសមភាពការ៉េ។
ប៉ុន្តែមុននឹងយើងឈានដល់ចំណុចនោះ សូមសង្ខេបរឿងខ្លះអំពីមុខងារការ៉េ។
តើអ្នករើសអើងទទួលខុសត្រូវចំពោះអ្វី? ត្រឹមត្រូវហើយ សម្រាប់ទីតាំងនៃក្រាហ្វដែលទាក់ទងទៅនឹងអ័ក្ស (ប្រសិនបើអ្នកមិនចាំរឿងនេះទេ សូមអានទ្រឹស្ដីអំពីមុខងារបួនជ្រុងឱ្យប្រាកដ)។
ក្នុងករណីណាក៏ដោយ នេះជាការរំលឹកតិចតួចសម្រាប់អ្នក៖

ឥឡូវនេះយើងបានធ្វើឲ្យសម្ភារៈទាំងអស់ក្នុងការចងចាំរបស់យើងស្រស់ស្អាតឡើងវិញហើយ ចូរចុះទៅរកជំនួញវិញ - យើងនឹងដោះស្រាយវិសមភាពជាក្រាហ្វិក។
ខ្ញុំនឹងប្រាប់អ្នកភ្លាមៗថាមានជម្រើសពីរសម្រាប់ដោះស្រាយវា។
ជម្រើសទី 1
យើងសរសេរប៉ារ៉ាបូឡារបស់យើងជាមុខងារ៖
ដោយប្រើរូបមន្ត យើងកំណត់កូអរដោណេនៃចំណុចកំពូលនៃប៉ារ៉ាបូឡា (ដូចគ្នានឹងពេលដោះស្រាយសមីការការ៉េ)៖
តើអ្នកបានរាប់ទេ? តើអ្នកទទួលបានអ្វីខ្លះ?
ឥឡូវយើងយកចំណុចពីរផ្សេងទៀតមកគណនាសម្រាប់ពួកគេ៖
យើងចាប់ផ្តើមបង្កើតសាខាមួយនៃប៉ារ៉ាបូឡា៖

យើងឆ្លុះបញ្ជាំងដោយស៊ីមេទ្រីលើចំណុចរបស់យើងលើសាខាមួយទៀតនៃប៉ារ៉ាបូឡា៖

ឥឡូវនេះត្រឡប់ទៅវិសមភាពរបស់យើង។
យើងត្រូវការវាឱ្យតិចជាងសូន្យរៀងៗខ្លួន៖

ដោយសារនៅក្នុងវិសមភាពរបស់យើងមានសញ្ញាតិចជាងយ៉ាងតឹងរ៉ឹង យើងដកចំនុចបញ្ចប់ចេញ - យើង "បញ្ចេញ"។
ចម្លើយ៖
ផ្លូវឆ្ងាយមែនទេ? ឥឡូវនេះខ្ញុំនឹងបង្ហាញអ្នកនូវកំណែសាមញ្ញនៃដំណោះស្រាយក្រាហ្វិកដោយប្រើវិសមភាពដូចគ្នាជាឧទាហរណ៍៖
ជម្រើសទី 2

យើងត្រឡប់ទៅវិសមភាពរបស់យើងវិញ ហើយសម្គាល់ចន្លោះពេលដែលយើងត្រូវការ៖

យល់ស្រប វាលឿនជាង។
តោះសរសេរចម្លើយឥឡូវនេះ៖
ចូរយើងពិចារណាវិធីសាស្រ្តដំណោះស្រាយមួយផ្សេងទៀតដែលជួយសម្រួលផ្នែកពិជគណិត ប៉ុន្តែរឿងសំខាន់គឺមិនត្រូវច្រឡំឡើយ។
គុណផ្នែកខាងឆ្វេង និងខាងស្តាំដោយ៖
ព្យាយាមដោះស្រាយវិសមភាពបួនជ្រុងខាងក្រោមដោយខ្លួនឯងតាមវិធីណាមួយដែលអ្នកចូលចិត្ត៖ .
តើអ្នកបានគ្រប់គ្រងទេ?
សូមមើលពីរបៀបដែលគំនូសតាងរបស់ខ្ញុំបានប្រែក្លាយ៖

ចម្លើយ៖ .
ដំណោះស្រាយក្រាហ្វិកនៃវិសមភាពចម្រុះ
ឥឡូវនេះ ចូរយើងបន្តទៅវិសមភាពដ៏ស្មុគស្មាញបន្ថែមទៀត!
តើអ្នកចូលចិត្តវាដោយរបៀបណា៖
រន្ធត់ណាស់មែនទេ? និយាយតាមត្រង់ទៅ ខ្ញុំមិនដឹងពីរបៀបដោះស្រាយពិជគណិតនេះទេ... ប៉ុន្តែ វាមិនចាំបាច់ទេ។ ក្រាហ្វិចមិនមានអ្វីស្មុគស្មាញក្នុងរឿងនេះទេ! ភ្នែកខ្លាចតែដៃធ្វើ!
រឿងដំបូងដែលយើងចាប់ផ្តើមគឺដោយការកសាងក្រាហ្វពីរ៖
ខ្ញុំនឹងមិនសរសេរតារាងសម្រាប់មនុស្សគ្រប់គ្នាទេ - ខ្ញុំប្រាកដថាអ្នកអាចធ្វើវាបានល្អឥតខ្ចោះដោយខ្លួនឯង (ជាការពិតណាស់ មានឧទាហរណ៍ជាច្រើនដែលត្រូវដោះស្រាយ!)
លាប? ឥឡូវនេះបង្កើតក្រាហ្វពីរ។
តោះប្រៀបធៀបគំនូររបស់យើង?

តើអ្នកមានដូចគ្នាទេ? មិនអីទេ! ឥឡូវនេះ ចូរយើងដាក់ចំនុចប្រសព្វ ហើយកំណត់ជាមួយនឹងពណ៌មួយណា ក្រាហ្វិចដែលយើងគួរមាន តាមទ្រឹស្តីគួរតែធំជាង។ សូមមើលអ្វីដែលបានកើតឡើងនៅទីបញ្ចប់៖

ហើយឥឡូវនេះយើងគ្រាន់តែពិនិត្យមើលថាតើតារាងដែលបានជ្រើសរើសរបស់យើងខ្ពស់ជាងគំនូសតាងណា? យកខ្មៅដៃមកលាបតំបន់នេះដោយសេរី! វានឹងក្លាយជាដំណោះស្រាយចំពោះវិសមភាពដ៏ស្មុគស្មាញរបស់យើង!

តើចន្លោះពេលប៉ុន្មានតាមអ័ក្សដែលយើងខ្ពស់ជាង? ត្រូវហើយ។ នេះជាចម្លើយ!
ឥឡូវនេះអ្នកអាចដោះស្រាយសមីការណាមួយ និងប្រព័ន្ធណាមួយ ហើយថែមទាំងមានវិសមភាពថែមទៀត!
សង្ខេបអំពីមេ
ក្បួនដោះស្រាយសមីការដោយប្រើក្រាហ្វមុខងារ៖
- បញ្ចេញមតិតាមរយៈ
- កំណត់ប្រភេទមុខងារ
- ចូរយើងបង្កើតក្រាហ្វនៃអនុគមន៍លទ្ធផល
- ស្វែងរកចំណុចប្រសព្វនៃក្រាហ្វ
- សរសេរចម្លើយឱ្យបានត្រឹមត្រូវ (ដោយគិតពីសញ្ញា ODZ និងវិសមភាព)
- ពិនិត្យចម្លើយ (ជំនួសឫសក្នុងសមីការ ឬប្រព័ន្ធ)
សម្រាប់ព័ត៌មានបន្ថែមអំពីការធ្វើផែនការក្រាហ្វិក សូមមើលប្រធានបទ ""។
ដំណោះស្រាយក្រាហ្វិកនៃសមីការ quadratic ដើម្បីពង្រឹងសមត្ថភាពបង្កើតក្រាហ្វនៃមុខងារផ្សេងៗ។ ដើម្បីបង្កើតសមត្ថភាពក្នុងការដោះស្រាយសមីការការ៉េជាក្រាហ្វិក។ Brdsk 2009 ស្ថាប័នអប់រំក្រុង - Economic Lyceum មេរៀនទូទៅលើប្រធានបទ "មុខងារបួនជ្រុង" ពិជគណិតថ្នាក់ទី 8 គ្រូបង្រៀន Fedoseeva T.M.
ការធ្វើផែនការអនុគមន៍ quadratic កំណត់ទិសដៅនៃសាខា៖ a> 0 branch up; ក 0 សាខាឡើង; a"> 0 សាខាឡើង; a"> 0 សាខាឡើង; a" title="(!LANG:ការកំណត់មុខងាររាងការ៉េ កំណត់ទិសដៅសាខា៖ a>0 សាខាឡើងលើ; a"> title="ការធ្វើផែនការអនុគមន៍ quadratic កំណត់ទិសដៅនៃសាខា៖ a> 0 branch up; ក"> !}
0 សាខាត្រូវបានដឹកនាំឡើងលើ; 2) ចំនុចកំពូល y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - អ័ក្សនៃប៉ារ៉ាបូឡា ចំណុចត្រួតពិនិត្យ៖ (0: -3), (3 ; 0) និងស៊ីមេទ្រីចំពោះពួកគេអំពីអ័ក្ស x = 1 យើងបង្កើតប៉ារ៉ាបូឡា។ ស្វែងរកចំណុច "title="(!LANG៖ ចូរបង្កើតក្រាហ្វនៃអនុគមន៍ y=x 2 -2x-3 ដោយប្រើក្បួនដោះស្រាយ៖ 1) a=1>0 សាខាត្រូវបានតម្រង់ទៅខាងលើ។ 2) ចំនុចកំពូល y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - អ័ក្សនៃប៉ារ៉ាបូឡា ចំណុចត្រួតពិនិត្យ៖ (0: -3), (3 ; 0) និងស៊ីមេទ្រីចំពោះពួកគេអំពីអ័ក្ស x = 1 យើងបង្កើតប៉ារ៉ាបូឡា។ ការស្វែងរកចំណុចមួយ។" class="link_thumb"> 3 !}ចូរយើងបង្កើតក្រាហ្វនៃអនុគមន៍ y=x 2 -2x-3 ដោយប្រើក្បួនដោះស្រាយ៖ 1) a=1> 0 សាខាត្រូវបានតម្រង់ទៅខាងលើ។ 2) ចំនុចកំពូល y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - អ័ក្សនៃប៉ារ៉ាបូឡា ចំណុចត្រួតពិនិត្យ៖ (0: -3), (3 ; 0) និងស៊ីមេទ្រីចំពោះពួកគេអំពីអ័ក្ស x = 1 យើងបង្កើតប៉ារ៉ាបូឡា។ យើងរកឃើញចំនុចប្រសព្វជាមួយអ័ក្ស OX: x 1 \u003d -1; x 2 \u003d 3 1 វិធីដើម្បីដោះស្រាយសមីការ x 2 -2x-3 \u003d 0 y x ដោះស្រាយសមីការ x 2 +2x-3 \u003d 0 0 សាខាត្រូវបានដឹកនាំឡើងលើ; 2) ចំនុចកំពូល y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - អ័ក្សនៃប៉ារ៉ាបូឡា ចំណុចត្រួតពិនិត្យ៖ (0: -3), (3 ; 0) និងស៊ីមេទ្រីចំពោះពួកគេអំពីអ័ក្ស x = 1 យើងបង្កើតប៉ារ៉ាបូឡា។ យើងរកឃើញចំណុច "\u003e 0 សាខាត្រូវបានតម្រង់ទៅខាងលើ; 2) កំពូល y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - អ័ក្ស ចំណុចត្រួតពិនិត្យប៉ារ៉ាបូឡា៖ (0: -3), (3; 0) និងស៊ីមេទ្រីអំពីអ័ក្ស x = 1 យើងបង្កើតប៉ារ៉ាបូឡា។ ស្វែងរកចំណុចប្រសព្វជាមួយអ័ក្ស OX៖ x 1 \u003d -1; x 2 \u003d 3 1 វិធីដើម្បីដោះស្រាយសមីការ x 2 -2x-3 \u003d 0 y x 0 1 - 4 23 ដោះស្រាយសមីការ x 2 + 2x-3 \u003d 0 "\u003e 0 សាខាត្រូវបានដឹកនាំឡើងលើ; 2) ចំនុចកំពូល y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - អ័ក្សនៃប៉ារ៉ាបូឡា ចំណុចត្រួតពិនិត្យ៖ (0: -3), (3 ; 0) និងស៊ីមេទ្រីចំពោះពួកគេអំពីអ័ក្ស x = 1 យើងបង្កើតប៉ារ៉ាបូឡា។ ស្វែងរកចំណុច "title="(!LANG៖ ចូរបង្កើតក្រាហ្វនៃអនុគមន៍ y=x 2 -2x-3 ដោយប្រើក្បួនដោះស្រាយ៖ 1) a=1>0 សាខាត្រូវបានតម្រង់ទៅខាងលើ។ 2) ចំនុចកំពូល y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - អ័ក្សនៃប៉ារ៉ាបូឡា ចំណុចត្រួតពិនិត្យ៖ (0: -3), (3 ; 0) និងស៊ីមេទ្រីចំពោះពួកគេអំពីអ័ក្ស x = 1 យើងបង្កើតប៉ារ៉ាបូឡា។ ការស្វែងរកចំណុចមួយ។"> title="ចូរយើងបង្កើតក្រាហ្វនៃអនុគមន៍ y=x 2 -2x-3 ដោយប្រើក្បួនដោះស្រាយ៖ 1) a=1> 0 សាខាត្រូវបានតម្រង់ទៅខាងលើ។ 2) ចំនុចកំពូល y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - អ័ក្សនៃប៉ារ៉ាបូឡា ចំណុចត្រួតពិនិត្យ៖ (0: -3), (3 ; 0) និងស៊ីមេទ្រីចំពោះពួកគេអំពីអ័ក្ស x = 1 យើងបង្កើតប៉ារ៉ាបូឡា។ ការស្វែងរកចំណុចមួយ។"> !}
វិធីទីពីរ៖ ក) ។ ចូរបែងចែកសមីការ x 2 −2x-3=0 ជាផ្នែក x 2 = 2x+3 ចូរយើងសរសេរអនុគមន៍ពីរ y= x 2 ; y \u003d 2x + 3 យើងបង្កើតក្រាហ្វនៃមុខងារទាំងនេះនៅក្នុងប្រព័ន្ធកូអរដោនេមួយ។ abscissas នៃចំនុចប្រសព្វគឺជាឫសគល់នៃសមីការ។ 0 1 x y ដោះស្រាយសមីការ x 2 +2x-3=0

វិធីទីបី៖ x 2 -3 \u003d 2x y \u003d x 2 -3; y=2x យើងបង្កើតក្រាហ្វនៃមុខងារទាំងនេះនៅក្នុងប្រព័ន្ធកូអរដោនេមួយ។ abscissas នៃចំនុចប្រសព្វគឺជាឫសគល់នៃសមីការ។ 0 1 x y ដោះស្រាយសមីការ x 2 +2x-3=0



វិទ្យាស្ថាន DAGESTAN សម្រាប់ការអភិវឌ្ឍន៍វិជ្ជាជីវៈ
បុគ្គលិកគរុកោសល្យ
នាយកដ្ឋានអប់រំរូបវិទ្យា និងគណិតវិទ្យា និង ICT
គម្រោង
លើប្រធានបទ៖
« សំណង់ និង ទំ កំណែទម្រង់
ក្រាហ្វិកមុខងារ
នៅក្នុងគណិតវិទ្យាសាលា »
Rabadanov P.A.
គ្រូបង្រៀនគណិតវិទ្យា
MBOU "អនុវិទ្យាល័យ Kochubey"
ស្រុក Tarumovsky
ឆ្នាំ 2015
1. សេចក្តីផ្តើម…………………………………………………………………..៣
2. ជំពូក ខ្ញុំ. ការពិនិត្យឡើងវិញនៃអក្សរសិល្ប៍លើប្រធានបទនៃគម្រោង…………………………………….៥
3. ជំពូក II. ផ្នែកជាក់ស្តែង៖
៣.១. វិធីសាស្រ្តជាមូលដ្ឋានសម្រាប់បំប្លែងក្រាហ្វមុខងារ …………. ៧
3.2. ការធ្វើផែនការស្មើគ្នានិងមុខងារសេស…………….. 10
3.3. ការធ្វើផែនការមុខងារបញ្ច្រាស………………………… 11
3.4. ការខូចទ្រង់ទ្រាយ (ការបង្ហាប់និងភាពតានតឹង) នៃក្រាហ្វ………………….12
3.5 ការរួមបញ្ចូលគ្នានៃការផ្ទេរ ការឆ្លុះបញ្ចាំង និងការខូចទ្រង់ទ្រាយ……………………13
៤.ភារកិច្ចសម្រាប់ដំណោះស្រាយឯករាជ្យ……………………………...១៤
៥.សេចក្តីសន្និដ្ឋាន………………………………………………………………… ១៥
៦.សេចក្តីសន្និដ្ឋាន…………………………………………………………………..១៧
ការណែនាំ
ការបំប្លែងក្រាហ្វមុខងារគឺជាគោលគំនិតគណិតវិទ្យាជាមូលដ្ឋានដែលទាក់ទងដោយផ្ទាល់ទៅនឹងសកម្មភាពជាក់ស្តែង។ ក្រាហ្វឆ្លុះបញ្ចាំងពីភាពប្រែប្រួល និងថាមវន្តនៃពិភពពិត ទំនាក់ទំនងទៅវិញទៅមកនៃវត្ថុពិត និងបាតុភូត។
បន្ទាត់មុខងារគឺជាប្រធានបទមូលដ្ឋានដែលគ្របដណ្តប់នៅក្នុងការប្រឡងថ្នាក់មូលដ្ឋាន និងបង្រួបបង្រួមរដ្ឋ។ដូចគ្នានេះផងដែរគំនិតគណិតវិទ្យាជាច្រើនត្រូវបានពិចារណាដោយវិធីសាស្ត្រក្រាហ្វិក។ ឧទាហរណ៍ទៅបួនជ្រុងមុខងារត្រូវបានណែនាំ និងសិក្សាដោយទំនាក់ទំនងជិតស្និទ្ធជាមួយសមីការ quadratic និងវិសមភាព។ដូច្នេះវាធ្វើតាមនោះ។ការបង្រៀនសិស្សពីរបៀបបង្កើត និងបំប្លែងក្រាហ្វនៃមុខងារ គឺជាកិច្ចការសំខាន់មួយនៃការបង្រៀនគណិតវិទ្យានៅសាលា។
ការសិក្សាអំពីមុខងារធ្វើឱ្យវាអាចរកឃើញអំពីដែននៃនិយមន័យ និងវិសាលភាពនៃមុខងារ វិសាលភាពការថយចុះឬបង្កើនអត្រា, asymtotes, ចន្លោះពេលsign constancy ។ល។ ទោះយ៉ាងណាក៏ដោយ ដើម្បីបង្កើតក្រាហ្វkov មុខងារជាច្រើនអាចជាប្រើវិធីសាស្រ្តមួយចំនួនធ្វើឱ្យវាកាន់តែងាយស្រួលអគារ។ ដូច្នេះ សិស្សគួរមានសមត្ថភាពក្នុងការបង្កើតក្រាហ្វតាមគ្រោងការណ៍វិធីសាស្ត្រ។
ខាងលើកំណត់ភាពពាក់ព័ន្ធ ប្រធានបទស្រាវជ្រាវ។
វត្ថុនៃការសិក្សា គឺជាការសិក្សាអំពីការបំប្លែងក្រាហ្វបន្ទាត់មុខងារក្នុងគណិតវិទ្យាសាលា។
មុខវិជ្ជាសិក្សា - ដំណើរការនៃការបង្កើត និងបំប្លែងក្រាហ្វមុខងារនៅក្នុងអនុវិទ្យាល័យ។
គោលបំណងនៃការសិក្សា៖ ការអប់រំ មាននៅក្នុងការកំណត់អត្តសញ្ញាណគ្រោងការណ៍វិធីសាស្រ្តសម្រាប់ការសាងសង់ និងការបំប្លែងក្រាហ្វនៃមុខងារមួយ;កំពុងអភិវឌ្ឍ - ការអភិវឌ្ឍនៃអរូបី, ក្បួនដោះស្រាយ, ការគិតឡូជីខល, ការស្រមើលស្រមៃទំហំ;អប់រំ - ការអប់រំនៃវប្បធម៌ក្រាហ្វិករបស់សិស្សសាលា, ការបង្កើតជំនាញផ្លូវចិត្ត។
គោលដៅនាំឱ្យមានការសម្រេចចិត្តដូចខាងក្រោមភារកិច្ច:
1. វិភាគការអប់រំ និងវិធីសាស្រ្តលើបញ្ហាដែលកំពុងសិក្សា។
2. កំណត់គ្រោងការណ៍វិធីសាស្រ្តការបំប្លែងក្រាហ្វមុខងារក្នុងវគ្គសិក្សាគណិតវិទ្យា។
3. ជ្រើសរើសមធ្យោបាយ និងមធ្យោបាយដែលមានប្រសិទ្ធភាពបំផុត។ការសាងសង់ និងការផ្លាស់ប្តូរក្រាហ្វមុខងារនៅក្នុងសាលាមធ្យមសិក្សារួមចំណែកដល់៖ ការបញ្ចូលអត្ថន័យនៃសម្ភារៈអប់រំ; បង្កើនសកម្មភាពយល់ដឹងរបស់សិស្ស; ការអភិវឌ្ឍសមត្ថភាពច្នៃប្រឌិតរបស់ពួកគេ។
សម្មតិកម្មស្រាវជ្រាវ៖ ការបង្កើតជំនាញក្រាហ្វិកក្នុងដំណើរការសិក្សាមុខងារ និងការអប់រំនៃវប្បធម៌ក្រាហ្វិករបស់សិស្សនឹង មានប្រសិទ្ធភាពប្រសិនបើសិស្សមានគ្រោងការណ៍វិធីសាស្រ្តសម្រាប់ការសាងសង់ និងបំប្លែងក្រាហ្វមុខងារនៅក្នុងវគ្គសិក្សាគណិតវិទ្យារបស់សាលា។
ជំពូក ខ្ញុំ . ការវាយតម្លៃអក្សរសិល្ប៍លើប្រធានបទនៃគម្រោង។
ក្នុងការរៀបចំសម្រាប់គម្រោង យើងបានសិក្សាអក្សរសិល្ប៍ដូចខាងក្រោមៈ
Sivashinsky, I. Kh. ទ្រឹស្តីបទ និងបញ្ហាក្នុងពិជគណិត មុខងារបឋម - M., 2002. - 115 p.
Gelfand, I. M., Glagoleva, E. G., Shnol, E. E. មុខងារ និងក្រាហ្វ (បច្ចេកទេសមូលដ្ឋាន) - M., 1985. - 120 s
V.Z.Zaitsev, V.V. Ryzhkov, M.I. ស្កែនវី។ គណិតវិទ្យាបឋម - អិម, ឆ្នាំ ២០១០ (ផ្សាយឡើងវិញ) ។ - 590 ទំ។
Kuzmin, M. K. ការសាងសង់ក្រាហ្វនៃអនុគមន៍ - J. គណិតវិទ្យានៅសាលា។ - 2003. - លេខ 5 ។ - ស ៦១-៦២។
Shilov G.E. តើធ្វើដូចម្តេចដើម្បីកសាងតារាង? - M. , 1982 ។
អ៊ីសាក តាណាតា។ ការបំប្លែងធរណីមាត្រនៃក្រាហ្វនៃមុខងារ - MTsNMO, 2012
អេវាត្រូវបានកត់សម្គាល់ថាសមត្ថភាពក្នុងការ "អាន" ឥរិយាបទនៃមុខងារនៅលើសំណុំជាក់លាក់មួយដោយប្រើក្រាហ្វត្រូវបានប្រើមិនត្រឹមតែនៅក្នុងវគ្គសិក្សានៃគណិតវិទ្យាប៉ុណ្ណោះទេប៉ុន្តែថែមទាំងនៅក្នុងសកម្មភាពជាក់ស្តែងនៃមនុស្សម្នាក់ដែលគាត់ត្រូវដោះស្រាយជាមួយក្រាហ្វិកជាក់លាក់ផងដែរ។ តំណាងនៃភាពអាស្រ័យ។ ដូច្នេះ សិស្សគួរតែអាចកំណត់លក្ខណៈសម្បត្តិមួយចំនួនរបស់វាពីក្រាហ្វនៃអនុគមន៍មួយ។
សម្ភារៈទ្រឹស្តីសម្រាប់ការផ្លាស់ប្តូរក្រាហ្វត្រូវបានបញ្ជាក់យ៉ាងតឹងរ៉ឹងនៅក្នុង។ បច្ចេកទេសនេះត្រូវបានអមដោយរូបភាពជាមួយគំនូរ ឧទាហរណ៍នៃភាពស្មុគស្មាញផ្សេងៗគ្នា និងដំណោះស្រាយរបស់ពួកគេ ដែលធ្វើឱ្យវាអាចធ្វើទៅបានដើម្បីពង្រឹងចំណេះដឹង និងគ្រោងមុខងារស្មុគស្មាញ។
តំណាងឱ្យវគ្គបណ្តុះបណ្តាលអេឡិចត្រូនិច បរិមាណ និងខ្លឹមសារដែលត្រូវនឹងតម្រូវការសម្រាប់វគ្គសិក្សាគណិតវិទ្យានៅវិទ្យាល័យ។ សម្ភារៈទ្រឹស្តីត្រូវបានគាំទ្រដោយគំនូរជីវចលក្រាហ្វិកដែលផ្តល់នូវការតំណាងដែលមើលឃើញនៃប្រធានបទដែលកំពុងសិក្សា។ វគ្គសិក្សារួមមានម៉ូឌុលចំនួនបី៖ ម៉ូឌុលសិក្សាសម្ភារៈទ្រឹស្តី ម៉ូឌុលពិនិត្យដោយខ្លួនឯង និងម៉ូឌុលត្រួតពិនិត្យចំណេះដឹង។
ពី , , គ្រោងការណ៍គំនូសតាងវិធីសាស្រ្ត ឧទាហរណ៍សម្រាប់ការងារឯករាជ្យត្រូវបានប្រើសម្រាប់ផ្នែកជាក់ស្តែងនៃគម្រោង។
ការសន្និដ្ឋានទៅជំពូកទី 1
ការសិក្សាអក្សរសិល្ប៍អប់រំ និងវិធីសាស្រ្តត្រូវបានអនុញ្ញាត៖
1. កំណត់គ្រោងការណ៍វិធីសាស្រ្តសិក្សា បង្កើត និងបំប្លែងក្រាហ្វនៃមុខងារក្នុងវគ្គសិក្សាគណិតវិទ្យារបស់សាលា។
2. ជ្រើសរើសមធ្យោបាយ និងមធ្យោបាយដែលមានប្រសិទ្ធភាពបំផុត។ការស្ថាបនា និងការផ្លាស់ប្តូរក្រាហ្វមុខងារក្នុងគណិតវិទ្យាសាលា,រួមចំណែក៖
assimilation អត្ថន័យនៃសម្ភារៈអប់រំ;
បង្កើនសកម្មភាពយល់ដឹងរបស់សិស្ស;
ការអភិវឌ្ឍសមត្ថភាពច្នៃប្រឌិតរបស់ពួកគេ។
3. បង្ហាញថា បន្ទាត់មុខងារមានឥទ្ធិពលយ៉ាងសំខាន់ក្នុងការសិក្សាអំពីគោលគំនិតផ្សេងៗក្នុងគណិតវិទ្យា។
ជំពូកទី 2. ផ្នែក EMPIRICAL
នៅក្នុងជំពូកនេះ យើងនឹងពិចារណាអំពីវិធីសាស្ត្រសំខាន់ៗសម្រាប់បំប្លែងក្រាហ្វមុខងារ និងផ្តល់នូវគ្រោងការណ៍វិធីសាស្រ្តសម្រាប់ការសាងសង់បន្សំផ្សេងៗនៃក្រាហ្វសម្រាប់មុខងារផ្សេងៗ។
២.១. បច្ចេកទេសជាមូលដ្ឋានសម្រាប់ការបំប្លែងក្រាហ្វមុខងារ
ការបកប្រែតាមអ័ក្ស y
f ( x ) f ( x )+ ខ .
សម្រាប់ការធ្វើផែនការមុខងារy = f( x) + ខដានអ៊ីម៖
1. បង្កើតក្រាហ្វមុខងារy= f( x)
2. ផ្លាស់ទីអ័ក្សabscissa នៅលើ| ខ| ឯកតាឡើងនៅខ>0 ឬនៅ| ខ| បរិភោគក្រាបចុះនៅខ < 0. ទទួលបាននៅក្នុងប្រព័ន្ធថ្មី។ក្រាហ្វឌីណាត គឺជាក្រាហ្វនៃមុខងារមួយ។y = f( x) + ខ.
2. ផ្ទេរ តាម អ័ក្ស abscissa
f ( x ) f ( x + ក ) .
y = f( x+ ក) ដានអ៊ីម៖

3. កំណត់មុខងារនៃទម្រង់ y = f (- x )
f (x ) f (- x ).
ដើម្បីគូរមុខងារy = f( - x) ដូចតទៅ៖
គ្រោងមុខងារមួយ។y = f( x)
ឆ្លុះបញ្ចាំងវាមកវិញទាក់ទងទៅនឹងអ័ក្ស y
ក្រាហ្វលទ្ធផលគឺក្រាហ្វមុខងារy = f( - X).
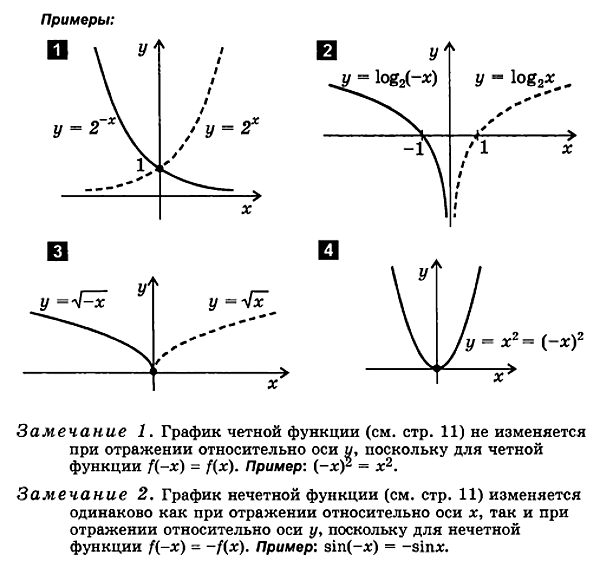
4. កំណត់មុខងារនៃទម្រង់ y= - f ( x )
f ( x ) - f ( x )
- f( x) ដូចតទៅ៖
គ្រោងមុខងារមួយ។y= f( x)
ឆ្លុះបញ្ចាំងពីអ័ក្ស x

២.២. ការធ្វើផែនការស្មើគ្នា និង លក្ខណៈពិសេសប្លែក
នៅពេលគ្រោងសម្រាប់មុខងារគូ និងសេស វាងាយស្រួលប្រើលក្ខណៈសម្បត្តិខាងក្រោម៖
1. ក្រាហ្វនៃស៊ីមមេតមុខងារគូអង្ករទាក់ទងនឹងអ័ក្ស y ។
2. ក្រាហ្វនៃមុខងារសេសគឺស៊ីមេទ្រីអំពីប្រភពដើម។
ដើម្បីបង្កើតក្រាហ្វនៃអនុគមន៍គូ និងសេស វាគ្រប់គ្រាន់ដើម្បីកំណត់តែសាខាត្រឹមត្រូវនៃក្រាហ្វសម្រាប់តម្លៃវិជ្ជមាននៃអាគុយម៉ង់។ សាខាខាងឆ្វេងត្រូវបានបញ្ចប់ដោយស៊ីមេទ្រីអំពីប្រភពដើមសម្រាប់មុខងារសេស និងអំពីអ័ក្ស y សម្រាប់អនុគមន៍គូ។
ដើម្បីកំណត់មុខងារស្មើ y = f ( x ) បន្ទាប់ពី បទភ្លេង៖
បង្កើតសាខានៃក្រាហ្វនៃមុខងារនេះតែនៅក្នុងជួរនៃតម្លៃវិជ្ជមាននៃអាគុយម៉ង់ x≥0 ។
អូតាមដានសាខានេះអំពីអ័ក្ស y

ដើម្បីរៀបចំមុខងារសេស y = f ( x ) ដូចខាងក្រោម៖
បង្កើតសាខាក្រាហ្វនៃមុខងារនេះតែនៅក្នុងផ្ទៃដីនៃតម្លៃវិជ្ជមាននៃអាគុយម៉ង់ (х≥0) ។
អូតាមដានសាខានេះដោយគោរពតាមប្រភពដើមទៅតំបន់នៃតម្លៃ x អវិជ្ជមាន។

២.៣. ការធ្វើផែនការមុខងារបញ្ច្រាស
ដូចដែលបានកត់សម្គាល់រួចហើយ មុខងារផ្ទាល់ និងបញ្ច្រាសបង្ហាញទំនាក់ទំនងដូចគ្នារវាងអថេរx និង y ជាមួយនឹងភាពខុសគ្នាតែមួយគត់ដែលនៅក្នុងមុខងារបញ្ច្រាសទាំងនេះអថេរបានផ្លាស់ប្តូរតួនាទី ដែលស្មើនឹងការផ្លាស់ប្តូរសញ្ញាណនៃអ័ក្សកូអរដោនេ។ ដូច្នេះកាលវិភាគអនុគមន៍បញ្ច្រាសគឺស៊ីមេទ្រីទៅនឹងក្រាហ្វនៃអនុគមន៍ផ្ទាល់អំពី bisectorខ្ញុំនិងIIIមុំសំរបសំរួល,i.e. ត្រង់y = x ។ ដូច្នេះយើងទទួលបានច្បាប់បន្ទាប់។
ដើម្បីកំណត់មុខងារ y = (x) បញ្ច្រាសទៅមុខងារy = f( x) គួរតែត្រូវបានសាងសង់កាលវិភាគy = f( x) ហើយឆ្លុះបញ្ចាំងវាដោយគោរពតាមបន្ទាត់ត្រង់ y = x ។

២.៤. ការខូចទ្រង់ទ្រាយ (ការបង្ហាប់និងភាពតានតឹង) នៃក្រាហ្វ
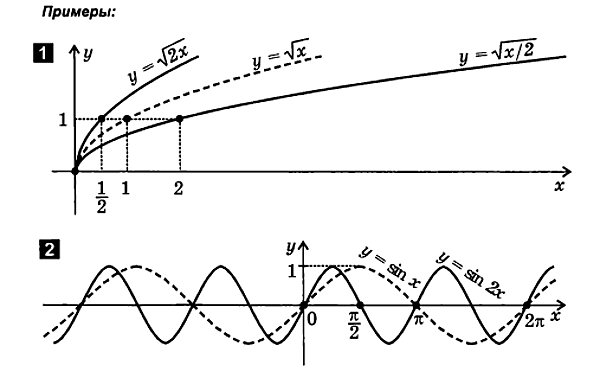
1. ការបង្ហាប់ (ការពង្រីក) នៃក្រាហ្វតាមអ័ក្ស y
f ( x ) ក ∙ f ( x ).
ដើម្បីគូរមុខងារy= ក∙ f( x) ដូចតទៅ៖

8. ការបង្ហាប់ (ការពង្រីក) នៃក្រាហ្វតាមអ័ក្ស x
f( x)
ដើម្បីកំណត់មុខងារ y= f( x) ដូចខាងក្រោម៖
២.៥. ការរួមបញ្ចូលគ្នានៃការបកប្រែ ការឆ្លុះបញ្ចាំង និងការខូចទ្រង់ទ្រាយ
ជាញឹកញាប់ណាស់នៅពេលគូរក្រាហ្វិកមុខងារសម្រាប់ផ្លាស់ប្តូរការរួមបញ្ចូលគ្នា.
ការអនុវត្តប្រកបដោយនិរន្តរភាពនៃបច្ចេកទេសឥរិយាបថបែបនេះមួយចំនួនអនុញ្ញាតឱ្យមានភាពសាមញ្ញយ៉ាងខ្លាំងក្នុងការកសាងក្រាហ្វដោយប្រើមុខងារដែលកំពុងដំណើរការហើយជារឿយៗកាត់បន្ថយវានៅចុងបញ្ចប់ទៅការស្ថាបនាមុខងារបឋមដ៏សាមញ្ញបំផុតមួយ។កិច្ចការ។ ពិចារណាពីរបៀបដែលនៅក្នុងទិដ្ឋភាពខាងលើវាដូចខាងក្រោមបង្កើតក្រាហ្វិកមុខងារ។
ចូរយើងកត់សំគាល់ថាវាដល់ពេលហើយ។វាគឺជាទីប្រឹក្សាដើម្បីអនុវត្តការចតសាមញ្ញនៅក្នុងអ្នកស្នងបន្ទាប់ភាព។
ការប្រើភាពស្មើគ្នាឬមុខងារចម្លែក។
ការផ្ទេរអ័ក្ស។
ការឆ្លុះបញ្ចាំងនិងការខូចទ្រង់ទ្រាយ។
ការសាងសង់ក្រាហ្វត្រូវបានអនុវត្តតាមលំដាប់បញ្ច្រាស។
ឧទាហរណ៍។
គ្រោងមុខងារមួយ។![]()
ការសាងសង់នឹងត្រូវបានអនុវត្តតាមជំហានដូចខាងក្រោមៈ
1. គ្រោងលោការីតធម្មជាតិ:
2. ច្របាច់ទៅអ័ក្សអូយ2 ដង:;
3.
បង្ហាញស៊ីមេទ្រីអំពីអ័ក្សអូយ:
;
4. ផ្លាស់ទីតាមអ័ក្សOXនៅលើ(!!!) ទៅខាងស្តាំ៖![]() :
:

5. បង្ហាញស៊ីមេទ្រីអំពីអ័ក្សOX:
;
6. ផ្លាស់ទីតាមអ័ក្សអូយ3 គ្រឿងឡើង៖![]() :
:

ឧទាហរណ៍នៃការសាងសង់ និងការបំប្លែងក្រាហ្វិកមុខងារ
ឧទាហរណ៍ ១ គ្រោងមុខងារមួយ។.
ដំបូងគូរក្រាហ្វស៊ីនុស រយៈពេលរបស់វាគឺស្មើនឹង:

ក្រាហ្វមុខងារទទួលបានដោយការបង្ហាប់ក្រាហ្វពីរដងទៅអ័ក្ស y ។កំណត់ហេតុ .
គ្រោងមុខងារមួយ។នៅ = 2 cosX.
គ្រោងមុខងារមួយ។y = អំពើបាបx .
សេចក្តីសន្និដ្ឋាន
ក្នុងអំឡុងពេលនៃការងារលើការងារគម្រោង អក្សរសិល្ប៍អប់រំ និងវិធីសាស្រ្តផ្សេងៗលើបញ្ហានេះត្រូវបានវិភាគ។ លទ្ធផលនៃការសិក្សាបានធ្វើឱ្យវាអាចកំណត់អត្តសញ្ញាណលក្ខណៈវិជ្ជមានបំផុតនៃការសិក្សាការសាងសង់ និងការបំប្លែងក្រាហ្វនៃអនុគមន៍នៅក្នុងវគ្គសិក្សាគណិតវិទ្យារបស់សាលា
គោលដៅចម្បងនៃគម្រោងគឺដើម្បីអភិវឌ្ឍជំនាញ និងសមត្ថភាពរបស់សិស្សក្នុងការអាន និងគូរគំនូរ ដើម្បីបង្កើតវិធីសាស្រ្តសមហេតុផលនៃសកម្មភាពឯករាជ្យ។
តម្រូវការក្នុងការធ្វើឱ្យប្រសើរឡើងនូវការអប់រំក្រាហ្វិកទាំងមូលត្រូវបានកំណត់មិនត្រឹមតែដោយតម្រូវការផលិតកម្មទំនើបប៉ុណ្ណោះទេ ប៉ុន្តែថែមទាំងដោយតួនាទីនៃក្រាហ្វិកក្នុងការអភិវឌ្ឍន៍ការគិតបច្ចេកទេស និងសមត្ថភាពយល់ដឹងរបស់សិស្សផងដែរ។ សមត្ថភាពរបស់មនុស្សម្នាក់ក្នុងដំណើរការព័ត៌មានក្រាហ្វិកគឺជាសូចនាករមួយនៃការអភិវឌ្ឍន៍ផ្លូវចិត្តរបស់គាត់។ ដូច្នេះ ការបណ្តុះបណ្តាលក្រាហ្វិកគួរតែក្លាយជាធាតុសំខាន់នៃការបណ្តុះបណ្តាលអប់រំទូទៅ។
ការរកឃើញ
ដូច្នេះ គម្រោងដែលបានបង្កើត "ការសាងសង់ និងការផ្លាស់ប្តូរក្រាហ្វមុខងារ" ដែលឧទ្ទិសដល់គោលគំនិតកណ្តាលនៃគណិតវិទ្យា - ការពឹងផ្អែកមុខងារ គឺផ្តោតលើការរៀបចំប្រព័ន្ធ និងការពង្រីកចំណេះដឹងរបស់សិស្ស។ ការសិក្សាអំពីវិធីសាស្រ្តជាក់លាក់សម្រាប់បំប្លែងក្រាហ្វមុខងារត្រូវបានអនុវត្តតាមវិធីវិភាគ និងក្រាហ្វិកតាមគ្រោងការណ៍វិធីសាស្រ្តដ៏តឹងរឹង។ សម្ភារៈដែលប្រមូលបានអាចប្រើប្រាស់ក្នុងថ្នាក់រៀន និងសម្រាប់ការបណ្តុះបណ្តាលសិស្សដោយខ្លួនឯង។ ទម្រង់ និងវិធីសាស្រ្តផ្សេងៗនៃការរៀបចំ និងការបណ្តុះបណ្តាលអាចត្រូវបានប្រើដើម្បីដឹកនាំថ្នាក់។
