អាំងតេក្រាលជាក់លាក់នៅលើអ៊ីនធឺណិតទៅកាន់គេហទំព័រ ដើម្បីបង្រួបបង្រួមសម្ភារៈដែលគ្របដណ្តប់ដោយសិស្ស និងសិស្សសាលា។ ហើយអនុវត្តជំនាញជាក់ស្តែងរបស់អ្នក។ ដំណោះស្រាយ​ពេញលេញ​នៃ​អាំងតេក្រាល​ជាក់លាក់​លើ​អ៊ីនធឺណិត​សម្រាប់​អ្នក​ក្នុង​ពេល​មួយ​នឹង​ជួយ​អ្នក​កំណត់​ដំណាក់កាល​ទាំងអស់​នៃ​ដំណើរការ។ អាំងតេក្រាលតាមអ៊ីនធឺណិតជាក់លាក់នៅលើគេហទំព័រសម្រាប់ការបង្រួបបង្រួមពេញលេញនៃសម្ភារៈដែលគ្របដណ្តប់ដោយសិស្ស និងសិស្សសាលា និងការបណ្តុះបណ្តាលជំនាញជាក់ស្តែងរបស់ពួកគេ។ ដំណោះស្រាយ​ពេញលេញ​នៃ​អាំងតេក្រាល​ជាក់លាក់​លើ​អ៊ីនធឺណិត​សម្រាប់​អ្នក​ក្នុង​ពេល​មួយ​នឹង​ជួយ​អ្នក​កំណត់​ដំណាក់កាល​ទាំងអស់​នៃ​ដំណើរការ។ សម្រាប់ពួកយើង ការទទួលយកអាំងតេក្រាលច្បាស់លាស់តាមអ៊ីនធឺណិត ហាក់ដូចជាមិនមែនជារឿងធម្មជាតិទេ ដោយបានសិក្សាប្រធានបទនេះពីសៀវភៅដោយអ្នកនិពន្ធល្បីៗ។ អរគុណច្រើនចំពោះពួកគេ ហើយយើងបង្ហាញពីការគោរពចំពោះបុគ្គលទាំងនេះ។ វានឹងជួយកំណត់ជាក់លាក់នៃសេវាកម្មអនឡាញអាំងតេក្រាលសម្រាប់ការគណនាបញ្ហាបែបនេះនៅក្នុង jiffy មួយ។ គ្រាន់តែបញ្ចូលទិន្នន័យត្រឹមត្រូវ នោះអ្វីៗនឹងល្អ! អាំងតេក្រាលច្បាស់លាស់ណាមួយជាដំណោះស្រាយចំពោះបញ្ហានឹងបង្កើនអក្ខរកម្មរបស់សិស្ស។ នេះ​ជា​សុបិន​របស់​មនុស្ស​ស្លូត​បូត​គ្រប់​រូប ហើយ​យើង​ក៏​មិន​លើកលែង​ដែរ យើង​សារភាព​ដោយ​ស្មោះត្រង់។ ប្រសិនបើអ្នកនៅតែគ្រប់គ្រងដើម្បីគណនាអាំងតេក្រាលច្បាស់លាស់តាមអ៊ីនធឺណិតជាមួយនឹងដំណោះស្រាយដោយឥតគិតថ្លៃនោះ សូមសរសេរអាសយដ្ឋានគេហទំព័រទៅកាន់អ្នកគ្រប់គ្នាដែលចង់ប្រើវា។ ដូចដែលពួកគេនិយាយ ចែករំលែកតំណមានប្រយោជន៍ ហើយមនុស្សដែលមានចិត្តល្អនឹងអរគុណអ្នកសម្រាប់អំណោយ។ វានឹងគួរឱ្យចាប់អារម្មណ៍ខ្លាំងណាស់ក្នុងការវិភាគបញ្ហាដែលអាំងតេក្រាលច្បាស់លាស់នឹងត្រូវបានដោះស្រាយដោយម៉ាស៊ីនគិតលេខដោយខ្លួនឯង និងមិនខ្ជះខ្ជាយពេលវេលាដ៏មានតម្លៃរបស់អ្នកឡើយ។ ហេតុ​នេះ​ហើយ​បាន​ជា​ពួក​គេ​ជា​ម៉ាស៊ីន​ភ្ជួរ​រាស់​មនុស្ស។ ទោះជាយ៉ាងណាក៏ដោយ ដំណោះស្រាយនៃអាំងតេក្រាលជាក់លាក់លើអ៊ីនធឺណិតគឺមិនមែនសម្រាប់គ្រប់គេហទំព័រនោះទេ ហើយនេះជាការងាយស្រួលក្នុងការត្រួតពិនិត្យ ពោលគឺវាគ្រប់គ្រាន់ដើម្បីយកឧទាហរណ៍ដ៏ស្មុគស្មាញមួយ ហើយព្យាយាមដោះស្រាយវាដោយប្រើសេវាកម្មនីមួយៗ។ អ្នកនឹងមានអារម្មណ៍ថាមានភាពខុសគ្នានៃស្បែករបស់អ្នក។ ជាញឹកញាប់ ការស្វែងរកអាំងតេក្រាលជាក់លាក់មួយតាមអ៊ីនធឺណិតដោយគ្មានការប្រឹងប្រែងណាមួយនឹងក្លាយទៅជាការលំបាក ហើយចម្លើយរបស់អ្នកនឹងមើលទៅគួរឱ្យអស់សំណើចប្រឆាំងនឹងផ្ទៃខាងក្រោយនៃរូបភាពទាំងមូលនៃលទ្ធផល។ យក​វគ្គ​អ្នក​ប្រដាល់​វ័យ​ក្មេង​ជា​ការ​ប្រសើរ​ជា​មុន​សិន។ ដំណោះស្រាយនៃអាំងតេក្រាលមិនត្រឹមត្រូវតាមអ៊ិនធរណេត កាត់បន្ថយជាដំបូងចំពោះការគណនាអកំណត់ ហើយបន្ទាប់មកតាមទ្រឹស្តីនៃដែនកំណត់ ដើម្បីគណនាជាក្បួន ដែនកំណត់ម្ខាងពីកន្សោមដែលទទួលបានជាមួយព្រំដែនជំនួស A និង B ។ ដោយបានពិចារណា អាំងតេក្រាលច្បាស់លាស់តាមអ៊ីនធឺណិតជាមួយនឹងដំណោះស្រាយលម្អិតដែលអ្នកបានបង្ហាញ យើងបានសន្និដ្ឋានថាអ្នកបានធ្វើខុសនៅជំហានទីប្រាំ ពោលគឺនៅពេលប្រើរូបមន្តផ្លាស់ប្តូរអថេរ Chebyshev ។ សូមប្រយ័ត្នក្នុងការសម្រេចចិត្តបន្ទាប់របស់អ្នក។ ប្រសិនបើម៉ាស៊ីនគិតលេខអនឡាញរបស់អ្នកមិនអាចយកអាំងតេក្រាលច្បាស់លាស់របស់អ្នកជាលើកដំបូងបានទេ នោះជាដំបូងវាមានតម្លៃពិនិត្យមើលទិន្នន័យដែលបានសរសេរជាពីរដងក្នុងទម្រង់សមស្របនៅលើគេហទំព័រ។ ត្រូវប្រាកដថាអ្វីៗស្ថិតក្នុងលំដាប់ហើយទៅ Go-Go! សម្រាប់សិស្សម្នាក់ៗ ឧបសគ្គគឺការគណនានៃអាំងតេក្រាលមិនត្រឹមត្រូវតាមអ៊ីនធឺណិតជាមួយគ្រូផ្ទាល់ ព្រោះនេះគឺជាការប្រឡង ឬជាពាក្យបញ្ជា ឬគ្រាន់តែជាការសាកល្បងលើគូ។ ដរាបណាការគណនាអាំងតេក្រាលតាមអ៊ីនធឺណិតដែលមិនសមស្របត្រូវបានផ្តល់ឱ្យអ្នក បន្ទាប់មកបើកបរភ្លាមៗនៅក្នុងមុខងារដែលបានផ្តល់ឱ្យ ជំនួសដែនកំណត់នៃការរួមបញ្ចូលដែលបានផ្តល់ឱ្យ ហើយចុចលើប៊ូតុង ដោះស្រាយ បន្ទាប់មកចម្លើយលម្អិតពេញលេញនឹងមានសម្រាប់អ្នក។ ហើយនៅតែជាការល្អនៅពេលដែលមានគេហទំព័រដ៏អស្ចារ្យបែបនេះជាគេហទំព័រមួយ ព្រោះវាទាំងឥតគិតថ្លៃ និងងាយស្រួលប្រើ វាក៏មានផ្នែកជាច្រើនផងដែរ។ ដែលសិស្សប្រើជារៀងរាល់ថ្ងៃ មួយក្នុងចំណោមពួកគេគឺគ្រាន់តែជាអាំងតេក្រាលច្បាស់លាស់លើអ៊ីនធឺណិតជាមួយនឹងដំណោះស្រាយពេញលេញ។ នៅក្នុងផ្នែកដូចគ្នា អ្នកអាចគណនាអាំងតេក្រាលមិនត្រឹមត្រូវតាមអ៊ីនធឺណិត ជាមួយនឹងដំណោះស្រាយលម្អិតសម្រាប់កម្មវិធីបន្ថែមនៃចម្លើយទាំងនៅវិទ្យាស្ថាន និងក្នុងការងារវិស្វកម្ម។ វាហាក់ដូចជាថាវាមិនពិបាកសម្រាប់មនុស្សគ្រប់គ្នាក្នុងការកំណត់អាំងតេក្រាលច្បាស់លាស់លើអ៊ីនធឺណិត ប្រសិនបើឧទាហរណ៍បែបនេះត្រូវបានដោះស្រាយជាមុនដោយគ្មានព្រំដែនខាងលើ និងខាងក្រោម នោះមិនមែនជាអាំងតេក្រាល Leibniz ប៉ុន្តែអាំងតេក្រាលមិនកំណត់។ ប៉ុន្តែនៅទីនេះ ពួកយើងមិនយល់ស្របជាមួយអ្នកជាដាច់ខាត ព្រោះនៅក្រឡេកមើលដំបូង វាអាចហាក់ដូចជាបែបនោះ ប៉ុន្តែមានភាពខុសប្លែកគ្នាយ៉ាងសំខាន់ ចូរយើងបែងចែកអ្វីៗគ្រប់យ៉ាងដោយឡែកពីគ្នា។ ដំណោះស្រាយផ្តល់នូវអាំងតេក្រាលច្បាស់លាស់បែបនេះ មិនមែនក្នុងទម្រង់ច្បាស់លាស់ទេ ប៉ុន្តែជាលទ្ធផលនៃការផ្លាស់ប្តូរកន្សោមទៅជាតម្លៃកំណត់។ ម្យ៉ាងវិញទៀត ទីមួយត្រូវតែដោះស្រាយអាំងតេក្រាលជាមួយនឹងការជំនួសតម្លៃនិមិត្តសញ្ញានៃព្រំដែន ហើយបន្ទាប់មកគណនាដែនកំណត់ទាំងនៅគ្មានកំណត់ ឬនៅចំណុចជាក់លាក់មួយ។ ពីទីនេះ ការគណនាអាំងតេក្រាលច្បាស់លាស់តាមអ៊ីនធឺណិតជាមួយនឹងដំណោះស្រាយដោយឥតគិតថ្លៃ មានន័យថាគ្មានអ្វីក្រៅពីការតំណាងឱ្យដំណោះស្រាយពិតប្រាកដដោយប្រើរូបមន្ត Newton-Leibniz នោះទេ។ ប្រសិនបើយើងពិចារណាអាំងតេក្រាលច្បាស់លាស់របស់យើង ម៉ាស៊ីនគិតលេខនឹងជួយអ្នកគណនាវាក្នុងរយៈពេលពីរបីវិនាទីមុនភ្នែករបស់អ្នក។ ការប្រញាប់ប្រញាល់បែបនេះគឺត្រូវការដោយអ្នកគ្រប់គ្នាដែលចង់ស៊ូទ្រាំនឹងកិច្ចការឱ្យបានលឿនតាមដែលអាចធ្វើទៅបាន ហើយត្រូវបានដោះលែងសម្រាប់កិច្ចការផ្ទាល់ខ្លួន។ អ្នកមិនគួរស្វែងរកគេហទំព័រនៅលើអ៊ីនធឺណិតដែលនឹងស្នើសុំឱ្យអ្នកចុះឈ្មោះ បន្ទាប់មកបញ្ចូលលុយទៅក្នុងសមតុល្យ ហើយទាំងអស់សម្រាប់ជាប្រយោជន៍សម្រាប់បុរសឆ្លាតវៃមួយចំនួនដែលរៀបចំដំណោះស្រាយនៃអាំងតេក្រាលមួយចំនួនដែលសន្មត់ថានៅលើអ៊ីនធឺណិត។ ចងចាំអាសយដ្ឋាន Math24 គឺជាសេវាកម្មឥតគិតថ្លៃសម្រាប់ដោះស្រាយបញ្ហាគណិតវិទ្យាជាច្រើន រួមទាំងយើងនឹងជួយអ្នកស្វែងរកអាំងតេក្រាលច្បាស់លាស់តាមអ៊ីនធឺណិត ហើយដើម្បីប្រាកដថាវា សូមពិនិត្យមើលសេចក្តីថ្លែងការណ៍របស់យើងជាមួយនឹងឧទាហរណ៍ជាក់លាក់។ បញ្ចូលអាំងតេក្រាលក្នុងវាលសមស្រប បន្ទាប់មកបញ្ជាក់តម្លៃដែនកំណត់គ្មានកំណត់ (ក្នុងករណីនេះ ដំណោះស្រាយនៃអាំងតេក្រាលមិនត្រឹមត្រូវនឹងត្រូវបានគណនា និងទទួលបានតាមអ៊ីនធឺណិត) ឬកំណត់ព្រំដែនជាលេខ ឬនិមិត្តសញ្ញារបស់អ្នក និងអាំងតេក្រាលលើអ៊ីនធឺណិតច្បាស់លាស់ជាមួយនឹងដំណោះស្រាយលម្អិត។ នឹងត្រូវបានបង្ហាញនៅលើទំព័របន្ទាប់ពីចុចលើប៊ូតុង "ដំណោះស្រាយ" ។ តើវាមិនពិតទេ - វាគឺសាមញ្ញណាស់ មិនត្រូវការសកម្មភាពបន្ថែមណាមួយពីអ្នក ដោយមិនគិតថ្លៃ ដែលជារឿងសំខាន់បំផុត ហើយក្នុងពេលតែមួយមានប្រសិទ្ធភាព។ អ្នកអាចប្រើប្រាស់សេវាកម្មដោយខ្លួនឯង ដើម្បីឱ្យម៉ាស៊ីនគិតលេខតាមអ៊ីនធឺណិតជាក់លាក់នឹងនាំមកជូនអ្នកនូវអត្ថប្រយោជន៍ជាអតិបរមា ហើយអ្នកនឹងទទួលបានស្ថានភាពសុខស្រួលដោយមិនមានភាពតានតឹងលើភាពស្មុគស្មាញនៃដំណើរការកុំព្យូទ័រទាំងអស់ អនុញ្ញាតឱ្យពួកយើងធ្វើអ្វីគ្រប់យ៉ាងសម្រាប់អ្នក និងបង្ហាញពីថាមពលពេញលេញនៃបច្ចេកវិទ្យាកុំព្យូទ័រ។ នៅក្នុងពិភពទំនើប។ ប្រសិនបើអ្នកចូលទៅក្នុងព្រៃនៃរូបមន្តដ៏ស្មុគស្មាញបំផុត ហើយសិក្សាពីការគណនាអាំងតេក្រាលមិនត្រឹមត្រូវតាមអ៊ីនធឺណិតដោយខ្លួនឯង នោះជាការសរសើរ ហើយអ្នកអាចទាមទារឱកាសដើម្បីសរសេរនិក្ខេបបទថ្នាក់បណ្ឌិត ប៉ុន្តែសូមត្រលប់ទៅការពិតនៃជីវិតសិស្សវិញ។ . ហើយអ្នកណាជាសិស្ស? ទី​១​នេះ​ជា​យុវជន​ស្វាហាប់​និង​រីករាយ​ដែល​ចង់​មាន​ពេល​សម្រាក​និង​ធ្វើ​កិច្ចការ​ផ្ទះ! ហេតុដូច្នេះហើយ យើងបានយកចិត្តទុកដាក់ចំពោះសិស្សានុសិស្សដែលកំពុងព្យាយាមស្វែងរកម៉ាស៊ីនគិតលេខតាមអ៊ីនធឺណិតដែលមិនត្រឹមត្រូវនៅក្នុងបណ្តាញសកលលោក ហើយនៅទីនេះវាគឺសម្រាប់ការយកចិត្តទុកដាក់របស់អ្នក - គេហទំព័រនេះគឺជាកម្មវិធីដោះស្រាយបញ្ហាអនឡាញដែលមានប្រយោជន៍បំផុតសម្រាប់មនុស្សវ័យក្មេង។ ដោយវិធីនេះ បើទោះបីជាសេវាកម្មរបស់យើងត្រូវបានបង្ហាញជាជំនួយការដល់សិស្សានុសិស្ស និងសិស្សសាលាក៏ដោយ វាគឺសមរម្យពេញលេញសម្រាប់វិស្វករណាមួយ ព្រោះយើងអាចធ្វើកិច្ចការគ្រប់ប្រភេទ ហើយដំណោះស្រាយរបស់ពួកគេត្រូវបានបង្ហាញជាទម្រង់វិជ្ជាជីវៈ។ ឧទាហរណ៍ យើងផ្តល់ជូននូវអាំងតេក្រាលច្បាស់លាស់លើអ៊ីនធឺណិតជាមួយនឹងដំណោះស្រាយក្នុងទម្រង់ពេញលេញជាដំណាក់កាល ពោលគឺប្លុកឡូជីខលនីមួយៗ (កិច្ចការរង) ត្រូវបានផ្តល់កំណត់ត្រាដាច់ដោយឡែកជាមួយនឹងការគណនាទាំងអស់នៅក្នុងដំណើរការនៃដំណើរការដំណោះស្រាយទូទៅ។ នេះជាការពិតណាស់ សម្រួលដល់ការយល់ឃើញនៃប្លង់បន្តបន្ទាប់គ្នាច្រើនដំណាក់កាល ហើយដូច្នេះគឺជាអត្ថប្រយោជន៍នៃគម្រោងគេហទំព័រលើសេវាកម្មស្រដៀងគ្នាសម្រាប់ការស្វែងរកអាំងតេក្រាលមិនត្រឹមត្រូវតាមអ៊ីនធឺណិតជាមួយនឹងដំណោះស្រាយលម្អិត។

តើអ្នកនៅទីនេះទេ? =) ទេ ខ្ញុំមិនបានព្យាយាមបំភិតបំភ័យនរណាម្នាក់ទេ វាគ្រាន់តែថាប្រធានបទនៃអាំងតេក្រាលមិនត្រឹមត្រូវ គឺជាឧទាហរណ៍ដ៏ល្អមួយអំពីសារៈសំខាន់ដែលវាមិនដំណើរការគណិតវិទ្យាខ្ពស់ជាង និងវិទ្យាសាស្ត្រពិតប្រាកដផ្សេងទៀត។ ដើម្បីធ្វើជាម្ចាស់មេរៀននៅលើគេហទំព័រ អ្វីគ្រប់យ៉ាងគឺនៅទីនោះ - ក្នុងទម្រង់លម្អិត និងអាចចូលដំណើរការបាន នោះនឹងមានបំណងប្រាថ្នាមួយ ...។

ដូច្នេះសូមចាប់ផ្តើម។ និយាយក្នុងន័យធៀប អាំងតេក្រាលមិនត្រឹមត្រូវគឺជាអាំងតេក្រាលកំណត់ "កម្រិតខ្ពស់" ហើយតាមពិតមិនមានការលំបាកច្រើនជាមួយពួកគេ លើសពីនេះ អាំងតេក្រាលមិនត្រឹមត្រូវមានអត្ថន័យធរណីមាត្រល្អណាស់។

តើការគណនាអាំងតេក្រាលមិនត្រឹមត្រូវមានន័យដូចម្តេច?

គណនាអាំងតេក្រាលមិនត្រឹមត្រូវ - វាមានន័យថាស្វែងរកលេខ NUMBER(ដូចគ្នាទៅនឹងអាំងតេក្រាលច្បាស់លាស់), ឬបង្ហាញថាវាខុសគ្នា(នោះគឺបញ្ចប់ដោយភាពគ្មានទីបញ្ចប់ជំនួសឱ្យលេខ) ។

អាំងតេក្រាលមិនត្រឹមត្រូវមានពីរប្រភេទ។

អាំងតេក្រាលមិនត្រឹមត្រូវជាមួយនឹងដែនកំណត់គ្មានកំណត់នៃការរួមបញ្ចូល

ជួនកាលអាំងតេក្រាលមិនសមរម្យបែបនេះត្រូវបានគេហៅថា អាំងតេក្រាលមិនត្រឹមត្រូវនៃប្រភេទទីមួយ. ជាទូទៅ អាំងតេក្រាលមិនត្រឹមត្រូវដែលមានដែនកំណត់គ្មានកំណត់ ភាគច្រើនមើលទៅដូចនេះ៖ . តើវាខុសពីអាំងតេក្រាលច្បាស់លាស់យ៉ាងដូចម្តេច? នៅក្នុងដែនកំណត់ខាងលើ។ វាគ្មានទីបញ្ចប់៖

ភាគតិចគឺអាំងតេក្រាលដែលមានដែនកំណត់ទាបគ្មានកំណត់ ឬមានដែនកំណត់គ្មានដែនកំណត់ពីរ៖ ហើយយើងនឹងពិចារណាពួកវានៅពេលក្រោយ - នៅពេលអ្នកទទួលបានរសជាតិ :)

មែនហើយឥឡូវនេះសូមវិភាគករណីពេញនិយមបំផុត។ នៅក្នុងឧទាហរណ៍ភាគច្រើន មុខងារអាំងតេក្រាល។ បន្តនៅចន្លោះនិងមួយនេះ ការពិតសំខាន់ត្រូវពិនិត្យជាមុន!សម្រាប់​ប្រសិនបើ​មាន​ចន្លោះ​ប្រហោង នោះ​មាន nuances បន្ថែម។ សម្រាប់ភាពច្បាស់លាស់ យើងសន្មត់ថាសូម្បីតែធម្មតាក៏ដោយ។ រាងចតុកោណកែងនឹងមើលទៅដូចនេះ៖

ចំណាំថាវាគ្មានកំណត់ (មិនកំណត់នៅខាងស្តាំ) និង អាំងតេក្រាលមិនត្រឹមត្រូវជាលេខស្មើនឹងតំបន់របស់វា។. ក្នុងករណីនេះ ជម្រើសខាងក្រោមអាចធ្វើទៅបាន៖

១) គំនិតដំបូងដែលគិតក្នុងចិត្តគឺ៖ “ចាប់តាំងពីតួលេខគឺគ្មានកំណត់ ដូច្នេះ ” និយាយម្យ៉ាងទៀត តំបន់នេះក៏គ្មានដែនកំណត់ដែរ។ ដូច្នេះវាប្រហែលជា។ក្នុងករណីនេះយើងនិយាយថាអាំងតេក្រាលមិនត្រឹមត្រូវ ខុសគ្នា.

2) ប៉ុន្តែ. ដូច​ជា paradoxical ដូច​ដែល​វា​អាច​នឹង​ស្តាប់​ទៅ​តំបន់​នៃ​តួ​លេខ​ដែល​គ្មាន​ដែន​កំណត់​អាច​ស្មើ​នឹង ... ចំនួន​កំណត់! ឧទាហរណ៍: ។ តើវាអាចទេ? ងាយស្រួល។ ក្នុងករណីទី 2 អាំងតេក្រាលមិនត្រឹមត្រូវ បញ្ចូលគ្នា.

3) អំពីជម្រើសទីបីបន្តិចក្រោយមក។

តើនៅពេលណាដែលអាំងតេក្រាលមិនសមគួរបែងចែក ហើយតើវាបញ្ចូលគ្នានៅពេលណា? នេះអាស្រ័យលើអាំងតេក្រាល ហើយយើងនឹងពិនិត្យមើលឧទាហរណ៍ជាក់ស្តែងក្នុងពេលឆាប់ៗនេះ។

ប៉ុន្តែតើមានអ្វីកើតឡើងប្រសិនបើ trapezoid curvilinear គ្មានដែនកំណត់មានទីតាំងនៅខាងក្រោមអ័ក្ស? ក្នុងករណីនេះអាំងតេក្រាលមិនត្រឹមត្រូវ (diverges) ឬស្មើនឹងចំនួនអវិជ្ជមានកំណត់។

ដោយវិធីនេះ អាំងតេក្រាលមិនត្រឹមត្រូវអាចជាអវិជ្ជមាន.

សំខាន់!នៅពេលដែលអាំងតេក្រាលមិនត្រឹមត្រូវណាមួយត្រូវបានផ្តល់ជូនអ្នកដើម្បីដោះស្រាយ បន្ទាប់មកនិយាយជាទូទៅ មិនមានការនិយាយអំពីតំបន់ណាមួយទេហើយមិនចាំបាច់សាងសង់គំនូរទេ។. ខ្ញុំបានប្រាប់អត្ថន័យធរណីមាត្រនៃអាំងតេក្រាលមិនសមរម្យតែប៉ុណ្ណោះដើម្បីធ្វើឱ្យវាកាន់តែងាយស្រួលក្នុងការយល់អំពីសម្ភារៈ។

ដោយសារ​អាំងតេក្រាល​មិន​ត្រឹមត្រូវ​គឺ​ស្រដៀង​គ្នា​នឹង​អាំងតេក្រាល​ច្បាស់លាស់ ដូច្នេះ​យើង​នឹកឃើញ​រូបមន្ត​ញូតុន-លីបនីស៖ . តាមការពិត រូបមន្តក៏អាចអនុវត្តបានចំពោះអាំងតេក្រាលមិនត្រឹមត្រូវដែរ មានតែវាត្រូវកែប្រែបន្តិចប៉ុណ្ណោះ។ អ្វី​ដែល​ជា​ភាព​ខុសគ្នា? នៅក្នុងដែនកំណត់ខាងលើគ្មានដែនកំណត់នៃការរួមបញ្ចូល: . ប្រហែលជា មនុស្សជាច្រើនបានទាយថា ការអនុវត្តទ្រឹស្តីដែនកំណត់រួចហើយ រូបមន្តនឹងត្រូវបានសរសេរដូចខាងក្រោម៖ .

តើវាខុសពីអាំងតេក្រាលច្បាស់លាស់យ៉ាងដូចម្តេច? បាទ គ្មានអ្វីពិសេសទេ! ដូចនៅក្នុងអាំងតេក្រាលច្បាស់លាស់ អ្នកត្រូវតែអាចស្វែងរកអនុគមន៍ប្រឆាំងដេរីវេ (អាំងតេក្រាលមិនកំណត់) អាចអនុវត្តរូបមន្តញូតុន-លីបនីស។ រឿងតែមួយគត់ដែលត្រូវបានបន្ថែមគឺការគណនាដែនកំណត់។ អ្នកណាអាក្រក់ជាមួយគេ រៀនមេរៀន ដែនកំណត់នៃមុខងារ។ ឧទាហរណ៍នៃដំណោះស្រាយព្រោះយឺតជាងក្នុងជួរកងទ័ព។

ពិចារណាឧទាហរណ៍បុរាណពីរ៖

ឧទាហរណ៍ ១

ដើម្បីភាពច្បាស់លាស់ ខ្ញុំនឹងបង្កើតគំនូរមួយ ទោះបីជាខ្ញុំបញ្ជាក់ម្តងទៀតក៏ដោយ នៅលើការអនុវត្ត វាមិនចាំបាច់ក្នុងការបង្កើតគំនូរនៅក្នុងកិច្ចការនេះទេ។.

អាំងតេក្រាលគឺបន្តនៅពាក់កណ្តាលចន្លោះ ដែលមានន័យថាអ្វីគ្រប់យ៉ាងគឺល្អ ហើយអាំងតេក្រាលមិនត្រឹមត្រូវអាចត្រូវបានគណនាដោយប្រើវិធីសាស្ត្រ "ទៀងទាត់" ។

ការអនុវត្តរូបមន្តរបស់យើង។ ហើយដំណោះស្រាយមើលទៅដូចនេះ៖

នោះគឺការបង្វែរអាំងតេក្រាលមិនត្រឹមត្រូវ ហើយផ្ទៃនៃរាងចតុកោណកែងដែលមានស្រមោលគឺស្មើនឹងភាពគ្មានកំណត់។

នៅក្នុងឧទាហរណ៍ដែលបានពិចារណា យើងមានអាំងតេក្រាលតារាងសាមញ្ញបំផុត និងបច្ចេកទេសដូចគ្នាសម្រាប់ការអនុវត្តរូបមន្ត Newton-Leibniz ដូចនៅក្នុងអាំងតេក្រាលច្បាស់លាស់។ ប៉ុន្តែរូបមន្តនេះត្រូវបានអនុវត្តនៅក្រោមសញ្ញានៃដែនកំណត់។ ជំនួសឱ្យអក្សរធម្មតានៃអថេរ "ថាមវន្ត" អក្សរ "be" លេចឡើង។ នេះ​មិន​គួរ​ច្រឡំ ឬ​ច្រឡំ​ទេ ព្រោះ​អក្សរ​ណា​ក៏​មិន​អន់​ជាង​អក្សរ “X” ដែរ។

ប្រសិនបើអ្នកមិនយល់ថាហេតុអ្វីនៅពេលណា នោះវាអាក្រក់ណាស់ ទាំងអ្នកមិនយល់ពីដែនកំណត់សាមញ្ញបំផុត (ហើយមិនយល់ថាដែនកំណត់គឺជាអ្វី) ឬអ្នកមិនដឹងថាក្រាហ្វនៃលោការីត មុខងារមើលទៅដូច។ ក្នុងករណីទីពីរ សូមចូលមើលមេរៀន ក្រាហ្វនិងលក្ខណៈសម្បត្តិនៃអនុគមន៍បឋម.

នៅពេលដោះស្រាយអាំងតេក្រាលមិនត្រឹមត្រូវ វាមានសារៈសំខាន់ខ្លាំងណាស់ក្នុងការដឹងពីរបៀបដែលក្រាហ្វនៃមុខងារបឋមសំខាន់ៗមើលទៅដូច!

ការរចនាការងារស្អាតគួរមើលទៅដូចនេះ៖

“

! នៅពេលរចនាឧទាហរណ៍ យើងតែងតែរំខានដំណោះស្រាយ និងបង្ហាញពីអ្វីដែលកើតឡើងចំពោះអាំងតេក្រាល។ – តើវាបន្តនៅលើចន្លោះពេលនៃការរួមបញ្ចូលឬអត់. តាមរយៈនេះ យើងកំណត់ប្រភេទនៃអាំងតេក្រាលមិនត្រឹមត្រូវ និងសកម្មភាពបន្ថែមទៀត។

ឧទាហរណ៍ ២

គណនាអាំងតេក្រាលមិនត្រឹមត្រូវ ឬបង្កើតភាពខុសគ្នារបស់វា។

តោះធ្វើគំនូរ៖

ដំបូង​យើង​សម្គាល់​ឃើញ​ដូច​ខាង​ក្រោម៖ អាំងតេក្រាល​គឺ​បន្ត​នៅ​ចន្លោះ​ពាក់កណ្តាល។ ល្អ ដោះស្រាយជាមួយរូបមន្ត :

(1) យើងយកអាំងតេក្រាលសាមញ្ញបំផុតនៃមុខងារថាមពល (ករណីពិសេសនេះមាននៅក្នុងតារាងជាច្រើន)។ វាជាការប្រសើរក្នុងការរំកិលដកភ្លាមៗឱ្យលើសពីសញ្ញាកំណត់ ដើម្បីកុំឱ្យវាស្ថិតនៅក្រោមបាតជើងក្នុងការគណនាបន្ថែមទៀត។

(2) យើងជំនួសដែនកំណត់ខាងលើ និងខាងក្រោមដោយយោងតាមរូបមន្ត Newton-Leibniz ។

(3) យើងបង្ហាញថានៅពេលដែល (សុភាពបុរស, នេះត្រូវបានយល់ជាយូរមកហើយ) និងសាមញ្ញចម្លើយ។

ត្រង់នេះ ផ្ទៃនៃរាងចតុកោណកែងគ្មានកំណត់ ស្មើនឹងចំនួនកំណត់! មិនគួរឱ្យជឿប៉ុន្តែវាជាការពិត។

ការរចនាស្អាតនៃឧទាហរណ៍គួរតែមើលទៅដូចនេះ៖

“

អាំងតេក្រាលកំពុងបន្ត

“

អ្វីដែលត្រូវធ្វើប្រសិនបើអ្នកឆ្លងកាត់អាំងតេក្រាលដូចជា - ជាមួយ ចំណុចបំបែកនៅលើចន្លោះពេលនៃការរួមបញ្ចូល? នេះមានន័យថាមានការវាយខុសនៅក្នុងឧទាហរណ៍ (ភាគ​ច្រើន​ទំនង)ឬកម្រិតអប់រំកម្រិតខ្ពស់។ ក្នុងករណីចុងក្រោយដោយសារតែ លក្ខណៈសម្បត្តិបន្ថែមមួយគួរតែពិចារណាអាំងតេក្រាលមិនត្រឹមត្រូវចំនួនពីរនៅលើចន្លោះពេល ហើយបន្ទាប់មកដោះស្រាយជាមួយផលបូក។

ពេលខ្លះ ដោយសារការវាយអក្សរ ឬចេតនានៃអាំងតេក្រាលមិនត្រឹមត្រូវ វាអាចទៅរួច មិនមានទាល់តែសោះដូច្នេះ ជាឧទាហរណ៍ ប្រសិនបើឫសការ៉េនៃ "x" ត្រូវបានដាក់ក្នុងភាគបែងនៃអាំងតេក្រាលខាងលើ នោះផ្នែកនៃចន្លោះពេលសមាហរណកម្មនឹងមិនចូលទៅក្នុងដែននៃនិយមន័យនៃអាំងតេក្រាលនោះទេ។

ជាងនេះទៅទៀត អាំងតេក្រាលមិនត្រឹមត្រូវអាចមិនមានសូម្បីតែ "សុខុមាលភាពជាក់ស្តែង" ទាំងអស់។ ឧទាហរណ៍បុរាណ៖ ទោះបីជាមានភាពច្បាស់លាស់ និងបន្តនៃកូស៊ីនុសក៏ដោយ ក៏អាំងតេក្រាលមិនត្រឹមត្រូវបែបនេះមិនមានទេ! ហេតុអ្វី? វាសាមញ្ញណាស់ព្រោះ៖
- មិន​មាន ដែនកំណត់ដែលត្រូវគ្នា។.

ហើយ​ឧទាហរណ៍​បែប​នេះ ទោះ​បី​ជា​កម្រ​មាន​ក្នុង​ការ​អនុវត្ត! ដូច្នេះ បន្ថែមពីលើការបញ្ចូលគ្នា និងការបង្វែរ ក៏មានលទ្ធផលទីបីនៃដំណោះស្រាយជាមួយនឹងចម្លើយពេញលេញផងដែរ៖ "មិនមានអាំងតេក្រាលមិនត្រឹមត្រូវទេ"។

គួរកត់សំគាល់ផងដែរថា និយមន័យយ៉ាងម៉ឺងម៉ាត់នៃអាំងតេក្រាលមិនសមរម្យត្រូវបានផ្តល់ឱ្យយ៉ាងជាក់លាក់តាមរយៈដែនកំណត់ ហើយអ្នកដែលប្រាថ្នាអាចស្គាល់វានៅក្នុងអក្សរសិល្ប៍អប់រំ។ ជាការប្រសើរណាស់ យើងបន្តមេរៀនជាក់ស្តែង ហើយបន្តទៅកិច្ចការដែលមានអត្ថន័យបន្ថែមទៀត៖

ឧទាហរណ៍ ៣

គណនាអាំងតេក្រាលមិនត្រឹមត្រូវ ឬបង្កើតភាពខុសគ្នារបស់វា។

ជាដំបូង ចូរយើងព្យាយាមស្វែងរកមុខងារ antiderivative (អាំងតេក្រាលមិនកំណត់)។ ប្រសិនបើ​យើង​បរាជ័យ​ក្នុង​ការ​ធ្វើ​បែប​នេះ នោះ​តាម​ធម្មជាតិ យើង​នឹង​មិន​ដោះស្រាយ​អាំងតេក្រាល​ដែល​មិន​ត្រឹមត្រូវ​នោះ​ទេ។

តើអាំងតេក្រាលតារាងមួយណាមើលទៅដូច? វារំឭកខ្ញុំអំពីតង់សង់ធ្នូ៖ . ពីការពិចារណាទាំងនេះ គំនិតបង្ហាញខ្លួនឯងថា វាជាការល្អក្នុងការទទួលបានការ៉េនៅក្នុងភាគបែង។ នេះត្រូវបានធ្វើដោយការជំនួស។

តោះជំនួស៖

អាំងតេក្រាលមិនកំណត់ត្រូវបានរកឃើញ វាគ្មានន័យទេក្នុងការបន្ថែមចំនួនថេរក្នុងករណីនេះ។

នៅលើសេចក្តីព្រាង វាតែងតែមានប្រយោជន៍ក្នុងការអនុវត្តការត្រួតពិនិត្យ ពោលគឺដើម្បីបែងចែកលទ្ធផលខុសគ្នា៖

អាំងតេក្រាលដើមត្រូវបានទទួល ដែលមានន័យថា អាំងតេក្រាលមិនកំណត់ត្រូវបានរកឃើញត្រឹមត្រូវ។

ឥឡូវនេះយើងរកឃើញអាំងតេក្រាលមិនត្រឹមត្រូវ៖

(1) យើងសរសេរដំណោះស្រាយស្របតាមរូបមន្ត . វាជាការល្អប្រសើរជាងមុនដើម្បីផ្លាស់ទីថេរភ្លាមៗលើសពីសញ្ញាកំណត់ដើម្បីកុំឱ្យរំខានដល់ការគណនាបន្ថែមទៀត។

(2) យើងជំនួសដែនកំណត់ខាងលើ និងខាងក្រោមដោយអនុលោមតាមរូបមន្ត Newton-Leibniz ។ ហេតុអ្វី? នៅ? សូមមើលក្រាហ្វតង់សង់ធ្នូនៅក្នុងអត្ថបទដែលបានណែនាំម្តងហើយម្តងទៀត។

(3) យើងទទួលបានចម្លើយចុងក្រោយ។ ការពិតដែលថាវាមានប្រយោជន៍ក្នុងការដឹងដោយបេះដូង។

សិស្សកម្រិតខ្ពស់អាចមិនស្វែងរកអាំងតេក្រាលមិនកំណត់ដាច់ដោយឡែកពីគ្នា និងមិនប្រើវិធីជំនួស ប៉ុន្តែប្រើវិធីសាស្រ្តនៃការបូកសរុបអនុគមន៍នៅក្រោមសញ្ញាឌីផេរ៉ង់ស្យែល ហើយដោះស្រាយអាំងតេក្រាលមិនត្រឹមត្រូវ "ភ្លាមៗ"។ ក្នុងករណីនេះដំណោះស្រាយគួរតែមើលទៅដូចនេះ:

“

អាំងតេក្រាលកំពុងបន្ត។

“

ឧទាហរណ៍ 4

គណនាអាំងតេក្រាលមិនត្រឹមត្រូវ ឬបង្កើតភាពខុសគ្នារបស់វា។

! នេះគឺជាឧទាហរណ៍ធម្មតា ហើយអាំងតេក្រាលស្រដៀងគ្នាគឺជារឿងធម្មតាណាស់។ ធ្វើវាឱ្យបានល្អ! មុខងារ antiderivative ត្រូវបានរកឃើញនៅទីនេះដោយវិធីសាស្រ្តនៃការជ្រើសរើសការ៉េពេញលេញ ព័ត៌មានលម្អិតបន្ថែមអំពីវិធីសាស្រ្តអាចត្រូវបានរកឃើញនៅក្នុងមេរៀន ការរួមបញ្ចូលប្រភាគមួយចំនួន.

ឧទាហរណ៍ ៥

គណនាអាំងតេក្រាលមិនត្រឹមត្រូវ ឬបង្កើតភាពខុសគ្នារបស់វា។

អាំងតេក្រាលនេះអាចត្រូវបានដោះស្រាយយ៉ាងលម្អិត នោះគឺជាដំបូងស្វែងរកអាំងតេក្រាលមិនកំណត់ដោយការផ្លាស់ប្តូរអថេរ។ ហើយអ្នកអាចដោះស្រាយវាបាន "ភ្លាមៗ" - ដោយសង្ខេបមុខងារនៅក្រោមសញ្ញានៃឌីផេរ៉ង់ស្យែល។ អ្នកណាខ្លះមានប្រវត្តិគណិតវិទ្យា។

បំពេញដំណោះស្រាយ និងចម្លើយនៅចុងបញ្ចប់នៃមេរៀន។

ឧទាហរណ៍នៃដំណោះស្រាយនៃអាំងតេក្រាល។ វិធីសាស្រ្តដ៏មានប្រសិទ្ធភាពសម្រាប់ការដោះស្រាយអាំងតេក្រាលមិនត្រឹមត្រូវ. ករណីដែលដែនកំណត់នៃការរួមបញ្ចូលទាំងពីរគឺគ្មានដែនកំណត់ក៏ត្រូវបានពិចារណានៅទីនោះផងដែរ។

អាំងតេក្រាលមិនត្រឹមត្រូវនៃមុខងារគ្មានដែនកំណត់

ឬ អាំងតេក្រាលមិនត្រឹមត្រូវនៃប្រភេទទីពីរ. អាំងតេក្រាលមិនត្រឹមត្រូវនៃប្រភេទទីពីរត្រូវបាន "ciphered" យ៉ាងប៉ិនប្រសប់នៅក្រោមអាំងតេក្រាលច្បាស់លាស់ធម្មតា ហើយមើលទៅដូចគ្នាបេះបិទ៖ ប៉ុន្តែ មិនដូចអាំងតេក្រាលច្បាស់លាស់ទេ អាំងតេក្រាលទទួលរងនូវភាពមិនទៀងទាត់ (មិនមានទេ): 1) នៅចំណុច , 2) ឬ នៅចំណុច 3) ​​ឬនៅចំណុចទាំងពីរក្នុងពេលតែមួយ 4) ឬសូម្បីតែនៅចន្លោះពេលនៃការរួមបញ្ចូល។ យើងនឹងពិចារណាករណីពីរដំបូង សម្រាប់ករណីទី 3-4 នៅចុងបញ្ចប់នៃអត្ថបទ មានតំណភ្ជាប់ទៅកាន់មេរៀនបន្ថែម។

គ្រាន់​តែ​ជា​ឧទាហរណ៍​ដើម្បី​បញ្ជាក់​ឱ្យ​បាន​ច្បាស់​: ។ វាហាក់ដូចជាអាំងតេក្រាលច្បាស់លាស់។ ប៉ុន្តែតាមការពិត នេះគឺជាអាំងតេក្រាលដែលមិនសមស្របនៃប្រភេទទីពីរ ប្រសិនបើយើងជំនួសតម្លៃនៃដែនកំណត់ទាបទៅជាអាំងតេក្រាល នោះភាគបែងនឹងរលាយបាត់ ពោលគឺអាំងតេក្រាលមិនមាននៅត្រង់ចំណុចនេះទេ!

ជាទូទៅនៅពេលវិភាគអាំងតេក្រាលមិនត្រឹមត្រូវ វាតែងតែចាំបាច់ដើម្បីជំនួសដែនកំណត់នៃការរួមបញ្ចូលទាំងពីរទៅក្នុងអាំងតេក្រាល។. ក្នុងន័យនេះ យើងក៏ពិនិត្យមើលដែនកំណត់ខាងលើផងដែរ៖ . អ្វីគ្រប់យ៉ាងគឺល្អនៅទីនេះ។

curvilinear trapezoid សម្រាប់ភាពខុសគ្នាដែលបានពិចារណានៃអាំងតេក្រាលមិនសមរម្យជាមូលដ្ឋានមើលទៅដូចនេះ:

នៅទីនេះស្ទើរតែទាំងអស់គឺដូចគ្នាទៅនឹងអាំងតេក្រាលនៃប្រភេទទីមួយ។

អាំងតេក្រាលរបស់យើងជាលេខស្មើនឹងផ្ទៃនៃរាងចតុកោណកែងរាងពងក្រពើដែលមិនមានព្រំប្រទល់ពីខាងលើ។ ក្នុងករណីនេះ វាអាចមានជម្រើសពីរ *៖ អាំងតេក្រាលមិនសមរម្យ (ផ្ទៃគឺគ្មានកំណត់) ឬអាំងតេក្រាលមិនត្រឹមត្រូវគឺស្មើនឹងចំនួនកំណត់ (នោះគឺតំបន់នៃតួរលេខគ្មានកំណត់!)។

* តាមលំនាំដើម យើងសន្មត់ជាទម្លាប់ថាមានអាំងតេក្រាលមិនសមរម្យ

វានៅសល់តែដើម្បីកែប្រែរូបមន្ត Newton-Leibniz ប៉ុណ្ណោះ។ វាក៏ត្រូវបានកែប្រែផងដែរ ដោយមានជំនួយពីដែនកំណត់ ប៉ុន្តែដែនកំណត់លែងមានទំនោរទៅរកភាពគ្មានទីបញ្ចប់ទៀតហើយ ប៉ុន្តែ ទៅតម្លៃនៅខាងស្តាំ។វាងាយស្រួលក្នុងការធ្វើតាមគំនូរ៖ តាមអ័ក្ស យើងត្រូវចូលទៅជិតចំណុចបំបែកដោយបិទមិនដាច់ នៅខាងស្ដាំ.

តោះមើលរបៀបដែលវាត្រូវបានអនុវត្តនៅក្នុងការអនុវត្ត។

ឧទាហរណ៍ ៦

គណនាអាំងតេក្រាលមិនត្រឹមត្រូវ ឬបង្កើតភាពខុសគ្នារបស់វា។

អាំងតេក្រាលទទួលរងនូវការបំបែកគ្មានកំណត់នៅចំណុចមួយ (កុំភ្លេចពិនិត្យដោយពាក្យសំដី ឬនៅលើសេចក្តីព្រាង ប្រសិនបើអ្វីៗដំណើរការល្អជាមួយដែនកំណត់ខាងលើ!)

ដំបូងយើងគណនាអាំងតេក្រាលមិនកំណត់៖

ការជំនួស៖

សម្រាប់​អ្នក​ដែល​មាន​ការ​លំបាក​ក្នុង​ការ​ជំនួស សូម​មើល​មេរៀន វិធីសាស្រ្តជំនួសក្នុងអាំងតេក្រាលមិនកំណត់.

យើងគណនាអាំងតេក្រាលមិនត្រឹមត្រូវ៖

(1) តើមានអ្វីថ្មីនៅទីនេះ? ជាក់ស្តែងគ្មានអ្វីទាក់ទងនឹងបច្ចេកទេសទេ។ រឿងតែមួយគត់ដែលបានផ្លាស់ប្តូរគឺធាតុនៅក្រោមរូបតំណាងដែនកំណត់: . ការបន្ថែមមានន័យថាយើងមានបំណងតម្លៃនៅខាងស្តាំ (ដែលជាឡូជីខល - មើលក្រាហ្វ) ។ ដែនកំណត់បែបនេះនៅក្នុងទ្រឹស្តីនៃដែនកំណត់ត្រូវបានគេហៅថា ដែនកំណត់ឯកតោភាគី. ក្នុងករណីនេះយើងមាន ដែនកំណត់ខាងស្តាំ.

(2) យើងជំនួសដែនកំណត់ខាងលើ និងខាងក្រោមដោយយោងតាមរូបមន្ត Newton-Leibniz ។

(3​) ការ​ដោះស្រាយ​នៅ . តើអ្នកកំណត់ថាកន្សោមមួយត្រូវបានដឹកនាំដោយរបៀបណា? និយាយជារួម អ្នកគ្រាន់តែត្រូវការជំនួសតម្លៃទៅក្នុងវា ជំនួសបីភាគបួន ហើយបង្ហាញថា . ផ្សំចម្លើយ។

ក្នុងករណីនេះអាំងតេក្រាលមិនត្រឹមត្រូវគឺស្មើនឹងចំនួនអវិជ្ជមាន។ មិនមានឧក្រិដ្ឋកម្មនៅក្នុងនេះទេគ្រាន់តែអង្កាញ់ curvilinear ដែលត្រូវគ្នាមានទីតាំងនៅក្រោមអ័ក្ស។

ហើយឥឡូវនេះឧទាហរណ៍ពីរសម្រាប់ការសម្រេចចិត្តឯករាជ្យ។

ឧទាហរណ៍ ៧

គណនាអាំងតេក្រាលមិនត្រឹមត្រូវ ឬបង្កើតភាពខុសគ្នារបស់វា។

ឧទាហរណ៍ ៨

គណនាអាំងតេក្រាលមិនត្រឹមត្រូវ ឬបង្កើតភាពខុសគ្នារបស់វា។

ប្រសិនបើអាំងតេក្រាលមិនមាននៅចំណុច

រាងចតុកោណកែងគ្មានកំណត់សម្រាប់អាំងតេក្រាលដែលមិនសមរម្យ មើលទៅដូចនេះ។

អាំងតេក្រាលច្បាស់លាស់

\[ I=\int_a^bf(x)dx \]

ត្រូវបានសាងសង់ក្រោមការសន្មត់ថាលេខ $a,\,b$ គឺកំណត់ ហើយ $f(x)$ គឺជាមុខងារបន្ត។ ប្រសិនបើការសន្មត់មួយក្នុងចំណោមការសន្មត់ទាំងនេះត្រូវបានរំលោភ នោះគេនិយាយអំពីអាំងតេក្រាលមិនសមរម្យ។

10.1 អាំងតេក្រាលមិនត្រឹមត្រូវនៃប្រភេទទី 1

អាំងតេក្រាលមិនត្រឹមត្រូវនៃប្រភេទទីមួយកើតឡើងនៅពេលដែលយ៉ាងហោចណាស់លេខមួយ $a,\,b$ គឺគ្មានកំណត់។

10.1.1 និយមន័យ និងលក្ខណៈសម្បត្តិមូលដ្ឋាន

ចូរយើងពិចារណាជាមុនអំពីស្ថានភាពនៅពេលដែលដែនកំណត់ទាបនៃការរួមបញ្ចូលគឺកំណត់ ហើយដែនកំណត់ខាងលើគឺស្មើនឹង $+\infty$ ជម្រើសផ្សេងទៀតនឹងត្រូវបានពិភាក្សានៅពេលក្រោយ។ សម្រាប់ $f(x)$ បន្តសម្រាប់ការប្រាក់ $x$ ទាំងអស់សម្រាប់ពួកយើង សូមពិចារណាអាំងតេក្រាល។

\begin(សមីការ) I=\int _a^(+\infty)f(x)dx ។ \quad(19) \label(inf1) \end(សមីការ)

ជាដំបូង ចាំបាច់ត្រូវកំណត់អត្ថន័យនៃការបញ្ចេញមតិនេះ។ ដើម្បីធ្វើដូចនេះយើងណែនាំមុខងារ

\[ I(N)=\int _a^(N)f(x)dx \\]

ហើយពិចារណាឥរិយាបថរបស់វាជា $N\rightarrow +\infty$ ។

និយមន័យ។ សូមឱ្យមានដែនកំណត់

\[ A=\lim_(N \rightarrow +\infty)I(N)=\lim_(N \rightarrow +\infty)\int _a^(N)f(x)dx ។ \]

បន្ទាប់មកអាំងតេក្រាលមិនត្រឹមត្រូវនៃប្រភេទទី 1 (19) ត្រូវបានគេនិយាយថាជា convergent ហើយតម្លៃ $A$ ត្រូវបានផ្តល់ទៅឱ្យវា មុខងារខ្លួនវាត្រូវបានគេហៅថា integable នៅចន្លោះ $\left[a,\, +\infty \right) $ ប្រសិនបើដែនកំណត់ដែលបានបញ្ជាក់មិនមាន ឬវាស្មើនឹង $\pm \infty$ នោះអាំងតេក្រាល (19) ត្រូវបានគេនិយាយថា diverge ។

ពិចារណាលើអាំងតេក្រាល។

\[ I=\int _0^(+\infty) \frac(dx)(1+x^2)។ \]

\[ I(N)=\int _0^(N) \frac(dx)(1+x^2)។ \]

ក្នុងករណីនេះ antiderivative នៃ integrand ត្រូវបានគេស្គាល់, ដូច្នេះ

\[ I(N)=\int _0^(N) \frac(dx)(1+x^2)=arctgx|_0^(N)=arctgN។ \]

វាត្រូវបានគេដឹងថា $arctg N \rightarrow \pi /2$ សម្រាប់ $N \rightarrow +\infty$ ។ ដូច្នេះ $I(N)$ មានដែនកំណត់កំណត់ អាំងតេក្រាលមិនសមរម្យរបស់យើងនឹងបញ្ចូលគ្នា ហើយស្មើនឹង $\pi /2$។

ការបង្រួបបង្រួមអាំងតេក្រាលមិនត្រឹមត្រូវនៃប្រភេទទី 1 មានលក្ខណៈសម្បត្តិស្តង់ដារទាំងអស់នៃអាំងតេក្រាលច្បាស់លាស់ធម្មតា។

1. ប្រសិនបើ $f(x)$, $g(x)$ អាចបញ្ចូលក្នុងចន្លោះពេល $\left[a,\,+\infty \right)$ នោះផលបូករបស់ពួកគេ $f(x)+g(x) $ ក៏មិនអាចបញ្ចូលក្នុងចន្លោះនេះបានទេ ហើយ \[ \int _a^(+\infty)\left(f(x)+g(x)\right)dx=\int _a^(+\infty)f(x )dx+\int _a^(+\infty)g(x)dx ។ \] 2. ប្រសិនបើ $f(x)$ មិនអាចបញ្ចូលក្នុងចន្លោះពេល $\left[a, \, +\infty \right)$ នោះសម្រាប់តម្លៃថេរ $C$ មុខងារ $C\cdot f(x)$ ក៏​អាច​បញ្ចូល​គ្នា​បាន​នៅ​ចន្លោះ​ពេល​នេះ ហើយ \[ \int _a^(+\infty)C\cdot f(x)dx=C \cdot \int _a^(+\infty)f(x)dx ។ \] 3. ប្រសិនបើ $f(x)$ អាចបញ្ចូលក្នុងចន្លោះពេល $\left[a, \, +\infty \right)$ និង $f(x)>0$ នៅលើចន្លោះពេលនេះ នោះ \[ \int _a ^ (+\infty) f(x)dx\,>\,0. \] 4. ប្រសិនបើ $f(x)$ អាចបញ្ចូលក្នុងចន្លោះពេល $\left[a,\,+\infty \right)$ បន្ទាប់មកសម្រាប់ $b>a$ អាំងតេក្រាល \[ \int _b^(+ \infty) f(x)dx \\] បញ្ចូលគ្នា ហើយ \[ \int _a^(+\infty)f(x)dx=\int _a^(b) f(x)dx+\int _b^(+\infty ) f(x)dx \\] (ការបន្ថែមនៃអាំងតេក្រាលលើចន្លោះពេល)។

រូបមន្តសម្រាប់ការផ្លាស់ប្តូរអថេរ ការរួមបញ្ចូលដោយផ្នែក។ល។ ក៏មានសុពលភាពផងដែរ។ (ជាមួយនឹងការកក់ធម្មជាតិ) ។

ពិចារណាលើអាំងតេក្រាល។

\begin(សមីការ) I=\int _1^(+\infty)\frac(1)(x^k)\,dx. \quad (20) \label(mod) \end(សមីការ)

យើងណែនាំមុខងារ

\[ I(N)=\int _1^(N)\frac(1)(x^k)\,dx. \]

ក្នុងករណីនេះ antiderivative ត្រូវបានគេស្គាល់, ដូច្នេះ

\[ I(N)=\int _1^(N)\frac(1)(x^k)\,dx\,=\frac(x^(1-k))(1-k)|_1^N = \frac(N^(1-k))(1-k)-\frac(1)(1-k) \\]

សម្រាប់ $k \neq 1$,

\[ I(N)=\int _1^(N)\frac(1)(x)\,dx\,=lnx|_1^N=lnN \]

សម្រាប់ $k = 1$ ។ ដោយពិចារណាលើឥរិយាបទសម្រាប់ $N \rightarrow +\infty$ យើងសន្និដ្ឋានថាអាំងតេក្រាល (20) បញ្ចូលគ្នាសម្រាប់ $k>1$ និង diverges សម្រាប់ $k \leq 1$ ។

ឥឡូវនេះ ចូរយើងពិចារណាករណីនៅពេលដែលដែនកំណត់ទាបនៃការរួមបញ្ចូលគឺស្មើនឹង $-\infty$ ហើយផ្នែកខាងលើគឺកំណត់ ពោលគឺឧ។ ពិចារណាលើអាំងតេក្រាល។

\[ I=\int _(-\infty)^af(x)dx ។ \]

ទោះយ៉ាងណាក៏ដោយ វ៉ារ្យ៉ង់នេះអាចត្រូវបានកាត់បន្ថយទៅលេខមុន ប្រសិនបើយើងធ្វើការផ្លាស់ប្តូរអថេរ $x=-s$ ហើយបន្ទាប់មកប្តូរដែនកំណត់នៃការរួមបញ្ចូល ដូច្នេះ

\[ I=\int _(-a)^(+\infty)g(s)ds, \]

$g(s)=f(-s)$។ ឥឡូវ​នេះ ចូរ​យើង​ពិចារណា​ករណី​ដែល​មាន​ចំនួន​ពីរ​ដែល​គ្មាន​ដែន​កំណត់ ពោល​គឺ អាំងតេក្រាល

\begin(សមីការ) I=\int _(-\infty)^(+\infty)f(x)dx, \quad (21) \label(intr) \end(សមីការ)

ដែល $f(x)$ គឺបន្តសម្រាប់ $x \in \mathbb(R)$។ ចូរបែងចែកចន្លោះពេលជាពីរផ្នែក៖ យក $c \in \mathbb(R)$ ហើយពិចារណាអាំងតេក្រាលពីរ

\[ I_1=\int _(-\infty)^(c)f(x)dx, \quad I_2=\int _(c)^(+\infty)f(x)dx ។ \]

និយមន័យ។ ប្រសិនបើអាំងតេក្រាលទាំងពីរ $I_1$, $I_2$ បញ្ចូលគ្នា នោះអាំងតេក្រាល (21) ត្រូវបានគេហៅថា convergent វាត្រូវបានផ្តល់តម្លៃ $I=I_1+I_2$ (យោងទៅតាមការបន្ថែមចន្លោះពេល)។ ប្រសិនបើអាំងតេក្រាលយ៉ាងហោចណាស់មួយ $I_1$, $I_2$ diverges អាំងតេក្រាល (21) ត្រូវបានគេនិយាយថាខុសគ្នា។

វាអាចត្រូវបានបង្ហាញថាការបញ្ចូលគ្នានៃអាំងតេក្រាល (21) មិនអាស្រ័យលើជម្រើសនៃចំណុច $c$ ទេ។

អាំងតេក្រាលមិនត្រឹមត្រូវនៃប្រភេទទី 1 ជាមួយនឹងចន្លោះពេលនៃការរួមបញ្ចូល $\left(-\infty, \, c \right]$ ឬ $(-\infty, \, +\infty)$ ក៏មានលក្ខណៈសម្បត្តិស្តង់ដារទាំងអស់នៃអាំងតេក្រាលច្បាស់លាស់ (ជាមួយ កំណែទម្រង់ដែលត្រូវគ្នាដែលគិតដល់ចន្លោះពេលសមាហរណកម្មជម្រើស)។

10.1.2 លក្ខណៈវិនិច្ឆ័យសម្រាប់ការបញ្ចូលគ្នានៃអាំងតេក្រាលមិនត្រឹមត្រូវនៃប្រភេទទី 1

ទ្រឹស្តីបទ (សញ្ញាដំបូងនៃការប្រៀបធៀប) ។ អនុញ្ញាតឱ្យ $f(x)$, $g(x)$ បន្តសម្រាប់ $x>a$ ហើយទុកឱ្យ $0 a$។ បន្ទាប់មក

1. ប្រសិនបើអាំងតេក្រាល \[ \int _a^(+\infty)g(x)dx \] បញ្ចូលគ្នា នោះអាំងតេក្រាល \[ \int _a^(+\infty)f(x)dx ចូលគ្នាផងដែរ។ \] 2. ប្រសិនបើអាំងតេក្រាល \[ \int _a^(+\infty)f(x)dx \] ខុសគ្នា នោះអាំងតេក្រាល \[ \int _a^(+\infty)g(x)dx ក៏ខុសគ្នាដែរ។ \]

ទ្រឹស្តីបទ (សញ្ញាទីពីរនៃការប្រៀបធៀប) ។ អនុញ្ញាតឱ្យ $f(x)$, $g(x)$ បន្ត និងវិជ្ជមានសម្រាប់ $x>a$ ហើយអនុញ្ញាតឱ្យមានដែនកំណត់កំណត់

\[ \theta = \lim_(x \rightarrow +\infty) \frac(f(x))(g(x)), \quad \theta \neq 0, \, +\infty ។ \]

បន្ទាប់មកអាំងតេក្រាល។

\[ \int _a^(+\infty)f(x)dx, \quad \int _a^(+\infty)g(x)dx \]

បង្រួបបង្រួម ឬបង្វែរក្នុងពេលតែមួយ។

ពិចារណាលើអាំងតេក្រាល។

\[ I=\int _1^(+\infty)\frac(1)(x+\sin x)\,dx. \]

អាំងតេក្រាលគឺជាមុខងារវិជ្ជមាននៅលើចន្លោះពេលនៃការរួមបញ្ចូល។ លើសពីនេះ សម្រាប់ $x \rightarrow +\infty$ យើងមាន៖

$\sin x$ គឺជាការកែតម្រូវ "តូច" ទៅកាន់ភាគបែង។ កាន់តែច្បាស់ ប្រសិនបើយើងយក $f(x)=1/(x+\sin x)$, \, $g(x)=1/x$ នោះ

\[ \lim _(x \rightarrow +\infty)\frac(f(x))(g(x))=\lim _(x \rightarrow +\infty)\frac(x)(x+\sin x) =1. \]

ដោយអនុវត្តលក្ខណៈវិនិច្ឆ័យទីពីរនៃការប្រៀបធៀប យើងឈានដល់ការសន្និដ្ឋានថា អាំងតេក្រាលរបស់យើងបញ្ចូលគ្នា ឬខុសគ្នាក្នុងពេលដំណាលគ្នាជាមួយនឹងអាំងតេក្រាល

\[ \int _1^(+\infty)\frac(1)(x)\,dx ។ \]

ដូចដែលបានបង្ហាញក្នុងឧទាហរណ៍មុន អាំងតេក្រាលនេះខុសគ្នា ($k=1$)។ ដូច្នេះ អាំងតេក្រាលដើមមានភាពខុសគ្នា។

គណនាអាំងតេក្រាលមិនត្រឹមត្រូវ ឬបង្កើតការបញ្ចូលគ្នារបស់វា (ភាពខុសគ្នា)។

1. \[ \int _(0)^(+\infty)e^(-ax)\,dx. \] 2. \[ \int _(0)^(+\infty)xe^(-x^2)\,dx. \] 3. \[ \int _(-\infty)^(+\infty)\frac(2xdx)(x^2+1)។ \] 4. \[ \int _(0)^(+\infty)\frac(xdx)((x+2)^3)។ \] 5. \[ \int _(-\infty)^(+\infty)\frac(dx)(x^2+2x+2)។ \] 6. \[ \int _(1)^(+\infty)\frac(lnx)(x^2)\,dx. \] 7. \[ \int _(1)^(+\infty)\frac(dx)((1+x)\sqrt(x)). \] 8. \[ \int _(0)^(+\infty)e^(-\sqrt(x))\,dx. \] 9. \[ \int _(0)^(+\infty)e^(-ax)\cos x\,dx. \] 10. \[ \int _(0)^(+\infty)\frac(xdx)(x^3+1)។ \]

អាំងតេក្រាលមិនត្រឹមត្រូវនៃប្រភេទទីមួយ៖ផ្នែកបន្ថែមនៃគំនិតនៃអាំងតេក្រាលច្បាស់លាស់ទៅនឹងករណីនៃអាំងតេក្រាលដែលមានដែនកំណត់ខាងលើ ឬខាងក្រោមនៃការរួមបញ្ចូលគ្មានដែនកំណត់ ឬដែនកំណត់ទាំងពីរនៃការរួមបញ្ចូលគឺគ្មានកំណត់។

អាំងតេក្រាលមិនត្រឹមត្រូវនៃប្រភេទទីពីរ៖ផ្នែកបន្ថែមនៃគោលគំនិតនៃអាំងតេក្រាលច្បាស់លាស់ទៅនឹងករណីនៃអាំងតេក្រាលនៃអនុគមន៍គ្មានដែនកំណត់ អាំងតេក្រាលមិនមាននៅចំនួនកំណត់នៃចំណុចនៃចន្លោះពេលកំណត់នៃការធ្វើសមាហរណកម្ម ដោយងាកទៅរកភាពគ្មានកំណត់។

សម្រាប់ការប្រៀបធៀប។នៅពេលណែនាំគំនិត អាំងតេក្រាលច្បាស់លាស់វាត្រូវបានសន្មត់ថាមុខងារ f(x) គឺបន្តនៅចន្លោះពេល [ ក, ខ] ហើយចន្លោះពេលនៃការធ្វើសមាហរណកម្មមានកំណត់ ពោលគឺវាត្រូវបានកំណត់ដោយលេខ និងមិនមែនដោយភាពគ្មានកំណត់នោះទេ។ កិច្ចការមួយចំនួននាំឱ្យមានតម្រូវការក្នុងការបោះបង់ចោលការរឹតបន្តឹងទាំងនេះ។ នេះជារបៀបដែលអាំងតេក្រាលមិនត្រឹមត្រូវលេចឡើង។

អត្ថន័យធរណីមាត្រនៃអាំងតេក្រាលមិនត្រឹមត្រូវប្រែទៅជាសាមញ្ញណាស់។ នៅពេលដែលក្រាហ្វនៃមុខងារ y = f(x) គឺនៅពីលើអ័ក្ស គោអាំងតេក្រាល។ y = f(x) , abscissa និង ordinates x = ក , x = ខ. នៅក្នុងវេន អាំងតេក្រាលមិនត្រឹមត្រូវបង្ហាញពីតំបន់នៃអន្ទាក់កោង (គ្មានដែនកំណត់) ដែលរុំព័ទ្ធរវាងបន្ទាត់ y = f(x) (រូបភាពខាងក្រោមពណ៌ក្រហម) x = កនិងអ័ក្ស abscissa ។

អាំងតេក្រាល​មិន​ត្រឹមត្រូវ​ត្រូវ​បាន​កំណត់​ស្រដៀង​គ្នា​នេះ​សម្រាប់​ចន្លោះ​ពេល​គ្មាន​កំណត់​ផ្សេង​ទៀត៖

តំបន់នៃរាងចតុកោណកែងគ្មានកំណត់អាចជាចំនួនកំណត់ ដែលក្នុងករណីដែលអាំងតេក្រាលមិនត្រឹមត្រូវត្រូវបានគេហៅថា convergent ។ តំបន់ក៏អាចជាភាពគ្មានកំណត់ ដែលក្នុងករណីនេះអាំងតេក្រាលមិនត្រឹមត្រូវត្រូវបានគេហៅថា divergent ។

ការប្រើដែនកំណត់នៃអាំងតេក្រាលមួយជំនួសឱ្យអាំងតេក្រាលមិនសមរម្យដោយខ្លួនវាផ្ទាល់។ដើម្បីគណនាអាំងតេក្រាលមិនត្រឹមត្រូវ អ្នកត្រូវប្រើដែនកំណត់នៃអាំងតេក្រាលច្បាស់លាស់។ ប្រសិនបើដែនកំណត់នេះមាន ហើយមានកំណត់ (មិនស្មើភាពគ្មានកំណត់) នោះអាំងតេក្រាលមិនត្រឹមត្រូវត្រូវបានគេហៅថា convergent បើមិនដូច្នេះទេ វាខុសគ្នា។ អ្វីដែលអថេរនៅក្រោមសញ្ញាកំណត់មាននិន្នាការអាស្រ័យលើថាតើយើងកំពុងដោះស្រាយជាមួយអាំងតេក្រាលមិនត្រឹមត្រូវនៃប្រភេទទីមួយ ឬប្រភេទទីពីរ។ ចូរយើងស្វែងយល់អំពីវាឥឡូវនេះ។

អាំងតេក្រាលមិនត្រឹមត្រូវនៃប្រភេទទីមួយ - ជាមួយនឹងដែនកំណត់គ្មានកំណត់ និងការបញ្ចូលគ្នារបស់ពួកគេ។

អាំងតេក្រាលមិនត្រឹមត្រូវដែលមានដែនកំណត់ខាងលើគ្មានកំណត់

ដូច្នេះ កំណត់ត្រានៃអាំងតេក្រាលមិនត្រឹមត្រូវ ខុសពីអាំងតេក្រាលកំណត់ធម្មតា ដែលដែនកំណត់ខាងលើនៃការរួមបញ្ចូលគឺគ្មានកំណត់។

និយមន័យ។ អាំងតេក្រាល​មិន​ត្រឹមត្រូវ​ជាមួយ​ដែន​កំណត់​ខាង​លើ​គ្មាន​កំណត់​នៃ​ការ​រួម​បញ្ចូល​គ្នា​ពី​អនុគមន៍​បន្ត f(x) រវាង ក ពីមុន ∞ ត្រូវបានគេហៅថាដែនកំណត់នៃអាំងតេក្រាលនៃអនុគមន៍នេះជាមួយនឹងដែនកំណត់ខាងលើនៃការរួមបញ្ចូល ខ និងដែនកំណត់ទាបនៃការរួមបញ្ចូល ក បានផ្តល់ថាដែនកំណត់ខាងលើនៃការរួមបញ្ចូលកើនឡើងដោយគ្មានកំណត់, i.e.

.

ប្រសិនបើដែនកំណត់នេះមាន ហើយស្មើនឹងចំនួនមួយចំនួន ហើយមិនមែនរហូតដល់គ្មានកំណត់ទេនោះ អាំងតេក្រាលមិនត្រឹមត្រូវត្រូវបានគេហៅថា convergentហើយចំនួនដែលស្មើនឹងដែនកំណត់ត្រូវបានយកជាតម្លៃរបស់វា។ បើមិនដូច្នេះទេ។ អាំងតេក្រាលមិនត្រឹមត្រូវត្រូវបានគេហៅថា divergentហើយ​គ្មាន​តម្លៃ​ត្រូវ​បាន​កំណត់​ចំពោះ​វា​ទេ។

ឧទាហរណ៍ 1. គណនាអាំងតេក្រាលមិនត្រឹមត្រូវ(ប្រសិនបើវាបញ្ចូលគ្នា) ។

ដំណោះស្រាយ។ ដោយផ្អែកលើនិយមន័យនៃអាំងតេក្រាលមិនត្រឹមត្រូវយើងរកឃើញ

ដោយសារដែនកំណត់មាន ហើយស្មើនឹង 1 នោះបានផ្តល់ អាំងតេក្រាល​មិន​ត្រឹមត្រូវ​ចូល​រួមនិងស្មើនឹង 1 ។

ក្នុងឧទាហរណ៍ខាងក្រោម អាំងតេក្រាលគឺស្ទើរតែដូចគ្នានឹងឧទាហរណ៍ទី 1 ដែរ មានតែដឺក្រេនៃ x មិនមែនជាពីរទេ ប៉ុន្តែជាអក្សរ alpha ហើយភារកិច្ចគឺដើម្បីសិក្សាអាំងតេក្រាលមិនត្រឹមត្រូវសម្រាប់ការបញ្ចូលគ្នា។ នោះហើយជាសំណួរនៅតែត្រូវឆ្លើយ៖ តើតម្លៃអាល់ហ្វាណាដែលអាំងតេក្រាលមិនសមរម្យនេះបញ្ចូលគ្នា ហើយតើតម្លៃអ្វីដែលវាខុសគ្នា?

ឧទាហរណ៍ 2. ស៊ើបអង្កេតការបញ្ចូលគ្នានៃអាំងតេក្រាលដែលមិនត្រឹមត្រូវ។(ដែនកំណត់នៃការរួមបញ្ចូលទាបគឺធំជាងសូន្យ)។

ដំណោះស្រាយ។ ឧបមាថាដំបូងនោះបន្ទាប់មក

នៅក្នុងកន្សោមលទ្ធផល យើងឆ្លងទៅដែនកំណត់នៅ៖

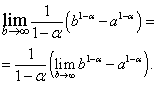
វាងាយមើលឃើញថាដែនកំណត់នៅខាងស្តាំមាន ហើយស្មើនឹងសូន្យនៅពេលដែល , i.e. , និងមិនមាននៅពេលដែល , i.e.

ក្នុងករណីដំបូង នោះគឺពេលណា។ បើអញ្ចឹង ហើយមិនមានទេ។

សេចក្តីសន្និដ្ឋាននៃការសិក្សារបស់យើងមានដូចខាងក្រោម៖ អាំងតេក្រាល​មិន​ត្រឹមត្រូវ​ចូល​រួមនៅ និង ខុសគ្នានៅ។

ការ​អនុវត្ត​ទៅ​នឹង​ប្រភេទ​ដែល​បាន​សិក្សា​នៃ​អាំងតេក្រាល​មិន​ត្រឹមត្រូវ រូបមន្ត Newton-Leibniz យើងអាចទាញយករូបមន្តស្រដៀងគ្នាខាងក្រោម៖

.

នេះគឺជារូបមន្តទូទៅ ញូតុន-លីបនីស។

ឧទាហរណ៍ 3. គណនាអាំងតេក្រាលមិនសមរម្យ(ប្រសិនបើវាបញ្ចូលគ្នា) ។

ដែនកំណត់នៃអាំងតេក្រាលនេះមាន៖

អាំងតេក្រាលទីពីរ ដែលជាផលបូកបង្ហាញពីអាំងតេក្រាលដើម៖

ដែនកំណត់នៃអាំងតេក្រាលនេះក៏មានផងដែរ៖

.

យើងរកឃើញផលបូកនៃអាំងតេក្រាលពីរ ដែលជាតម្លៃនៃអាំងតេក្រាលមិនត្រឹមត្រូវដើមដែលមានដែនកំណត់គ្មានកំណត់ពីរ៖

អាំងតេក្រាលមិនត្រឹមត្រូវនៃប្រភេទទីពីរ - ពីមុខងារគ្មានដែនកំណត់និងការបញ្ចូលគ្នារបស់វា។

អនុញ្ញាតឱ្យមុខងារ f(x) កំណត់នៅលើផ្នែកពី ក ពីមុន ខ និងគ្មានដែនកំណត់លើវា។ ឧបមាថាអនុគមន៍ទៅគ្មានដែនកំណត់នៅចំណុច ខ ខណៈពេលដែលនៅចំណុចផ្សេងទៀតទាំងអស់នៃផ្នែកវាបន្ត។

និយមន័យ។ អាំងតេក្រាលមិនត្រឹមត្រូវនៃមុខងារ f(x) នៅលើផ្នែកពី ក ពីមុន ខ ត្រូវបានគេហៅថាដែនកំណត់នៃអាំងតេក្រាលនៃអនុគមន៍នេះជាមួយនឹងដែនកំណត់ខាងលើនៃការរួមបញ្ចូល គ ប្រសិនបើនៅពេលដែលខិតខំ គ ទៅ ខ មុខងារកើនឡើងឥតកំណត់ ហើយនៅចំណុច x = ខ មុខងារមិនត្រូវបានកំណត់, i.e.

.

ប្រសិនបើមានដែនកំណត់នេះ នោះអាំងតេក្រាលមិនត្រឹមត្រូវនៃប្រភេទទីពីរត្រូវបានគេហៅថា convergent បើមិនដូច្នេះទេ divergent ។

ដោយប្រើរូបមន្ត Newton-Leibniz យើងទទួលបាន។