ជាមួយនឹងម៉ាទ្រីស A ប្រសិនបើមានលេខ l នោះ AX = lX ។

ក្នុងករណីនេះលេខ l ត្រូវបានហៅ eigenvalueប្រតិបត្តិករ (ម៉ាទ្រីស A) ដែលត្រូវគ្នានឹងវ៉ិចទ័រ X ។

នៅក្នុងពាក្យផ្សេងទៀត eigenvector គឺជាវ៉ិចទ័រដែលនៅក្រោមសកម្មភាពរបស់ប្រតិបត្តិករលីនេអ៊ែរបំលែងទៅជាវ៉ិចទ័រ collinear ពោលគឺឧ។ គ្រាន់តែគុណនឹងចំនួនមួយចំនួន។ ផ្ទុយ​ទៅ​វិញ វ៉ិចទ័រ​មិន​ត្រឹមត្រូវ​គឺ​ពិបាក​ក្នុង​ការ​បំប្លែង​ជាង។

យើងសរសេរនិយមន័យនៃ eigenvector ជាប្រព័ន្ធនៃសមីការ៖

ចូរផ្លាស់ទីលក្ខខណ្ឌទាំងអស់ទៅផ្នែកខាងឆ្វេង៖

ប្រព័ន្ធចុងក្រោយអាចត្រូវបានសរសេរជាទម្រង់ម៉ាទ្រីសដូចខាងក្រោមៈ

(A - lE)X \u003d O

ប្រព័ន្ធលទ្ធផលតែងតែមានដំណោះស្រាយសូន្យ X = O ។ ប្រព័ន្ធបែបនេះដែលលក្ខខណ្ឌឥតគិតថ្លៃទាំងអស់ស្មើនឹងសូន្យត្រូវបានគេហៅថា ដូចគ្នា. ប្រសិនបើម៉ាទ្រីសនៃប្រព័ន្ធបែបនេះគឺការ៉េហើយកត្តាកំណត់របស់វាមិនស្មើនឹងសូន្យទេនោះយោងទៅតាមរូបមន្តរបស់ Cramer យើងនឹងទទួលបានដំណោះស្រាយតែមួយគត់ - សូន្យ។ វាអាចត្រូវបានបង្ហាញថាប្រព័ន្ធមានដំណោះស្រាយមិនសូន្យប្រសិនបើនិងលុះត្រាតែកត្តាកំណត់នៃម៉ាទ្រីសនេះគឺស្មើនឹងសូន្យពោលគឺឧ។

|A - lE| = = 0

សមីការនេះជាមួយ l មិនស្គាល់ត្រូវបានគេហៅថា សមីការលក្ខណៈ (ពហុនាមលក្ខណៈ) ម៉ាទ្រីស A (ប្រតិបត្តិករលីនេអ៊ែរ) ។

វាអាចត្រូវបានបង្ហាញថាពហុនាមលក្ខណៈនៃប្រតិបត្តិករលីនេអ៊ែរមិនអាស្រ័យលើជម្រើសនៃមូលដ្ឋានទេ។

ជាឧទាហរណ៍ ចូរយើងស្វែងរក eigenvalues ​​និង eigenvectors នៃ linear operator ដែលផ្តល់ដោយ matrix A = .

ដើម្បីធ្វើដូចនេះយើងបង្កើតសមីការលក្ខណៈ |А - lЕ| = \u003d (1 - l) 2 - 36 \u003d 1 - 2l + l 2 - 36 \u003d l 2 - 2l - 35 \u003d 0; ឃ \u003d 4 + 140 \u003d 144; eigenvalues ​​​​l 1 = (2 - 12)/2 = -5; l 2 \u003d (2 + 12) / 2 \u003d ៧.

ដើម្បីស្វែងរក eigenvectors យើងដោះស្រាយប្រព័ន្ធសមីការពីរ

(A + 5E) X = O

(A - 7E) X = O

សម្រាប់ទីមួយនៃពួកគេ ម៉ាទ្រីសដែលបានពង្រីកនឹងយកទម្រង់

,

ពេលណា x 2 \u003d c, x 1 + (2/3) c \u003d 0; x 1 \u003d - (2/3) s, i.e. X (1) \u003d (- (2/3) s; s) ។

សម្រាប់ទីពីរនៃពួកគេ ម៉ាទ្រីសពង្រីកនឹងយកទម្រង់

,

ពេលណា x 2 \u003d c 1, x 1 - (2/3) c 1 \u003d 0; x 1 \u003d (2/3) s 1, i.e. X (2) \u003d ((2/3) s 1; s 1) ។

ដូច្នេះ eigenvectors នៃប្រតិបត្តិករលីនេអ៊ែរនេះគឺជាវ៉ិចទ័រទាំងអស់នៃទម្រង់ (-(2/3)c; c) ជាមួយ eigenvalue (-5) និងវ៉ិចទ័រទាំងអស់នៃទម្រង់ ((2/3)c 1 ; c 1) ជាមួយ eigenvalue ៧.

វាអាចត្រូវបានបង្ហាញថាម៉ាទ្រីសនៃប្រតិបត្តិករ A នៅក្នុងមូលដ្ឋានដែលមាន eigenvectors របស់វាគឺអង្កត់ទ្រូងហើយមានទម្រង់:

,

ដែលជាកន្លែងដែលខ្ញុំគឺជា eigenvalues ​​នៃម៉ាទ្រីសនេះ។

ការសន្ទនាក៏ពិតដែរ៖ ប្រសិនបើម៉ាទ្រីស A ក្នុងមូលដ្ឋានខ្លះជាអង្កត់ទ្រូង នោះវ៉ិចទ័រទាំងអស់នៃមូលដ្ឋាននេះនឹងក្លាយជា eigenvectors នៃម៉ាទ្រីសនេះ។

វាក៏អាចបញ្ជាក់បានថា ប្រសិនបើប្រតិបត្តិករលីនេអ៊ែរមាន eigenvalues ​​ខុសគ្នាជាគូ នោះ eigenvectors ដែលត្រូវគ្នាគឺឯករាជ្យលីនេអ៊ែរ ហើយម៉ាទ្រីសនៃប្រតិបត្តិករនេះក្នុងមូលដ្ឋានដែលត្រូវគ្នាមានទម្រង់អង្កត់ទ្រូង។

ចូរយើងពន្យល់រឿងនេះជាមួយឧទាហរណ៍មុន។ អនុញ្ញាតឱ្យយើងយកតម្លៃមិនសូន្យតាមអំពើចិត្ត c និង c 1 ប៉ុន្តែដូចជាវ៉ិចទ័រ X (1) និង X (2) គឺឯករាជ្យលីនេអ៊ែរ ឧ។ នឹងបង្កើតជាមូលដ្ឋាន។ ឧទាហរណ៍ អនុញ្ញាតឱ្យ c \u003d c 1 \u003d 3 បន្ទាប់មក X (1) \u003d (-2; 3), X (2) \u003d (2; 3) ។

អនុញ្ញាតឱ្យយើងផ្ទៀងផ្ទាត់ឯករាជ្យលីនេអ៊ែរនៃវ៉ិចទ័រទាំងនេះ:

12 ≠ 0. ក្នុងមូលដ្ឋានថ្មីនេះ ម៉ាទ្រីស A នឹងយកទម្រង់ A * = ។

ដើម្បីផ្ទៀងផ្ទាត់នេះយើងប្រើរូបមន្ត A * = C -1 AC ។ តោះរក C-1 ជាមុនសិន។

គ −1 = ;

ទម្រង់បួនជ្រុង

ទម្រង់បួនជ្រុង f (x 1, x 2, x n) ពីអថេរ n ត្រូវបានគេហៅថាផលបូក ដែលពាក្យនីមួយៗគឺជាការ៉េនៃអថេរមួយ ឬផលគុណនៃអថេរពីរផ្សេងគ្នា ដែលយកដោយមេគុណជាក់លាក់មួយ៖ f (x 1 , x 2, x n) = (a ij = a ji) ។

ម៉ាទ្រីស A ដែលផ្សំឡើងដោយមេគុណទាំងនេះត្រូវបានគេហៅថា ម៉ាទ្រីសទម្រង់បួនជ្រុង។ វាតែងតែ ស៊ីមេទ្រីម៉ាទ្រីស (ឧ. ស៊ីមេទ្រីម៉ាទ្រីសអំពីអង្កត់ទ្រូងសំខាន់ a ij = a ji) ។

នៅក្នុងសញ្ញាណម៉ាទ្រីស ទម្រង់បួនជ្រុងមានទម្រង់ f(X) = X T AX ដែលជាកន្លែងដែល

ជា​ការ​ពិត

ឧទាហរណ៍ ចូរយើងសរសេរទម្រង់ quadratic ក្នុងទម្រង់ម៉ាទ្រីស។

ដើម្បីធ្វើដូចនេះយើងរកឃើញម៉ាទ្រីសនៃទម្រង់បួនជ្រុង។ ធាតុអង្កត់ទ្រូងរបស់វាគឺស្មើនឹងមេគុណនៅការ៉េនៃអថេរ ហើយធាតុដែលនៅសល់គឺស្មើនឹងពាក់កណ្តាលនៃមេគុណដែលត្រូវគ្នានៃទម្រង់ការ៉េ។ នោះ​ហើយ​ជា​មូល​ហេតុ​ដែល

អនុញ្ញាតឱ្យ​ជួរ​ឈរ​ម៉ាទ្រីស​នៃ​អថេរ X ត្រូវ​បាន​ទទួល​ដោយ​ការ​បំប្លែង​លីនេអ៊ែរ​ដែល​មិន​កើត​ចេញ​នៃ​ជួរ​ឈរ​ម៉ាទ្រីស Y, i.e. X = CY ដែល C ជាម៉ាទ្រីសមិន degenerate នៃលំដាប់ n ។ បន្ទាប់មកទម្រង់ការ៉េ f(X) = X T AX = (CY) T A(CY) = (Y T C T)A(CY) = Y T (C T AC)Y ។

ដូច្នេះនៅក្រោមការបំលែងលីនេអ៊ែរដែលមិន degenerate C ម៉ាទ្រីសនៃទម្រង់បួនជ្រុងយកទម្រង់៖ A * = C T AC ។

ឧទាហរណ៍ ចូរយើងស្វែងរកទម្រង់ការ៉េ f(y 1, y 2) ដែលទទួលបានពីទម្រង់រាងចតុកោណ f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 ដោយការបំលែងលីនេអ៊ែរ។

ទម្រង់បួនជ្រុងត្រូវបានគេហៅថា Canonical(វា​មាន ទិដ្ឋភាព Canonical) ប្រសិនបើមេគុណរបស់វា a ij = 0 សម្រាប់ i ≠ j, i.e.
f(x 1, x 2, x n) = a 11 x 1 2 + a 22 x 2 2 + a nn x n 2 = ។

ម៉ាទ្រីសរបស់វាគឺអង្កត់ទ្រូង។

ទ្រឹស្តីបទ(ភស្តុតាងមិនត្រូវបានផ្តល់ឱ្យនៅទីនេះ) ។ ទម្រង់បួនជ្រុងណាមួយអាចត្រូវបានកាត់បន្ថយទៅជាទម្រង់ Canonical ដោយប្រើការបំប្លែងលីនេអ៊ែរដែលមិន degenerate ។

ជាឧទាហរណ៍ អនុញ្ញាតឱ្យយើងកាត់បន្ថយទៅជាទម្រង់ Canonical ទម្រង់បួនជ្រុង
f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 ។

ដើម្បីធ្វើដូចនេះដំបូងត្រូវជ្រើសរើសការ៉េពេញសម្រាប់អថេរ x 1៖

f (x 1, x 2, x 3) \u003d 2 (x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 \u003d 2 (x 1 + x 2 ) 2 − 5x 2 2 − x 2 x 3 ។

ឥឡូវនេះយើងជ្រើសរើសការ៉េពេញសម្រាប់អថេរ x 2៖

f (x 1, x 2, x 3) \u003d 2 (x 1 + x 2) 2 - 5 (x 2 2 + 2 * x 2 * (1/10) x 3 + (1/100) x 3 2 ) + (5/100) x 3 2 =
\u003d 2 (x 1 + x 2) 2 - 5 (x 2 - (1/10) x 3) 2 + (1/20) x 3 2 ។

បន្ទាប់មកការផ្លាស់ប្តូរលីនេអ៊ែរមិន degenerate y 1 \u003d x 1 + x 2, y 2 \u003d x 2 + (1/10) x 3 និង y 3 \u003d x 3 នាំទម្រង់ការ៉េនេះទៅជាទម្រង់ Canonical f (y 1 , y 2, y 3) = 2y 1 2 - 5y 2 2 + (1/20)y 3 2 ។

ចំណាំថាទម្រង់ Canonical នៃទម្រង់បួនជ្រុងត្រូវបានកំណត់មិនច្បាស់លាស់ (ទម្រង់ការ៉េដូចគ្នាអាចត្រូវបានកាត់បន្ថយទៅជាទម្រង់ Canonical ក្នុងវិធីផ្សេងគ្នា)។ ទោះជាយ៉ាងណាក៏ដោយទម្រង់ Canonical ដែលទទួលបានដោយវិធីសាស្រ្តផ្សេងៗមានលក្ខណៈសម្បត្តិទូទៅមួយចំនួន។ ជាពិសេស ចំនួននៃពាក្យដែលមានមេគុណវិជ្ជមាន (អវិជ្ជមាន) នៃទម្រង់បួនជ្រុងមិនអាស្រ័យលើរបៀបដែលទម្រង់ត្រូវបានកាត់បន្ថយទៅជាទម្រង់នេះទេ (ឧទាហរណ៍ ក្នុងឧទាហរណ៍ដែលបានពិចារណា វាតែងតែមានមេគុណអវិជ្ជមានពីរ និងមេគុណវិជ្ជមានមួយ)។ ទ្រព្យសម្បត្តិនេះត្រូវបានគេហៅថាច្បាប់នៃនិចលភាពនៃទម្រង់បួនជ្រុង។

អនុញ្ញាតឱ្យយើងផ្ទៀងផ្ទាត់វាដោយកាត់បន្ថយទម្រង់បួនជ្រុងដូចគ្នាទៅជាទម្រង់ Canonical ក្នុងវិធីផ្សេងគ្នា។ ចូរចាប់ផ្តើមការបំប្លែងដោយអថេរ x 2៖

f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 \u003d -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 \u003d - 3(x 2 2 +
+ 2 * x 2 ((1/6) x 3 - (2/3) x 1) + ((1/6) x 3 - (2/3) x 1) 2) + 3 ((1/6) x 3 − (2/3) x 1) 2 + 2x 1 2 =
\u003d -3 (x 2 + (1/6) x 3 - (2/3) x 1) 2 + 3 ((1/6) x 3 + (2/3) x 1) 2 + 2x 1 2 \ u003d f (y 1, y 2, y 3) = -3y 1 2 -
+ 3y 2 2 + 2y 3 2 ដែល y 1 \u003d - (2/3) x 1 + x 2 + (1/6) x 3, y 2 \u003d (2/3) x 1 + (1/6) ) x 3 និង y 3 = x 1 ។ នៅទីនេះ មេគុណអវិជ្ជមាន -3 នៅ y 1 និងមេគុណវិជ្ជមានពីរ 3 និង 2 នៅ y 2 និង y 3 (ហើយដោយប្រើវិធីមួយផ្សេងទៀត យើងទទួលបានមេគុណអវិជ្ជមាន (-5) នៅ y 2 និងមេគុណវិជ្ជមានពីរ៖ 2 នៅ y 1 និង 1/20 សម្រាប់ y ​​3) ។

វាគួរតែត្រូវបានគេកត់សម្គាល់ផងដែរថាចំណាត់ថ្នាក់នៃម៉ាទ្រីសនៃទម្រង់រាងបួនជ្រុងត្រូវបានគេហៅថា ចំណាត់ថ្នាក់នៃទម្រង់បួនជ្រុង, គឺស្មើនឹងចំនួនមេគុណមិនសូន្យនៃទម្រង់ Canonical និងមិនផ្លាស់ប្តូរក្រោមការបំប្លែងលីនេអ៊ែរ។

ទម្រង់បួនជ្រុង f(X) ត្រូវបានគេហៅថា ជាវិជ្ជមាន (អវិជ្ជមាន) ជាក់លាក់, ប្រសិនបើសម្រាប់តម្លៃទាំងអស់នៃអថេរដែលមិនក្នុងពេលដំណាលគ្នាស្មើនឹងសូន្យនោះវាវិជ្ជមាន, i.e. f(X) > 0 (អវិជ្ជមាន, i.e.
f(X)< 0).

ឧទាហរណ៍ ទម្រង់រាងបួនជ្រុង f 1 (X) \u003d x 1 2 + x 2 2 ត្រូវបានកំណត់ជាវិជ្ជមាន ពីព្រោះ គឺជាផលបូកនៃការ៉េ ហើយទម្រង់ចតុកោណ f 2 (X) \u003d -x 1 2 + 2x 1 x 2 - x 2 2 គឺជានិយមន័យអវិជ្ជមាន ពីព្រោះ តំណាងវាអាចត្រូវបានតំណាងជា f 2 (X) \u003d - (x 1 - x 2) 2 ។

នៅក្នុងស្ថានភាពជាក់ស្តែងភាគច្រើន វាមានការលំបាកជាងក្នុងការកំណត់សញ្ញា-កំណត់នៃទម្រង់បួនជ្រុង ដូច្នេះទ្រឹស្តីបទមួយក្នុងចំណោមទ្រឹស្តីបទខាងក្រោមត្រូវបានប្រើសម្រាប់ការនេះ (យើងបង្កើតពួកវាដោយគ្មានភស្តុតាង)។

ទ្រឹស្តីបទ. ទម្រង់បួនជ្រុងគឺវិជ្ជមាន (អវិជ្ជមាន) កំណត់ប្រសិនបើ និងលុះត្រាតែតម្លៃ eigenvalue ទាំងអស់នៃម៉ាទ្រីសរបស់វាគឺវិជ្ជមាន (អវិជ្ជមាន)។

ទ្រឹស្តីបទ(លក្ខណៈវិនិច្ឆ័យរបស់ Sylvester) ។ ទម្រង់ quadratic គឺវិជ្ជមានកំណត់ប្រសិនបើ និងលុះត្រាតែអនីតិជនសំខាន់ៗទាំងអស់នៃម៉ាទ្រីសនៃទម្រង់នេះគឺវិជ្ជមាន។

ធំ (ជ្រុង) អនីតិជនលំដាប់ k-th នៃម៉ាទ្រីស A នៃលំដាប់ n-th ត្រូវបានគេហៅថា កត្តាកំណត់នៃម៉ាទ្រីស ដែលផ្សំឡើងពីជួរ k ដំបូង និងជួរឈរនៃម៉ាទ្រីស A ()។

ចំណាំថាសម្រាប់ទម្រង់រាងចតុកោណដែលកំណត់និយមន័យអវិជ្ជមាន សញ្ញានៃអនីតិជនចម្បងឆ្លាស់គ្នា ហើយអនីតិជនលំដាប់ទីមួយត្រូវតែអវិជ្ជមាន។

ឧទាហរណ៍ យើងពិនិត្យទម្រង់រាងការ៉េ f (x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 សម្រាប់ការកំណត់សញ្ញា។

= (2 - លីត្រ)*
*(3 - លីត្រ) - 4 \u003d (6 - 2l - 3l + l 2) - 4 \u003d l 2 - 5l + 2 \u003d 0; ឃ = 25 - 8 = 17;
. ដូច្នេះទម្រង់ quadratic គឺវិជ្ជមានកំណត់។

វិធីសាស្រ្ត 2. អនីតិជនសំខាន់នៃលំដាប់ទីមួយនៃម៉ាទ្រីស A D 1 = a 11 = 2 > 0. អនីតិជនសំខាន់នៃលំដាប់ទីពីរ D 2 = = 6 - 4 = 2 > 0. ដូច្នេះយោងទៅតាមលក្ខណៈវិនិច្ឆ័យរបស់ Sylvester ។ ទម្រង់​បួន​ជ្រុង​គឺ​ជា​ការ​កំណត់​វិជ្ជមាន។

យើងពិនិត្យមើលទម្រង់បួនជ្រុងផ្សេងទៀតសម្រាប់ការកំណត់សញ្ញា f (x 1, x 2) \u003d -2x 1 2 + 4x 1 x 2 - 3x 2 2 ។

វិធីសាស្រ្ត 1. ចូរយើងបង្កើតម៉ាទ្រីសនៃទម្រង់បួនជ្រុង А = ។ សមីការលក្ខណៈនឹងមានទម្រង់ = (-2 - លីត្រ)*
*(−3 − l) - 4 = (6 + 2l + 3l + l 2) - 4 = l 2 + 5l + 2 = 0; ឃ = 25 - 8 = 17;
. ដូច្នេះទម្រង់ quadratic គឺអវិជ្ជមានកំណត់។

វិធីសាស្រ្ត 2. អនីតិជនសំខាន់នៃលំដាប់ទីមួយនៃម៉ាទ្រីស A D 1 = a 11 =
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 >0. ដូច្នេះយោងទៅតាមលក្ខណៈវិនិច្ឆ័យរបស់ Sylvester ទម្រង់រាងចតុកោណគឺអវិជ្ជមានកំណត់ (សញ្ញានៃអនីតិជនចម្បងឆ្លាស់គ្នា ចាប់ផ្តើមពីដក)។

ហើយជាឧទាហរណ៍មួយទៀត យើងពិនិត្យមើលទម្រង់ការ៉េ f (x 1, x 2) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 សម្រាប់ការកំណត់សញ្ញា។

វិធីសាស្រ្ត 1. ចូរយើងបង្កើតម៉ាទ្រីសនៃទម្រង់បួនជ្រុង А = ។ សមីការលក្ខណៈនឹងមានទម្រង់ = (2 - លីត្រ)*
*(−3 − l) - 4 = (−6 − 2l + 3l + l 2) - 4 = l 2 + l − 10 = 0; ឃ = 1 + 40 = 41;
.

លេខមួយក្នុងចំណោមលេខទាំងនេះគឺអវិជ្ជមាន ហើយមួយទៀតគឺវិជ្ជមាន។ សញ្ញានៃ eigenvalues ​​គឺខុសគ្នា។ ដូច្នេះ ទម្រង់​រាង​បួនជ្រុង​មិន​អាច​កំណត់​បាន​ទាំង​អវិជ្ជមាន ឬ​វិជ្ជមាន​ទេ ឧ. ទម្រង់​ការ៉េ​នេះ​មិន​មាន​សញ្ញា​កំណត់​ទេ (វា​អាច​យក​តម្លៃ​នៃ​សញ្ញា​ណាមួយ)។

វិធីសាស្រ្ត 2. អនីតិជនសំខាន់នៃលំដាប់ទីមួយនៃម៉ាទ្រីស A D 1 = a 11 = 2 > 0. អនីតិជនសំខាន់នៃលំដាប់ទីពីរ D 2 = = -6 - 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).

"។ ផ្នែកទីមួយមានបទប្បញ្ញត្តិដែលចាំបាច់តិចតួចបំផុតសម្រាប់ការយល់ដឹងអំពីគីមីវិទ្យា ហើយផ្នែកទីពីរមានការពិតដែលអ្នកត្រូវដឹងសម្រាប់ការយល់ដឹងកាន់តែស៊ីជម្រៅអំពីវិធីសាស្រ្តនៃការវិភាគពហុវ៉ារ្យង់។ បទបង្ហាញត្រូវបានបង្ហាញដោយឧទាហរណ៍ដែលបានធ្វើនៅក្នុងសៀវភៅការងារ Excel ម៉ាទ្រីស.xlsដែលភ្ជាប់មកជាមួយឯកសារនេះ។

តំណភ្ជាប់ទៅកាន់ឧទាហរណ៍ត្រូវបានដាក់ក្នុងអត្ថបទជាវត្ថុ Excel ។ ឧទាហរណ៍ទាំងនេះមានលក្ខណៈអរូបី វាមិនជាប់ទាក់ទងនឹងបញ្ហានៃគីមីវិទ្យាវិភាគទេ។ ឧទាហរណ៍ជាក់ស្តែងនៃការប្រើប្រាស់ពិជគណិតម៉ាទ្រីសក្នុងគីមីវិទ្យាត្រូវបានពិភាក្សានៅក្នុងអត្ថបទផ្សេងទៀតដែលឧទ្ទិសដល់កម្មវិធីគីមីវិទ្យាផ្សេងៗ។

ការវាស់វែងភាគច្រើនដែលធ្វើឡើងក្នុងគីមីវិទ្យាវិភាគគឺមិនមែនដោយផ្ទាល់ទេ ប៉ុន្តែ ដោយប្រយោល។. នេះមានន័យថានៅក្នុងការពិសោធន៍ជំនួសឱ្យតម្លៃនៃការវិភាគដែលចង់បាន C (ការប្រមូលផ្តុំ) តម្លៃមួយផ្សេងទៀតត្រូវបានទទួល។ x(សញ្ញា) ដែលទាក់ទងនឹងប៉ុន្តែមិនស្មើនឹង C, i.e. x(C) ≠ C. តាមក្បួនមួយប្រភេទនៃភាពអាស្រ័យ x(C) មិនត្រូវបានគេស្គាល់ទេ ប៉ុន្តែជាសំណាងល្អនៅក្នុងគីមីវិទ្យាវិភាគ ការវាស់វែងភាគច្រើនគឺសមាមាត្រ។ នេះមានន័យថាជាការផ្តោតអារម្មណ៍នៃ C in កដង, សញ្ញា X នឹងកើនឡើងដោយចំនួនដូចគ្នា។, i.e. x(កគ) = ក x(គ). លើសពីនេះ សញ្ញាក៏ជាការបន្ថែមផងដែរ ដូច្នេះសញ្ញាពីគំរូដែលមានសារធាតុពីរដែលមានកំហាប់ C 1 និង C 2 នឹងស្មើនឹងផលបូកនៃសញ្ញាពីសមាសធាតុនីមួយៗ i.e. x(C1 + C2) = x(C1)+ x(C2) ។ សមាមាត្រ និងការបន្ថែមរួមគ្នាផ្តល់ឱ្យ លីនេអ៊ែរ. ឧទាហរណ៍ជាច្រើនអាចត្រូវបានផ្តល់ឱ្យដើម្បីបង្ហាញពីគោលការណ៍នៃលីនេអ៊ែរ ប៉ុន្តែវាគ្រប់គ្រាន់ដើម្បីនិយាយអំពីឧទាហរណ៍ដ៏ទាក់ទាញបំផុតពីរ - chromatography និង spectroscopy ។ លក្ខណៈពិសេសទីពីរដែលមាននៅក្នុងការពិសោធន៍ក្នុងគីមីវិទ្យាវិភាគគឺ ពហុឆានែល. ឧបករណ៍វិភាគទំនើបក្នុងពេលដំណាលគ្នាវាស់វែងសញ្ញាសម្រាប់បណ្តាញជាច្រើន។ ឧទាហរណ៍ អាំងតង់ស៊ីតេនៃការបញ្ជូនពន្លឺត្រូវបានវាស់សម្រាប់ប្រវែងរលកជាច្រើនក្នុងពេលតែមួយ i.e. វិសាលគម។ ដូច្នេះហើយ នៅក្នុងការពិសោធន៍ យើងកំពុងដោះស្រាយជាមួយនឹងសញ្ញាផ្សេងៗគ្នា x 1 , x 2 ,...., x n កំណត់លក្ខណៈនៃកំហាប់ C 1 , C 2 , ... , C m នៃសារធាតុដែលមាននៅក្នុងប្រព័ន្ធដែលកំពុងសិក្សា។

អង្ករ។ 1 Spectra

ដូច្នេះ ការពិសោធន៍វិភាគត្រូវបានកំណត់លក្ខណៈដោយលីនេអ៊ែរ និងពហុវិមាត្រ។ ដូច្នេះ វាជាការងាយស្រួលក្នុងការពិចារណាទិន្នន័យពិសោធន៍ជាវ៉ិចទ័រ និងម៉ាទ្រីស ហើយរៀបចំពួកវាដោយប្រើឧបករណ៍នៃម៉ាទ្រីសពិជគណិត។ ផលផ្លែនៃវិធីសាស្រ្តនេះត្រូវបានបង្ហាញដោយឧទាហរណ៍ដែលបានបង្ហាញនៅក្នុង ដែលបង្ហាញពីវិសាលគមចំនួនបីដែលបានយកសម្រាប់ 200 រលកប្រវែងពី 4000 ទៅ 4796 សង់ទីម៉ែត្រ-1 ។ ដំបូង ( x 1) និងទីពីរ ( x 2) វិសាលគមត្រូវបានទទួលសម្រាប់សំណាកស្តង់ដារដែលកំហាប់នៃសារធាតុពីរ A និង B ត្រូវបានគេដឹង: នៅក្នុងគំរូទីមួយ [A] = 0.5, [B] = 0.1 និងនៅក្នុងគំរូទីពីរ [A] = 0.2, [ ខ] = 0.6 ។ អ្វីដែលអាចត្រូវបាននិយាយអំពីគំរូថ្មីដែលមិនស្គាល់ វិសាលគមដែលត្រូវបានចង្អុលបង្ហាញ x 3 ?

ពិចារណាលើវិសាលគមពិសោធន៍បី x 1 , x 2 និង x 3 ជាវ៉ិចទ័របីនៃវិមាត្រ 200។ ដោយប្រើពិជគណិតលីនេអ៊ែរ មួយអាចបង្ហាញយ៉ាងងាយស្រួលនោះ។ x 3 = 0.1 x 1 +0.3 x 2 ដូច្នេះគំរូទី 3 ជាក់ស្តែងមានតែសារធាតុ A និង B ក្នុងកំហាប់ [A] = 0.5 × 0.1 + 0.2 × 0.3 = 0.11 និង [B] = 0.1 × 0.1 + 0.6 × 0.3 = 0.19 ។

1. ព័ត៌មានមូលដ្ឋាន

1.1 ម៉ាទ្រីស

ម៉ាទ្រីសឧទាហរណ៍ គេហៅថាតារាងចតុកោណនៃលេខ

អង្ករ។ 2 ម៉ាទ្រីស

Matrices ត្រូវបានតាងដោយអក្សរដិតធំ ( ក) និងធាតុរបស់ពួកគេ - ជាមួយអក្សរតូចដែលត្រូវគ្នាជាមួយសន្ទស្សន៍ ឧ។ កអ៊ី. លិបិក្រមទីមួយដាក់លេខជួរ និងលេខទីពីរជាជួរ។ នៅក្នុងគីមីវិទ្យា វាជាទម្លាប់ក្នុងការកំណត់តម្លៃអតិបរមានៃលិបិក្រមដោយអក្សរដូចគ្នាទៅនឹងសន្ទស្សន៍ខ្លួនវា ប៉ុន្តែជាអក្សរធំ។ ដូច្នេះម៉ាទ្រីស កក៏អាចសរសេរជា ( ក អ៊ី , ខ្ញុំ = 1,..., ខ្ញុំ; j = 1,..., ជ) សម្រាប់ឧទាហរណ៍ម៉ាទ្រីស ខ្ញុំ = 4, ជ= 3 និង ក 23 = −7.5.

លេខគូ ខ្ញុំនិង ជត្រូវបានគេហៅថាវិមាត្រនៃម៉ាទ្រីសហើយត្រូវបានតំណាងថាជា ខ្ញុំ× ជ. ឧទាហរណ៍នៃម៉ាទ្រីសក្នុងគីមីវិទ្យាគឺជាសំណុំនៃវិសាលគមដែលទទួលបានសម្រាប់ ខ្ញុំគំរូនៅលើ ជប្រវែងរលក។

១.២. ប្រតិបត្តិការសាមញ្ញបំផុតជាមួយម៉ាទ្រីស

ម៉ាទ្រីសអាច គុណនឹងលេខ. ក្នុងករណីនេះធាតុនីមួយៗត្រូវបានគុណនឹងលេខនេះ។ ឧទាហរណ៍ -

អង្ករ។ 3 ការគុណម៉ាទ្រីសដោយលេខ

ម៉ាទ្រីសពីរនៃវិមាត្រដូចគ្នាអាចជាធាតុដែលមានប្រាជ្ញា បត់និង ដក. ឧទាហរណ៍,

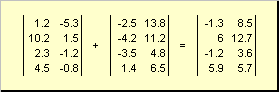
អង្ករ។ 4 ការបន្ថែមម៉ាទ្រីស

ជាលទ្ធផលនៃការគុណដោយលេខមួយ និងការបូកមួយ ម៉ាទ្រីសនៃវិមាត្រដូចគ្នាត្រូវបានទទួល។

ម៉ាទ្រីសសូន្យគឺជាម៉ាទ្រីសដែលមានលេខសូន្យ។ វាត្រូវបានកំណត់ អូ. វាច្បាស់ណាស់។ ក+អូ = ក, ក−ក = អូនិង 0 ក = អូ.

ម៉ាទ្រីសអាច បញ្ជូន. ក្នុងអំឡុងពេលប្រតិបត្តិការនេះម៉ាទ្រីសត្រូវបានត្រឡប់, i.e. ជួរ​ដេក​និង​ជួរ​ឈរ​ត្រូវ​បាន​ផ្លាស់​ប្តូ​រ​។ ការផ្លាស់ប្តូរត្រូវបានចង្អុលបង្ហាញដោយសញ្ញាចុច ក" ឬសន្ទស្សន៍ ក t ដូច្នេះប្រសិនបើ ក = {ក អ៊ី , ខ្ញុំ = 1,..., ខ្ញុំ; j = 1,...,ជ) បន្ទាប់មក ក t = ( ក ជី , j = 1,...,ជ; i = 1,..., ខ្ញុំ) ឧទាហរណ៍

អង្ករ។ 5 ការផ្ទេរម៉ាទ្រីស

វាច្បាស់ណាស់ថា ( ក t) t = ក, (ក+ខ) t = ក t + ខ t

១.៣. គុណម៉ាទ្រីស

ម៉ាទ្រីសអាច គុណប៉ុន្តែលុះត្រាតែពួកគេមានវិមាត្រសមស្រប។ ហេតុអ្វីបានជាវាដូច្នេះនឹងច្បាស់ពីនិយមន័យ។ ផលិតផលម៉ាទ្រីស ក, វិមាត្រ ខ្ញុំ× ខេនិងម៉ាទ្រីស ខ, វិមាត្រ ខេ× ជត្រូវបានគេហៅថាម៉ាទ្រីស គ, វិមាត្រ ខ្ញុំ× ជដែលធាតុទាំងនោះជាលេខ

ដូច្នេះសម្រាប់ផលិតផល ABវាចាំបាច់ដែលចំនួនជួរឈរនៅក្នុងម៉ាទ្រីសខាងឆ្វេង កគឺស្មើនឹងចំនួនជួរដេកក្នុងម៉ាទ្រីសខាងស្តាំ ខ. ឧទាហរណ៍ផលិតផលម៉ាទ្រីស -

រូបភាពទី ៦ ផលិតផលនៃម៉ាទ្រីស

ក្បួនគុណម៉ាទ្រីសអាចត្រូវបានបង្កើតដូចខាងក្រោម។ ដើម្បីស្វែងរកធាតុនៃម៉ាទ្រីស គឈរនៅចំនុចប្រសព្វ ខ្ញុំ- បន្ទាត់ទី និង j- ជួរ​ឈរ ( គ អ៊ី) ត្រូវតែគុណធាតុដោយធាតុ ខ្ញុំ- ជួរទី 1 នៃម៉ាទ្រីសទីមួយ កនៅ​លើ j- ជួរទី 2 នៃម៉ាទ្រីសទីពីរ ខហើយបន្ថែមលទ្ធផលទាំងអស់។ ដូច្នេះក្នុងឧទាហរណ៍ដែលបានបង្ហាញ ធាតុពីជួរទីបី និងជួរទីពីរត្រូវបានទទួលជាផលបូកនៃផលិតផលដែលមានប្រាជ្ញានៃជួរទីបី។ កនិងជួរទីពីរ ខ

រូបភាពទី 7 ធាតុនៃផលិតផលនៃម៉ាទ្រីស

ផលិតផលនៃម៉ាទ្រីសអាស្រ័យលើលំដាប់, i.e. AB ≠ បយ៉ាងហោចណាស់សម្រាប់ហេតុផលវិមាត្រ។ វាត្រូវបានគេនិយាយថាមិនផ្លាស់ប្តូរ។ ទោះជាយ៉ាងណាក៏ដោយផលិតផលនៃម៉ាទ្រីសគឺពាក់ព័ន្ធ។ វាមានន័យថា ABC = (AB)គ = ក(BC) លើសពីនេះទៅទៀត វាក៏មានការចែកចាយផងដែរ i.e. ក(ខ+គ) = AB+AC. វាច្បាស់ណាស់។ អូ = អូ.

១.៤. ម៉ាទ្រីសការ៉េ

ប្រសិនបើចំនួនជួរឈរនៃម៉ាទ្រីសគឺស្មើនឹងចំនួនជួរដេករបស់វា ( ខ្ញុំ = J=N) បន្ទាប់មកម៉ាទ្រីសបែបនេះត្រូវបានគេហៅថាការ៉េ។ នៅក្នុងផ្នែកនេះ យើងនឹងពិចារណាតែម៉ាទ្រីសបែបនេះប៉ុណ្ណោះ។ ក្នុង​ចំណោម​ម៉ាទ្រីស​ទាំងនេះ គេ​អាច​បែងចែក​ម៉ាទ្រីស​ដែល​មាន​លក្ខណៈ​ពិសេស។

នៅលីវម៉ាទ្រីស (បញ្ជាក់ ខ្ញុំហើយពេលខ្លះ អ៊ី) គឺជាម៉ាទ្រីសដែលធាតុទាំងអស់ស្មើនឹងសូន្យ លើកលែងតែអង្កត់ទ្រូងដែលស្មើនឹង 1 ពោលគឺឧ។

ជាក់ស្តែង អាយ = អាយ.អេ = ក.

ម៉ាទ្រីសត្រូវបានគេហៅថា អង្កត់ទ្រូងប្រសិនបើធាតុទាំងអស់របស់វា លើកលែងតែអង្កត់ទ្រូង ( ក ii) ស្មើនឹងសូន្យ។ ឧទាហរណ៍

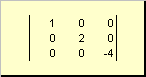
អង្ករ។ 8 ម៉ាទ្រីសអង្កត់ទ្រូង

ម៉ាទ្រីស កហៅថាកំពូល ត្រីកោណប្រសិនបើធាតុទាំងអស់របស់វាស្ថិតនៅខាងក្រោមអង្កត់ទ្រូងគឺស្មើនឹងសូន្យ ពោលគឺឧ។ ក អ៊ី= 0, នៅ ខ្ញុំ>j. ឧទាហរណ៍

អង្ករ។ 9 ម៉ាទ្រីសត្រីកោណខាងលើ

ម៉ាទ្រីសត្រីកោណទាបត្រូវបានកំណត់ស្រដៀងគ្នា។

ម៉ាទ្រីស កបានហៅ ស៊ីមេទ្រី, ប្រសិនបើ ក t = ក. ក្នុង​ន័យ​ផ្សេងទៀត ក អ៊ី = ក ជី. ឧទាហរណ៍

អង្ករ។ 10 ម៉ាទ្រីសស៊ីមេទ្រី

ម៉ាទ្រីស កបានហៅ រាងមូល, ប្រសិនបើ

ក t ក = អេ t = ខ្ញុំ.

ម៉ាទ្រីសត្រូវបានគេហៅថា ធម្មតា។ប្រសិនបើ

១.៥. ដាននិងកត្តាកំណត់

កំពុងតាមម៉ាទ្រីសការ៉េ ក(តំណាង Tr( ក) ឬ Sp( ក)) គឺជាផលបូកនៃធាតុអង្កត់ទ្រូងរបស់វា

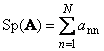
ឧទាហរណ៍,

អង្ករ។ 11 ដានម៉ាទ្រីស

វាច្បាស់ណាស់។

Sp(α ក) = α Sp( ក) និង

Sp( ក+ខ) = Sp( ក) + Sp( ខ).

វាអាចត្រូវបានបង្ហាញថា

Sp( ក) = Sp( ក t), Sp( ខ្ញុំ) = ន,

ហើយនោះផងដែរ។

Sp( AB) = Sp( ប).

លក្ខណៈសំខាន់មួយទៀតនៃម៉ាទ្រីសការ៉េគឺរបស់វា។ កត្តាកំណត់(តំណាងដោយ det( ក)). និយមន័យនៃកត្តាកំណត់នៅក្នុងករណីទូទៅគឺស្មុគស្មាញជាង ដូច្នេះយើងនឹងចាប់ផ្តើមជាមួយនឹងជម្រើសដ៏សាមញ្ញបំផុត - ម៉ាទ្រីស កវិមាត្រ (២ × ២) ។ បន្ទាប់មក

សម្រាប់ម៉ាទ្រីស (3×3) កត្តាកំណត់នឹងស្មើនឹង

ក្នុងករណីម៉ាទ្រីស ( ន× ន) កត្តាកំណត់ត្រូវបានគណនាជាផលបូក 1 2 3 ... ន= ន! លក្ខខណ្ឌនីមួយៗគឺស្មើនឹង

សន្ទស្សន៍ k 1 , k 2 ,..., k Nត្រូវបានកំណត់ថាជាការផ្លាស់ប្តូរតាមលំដាប់ដែលអាចធ្វើបានទាំងអស់។ rលេខនៅក្នុងសំណុំ (1, 2, ... , ន) ការគណនានៃកត្តាកំណត់ម៉ាទ្រីសគឺជានីតិវិធីដ៏ស្មុគស្មាញដែលក្នុងការអនុវត្តត្រូវបានអនុវត្តដោយប្រើកម្មវិធីពិសេស។ ឧទាហរណ៍,

អង្ករ។ 12 កត្តាកំណត់ម៉ាទ្រីស

យើងកត់សំគាល់តែលក្ខណៈសម្បត្តិជាក់ស្តែង៖

det( ខ្ញុំ) = 1, det( ក) = det( ក t)

det( AB) = det( ក)det( ខ).

១.៦. វ៉ិចទ័រ

ប្រសិនបើម៉ាទ្រីសមានជួរឈរតែមួយ ( ជ= 1) បន្ទាប់មកវត្ថុបែបនេះត្រូវបានគេហៅថា វ៉ិចទ័រ. ច្បាស់ជាងនេះទៅទៀត វ៉ិចទ័រជួរឈរ។ ឧទាហរណ៍

ឧទាហរណ៍ Matrices ដែល​មាន​ជួរ​មួយ​ក៏​អាច​ត្រូវ​បាន​ពិចារណា​ផង​ដែរ​

វត្ថុនេះក៏ជាវ៉ិចទ័រដែរ ប៉ុន្តែ វ៉ិចទ័រជួរ. នៅពេលវិភាគទិន្នន័យ វាជារឿងសំខាន់ក្នុងការយល់ដឹងថាតើវ៉ិចទ័រមួយណាដែលយើងកំពុងដោះស្រាយ - ជួរឈរ ឬជួរដេក។ ដូច្នេះវិសាលគមដែលបានយកសម្រាប់គំរូមួយអាចត្រូវបានចាត់ទុកថាជាវ៉ិចទ័រជួរដេក។ បន្ទាប់មកសំណុំនៃអាំងតង់ស៊ីតេវិសាលគមនៅចម្ងាយរលកមួយចំនួនសម្រាប់គំរូទាំងអស់គួរតែត្រូវបានចាត់ទុកជាវ៉ិចទ័រជួរឈរ។

វិមាត្រនៃវ៉ិចទ័រគឺជាចំនួនធាតុរបស់វា។

វាច្បាស់ណាស់ថាវ៉ិចទ័រជួរឈរណាមួយអាចត្រូវបានបំលែងទៅជាវ៉ិចទ័រជួរដេកដោយការផ្លាស់ប្តូរ ពោលគឺឧ។

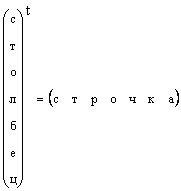
ក្នុងករណីទាំងនោះដែលទម្រង់នៃវ៉ិចទ័រមិនត្រូវបានបញ្ជាក់ជាក់លាក់ទេ ប៉ុន្តែគ្រាន់តែនិយាយវ៉ិចទ័រ នោះពួកវាមានន័យថាវ៉ិចទ័រជួរឈរ។ យើងក៏នឹងប្រកាន់ខ្ជាប់នូវច្បាប់នេះដែរ។ វ៉ិចទ័រត្រូវបានតំណាងដោយអក្សរដិតដោយផ្ទាល់អក្សរតូច។ វ៉ិចទ័រសូន្យគឺជាវ៉ិចទ័រធាតុទាំងអស់ដែលស្មើនឹងសូន្យ។ វាត្រូវបានតំណាង 0 .

១.៧. ប្រតិបត្តិការសាមញ្ញបំផុតជាមួយវ៉ិចទ័រ

វ៉ិចទ័រ​អាច​ត្រូវ​បាន​បន្ថែម​និង​គុណ​ដោយ​លេខ​ក្នុង​វិធី​ដូច​គ្នា​នឹង​ម៉ាទ្រីស។ ឧទាហរណ៍,

អង្ករ។ 13 ប្រតិបត្តិការជាមួយវ៉ិចទ័រ

វ៉ិចទ័រពីរ xនិង yបានហៅ collinearប្រសិនបើមានលេខ α បែបនេះ

១.៨. ផលិតផលវ៉ិចទ័រ

វ៉ិចទ័រពីរនៃវិមាត្រដូចគ្នា។ នអាចត្រូវបានគុណ។ សូមឱ្យមានវ៉ិចទ័រពីរ x = (x 1 , x 2 ,...,xន) t និង y = (y 1 , y 2 ,...,yន) t ។ ណែនាំដោយច្បាប់គុណ "ជួរដេកតាមជួរឈរ" យើងអាចបង្កើតផលិតផលពីរពីពួកវា៖ x t yនិង xy t ការងារដំបូង

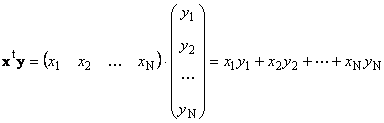
បានហៅ មាត្រដ្ឋានឬ ខាងក្នុង. លទ្ធផលរបស់វាគឺលេខ។ វាក៏ប្រើសញ្ញាសម្គាល់ ( x,y)= x t y. ឧទាហរណ៍,

អង្ករ។ 14 ផលិតផលខាងក្នុង (មាត្រដ្ឋាន)

ការងារទីពីរ

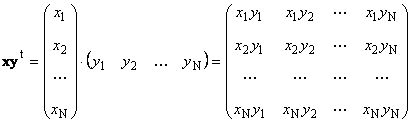
បានហៅ ខាងក្រៅ. លទ្ធផលរបស់វាគឺម៉ាទ្រីសវិមាត្រ ( ន× ន) ឧទាហរណ៍,

អង្ករ។ 15 ផលិតផលខាងក្រៅ

វ៉ិចទ័រដែលផលិតផលមាត្រដ្ឋានស្មើនឹងសូន្យត្រូវបានហៅ រាងមូល.

១.៩. បទដ្ឋានវ៉ិចទ័រ

ផលិតផលមាត្រដ្ឋាននៃវ៉ិចទ័រជាមួយខ្លួនវាត្រូវបានគេហៅថាការេ scalar ។ តម្លៃនេះ។

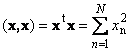
កំណត់ការ៉េ ប្រវែងវ៉ិចទ័រ x. ដើម្បីសម្គាល់ប្រវែង (ហៅផងដែរថា បទដ្ឋានវ៉ិចទ័រ) សញ្ញាណត្រូវបានប្រើ

ឧទាហរណ៍,

អង្ករ។ 16 បទដ្ឋានវ៉ិចទ័រ

វ៉ិចទ័រប្រវែងឯកតា (|| x|| = 1) ត្រូវបានគេហៅថាធម្មតា។ វ៉ិចទ័រមិនសូន្យ ( x ≠ 0 ) អាច​ត្រូវ​បាន​ធម្មតា​ដោយ​ការ​បែង​ចែក​វា​ដោយ​ប្រវែង, i.e. x = ||x|| (x/||x||) = ||x|| អ៊ី. នៅទីនេះ អ៊ី = x/||x|| គឺជាវ៉ិចទ័រធម្មតា។

វ៉ិចទ័រត្រូវបានគេហៅថា orthonormal ប្រសិនបើពួកវាត្រូវបានធ្វើឱ្យមានលក្ខណៈធម្មតា និងរាងជាគូ។

១.១០. មុំរវាងវ៉ិចទ័រ

ផលិតផលមាត្រដ្ឋានកំណត់និង ជ្រុងφ រវាងវ៉ិចទ័រពីរ xនិង y

ប្រសិនបើវ៉ិចទ័រមានរាងមូល នោះ cosφ = 0 និង φ = π/2 ហើយប្រសិនបើវាជា collinear បន្ទាប់មក cosφ = 1 និង φ = 0 ។

១.១១. តំណាងវ៉ិចទ័រនៃម៉ាទ្រីស

ម៉ាទ្រីសនីមួយៗ កទំហំ ខ្ញុំ× ជអាចត្រូវបានតំណាងជាសំណុំនៃវ៉ិចទ័រ

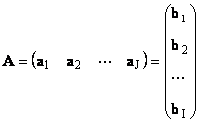
នៅទីនេះវ៉ិចទ័រនីមួយៗ ក jគឺ j-th ជួរឈរនិងវ៉ិចទ័រជួរដេក ខ ខ្ញុំគឺ ខ្ញុំ- ជួរទីនៃម៉ាទ្រីស ក

១.១២. វ៉ិចទ័រអាស្រ័យលីនេអ៊ែរ

វ៉ិចទ័រដែលមានវិមាត្រដូចគ្នា ( ន) អាច​ត្រូវ​បាន​បន្ថែម​និង​គុណ​ដោយ​ចំនួន​ដូច​ជា​ម៉ាទ្រីស។ លទ្ធផលគឺជាវ៉ិចទ័រនៃវិមាត្រដូចគ្នា។ សូមឱ្យមានវ៉ិចទ័រជាច្រើននៃវិមាត្រដូចគ្នា។ x 1 , x 2 ,...,x K និងចំនួនដូចគ្នានៃលេខ α α 1 , α 2 , ... , α ខេ. វ៉ិចទ័រ

y= α ១ x 1 + α 2 x 2 +...+α ខេ x ខេ

បានហៅ ការរួមបញ្ចូលគ្នាលីនេអ៊ែរវ៉ិចទ័រ x k .

ប្រសិនបើមានលេខមិនមែនសូន្យបែបនេះ α k ≠ 0, k = 1,..., ខេអ្វី y = 0 បន្ទាប់មកសំណុំនៃវ៉ិចទ័របែបនេះ x kបានហៅ អាស្រ័យតាមលីនេអ៊ែរ. បើមិនដូច្នោះទេ វ៉ិចទ័រត្រូវបានគេហៅថាឯករាជ្យលីនេអ៊ែរ។ ឧទាហរណ៍ វ៉ិចទ័រ x 1 = (2, 2) t និង x 2 = (−1, −1) t គឺអាស្រ័យតាមលីនេអ៊ែរ ចាប់តាំងពី x 1 +2x 2 = 0

១.១៣. ចំណាត់ថ្នាក់ម៉ាទ្រីស

ពិចារណាសំណុំនៃ ខេវ៉ិចទ័រ x 1 , x 2 ,...,x ខេវិមាត្រ ន. ចំណាត់ថ្នាក់នៃប្រព័ន្ធវ៉ិចទ័រនេះគឺជាចំនួនអតិបរមានៃវ៉ិចទ័រឯករាជ្យលីនេអ៊ែរ។ ឧទាហរណ៍នៅក្នុងឈុត

ឧទាហរណ៍មានតែវ៉ិចទ័រឯករាជ្យពីរ x 1 និង x 2 ដូច្នេះចំណាត់ថ្នាក់របស់វាគឺ 2 ។

ជាក់ស្តែងប្រសិនបើមានវ៉ិចទ័រច្រើននៅក្នុងសំណុំជាងវិមាត្ររបស់វា ( ខេ>ន) បន្ទាប់មក ពួកវាពឹងផ្អែកជាលីនេអ៊ែរ។

ចំណាត់ថ្នាក់ម៉ាទ្រីស(កំណត់ដោយចំណាត់ថ្នាក់ ( ក)) គឺជាចំណាត់ថ្នាក់នៃប្រព័ន្ធវ៉ិចទ័រដែលវាមាន។ ទោះបីជាម៉ាទ្រីសណាមួយអាចត្រូវបានតំណាងជាពីរវិធី (វ៉ិចទ័រជួរឈរ ឬវ៉ិចទ័រជួរ) វាមិនប៉ះពាល់ដល់តម្លៃចំណាត់ថ្នាក់ទេ ចាប់តាំងពី

១.១៤. ម៉ាទ្រីសបញ្ច្រាស

ម៉ាទ្រីសការ៉េ កត្រូវបានគេហៅថា non-degenerate ប្រសិនបើវាមានតែមួយគត់ បញ្ច្រាសម៉ាទ្រីស ក-១ កំណត់ដោយលក្ខខណ្ឌ

អេ −1 = ក −1 ក = ខ្ញុំ.

ម៉ាទ្រីសបញ្ច្រាសមិនមានសម្រាប់ម៉ាទ្រីសទាំងអស់ទេ។ លក្ខខណ្ឌចាំបាច់ និងគ្រប់គ្រាន់សម្រាប់ការមិនវិវឌ្ឍន៍គឺ

det( ក) ≠ 0 ឬចំណាត់ថ្នាក់( ក) = ន.

ការ​បញ្ច្រាស​ម៉ាទ្រីស​គឺ​ជា​នីតិវិធី​ស្មុគស្មាញ​ដែល​មាន​កម្មវិធី​ពិសេស។ ឧទាហរណ៍,

អង្ករ។ 17 ការបញ្ច្រាសម៉ាទ្រីស

យើងផ្តល់រូបមន្តសម្រាប់ករណីសាមញ្ញបំផុត - ម៉ាទ្រីស 2 × 2

ប្រសិនបើម៉ាទ្រីស កនិង ខគឺមិន degenerate បន្ទាប់មក

(AB) −1 = ខ −1 ក −1 .

១.១៥. ម៉ាទ្រីស Pseudo-បញ្ច្រាស

ប្រសិនបើម៉ាទ្រីស កគឺ degenerate ហើយម៉ាទ្រីសបញ្ច្រាសមិនមានទេ បន្ទាប់មកក្នុងករណីខ្លះគេអាចប្រើបាន។ pseudo-បញ្ច្រាសម៉ាទ្រីស ដែលត្រូវបានកំណត់ថាជាម៉ាទ្រីស ក+ នោះ។

អេ + ក = ក.

ម៉ាទ្រីស pseudo-inverse matrix មិនមែនតែមួយទេ ហើយទម្រង់របស់វាអាស្រ័យលើវិធីសាស្ត្រសាងសង់។ ឧទាហរណ៍ សម្រាប់ម៉ាទ្រីសរាងចតុកោណ អ្នកអាចប្រើវិធីសាស្ត្រ Moore-Penrose ។

ប្រសិនបើចំនួនជួរឈរតិចជាងចំនួនជួរដេក

ក + =(ក t ក) −1 ក t

ឧទាហរណ៍,

អង្ករ។ 17a ការបញ្ច្រាសម៉ាទ្រីស Pseudo

ប្រសិនបើចំនួនជួរឈរធំជាងចំនួនជួរដេក

ក + =ក t ( អេ t) −1

១.១៦. គុណនៃវ៉ិចទ័រដោយម៉ាទ្រីស

វ៉ិចទ័រ xអាចត្រូវបានគុណដោយម៉ាទ្រីស កវិមាត្រសមរម្យ។ ក្នុងករណីនេះវ៉ិចទ័រជួរឈរត្រូវបានគុណនៅខាងស្តាំ ពូថៅហើយខ្សែវ៉ិចទ័រនៅខាងឆ្វេង x t ក. ប្រសិនបើវិមាត្រនៃវ៉ិចទ័រ ជនិងវិមាត្រនៃម៉ាទ្រីស ខ្ញុំ× ជបន្ទាប់មកលទ្ធផលគឺជាវ៉ិចទ័រនៃវិមាត្រ ខ្ញុំ. ឧទាហរណ៍,

អង្ករ។ 18 ការគុណវ៉ិចទ័រ-ម៉ាទ្រីស

ប្រសិនបើម៉ាទ្រីស ក- ការ៉េ ( ខ្ញុំ× ខ្ញុំ) បន្ទាប់មកវ៉ិចទ័រ y = ពូថៅមានវិមាត្រដូចគ្នានឹង x. វាច្បាស់ណាស់។

ក(α ១ x 1 + α 2 x២) = α ១ ពូថៅ 1 + α 2 ពូថៅ 2 .

ដូច្នេះ matrices អាច​ត្រូវ​បាន​ចាត់​ទុក​ថា​ជា​ការ​បំប្លែង​លីនេអ៊ែរ​នៃ​វ៉ិចទ័រ។ ជាពិសេស x = x, គោ = 0 .

2. ព័ត៌មានបន្ថែម

២.១. ប្រព័ន្ធនៃសមីការលីនេអ៊ែរ

អនុញ្ញាតឱ្យ ក- ទំហំម៉ាទ្រីស ខ្ញុំ× ជ, ក ខ- វ៉ិចទ័រវិមាត្រ ជ. ពិចារណាសមីការ

ពូថៅ = ខ

ទាក់ទងនឹងវ៉ិចទ័រ x, វិមាត្រ ខ្ញុំ. សំខាន់នេះគឺជាប្រព័ន្ធនៃ ខ្ញុំសមីការលីនេអ៊ែរជាមួយ ជមិនស្គាល់ x 1 ,...,x ជ. ដំណោះ​ស្រាយ​មាន​ប្រសិន​បើ​និង​បាន​តែ​ប្រសិន​បើ​

ចំណាត់ថ្នាក់ ( ក) = ចំណាត់ថ្នាក់( ខ) = រ,

កន្លែងណា ខគឺជាម៉ាទ្រីសវិមាត្របន្ថែម ខ្ញុំ×( J+1) ដែលរួមមានម៉ាទ្រីស ក, padded ជាមួយជួរឈរមួយ។ ខ, ខ = (ក ខ) បើមិនដូច្នោះទេ សមីការមិនស៊ីសង្វាក់គ្នា។

ប្រសិនបើ ក រ = ខ្ញុំ = ជបន្ទាប់មកដំណោះស្រាយគឺប្លែក

x = ក −1 ខ.

ប្រសិនបើ ក រ < ខ្ញុំបន្ទាប់មកមានដំណោះស្រាយផ្សេងៗគ្នាជាច្រើនដែលអាចបញ្ជាក់បានក្នុងន័យនៃការរួមបញ្ចូលគ្នាលីនេអ៊ែរ ជ−រវ៉ិចទ័រ។ ប្រព័ន្ធនៃសមីការដូចគ្នា។ ពូថៅ = 0 ជាមួយម៉ាទ្រីសការ៉េ ក (ន× ន) មានដំណោះស្រាយមិនសំខាន់ ( x ≠ 0 ) ប្រសិនបើ និង លុះត្រាតែ det( ក) = 0. ប្រសិនបើ រ= ចំណាត់ថ្នាក់( ក)<នបន្ទាប់មកមាន ន−រដំណោះស្រាយឯករាជ្យលីនេអ៊ែរ។

២.២. ទម្រង់ Bilinear និង quadratic

ប្រសិនបើ ក កគឺជាម៉ាទ្រីសការ៉េ និង xនិង y- វ៉ិចទ័រនៃវិមាត្រដែលត្រូវគ្នា បន្ទាប់មកផលិតផលមាត្រដ្ឋាននៃទម្រង់ x t អាយបានហៅ bilinearរូបរាងដែលកំណត់ដោយម៉ាទ្រីស ក. នៅ x = yកន្សោម x t ពូថៅបានហៅ បួនជ្រុងទម្រង់។

២.៣. ម៉ាទ្រីសច្បាស់លាស់វិជ្ជមាន

ម៉ាទ្រីសការ៉េ កបានហៅ និយមន័យវិជ្ជមានប្រសិនបើសម្រាប់វ៉ិចទ័រដែលមិនសូន្យ x ≠ 0 ,

x t ពូថៅ > 0.

នេះ។ អវិជ្ជមាន (x t ពូថៅ < 0), មិនអវិជ្ជមាន (x t ពូថៅ≥ 0) និង មិនវិជ្ជមាន (x t ពូថៅ≤ 0) ម៉ាទ្រីសជាក់លាក់។

២.៤. ការរលួយ Cholesky

ប្រសិនបើម៉ាទ្រីសស៊ីមេទ្រី កមានភាពវិជ្ជមានច្បាស់លាស់ បន្ទាប់មកមានម៉ាទ្រីសត្រីកោណតែមួយគត់ យូជាមួយនឹងធាតុវិជ្ជមាន

ក = យូ t យូ.

ឧទាហរណ៍,

អង្ករ។ 19 ការរលួយ Cholesky

២.៥. ការរលួយប៉ូល

អនុញ្ញាតឱ្យ កគឺ​ជា​ម៉ាទ្រីស​ការ៉េ​ដែល​មិន​ខូច​ទ្រង់ទ្រាយ​នៃ​វិមាត្រ ន× ន. បន្ទាប់មកមានតែមួយគត់ ប៉ូលការសម្តែង

ក = SR

កន្លែងណា សគឺជាម៉ាទ្រីសស៊ីមេទ្រីដែលមិនអវិជ្ជមាន និង រគឺជាម៉ាទ្រីស orthogonal ។ ម៉ាទ្រីស សនិង រអាច​កំណត់​យ៉ាង​ច្បាស់៖

ស 2 = អេ t ឬ ស = (អេ t) ½ និង រ = ស −1 ក = (អេ t) − ½ ក.

ឧទាហរណ៍,

អង្ករ។ 20 ការរលួយប៉ូល

ប្រសិនបើម៉ាទ្រីស កគឺ degenerate បន្ទាប់មក decomposition គឺមិនមានតែមួយគត់ - គឺ: សនៅ​តែ​ម្នាក់​ឯង, ប៉ុន្តែ រអាចមានច្រើន។ ការរលួយប៉ូលតំណាងឱ្យម៉ាទ្រីស កជាការរួមបញ្ចូលគ្នានៃការបង្ហាប់ / លាតសន្ធឹង សនិងងាក រ.

២.៦. Eigenvectors និង eigenvalues

អនុញ្ញាតឱ្យ កគឺជាម៉ាទ្រីសការ៉េ។ វ៉ិចទ័រ vបានហៅ វ៉ិចទ័រផ្ទាល់ខ្លួនម៉ាទ្រីស ក, ប្រសិនបើ

Av = λ v,

កន្លែងដែលលេខ λ ត្រូវបានហៅ eigenvalueម៉ាទ្រីស ក. ដូច្នេះការផ្លាស់ប្តូរដែលម៉ាទ្រីសអនុវត្ត កលើវ៉ិចទ័រ v, ត្រូវបានកាត់បន្ថយទៅជាការលាតសន្ធឹង ឬបង្ហាប់សាមញ្ញជាមួយនឹងកត្តា λ ។ eigenvector ត្រូវបានកំណត់រហូតដល់គុណដោយថេរ α ≠ 0, i.e. ប្រសិនបើ vគឺជា eigenvector បន្ទាប់មក α vក៏ជា eigenvector ផងដែរ។

២.៧. Eigenvalues

នៅម៉ាទ្រីស ក, វិមាត្រ ( ន× ន) មិនអាចធំជាង ន eigenvalues ​​។ ពួកគេពេញចិត្ត សមីការលក្ខណៈ

det( ក − λ ខ្ញុំ) = 0,

ដែលជាសមីការពិជគណិត ន- លំដាប់។ ជាពិសេស សម្រាប់ម៉ាទ្រីស 2×2 សមីការលក្ខណៈមានទម្រង់

ឧទាហរណ៍,

អង្ករ។ 21 Eigenvalues

សំណុំនៃ eigenvalues ​​λ 1 ,... , λ នម៉ាទ្រីស កបានហៅ វិសាលគម ក.

វិសាលគមមានលក្ខណៈសម្បត្តិផ្សេងៗ។ ជាពិសេស

det( ក) = λ 1 ×... ×λ ន, Sp( ក) = λ 1 +...+λ ន.

eigenvalues ​​នៃ​ម៉ាទ្រីស​បំពាន​អាច​ជា​ចំនួន​កុំផ្លិច ប៉ុន្តែ​ប្រសិនបើ​ម៉ាទ្រីស​គឺ​ស៊ីមេទ្រី ( ក t = ក) បន្ទាប់មក eigenvalues ​​របស់វាគឺពិតប្រាកដ។

២.៨. Eigenvectors

នៅម៉ាទ្រីស ក, វិមាត្រ ( ន× ន) មិនអាចធំជាង ន eigenvectors ដែលនីមួយៗត្រូវគ្នាទៅនឹងតម្លៃរបស់វា។ ដើម្បីកំណត់ eigenvector v នអ្នកត្រូវដោះស្រាយប្រព័ន្ធនៃសមីការដូចគ្នា។

(ក − λ ន ខ្ញុំ)v ន = 0 .

វាមានដំណោះស្រាយមិនសំខាន់ព្រោះ det( ក-λ ន ខ្ញុំ) = 0.

ឧទាហរណ៍,

អង្ករ។ 22 Eigenvectors

eigenvectors នៃម៉ាទ្រីសស៊ីមេទ្រីគឺ orthogonal ។

eigenvector នៃ​ម៉ាទ្រីស​ការ៉េ​គឺ​ជា​មួយ​ដែល​នៅ​ពេល​ដែល​គុណ​នឹង​ម៉ាទ្រីស​ដែល​បាន​ផ្តល់​ឱ្យ​លទ្ធផល​ជា​វ៉ិចទ័រ​រួម។ នៅក្នុងពាក្យសាមញ្ញ នៅពេលដែលម៉ាទ្រីសមួយត្រូវបានគុណដោយ eigenvector ក្រោយមកទៀតនៅតែដដែល ប៉ុន្តែគុណនឹងចំនួនមួយចំនួន។

និយមន័យ

eigenvector គឺជាវ៉ិចទ័រមិនសូន្យ V ដែលនៅពេលគុណនឹងម៉ាទ្រីសការ៉េ M ក្លាយជាខ្លួនវា កើនឡើងដោយចំនួន λ ។ នៅក្នុងការសម្គាល់ពិជគណិត វាមើលទៅដូចនេះ៖

M × V = λ × V,

ដែល λ គឺជា eigenvalue នៃម៉ាទ្រីស M.

ចូរយើងពិចារណាឧទាហរណ៍ជាលេខ។ ដើម្បីភាពងាយស្រួលនៃការសរសេរ លេខនៅក្នុងម៉ាទ្រីសនឹងត្រូវបានបំបែកដោយសញ្ញាក្បៀស។ ឧបមាថាយើងមានម៉ាទ្រីស៖

• M = 0; បួន;
• 6; 10.

ចូរគុណវាដោយវ៉ិចទ័រជួរឈរ៖

• V = -2;

នៅពេលគុណម៉ាទ្រីសដោយវ៉ិចទ័រជួរឈរ យើងក៏ទទួលបានវ៉ិចទ័រជួរឈរផងដែរ។ នៅក្នុងភាសាគណិតវិទ្យាដ៏តឹងរឹង រូបមន្តសម្រាប់គុណម៉ាទ្រីស 2 × 2 ដោយវ៉ិចទ័រជួរឈរនឹងមើលទៅដូចនេះ៖

• M × V = M11 × V11 + M12 × V21;
• M21 x V11 + M22 x V21 ។

M11 មានន័យថាធាតុនៃម៉ាទ្រីស M ដែលឈរនៅជួរទីមួយ និងជួរទីមួយ ហើយ M22 គឺជាធាតុដែលមានទីតាំងនៅជួរទីពីរ និងជួរទីពីរ។ សម្រាប់ម៉ាទ្រីសរបស់យើង ធាតុទាំងនេះគឺ M11 = 0, M12 = 4, M21 = 6, M22 10. សម្រាប់វ៉ិចទ័រជួរឈរ តម្លៃទាំងនេះគឺ V11 = –2, V21 = 1 ។ យោងតាមរូបមន្តនេះ យើងទទួលបានដូចខាងក្រោម លទ្ធផលនៃផលគុណនៃម៉ាទ្រីសការ៉េដោយវ៉ិចទ័រ៖

• M × V = 0 × (−2) + (4) × (1) = 4;
• 6 × (−2) + 10 × (1) = −2 ។

ដើម្បីភាពងាយស្រួលយើងសរសេរវ៉ិចទ័រជួរឈរទៅជាជួរដេកមួយ។ ដូច្នេះ យើង​បាន​គុណ​ម៉ាទ្រីស​ការេ​ដោយ​វ៉ិចទ័រ (-2; 1) លទ្ធផល​ជា​វ៉ិចទ័រ (4; -2) ។ ជាក់ស្តែងនេះគឺជាវ៉ិចទ័រដូចគ្នាគុណនឹង λ = -2 ។ Lambda ក្នុងករណីនេះតំណាងឱ្យតម្លៃ eigenvalue នៃម៉ាទ្រីស។

eigenvector នៃម៉ាទ្រីសគឺជាវ៉ិចទ័រ collinear ពោលគឺវត្ថុដែលមិនផ្លាស់ប្តូរទីតាំងរបស់វានៅក្នុងលំហ នៅពេលដែលវាត្រូវបានគុណដោយម៉ាទ្រីសមួយ។ គោលគំនិតនៃភាពជាប់គ្នានៅក្នុងពិជគណិតវ៉ិចទ័រគឺស្រដៀងទៅនឹងពាក្យនៃភាពស្របគ្នានៅក្នុងធរណីមាត្រ។ នៅក្នុងការបកស្រាយធរណីមាត្រ វ៉ិចទ័រ collinear គឺជាផ្នែកដឹកនាំស្របគ្នាដែលមានប្រវែងខុសៗគ្នា។ ចាប់តាំងពីសម័យ Euclid យើងដឹងថាបន្ទាត់តែមួយមានចំនួនបន្ទាត់គ្មានកំណត់ដែលស្របនឹងវា ដូច្នេះវាជាឡូជីខលក្នុងការសន្មត់ថាម៉ាទ្រីសនីមួយៗមានចំនួន eigenvectors គ្មានដែនកំណត់។

ពីឧទាហរណ៍មុន វាអាចត្រូវបានគេមើលឃើញថាទាំងពីរ (-8; 4) និង (16; -8) និង (32, -16) អាចជា eigenvectors ។ ទាំងអស់នេះគឺជាវ៉ិចទ័រ collinear ដែលត្រូវគ្នានឹង eigenvalue λ = -2 ។ នៅពេលគុណម៉ាទ្រីសដើមដោយវ៉ិចទ័រទាំងនេះ យើងនឹងនៅតែទទួលបានវ៉ិចទ័រជាលទ្ធផល ដែលខុសពីដើម 2 ដង។ នោះហើយជាមូលហេតុដែលនៅពេលដោះស្រាយបញ្ហាសម្រាប់ការស្វែងរក eigenvector វាត្រូវបានទាមទារដើម្បីស្វែងរកតែវត្ថុវ៉ិចទ័រឯករាជ្យលីនេអ៊ែរប៉ុណ្ណោះ។ ភាគច្រើនជាញឹកញាប់សម្រាប់ម៉ាទ្រីស n × n មាន n-th នៃ eigenvectors ។ ម៉ាស៊ីនគិតលេខរបស់យើងត្រូវបានរចនាឡើងសម្រាប់ការវិភាគនៃម៉ាទ្រីសការ៉េលំដាប់ទីពីរ ដូច្នេះស្ទើរតែតែងតែមាន eigenvectors ពីរនឹងត្រូវបានរកឃើញជាលទ្ធផល លើកលែងតែនៅពេលដែលវាស្របគ្នា។

នៅក្នុងឧទាហរណ៍ខាងលើ យើងបានដឹងជាមុនអំពី eigenvector នៃម៉ាទ្រីសដើម ហើយបានកំណត់ដោយមើលឃើញនូវចំនួន lambda ។ ទោះយ៉ាងណាក៏ដោយនៅក្នុងការអនុវត្តអ្វីគ្រប់យ៉ាងកើតឡើងតាមរបៀបផ្សេងទៀត: នៅដើមដំបូងមាន eigenvalues ​​ហើយមានតែ eigenvectors ប៉ុណ្ណោះ។

ក្បួនដោះស្រាយដំណោះស្រាយ

សូមក្រឡេកមើលម៉ាទ្រីសដើម M ម្តងទៀត ហើយព្យាយាមស្វែងរក eigenvectors ទាំងពីររបស់វា។ ដូច្នេះម៉ាទ្រីសមើលទៅដូចនេះ៖

• M = 0; បួន;
• 6; 10.

ដើម្បីចាប់ផ្តើម យើងត្រូវកំណត់ eigenvalue λ ដែលយើងត្រូវគណនាកត្តាកំណត់នៃម៉ាទ្រីសខាងក្រោម៖

• (0 − λ); បួន;
• ៦; (១០ − λ)។

ម៉ាទ្រីស​នេះ​ត្រូវ​បាន​ទទួល​ដោយ​ដក​មិន​ស្គាល់ λ ពី​ធាតុ​នៅ​លើ​អង្កត់ទ្រូង​មេ។ កត្តាកំណត់ត្រូវបានកំណត់ដោយរូបមន្តស្តង់ដារ៖

• detA = M11 × M21 − M12 × M22
• detA = (0 − λ) × (10 − λ) − 24

ដោយសារវ៉ិចទ័ររបស់យើងមិនត្រូវជាសូន្យទេ យើងយកសមីការលទ្ធផលដែលពឹងផ្អែកលីនេអ៊ែរ ហើយស្មើនឹង detA កត្តាកំណត់របស់យើងទៅសូន្យ។

(0 − λ) × (10 − λ) − 24 = 0

ចូរបើកតង្កៀប និងទទួលបានសមីការលក្ខណៈនៃម៉ាទ្រីស៖

λ 2 − 10λ − 24 = 0

នេះគឺជាសមីការការ៉េស្ដង់ដារដែលចាំបាច់ត្រូវដោះស្រាយក្នុងន័យនៃអ្នករើសអើង។

ឃ \u003d b 2 - 4ac \u003d (-10) × 2 - 4 × (-1) × 24 \u003d 100 + 96 \u003d 196

ឫសគល់នៃការរើសអើងគឺ sqrt(D) = 14 ដូច្នេះ λ1 = -2, λ2 = 12. ឥឡូវនេះសម្រាប់តម្លៃ lambda នីមួយៗ យើងត្រូវស្វែងរក eigenvector ។ ចូរយើងបង្ហាញពីមេគុណនៃប្រព័ន្ធសម្រាប់ λ = -2 ។

• M − λ × E = 2; បួន;
• 6; 12.

នៅក្នុងរូបមន្តនេះ E គឺជាម៉ាទ្រីសអត្តសញ្ញាណ។ ផ្អែកលើម៉ាទ្រីសដែលទទួលបាន យើងបង្កើតប្រព័ន្ធសមីការលីនេអ៊ែរ៖

2x + 4y = 6x + 12y

ដែល x និង y គឺជាធាតុនៃ eigenvector ។

តោះប្រមូល X ទាំងអស់នៅខាងឆ្វេង និង Y ទាំងអស់នៅខាងស្តាំ។ ជាក់ស្តែង - 4x = 8y ។ ចែកកន្សោមដោយ − 4 ហើយទទួលបាន x = −2y ។ ឥឡូវនេះយើងអាចកំណត់ eigenvector ដំបូងនៃម៉ាទ្រីសដោយយកតម្លៃណាមួយនៃមិនស្គាល់ (ចងចាំអំពីភាពគ្មានទីបញ្ចប់នៃ eigenvectors អាស្រ័យលីនេអ៊ែរ) ។ ចូរយក y = 1 បន្ទាប់មក x = −2 ។ ដូច្នេះ eigenvector ដំបូងមើលទៅដូចជា V1 = (–2; 1) ។ ត្រលប់ទៅដើមអត្ថបទ។ វា​ជា​វត្ថុ​វ៉ិចទ័រ​នេះ​ដែល​យើង​គុណ​ម៉ាទ្រីស​ដោយ​ដើម្បី​បង្ហាញ​ពី​គោល​គំនិត​នៃ eigenvector ។

ឥឡូវនេះ ចូរយើងស្វែងរក eigenvector សម្រាប់ λ = 12 ។

• M − λ × E = −12; បួន
• 6; -2.

អនុញ្ញាតឱ្យយើងបង្កើតប្រព័ន្ធដូចគ្នានៃសមីការលីនេអ៊ែរ;

• −12x + 4y = 6x − 2y
• −18x = −6y
• 3x=y។

ឥឡូវយើងយក x = 1 ដូច្នេះ y = 3 ។ ដូច្នេះ eigenvector ទីពីរមើលទៅដូចជា V2 = (1; 3) ។ នៅពេលគុណម៉ាទ្រីសដើមដោយវ៉ិចទ័រនេះ លទ្ធផលនឹងតែងតែជាវ៉ិចទ័រដូចគ្នាគុណនឹង 12។ វាបញ្ចប់ក្បួនដោះស្រាយដំណោះស្រាយ។ ឥឡូវអ្នកដឹងពីរបៀបកំណត់ eigenvector នៃម៉ាទ្រីសដោយដៃ។

• កត្តាកំណត់;
• ដាន, នោះគឺ, ផលបូកនៃធាតុនៅលើអង្កត់ទ្រូងមេ;
• ចំណាត់ថ្នាក់ ពោលគឺចំនួនអតិបរមានៃជួរ/ជួរឈរឯករាជ្យលីនេអ៊ែរ។

កម្មវិធីនេះដំណើរការដោយយោងតាមក្បួនដោះស្រាយខាងលើ ដោយកាត់បន្ថយដំណើរការដំណោះស្រាយ។ វាជាការសំខាន់ក្នុងការចង្អុលបង្ហាញថានៅក្នុងកម្មវិធី lambda ត្រូវបានតំណាងដោយអក្សរ "c" ។ សូមក្រឡេកមើលឧទាហរណ៍លេខ។

ឧទាហរណ៍កម្មវិធី

តោះព្យាយាមកំណត់ eigenvectors សម្រាប់ម៉ាទ្រីសខាងក្រោម៖

• M=5; ១៣;
• 4; 14.

ចូរយើងបញ្ចូលតម្លៃទាំងនេះទៅក្នុងក្រឡានៃម៉ាស៊ីនគិតលេខ ហើយទទួលបានចម្លើយក្នុងទម្រង់ខាងក្រោម៖

• ចំណាត់ថ្នាក់ម៉ាទ្រីស៖ ២;
• កត្តាកំណត់ម៉ាទ្រីស៖ ១៨;
• ដានម៉ាទ្រីស: 19;
• ការគណនា Eigenvector: c 2 − 19.00c + 18.00 (សមីការលក្ខណៈ);
• ការគណនា Eigenvector: 18 (តម្លៃ lambda ដំបូង);
• ការគណនា Eigenvector: 1 (តម្លៃ lambda ទីពីរ);
• ប្រព័ន្ធនៃសមីការវ៉ិចទ័រ 1: −13x1 + 13y1 = 4x1 − 4y1;
• ប្រព័ន្ធសមីការវ៉ិចទ័រ 2: 4x1 + 13y1 = 4x1 + 13y1;
• Eigenvector 1: (1; 1);
• Eigenvector 2: (-3.25; 1) ។

ដូច្នេះហើយ យើងបានទទួល eigenvectors ឯករាជ្យលីនេអ៊ែរពីរ។

សេចក្តីសន្និដ្ឋាន

ពិជគណិតលីនេអ៊ែរ និងធរណីមាត្រវិភាគគឺជាមុខវិជ្ជាស្ដង់ដារសម្រាប់និស្សិតថ្មីផ្នែកវិស្វកម្ម។ វ៉ិចទ័រ និងម៉ាទ្រីសមួយចំនួនធំគួរឱ្យខ្លាច ហើយវាងាយស្រួលក្នុងការធ្វើកំហុសក្នុងការគណនាដ៏ស្មុគស្មាញបែបនេះ។ កម្មវិធីរបស់យើងនឹងអនុញ្ញាតឱ្យសិស្សពិនិត្យមើលការគណនារបស់ពួកគេ ឬដោះស្រាយបញ្ហានៃការស្វែងរក eigenvector ដោយស្វ័យប្រវត្តិ។ មានម៉ាស៊ីនគិតលេខពិជគណិតលីនេអ៊ែរផ្សេងទៀតនៅក្នុងកាតាឡុករបស់យើង ប្រើវាក្នុងការសិក្សា ឬការងាររបស់អ្នក។

www.siteអនុញ្ញាតឱ្យអ្នកស្វែងរក។ គេហទំព័រធ្វើការគណនា។ ក្នុងរយៈពេលពីរបីវិនាទី ម៉ាស៊ីនមេនឹងផ្តល់ដំណោះស្រាយត្រឹមត្រូវ។ សមីការលក្ខណៈសម្រាប់ម៉ាទ្រីសនឹងជាកន្សោមពិជគណិតដែលរកឃើញដោយច្បាប់សម្រាប់គណនាកត្តាកំណត់ ម៉ាទ្រីស ម៉ាទ្រីសខណៈពេលដែលនៅលើអង្កត់ទ្រូងមេនឹងមានភាពខុសគ្នានៅក្នុងតម្លៃនៃធាតុអង្កត់ទ្រូងនិងអថេរ។ នៅពេលគណនា សមីការលក្ខណៈសម្រាប់ម៉ាទ្រីសតាមអ៊ីនធឺណិត, ធាតុនីមួយៗ ម៉ាទ្រីសនឹងត្រូវបានគុណជាមួយនឹងធាតុផ្សេងទៀតដែលត្រូវគ្នា។ ម៉ាទ្រីស. ស្វែងរកនៅក្នុងរបៀប លើបណ្តាញអាចធ្វើទៅបានសម្រាប់តែការ៉េ ម៉ាទ្រីស. ស្វែងរកប្រតិបត្តិការ សមីការលក្ខណៈសម្រាប់ម៉ាទ្រីសតាមអ៊ីនធឺណិតកាត់បន្ថយដល់ការគណនាផលបូកពិជគណិតនៃផលិតផលនៃធាតុ ម៉ាទ្រីសជាលទ្ធផលនៃការស្វែងរកកត្តាកំណត់ ម៉ាទ្រីសសម្រាប់គោលបំណងកំណត់តែប៉ុណ្ណោះ សមីការលក្ខណៈសម្រាប់ម៉ាទ្រីសតាមអ៊ីនធឺណិត. ប្រតិបត្តិការនេះកាន់កាប់កន្លែងពិសេសមួយនៅក្នុងទ្រឹស្តី ម៉ាទ្រីសអនុញ្ញាតឱ្យអ្នកស្វែងរក eigenvalues ​​និង vectors ដោយប្រើ root ។ ស្វែងរកកិច្ចការ សមីការលក្ខណៈសម្រាប់ម៉ាទ្រីសតាមអ៊ីនធឺណិតគឺគុណធាតុ ម៉ាទ្រីសជាមួយនឹងការបូកសរុបជាបន្តបន្ទាប់នៃផលិតផលទាំងនេះយោងទៅតាមច្បាប់ជាក់លាក់មួយ។ www.siteរកឃើញ សមីការលក្ខណៈសម្រាប់ម៉ាទ្រីសវិមាត្រដែលបានផ្តល់ឱ្យនៅក្នុងរបៀប លើបណ្តាញ. ការគណនា សមីការលក្ខណៈសម្រាប់ម៉ាទ្រីសតាមអ៊ីនធឺណិតសម្រាប់វិមាត្រដែលបានផ្តល់ឱ្យ នេះគឺជាការស្វែងរកពហុនាមដែលមានមេគុណលេខ ឬនិមិត្តសញ្ញាដែលរកឃើញដោយច្បាប់សម្រាប់គណនាកត្តាកំណត់ ម៉ាទ្រីស- ជាផលបូកនៃផលិតផលនៃធាតុដែលត្រូវគ្នា។ ម៉ាទ្រីសសម្រាប់គោលបំណងកំណត់តែប៉ុណ្ណោះ សមីការលក្ខណៈសម្រាប់ម៉ាទ្រីសតាមអ៊ីនធឺណិត. ការស្វែងរកពហុនាមទាក់ទងនឹងអថេរសម្រាប់ការ៉េ ម៉ាទ្រីសជានិយមន័យ សមីការលក្ខណៈសម្រាប់ម៉ាទ្រីសជាទូទៅនៅក្នុងទ្រឹស្តី ម៉ាទ្រីស. តម្លៃនៃឫសនៃពហុធា សមីការលក្ខណៈសម្រាប់ម៉ាទ្រីសតាមអ៊ីនធឺណិតប្រើដើម្បីកំណត់ eigenvectors និង eigenvalues ​​សម្រាប់ ម៉ាទ្រីស. ទោះយ៉ាងណាក៏ដោយប្រសិនបើកត្តាកំណត់ ម៉ាទ្រីសនោះនឹងជាសូន្យ សមីការលក្ខណៈម៉ាទ្រីសនឹងនៅតែមាន មិនដូចការបញ្ច្រាស ម៉ាទ្រីស. ដើម្បីគណនា សមីការលក្ខណៈសម្រាប់ម៉ាទ្រីសឬស្វែងរកច្រើនក្នុងពេលតែមួយ សមីការលក្ខណៈម៉ាទ្រីសអ្នកត្រូវចំណាយពេលវេលា និងការខិតខំប្រឹងប្រែងច្រើន ខណៈពេលដែលម៉ាស៊ីនមេរបស់យើងនឹងស្វែងរក សមីការលក្ខណៈសម្រាប់ម៉ាទ្រីសអនឡាញ. ក្នុងករណីនេះចម្លើយដោយការស្វែងរក សមីការលក្ខណៈសម្រាប់ម៉ាទ្រីសតាមអ៊ីនធឺណិតនឹងត្រឹមត្រូវ និងមានភាពត្រឹមត្រូវគ្រប់គ្រាន់ បើទោះបីជាលេខនៅពេលស្វែងរកក៏ដោយ។ សមីការលក្ខណៈសម្រាប់ម៉ាទ្រីសតាមអ៊ីនធឺណិតនឹងមិនសមហេតុផល។ នៅលើគេហទំព័រ www.siteការបញ្ចូលតួអក្សរត្រូវបានអនុញ្ញាតនៅក្នុងធាតុ ម៉ាទ្រីសនោះគឺ សមីការលក្ខណៈសម្រាប់ម៉ាទ្រីសអនឡាញអាចត្រូវបានតំណាងជាទម្រង់និមិត្តសញ្ញាទូទៅនៅពេលគណនា ម៉ាទ្រីសសមីការលក្ខណៈតាមអ៊ីនធឺណិត. វាមានប្រយោជន៍ក្នុងការពិនិត្យមើលចម្លើយដែលទទួលបាននៅពេលដោះស្រាយបញ្ហានៃការស្វែងរក សមីការលក្ខណៈសម្រាប់ម៉ាទ្រីសតាមអ៊ីនធឺណិតដោយប្រើគេហទំព័រ www.site. នៅពេលអនុវត្តប្រតិបត្តិការនៃការគណនាពហុធា - សមីការលក្ខណៈនៃម៉ាទ្រីសវាចាំបាច់ក្នុងការយកចិត្តទុកដាក់ និងផ្តោតអារម្មណ៍យ៉ាងខ្លាំងក្នុងការដោះស្រាយបញ្ហានេះ។ នៅក្នុងវេន គេហទំព័ររបស់យើងនឹងជួយអ្នកពិនិត្យមើលការសម្រេចចិត្តរបស់អ្នកលើប្រធានបទ ម៉ាទ្រីសសមីការលក្ខណៈតាមអ៊ីនធឺណិត. ប្រសិនបើអ្នកមិនមានពេលវេលាសម្រាប់ការត្រួតពិនិត្យរយៈពេលយូរនៃបញ្ហាដែលបានដោះស្រាយនោះបន្ទាប់មក www.siteប្រាកដជានឹងជាឧបករណ៍ដ៏ងាយស្រួលសម្រាប់ពិនិត្យមើលនៅពេលស្វែងរក និងគណនា សមីការលក្ខណៈសម្រាប់ម៉ាទ្រីសតាមអ៊ីនធឺណិត.

និយមន័យ ៩.៣.វ៉ិចទ័រ X បានហៅ វ៉ិចទ័រផ្ទាល់ខ្លួនម៉ាទ្រីស ប៉ុន្តែប្រសិនបើមានលេខបែបនេះ λ, ដែលសមភាពទទួលបាន៖ ប៉ុន្តែ X= λ X, នោះគឺជាលទ្ធផលនៃការអនុវត្តទៅ X ការបំប្លែងលីនេអ៊ែរដែលផ្តល់ដោយម៉ាទ្រីស ប៉ុន្តែ, គឺជាគុណនៃវ៉ិចទ័រនេះដោយចំនួន λ . លេខខ្លួនឯង λ បានហៅ លេខផ្ទាល់ខ្លួនម៉ាទ្រីស ប៉ុន្តែ.

ការជំនួសរូបមន្ត (៩.៣) x` j = λx j ,យើងទទួលបានប្រព័ន្ធនៃសមីការសម្រាប់កំណត់កូអរដោនេនៃ eigenvector:

. (9.5)

ប្រព័ន្ធលីនេអ៊ែរដូចគ្នានេះនឹងមានដំណោះស្រាយមិនសំខាន់ លុះត្រាតែកត្តាកំណត់សំខាន់របស់វាគឺ 0 (ច្បាប់របស់ Cramer)។ ដោយសរសេរលក្ខខណ្ឌនេះក្នុងទម្រង់៖

យើងទទួលបានសមីការសម្រាប់កំណត់ eigenvalues λ បានហៅ សមីការលក្ខណៈ. ដោយសង្ខេប វាអាចត្រូវបានតំណាងដូចខាងក្រោមៈ

| អេ-ល | = 0, (9.6)

ដោយសារផ្នែកខាងឆ្វេងរបស់វាគឺជាកត្តាកំណត់នៃម៉ាទ្រីស អេ-ល. ពហុនាមទាក់ទងនឹង λ | អេ-ល| បានហៅ ពហុនាមលក្ខណៈម៉ាទ្រីស ក

លក្ខណៈសម្បត្តិនៃពហុនាមលក្ខណៈ៖

1) ពហុនាមលក្ខណៈនៃការផ្លាស់ប្តូរលីនេអ៊ែរមិនអាស្រ័យលើជម្រើសនៃមូលដ្ឋានទេ។ ភស្តុតាង។ (សូមមើល (៩.៤)) ប៉ុន្តែ ជាលទ្ធផល, ។ ដូច្នេះមិនអាស្រ័យលើជម្រើសនៃមូលដ្ឋាន។ ដូច្នេះហើយ | អេ-ល| មិនផ្លាស់ប្តូរនៅពេលផ្លាស់ប្តូរទៅមូលដ្ឋានថ្មី។

2) ប្រសិនបើម៉ាទ្រីស ប៉ុន្តែការផ្លាស់ប្តូរលីនេអ៊ែរគឺ ស៊ីមេទ្រី(ទាំងនោះ។ a ij = a ji) បន្ទាប់មកឫសទាំងអស់នៃសមីការលក្ខណៈ (9.6) គឺជាចំនួនពិត។

លក្ខណៈសម្បត្តិនៃ eigenvalues ​​និង eigenvectors:

1) ប្រសិនបើយើងជ្រើសរើសមូលដ្ឋានពី eigenvectors x 1, x 2, x 3 ដែលត្រូវគ្នាទៅនឹង eigenvalues λ 1 , λ 2 , λ ៣ម៉ាទ្រីស ប៉ុន្តែបន្ទាប់មកនៅក្នុងមូលដ្ឋាននេះ ការបំលែងលីនេអ៊ែរ A មានម៉ាទ្រីសអង្កត់ទ្រូង៖

(9.7) ភស្តុតាងនៃទ្រព្យសម្បត្តិនេះធ្វើតាមនិយមន័យនៃ eigenvectors ។

2) ប្រសិនបើការផ្លាស់ប្តូរ eigenvalues ប៉ុន្តែមានភាពខុសប្លែកគ្នា បន្ទាប់មក eigenvectors ដែលត្រូវគ្នានឹងពួកវាគឺឯករាជ្យលីនេអ៊ែរ។

3) ប្រសិនបើពហុនាមលក្ខណៈនៃម៉ាទ្រីស ប៉ុន្តែមានឫសបីផ្សេងគ្នា បន្ទាប់មកក្នុងមូលដ្ឋានខ្លះ ម៉ាទ្រីស ប៉ុន្តែមានរាងអង្កត់ទ្រូង។

ចូរយើងស្វែងរក eigenvalues ​​និង eigenvectors នៃ matrix ចូរយើងបង្កើតសមីការលក្ខណៈ៖ (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - ៧ λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

ស្វែងរកកូអរដោនេនៃ eigenvectors ដែលត្រូវគ្នានឹងតម្លៃដែលបានរកឃើញនីមួយៗ λ. ពី (9.5) វាធ្វើតាមថាប្រសិនបើ X (1) ={x 1 , x 2 , x 3) គឺជា eigenvector ដែលត្រូវគ្នា។ λ 1 = -2 បន្ទាប់មក

គឺជាប្រព័ន្ធសហការ ប៉ុន្តែមិនអាចកំណត់បាន។ ដំណោះស្រាយរបស់វាអាចត្រូវបានសរសេរជា X (1) ={ក,0,-ក) ដែល a ជាលេខណាមួយ។ ជាពិសេសប្រសិនបើអ្នកទាមទារនោះ | x (1) |=1, X (1) =

ការជំនួសប្រព័ន្ធ (៩.៥) λ 2 =3 យើងទទួលបានប្រព័ន្ធសម្រាប់កំណត់កូអរដោនេនៃ eigenvector ទីពីរ - x (2) ={y1,y2,y3}:

កន្លែងណា X (2) ={b,-b, ខ) ឬផ្តល់ | x (2) |=1, x (2) =

សម្រាប់ λ 3 = 6 ស្វែងរក eigenvector x (3) ={z1, z2, z3}:

, x (3) ={គ,2c, គ) ឬនៅក្នុងកំណែធម្មតា។

x (3) = វាអាចត្រូវបានគេមើលឃើញថា X (1) X (2) = ab-ab= 0, x (1) x (3) = ac-ac= 0, x (2) x (3) = bc- 2bc + bc= 0. ដូច្នេះ eigenvectors នៃ matrix នេះ គឺ​ជា​គូ​ orthogonal ។

ធម្មទេសនា ១០

ទម្រង់បួនជ្រុង និងការភ្ជាប់របស់ពួកគេជាមួយម៉ាទ្រីសស៊ីមេទ្រី។ លក្ខណៈសម្បត្តិនៃ eigenvectors និង eigenvalues ​​នៃម៉ាទ្រីសស៊ីមេទ្រី។ ការកាត់បន្ថយទម្រង់បួនជ្រុងទៅជាទម្រង់ Canonical ។

និយមន័យ 10.1 ។ទម្រង់បួនជ្រុងអថេរពិតប្រាកដ x 1, x 2,…, x nពហុធានៃសញ្ញាបត្រទីពីរទាក់ទងនឹងអថេរទាំងនេះត្រូវបានគេហៅថា ដែលមិនមានពាក្យឥតគិតថ្លៃ និងលក្ខខណ្ឌនៃសញ្ញាបត្រទីមួយ។

ឧទាហរណ៍នៃទម្រង់ការ៉េ៖

(ន = 2),

(ន = 3). (10.1)

រំលឹកឡើងវិញនូវនិយមន័យនៃម៉ាទ្រីសស៊ីមេទ្រីដែលបានផ្តល់ឱ្យនៅក្នុងការបង្រៀនចុងក្រោយនេះ៖

និយមន័យ 10.2 ។ម៉ាទ្រីសការ៉េត្រូវបានគេហៅថា ស៊ីមេទ្រីប្រសិនបើ នោះគឺប្រសិនបើធាតុម៉ាទ្រីសស៊ីមេទ្រីទាក់ទងនឹងអង្កត់ទ្រូងសំខាន់គឺស្មើគ្នា។

លក្ខណៈសម្បត្តិនៃ eigenvalues ​​និង eigenvectors នៃម៉ាទ្រីសស៊ីមេទ្រី៖

1) eigenvalues ​​ទាំងអស់នៃម៉ាទ្រីសស៊ីមេទ្រីគឺពិតប្រាកដ។

ភស្តុតាង (សម្រាប់ ន = 2).

អនុញ្ញាតឱ្យម៉ាទ្រីស ប៉ុន្តែមើល​ទៅ​ដូច​ជា: . ចូរយើងបង្កើតសមីការលក្ខណៈ៖

(១០.២) ស្វែងរកអ្នករើសអើង៖

ដូច្នេះ សមីការ​មាន​ឫស​ពិត​តែ​ប៉ុណ្ណោះ។

2) eigenvectors នៃម៉ាទ្រីសស៊ីមេទ្រីគឺ orthogonal ។

ភស្តុតាង (សម្រាប់ ន= 2).

កូអរដោនេនៃ eigenvectors និងត្រូវតែបំពេញសមីការ។