Nakreslite mnohouholník na kockovaný papier. Napríklad, ako je znázornené na obrázku 1.
Skúsme teraz vypočítať jeho plochu. Ako to spraviť? Asi najjednoduchšie je rozložiť to na pravouhlé trojuholníky a obdĺžniky, ktorých plochy sa už dajú ľahko vypočítať a výsledky sčítať. Metóda, ktorú som použil, je jednoduchá, ale veľmi ťažkopádna a okrem toho nie je vhodná pre všetky polygóny.
Uvažujme nedegenerovaný jednoduchý celočíselný mnohouholník (to znamená, že je spojený – ľubovoľné dva jeho body môžu byť spojené súvislou krivkou, ktorá je v ňom celá obsiahnutá, a všetky jeho vrcholy majú celočíselné súradnice, jeho hranica je spojená lomená čiara bez vlastné križovatky a má nenulový štvorec). Na výpočet plochy takéhoto mnohouholníka môžete použiť nasledujúcu vetu:
Pickova veta. Nech je počet celočíselných bodov vo vnútri mnohouholníka, počet celočíselných bodov na jeho hranici a nech je jeho plocha. Potom Pickov vzorec:
Príklad. Pre mnohouholník na obrázku 1 (žlté bodky), (modré bodky, nezabudnite na vrcholy!), teda štvorcové jednotky.
Dôkaz Pickovej vety. Najprv si všimnite, že Pickov vzorec platí pre jednotkový štvorec. Naozaj, v tomto prípade máme
Zvážte obdĺžnik so stranami ležiacimi na mriežkových čiarach. Nech sa dĺžky jeho strán rovnajú a. V tomto prípade a podľa vzorca Pick,
Zvážte teraz pravouhlý trojuholník s nohami ležiacimi na súradnicových osiach. Takýto trojuholník sa získa z obdĺžnika so stranami a, uvažované v predchádzajúcom prípade, jeho diagonálnym rezom. Nech celočíselné body ležia na diagonále. Potom to v tomto prípade dostaneme
Teraz zvážte ľubovoľný trojuholník. Dá sa získať odrezaním niekoľkých pravouhlých trojuholníkov a prípadne obdĺžnika z obdĺžnika (pozri obrázky 2 a 3). Keďže Pickov vzorec platí pre obdĺžnik aj pravouhlý trojuholník, dostaneme, že bude platiť aj pre ľubovoľný trojuholník.
Zostáva urobiť posledný krok: prejsť od trojuholníkov k mnohouholníkom. Akýkoľvek mnohouholník môže byť rozdelený na trojuholníky (napríklad pomocou uhlopriečok). Preto musíme len dokázať, že pri pridávaní ľubovoľného trojuholníka do ľubovoľného mnohouholníka zostáva Pickov vzorec pravdivý.
Nech mnohouholník a trojuholník majú spoločnú stranu. Predpokladajme, že Pickov vzorec platí pre a dokážeme, že bude platiť aj pre mnohouholník získaný sčítaním. Keďže a majú spoločnú stranu, všetky celočíselné body ležiace na tejto strane, okrem dvoch vrcholov, sa stanú vnútornými bodmi nového mnohouholníka. Vrcholy budú hraničnými bodmi. Označme počet spoločných bodov a získajme
Počet vnútorných celočíselných bodov nového mnohouholníka,
Počet hraničných bodov pre nový polygón.
Z týchto rovnosti dostávame
Keďže sme predpokladali, že teorém platí pre a pre oddelene, potom
Tým je dokázaný výberový vzorec.
Tento vzorec objavil rakúsky matematik Peak Georg Alexandrov (1859 - 1943) v roku 1899. Okrem tohto vzorca Georg Pick objavil vety Pick, Pick - Julia, Pick - Nevalina, dokázal Schwarz - Pick nerovnosť. AT Dodatok 1 môžete vidieť neštandardné úlohy, ktoré som zvažoval pri použití vzorca Vybrať.
Vrcholový vzorec
1. Úvod
2. Vzorec vrcholu. Dôkaz I.
Dôkaz II.
Dôkaz Sh.
3. Úlohy.
4. Vzorec pre oblasť mnohouholníka z hľadiska súradníc vrcholov.
5. Úlohy.
6. Literatúra
Vrcholový vzorec.
1. Úvod.
Múdrosť čerpáme z histórie,
v poézii - vtip,
v matematike - vhľad.
F. Bacon
Dej sa bude odvíjať na bežnom károvanom papieri.
Čiary idúce po stranách buniek tvoria mriežku a vrcholy buniek sú uzlami tejto mriežky. Nakreslíme na list mnohouholník s vrcholmi v uzloch a nájdeme jeho plochu.
Môžete ho hľadať rôznymi spôsobmi. Môžete napríklad rozrezať mnohouholník na pomerne jednoduché tvary, nájsť ich oblasti a sčítať ich.
Ale tu nás čaká veľa problémov. Figúrka sa dá ľahko rozdeliť na obdĺžniky, lichobežníky a trojuholníky a jej plocha sa vypočíta bez námahy.
Hoci polygón vyzerá dostatočne jednoducho, výpočet jeho plochy si vyžiada veľa práce. Čo keby polygón vyzeral krajšie? Ukazuje sa, že oblasti polygónov, ktorých vrcholy sa nachádzajú v uzloch mriežky, sa dajú vypočítať oveľa jednoduchšie: existuje vzorec, ktorý spája ich plochu s počtom uzlov ležiacich vo vnútri a na hranici mnohouholníka. Tento úžasný a jednoduchý vzorec sa nazýva Pickov vzorec.
2. Vzorec vrcholu.
Vrcholy mnohouholníka (nie nevyhnutne konvexné) sa nachádzajú v uzloch celočíselnej mriežky. Vo vnútri leží B uzly mriežky a na hranici G uzlov. Dokážme, že jeho plocha je B + 
– 1 (Peakov vzorec).
Dôkaz I.
Uvažujme mnohouholník, ktorého vrcholy sú v uzloch celočíselnej mriežky, to znamená, že majú celočíselné súradnice.
Mnohouholník rozdelíme na trojuholníky s vrcholmi v uzloch mriežky, ktoré neobsahujú uzly ani vo vnútri, ani po stranách.
Označiť:
n je počet strán mnohouholníka,
m je počet trojuholníkov s vrcholmi v uzloch mriežky, ktoré neobsahujú uzly ani vo vnútri, ani na stranách,
B je počet uzlov vo vnútri polygónu,
Г je počet uzlov na stranách vrátane vrcholov.
Plochy všetkých týchto trojuholníkov sú rovnaké a rovnaké.
Preto je plocha polygónu 
.
180 0 m .
Teraz nájdime túto sumu iným spôsobom.
Súčet uhlov s vrcholom v akomkoľvek vnútornom uzle je 360 0 .
Potom súčet uhlov s vrcholmi vo všetkých vnútorných uzloch je 360 0 V.
Celkový súčet uhlov v uzloch na stranách, ale nie vo vrcholoch, je 180 0 (G - n).
Súčet uhlov vo vrcholoch mnohouholníka je 180 0 ( n – 2) .
Celkový súčet uhlov všetkých trojuholníkov je 360 0 V + 180 0 (G - n) + 180 0 (n – 2).
Takže 1800 m\u003d 360 0 V + 180 0 (G - n) + 180 0 (n – 2),
180 0 m\u003d 360 0 V + 180 0 G - 180 0 n + 180 0 n– 180 0 2,
180 0 m\u003d 360 0 V + 180 0 G– 360 0,
= B+ 
– 1 ,
odkiaľ dostaneme výraz pre oblasť S mnohouholníka:
S= B+ – 1 ,
známy ako Pickov vzorec.
Na obrázku: V = 24, D = 9, tedaS = 24 + – 1 = 27,5.
Nájdite oblasť prvého mnohouholníka pomocou vzorca Peak:
B = 28 (zelené bodky);
D = 20 (modré bodky).
Dostávame, S =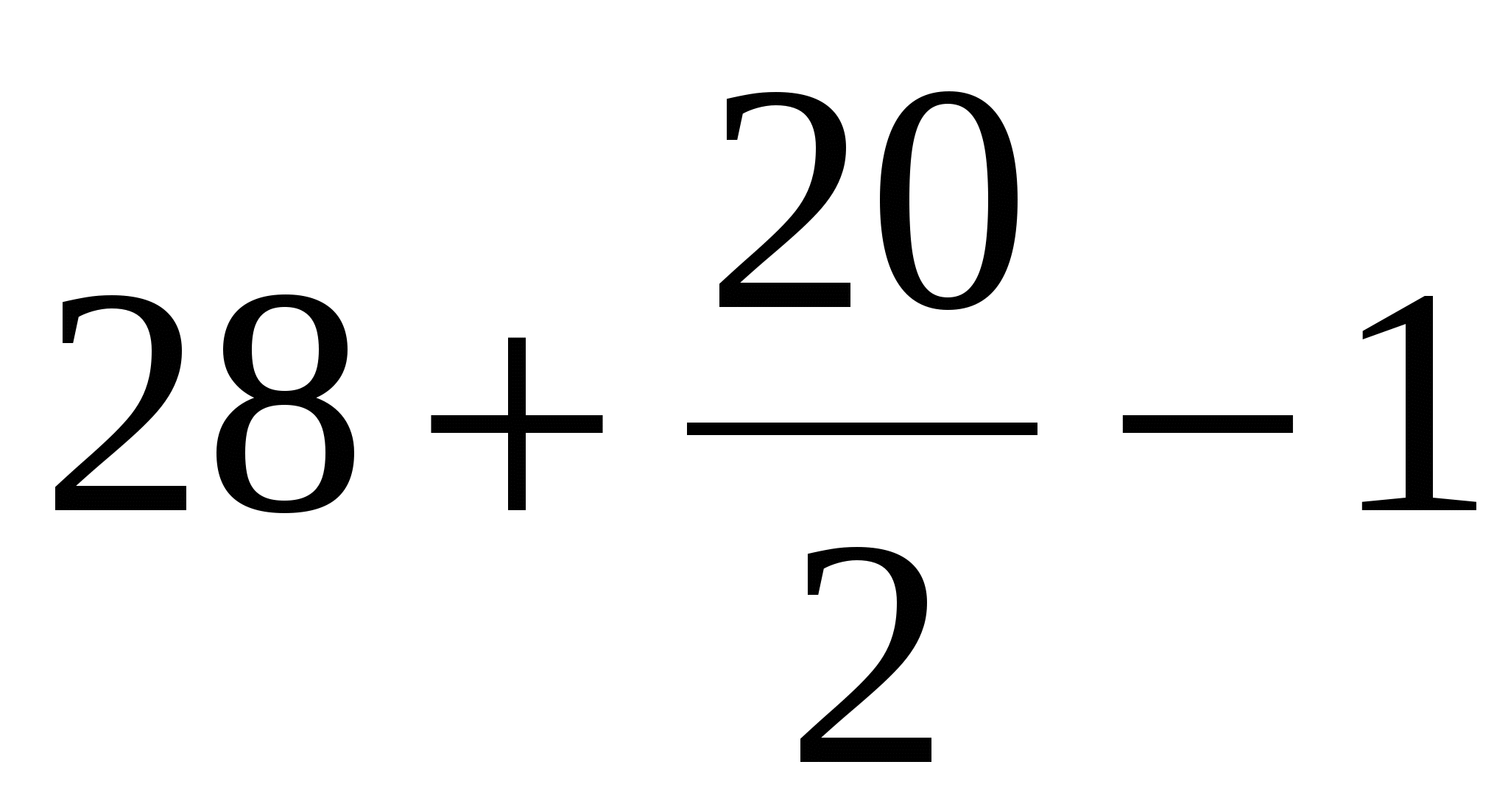 
= 37 štvorcových jednotiek
Dôkaz II.
Každému polygónu M s vrcholmi v uzloch celočíselnej mriežky priradíme číslo f (M) = 
, kde súčet je cez všetky uzly mriežky patriace do M a uhol 
je definovaný nasledovne: 
= 
pre vnútorný bod mnohouholníka, 
= 
pre hraničný bod iný ako vrchol a – uhol vo vrchole, ak je daný uzol vrcholom. Je ľahké vidieť, že f (M) = 
+ 
= B+ – 1. Zostáva skontrolovať, či sa číslo f (M) rovná ploche mnohouholníka M.
Nech je mnohouholník M rozrezaný na mnohouholníky M 1 a M 2 s vrcholmi v uzloch mriežky. Potom f(M) = f(M 1) + f(M 2), pretože pre každý uzol sa uhly sčítavajú. Ak teda Pickov vzorec platí pre dva z polygónov M, M 1 a M 2, platí to aj pre tretí.
Ak M je obdĺžnik so stranami p a q, smerované pozdĺž mriežkových línií, potom
f (M) = (p – 1) (q – 1) + 
= pq.
V tomto prípade platí Pickov vzorec. Rozrezaním obdĺžnika M diagonálne na trojuholníky M 1 a M 2 a využitím skutočnosti, že f (M) = f (M 1) + f (M 2) a f (M 1) = f (M 2), je ľahké dokázať platnosť Pickovho vzorca pre ľubovoľný pravouhlý trojuholník s nohami nasmerovanými pozdĺž čiar mriežky. Odrezaním niekoľkých takýchto trojuholníkov z obdĺžnika je možné získať akýkoľvek trojuholník.
Na dokončenie dôkazu Pickovho vzorca zostáva poznamenať, že ľubovoľný mnohouholník môže byť rozrezaný na trojuholníky pomocou nepretínajúcich sa uhlopriečok.
Dôkaz Sh.
Spojenie medzi plochou obrázku a počtom uzlov, ktoré spadajú do tohto obrázku, je obzvlášť jasné v prípade obdĺžnika.
Nechať byť A B C D- obdĺžnik s vrcholmi v uzloch a na stranách pozdĺž mriežky.
Označiť podľa AT počet uzlov ležiacich vo vnútri obdĺžnika a cez G je počet uzlov na jeho hranici. Posuňte mriežku o polovicu bunky doprava a o polovicu nadol.
Potom môže byť územie obdĺžnika "rozložené" medzi uzlami takto: každý z AT uzly "ovládajú" celú bunku posunutej mriežky, každý z G- 4 hraničné nerohové uzly - polovica bunky a každý z rohových bodov - štvrtina bunky. Preto je plocha obdĺžnika S
Takže pre obdĺžniky s vrcholmi v uzloch a stranami pozdĺž čiar mriežky sme vytvorili vzorec 
Dokážme, že tento vzorec platí nielen pre obdĺžniky, ale aj pre ľubovoľné polygóny s vrcholmi v uzloch mriežky.
Označiť podľa S
m
oblasť polygónuM
s vrcholmi v uzloch a cezP
m
- hodnota 
, kdeAT
m
je počet uzlov vo vnútriM, a G
m
je počet uzlov na hranici. Potom vzorec Pick môže byť napísaný ako 
.
Dôkaz vzorca rozdeľujeme do niekoľkých krokov.
Krok 1.
Ak polygónM
s vrcholmi v uzloch mriežky rozrezanými na 2 polygónyM
1
a M
2
,
majú tiež vrcholy iba v uzloch mriežky 
. Nechajte polygónM
rozrezané na mnohouholníkyM
1
a M
2
s vrcholmi v uzloch po segmente AB. Všetky uzly, okrem tých, ktoré spadajú do segmentuAB,
dajte rovnaký príspevok do ľavej a pravej časti vzorca. Zvážte uzly ležiace na segmente AB.
Ak takýto uzol leží medzi A a B (napríklad C), potom pre mnohouholníkM
je vnútorný a pre mnohouholníkyM
1
a M
2
- hranica. Preto jeho príspevok kP
m
sa rovná 1 a v každom z výrazov 
a 
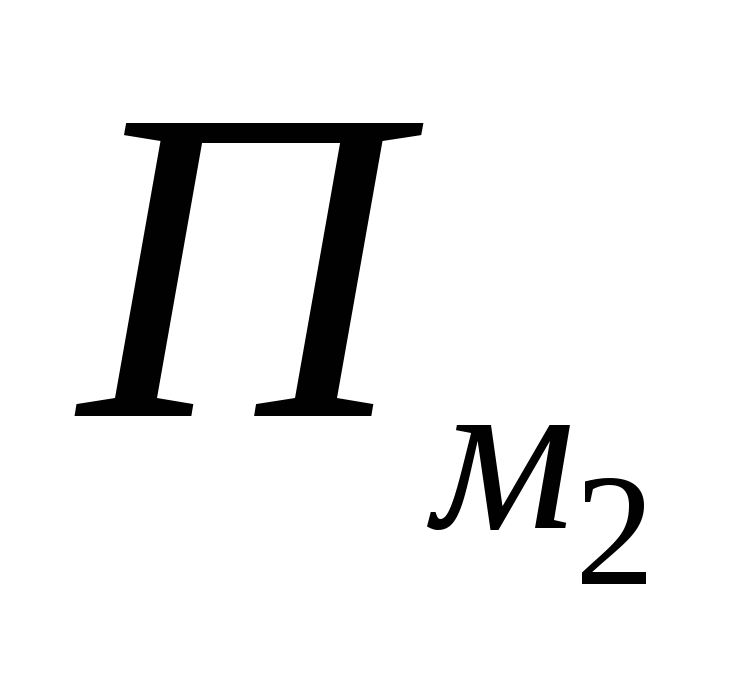– 0,5 každý, to znamená príspevky takéhoto uzla doP
m
a 
sú si rovní.
Uvažujme uzly A a B. Obidva sú hraničné M, a pre M 1 , M 2 .
Preto príspevok každého z týchto uzlov kP
m
je 0,5 a -
jednotka. To znamená, že celkový príspevok uzlov A a B kP
m
sa rovná 1, čo je o 1 menej ako ich príspevok .
ale 
, a.
Z celkového „príspevku“ všetkých uzlov P m 1 sa odpočíta 2 sa odpočíta a to kompenzuje rozdiel v príspevkoch uzlov A a B.
takze .
Krok 2
Ak polygón M s vrcholmi v uzloch mriežky rozrezanými na dva polygóny M 1 a M 2 (aj s vrcholmi v uzloch) a vzorec platí pre niektoré dva polygóny MM 1 , M 2 , potom to platí aj pre tretí polygón.
Nech platí napríklad preM
1
a M
2
,
t.j 
. Potom (v prvom kroku),
ale na
prvý krok), posledný výraz sa rovnáP
m
,
a rovnosť 
a tam je výberový vzorec.
Krok 3
Dokážme Pickov vzorec pre pravouhlý trojuholník s vrcholmi v uzloch mriežky a nohami ležiacimi na čiarach mriežky.
Trojuholník ABC postaviť do obdĺžnika A B C D .
Pre obdĺžniky je Pickov vzorec správny: S A B C D = P A B C D . Podľa prvého kroku P A B C D = P ABC + P ACD , P ABC = P ACD , tak P A B C D = 2P ABC . ale S A B C D = 2 S ABC . Takže S ABC = P ABC .
Krok 4
Pickov vzorec je správny pre ľubovoľný trojuholník s vrcholmi v uzloch mriežky.
Po preskúmaní obrázku je ľahké pochopiť: každý takýto trojuholník možno získať „odrezaním“ z nejakého obdĺžnika so stranami pozdĺž čiar mriežky, niekoľkých obdĺžnikov a pravouhlých trojuholníkov s nohami na čiarach mriežky. A keďže Pickov vzorec platí pre obdĺžniky a pravouhlé trojuholníky, potom (zapamätajte si krok 2) platí aj pre pôvodný trojuholník.
Dokázali sme, že ak je možné polygón rozrezať na trojuholníky s vrcholmi v uzloch mriežky, potom preň platí Pickov vzorec.
3. Úlohy.
Nájdite oblasť figúr:
1
.
B = 9
G = 4
B = 9
G = 5
Výpočet plochy postavy.
Vyberte metódu
Práca študenta triedy 5B MBOU strednej školy č. 23 v Irkutsku
Balšuková Alexandra
Vedúci: Khodyreva T.G.
2014
Výpočet plochy postavy. Vyberte metódu
Predmet štúdia : úlohy na kockovanom papieri
Predmet štúdia : úlohy na výpočet plochy mnohouholníka na kockovanom papieri, metódy a techniky ich riešenia.
Výskumné metódy Kľúčové slová: porovnanie, zovšeobecnenie, analógia, štúdium literatúry a internetových zdrojov, analýza informácií.
Účel štúdie:
vybrať hlavné, zaujímavé a zrozumiteľné informácie
Analyzujte a usporiadajte prijaté informácie
Nájdite rôzne metódy a techniky riešenia problémov na kockovanom papieri
skontrolujte vzorce na výpočet plôch geometrických tvarov pomocou vzorca Peak
Vytvorte elektronickú prezentáciu práce na prezentáciu zozbieraného materiálu
Geometria je najmocnejším nástrojom na zdokonaľovanie našich mentálnych schopností a umožňuje nám správne myslieť a uvažovať.
(G. Galileo)
Relevantnosť témy
Vášeň pre matematiku často začína premýšľaním o probléme. Pri štúdiu témy „Oblasti polygónov“ teda vyvstáva otázka, či existujú úlohy, ktoré sa líšia od úloh zvažovaných v učebnici. Medzi takéto úlohy patria úlohy na kockovanom papieri. Aká je zvláštnosť takýchto problémov, existujú špeciálne metódy a techniky na riešenie problémov na kockovanom papieri. Na hodine matematiky nám pani učiteľka predstavila zaujímavú metódu výpočtu mnohouholníkov. Začal som študovať literatúru, internetové zdroje na túto tému. Zdalo by sa, že na kockovanej rovine, teda na nekonečnom papieri, vyskladanom do rovnakých štvorcov, sa dajú nájsť fascinujúce veci. Ukazuje sa, že úlohy spojené s kockovaným papierom sú dosť rôznorodé. Naučil som sa vypočítať plochy mnohouholníkov nakreslených na kockovanom papieri. Pre mnohé úlohy na papieri v klietke neexistuje všeobecné pravidlo riešenia, konkrétne metódy a techniky. Toto je ich vlastnosť, ktorá určuje ich hodnotu pre rozvoj nie špecifickej vzdelávacej zručnosti alebo zručnosti, ale vo všeobecnosti schopnosti myslieť, reflektovať, analyzovať, hľadať analógie, to znamená, že tieto úlohy rozvíjajú myslenie v ich najširšom zmysle.
A tiež som sa dozvedel, že s takýmito úlohami sa počíta v kontrolných a meracích materiáloch GIA a Jednotnej štátnej skúšky. Štúdium tohto materiálu preto považujem za užitočné pre jeho uplatnenie nielen v ďalšom vzdelávacom procese, ale aj pri riešení neštandardných problémov olympiády.
2.Pojem oblasti
Námestie- číselná charakteristika dvojrozmerného geometrického útvaru, znázorňujúca veľkosť tohto útvaru. Historicky bol výpočet plochy tzv . Figúra, ktorá má plochu, sa nazýva kvadratúra .
Oblasť plochej postavy z hľadiska geometrie
1. Námestie- miera plochého obrazca vo vzťahu k štandardnému obrazcu, čo je štvorec so stranou rovnajúcou sa jednej dĺžke.
2. Námestie- číselná charakteristika pripisovaná plochým obrazcom určitej triedy (napríklad mnohouholníkom). Plocha štvorca so stranou rovnajúcou sa jednotke dĺžky, ktorá sa rovná jednotke plochy
3. Námestie- kladná hodnota, ktorej číselná hodnota má tieto vlastnosti:
Rovnaké čísla majú rovnaké oblasti;
Ak je obrázok rozdelený na časti, ktoré sú jednoduchými obrázkami (t. j. tie, ktoré možno rozdeliť na konečný počet plochých trojuholníkov), potom sa plocha tohto obrázku rovná súčtu jeho plôch. časti;
Plocha štvorca so stranou rovnajúcou sa jednotke merania sa rovná jednej.
Môžeme teda dospieť k záveru, že oblasť nie je špecifickou hodnotou, ale dáva iba určitú podmienenú charakteristiku plochej postavy. Na nájdenie plochy ľubovoľnej postavy je potrebné určiť, koľko štvorcov so stranou rovnajúcou sa jednej dĺžke obsahuje. Zoberme si napríklad obdĺžnik, do ktorého sa presne 6-krát zmestí štvorcový centimeter. To znamená, že plocha obdĺžnika je 6 cm2.
Výber plochy štvorca so stranou rovnajúcou sa jednotke merania ako minimálnej jednotky merania pre všetky plochy nie je náhodný. Je to výsledok dohody medzi ľuďmi, ktorá vznikla v priebehu „prirodzenej“ stáročnej selekcie. Okrem toho existovali ďalšie návrhy na mernú jednotku. Napríklad sa navrhlo brať plochu rovnostranného trojuholníka ako takú jednotku (t. j. každý plochý útvar by mohol byť reprezentovaný ako „súčet“ určitého počtu rovnostranných trojuholníkov), čo by viedlo k zmena v číselnom zastúpení plôch.
Vzorce na výpočet oblastí sa teda objavili v matematike a človek ich okamžite nerealizoval - to je veľa vedcov žijúcich v rôznych obdobiach a rôznych krajinách. (Chybné vzorce nenašli miesto vo vede a upadli do zabudnutia). Pravdivé vzorce sa tisícročia dopĺňali, opravovali a odôvodňovali, až sa k nám dostali vo svojej modernej podobe.
Samozrejme meranie plochy spočíva v porovnaní plochy daného obrázku s plochou obrázku branou ako merná jednotka. V dôsledku porovnania sa získa určité číslo - číselná hodnota plochy daného čísla. Toto číslo ukazuje, koľkokrát je plocha daného obrázku väčšia (alebo menšia) ako plocha obrázku, braná ako jednotka plochy.
T 
Môžeme teda konštatovať, že plocha je umelá veličina, historicky zavedená človekom na meranie nejakej vlastnosti plochej postavy. Potreba zadať takúto hodnotu bola spôsobená rastúcou potrebou vedieť, aké veľké je to alebo ono územie, koľko obilia je potrebné na zasiatie poľa alebo na výpočet podlahovej plochy na zdobenie okrasných dlaždíc.
Vrcholový vzorec
Na odhadnutie plochy mnohouholníka na kockovanom papieri stačí vypočítať, koľko buniek tento mnohouholník pokrýva (plochu bunky berieme ako jednotku). Presnejšie, akS je plocha mnohouholníka, B je počet buniek, ktoré ležia úplne vo vnútri mnohouholníka, a G je počet buniek, ktoré majú vnútro. Budeme uvažovať len také polygóny, ktorých všetky vrcholy ležia v uzloch kockovaného papiera - v tých, kde mriežkové čiary mnohouholníka pretínajú aspoň jeden spoločný bod.
Plochu ľubovoľného trojuholníka nakresleného na kockovanom papieri možno ľahko vypočítať tak, že ju predstavíte ako súčet alebo rozdiel plôch pravouhlých trojuholníkov a obdĺžnikov, ktorých strany sledujú čiary mriežky prechádzajúce cez vrcholy nakresleného trojuholníka.
Na výpočet plochy takéhoto mnohouholníka môžete použiť nasledujúcu vetu:
Veta . Nechať byť - počet celočíselných bodov vo vnútri mnohouholníka, - počet celočíselných bodov na jeho hranici, - jeho oblasť. PotomPickov vzorec:
Príklad. Pre mnohouholník na obrázkuL = 7 (červené bodky), 9 (zelené bodky), takS = 7+ 9/2 -1 = 10,5 štvorcových jednotiek.
Pickova veta- klasický výsledok a .
Plocha trojuholníka s vrcholmi v uzloch a bez uzlov vo vnútri ani po stranách (okrem vrcholov) sa rovná 1/2. Tento fakt.
3. História
Pickov vzorec objavil rakúsky matematik Georg Alexander (1859-1942) v St. . Vo veku 16 rokov Georg dokončil školu a vstúpil. Vo veku 20 rokov získal právo vyučovať fyziku a matematiku. V roku 1884 Peak odišiel do do . Tam stretol ďalšieho Kleinovho študenta,. Neskôr, v roku 1885, sa vrátil dokde strávil zvyšok svojej vedeckej kariéry.
Georg Pick bol priateľom s Einsteinom. Pick a Einstein mali nielen spoločné vedecké záujmy, ale boli nadšení aj pre hudbu. Pick, ktorý hral v kvartete zloženom z univerzitných profesorov, uviedol Einsteina do pražských vedeckých a hudobných spoločností.
Okruh matematických záujmov Peaka bol mimoriadne široký. Predovšetkým má viac ako 50 vedeckých prác. Pickova veta, ktorú objavil v roku 1899, bola všeobecne známa pre výpočet plochy mnohouholníka. V Nemecku je táto veta súčasťou školských učebníc.
4.Aplikácie Pickovho vzorca
Vzorec Pick sa používa nielen na výpočet plôch polygónov, ale aj na riešenie mnohých problémov na úrovni olympiády.
Niekoľko príkladov použitia Pickovho vzorca pri riešení problémov:
1) Šachový kráľ obišiel hraciu plochu 8 × 8 buniek, pričom každú navštívil
domáce ihrisko presne raz a posledným ťahom sa vracia k pôvodnému
lúka. Prerušovaná čiara spájajúca v sérii stredy polí, ktoré
kráľ prešiel, nemá žiadne sebapriesečníky. Aká oblasť môže
obmedziť túto prerušovanú čiaru? (Strana bunky je 1.)
Z Pickovho vzorca okamžite vyplýva, že plocha ohraničená lo-
mana je 64/2 − 1 = 31; tu sú uzly mriežky stredy 64
polia a podľa predpokladu všetky ležia na hranici polygónu. Takže
Teda takých „trajektórií“ kráľa je síce pomerne veľa, ale všetky
obmedziť polygóny s rovnakými plochami.
Úlohy z kontrolných a meracích materiálov GIA a Jednotnej štátnej skúšky
Úloha B3
Nájdite oblasť obrázku zobrazenú na kockovanom papieri s veľkosťou buniek 1 cm 1 cm (pozri obr.). Svoju odpoveď uveďte v centimetroch štvorcových.
4. Záver
V procese výskumu som študoval referenčnú, populárno-náučnú literatúru. Dozvedel som sa, že problém nájsť oblasť polygónu s vrcholmi v uzloch mriežky inšpiroval rakúskeho matematika Picka v roku 1899, aby dokázal úžasný Pickov vzorec.
Vďaka práci som si rozšíril vedomosti o riešení úloh na kockovanom papieri, určil som si klasifikáciu skúmaných problémov a presvedčil som sa o ich rôznorodosti.
Naučil som sa vypočítať plochy mnohouholníkov nakreslených na kockovanom hárku.Uvažované úlohy majú rôznu náročnosť – od jednoduchých až po olympiádu. Každý si medzi nimi nájde úlohy na realizovateľnej úrovni zložitosti, od ktorej bude možné prejsť k riešeniu náročnejších.
Prišiel som na to, že téma, ktorá ma zaujala, je dosť mnohostranná, úlohy na kockovanom papieri sú rôznorodé, rôznorodé sú aj metódy a techniky ich riešenia. Preto som sa rozhodol pokračovať v práci týmto smerom.
5. Použitá literatúra:
1. N. B. Vasiľjev, „Okolo vzorca Pick“, Kvant. - 1974. - č.12
2. Kokse Prasolov VV Úlohy z planimetrie. - M.: MTsNMO, 2006.t e r G.S.M. Úvod do geometrie. - M.: Nauka, 1966
3. Roslova L.O., Sharygin I.F. Merania. - M.: Ed. "Otvorený svet", 2005.
internetové zdroje:
:
Spätná väzba na prácu
„Výpočet plôch rovinných útvarov. Vybrať metódu"
Zohľadnenie tejto témy zvýši kognitívnu aktivitu žiaka, ktorý neskôr na hodinách geometrie začne vidieť harmóniu kresby a prestane vnímať geometriu (a matematiku vôbec) ako nudnú vedu.
Posúdené učiteľom matematiky
Khodyreva Tatyana Georgievna
Existuje úžasný vzorec, ktorý vám umožňuje počítať oblasť polygónu na súradnicovej sieti takmer bez chýb. Nie je to ani vzorec, je to skutočné teorém. Na prvý pohľad sa to môže zdať komplikované. Stačí však vyriešiť niekoľko úloh - a pochopíte, aká skvelá je táto funkcia. Tak do toho!
Začnime s novou definíciou:
Uzol súradnicového zásobníka je akýkoľvek bod, ktorý leží v priesečníku zvislých a vodorovných čiar tejto mriežky.
Označenie:
Na prvom obrázku nie sú uzly vôbec označené. Druhý má 4 uzly. Nakoniec na treťom obrázku je označených všetkých 16 uzlov.
Čo to má spoločné s problémom B5? Faktom je, že vrcholy polygónu v takýchto problémoch vždy ležia v uzloch mriežky. V dôsledku toho pre nich funguje nasledujúca veta:
Veta. Uvažujme mnohouholník na súradnicovej mriežke, ktorého vrcholy ležia v uzloch tejto mriežky. Potom je plocha mnohouholníka:
kde n je počet uzlov vo vnútri daného polygónu, k je počet uzlov, ktoré ležia na jeho hranici (hraničné uzly).
Ako príklad uvažujme obyčajný trojuholník na súradnicovej mriežke a skúsme označiť vnútorné a hraničné uzly.
Prvý obrázok ukazuje obyčajný trojuholník. Na druhom obrázku sú vyznačené jeho vnútorné uzly, ktorých počet je n = 10. Na treťom obrázku sú vyznačené uzly ležiace na hranici, spolu je ich k = 6.
Možno mnohí čitatelia nechápu, ako počítať čísla n a k. Začnite s vnútornými uzlami. Tu je všetko zrejmé: namaľujeme trojuholník ceruzkou a vidíme, koľko uzlov je zatienených.
S hraničnými uzlami je to trochu komplikovanejšie. polygónové ohraničenie - uzavretá prerušovaná čiara, ktorý pretína súradnicovú mriežku v mnohých bodoch. Najjednoduchší spôsob je označiť nejaký „východiskový“ bod a zvyšok potom obísť.
Hraničné uzly budú len tie body na lomenej čiare, v ktorých sa súčasne pretínajú tri riadky:
- Vlastne prerušovaná čiara;
- Horizontálna mriežka;
- vertikálna čiara.
Pozrime sa, ako to celé funguje v reálnych problémoch.
Úloha. Nájdite obsah trojuholníka, ak je veľkosť bunky 1 x 1 cm:
Najprv označme uzly, ktoré ležia vo vnútri trojuholníka, ako aj na jeho hranici:
Ukazuje sa, že existuje iba jeden vnútorný uzol: n = 1. Existuje šesť hraničných uzlov: tri sa zhodujú s vrcholmi trojuholníka, a tri ďalšie ležia na bokoch. Celkom k = 6.
Teraz vypočítame plochu pomocou vzorca:
To je všetko! Problém je vyriešený.
Úloha. Nájdite plochu štvoruholníka nakreslenú na kockovanom papieri s veľkosťou bunky 1 cm x 1 cm. Odpoveď uveďte v centimetroch štvorcových.
Opäť označíme vnútorné a hraničné uzly. Vnútorných uzlov je n = 2. Hraničné uzly: k = 7, z toho 4 vrcholy štvoruholníka, a 3 ďalšie ležia na bokoch.
Zostáva nahradiť čísla n a k vo vzorci oblasti:
Venujte pozornosť poslednému príkladu. Tento problém bol skutočne navrhnutý pri diagnostických prácach v roku 2012. Ak pracujete podľa štandardnej schémy, budete musieť urobiť veľa dodatočných konštrukcií. A metódou uzlov sa všetko rieši takmer ústne.
Dôležitá poznámka k oblastiam
Ale vzorec nie je všetko. Poďme trochu prepísať vzorec a uviesť výrazy na pravú stranu na spoločného menovateľa. Dostaneme:
Čísla n a k sú počet uzlov, sú to vždy celé čísla. Takže celý čitateľ je tiež celé číslo. Delíme ho 2, z čoho vyplýva dôležitý fakt:
Plocha je vždy vyjadrená celé číslo alebo zlomok. Navyše na konci zlomku je vždy „päť desatín“: 10,5; 17,5 atď.
Oblasť v úlohe B5 je teda vždy vyjadrená ako celé číslo alebo zlomok tvaru ***.5. Ak je odpoveď iná, znamená to, že sa niekde stala chyba. Majte to na pamäti, keď budete robiť skutočnú skúšku z matematiky!
Ak chcete použiť ukážku prezentácií, vytvorte si Google účet (účet) a prihláste sa: https://accounts.google.com
Popisy snímok:
Ukončil študent strednej školy č. 7 8 "A" triedy Yunosheva Ksenia Inštruktor: Babina Natalya Alekseevna Salsk 2011 "Peak Formula"
Ciele práce: Zistiť existenciu iného, odlišného od školských osnov, vzorca na nájdenie plochy mriežkového mnohouholníka. Oblasti použitia požadovaného vzorca.
Úvod. Matematické vzdelanie získané na všeobecnovzdelávacích školách je základnou súčasťou všeobecného vzdelania a všeobecnej kultúry moderného človeka. V tomto štádiu je školský systém navrhnutý na jedenásťročné vzdelávanie. Všetci žiaci na konci jedenásteho ročníka budú musieť zložiť Jednotnú štátnu skúšku, ktorá preukáže úroveň vedomostí získaných štúdiom v škole. Školské osnovy však nie vždy poskytujú najracionálnejšie spôsoby riešenia akýchkoľvek problémov. Napríklad pri pohľade na výsledky POUŽITIA v roku 2010 je vidieť, že veľa študentov stráca body kvôli úlohe B6. Dal som si za cieľ zistiť, ako ušetriť čas a správne vyriešiť tento problém.
Úloha B6. Obrázky sú zobrazené na kockovanom papieri s bunkami s rozmermi 1 cm x 1 cm (pozri obrázok). Nájdite ich plochu v centimetroch štvorcových.
Takže, aby som túto úlohu ešte vyriešil, musím použiť vzorce na nájdenie oblasti, ktorú študujeme v 8. ročníku. Ale zaberie to veľa času a potrebujem na otázku odpovedať čo najrýchlejšie, pretože čas na skúšku je prísne obmedzený. Preto som po prieskume zistil, že existuje Pickova veta, ktorá sa v školských osnovách neuvádza, ale pomôže mi rýchlejšie sa s úlohou vyrovnať.
Odkaz na históriu. Georg Alexander Pick (10. august 1859 – 26. júl 1942) bol rakúsky matematik. Zomrel v koncentračnom tábore Terezín. Dnes je známy vďaka Pickovmu vzorcu na určenie plochy mriežky mnohouholníkov. Svoj vzorec publikoval v novinách v roku 1899 a stal sa populárnym, keď ho Hugo Steinhaus zahrnul do vydania Mathematical Pictures v roku 1969. Pick študoval na Viedenskej univerzite a doktorát ukončil v roku 1880. Po získaní doktorátu bol vymenovaný za asistenta Ernesta Macha na Scherl-Ferdinandovej univerzite v Prahe. V roku 1881 sa tam stal učiteľom. V roku 1884 si vzal na univerzite dovolenku a začal pracovať s Felixom Kleinom na univerzite v Lipsku. V Prahe zostal až do odchodu do dôchodku v roku 1927, kedy sa vrátil do Viedne. Pick predsedal výboru na (vtedy) Nemeckej univerzite v Prahe, ktorý v roku 1911 vymenoval Alberta Einsteina za profesora matematickej fyziky. Picka bol zvolený za člena českej akadémie vied a umení, ale po ovládnutí Prahy nacistami bol vylúčený. Po odchode do dôchodku v roku 1927 sa Pick vrátil do Viedne, mesta, kde sa narodil. Po anšluse, keď nacisti 12. marca 1938 vstúpili do Rakúska, sa Pieck vrátil do Prahy. V marci 1939 nacisti napadli Československo. Georga poslali do koncentračného tábora Terezín 13. júla 1942. O dva týždne zomrel.
Pickova veta. Pickova veta je klasickým výsledkom kombinatorickej geometrie a geometrie čísel. Plocha mnohouholníka s celočíselnými vrcholmi sa rovná súčtu B + D/2 - 1, kde B je počet celočíselných bodov vo vnútri mnohouholníka a D je počet celočíselných bodov na hranici mnohouholníka.
Lichotivý dôkaz Pickovej vety. Každý takýto mnohouholník možno ľahko rozdeliť na trojuholníky s vrcholmi v uzloch mriežky, ktoré neobsahujú žiadne uzly ani vo vnútri, ani na stranách. Dá sa ukázať, že plochy všetkých týchto trojuholníkov sú rovnaké a rovné 1/2, a preto sa plocha mnohouholníka rovná polovici ich čísla T. Aby sme našli toto číslo, označíme n počet strán mnohouholníka, b - počet uzlov v ňom a b - počet uzlov na stranách vrátane vrcholov. Celkový súčet uhlov všetkých trojuholníkov je πТ. Teraz nájdime túto sumu iným spôsobom. Súčet uhlov s vrcholom v ktoromkoľvek vnútornom uzle je 2 π, t. j. celkový súčet takýchto uhlov je 2 π i; celkový súčet uhlov v uzloch na stranách, ale nie vo vrcholoch, je (b - n) π a súčet uhlov vo vrcholoch mnohouholníka je (n - 2) π. Teda π T \u003d 2i π + (b - n) π + (n - 2) π, z čoho získame výraz pre oblasť S mnohouholníka, známy ako Pickov vzorec. Napríklad na obrázku b = 9, i = 24, a preto je plocha polygónu 27,5.
Aplikácia. Takže späť k úlohe B6. Teraz, keď poznáme nový vzorec, môžeme ľahko nájsť oblasť tohto štvoruholníka. Pretože B je 5; D - 14, potom 5 + 14: 2-1 \u003d 11 (cm na druhú) Plocha tohto štvoruholníka je 11 cm na druhú.
Pomocou rovnakého vzorca môžeme nájsť oblasť trojuholníka. Od B-14, G-10, potom 14+10:2-1=18 (cm štvorcový) Plocha tohto trojuholníka je 18 cm štvorcových.
Ak B-9, D-12, potom: 9+12:2-1=14 (cm na druhú) Plocha tohto štvoruholníka je 14 cm na druhú.
Rozsah vzorca. Okrem toho, že sa vzorec používa pri rôznych druhoch skúšok, úloh a podobne, sprevádza celý svet okolo nás.
Podľa Peakovho vzorca S = B + ½ G-1 1) telo B=9, G=26, S=9+½ 26-1=9+13-1= 21 2) chvost B=0, G=8, S = 0 + 1/28-1 = 3 3) S = 21 + 3 = 24
Podľa Peakovho vzorca S \u003d B + ½ G-1 B \u003d 36, G \u003d 21 S \u003d 36 + ½ 21 -1 \u003d 36 + 10,5-1 \u003d 45,5
Záver. Výsledkom bolo, že som dospel k záveru, že existuje mnoho rôznych spôsobov riešenia plošných problémov, ktoré nie sú študované v školských osnovách, a ukázal som ich na príklade Pickovho vzorca.
Adresár. Mnohouholník bez sebapriesečníkov sa nazýva mriežkový mnohouholník, ak sú všetky jeho vrcholy v bodoch s celočíselnými súradnicami (v karteziánskom súradnicovom systéme). Bod v rovine súradníc sa nazýva celé číslo, ak sú obe jeho súradnice celými číslami.
