Je to štvoruholník, ktorého protiľahlé strany sú párovo rovnobežné.

Nehnuteľnosť 1 . Akákoľvek uhlopriečka rovnobežníka ho rozdeľuje na dva rovnaké trojuholníky.

Dôkaz . Podľa značky II (krížom ležiace rohy a spoločná strana).

Veta dokázaná.

Nehnuteľnosť 2. V rovnobežníku sú protiľahlé strany rovnaké a opačné uhly sú rovnaké.

Dôkaz .
podobne,

Veta dokázaná.

Vlastnosť 3. V diagonálnom rovnobežníku je priesečník rozdelený na polovicu.

Dôkaz .

Veta dokázaná.

Nehnuteľnosť 4. Stred uhla rovnobežníka, ktorý pretína opačnú stranu, ho rozdeľuje na rovnoramenný trojuholník a lichobežník. (Ch. slovo - vrchol - dva rovnoramenné? -ka).

Dôkaz .

Veta dokázaná.

Nehnuteľnosť 5. V rovnobežníku je segment s koncami na opačných stranách, ktorý prechádza priesečníkom uhlopriečok, rozpolený týmto bodom.

Dôkaz .

Veta dokázaná.

Nehnuteľnosť 6. Uhol medzi výškami spustenými z vrcholu tupého uhla rovnobežníka sa rovná ostrému uhlu rovnobežníka.

Dôkaz .

Veta dokázaná.

Nehnuteľnosť 7 . Súčet uhlov rovnobežníka susediaceho s jednou stranou je 180°.

Dôkaz .

Veta dokázaná.

Konštrukcia osy uhla. Vlastnosti osy uhla trojuholníka.

1) Zostrojte ľubovoľný lúč DE.

2) Na danom lúči zostrojte ľubovoľnú kružnicu so stredom vo vrchole a to isté
so stredom na začiatku zostrojeného lúča.

3) F a G - priesečník kružnice so stranami daného uhla, H - priesečník kružnice so zostrojeným lúčom

Zostrojte kružnicu so stredom v bode H a polomerom rovným FG.

5) I - priesečník kružníc zostrojeného nosníka.

6) Nakreslite čiaru cez vrchol a I.

IDH - požadovaný uhol.
)

Nehnuteľnosť 1 . Osa uhla trojuholníka rozdeľuje opačnú stranu v pomere k susedným stranám.

Dôkaz . Nech x, y sú segmenty strany c. Pokračujeme lúčom BC. Na lúč BC vynesieme segment CK z C rovný AC.

Dôkaz

Najprv nakreslíme uhlopriečku AC. Získajú sa dva trojuholníky: ABC a ADC.

Keďže ABCD je rovnobežník, platí nasledovné:

AD || BC \Pravá šípka \uhol 1 = \uhol 2 ako ležať naprieč.

AB || CD \Rightarrow \uhol3 = \uholník 4 ako ležať naprieč.

Preto \triangle ABC = \triangle ADC (podľa druhého znaku: a AC je spoločný).

A preto \triangle ABC = \triangle ADC , potom AB = CD a AD = BC .

Osvedčené!

2. Opačné uhly sú rovnaké.

Dôkaz

Podľa dôkazu vlastnosti 1 My to vieme \uhol 1 = \uhol 2, \uhol 3 = \uhol 4. Takže súčet opačných uhlov je: \uhol 1 + \uhol 3 = \uhol 2 + \uhol 4. Ak vezmeme do úvahy, že \triangle ABC = \triangle ADC dostaneme \uholník A = \uholník C , \uholník B = \uholník D .

Osvedčené!

3. Uhlopriečky sú rozpolené priesečníkom.

Dôkaz

Nakreslíme ďalšiu uhlopriečku.

Autor: majetok 1 vieme, že protiľahlé strany sú totožné: AB = CD . Opäť si všimneme rovnaké uhly ležiace naprieč.

Podľa druhého znamienka rovnosti trojuholníkov (dva uhly a strana medzi nimi) je teda možné vidieť, že \triangle AOB = \triangle COD. To znamená, že BO = OD (opačný \uhol 2 a \uhol 1 ) a AO = OC (opačný \uhol 3 a \uhol 4).

Osvedčené!

Vlastnosti paralelogramu

Ak je vo vašom probléme prítomný iba jeden znak, potom je obrázok rovnobežník a môžete použiť všetky vlastnosti tohto obrázku.

Pre lepšie zapamätanie si všimnite, že znak rovnobežníka odpovie na nasledujúcu otázku − "ako to zistiť?". Teda ako zistiť, že daný obrazec je rovnobežník.

1. Rovnobežník je štvoruholník, ktorého dve strany sú rovnaké a rovnobežné.

AB=CD; AB || CD \Rightarrow ABCD je rovnobežník.

Dôkaz

Uvažujme podrobnejšie. Prečo AD || pred Kristom?

\triangle ABC = \triangle ADC by majetok 1: AB = CD , AC je spoločné a \uhol 1 = \uhol 2 ako krížový s AB a CD rovnobežný a sečnicový AC .

Ale ak \triangle ABC = \triangle ADC , potom \uholník 3 = \uhol 4 (ležia oproti AB a CD). A preto AD || BC (\uhol 3 a \uhol 4 - ležiace naprieč sú tiež rovnaké).

Prvý znak je správny.

2. Rovnobežník je štvoruholník, ktorého protiľahlé strany sú rovnaké.

AB = CD , AD = BC \Šípka doprava ABCD je rovnobežník.

Dôkaz

Zoberme si túto funkciu. Opäť nakreslíme uhlopriečku AC.

Autor: majetok 1\triangle ABC = \triangle ACD .

Z toho vyplýva, že: \uhol 1 = \uhol 2 \Šípka doprava || pred Kr a \uhol 3 = \uhol 4 \Šípka doprava AB || CD, to znamená, že ABCD je rovnobežník.

Druhý znak je správny.

3. Rovnobežník je štvoruholník, ktorého opačné uhly sú rovnaké.

\uhol A = \uhol C , \uhol B = \uholník D \Šípka doprava ABCD- rovnobežník.

Dôkaz

2 \alfa + 2 \beta = 360^(\circ)(pretože ABCD je štvoruholník a \uhol A = \uhol C , \uholník B = \uhol D podľa konvencie).

Takže \alpha + \beta = 180^(\circ) . Ale \alpha a \beta sú interné jednostranné na sečne AB .

A to, že \alpha + \beta = 180^(\circ) tiež znamená, že AD || pred Kr.

Zároveň sú \alpha a \beta vnútorné jednostranné so sečnicou AD . A to znamená AB || CD.

Tretí znak je správny.

4. Rovnobežník je štvoruholník, ktorého uhlopriečky sú rozpolené priesečníkom.

AO = OC; BO = OD \Pravý rovnobežník.

Dôkaz

BO=OD; AO = OC , \uhol 1 = \uhol 2 ako zvislý \Rightarrow \triangle AOB = \trojuholník COD, \Vpravo \uhol 3 = \uhol 4 a \Rightarrow AB || CD.

Podobne BO = OD ; AO=OC, \uholník 5 = \uhol 6 \šípka doprava \trojuholník AOD = \trojuholník BOC \šípka doprava \uhol 7 = \uhol 8 a \Rightarrow AD || pred Kr.

Štvrtý znak je správny.

Téma lekcie

• Vlastnosti uhlopriečok rovnobežníka.

Ciele lekcie

• Zoznámte sa s novými definíciami a pripomeňte si niektoré už naštudované.
• Formulujte a dokážte vlastnosť uhlopriečok rovnobežníka.
• Naučiť sa aplikovať vlastnosti tvarov pri riešení úloh.
• Rozvíjajúce – rozvíjať pozornosť žiakov, vytrvalosť, vytrvalosť, logické myslenie, matematickú reč.
• Vzdelávacie - prostredníctvom lekcie pestovať pozorný postoj k sebe navzájom, vštepovať schopnosť počúvať kamarátov, vzájomnú pomoc, nezávislosť.

Ciele lekcie

• Skontrolujte schopnosť študentov riešiť problémy.

Plán lekcie

1. Úvod.
2. Opakovanie predtým naučeného učiva.
3. Rovnobežník, jeho vlastnosti a znaky.
4. Príklady úloh.
5. Samokontrola.

Úvod

"Veľký vedecký objav poskytuje riešenie na veľký problém, ale v riešení akéhokoľvek problému je zrnko objavu."

Vlastnosti protiľahlých strán rovnobežníka

Rovnobežník má rovnaké protiľahlé strany.

Dôkaz.

Nech ABCD je daný rovnobežník. A nech sa jeho diagonály pretínajú v bode O.
Keďže Δ AOB = Δ COD podľa prvého znamienka rovnosti trojuholníkov (∠ AOB = ∠ COD, ako zvislé, AO=OC, DO=OB, podľa vlastnosti uhlopriečok rovnobežníka), potom AB=CD. Podobne z rovnosti trojuholníkov BOC a DOA vyplýva, že BC=DA. Veta bola dokázaná.

Vlastnosť opačných uhlov rovnobežníka

Rovnobežník má opačné uhly.

Dôkaz.

Nech ABCD je daný rovnobežník. A nech sa jeho diagonály pretínajú v bode O.
Z vlastností protiľahlých strán rovnobežníka dokázaného vo vete o Δ ABC = Δ CDA na troch stranách (AB=CD, BC=DA z dokázaného, ​​AC je všeobecné). Z rovnosti trojuholníkov vyplýva, že ∠ABC = ∠CDA.
Je tiež dokázané, že ∠ DAB = ∠ BCD, čo vyplýva z ∠ ABD = ∠ CDB. Veta bola dokázaná.

Vlastnosť uhlopriečok rovnobežníka

Uhlopriečky rovnobežníka sa pretínajú a priesečník je rozdelený na polovicu.

Dôkaz.

Nech ABCD je daný rovnobežník. Nakreslíme uhlopriečku AC. Označíme na ňom stred O. Na pokračovanie úsečky DO odložíme úsečku OB 1 rovnú DO.
Podľa predchádzajúcej vety je AB 1 CD rovnobežník. Preto je čiara AB 1 rovnobežná s jednosmerným prúdom. Ale cez bod A možno nakresliť iba jednu čiaru rovnobežnú s DC. Čiara AB 1 sa teda zhoduje s čiarou AB.
Je tiež dokázané, že BC 1 sa zhoduje s BC. Takže bod C sa zhoduje s C 1 . rovnobežník ABCD sa zhoduje s rovnobežníkom AB 1 CD. Preto sa uhlopriečky rovnobežníka pretínajú a priesečník je rozpoltený. Veta bola dokázaná.

V učebniciach pre bežné školy (napríklad v Pogorelove) sa to dokazuje takto: uhlopriečky rozdeľujú rovnobežník na 4 trojuholníky. Zvážte jeden pár a zistite - sú rovnaké: ich základne sú protiľahlé strany, zodpovedajúce uhly, ktoré k nemu priliehajú, sú rovnaké ako vertikálne s rovnobežnými čiarami. To znamená, že segmenty uhlopriečok sú párovo rovnaké. Všetko.

Je to všetko?
Vyššie bolo dokázané, že priesečník pretína uhlopriečky - ak existuje. Vyššie uvedené zdôvodnenie jeho existenciu nijako nedokazuje. To znamená, že časť vety "úhlopriečky rovnobežníka sa pretínajú" zostáva nedokázaná.

Je smiešne, že túto časť je oveľa ťažšie dokázať. To mimochodom vyplýva zo všeobecnejšieho výsledku: pre akýkoľvek konvexný štvoruholník sa uhlopriečky pretínajú, pre akýkoľvek nekonvexný nie.

O rovnosti trojuholníkov pozdĺž strany a dvoch uhlov k nej priľahlých (druhé znamenie rovnosti trojuholníkov) a ďalšie.

Veta o rovnosti dvoch trojuholníkov pozdĺž strany a dvoch uhlov priľahlých k nej Thales našla dôležité praktické uplatnenie. V prístave Miletus bol zostrojený diaľkomer, ktorý určuje vzdialenosť lode na mori. Pozostával z troch zarazených kolíkov A, B a C (AB = BC) a vyznačenej priamky SK, kolmej na CA. Keď sa loď objavila na priamke SC, našiel sa bod D taký, že body D, .B a E boli na rovnakej priamke. Ako je zrejmé z nákresu, vzdialenosť CD na zemi je požadovaná vzdialenosť od lode.

Otázky

1. Sú uhlopriečky štvorca rozpolené priesečníkom?
   
2. Sú uhlopriečky rovnobežníka rovnaké?
3. Sú opačné uhly rovnobežníka rovnaké?
4. Aká je definícia rovnobežníka?
5. Koľko vlastností má rovnobežník?
   
6. Môže byť kosoštvorec rovnobežníkom?
   

Zoznam použitých zdrojov

1. Kuznecov A. V., učiteľ matematiky (5.-9. ročník), Kyjev
2. „Jednotná štátna skúška 2006. Matematika. Vzdelávacie a školiace materiály pre prípravu študentov / Rosobrnadzor, ISOP - M .: Intellect-Center, 2006 "
3. Mazur K. I. "Riešenie hlavných súťažných problémov v matematike zborníka edited by M. I. Scanavi"
4. L. S. Atanasyan, V. F. Butuzov, S. B. Kadomtsev, E. G. Poznyak, I. I. Yudina "Geometria, 7 - 9: učebnica pre vzdelávacie inštitúcie"

Práca na lekcii

Kuznecov A.V.

Poturnak S.A.

Jevgenij Petrov

Môžete položiť otázku o modernom vzdelávaní, vyjadriť myšlienku alebo vyriešiť naliehavý problém na Vzdelávacie fórum kde sa na medzinárodnej úrovni stretáva vzdelávacia rada nových myšlienok a činov. Po vytvorení blog, Zlepšíte si nielen svoj status kompetentného učiteľa, ale výrazne prispejete aj k rozvoju školy budúcnosti. Cech vedúcich vzdelávania otvára dvere špičkovým odborníkom a pozýva vás k spolupráci v smere vytvárania najlepších škôl na svete.

Predmety > Matematika > Matematika 8. ročník

Rovnobežník je štvoruholník, ktorého protiľahlé strany sú rovnobežné, t.j. ležať na rovnobežných čiarach

Vlastnosti rovnobežníka:
Veta 22. Opačné strany rovnobežníka sú rovnaké.
Dôkaz. Nakreslite uhlopriečku AC do rovnobežníka ABCD. Trojuholníky ACD a ACB sú zhodné, pretože majú spoločnú stranu AC a dva páry rovnakých uhlov. vedľa nej: ∠ CAB=∠ ACD, ∠ ASV=∠ DAC (ako priečne ležiace uhly s rovnobežnými priamkami AD a BC). Preto AB=CD a BC=AD ako zodpovedajúce strany rovnakých trojuholníkov atď. Z rovnosti týchto trojuholníkov vyplýva aj rovnosť zodpovedajúcich uhlov trojuholníkov:
Veta 23. Opačné uhly rovnobežníka sú: ∠ A=∠ C a ∠ B=∠ D.
Rovnosť prvého páru pochádza z rovnosti trojuholníkov ABD a CBD a druhého - ABC a ACD.
Veta 24. Susedné rohy rovnobežníka, t.j. uhly susediace s jednou stranou sú 180 stupňov.
Ide totiž o vnútorné jednostranné rohy.
Veta 25. Uhlopriečky rovnobežníka sa navzájom pretínajú v bode svojho priesečníka.
Dôkaz. Zvážte trojuholníky BOC a AOD. Podľa prvej vlastnosti AD=BC ∠ ОАD=∠ OSV a ∠ ОDA=∠ ОВС ako ležiace naprieč s rovnobežkami AD a BC. Preto majú trojuholníky BOC a AOD rovnakú stranu a uhly, ktoré k nim priliehajú. Preto BO=OD a AO=OC ako zodpovedajúce strany rovnakých trojuholníkov atď.

Vlastnosti paralelogramu
Veta 26. Ak sú protiľahlé strany štvoruholníka rovnaké v pároch, potom ide o rovnobežník.
Dôkaz. Nech má štvoruholník ABCD strany AD a BC, AB a CD rovnaké (obr. 2). Nakreslíme uhlopriečku AC. Trojuholník ABC a ACD majú tri rovnaké strany. Potom sú uhly BAC a DCA rovnaké, a preto je AB rovnobežná s CD. Rovnobežnosť strán BC a AD vyplýva z rovnosti uhlov CAD a DIA.
Veta 27. Ak sú opačné uhly štvoruholníka rovnaké v pároch, potom ide o rovnobežník.
Nech ∠ A=∠ C a ∠ B=∠ D. ∠ A+∠ B+∠ C+∠ D=360 o, potom ∠ A+∠ B=180 o a strany AD a BC sú rovnobežné (na základe rovnobežiek). Tiež dokážeme rovnobežnosť strán AB a CD a dospejeme k záveru, že ABCD je podľa definície rovnobežník.
Veta 28. Ak priľahlé rohy štvoruholníka, t.j. uhly susediace s jednou stranou sú 180 stupňov, potom ide o rovnobežník.
Ak súčet vnútorných jednostranných uhlov je 180 stupňov, potom sú čiary rovnobežné. To znamená, že AB je pár CD a BC je pár AD. Štvoruholník sa podľa definície javí ako rovnobežník.
Veta 29. Ak sú uhlopriečky štvoruholníka vzájomne rozdelené v priesečníku na polovicu, potom je štvoruholník rovnobežník.
Dôkaz. Ak AO=OC, BO=OD, potom sú trojuholníky AOD a BOC rovnaké, pretože majú rovnaké uhly (vertikálne) vo vrchole O, uzavreté medzi pármi rovnakých strán. Z rovnosti trojuholníkov usudzujeme, že AD a BC sú rovnaké. Strany AB a CD sú tiež rovnaké a štvoruholník sa ukáže ako rovnobežník podľa funkcie 1.
Veta 30. Ak má štvoruholník pár rovnakých rovnobežných strán, ide o rovnobežník.
Nech sú strany AB a CD rovnobežné a rovnaké v štvoruholníku ABCD. Nakreslite uhlopriečky AC a BD. Z rovnobežnosti týchto priamok vyplýva rovnosť priečne ležiacich uhlov ABO=CDO a BAO=OCD. Trojuholníky ABO a CDO sú rovnaké v bočných a susedných uhloch. Preto AO=OC, BO=OD, t.j. diagonály priesečníka sú rozdelené na polovicu a štvoruholník sa ukáže ako rovnobežník podľa znaku 4.

V geometrii sa berú do úvahy špeciálne prípady rovnobežníka.

Koncept rovnobežníka

Definícia 1

Paralelogram je štvoruholník, v ktorom sú protiľahlé strany navzájom rovnobežné (obr. 1).

Obrázok 1.

Rovnobežník má dve hlavné vlastnosti. Uvažujme o nich bez dôkazov.

Vlastnosť 1: Protiľahlé strany a uhly rovnobežníka sú si navzájom rovnaké.

Vlastnosť 2: Uhlopriečky nakreslené v rovnobežníku sú rozpolené ich priesečníkom.

Vlastnosti paralelogramu

Zvážte tri vlastnosti rovnobežníka a prezentujte ich vo forme viet.

Veta 1

Ak sú dve strany štvoruholníka rovnaké a tiež rovnobežné, potom tento štvoruholník bude rovnobežník.

Dôkaz.

Dajme nám štvoruholník $ABCD$. Do ktorej $AB||CD$ a $AB=CD$ Narysujme do nej uhlopriečku $AC$ (obr. 2).

Obrázok 2

Uvažujme rovnobežné čiary $AB$ a $CD$ a ich sečnicu $AC$. Potom

\[\uhol CAB=\uhol DCA\]

ako priečne rohy.

Podľa $I$ kritéria pre rovnosť trojuholníkov,

pretože $AC$ je ich spoločná strana a $AB=CD$ podľa predpokladu. Prostriedky

\[\uhol DAC=\uhol ACB\]

Uvažujme priamky $AD$ a $CB$ a ich sečnicu $AC$; poslednou rovnosťou krížových uhlov dostaneme $AD||CB$.) Preto podľa definície $1$ tento štvoruholník je rovnobežník.

Veta bola dokázaná.

Veta 2

Ak sú protiľahlé strany štvoruholníka rovnaké, ide o rovnobežník.

Dôkaz.

Dajme nám štvoruholník $ABCD$. V ktorých $AD=BC$ a $AB=CD$. Nakreslíme do nej uhlopriečku $AC$ (obr. 3).

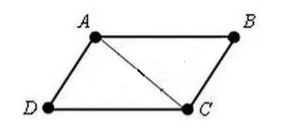
Obrázok 3

Keďže $AD=BC$, $AB=CD$ a $AC$ je spoločná strana, potom pomocou testu trojuholníkovej rovnosti $III$,

\[\triangle DAC=\triangle ACB\]

\[\uhol DAC=\uhol ACB\]

Zoberme si priamky $AD$ a $CB$ a ich sečnicu $AC$, podľa poslednej rovnosti medzi sebou ležiacich uhlov dostaneme $AD||CB$. Preto podľa definície $1$ je tento štvoruholník rovnobežníkom.

\[\uhol DCA=\uhol CAB\]

Zoberme do úvahy čiary $AB$ a $CD$ a ich sečnicu $AC$, pri poslednej rovnosti medzi sebou ležiacich uhlov dostaneme $AB||CD$. Preto podľa definície 1 je tento štvoruholník rovnobežníkom.

Veta bola dokázaná.

Veta 3

Ak sú uhlopriečky nakreslené v štvoruholníku ich priesečníkom rozdelené na dve rovnaké časti, potom je tento štvoruholník rovnobežníkom.

Dôkaz.

Dajme nám štvoruholník $ABCD$. Nakreslíme do nej uhlopriečky $AC$ a $BD$. Nech sa pretínajú v bode $O$ (obr. 4).

Obrázok 4

Keďže podľa podmienky $BO=OD,\ AO=OC$ a uhly $\uhol COB=\uhol DOA$ sú vertikálne, potom pomocou $I$ testu rovnosti trojuholníka,

\[\triangle BOC=\triangle AOD\]

\[\uhol DBC=\uhol BDA\]

Zoberme si čiary $BC$ a $AD$ a ich sečnicu $BD$, pri poslednej rovnosti uhlov ležiacich naprieč dostaneme $BC||AD$. Tiež $BC=AD$. Preto podľa vety $1$ je tento štvoruholník rovnobežníkom.