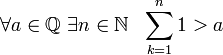Historiallisesti ensimmäinen kokonaislukuja$N$, pierujen uudelleenlaskennan seurauksena. Näiden lukujen joukko on ääretön ja muodostaa luonnollisen sarjan $N=\(1, 2, 3, ..., n, ...\)$. Tässä joukossa yhteen- ja kertolaskuoperaatiot ovat mahdollisia. Vähennysoperaation suorittamiseksi vaadittiin uusia lukuja, jotka johtivat kokonaislukujoukon ilmestymiseen: $Z$. $Z=N_+\kuppi N_- \kuppi \(0\)$. Näin ollen kokonaislukujoukossa suoritetaan aina yhteen-, kerto- ja vähennysoperaatiot.
Rationaaliset luvut
Tarve suorittaa jako johti rationaalilukujen joukkoon $Q$. $Q=\(\frac(m)(n), m\in Z, n\in N\)$.
Määritelmä. Kaksi rationaalilukua ovat yhtä suuret: $\frac(m_1)(n_1)=\frac(m_2)(n_2)$ - jos $m_1\cdot n_2=n_1\cdot m_2$. Tämä tarkoittaa, että jokainen rationaalinen luku voidaan esittää yksiselitteisesti pelkistymättömänä murto-osana $\frac(m)(n)$. $gcd(m, n)=1$.
Rationaalilukujen joukon ominaisuudet
1. Tuloksena aritmeettiset operaatiot rationaalilukujen yli (yhteen-, kerto-, vähennys-, jakolasku, paitsi nollalla jako) saadaan rationaalinen luku.
2. Rationaalilukujen joukko on järjestetty, eli mille tahansa rationaalilukuparille $a$ ja $b$ tai $a
3. Rationaalilukujoukko on tiheä, eli mille tahansa rationaalilukuparille $a$ ja $b$ on olemassa rationaaliluku $c$, jolloin $a Mikä tahansa positiivinen rationaalinen luku voidaan aina esittää desimaalilukuna: joko äärellisenä tai äärettömänä jaksollisena. Esimerkki: $\frac(3)(5)=0.6$, $\frac(1)(3)=0.333...=0,(3)$. $\frac(m)(n)=a_0,a_1a_1...a_kb_1b_2b_3...b_nb_1b_2b_3...b_n...$. $b_1b_2b_3...b_n...$ - kutsutaan desimaaliluvun jaksoksi, jossa ei kaikki $b_i=0$. Huomaa, että äärellinen murto-osa voidaan kirjoittaa äärettömänä jaksollisena murtolukuna, jonka jaksossa on nolla. $\frac(m)(n)=a_0,a_1a_1...a_k000000...$, $a_k\ne0$. Toinen rationaalilukujen esitys desimaalilukuna on kuitenkin yleisempi: $\frac(m)(n)=a_0,a_1a_1...(a_k-1)999...$. Negatiiviset rationaaliluvut $-\frac(m)(n)$ kirjoitetaan muotoa $\frac(m)(n)$ olevan rationaaliluvun desimaalilaajennukseksi vastakkaisella merkillä. Numero $0$ esitetään muodossa $0,000...$. Siten mikä tahansa rationaalinen luku on aina esitettävissä äärettömänä desimaalilukuna, joka ei sisällä $0$ jaksossa, paitsi itse luku $0$. Tämä näkemys on ainoa. Rationaalilukujen joukko suljetaan neljällä aritmeettisella operaatiolla. Rationaalisten lukujen joukossa ei kuitenkaan aina tapahdu yksinkertaisimman yhtälön, joka on muotoa $x^2-n=0$, ratkaisu. Siksi on tarpeen ottaa käyttöön uusia numeroita. Osoitetaan, että rationaalisten lukujen joukossa ei ole lukua, jonka neliö on kolme. Todistus suoritetaan ristiriitamenetelmällä. Oletetaan, että on olemassa rationaaliluku $\frac(m)(n)$, jonka neliö on kolme: $\left(\frac(m)(n)\right)^2=3\;\;\;( 1 )$. $\frac(m^2)(n^2)=3$, $m^2=3n^2.\;\;\;(2)$ Yhtälön (2) oikea puoli on jaollinen kolmella. Siten $m^2$ on myös jaollinen kolmella, joten $m$ on jaollinen 3:lla, mikä tarkoittaa, että $m=3k$. Korvaamalla yhtälön (2), saamme: $3k^2=n^2.\;\;\;(3)$ $(3)$:n vasen puoli on jaollinen $3$:lla, joten oikea puoli on myös jaollinen $3$:lla. Siten $n^2$ on jaollinen $3$:lla, joten $n$ on myös jaollinen luvulla $3$, mistä $n=3p$. Lopputuloksena saadaan: $\frac(m)(n)=\frac(3k)(3p)$, eli murto-osa $\frac(m)(n)$ osoittautui pelkistäväksi, mikä on ristiriidassa oletuksen kanssa. . Tämä tarkoittaa, että rationaalisten lukujen joukossa ei ole sellaista lukua, jonka neliö on yhtä suuri kuin kolme. Mutta on luku, jonka neliö on kolme. Se voidaan esittää äärettömänä ei-jaksollisena murtolukuna. Ja meillä on uudenlaisia numeroita. Kutsukaamme niitä irrationaalisiksi. Määritelmä. Irrationaaliluku on mikä tahansa ääretön ei-jaksollinen murtoluku. Kaikkien äärettömien ei-jaksollisten murtolukujen joukkoa kutsutaan irrationaalisten lukujen joukoksi ja sitä merkitään $I$. Rationaalilukujen $Q$ ja irrationaalilukujen $I$ liitto antaa reaalilukujen joukon $R$: $Q\cup I=R$. Siten mikä tahansa reaaliluku voidaan esittää äärettömänä desimaalilukuna: jaksollinen rationaaliluvun tapauksessa ja ei-jaksollinen irrationaalisen luvun tapauksessa. Reaalilukujen $a=a_0,a_1a_2a_3\ldots a_n\ldots$, $b=b_0,b_1b_2b_3\ldots b_n\ldots$ vertailu on seuraava: 1) Olkoot $a$ ja $b$ molemmat positiivisia: $a>0$, $b>0$, sitten: $a=b$ jos jollekin $k$ $a_k=b_k$; $a>b$ jos $\olemassa s$ $\kaikki k 2) Olkoon $a>0$, $b<0$, или иначе: $b<0 3) Olkoot $a$ ja $b$ molemmat negatiivisia: $a<0$, $b<0$, тогда: $a=b$ jos $-a=-b$; On olemassa erilaisia lukuja - neliöjuuren erottaminen johtaa usein niihin (eikä vain sitä, emme vain tiedä sitä vielä). Joten meidän on tutustuttava uusiin numeroihin tarkemmin. Mutta ensin yritetään systematisoida tietomme "vanhoista", eli rationaalisista, numeroista. 1. Jotkut matemaattisen kielen symbolit
Nämä olivat kokonaislukuja, yhteisiä murtolukuja ja desimaalilukuja. Voit käyttää kaikkia näitä lukuja varten samaa merkintää, josta nyt keskustellaan. 5 = 5.00000... = 5,(0). Sama pätee numeroon 8,377: 8,377 = 8,377000... = 8,377(0). Jotta kaikki olisi siistiä, he sanovat näin: 8,377 on äärellinen desimaaliluku ja 8,377000 ... on ääretön desimaaliluku. Yleensä mikä tahansa rationaalinen luku voidaan kirjoittaa äärettömänä desimaalilukuna. Kommentti.
Tämä johtopäätös on kätevä teorialle, mutta ei kovin kätevä käytännölle. Loppujen lopuksi, jos viimeinen desimaaliluku 8,377 on annettu, niin miksi se on kirjoitettava muodossa 8,377 (0)? Siksi he yleensä sanovat näin: mikä tahansa rationaalinen luku voidaan kirjoittaa äärettömänä desimaalimurtolukuna tai äärettömänä desimaalilukuna. Rationaalilukujen joukko merkitään ja voidaan kirjoittaa seuraavasti: Osoittautuu, että eri merkinnät voivat edustaa samaa murtolukua, esimerkiksi ja , (kaikki murtoluvut, jotka voidaan saada toisistaan kertomalla tai jakamalla samalla luonnollisella luvulla, edustavat samaa rationaalilukua). Koska jakamalla murtoluvun osoittaja ja nimittäjä niiden suurimmalla yhteisellä jakajalla, voidaan saada rationaaliluvun ainoa pelkistymätön esitys, voidaan puhua niiden joukosta joukkona vähentymätön murtoluvut, joissa on kokonaisluku osoittaja ja luonnollinen nimittäjä: Tässä on suurin yhteinen jakaja numerot ja . Rationaalilukujen joukko on luonnollinen yleistys kokonaislukujen joukosta. On helppo nähdä, että jos rationaaliluvulla on nimittäjä , niin se on kokonaisluku. Rationaalilukujoukko on kaikkialla tiheä lukuakselilla: minkä tahansa kahden eri rationaaliluvun välissä on ainakin yksi rationaaliluku (ja siten ääretön joukko rationaalilukuja). Kuitenkin käy ilmi, että rationaalisten lukujen joukolla on laskettava kardinaliteetti (eli kaikki sen elementit voidaan numeroida uudelleen). Huomaa muuten, että jopa muinaiset kreikkalaiset olivat vakuuttuneita lukujen olemassaolosta, joita ei voida esittää murtolukuna (he esimerkiksi osoittivat, että ei ole olemassa rationaalilukua, jonka neliö on 2). Ominaisuudet Perusominaisuudet Rationaalilukujen joukko täyttää kuusitoista perusominaisuutta, jotka voidaan helposti saada kokonaislukujen ominaisuuksista. Lisäominaisuudet Kaikkia muita rationaalilukuihin sisältyviä ominaisuuksia ei eroteta perusominaisuuksiksi, koska yleisesti ottaen ne eivät enää perustu suoraan kokonaislukujen ominaisuuksiin, vaan ne voidaan todistaa annettujen perusominaisuuksien perusteella tai suoraan luvun määritelmällä. jokin matemaattinen objekti. Tällaisia lisäominaisuuksia on paljon. Tässä on järkevää mainita niistä vain muutama. 25..Jo irrationaalisia lukuja Esimerkkejä irrationaalisista luvuista: Irrationaalisten lukujen joukko on merkitty isolla englanninkielisellä kirjaimella [ai] - "I". Numerojoukon joukossa irrationaalisilla luvuilla on erityinen paikka. Ne eivät sisälly rationaalisiin lukuihin. Irrationaalisia lukuja(toisin kuin rationaaliset) ei voida esittää murtolukuna a / b , jossa a ∈ Z (a kuuluu kokonaislukuihin), b∈N (b kuuluu luonnollisiin lukuihin). 26. Reaalilukujen joukko R oikea numero Wikipediasta, ilmaisesta tietosanakirjasta Hyppää: navigointi, haku Todellinen, tai oikea numero- matemaattinen abstraktio, joka syntyi tarpeesta mitata ympäröivän maailman geometriset ja fysikaaliset suureet sekä suorittaa sellaisia operaatioita kuin juurien erottaminen, logaritmien laskeminen, algebrallisten yhtälöiden ratkaiseminen. Numerorivi Jos luonnolliset luvut syntyivät laskentaprosessissa, rationaaliset luvut - tarpeesta toimia kokonaisuuden osien kanssa, niin reaaliluvut on tarkoitettu jatkuvien määrien mittaamiseen. Näin ollen tarkasteltavana olevan lukukannan laajentaminen on johtanut reaalilukujen joukkoon, joka sisältää rationaalilukujen lisäksi myös muita elementtejä ns. irrationaalisia lukuja. Reaaliluvun käsite voidaan visualisoida käyttämällä numeroviiva. Jos valitset suoran suunnan, aloituspisteen ja pituusyksikön segmenttien mittaamiseen, niin jokainen reaaliluku voidaan liittää tiettyyn pisteeseen tällä suoralla ja päinvastoin, jokainen piste edustaa jotakin, ja lisäksi , vain yksi, todellinen luku. Tämän vastaavuuden vuoksi termiä numerorivi käytetään yleensä synonyyminä reaalilukujoukolle. Reaaliluvun käsite on kehittynyt pitkän matkan. Jo muinaisessa Kreikassa, Pythagoraan koulukunnassa, jossa kokonaisluvut ja niiden suhteet asetettiin kaiken perustaksi, suhteettomia määriä(neliön sivun ja diagonaalin yhteensopimattomuus), eli nykyajan terminologiassa lukuja, jotka eivät ole rationaalisia. Tämän jälkeen Eudoxus of Cnidus yritti rakentaa yleisen lukuteorian, joka sisälsi suhteettomia määriä. Sen jälkeen yli kahteen tuhanteen vuoteen kukaan ei tuntenut tarvetta reaaliluvun käsitteen tarkkaan määrittelyyn huolimatta tämän käsitteen asteittaisesta laajentumisesta. Vasta 1800-luvun jälkipuoliskolla, kun matemaattisen analyysin kehittyminen edellytti sen perusteiden uudelleenjärjestelyä uudelle, korkeammalle tasolle, K. Weierstrassin, R. Dedekindin teoksissa luotiin tiukka reaalilukuteoria. , G. Cantor, E. Heine, S. Mere. Modernin matematiikan näkökulmasta reaalilukujen joukko on jatkuva järjestyskenttä. Tämä määritelmä tai vastaava aksioomajärjestelmä määrittelee tarkalleen reaaliluvun käsitteen siinä mielessä, että on olemassa vain yksi, isomorfismiin asti jatkuva järjestyskenttä. Reaalilukujoukolla on standardi merkintätapa - R("lihavoitu R") tai (eng. liitutaulu lihavoitu"R") lat. realis- pätevä. 27. Numerojärjestelmät Merkintä- symbolinen tapa kirjoittaa numeroita, jotka edustavat numeroita kirjoitetuilla merkeillä. Merkintä: Numerojärjestelmät on jaettu paikallinen, ei-positiaalinen ja sekoitettu.Irrationaalisia lukuja
Oikeita lukuja
Reaalilukujen vertailu
Tarkastellaan esimerkiksi kokonaislukua 5, yhteistä murtolukua ja desimaalilukua 8,377. Kokonaisluku 5 voidaan kirjoittaa äärettömänä desimaalilukuna: 5,0000... Desimaaliluku 8,377 voidaan kirjoittaa myös äärettömänä desimaaliluku: 8.377000... Käytämme lukua varten "kulmajako"-menetelmää:
Kuten näet, alkaen toisesta numerosta desimaalipilkun jälkeen, sama numeroryhmä toistetaan: 18, 18, 18, .... Siten = 0,3181818... . Lyhyesti sanottuna se kirjoitetaan näin: 0,3 (18). Desimaalipilkun jälkeen toistuvaa numeroryhmää kutsutaan pisteeksi, ja itse desimaalimurtolukua kutsutaan äärettömäksi desimaalilukujaksoksi.
ääretön desimaaliluku. Voit tehdä tämän kirjoittamalla pisteen numeron 0:
Siten luku 5, luku ja luku 8,377 kirjoitettiin äärettömänä desimaalilukuna.![]()