Numeroiden tyypit. Naturalit, kokonaisluvut, rationaalit ja realit. Numero on abstraktio, jota käytetään määrälliset ominaisuudet esineitä. Numerot ovat peräisin v primitiivinen yhteiskunta ihmisten tarpeeseen laskea esineitä. Ajan myötä tieteen kehittyessä numerosta on tullut tärkein matemaattinen käsite.

Ongelmanratkaisuun ja todisteisiin erilaisia ​​lauseita sinun on ymmärrettävä, minkä tyyppiset numerot ovat. Pääasiallisia lukutyyppejä ovat: luonnolliset luvut, kokonaisluvut, rationaaliluvut, reaaliluvut.

Kokonaisluvut- nämä ovat numeroita, jotka on saatu esineiden luonnollisella laskennalla tai pikemminkin niiden numeroinnilla ("ensimmäinen", "toinen", "kolmas" ...). Paljon luonnolliset luvut merkitty Latinalainen kirjain N(voidaan muistaa sen perusteella Englanninkielinen sana luonnollinen). Sen voi sanoa N ={1,2,3,....}

Kokonaislukuja ovat numeroita joukosta (0, 1, -1, 2, -2, ....). Tämä joukko koostuu kolmesta osasta - luonnolliset luvut, negatiiviset kokonaisluvut (luonnollisten lukujen vastakohta) ja numero 0 (nolla). Kokonaisluvut on merkitty latinalaisella kirjaimella Z. Sen voi sanoa Z={...,-3,-2,-1,0,1,2,3,....}.

Rationaaliset luvut ovat lukuja, jotka voidaan esittää murtolukuna, missä m on kokonaisluku ja n on luonnollinen luku. Tässä tapauksessa kutsutaan numeroa m osoittaja, ja numero n - nimittäjä murto-osia. Tällainen murtoluku tulee ymmärtää m:n jakamisen tuloksena n:llä, vaikka sitä ei voidakaan jakaa kokonaan. Latinalaista kirjainta käytetään merkitsemään rationaalisia lukuja K. Q={... ;-3;-2,5;-2;-1;0; ;1;2;3;3,5....}. Kaikki luonnolliset ja kokonaisluvut ovat rationaalisia. Esimerkkeinä rationaaliluvuista voit myös antaa: , , . AT oikea elämä rationaalilukuja käytetään joidenkin kokonaisten mutta jaettavissa olevien esineiden, kuten kakkujen tai muiden useisiin paloiksi leikattujen ruokien osien laskemiseen tai laajennettujen esineiden tilasuhteiden karkeasti arvioimiseen.

Oikeat (oikeat) numerot ovat numeroita, joita käytetään mittaamiseen jatkuvat määrät. Paljon todellisia lukuja merkitty latinalaisella kirjaimella R. Reaaliluvut sisältävät rationaaliluvut ja irrationaaliset luvut. Irrationaalisia lukuja- nämä ovat lukuja, jotka saadaan suorittamalla erilaisia ​​​​toimintoja rationaalisilla luvuilla (esimerkiksi juuren erottaminen, logaritmien laskeminen), mutta jotka eivät ole rationaalisia. Esimerkkejä irrationaalisista luvuista ovat , , .

Mikä tahansa reaaliluku voidaan näyttää numerorivillä:

Yllä luetelluille numerosarjoille seuraava väite pitää paikkansa:

Eli luonnollisten lukujen joukko sisältyy kokonaislukujen joukkoon. Kokonaislukujen joukko sisältyy rationaalilukujen joukkoon. Ja rationaalilukujen joukko sisältyy reaalilukujen joukkoon. Tämä väite voidaan havainnollistaa käyttämällä Eulerin ympyröitä.

Luonnollisten lukujen määritelmät ovat kokonaislukuja positiivisia lukuja. Luonnollisia lukuja käytetään esineiden laskemiseen ja moniin muihin tarkoituksiin. Nämä luvut ovat: 1; 2; 3; neljä;...

Tämä on luonnollinen numerosarja.
Onko nolla luonnollinen luku? Ei, nolla ei ole luonnollinen luku.
Kuinka monta luonnollista lukua on? Olemassa ääretön joukko luonnolliset luvut.
Mikä on pienin luonnollinen luku? Yksi on pienin luonnollinen luku.
Mikä on suurin luonnollinen luku? Sitä ei voida määrittää, koska luonnollisia lukuja on ääretön joukko.

Luonnollisten lukujen summa on luonnollinen luku. Joten luonnollisten lukujen a ja b yhteenlasku:

Luonnollisten lukujen tulo on luonnollinen luku. Joten luonnollisten lukujen a ja b tulo:

c on aina luonnollinen luku.

Luonnollisten lukujen ero Aina ei ole luonnollista lukua. Jos minuendi on suurempi kuin osaluku, niin luonnollisten lukujen erotus on luonnollinen luku, muuten se ei ole.

Luonnollisten lukujen osamäärä Luonnollista lukua ei aina ole. Jos luonnollisille luvuille a ja b

missä c on luonnollinen luku, se tarkoittaa, että a on tasaisesti jaollinen b:llä. Tässä esimerkissä a on osinko, b on jakaja, c on osamäärä.

Luonnollisen luvun jakaja on luonnollinen luku, jolla ensimmäinen luku on tasan jaollinen.

Jokainen luonnollinen luku on jaollinen 1:llä ja itsellään.

Yksinkertaiset luonnolliset luvut ovat jaollisia vain 1:llä ja itsellään. Tässä se tarkoittaa, että ne ovat täysin jakautuneet. Esimerkki, numerot 2; 3; 5; 7 on jaollinen vain 1:llä ja itsellään. Nämä ovat yksinkertaisia ​​luonnollisia lukuja.

Yhtä ei pidetä alkulukuna.

Lukuja, jotka ovat suurempia kuin yksi ja jotka eivät ole alkulukuja, kutsutaan yhdistelmäluvuiksi. Esimerkkejä yhdistetyt numerot: 4; 6; 8; 9; 10

Yhtä ei pidetä yhdistelmälukuna.

Luonnollisten lukujen joukko on yksi, alkuluvut ja yhdistelmäluvut.

Luonnollisten lukujen joukko on merkitty latinalaisella kirjaimella N.

Luonnollisten lukujen yhteen- ja kertolaskuominaisuudet:

lisäyksen kommutatiivinen ominaisuus

assosiatiivista omaisuutta lisäyksiä

(a + b) + c = a + (b + c);

kertolasku kommutatiivinen ominaisuus

kertomisen assosiatiivinen ominaisuus

(ab)c = a(bc);

jakeluomaisuutta kertolasku

a (b + c) = ab + ac;

Kokonaislukuja

Kokonaisluvut ovat luonnollisia lukuja, nolla ja luonnollisten lukujen vastakohta.

Luonnollisten lukujen vastaiset luvut ovat kokonaislukuja. negatiivisia lukuja, esimerkiksi: -1; -2; -3; - neljä;...

Kokonaislukujoukkoa merkitään latinalaisella kirjaimella Z.

Rationaaliset luvut

Rationaaliluvut ovat kokonaislukuja ja murtolukuja.

Mikä tahansa rationaalinen luku voidaan esittää jaksollisena murtolukuna. Esimerkkejä: -1, (0); 3, (6); 0, (0);...

Esimerkeistä on selvää, että mikä tahansa kokonaisluku on jaksollinen murto-osa jaksolla nolla.

Mikä tahansa rationaalinen luku voidaan esittää murto-osana m/n, missä m kokonaisluku, n luonnollinen luku. Esitetään edellisen esimerkin luku 3,(6) sellaisena murto-osana: 22/6 = 3,(6);

Toinen esimerkki: rationaalinen luku 9 voidaan esittää yksinkertaisena murtolukuna 18/2 tai 36/4.

Toinen esimerkki: rationaalinen luku -9 voidaan esittää yksinkertaisena murtolukuna -18/2 tai -72/8.

Rationaalilukujen joukko on merkitty latinalaisella kirjaimella Q.

Irrationaalisia lukuja

Irrationaaliset luvut ovat äärettömiä ei-toistuvia desimaalilukuja.

Esimerkkejä: pi = 3,141592... e = 2,718281...

Oikeita lukuja

Reaaliluvut ovat kaikki rationaalisia ja kaikki irrationaalisia lukuja.

Reaalilukujoukkoa merkitään latinalaisella kirjaimella R.

Tarkoitus: Tietää mikä luonnollinen, kokonaisluku, rationaalinen luku, jaksollinen murtoluku on; osaa kirjoittaa loputtomasti desimaali tavallisen muodossa, osaa suorittaa toimintoja desimaali- ja tavallisilla murtoluvuilla.

1. Yhdistää opiskelumateriaalia muuttamalla työtyyppejä aiheesta "Kokonaisluvut ja rationaaliset luvut".
2. Kehittää taitoja ja kykyjä suorittaa toimintoja desimaali- ja tavallisilla murtoluvuilla, kehittyä looginen ajattelu, oikeaa ja osaavaa matemaattista puhetta, itsenäisyyden kehittymistä ja luottamusta tietoihinsa ja taitoihinsa suorituksessa eri tyyppejä toimii.
3. Lisää kiinnostusta matematiikkaa kohtaan ottamalla käyttöön erilaisia ​​materiaalin konsolidointityyppejä: suullinen työ, työskentely oppikirjan kanssa, työskentely taulun ääressä, kysymyksiin vastaaminen ja itsetutkiskelukyky, itsenäinen työskentely; kannustaa ja kannustaa opiskelijoiden toimintaan.

minä Ajan järjestäminen.
II. Uusi aihe:
"Kokonaisluvut ja rationaaliluvut".
1. Teoreettinen osa.
2. Käytännön osa.
3. Työskentele oppikirjan mukaan ja taulun ääressä.
4. Itsenäinen työ vaihtoehtojen mukaan.
III. Tulokset.
1. Kysymyksiin.
IV. Kotitehtävät.

Tuntien aikana

I. Organisatorinen hetki.

Opettajan ja oppilaiden emotionaalinen mieliala ja valmius oppitunnille. Tavoitteiden ja tavoitteiden viestintä.

II. Uusi aihe: "Kokonaisluvut ja rationaaliset luvut":

Teoreettinen osa.

1. Aluksi luku ymmärrettiin vain luonnollisina lukuina. Mikä riittää yksittäisten kohteiden laskemiseen.

Aseta N = (1; 2; 3...) luonnolliset luvut on suljettu yhteen- ja kertolaskuoperaatioiden alla. Tämä tarkoittaa, että luonnollisten lukujen summa ja tulo ovat luonnollisia lukuja.

2. Kahden luonnollisen luvun ero ei kuitenkaan ole enää aina luonnollinen luku.

(Anna esimerkkejä: 5 - 5 = 0; 5 - 7 = - 2, luvut 0 ja - 2 eivät ole luonnollisia).

Siten kahden identtisen luonnollisen luvun vähentämisen tulos johtaa nollan käsitteeseen ja johdatukseen ei-negatiivisten kokonaislukujen joukkoa

Z0 = (0; 1; 2;...).

3. Jotta vähennysoperaatio olisi mahdollista, syötä negatiivisia kokonaislukuja eli luonnollisten lukujen vastaisia ​​lukuja. Siten saadaan joukko kokonaislukuja Z={...; -3; -2; -1; 0; 1; 2;...}.

Jotta jakaminen millä tahansa luvulla ei ole nolla mahdollista, kaikkien kokonaislukujen joukkoon on lisättävä kaikkien positiivisten ja negatiiviset murtoluvut. Tulos on joukko rationaalilukuja Q=.

Kun teet neljä aritmeettiset operaatiot(paitsi nollalla jakoa) rationaalilukujen yli, rationaaliluvut saadaan aina.

4. Jokainen rationaalinen luku voidaan esittää jaksollisena desimaalilukuna.

Muistetaan mikä on jaksollinen murto-osa. Tämä on ääretön desimaaliluku, jossa tietystä desimaalista alkaen toistetaan sama numero tai useita numeroita - murto-osan jakso. Esimerkiksi 0,3333…= 0,(3);

1,057373…=1,05(73).

Nämä murtoluvut luetaan seuraavasti: "0 kokonaista ja 3 jaksossa", "1 kokonaisuus, 5 sadasosaa ja 73 jaksossa".

Kirjoitamme rationaaliset luvut äärettömänä jaksollisena desimaalilukuna:

luonnollinen luku 25 = 25.00…= 25,(0);

kokonaisluku -7 = -7,00…= -7,(0);

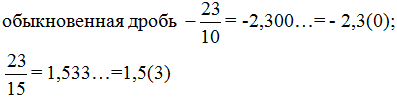
(käytämme kulmanjakoalgoritmia).

5. Myös käänteinen väite on totta: jokainen ääretön jaksollinen desimaalimurto on rationaalinen luku, koska se voidaan esittää murtolukuna, missä m on kokonaisluku, n on luonnollinen luku.

Harkitse esimerkkiä:

1) Olkoon x \u003d 0,2 (18) kertomalla 10:llä, saamme 10x \u003d 2,1818 ... (Sinun on kerrottava murtoluku 10 n:llä, missä n on tämän murto-osan tietueen sisältämien desimaalien määrä ylös ajanjaksolle: x10 n).

2) Kerrotaan viimeisen yhtälön molemmat puolet 100:lla, saadaan

1000x = 218,1818…(Kertomalla 10 k:lla, missä k on numeroiden lukumäärä jaksolla x10 n 10 k = x10 n+k).

3) Vähentämällä yhtälöstä (2) yhtäläisyydestä (1), saadaan 990x = 216, x = .

Käytännön osa.

1. Kirjoita desimaalilukuna:

1) - laudalla;

3) - taululle yksi opiskelija kirjoittaa päätöksensä, loput päättävät kentällä ja tarkistavat sitten toisensa;

4) - sanelussa kaikki suorittavat tehtävän, ja yksi puhuu ääneen.

2. Suorita toiminnot ja kirjoita tulos desimaalilukuna:

1) - laudalla;

3) - sanelussa kaikki suorittavat tehtävän, ja yksi puhuu ääneen;

5) - itsenäisesti jälkitarkastuksen kanssa.

3. Kirjoita nimellä murtolukuääretön desimaali:

6) -2.3(82) - opettaja näyttää ratkaisun taululle algoritmin perusteella.