Funktiota y=f(x) kutsutaan differentioituvaksi jossain pisteessä x 0, jos sillä on siinä pisteessä määrätty derivaatta, ts. jos suhteen raja on olemassa ja on äärellinen.

Jos funktio on differentioituva jonkin janan [a; b] tai väli (a; b), niin sen sanotaan olevan differentioituva segmentillä [a; b] tai vastaavasti välissä (a; b).

Pätee seuraava lause, joka muodostaa yhteyden differentioituvien ja jatkuvien funktioiden välille.

Lause. Jos funktio y=f(x) on differentioituva jossain pisteessä x 0 , niin se on jatkuva siinä pisteessä.

Siten funktion erilaistuvuus merkitsee sen jatkuvuutta.

Todiste. Jos sitten

missä b on äärettömän pieni arvo, ts. määrä, joka pyrkii nollaan, kun Ax>0. Mutta toisaalta

Dy=f "(x 0) Dx+bDx=> Dy>0, kun Dx>0, eli f(x) - f(x 0)>0, kun x>x 0,

ja tämä tarkoittaa, että funktio f(x) on jatkuva pisteessä x 0 . Q.E.D.

Siten epäjatkuvuuspisteissä funktiolla ei voi olla derivaattia. Käänteinen väite ei pidä paikkaansa: on jatkuvia funktioita, jotka eivät ole differentioituvia joissakin pisteissä (eli niillä ei ole derivaatta näissä pisteissä).

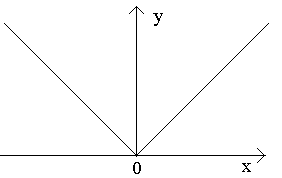
Tarkastellaan kuvan pistettä a, b, c.

Kohdassa a, kun Dx>0, suhteella ei ole rajaa (koska yksipuoliset rajat ovat erilaisia ​​Dx>0-0 ja Dx>0+0). Kuvaajan pisteessä A ei ole määriteltyä tangenttia, mutta on olemassa kaksi erilaista yksipuolista tangenttia, joiden kulmakertoimet ovat 1 ja 2 . Tämän tyyppistä pistettä kutsutaan kulmapisteeksi.

Pisteessä b Dx>0:lle suhde on etumerkkivakio, äärettömän suuri arvo. Funktiolla on ääretön derivaatta. Tässä vaiheessa kaaviolla on pystytangentti. Pistetyyppi - "käännepiste" pystytangentilla.

Kohdassa c yksipuoliset derivaatat ovat äärettömän suuria määriä eri merkkejä. Tässä vaiheessa kaaviossa on kaksi yhdistettyä pystytangenttia. Tyyppi - "kärki" pystytangentilla - kulmapisteen erikoistapaus.

1. Tarkastellaan funktiota y=|x|. Tämä toiminto on jatkuva pisteessä

Osoittakaamme, että sillä ei ole johdannaista tässä vaiheessa.

f(0+Dx) = f(Dx) = |Dx|. Siksi Dy = f(Dx) - f(0) = |Dx|

Mutta sitten Dx:lle< 0 (т.е. при Дx стремящемся к 0 слева)

Ja kun Dx > 0

Siten relaatiolla Dx> 0 on erilaiset rajat oikealla ja vasemmalla, mikä tarkoittaa, että suhteella ei ole rajaa, ts. funktion y=|x| derivaatta pisteessä x= 0 ei ole olemassa. Geometrisesti tämä tarkoittaa, että pisteessä x= 0 tällä "käyrällä" ei ole tarkkaa tangenttia (tässä pisteessä niitä on kaksi).

2. Funktio on määritelty ja jatkuva koko reaaliviivalla. Selvitetään, onko tällä funktiolla derivaatta kohdassa x= 0.

Siksi tarkasteltava funktio ei ole differentioituva pisteessä x= 0. Käyrän tangentti tässä pisteessä muodostaa kulman p/2 x-akselin kanssa, ts. osuu yhteen y-akselin kanssa.

3 Pisteessä olevan funktion derivaatan määritelmä. Olkoon funktio f(x) määritelty jossain pisteen x 0 ympäristössä. MÄÄRITELMÄ. Jos suhteella on (äärellinen) raja, niin f (x) kutsutaan differentioituvaksi pisteeksi x 0, ja itse rajaa kutsutaan funktion f (x) derivaatiksi pisteessä x 0 ja sitä merkitään f:llä. "(x 0), eli merkitsemme, että x \u003d x - x 0 on argumentin lisäys, kun siirrytään pisteestä x 0 pisteeseen x, ja y \u003d f (x 0 + x) - f (x 0) ) on funktion vastaava inkrementti. Silloin funktion f (x) derivaatta pisteessä x 0 on funktion inkrementin ja sen aiheuttaneen argumentin inkrementin suhteen raja, kun funktion inkrementti argumentti pyrkii nollaan.

4 Esimerkki 1. Annetaan esimerkkejä joidenkin yksinkertaisten alkeisfunktioiden derivaattojen laskemisesta derivaatan määritelmän perusteella. y = a x (0 0. Ottaen huomioon, että | x | 0 on mielivaltainen piste, niin 0. Ottaen huomioon, että | x | 0 on mielivaltainen piste, sitten ">

0. Ottaen huomioon, että | x | 0 on mielivaltainen piste, niin Esimerkki 4. y = sinx, x R. Otetaan x 0 R ja lasketaan funktion inkrementti tässä pisteessä: Joten (sinx) = cosx, x R." title=" 5 Esimerkki 3. Otetaan x 0 > 0. Ottaen huomioon, että |x | 0 on mielivaltainen piste, niin Esimerkki 4. y = sinx, x R. Otetaan x 0 R ja lasketaan funktion inkrementti tässä pisteessä: Joten (sinx) = cosx, x R." class="link_thumb"> 5 !} 5 Esimerkki 3. Otetaan x 0 > 0. Ottaen huomioon, että | x | 0 on mielivaltainen piste, niin Esimerkki 4. y = sinx, x R. Otetaan x 0 R ja lasketaan funktion inkrementti tässä pisteessä: Joten (sinx) = cosx, x R. 0. Ottaen huomioon, että | x | 0 on mielivaltainen piste, niin Esimerkki 4. y = sinx, x R. Otetaan x 0 R ja lasketaan funktion inkrementti tässä pisteessä: Joten (sinx) = cosx, x R. "> 0. Ottaen huomioon, että | x | 0 - mielivaltainen piste, sitten Esimerkki 4. y \u003d sinx, x R. Otetaan x 0 R ja lasketaan funktion inkrementti tässä pisteessä: Joten (sinx) \u003d cosx, x R. "> 0. | x | 0 on mielivaltainen piste, niin Esimerkki 4. y = sinx, x R. Otetaan x 0 R ja lasketaan funktion inkrementti tässä pisteessä: Joten (sinx) = cosx, x R." title=" 5 Esimerkki 3. Otetaan x 0 > 0. Ottaen huomioon, että |x | 0 on mielivaltainen piste, niin Esimerkki 4. y = sinx, x R. Otetaan x 0 R ja lasketaan funktion inkrementti tässä pisteessä: Joten (sinx) = cosx, x R."> title="5 Esimerkki 3. Otetaan x 0 > 0. Ottaen huomioon, että | x | 0 on mielivaltainen piste, niin Esimerkki 4. y = sinx, x R. Otetaan x 0 R ja lasketaan funktion inkrementti tässä pisteessä: Joten (sinx) = cosx, x R."> !}

6 LAUSE. Jos funktio f(x) on differentioituva pisteessä x 0, niin se on jatkuva siinä pisteessä. Todiste. Olkoon se olemassa. Tästä saadaan, että f (x) - f (x 0) \u003d f "(x 0) (x - x 0) + (x - x 0) α (x) x x 0:lle. , f ( x) on jatkuva pisteessä x 0. Differentioituvan funktion (1) jatkuvuus

7 HUOM. Funktion jatkuvuus pisteessä ei ole riittävä ehto derivaatan olemassaololle tässä pisteessä. Esimerkki 5. f (x) \u003d x. Tutkimme f (x):n käyttäytymistä x 0 = 0:n läheisyydessä. Tässä ja f (x) f (0) = 0 x 0:lle. funktio on jatkuva pisteessä x 0 \u003d 0. Tarkastellaan x y 0 Rajaa ei ole olemassa, koska siis funktiolla f (x) \u003d x ei ole derivaattia pisteessä x \u003d 0, vaikka se on jatkuva tässä vaiheessa

8 Esimerkki x y 0 kohdassa x 0. kohdassa x 0. Eli. f(x) on jatkuva kohdassa x = 0. f(x):llä ei ole derivaattia kohdassa x = 0, joten se ei ole differentioituva tässä pisteessä. Tutkimme f (x):n käyttäytymistä pisteen x = 0 läheisyydessä.

9 Olkoon funktio y \u003d f (x) differentioituva pisteessä x 0. Sitten (1) mukaan sen inkrementti pisteessä x 0 voidaan kirjoittaa muodossa y \u003d f (x 0 + x) - f (x 0) \u003d f ( x 0) x + o(x) kohdassa x. Funktion f (x 0) x differentiaalia - funktion y \u003d f (x) inkrementin päälineaariosaa pisteessä x 0, lineaarinen x:n suhteen, kutsutaan funktion differentiaaliksi pisteessä piste x 0 inkrementissä x ja sitä merkitään df (x 0; x) tai df (x 0 ) tai df tai dу. y \u003d f (x 0 + x) - f (x 0) \u003d df (x 0; x) + o (x) kohdassa x. MÄÄRITELMÄ. Inkrementin pääosa, lineaarinen x:ssä. Äärettömän pieni suuruusluokka kuin x. Nyt funktion inkrementti voidaan kirjoittaa näin:

10 HUOM. Inkrementtiä x merkitään usein symbolilla dx ja sitä kutsutaan itsenäisen muuttujan differentiaaliksi. Näin ollen funktion differentiaali pisteessä x 0 voidaan kirjoittaa muodossa df (x 0) \u003d f "(x 0) dx. Jos funktio on differentioituva tietyn intervallin jokaisessa pisteessä, niin sen differentiaali dy on a x:n ja dx:n funktio: dy \u003d f "(x)dx. Tästä saadaan erityisesti derivaatan lauseke eli derivaatta voidaan pitää funktion differentiaalin suhdetta riippumattoman muuttujan differentiaaliin.

11 Derivaatan ja differentiaalin geometrinen merkitys Olkoon funktio y \u003d f (x) määritelty U (x 0) ja differentioituva pisteessä x 0. M0M0 M x0x0 x 0 + x y x y = f (x) y0y0 y 0 + y 0 L on L 0 - tangentin x y \u003d f (x 0 + x) - f (x 0) sekantti kohdassa x funktion jatkuvuudesta johtuen. Funktion y \u003d f (x) kaavion tangentti pisteessä M 0 on sekantin L rajapaikka x:ssä. y Jos funktio on differentioituva pisteessä x 0, niin sekanttiyhtälössä y / x f (x 0) kohdassa x ja tangenttiyhtälö on muotoa y \u003d y 0 + f (x 0) (x - x 0) .

12 M0M0 M x0x0 x 0 + x dy = df(x 0; x) = f (x 0) x x y = f(x) f(x0)f(x0) f(x 0 + x) 0 x y F E EM = o (x) kohdassa x 0 L0L0 tg \u003d f (x 0) Jos y / x kohdassa x, niin sekanttiyhtälöstä saatua suoraa x \u003d x 0 kutsutaan pystytangentiksi funktion kuvaajalle kohdassa piste M 0. Tangenttiyhtälöstä saadaan y - y 0 \u003d f (x 0) (x - x 0) \u003d df (x 0) - tangentin ordinaatin lisäys siirryttäessä pisteestä x 0 pisteeseen x . Pisteessä M 0 olevan funktion kaavion normaali on suora, joka on kohtisuorassa pisteen M 0 kautta kulkevaan tangenttiin. Sen yhtälö on muotoa y \u003d y 0 - 1 / f (x 0) (x - x) 0). L 1 - normaali

13 Derivaatan ja differentiaalin fyysiset sovellukset Jos S (t) on materiaalin pisteen kulkema reitti ajassa t, niin S "(t) on materiaalipisteen hetkellinen nopeus ja dS \u003d S "(t) dt on etäisyys, jonka aineellinen piste kulkisi ajanjakson aikana pisteestä t paikkaan t + dt, jos se liikkuisi nopeudella, joka on yhtä suuri kuin hetkellinen nopeus hetkellä t. Jos Q (t) on sähkön määrä, joka virtaa johtimen poikkileikkauksen läpi hetkellä t, niin Q "(t) \u003d I on virran voimakkuus. Jos N (t) on aineen määrä, joka muodostuu hetkellä t kemiallisen reaktion aikana, sitten N "(t) - kemiallisen reaktion nopeus.

Jos toiminto y = f(x) on erilainen jossain vaiheessa x = x 0, niin se on jatkuva tässä pisteessä.

Siten epäjatkuvuuspisteissä funktiolla ei voi olla derivaattia. Käänteinen johtopäätös on väärä, ts. siitä, että jossain vaiheessa x = x 0 toiminto y = f(x) on jatkuva, siitä ei seuraa, että se olisi tässä vaiheessa differentioituva. Esimerkiksi funktio y = |x| jatkuvaa kaikille x (–< X < ), но в точке x= 0 ei ole derivaatta. Tässä vaiheessa kuvaajalla ei ole tangenttia. On oikea tangentti ja vasen tangentti, mutta ne eivät täsmää.

21 Sääntöjen löytäminen. tuotantoon määriä

Sääntö 1 Jos funktioilla y \u003d f (x) ja y \u003d g (x) on derivaatta pisteessä x, niin niiden summalla on myös derivaatta pisteessä x, ja summan derivaatta on yhtä suuri kuin johdannaiset:
(f (x) + 8 (x))" \u003d f (x) + (x).
Käytännössä tämä sääntö on muotoiltu lyhyemmällä tavalla: summan derivaatta on yhtä suuri kuin johdannaisten summa.
Esimerkiksi,
Sääntö 2 Jos funktiolla y \u003d f (x) on derivaatta pisteessä x, niin funktiolla y \u003d kf (x) on derivaatta pisteessä x, ja:

Käytännössä tämä sääntö on muotoiltu lyhyemmin: vakiotekijä voidaan ottaa pois derivaatan etumerkistä. Esimerkiksi,

Sääntö 3 Jos funktioilla y \u003d f (x) ja y \u003d g (x) on derivaatta pisteessä x, niin niiden tulolla on myös derivaatta pisteessä x, ja:

Käytännössä tämä sääntö on muotoiltu seuraavasti: kahden funktion tulon derivaatta on yhtä suuri kuin kahden termin summa. Ensimmäinen termi on ensimmäisen funktion ja toisen funktion derivaatan tulo, ja toinen termi on ensimmäisen funktion ja toisen funktion derivaatan tulo.
Esimerkiksi:
Sääntö 4 Jos funktioilla y \u003d f (x) ja y \u003d g (x) on derivaatta silloin ja osamäärällä on derivaatta pisteessä x, lisäksi:

Taulukko monimutkaisista johdannaisista

22 Diffir. funkt. pisteessä

Toiminto y=f(x) kutsutaan differentioituvaksi pisteessä x 0, jos sen lisäys Δ y(x 0,Δ x) voidaan esittää muodossa

Δ y(x 0,Δ x)=AΔ x+o(Δ x).

Lineaarinen pääosa AΔ x lisäykset Δ y kutsutaan tämän funktion differentiaaliksi pisteessä x 0, joka vastaa lisäystä Δ x, ja se on merkitty symbolilla dy(x 0,Δ x).

Toiminnon vuoksi y=f(x) oli eroava siinä vaiheessa x 0, on välttämätöntä ja riittävää, että derivaatta f′( x 0), kun taas tasa-arvo A=f′( x 0).

Differentiaalin lausekkeella on muoto

dy(x 0,dx)=f′( x 0)dx,

Missä dx=Δ x.

23 Tuot. Diff. Toiminnot

Monimutkaisen funktion johdannainen. Parametrisesti määritellyn funktion derivaatta

Antaa y - monimutkainen toiminto x, eli y = f(u), u = g(x), tai

Jos g(x) Ja f(u) ovat argumenttiensa differentioituvia funktioita, vastaavasti pisteissä x Ja u = g(x), silloin kompleksifunktio on myös differentioituva pisteessä x ja se löytyy kaavan mukaan

Parametrisesti annetun funktion derivaatta.

24 Tuot. ja ero. Ylempi määräys

Olkoon nyt kolmannen kertaluvun derivaatta määritelty jossain pisteen ympäristössä ja differentioituva. Sitten

Jos funktiolla on osittaisderivaata jonkin alueen D muuttujan suhteen, niin nimetyllä derivaatalla, joka on itse funktio, voi jossain vaiheessa olla osittaiset derivaatat saman tai minkä tahansa muun muuttujan suhteen. Alkuperäisessä funktiossa nämä derivaatat ovat toisen asteen osittaisia ​​derivaattoja (tai toisen asteen osittaisderivaataita).

Eri muuttujien suhteen otettua toisen tai korkeamman kertaluvun osittaisderivaata kutsutaan sekaosittaisderivaataksi. Esimerkiksi,

tilausero n, Missä n > 1, funktiota jossain vaiheessa kutsutaan differentiaaliksi tässä järjestysdifferentiaalin kohdassa (n - 1), tuo on

Yhdestä muuttujasta riippuvaisen funktion toinen ja kolmas differentiaali näyttävät tältä:

Tästä voimme johtaa differentiaalin yleisen muodon n-järjestys funktiosta:

25 Fermatin, Rollen, Langragen lauseet

v Fermatin lause: Määritetään funktio ja saavuttaa maksimi- ja minimiarvonsa ( M Ja m) joissakin . Jos kohdassa on derivaatta, se on välttämättä yhtä suuri kuin 0.

Todiste: On. Kaksi tapausta on mahdollista:

1) , => , => .

2) , => , => .

Kohdista 1) ja 2) seuraa, että

v Rollen lause (derivaatan juurista): Olkoon funktio jatkuva päällä ja differentioituva ja ota samat arvot segmentin päissä: . Sitten :ssä on ainakin yksi piste, jonka derivaatta on .

v Todistus: Jatkuva kurotus päällä M Ja m. Sitten kaksi tapausta on mahdollista:

2) suurin arvo saavutetaan Fermatin lauseen mukaisen intervallin sisällä.

v Langragen lause (noin äärellisillä askelilla): Olkoon funktio jatkuva päällä ja differentioituva päällä. Sitten on olemassa ainakin yksi, jolle seuraava yhtäläisyys pätee: .

Todistus: Esitellään funktio . (jatkuva päällä ja erotettava päällä ).

Funktio täyttää Rollen lauseen, jolle: , , , .

Funktiota kutsutaan tiukasti kasvaa jos

Funktiota kutsutaan vähenee jos

Funktiota kutsutaan tiukasti laskeva jos

Määritelmä: Funktion derivaatta pisteessä on raja, johon sen inkrementin suhde kyseisessä pisteessä suuntautuu argumentin vastaavaan lisäykseen, kun jälkimmäinen pyrkii nollaan:

Eli jos määritellään kohdassa, niin

Lause 1:

Funktion kuvaajalla on ei-pystytangentti silloin ja vain, jos tämän funktion derivaatalla on äärellinen arvo tietyssä pisteessä.

Todiste:

Olkoon siis f'()-äärellinen arvo

Olkoon ei-pystytangentti => olemassa - äärellinen.

Sekantti pyrkii tangenttiin.

Lause on todistettu.

Ticket 2 Jatkuvuus funktiolle, jolla on derivaatta.

Jossain pisteen a ympäristössä määriteltyä funktiota f (x) kutsutaan jatkuvaksi tässä pisteessä if

Lause: (välttämätön edellytys johdannaisen olemassaololle)

Jos funktiolla on äärellinen piste, se on jatkuva pisteessä.

Todiste:

Siksi - on jatkuva pisteessä.

Lause on todistettu.

Kommentti : päinvastoin ei pidä paikkaansa, jos funktio on jatkuva jossakin pisteessä, niin siitä ei seuraa, että sillä olisi derivaatta kyseisessä pisteessä.

lausunto : jos funktiolla on pisteessä oikea ja vasen derivaatta, niin se on jatkuva sekä oikealla että vasemmalla puolella.

Lippu 3

Summan, tuotteen, osamäärän derivaatta.

Käänteisfunktion derivaatta.

Differentioituvan funktion määritelmä. Erilaistuvuuden välttämätön ja riittävä ehto.

Olkoon funktiolla derivaatta pisteessä (lopullinen): .

Sitten riittävän pienelle voidaan kirjoittaa jonkin funktion summana, jota merkitsemme ja joka pyrkii nollaan yhdessä:,

ja pisteen lisäys voidaan kirjoittaa seuraavasti:

tai (1) ,

sillä lauseke ymmärretään funktiona siten, että sen suhde pyrkii nollaan yhdessä.

Selitys:

Määritelmä .

Funktiota kutsutaan differentioituvaksi pisteessä, jos sen inkrementti voidaan esittää seuraavasti: (2),

jossa A ei riipu , mutta yleensä riippuu .

Lause 1:

Jotta funktio olisi differentioituva jossakin pisteessä, on välttämätöntä ja riittävää, että sillä on äärellinen derivaatta tässä pisteessä.

Todiste:

Ehdon riittävyys edellä todistettu: äärellisen derivaatan olemassaolo merkitsi mahdollisuutta esittää muodossa (1), jossa voidaan asettaa

Välttämättömyys . Olkoon funktio differentioituva jossakin pisteessä. Sitten kohdasta (2), olettaen, saamme.

Oikean puolen raja on olemassa ja on yhtä suuri kuin A:.

Tämä tarkoittaa, että on olemassa johdannainen. Lause on todistettu.

Lippu 6 Funktion differentiaali, sen geometrinen merkitys.

Jos toiminto f on johdannainen f΄(x o ) pisteessä x o, silloin on raja , jossa Δ f=f(x o + Δ x)-f(x o ) , tai missä A=f΄(x o ) .

Määritelmä:

Toiminto f erottuva jossain kohdassa x o, jos sen lisäys voidaan esittää seuraavasti:

Missä AΔ x=df. (*)

Differentiaali on funktion inkrementin tärkein lineaarinen osa.

Jos on äärellinen derivaatta f΄(x o ) pisteessä x o, sitten toiminto f(x) on erotettavissa tässä vaiheessa.

Päinvastoin on myös totta: jos funktio f erottuva jossain kohdassa x o, eli sen inkrementti voidaan esittää muodossa (*), silloin sillä on derivaatta pisteessä x o yhtä kuin A:

Differentiaalin geometrinen merkitys:

A Ja B– kuvaajapisteet f(x), jotka vastaavat arvoja x o Ja (x o + Δ x) itsenäinen muuttuja. Piste-ordinaatit A Ja B vastaavasti yhtä suuret f(x o ) Ja f(x o + Δ x). Toiminnon lisäys Δ f=f(x o + Δ x)-f(x o ) pisteessä x o yhtä suuri kuin segmentin pituus BD ja se voidaan esittää summana Δ f=BD=DC+CB, Missä DC = tgaΔ x=f΄(x o ) Δ x Ja α on pisteen tangentin välinen kulma A kuvaajaan ja akselin positiiviseen suuntaan x. Tästä se on selvää DC on funktion differentiaali f pisteessä x o :

DC=df=f΄(x o ) Δ x.

Samaan aikaan toisen jäsenen osuus CB lisäykset Δ f huomioon koko . Tämä arvo suurella Δ x, ehkä jopa enemmän kuin päätermi, mutta se on äärettömästi korkeampi kertaluku kuin Δ x kun Δ x→0.

JATKUVIEN TOIMINTOJEN OMINAISUUDET

Tarkastellaan joitain intervallin jatkuvien funktioiden ominaisuuksia. Esittelemme nämä ominaisuudet ilman todisteita.

Toiminto y = f(x) nimeltään jatkuva segmentillä [a, b], jos se on jatkuva tämän janan kaikissa sisäpisteissä ja sen päissä, ts. kohdissa a Ja b, on jatkuva oikealla ja vasemmalla.

Lause 1. Jatkuva funktio segmentillä [ a, b], ainakin yhdessä tämän segmentin kohdassa on suurin arvo ja ainakin yhdessä kohdassa pienin arvo.

Lauseen mukaan jos funktio y = f(x) jatkuva aikavälillä [ a, b], silloin on vähintään yksi piste x 1 Î [ a, b] siten, että funktion arvo f(x) tässä vaiheessa on suurin kaikista sen arvoista tällä segmentillä: f(x1) ≥ f(x). Samoin on olemassa sellainen kohta x2, jossa funktion arvo on pienin kaikista segmentin arvoista: f(x 1) ≤ f(x).

On selvää, että tällaisia ​​pisteitä voi olla useita, esimerkiksi kuva osoittaa, että funktio f(x) ottaa pienimmän arvon kahdessa pisteessä x2 Ja x 2 ".

Kommentti. Lauseen lauseesta voi tulla väärä, jos huomioidaan funktion arvo välillä ( a, b). Todellakin, jos tarkastelemme funktiota y=x päällä (0, 2), niin se on jatkuva tällä välillä, mutta ei saavuta maksimi- tai minimiarvojaan siinä: se saavuttaa nämä arvot intervallin päissä, mutta päät eivät kuulu meidän alueella.

Myös lause lakkaa olemasta totta epäjatkuville funktioille. Anna esimerkki.

Seuraus. Jos toiminto f(x) jatkuva [ a, b], niin se rajoittuu tähän segmenttiin.

Lause 2. Anna toiminnon y = f(x) jatkuva segmentillä [ a, b] ja ottaa eri merkkien arvot tämän segmentin päistä, niin janan sisällä on ainakin yksi piste x=C, jossa funktio katoaa: f(C)= 0, missä a< C< b

Tällä lauseella on yksinkertainen geometrinen merkitys: jos jatkuvan funktion kuvaajan pisteet y = f(x), joka vastaa segmentin päitä [ a, b] sijaitsevat akselin vastakkaisilla puolilla Härkä, silloin tämä kuvaaja ainakin yhdessä janan pisteessä leikkaa akselin Härkä. Epäjatkuvilla toiminnoilla ei välttämättä ole tätä ominaisuutta.

Tämä lause hyväksyy seuraavan yleistyksen.

Lause 3 (väliarvojen lause). Anna toiminnon y = f(x) jatkuva segmentillä [ a, b] Ja f(a) = A, f(b) = B. Siis mille tahansa numerolle C välillä A Ja B, tämän segmentin sisällä on sellainen piste CÎ [ a, b], Mitä f(c) = C.

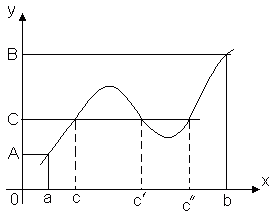
Tämä lause on geometrisesti ilmeinen. Tarkastellaan funktion kuvaajaa y = f(x). Antaa f(a) = A, f(b) = B. Sitten mikä tahansa rivi y = C, Missä C- mikä tahansa numero väliltä A Ja B, leikkaa funktion kuvaajan ainakin yhdessä pisteessä. Leikkauspisteen abskissa on tämä arvo x=C, jossa f(c) = C.

Näin ollen jatkuva funktio, joka siirtyy yhdestä arvostaan ​​toiseen, kulkee välttämättä kaikkien väliarvojen läpi. Erityisesti:

Seuraus. Jos toiminto y = f(x) on jatkuva jollain aikavälillä ja ottaa suurimman ja pienimmän arvon, niin tällä välillä se ottaa ainakin kerran minkä tahansa arvon sen pienimmän ja suurimman arvojen väliltä.

JOHDANNAISSOVELLUKSET JA SEN SOVELLUKSET. JOHDANNAISMÄÄRITELMÄ

Tehdään jokin toiminto y=f(x), määritelty tietyllä aikavälillä. Jokaiselle argumentin arvolle x tästä intervallista funktio y=f(x) on tietty merkitys.

Harkitse kahta argumenttiarvoa: iniciaali x 0 ja uusi x.

Ero x–x 0 kutsutaan argumentin x lisäys pisteessä x 0 ja merkitty Δx. Täten, ∆x = x – x 0 (argumentin lisäys voi olla joko positiivinen tai negatiivinen). Tästä tasa-arvosta seuraa se x=x 0 +Δx, eli muuttujan alkuarvo on saanut jonkin verran lisäystä. Sitten, jos pisteessä x 0 funktion arvo oli f(x 0 ), sitten uudessa kohdassa x funktio ottaa arvon f(x) = f(x 0 +∆x).

Ero y-y 0 = f(x) – f(x 0 ) nimeltään funktion lisäys y = f(x) pisteessä x 0 ja se on merkitty symbolilla Δy. Täten,

Δy = f(x) – f(x 0 ) = f(x 0 +Δx) - f(x 0 ) .

(1)

Yleensä argumentin alkuarvo x 0 katsotaan kiinteäksi ja uudeksi arvoksi x-muuttuva. Sitten y 0 = f(x 0 ) osoittautuu jatkuvaksi ja y = f(x)-muuttuva. lisäyksiä Δy Ja Δx on myös muuttujia ja kaava (1) osoittaa sen Dy on muuttujan funktio Δx.

Laadi funktion lisäyksen suhde argumentin kasvuun

Etsitään tämän suhteen raja kohdasta Δx→0. Jos tämä raja on olemassa, sitä kutsutaan tämän funktion derivaatiksi. f(x) pisteessä x 0 ja merkitse f "(x 0). Niin,

johdannainen tämä toiminto y = f(x) pisteessä x 0:ta kutsutaan funktion Δ lisäyssuhteen rajaksi y argumentin Δ lisäykseen x kun jälkimmäinen mielivaltaisesti pyrkii nollaan.

Huomaa, että saman funktion derivaatta eri pisteissä x voi saada erilaisia ​​arvoja, ts. derivaatta voidaan pitää argumentin funktiona x. Tämä toiminto on merkitty f "(x)

Johdannainen on merkitty symboleilla f "(x),y", . Johdannan erityinen arvo x = a merkitty f "(a) tai y "| x=a.

Toiminto funktion derivaatan löytämiseksi f(x) kutsutaan tämän funktion differentiaatioksi.

Voit etsiä johdannaisen suoraan määritelmän mukaan käyttämällä seuraavaa nyrkkisääntö:

Esimerkkejä.

JOHDANNAISEN MEKAANINEN MERKITYS

Fysiikasta tiedetään, että tasaisen liikkeen lailla on muoto s = v t, Missä s- polku kulki ajankohtaan asti t, v on tasaisen liikkeen nopeus.

Kuitenkin, koska suurin osa luonnossa tapahtuvista liikkeistä on epätasaisia, sitten yleensä nopeus ja siten etäisyys s riippuu ajasta t, eli tulee olemaan ajan funktio.

Annetaan siis materiaalipisteen liikkua suoraan yhteen suuntaan lain mukaan s=s(t).

Huomaa hetki aikaa t 0 . Tähän mennessä piste on ohittanut polun s=s(t 0 ). Määritetään nopeus v aineellinen hetki t 0 .

Voit tehdä tämän harkitsemalla jotakin muuta hetkeä t 0 + Δ t. Se vastaa kuljettua matkaa s =s(t 0 + Δ t). Sitten aikavälille Δ t piste on kulkenut polun Δs =s(t 0 + Δ t)–s(t).

Mietitään suhdetta. Sitä kutsutaan keskinopeudeksi aikavälillä Δ t. Keskinopeus ei pysty kuvaamaan tarkasti pisteen liikkeen nopeutta tällä hetkellä t 0 (koska liike on epätasainen). Jotta tämä todellinen nopeus voidaan ilmaista tarkemmin keskinopeudella, sinun on otettava pienempi aikaväli Δ t.

Eli liikkeen nopeus tiettynä ajankohtana t 0 (hetkellinen nopeus) on keskinopeuden raja aikavälillä alkaen t 0 - t 0 +Δ t kun Δ t→0:

,

nuo. epätasaisen liikkeen nopeus on kuljetun matkan johdannainen ajan suhteen.

JOHDANNAISEN GEOMETRIINEN MERKITYS

Otetaan ensin käyttöön käyrän tangentin määritelmä tietyssä pisteessä.

Olkoon meillä käyrä ja kiinteä piste siinä M 0(katso kuva) Harkitse toista kohtaa M tämä käyrä ja piirrä sekantti M 0 M. Jos kohta M alkaa liikkua käyrää ja pistettä pitkin M 0 pysyy paikallaan, sekantti muuttaa asentoaan. Jos, pisteen rajoittamattomalla approksimaatiolla M käyrästä pisteeseen M 0 millä tahansa puolella sekantti pyrkii ottamaan tietyn suoran paikan M 0 T, sitten suora viiva M 0 T kutsutaan käyrän tangentiksi annetussa pisteessä M 0.

Että., tangentti käyrään tietyssä pisteessä M 0 kutsutaan sekantin raja-asemaksi M 0 M kun piste M suuntautuu käyrää pitkin pisteeseen M 0.

Harkitse nyt jatkuvaa funktiota y=f(x) ja tätä funktiota vastaava käyrä. Jotain arvoa vastaan X 0-funktio ottaa arvon y0=f(x0). Nämä arvot x 0 ja y 0 käyrällä vastaa pistettä M 0 (x 0; y 0). Esitetään argumentti x0 lisäys Δ X. Argumentin uusi arvo vastaa funktion lisättyä arvoa y 0 +Δ y=f(x 0 –Δ x). Saamme pisteen M(x 0+Δ x; v 0+Δ y). Piirretään sekantti M 0 M ja merkitään φ:llä sekantin muodostama kulma akselin positiivisen suunnan kanssa Härkä. Tehdään suhde ja huomioidaan se.

Jos nyt Δ x→0, funktion Δ jatkuvuudesta johtuen klo→0, ja siksi piste M, liikkuu käyrää pitkin, lähestyy loputtomasti pistettä M 0. Sitten sekantti M 0 M on taipumus ottaa käyrän tangentin asema pisteessä M 0, ja kulma φ→α kohdassa Δ x→0, jossa α tarkoittaa tangentin ja akselin positiivisen suunnan välistä kulmaa Härkä. Koska funktio tg φ riippuu jatkuvasti φ:stä kohdassa φ≠π/2, niin kohdassa φ→α tg φ → tg α ja siten tangentin kaltevuus on:

nuo. f"(x)= tgα.

Siis geometrisesti y "(x 0) edustaa tämän funktion kaavion tangentin jyrkkyyttä pisteessä x0, eli argumentin tietylle arvolle x, derivaatta on yhtä suuri kuin funktion kaavion tangentin muodostaman kulman tangentti f(x) vastaavassa kohdassa M 0 (x; y) positiivisella akselisuunnalla Härkä.

Esimerkki. Etsi käyrän tangentin kaltevuus y = x 2 kohdassa M(-1; 1).

Olemme jo nähneet sen ( x 2)" = 2X. Mutta käyrän tangentin kaltevuus on tg α = y"| x=-1 = -2.

TOIMINTOJEN ERILAITTAVUUS. ERITTYVÄN TOIMINNON JATKUVUUS

Toiminto y=f(x) nimeltään erottuva jossain vaiheessa x 0, jos sillä on tietty derivaatta tässä vaiheessa, ts. jos suhteen raja on olemassa ja on äärellinen.

Jos funktio on differentioituva jossakin segmentin [ A; b] tai intervalli ( A; b), sitten he sanovat sen erottuva segmentillä [ A; b] tai vastaavasti välissä ( A; b).

Pätee seuraava lause, joka muodostaa yhteyden differentioituvien ja jatkuvien funktioiden välille.

Lause. Jos toiminto y=f(x) erottuva jossain vaiheessa x0, niin se on jatkuva tässä vaiheessa.

Siten funktion erilaistuvuus merkitsee sen jatkuvuutta.

Todiste. Jos , Tuo

,

jossa α on äärettömän pieni arvo, ts. määrä, joka pyrkii nollaan kohtaan Δ x→0. Mutta toisaalta

Δ y=f "(x0) Δ x+αΔ x=> Δ y→0 kohdassa Δ x→0, ts. f(x) – f(x0)→0 klo x→x 0, mikä tarkoittaa, että funktio f(x) jatkuva pisteessä x 0 . Q.E.D.

Siten epäjatkuvuuspisteissä funktiolla ei voi olla derivaattia. Käänteinen väite ei pidä paikkaansa: on jatkuvia funktioita, jotka eivät ole differentioituvia joissakin pisteissä (eli niillä ei ole derivaatta näissä pisteissä).

Harkitse kuvassa olevia kohtia a, b, c.

Pisteessä a klo Δ x→0 suhteella ei ole rajaa (koska Δ:n yksipuoliset rajat ovat erilaiset x→0–0 ja Δ x→0+0). Pisteessä A kaaviossa ei ole määriteltyä tangenttia, mutta siinä on kaksi erilaista yksipuolista tangenttia, joissa on kulmakertoimet Vastaanottaja 1 ja Vastaanottaja 2. Tämän tyyppistä pistettä kutsutaan kulmapisteeksi.

Pisteessä b klo Δ x→0 suhde on vakiomerkkinen äärettömän suuri arvo . Funktiolla on ääretön derivaatta. Tässä vaiheessa kaaviolla on pystytangentti. Pistetyyppi - "käännepiste" pystytangentilla.

Pisteessä c yksipuoliset johdannaiset ovat äärettömän suuria määriä erilaisia ​​merkkejä. Tässä vaiheessa kaaviossa on kaksi yhdistettyä pystytangenttia. Tyyppi - "kärki" pystytangentilla - kulmapisteen erikoistapaus.