चरम बिंदुओं की खोज करें। विषय पर पाठ: "कार्यों के चरम बिंदुओं का पता लगाना

यह गणित का एक दिलचस्प खंड है जिसका सामना सभी स्नातक छात्र और छात्र करते हैं। हालांकि, सभी को मटन पसंद नहीं होता है। कुछ तो बुनियादी बातों को भी समझने में असफल हो जाते हैं जैसे प्रतीत होता है कि मानक प्रकार्य अध्ययन। इस लेख का उद्देश्य इस भूल को ठीक करना है। फ़ंक्शन विश्लेषण के बारे में अधिक जानना चाहते हैं? क्या आप जानना चाहेंगे कि चरम बिंदु क्या हैं और उन्हें कैसे खोजा जाए? तब तो यह लेख तुम्हारे लिए है।

एक समारोह के ग्राफ की जांच

शुरू करने के लिए, यह समझने योग्य है कि चार्ट का विश्लेषण करना क्यों आवश्यक है। ऐसे सरल कार्य हैं जिन्हें आकर्षित करना आसान है। इस तरह के एक समारोह का एक उल्लेखनीय उदाहरण परवलय है। उसका चार्ट बनाना मुश्किल नहीं है। केवल एक साधारण परिवर्तन का उपयोग करके, उन संख्याओं को खोजने की आवश्यकता है, जिन पर फ़ंक्शन 0 का मान लेता है। और सिद्धांत रूप में, एक परवलय ग्राफ खींचने के लिए आपको बस इतना ही जानना होगा।

लेकिन क्या होगा यदि हमें जिस फ़ंक्शन को ग्राफ़ करने की आवश्यकता है वह अधिक जटिल है? चूंकि जटिल कार्यों के गुण स्पष्ट नहीं हैं, इसलिए संपूर्ण विश्लेषण करना आवश्यक है। तभी फलन को आलेखीय रूप से प्रदर्शित किया जा सकता है। यह कैसे करना है? इस सवाल का जवाब आप इस लेख में पा सकते हैं।

कार्य विश्लेषण योजना

पहली बात यह है कि फ़ंक्शन का सतही अध्ययन करना है, जिसके दौरान हम परिभाषा का क्षेत्र पाएंगे। तो, चलिए क्रम से शुरू करते हैं। परिभाषा का डोमेन उन मानों का समूह है जिनके द्वारा फ़ंक्शन को परिभाषित किया जाता है। सीधे शब्दों में कहें, तो ये वे संख्याएँ हैं जिनका उपयोग x के बजाय फ़ंक्शन में किया जा सकता है। दायरा निर्धारित करने के लिए, आपको केवल रिकॉर्ड देखने की जरूरत है। उदाहरण के लिए, यह स्पष्ट है कि फ़ंक्शन y (x) \u003d x 3 + x 2 - x + 43 में परिभाषा का एक डोमेन है - वास्तविक संख्याओं का समूह। खैर, (x 2 - 2x) / x जैसे फ़ंक्शन के साथ, सब कुछ थोड़ा अलग है। चूंकि हर में संख्या 0 के बराबर नहीं होनी चाहिए, तो इस फ़ंक्शन का डोमेन शून्य को छोड़कर सभी वास्तविक संख्याएं होंगी।

अगला, आपको फ़ंक्शन के तथाकथित शून्य को खोजने की आवश्यकता है। ये उस तर्क के मान हैं जिसके लिए संपूर्ण फ़ंक्शन मान शून्य लेता है। ऐसा करने के लिए, फ़ंक्शन को शून्य के बराबर करना आवश्यक है, इस पर विस्तार से विचार करें और कुछ परिवर्तन करें। आइए पहले से ही परिचित फलन y(x) = (x 2 - 2x)/x लें। स्कूल के पाठ्यक्रम से, हम जानते हैं कि अंश 0 होता है जब अंश शून्य होता है। इसलिए, हम हर को त्याग देते हैं और अंश के साथ काम करना शुरू करते हैं, इसे शून्य के बराबर करते हैं। हमें x 2 - 2x \u003d 0 मिलता है और x को कोष्ठक से बाहर निकालते हैं। इसलिए x (x - 2) \u003d 0. परिणामस्वरूप, हम पाते हैं कि हमारा कार्य शून्य के बराबर है जब x 0 या 2 के बराबर है।

किसी फलन के ग्राफ के अध्ययन के दौरान कई लोगों को चरम बिन्दुओं के रूप में समस्या का सामना करना पड़ता है। और यह अजीब है। आखिरकार, चरम सीमा एक साधारण विषय है। विश्वास मत करो? लेख के इस भाग को पढ़कर आप स्वयं देख लें, जिसमें हम न्यूनतम और अधिकतम बिंदुओं के बारे में बात करेंगे।

आरंभ करने के लिए, यह समझने योग्य है कि एक चरम सीमा क्या है। एक एक्सट्रीम वह सीमा मान है जो एक फ़ंक्शन ग्राफ़ पर पहुंचता है। इससे यह पता चलता है कि दो चरम मूल्य हैं - अधिकतम और न्यूनतम। स्पष्टता के लिए, आप ऊपर दी गई तस्वीर को देख सकते हैं। जांच किए गए क्षेत्र पर, बिंदु -1 अधिकतम फ़ंक्शन y (x) \u003d x 5 - 5x है, और बिंदु 1, क्रमशः न्यूनतम है।

इसके अलावा, अवधारणाओं को एक दूसरे के साथ भ्रमित न करें। किसी फ़ंक्शन के चरम बिंदु वे तर्क होते हैं जिन पर दिया गया फ़ंक्शन चरम मान प्राप्त करता है। बदले में, एक्सट्रीम फंक्शन के मिनिमा और मैक्सिमा का मान है। उदाहरण के लिए, ऊपर दिए गए चित्र पर फिर से विचार करें। -1 और 1 फ़ंक्शन के चरम बिंदु हैं, और 4 और -4 स्वयं चरम हैं।

चरम बिंदु ढूँढना

लेकिन आप किसी फ़ंक्शन के चरम बिंदु कैसे ढूंढते हैं? सब कुछ काफी सरल है। पहली बात यह है कि समीकरण के व्युत्पन्न को खोजना है। मान लीजिए कि हमें कार्य मिला है: "फ़ंक्शन y (x) के चरम बिंदु खोजें, x तर्क है। स्पष्टता के लिए, आइए फ़ंक्शन y (x) \u003d x 3 + 2x 2 + x + 54 लें। आइए अंतर करें और निम्नलिखित समीकरण प्राप्त करें: 3x 2 + 4x + 1. नतीजतन, हमें एक मानक द्विघात समीकरण मिला। केवल इतना करने की आवश्यकता है कि इसे शून्य के बराबर करें और मूल खोजें। चूंकि विवेचक शून्य से बड़ा है (D \u003d 16 - 12 \u003d 4), यह समीकरण दो जड़ों से निर्धारित होता है। हम उन्हें ढूंढते हैं और दो मान प्राप्त करते हैं: 1/3 और -1। ये फ़ंक्शन के चरम बिंदु होंगे। हालाँकि, आप अभी भी कैसे निर्धारित कर सकते हैं कौन है? कौन सा बिंदु अधिकतम है और कौन सा न्यूनतम है? ऐसा करने के लिए, आपको एक पड़ोसी बिंदु लेना होगा और उसका मान ज्ञात करना होगा। उदाहरण के लिए, आइए संख्या -2 लें, जो निर्देशांक के साथ बाईं ओर है -1 से रेखा। हम इस मान को अपने समीकरण y (-2) = 12 - 8 + 1 = 5 में प्रतिस्थापित करते हैं। नतीजतन, हमें एक सकारात्मक संख्या मिली। इसका मतलब है कि 1/3 से -1 के अंतराल पर फलन बढ़ता है, जिसका अर्थ है कि मिनट से अंतराल पर अनंत से 1/3 तक और -1 से प्लस अनंत तक, फ़ंक्शन घटता है। इस प्रकार, हम यह निष्कर्ष निकाल सकते हैं कि जांच किए गए अंतराल पर संख्या 1/3 फ़ंक्शन का न्यूनतम बिंदु है, और -1 अधिकतम बिंदु है।

यह भी ध्यान देने योग्य है कि परीक्षा में न केवल चरम बिंदुओं को खोजने की आवश्यकता होती है, बल्कि उनके साथ किसी प्रकार का ऑपरेशन (जोड़ना, गुणा करना, आदि) करना भी आवश्यक है। यही कारण है कि समस्या की स्थितियों पर विशेष ध्यान देना उचित है। आखिरकार, असावधानी के कारण आप अंक खो सकते हैं।

इस लेख से, पाठक इस बारे में जानेंगे कि कार्यात्मक मूल्य का चरम क्या है, साथ ही व्यवहार में इसके उपयोग की विशेषताओं के बारे में भी। उच्च गणित की नींव को समझने के लिए ऐसी अवधारणा का अध्ययन अत्यंत महत्वपूर्ण है। यह विषय पाठ्यक्रम के गहन अध्ययन के लिए मौलिक है।

संपर्क में

अति क्या है?

स्कूल के पाठ्यक्रम में, "चरम" की अवधारणा की कई परिभाषाएँ दी गई हैं। इस लेख का उद्देश्य उन लोगों के लिए शब्द की गहरी और स्पष्ट समझ देना है जो इस मुद्दे से अनभिज्ञ हैं। तो, शब्द को उस सीमा के रूप में समझा जाता है, जिस हद तक कार्यात्मक अंतराल किसी विशेष सेट पर न्यूनतम या अधिकतम मान प्राप्त करता है।

एक्स्ट्रीमम फ़ंक्शन का न्यूनतम मान और एक ही समय में अधिकतम दोनों है। एक न्यूनतम बिंदु और एक अधिकतम बिंदु होता है, यानी ग्राफ़ पर तर्क के चरम मान। मुख्य विज्ञान जिसमें इस अवधारणा का उपयोग किया जाता है:

  • सांख्यिकी;
  • मशीन नियंत्रण;
  • अर्थमिति।

किसी दिए गए फ़ंक्शन के अनुक्रम को निर्धारित करने में चरम बिंदु महत्वपूर्ण भूमिका निभाते हैं। ग्राफ पर समन्वय प्रणाली अपने सबसे अच्छे रूप में कार्यक्षमता में परिवर्तन के आधार पर चरम स्थिति में परिवर्तन दिखाती है।

व्युत्पन्न फ़ंक्शन का एक्स्ट्रेमा

"व्युत्पन्न" जैसी कोई चीज भी होती है। चरम बिंदु निर्धारित करना आवश्यक है। यह महत्वपूर्ण है कि न्यूनतम या अधिकतम बिंदुओं को सबसे बड़े और सबसे छोटे मूल्यों के साथ भ्रमित न करें। ये अलग-अलग अवधारणाएँ हैं, हालाँकि वे समान लग सकती हैं।

फ़ंक्शन का मान यह निर्धारित करने का मुख्य कारक है कि अधिकतम बिंदु कैसे खोजा जाए। व्युत्पन्न मूल्यों से नहीं बनता है, बल्कि विशेष रूप से एक क्रम या किसी अन्य में इसकी चरम स्थिति से बनता है।

व्युत्पन्न स्वयं चरम बिंदुओं के डेटा के आधार पर निर्धारित किया जाता है, न कि सबसे बड़ा या सबसे छोटा मान। रूसी स्कूलों में, इन दो अवधारणाओं के बीच की रेखा स्पष्ट रूप से नहीं खींची जाती है, जो सामान्य रूप से इस विषय की समझ को प्रभावित करती है।

आइए अब इस तरह की चीज़ को "तेज चरम" मानें। आज तक, एक तीव्र न्यूनतम मूल्य और एक तीव्र अधिकतम मूल्य है। परिभाषा किसी फ़ंक्शन के महत्वपूर्ण बिंदुओं के रूसी वर्गीकरण के अनुसार दी गई है। एक चरम बिंदु की अवधारणा एक चार्ट पर महत्वपूर्ण बिंदुओं को खोजने का आधार है।

इस तरह की अवधारणा को परिभाषित करने के लिए, Fermat के प्रमेय का उपयोग किया जाता है। यह चरम बिन्दुओं के अध्ययन में सबसे महत्वपूर्ण है और किसी न किसी रूप में उनके अस्तित्व का स्पष्ट विचार देता है। चरमता सुनिश्चित करने के लिए, चार्ट पर घटने या बढ़ने के लिए कुछ शर्तें बनाना महत्वपूर्ण है।

"अधिकतम बिंदु कैसे प्राप्त करें" प्रश्न का सटीक उत्तर देने के लिए, आपको इन प्रावधानों का पालन करना चाहिए:

  1. चार्ट पर परिभाषा का सटीक क्षेत्र ढूँढना।
  2. किसी फ़ंक्शन के व्युत्पन्न और एक चरम बिंदु की खोज करें।
  3. तर्क के क्षेत्र के लिए मानक असमानताओं को हल करें।
  4. यह साबित करने में सक्षम हो कि किस कार्य में एक ग्राफ पर एक बिंदु परिभाषित और निरंतर है।

ध्यान!किसी फ़ंक्शन के महत्वपूर्ण बिंदु की खोज तभी संभव है जब कम से कम दूसरे क्रम का व्युत्पन्न हो, जो एक चरम बिंदु की उपस्थिति के उच्च अनुपात द्वारा सुनिश्चित किया जाता है।

समारोह के चरम के लिए आवश्यक शर्त

एक चरम के अस्तित्व के लिए, यह महत्वपूर्ण है कि न्यूनतम अंक और अधिकतम अंक दोनों हों। यदि यह नियम केवल आंशिक रूप से मनाया जाता है, तो चरम सीमा के अस्तित्व की स्थिति का उल्लंघन होता है।

किसी भी स्थिति में प्रत्येक कार्य को उसके नए अर्थों की पहचान करने के लिए विभेदित किया जाना चाहिए। यह समझना महत्वपूर्ण है कि वह मामला जब कोई बिंदु गायब हो जाता है, एक अवकलनीय बिंदु खोजने का मुख्य सिद्धांत नहीं है।

एक तीक्ष्ण चरम, साथ ही न्यूनतम कार्य, चरम मूल्यों का उपयोग करके गणितीय समस्या को हल करने का एक अत्यंत महत्वपूर्ण पहलू है। इस घटक को बेहतर ढंग से समझने के लिए, कार्यात्मक के असाइनमेंट के लिए सारणीबद्ध मूल्यों को संदर्भित करना महत्वपूर्ण है।

अर्थ की पूरी खोज एक मूल्य प्लॉट करना
1. मूल्यों के बढ़ने और घटने के बिंदुओं का निर्धारण।

2. समन्वय अक्षों के साथ विराम बिंदु, चरम सीमा और प्रतिच्छेदन ढूँढना।

3. चार्ट पर स्थिति में परिवर्तन निर्धारित करने की प्रक्रिया।

4. स्पर्शोन्मुख की उपस्थिति को ध्यान में रखते हुए सूचकांक और उत्तलता और उत्तलता की दिशा का निर्धारण।

5. इसके निर्देशांक निर्धारित करने के संदर्भ में अध्ययन की एक सारांश तालिका का निर्माण।

6. चरम और तीव्र बिंदुओं के बढ़ने और घटने के अंतराल का पता लगाना।

7. वक्र की उत्तलता और अवतलता का निर्धारण।

8. अध्ययन के आधार पर एक ग्राफ बनाना आपको न्यूनतम या अधिकतम खोजने की अनुमति देता है।

 मुख्य तत्व, जब चरम सीमाओं के साथ काम करना आवश्यक होता है, तो इसके ग्राफ का सटीक निर्माण होता है।

स्कूल के शिक्षक अक्सर ऐसे महत्वपूर्ण पहलू पर अधिकतम ध्यान नहीं देते हैं, जो शैक्षिक प्रक्रिया का घोर उल्लंघन है।

ग्राफ का निर्माण केवल कार्यात्मक डेटा के अध्ययन के परिणामों के आधार पर होता है, तेज एक्स्ट्रेमा का निर्धारण, साथ ही ग्राफ पर अंक।

किसी फ़ंक्शन के व्युत्पन्न के तीव्र एक्स्ट्रेमा को सटीक मानों के ग्राफ़ पर प्रदर्शित किया जाता है, जिसमें स्पर्शोन्मुख को निर्धारित करने के लिए मानक प्रक्रिया का उपयोग किया जाता है।

एक सतत फलन के ग्राफ पर विचार करें वाई = एफ (एक्स)चित्र में दिखाया गया है।

बिंदु पर फ़ंक्शन मान एक्स 1 बाईं और दाईं ओर के सभी पड़ोसी बिंदुओं पर फ़ंक्शन के मानों से अधिक होगा एक्सएक । इस मामले में, फ़ंक्शन को बिंदु पर कहा जाता है एक्स 1 अधिकतम। बिंदु पर एक्स 3 फ़ंक्शन में स्पष्ट रूप से अधिकतम भी है। अगर हम बिंदु पर विचार करें एक्स 2 , तो इसमें फ़ंक्शन का मान सभी पड़ोसी मानों से कम है। इस मामले में, फ़ंक्शन को बिंदु पर कहा जाता है एक्स 2 न्यूनतम। इसी प्रकार बिंदु के लिए एक्स 4 .

समारोह वाई = एफ (एक्स)बिंदु पर एक्स 0 है ज्यादा से ज्यादा, यदि इस बिंदु पर फ़ंक्शन का मान बिंदु वाले कुछ अंतराल के सभी बिंदुओं पर इसके मानों से अधिक है एक्स 0, यानी अगर बिंदु का ऐसा पड़ोस है एक्स 0 , जो सभी के लिए है एक्स≠एक्स 0 , इस पड़ोस से संबंधित, हमारे पास असमानता है एफ (एक्स)<च (एक्स 0 ) .

समारोह वाई = एफ (एक्स)यह है न्यूनतमबिंदु पर एक्स 0 , अगर बिंदु का ऐसा पड़ोस है एक्स 0 , सबके लिए क्या है एक्स≠एक्स 0 इस पड़ोस से संबंधित, हमारे पास असमानता है एफ (एक्स)>च(x0.

जिन बिंदुओं पर फ़ंक्शन अपने अधिकतम और न्यूनतम तक पहुंचता है, उन्हें चरम बिंदु कहा जाता है, और इन बिंदुओं पर फ़ंक्शन के मान फ़ंक्शन के एक्स्ट्रेमा होते हैं।

आइए हम इस तथ्य पर ध्यान दें कि एक खंड पर परिभाषित एक फ़ंक्शन अपने अधिकतम और न्यूनतम तक केवल विचाराधीन खंड के भीतर निहित बिंदुओं पर पहुंच सकता है।

ध्यान दें कि यदि किसी फ़ंक्शन का एक बिंदु पर अधिकतम है, तो इसका मतलब यह नहीं है कि इस बिंदु पर फ़ंक्शन का पूरे डोमेन में अधिकतम मान है। ऊपर चर्चा की गई आकृति में, बिंदु पर फलन एक्स 1 में अधिकतम है, हालांकि ऐसे बिंदु हैं जिन पर फ़ंक्शन के मान बिंदु से अधिक हैं एक्स 1 . विशेष रूप से, एफ(एक्स 1) < एफ(एक्स 4) यानी फ़ंक्शन का न्यूनतम अधिकतम से अधिक है। अधिकतम की परिभाषा से, यह केवल इस प्रकार है कि यह अधिकतम बिंदु के काफी करीब बिंदुओं पर फ़ंक्शन का सबसे बड़ा मान है।

प्रमेय 1. (एक चरम के अस्तित्व के लिए एक आवश्यक शर्त।)यदि भिन्न कार्य वाई = एफ (एक्स)बिंदु पर है एक्स = एक्स 0 चरम, तो इस बिंदु पर इसका व्युत्पन्न गायब हो जाता है।

सबूत. चलो, निश्चितता के लिए, बिंदु पर एक्स 0 फ़ंक्शन में अधिकतम है। फिर पर्याप्त रूप से छोटे वेतन वृद्धि के लिए एक्सअपने पास च (एक्स 0 + Δ एक्स) 0 ) , अर्थात। परन्तु फिर

इन असमानताओं को सीमा तक . के रूप में पारित करना एक्स→ 0 और ध्यान में रखते हुए कि व्युत्पन्न एफ "(एक्स 0) मौजूद है, और इसलिए बाईं ओर की सीमा इस बात पर निर्भर नहीं करती है कि कैसे एक्स→ 0, हम पाते हैं: . के लिए एक्स → 0 – 0 एफ"(एक्स 0) 0 और . पर एक्स → 0 + 0 एफ"(एक्स 0) 0. चूँकि एफ"(एक्स 0) एक संख्या को परिभाषित करता है, तो ये दो असमानताएँ तभी संगत होती हैं जब एफ"(एक्स 0) = 0.

सिद्ध प्रमेय में कहा गया है कि अधिकतम और न्यूनतम अंक केवल तर्क के उन मूल्यों में से हो सकते हैं जिनके लिए व्युत्पन्न गायब हो जाता है।

हमने उस स्थिति पर विचार किया है जब किसी फलन का एक निश्चित खंड के सभी बिंदुओं पर व्युत्पन्न होता है। क्या होता है जब व्युत्पन्न मौजूद नहीं होता है? उदाहरणों पर विचार करें।

उदाहरण.

  1. आप=|एक्स|.

    फ़ंक्शन में एक बिंदु पर व्युत्पन्न नहीं होता है एक्स=0 (इस बिंदु पर, फ़ंक्शन के ग्राफ़ में एक निश्चित स्पर्शरेखा नहीं होती है), लेकिन इस बिंदु पर फ़ंक्शन का न्यूनतम होता है, क्योंकि आप(0) = 0, और सभी के लिए एक्स≠ 0आप > 0.

    2. फ़ंक्शन का कोई व्युत्पन्न नहीं है एक्स= 0, क्योंकि यह अनंत तक जाता है जब एक्स= 0। लेकिन इस बिंदु पर, फ़ंक्शन की अधिकतम है।

    फ़ंक्शन का कोई व्युत्पन्न नहीं है एक्स=0 क्योंकि पर एक्स→0। इस बिंदु पर, फ़ंक्शन में न तो अधिकतम और न ही न्यूनतम है। सचमुच, एफ (एक्स)=0 और at एक्स<0एफ (एक्स)<0, а при एक्स>0एफ (एक्स)>0.

    इस प्रकार, दिए गए उदाहरणों और सूत्रबद्ध प्रमेय से यह स्पष्ट है कि फ़ंक्शन का केवल दो मामलों में एक चरम हो सकता है: 1) उन बिंदुओं पर जहां व्युत्पन्न मौजूद है और शून्य के बराबर है; 2) उस बिंदु पर जहां व्युत्पन्न मौजूद नहीं है।

    हालांकि, अगर किसी बिंदु पर एक्स 0 हम जानते हैं कि च"(एक्स 0 ) = 0, तो इससे यह निष्कर्ष नहीं निकाला जा सकता है कि बिंदु पर एक्स 0 फ़ंक्शन में एक चरम सीमा होती है।

    उदाहरण के लिए. .

    लेकिन बिंदु एक्स=0 एक चरम बिंदु नहीं है, क्योंकि इस बिंदु के बाईं ओर फ़ंक्शन मान अक्ष के नीचे स्थित हैं बैल, और ऊपर दाईं ओर।

    किसी फ़ंक्शन के डोमेन से एक तर्क के मान, जिसके लिए फ़ंक्शन का व्युत्पन्न गायब हो जाता है या मौजूद नहीं है, कहलाते हैं महत्वपूर्ण बिंदु.


    उपरोक्त सभी से, यह इस प्रकार है कि फ़ंक्शन के चरम बिंदु महत्वपूर्ण बिंदुओं में से हैं, और, हालांकि, प्रत्येक महत्वपूर्ण बिंदु एक चरम बिंदु नहीं है। इसलिए, फ़ंक्शन के चरम को खोजने के लिए, आपको फ़ंक्शन के सभी महत्वपूर्ण बिंदुओं को ढूंढना होगा, और फिर इनमें से प्रत्येक बिंदु को अधिकतम और न्यूनतम के लिए अलग-अलग जांचना होगा। इसके लिए, निम्नलिखित प्रमेय कार्य करता है।

    प्रमेय 2। (एक चरम के अस्तित्व के लिए पर्याप्त शर्त।)मान लीजिए कि क्रान्तिक बिन्दु वाले किसी अन्तराल पर फलन सतत रहता है एक्स 0 , और इस अंतराल के सभी बिंदुओं पर अवकलनीय है (सिवाय, शायद, बिंदु को छोड़कर एक्स 0)। यदि, इस बिंदु से बाएं से दाएं जाने पर, व्युत्पन्न चिह्न प्लस से माइनस में बदल जाता है, तो बिंदु पर एक्स = एक्स 0 फ़ंक्शन में अधिकतम है। अगर, गुजरते समय एक्स 0 बाएं से दाएं, व्युत्पन्न परिवर्तन माइनस से प्लस पर हस्ताक्षर करते हैं, फिर इस बिंदु पर फ़ंक्शन का न्यूनतम होता है।

    इस प्रकार, यदि

    सबूत. आइए पहले मान लें कि जब से गुजरते हैं एक्स 0, व्युत्पन्न परिवर्तन संकेत प्लस से माइनस में, अर्थात। सभी के लिए एक्सबिंदु के करीब एक्स 0 एफ "(एक्स)> 0 के लिए एक्स< x 0 , च"(एक्स)< 0 के लिए एक्स > एक्स 0. आइए लैग्रेंज प्रमेय को अंतर पर लागू करें एफ(एक्स) - एफ(एक्स 0 ) = एफ "(सी) (एक्स- एक्स 0), जहां सीबीच मे स्थित एक्सतथा एक्स 0 .

    1. होने देना एक्स< x 0. फिर सी< x 0 और च "(सी)> 0. इसीलिए एफ "(सी) (एक्स-एक्स 0)< 0 और इसलिए,

      एफ(एक्स) - एफ(एक्स 0 )< 0, यानी एफ (एक्स)< f(x 0 ).

    2. होने देना एक्स > एक्स 0. फिर सी> एक्स 0 और च"(सी)< 0. माध्यम एफ "(सी) (एक्स-एक्स 0)< 0. इसीलिए एफ(एक्स) - एफ(एक्स 0 ) <0,т.е.एफ (एक्स)< च (एक्स 0 ) .

    इस प्रकार, सभी मूल्यों के लिए एक्सकाफी करीब एक्स 0 एफ (एक्स)< च (एक्स 0 ) . और इसका मतलब है कि बिंदु पर एक्स 0 फ़ंक्शन में अधिकतम है।

    न्यूनतम प्रमेय का दूसरा भाग इसी प्रकार सिद्ध होता है।

    आइए चित्र में इस प्रमेय का अर्थ स्पष्ट करें। होने देना च"(एक्स 1 ) = 0 और किसी के लिए एक्स,काफी करीब एक्स 1, असमानताएं

    च"(एक्स)< 0 बजे एक्स< x 1 , एफ "(एक्स)> 0 बजे एक्स > एक्स 1 .

    फिर बिंदु के बाईं ओर एक्स 1 फलन बढ़ रहा है, और दाईं ओर घट रहा है, इसलिए, जब एक्स = एक्स 1 फलन बढ़ते से घटते जाता है, अर्थात इसमें अधिकतम होता है।

    इसी तरह, कोई बिंदुओं पर विचार कर सकता है एक्स 2 और एक्स 3 .


    योजनाबद्ध रूप से, उपरोक्त सभी को चित्र में दर्शाया जा सकता है:

    एक चरम के लिए y=f(x) फलन का अध्ययन करने का नियम

    1. फ़ंक्शन का दायरा खोजें एफ (एक्स)।
    2. किसी फ़ंक्शन का पहला व्युत्पन्न खोजें च"(एक्स).
    3. इसके लिए महत्वपूर्ण बिंदु निर्धारित करें:
      1. समीकरण की वास्तविक जड़ें खोजें च"(एक्स)=0;
      2. सभी मान खोजें एक्सजिसके तहत व्युत्पन्न च"(एक्स)मौजूद नहीं।
    4. महत्वपूर्ण बिंदु के बाएँ और दाएँ व्युत्पन्न के चिह्न का निर्धारण करें। चूंकि व्युत्पन्न का चिह्न दो महत्वपूर्ण बिंदुओं के बीच स्थिर रहता है, इसलिए यह व्युत्पन्न के चिह्न को बाईं ओर किसी एक बिंदु पर और एक बिंदु पर महत्वपूर्ण बिंदु के दाईं ओर निर्धारित करने के लिए पर्याप्त है।
    5. चरम बिंदुओं पर फ़ंक्शन के मान की गणना करें।

    उदाहरण. न्यूनतम और अधिकतम के लिए कार्यों का अन्वेषण करें।


    इंटरसेप्ट पर सबसे बड़ा और न्यूनतम फ़ंक्शन मान

    सबसे बड़ाकिसी खंड पर किसी फ़ंक्शन का मान इस खंड पर उसके सभी मूल्यों में सबसे बड़ा है, और कम से कमअपने सभी मूल्यों में सबसे छोटा है।

    समारोह पर विचार करें वाई = एफ (एक्स)अंतराल पर निरंतर [ ए, बी]. जैसा कि ज्ञात है, ऐसा फ़ंक्शन अपने अधिकतम और न्यूनतम मूल्यों तक पहुंचता है, या तो खंड की सीमा पर, या इसके अंदर। यदि फ़ंक्शन का अधिकतम या न्यूनतम मान खंड के आंतरिक बिंदु पर पहुंच जाता है, तो यह मान फ़ंक्शन का अधिकतम या न्यूनतम होता है, अर्थात यह महत्वपूर्ण बिंदुओं पर पहुंच जाता है।

    इस प्रकार, हम निम्नलिखित प्राप्त करते हैं: खंड पर किसी फ़ंक्शन के सबसे बड़े और सबसे छोटे मान ज्ञात करने का नियम [ ए, बी] :

    1. अंतराल में किसी फ़ंक्शन के सभी महत्वपूर्ण बिंदु खोजें ( ए, बी) और इन बिंदुओं पर फ़ंक्शन मानों की गणना करें।
    2. के लिए खंड के सिरों पर फ़ंक्शन के मानों की गणना करें एक्स = ए, एक्स = बी.
    3. सभी प्राप्त मूल्यों में से, सबसे बड़ा और सबसे छोटा चुनें।

>> चरम

फंक्शन एक्सट्रीमम

चरम की परिभाषा

समारोह y = f(x) कहा जाता है की बढ़ती (घट) कुछ अंतराल में यदि x 1 . के लिए< x 2 выполняется неравенство (f (x 1) < f (x 2) (f (x 1) >एफ (एक्स 2))।

यदि एक खंड पर एक भिन्न कार्य y \u003d f (x) बढ़ता है (घटता है), तो इस खंड पर इसका व्युत्पन्न f " (एक्स )> 0

(एफ"(एक्स)< 0).

दूरसंचार विभाग एक्स के बारे में बुलाया स्थानीय अधिकतम बिंदु (न्यूनतम) फ़ंक्शन का f (x) यदि बिंदु का एक पड़ोस है एक्स ओ, उन सभी बिंदुओं के लिए जिनमें असमानता f (x) है≤ एफ (एक्स ओ) (एफ (एक्स)≥ एफ (एक्स ओ))।

अधिकतम और न्यूनतम अंक कहलाते हैं चरम बिंदु, और इन बिंदुओं पर फ़ंक्शन के मान इसके हैं एक्स्ट्रेमा।

चरम बिंदु

एक चरम के लिए आवश्यक शर्तें . अगर बिंदु एक्स के बारे में फ़ंक्शन f (x) का एक चरम बिंदु है, तो या तो f " (एक्स ओ) = 0, या एफ(एक्स ओ) मौजूद नहीं है। ऐसे बिंदु कहलाते हैं नाजुक,जहां फ़ंक्शन को महत्वपूर्ण बिंदु पर ही परिभाषित किया जाता है। किसी फ़ंक्शन की चरम सीमा को उसके महत्वपूर्ण बिंदुओं के बीच मांगा जाना चाहिए।

पहली पर्याप्त शर्त। होने देना एक्स के बारे में - महत्वपूर्ण बिंदु। अगर च" (x ) बिंदु से गुजरते समय एक्स के बारे में प्लस चिह्न को माइनस में बदल देता है, फिर बिंदु पर एक्स ओफ़ंक्शन में अधिकतम है, अन्यथा इसमें न्यूनतम है। यदि व्युत्पन्न एक महत्वपूर्ण बिंदु से गुजरते समय संकेत नहीं बदलता है, तो बिंदु पर एक्स के बारे में कोई चरम नहीं है।

दूसरी पर्याप्त शर्त। मान लें कि फलन f(x) में है
एफ" (x ) बिंदु के आसपास के क्षेत्र में एक्स के बारे में और दूसरा व्युत्पन्न बहुत ही बिंदु पर एक्स ओ. अगर च"(एक्स ओ) = 0, >0 ( <0), то точка एक्स ओफ़ंक्शन f(x) का स्थानीय न्यूनतम (अधिकतम) बिंदु है। यदि = 0 है, तो व्यक्ति को या तो पहली पर्याप्त शर्त का उपयोग करना चाहिए, या उच्चतर शर्तों को शामिल करना चाहिए।

एक खंड पर, फ़ंक्शन y \u003d f (x) महत्वपूर्ण बिंदुओं पर या खंड के सिरों पर सबसे छोटे या सबसे बड़े मान तक पहुंच सकता है।

उदाहरण 3.22।

समाधान।इसलिये एफ " (

किसी फ़ंक्शन के चरम को खोजने के लिए कार्य

उदाहरण 3.23। एक

समाधान। एक्सतथा आप आप
0 ≤ एक्स≤
> 0, जबकि एक्स >ए /4 एस " < 0, значит, в точке x=a /4 функция S имеет максимум. Значение कार्यों वर्ग. इकाइयों).

उदाहरण 3.24।पी

समाधान।पीपी
एस"
आर = 2, एच = 16/4 = 4।

उदाहरण 3.22।फलन f (x) = 2x 3 - 15x 2 + 36x - 14 का चरम ज्ञात कीजिए।

समाधान।इसलिये एफ " (x) \u003d 6x 2 - 30x +36 \u003d 6 (x -2) (x - 3), फिर फ़ंक्शन के महत्वपूर्ण बिंदु x 1 \u003d 2 और x 2 \u003d 3. चरम बिंदु केवल इन पर हो सकते हैं अंक। चूंकि बिंदु x 1 \u003d 2 से गुजरते समय, व्युत्पन्न परिवर्तन प्लस से माइनस में बदल जाता है, फिर इस बिंदु पर फ़ंक्शन में अधिकतम होता है। बिंदु x 2 \u003d 3 से गुजरते समय, व्युत्पन्न परिवर्तन माइनस से प्लस में बदल जाता है, इसलिए, बिंदु x 2 \u003d 3 पर, फ़ंक्शन में न्यूनतम होता है। अंक में फ़ंक्शन के मूल्यों की गणना
x 1 = 2 और x 2 = 3, हम फलन का एक्स्ट्रेमा पाते हैं: अधिकतम f (2) = 14 और न्यूनतम f (3) = 13।

उदाहरण 3.23।पत्थर की दीवार के पास एक आयताकार क्षेत्र बनाना आवश्यक है ताकि इसे तीन तरफ से तार की जाली से बंद कर दिया जाए और चौथी तरफ की दीवार को जोड़ दिया जाए। इसके लिए है एकग्रिड के रैखिक मीटर। किस पक्षानुपात पर साइट का क्षेत्रफल सबसे बड़ा होगा?

समाधान।के माध्यम से साइट के किनारों को निरूपित करें एक्सतथा आप. साइट का क्षेत्रफल S = xy के बराबर है। होने देना आपदीवार से सटे पक्ष की लंबाई है। फिर, शर्त के अनुसार, समता 2x + y = a अवश्य धारण करें। इसलिए y = a - 2x और S = x (a - 2x), जहाँ
0 ≤ एक्स≤ a/2 (पैड की लंबाई और चौड़ाई ऋणात्मक नहीं हो सकती)।एस "= ए - 4x, ए - 4x = 0 एक्स = ए / 4 के लिए, जहां से
वाई \u003d ए - 2 × ए / 4 \u003d ए / 2। क्यों कि x = a /4 एकमात्र महत्वपूर्ण बिंदु है, आइए देखें कि क्या इस बिंदु से गुजरते समय व्युत्पन्न का चिह्न बदलता है। एक्स ए / 4 एस के लिए "> 0, जबकि एक्स >ए /4 एस " < 0, значит, в точке x=a /4 функция S имеет максимум. Значение कार्यों एस(ए/4) = ए/4(ए - ए/2) = ए 2/8 (वर्ग. इकाइयों). चूँकि S निरंतर चालू है और S(0) और S(a/2) के सिरों पर इसके मान शून्य के बराबर हैं, तो पाया गया मान फ़ंक्शन का सबसे बड़ा मान होगा। इस प्रकार, समस्या की दी गई शर्तों के तहत साइट का सबसे अनुकूल पहलू अनुपात y = 2x है।

उदाहरण 3.24।V=16 . की क्षमता वाला एक बंद बेलनाकार टैंक बनाना आवश्यक हैपी 50 मीटर 3. इसके निर्माण के लिए कम से कम सामग्री का उपयोग करने के लिए टैंक (त्रिज्या आर और ऊंचाई एच) के आयाम क्या होने चाहिए?

समाधान।बेलन का कुल पृष्ठीय क्षेत्रफल S = 2 . हैपी आर (आर + एच)। हम बेलन का आयतन V = . जानते हैंपी आर 2 एन एन \u003d वी / पी आर 2 \u003d 16 पी / पी आर 2 \u003d 16 / आर 2। तो एस (आर) = 2पी (आर2+16/आर)। हम इस फ़ंक्शन का व्युत्पन्न पाते हैं:
एस"(आर) \u003d 2 पी (2 आर- 16 / आर 2) \u003d 4 पी (आर- 8 / आर 2)। एस" (आर) = 0 के लिए आर 3 = 8, इसलिए,
आर = 2, एच = 16/4 = 4।

कार्य, पहले और दूसरे डेरिवेटिव की उपस्थिति के बारे में जानना और उनके भौतिक अर्थ को समझना बिल्कुल भी आवश्यक नहीं है। पहले आपको निम्नलिखित को समझने की आवश्यकता है:

  • फ़ंक्शन का चरम अधिकतम या, इसके विपरीत, मनमाने ढंग से छोटे पड़ोस में फ़ंक्शन के मूल्य को कम करता है;
  • चरम बिंदु पर समारोह का विच्छेदन नहीं होना चाहिए।

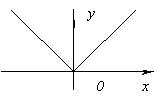
और अब वही बात, सरल शब्दों में। बॉलपॉइंट पेन की नोक को देखें। यदि कलम को लंबवत रखा जाता है, लेखन समाप्त होता है, तो गेंद का बिल्कुल मध्य चरम बिंदु होगा - उच्चतम बिंदु। इस मामले में, हम अधिकतम के बारे में बात करते हैं। अब, यदि आप लेखन के अंत के साथ कलम को मोड़ते हैं, तो गेंद के बीच में पहले से ही न्यूनतम कार्य होगा। यहां दी गई आकृति की सहायता से, आप एक स्टेशनरी पेंसिल के लिए सूचीबद्ध जोड़तोड़ की कल्पना कर सकते हैं। तो, किसी फ़ंक्शन का चरम हमेशा महत्वपूर्ण बिंदु होता है: इसका मैक्सिमा या मिनिमा। चार्ट का आसन्न खंड मनमाने ढंग से तेज या चिकना हो सकता है, लेकिन यह दोनों तरफ मौजूद होना चाहिए, केवल इस मामले में बिंदु एक चरम है। यदि चार्ट केवल एक तरफ मौजूद है, तो यह बिंदु चरम नहीं होगा, भले ही इसके एक तरफ चरम स्थितियां पूरी हों। आइए अब वैज्ञानिक दृष्टिकोण से फलन की चरम सीमा का अध्ययन करें। एक बिंदु को चरम सीमा माना जाने के लिए, यह आवश्यक और पर्याप्त है कि:

  • पहला व्युत्पन्न शून्य के बराबर था या बिंदु पर मौजूद नहीं था;
  • इस बिंदु पर पहला व्युत्पन्न परिवर्तन संकेत करता है।

उच्च-क्रम के डेरिवेटिव के दृष्टिकोण से स्थिति की व्याख्या कुछ अलग तरीके से की जाती है: एक बिंदु पर अलग-अलग फ़ंक्शन के लिए, यह पर्याप्त है कि एक विषम-क्रम व्युत्पन्न है जो शून्य के बराबर नहीं है, जबकि सभी निचले-क्रम के डेरिवेटिव को होना चाहिए मौजूद हैं और शून्य के बराबर हैं। पाठ्यपुस्तकों से प्रमेयों की यह सबसे सरल व्याख्या है, लेकिन सबसे सामान्य लोगों के लिए, इस बिंदु को एक उदाहरण के साथ समझाने लायक है। आधार एक साधारण परवलय है। तुरंत आरक्षण करें, शून्य बिंदु पर यह न्यूनतम है। बस थोड़ा सा गणित:

  • पहला व्युत्पन्न (एक्स 2) | = 2X, शून्य बिंदु 2X = 0 के लिए;
  • दूसरा व्युत्पन्न (2X) | = 2, शून्य बिंदु 2 = 2 के लिए

इस सरल तरीके से, पहले-क्रम डेरिवेटिव और उच्च-ऑर्डर डेरिवेटिव दोनों के लिए फ़ंक्शन के चरम को निर्धारित करने वाली स्थितियां सचित्र हैं। हम इसमें जोड़ सकते हैं कि दूसरा व्युत्पन्न एक विषम क्रम का समान व्युत्पन्न है, जो शून्य के बराबर नहीं है, जिसकी चर्चा थोड़ी अधिक की गई थी। जब दो चर के एक समारोह के चरम की बात आती है, तो दोनों तर्कों के लिए शर्तों को पूरा किया जाना चाहिए। जब सामान्यीकरण होता है, तो आंशिक व्युत्पन्न खेल में आते हैं। यही है, एक बिंदु पर एक चरम की उपस्थिति के लिए यह आवश्यक है कि दोनों प्रथम-क्रम डेरिवेटिव शून्य के बराबर हों, या उनमें से कम से कम एक मौजूद न हो। एक चरम की उपस्थिति की पर्याप्तता के लिए, एक अभिव्यक्ति की जांच की जाती है, जो दूसरे क्रम के डेरिवेटिव के उत्पाद और फ़ंक्शन के मिश्रित द्वितीय-क्रम व्युत्पन्न के वर्ग के बीच का अंतर है। यदि यह अभिव्यक्ति शून्य से अधिक है, तो एक चरम है, और यदि शून्य की समानता है, तो प्रश्न खुला रहता है, और अतिरिक्त शोध की आवश्यकता होती है।

संबंधित आलेख