Contoh

Temukan ekstrem dari fungsi asalkan X dan pada berhubungan dengan rasio: . Secara geometris, masalahnya berarti sebagai berikut: pada elips
pesawat terbang
.

Masalah ini dapat diselesaikan sebagai berikut: dari persamaan
Temukan
X:

dengan ketentuan
, direduksi menjadi masalah menemukan ekstrem dari fungsi satu variabel, pada interval
.

Secara geometris, masalahnya berarti sebagai berikut: pada elips diperoleh dengan melintasi silinder
pesawat terbang
, diperlukan untuk menemukan nilai maksimum atau minimum dari aplikasi (Gbr. 9). Masalah ini dapat diselesaikan sebagai berikut: dari persamaan
Temukan
. Mensubstitusikan nilai y yang ditemukan ke dalam persamaan bidang, kita memperoleh fungsi dari satu variabel X:

Jadi, masalah menemukan ekstrem dari fungsi
dengan ketentuan
, direduksi menjadi masalah menemukan ekstrem dari fungsi satu variabel, pada segmen.

Jadi, masalah menemukan ekstrem bersyarat adalah masalah menemukan ekstrem dari fungsi tujuan
, asalkan variabel X dan pada tunduk pada pembatasan
ditelepon persamaan koneksi.

Kami akan mengatakan itu dot
, memenuhi persamaan kendala, adalah titik maksimum bersyarat lokal (minimum) jika ada lingkungan
sedemikian rupa sehingga untuk setiap titik
, yang koordinatnya memenuhi persamaan kendala, pertidaksamaan berlaku.

Jika dari persamaan komunikasi dimungkinkan untuk menemukan ekspresi untuk pada, kemudian, dengan mensubstitusi ekspresi ini ke fungsi aslinya, kita ubah yang terakhir menjadi fungsi kompleks dari satu variabel X.

Metode umum untuk menyelesaikan masalah ekstrem bersyarat adalah Metode pengali Lagrange. Mari kita buat fungsi bantu, di mana beberapa nomor. Fungsi ini disebut Fungsi Lagrange, sebuah Pengganda Lagrange. Jadi, masalah menemukan ekstrem bersyarat telah direduksi menjadi menemukan titik ekstrem lokal untuk fungsi Lagrange. Untuk menemukan titik-titik dari kemungkinan ekstrem, perlu untuk menyelesaikan sistem 3 persamaan dengan tiga yang tidak diketahui x, y dan.

Maka seseorang harus menggunakan kondisi ekstrem yang cukup berikut ini.

DALIL. Biarkan titik tersebut menjadi titik ekstrem yang mungkin untuk fungsi Lagrange. Kami berasumsi bahwa di sekitar titik
ada turunan parsial orde dua kontinu dari fungsi dan . Menunjukkan

Lalu jika
, kemudian
titik ekstrem bersyarat dari fungsi
pada persamaan kendala
sementara itu, jika
, kemudian
titik minimum bersyarat, jika
, kemudian
titik maksimum bersyarat.

§delapan. Gradien dan turunan terarah

Biarkan fungsinya
didefinisikan dalam beberapa domain (terbuka). Pertimbangkan poin apa pun
daerah ini dan setiap garis lurus berarah (sumbu) melewati titik ini (Gbr. 1). Biarlah
- beberapa titik lain dari sumbu ini,
- panjang segmen antara
dan
, diambil dengan tanda tambah, jika arahnya
bertepatan dengan arah sumbu , dan dengan tanda minus jika arahnya berlawanan.

Biarlah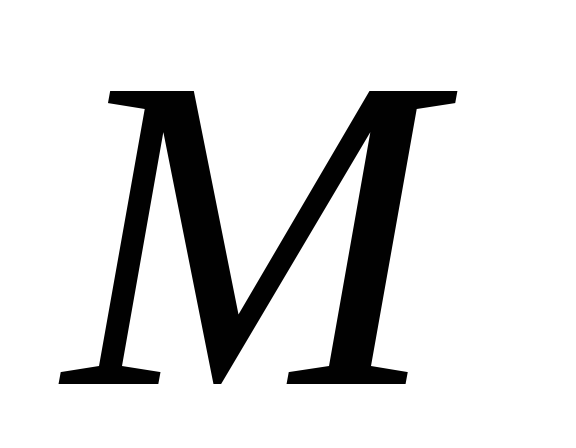
mendekati tanpa batas
. Membatasi

ditelepon turunan fungsi
menuju (atau sepanjang sumbu ) dan dilambangkan sebagai berikut:

.

Turunan ini mencirikan "laju perubahan" fungsi di titik
menuju . Khususnya, dan turunan parsial biasa ,juga dapat dianggap sebagai turunan "sehubungan dengan arah".

Misalkan sekarang fungsi
memiliki turunan parsial kontinu di daerah yang ditinjau. Biarkan poros membentuk sudut dengan sumbu koordinat
dan . Di bawah asumsi yang dibuat, turunan terarah ada dan dinyatakan dengan rumus

.

Jika vektor
ditentukan oleh koordinatnya
, maka turunan dari fungsi
dalam arah vektor
dapat dihitung dengan menggunakan rumus:

.

Vektor dengan koordinat
ditelepon vektor gradien fungsi
pada intinya
. Vektor gradien menunjukkan arah peningkatan tercepat fungsi pada titik tertentu.

Contoh

Diberikan fungsi , titik A(1, 1) dan vektor
. Cari: 1) lulusan z di titik A; 2) turunan di titik A searah dengan vektor .

Turunan parsial dari suatu fungsi tertentu di suatu titik
:

;
.

Maka vektor gradien fungsi pada titik ini adalah:
. Vektor gradien juga dapat ditulis menggunakan ekspansi vektor dan :

. turunan fungsi dalam arah vektor :

Jadi,
,
.◄

Kondisi yang cukup untuk ekstrem dari fungsi dua variabel

1. Biarkan fungsi terdiferensiasi secara kontinu di beberapa lingkungan titik dan memiliki turunan parsial orde dua kontinu (murni dan campuran).

2. Dilambangkan dengan determinan orde kedua

fungsi kuliah variabel ekstrem

Dalil

Jika titik dengan koordinat adalah titik stasioner untuk fungsi tersebut, maka:

A) Ketika itu adalah titik ekstrem lokal dan, pada maksimum lokal, - minimum lokal;

C) ketika titik tersebut bukan titik ekstrem lokal;

C) jika, mungkin keduanya.

Bukti

Kami menulis rumus Taylor untuk fungsi tersebut, membatasi diri pada dua anggota:

Karena, menurut kondisi teorema, titiknya stasioner, turunan parsial orde kedua sama dengan nol, mis. dan. Kemudian

Menunjukkan

Kemudian kenaikan fungsi akan berbentuk:

Karena kontinuitas turunan parsial orde kedua (murni dan campuran), menurut kondisi teorema pada suatu titik, kita dapat menulis:

Dimana atau; ,

1. Membiarkan dan, yaitu, atau.

2. Kami mengalikan kenaikan fungsi dan membaginya, kami mendapatkan:

3. Lengkapi ekspresi dalam kurung kurawal ke kuadrat penuh dari jumlah:

4. Ekspresi dalam kurung kurawal adalah non-negatif, karena

5. Oleh karena itu, jika dan karenanya, dan, maka dan, oleh karena itu, menurut definisi, titik tersebut adalah titik minimum lokal.

6. Jika dan berarti, dan, maka, menurut definisi, suatu titik dengan koordinat adalah titik maksimum lokal.

2. Pertimbangkan trinomial persegi, diskriminannya, .

3. Jika, maka ada titik-titik sedemikian rupa sehingga polinomial

4. Pertambahan total fungsi pada suatu titik sesuai dengan ekspresi yang diperoleh pada I, kita tuliskan dalam bentuk:

5. Karena kontinuitas turunan parsial orde kedua, dengan syarat teorema pada suatu titik, kita dapat menulis bahwa

oleh karena itu, terdapat lingkungan suatu titik sedemikian rupa sehingga, untuk sembarang titik, trinomial kuadrat lebih besar dari nol:

6. Pertimbangkan - lingkungan titik.

Mari kita pilih nilai apa saja, jadi itu intinya. Dengan asumsi bahwa dalam rumus untuk kenaikan fungsi

Apa yang kami dapatkan:

7. Sejak itu.

8. Berdebat dengan cara yang sama untuk akarnya, kita mendapatkan bahwa di setiap -tetangga dari titik ada titik yang, oleh karena itu, di sekitar titik itu tidak mempertahankan tanda, oleh karena itu tidak ada ekstrem pada titik tersebut.

Ekstrem bersyarat dari fungsi dua variabel

Ketika mencari ekstrem dari fungsi dua variabel, masalah sering muncul terkait dengan apa yang disebut ekstrem bersyarat. Konsep ini dapat dijelaskan dengan contoh fungsi dua variabel.

Biarkan fungsi dan garis L diberikan pada bidang 0xy. Tugasnya adalah menemukan titik P (x, y) seperti itu pada garis L, di mana nilai fungsi terbesar atau terkecil dibandingkan dengan nilai fungsi ini pada titik-titik garis L yang terletak di dekat titik P. Titik-titik P tersebut disebut fungsi titik ekstrem bersyarat pada garis L. Berbeda dengan titik ekstrem biasa, nilai fungsi pada titik ekstrem bersyarat dibandingkan dengan nilai fungsi tidak di semua titik beberapa lingkungannya, tetapi hanya pada yang terletak pada garis L.

Cukup jelas bahwa titik ekstrem biasa (mereka juga mengatakan ekstrem tak bersyarat) juga merupakan titik ekstrem bersyarat untuk setiap garis yang melewati titik ini. Kebalikannya, tentu saja, tidak benar: titik ekstrem bersyarat mungkin bukan titik ekstrem konvensional. Mari kita ilustrasikan apa yang telah dikatakan dengan sebuah contoh.

Contoh 1. Grafik fungsinya adalah belahan atas (Gbr. 2).

Beras. 2.

Fungsi ini memiliki maksimum di asal; itu sesuai dengan titik M dari belahan bumi. Jika garis L adalah garis lurus yang melalui titik A dan B (persamaannya), maka secara geometris jelas bahwa untuk titik-titik garis ini nilai maksimum fungsi dicapai pada titik yang terletak di tengah-tengah antara titik A dan B. Ini adalah fungsi titik ekstrem bersyarat (maksimum) pada baris ini; itu sesuai dengan titik M 1 di belahan bumi, dan dapat dilihat dari gambar bahwa tidak ada pertanyaan tentang ekstrem biasa di sini.

Perhatikan bahwa di bagian akhir dari masalah menemukan nilai terbesar dan terkecil dari suatu fungsi di daerah tertutup, kita harus menemukan nilai ekstrem dari fungsi pada batas daerah ini, yaitu. pada beberapa baris, dan dengan demikian memecahkan masalah untuk ekstrem bersyarat.

Definisi 1. Mereka mengatakan bahwa di mana memiliki maksimum bersyarat atau relatif (minimum) pada titik yang memenuhi persamaan: jika untuk setiap yang memenuhi persamaan, ketidaksetaraan

Definisi 2. Persamaan bentuk disebut persamaan kendala.

Dalil

Jika fungsi dan terdiferensiasi secara kontinu di sekitar suatu titik, dan turunan parsial dan titik tersebut adalah titik ekstrem bersyarat fungsi terhadap persamaan kendala, maka determinan orde kedua sama dengan nol:

Bukti

1. Karena, menurut ketentuan teorema, turunan parsial, dan nilai fungsi, maka dalam beberapa persegi panjang

fungsi implisit didefinisikan

Fungsi kompleks dari dua variabel pada suatu titik akan memiliki ekstrem lokal, oleh karena itu, atau.

2. Memang, menurut properti invarians dari rumus diferensial orde pertama

3. Persamaan koneksi dapat direpresentasikan dalam bentuk ini, yang berarti

4. Kalikan persamaan (2) dengan, dan (3) dengan dan tambahkan mereka

Oleh karena itu, pada

sewenang-wenang. h.t.d.

Konsekuensi

Pencarian titik ekstrem bersyarat dari fungsi dua variabel dalam praktiknya dilakukan dengan menyelesaikan sistem persamaan

Jadi, pada contoh di atas No 1 dari persamaan komunikasi yang kita miliki. Dari sini mudah untuk memeriksa apa yang mencapai maksimum di . Tapi kemudian dari persamaan komunikasi. Kami mendapatkan titik P, ditemukan secara geometris.

Contoh #2. Temukan titik ekstrem bersyarat dari fungsi terhadap persamaan kendala.

Mari kita cari turunan parsial dari fungsi yang diberikan dan persamaan koneksi:

Mari kita buat determinan orde kedua:

Mari kita tuliskan sistem persamaan untuk mencari titik ekstrem bersyarat:

karenanya, ada empat titik ekstrem bersyarat dari fungsi dengan koordinat: .

Contoh #3. Temukan titik ekstrem dari fungsi tersebut.

Menyamakan turunan parsial dengan nol: , kami menemukan satu titik stasioner - titik asal. Di Sini,. Oleh karena itu, titik (0, 0) juga bukan merupakan titik ekstrem. Persamaan tersebut merupakan persamaan paraboloid hiperbolik (Gbr. 3), gambar tersebut menunjukkan bahwa titik (0, 0) bukan merupakan titik ekstrem.

Beras. 3.

Nilai terbesar dan terkecil dari suatu fungsi di daerah tertutup

1. Biarkan fungsi didefinisikan dan kontinu dalam domain tertutup terbatas D.

2. Biarkan fungsi memiliki turunan parsial hingga di wilayah ini, kecuali untuk titik individu dari wilayah tersebut.

3. Sesuai dengan teorema Weierstrass, pada daerah ini terdapat titik dimana fungsi mengambil nilai terbesar dan terkecil.

4. Jika titik-titik ini adalah titik-titik interior daerah D, maka jelas bahwa mereka akan memiliki maksimum atau minimum.

5. Dalam hal ini, tempat-tempat menarik bagi kami termasuk di antara titik-titik yang mencurigakan di ekstrem.

6. Namun, fungsi tersebut juga dapat mengambil nilai maksimum atau minimum pada batas daerah D.

7. Untuk menemukan nilai terbesar (terkecil) dari fungsi di area D, Anda perlu menemukan semua titik internal yang mencurigakan untuk sebuah ekstrem, hitung nilai fungsi di dalamnya, lalu bandingkan dengan nilai fungsi di titik batas daerah, dan nilai terbesar dari semua yang ditemukan akan menjadi yang terbesar di daerah tertutup D.

8. Metode menemukan maksimum atau minimum lokal telah dibahas sebelumnya di Bagian 1.2. dan 1.3.

9. Tetap mempertimbangkan metode untuk menemukan nilai maksimum dan minimum fungsi pada batas wilayah.

10. Dalam kasus fungsi dua variabel, area biasanya dibatasi oleh sebuah kurva atau beberapa kurva.

11. Sepanjang kurva seperti itu (atau beberapa kurva), variabel dan keduanya bergantung satu sama lain, atau keduanya bergantung pada satu parameter.

12. Jadi, pada batas, fungsi tersebut ternyata bergantung pada satu variabel.

13. Metode menemukan nilai terbesar dari suatu fungsi dari satu variabel telah dibahas sebelumnya.

14. Biarkan batas daerah D diberikan oleh persamaan parametrik:

Kemudian pada kurva ini fungsi dua variabel akan menjadi fungsi kompleks dari parameter: . Untuk fungsi seperti itu, nilai terbesar dan terkecil ditentukan dengan metode penentuan nilai terbesar dan terkecil untuk fungsi satu variabel.

Biarkan fungsi z - f(x, y) didefinisikan dalam beberapa domain D dan biarkan Mo(xo, y0) menjadi titik interior domain ini. Definisi. Jika terdapat bilangan sedemikian rupa sehingga pertidaksamaan benar untuk semua yang memenuhi syarat, maka titik Mo(xo, yo) disebut titik maksimum lokal dari fungsi f(x, y); jika, bagaimanapun, untuk semua Dx, Du memenuhi kondisi | maka titik Mo(x0, y0) disebut minimum lokal halus. Dengan kata lain, titik M0(x0, y0) adalah titik maksimum atau minimum dari fungsi f(x, y) jika terdapat 6-tetangga dari titik A/o(x0, y0) sedemikian rupa sehingga sama sekali titik M(x, y) dari lingkungan ini, kenaikan fungsi mempertahankan tanda. Contoh. 1. Untuk suatu fungsi, titik adalah titik minimum (Gbr. 17). 2. Untuk fungsi, titik 0(0,0) adalah titik maksimum (Gbr. 18). 3. Untuk fungsi, titik 0(0,0) adalah titik maksimum lokal. 4 Memang, ada lingkungan dari titik 0(0, 0), misalnya, lingkaran dengan jari-jari j (lihat Gambar 19), di setiap titik yang berbeda dari titik 0(0, 0), nilai fungsi f(x, y) kurang dari 1 = Kami hanya akan mempertimbangkan titik-titik dari fungsi maksimum dan minimum yang ketat ketika pertidaksamaan ketat atau pertidaksamaan ketat berlaku untuk semua titik M(x) y) dari beberapa 6-tetangga tertusuk dari titik Mq. Nilai fungsi pada titik maksimum disebut maksimum, dan nilai fungsi pada titik minimum disebut minimum fungsi ini. Titik maksimum dan minimum dari suatu fungsi disebut titik ekstrem dari fungsi tersebut, dan titik maksimum dan minimum dari fungsi itu sendiri disebut titik ekstremnya. Teorema 11 (kondisi yang diperlukan untuk suatu ekstrem). Jika fungsi Ekstrem dari fungsi beberapa variabel Konsep ekstrem dari fungsi beberapa variabel. Kondisi yang diperlukan dan cukup untuk suatu ekstrem Ekstrem bersyarat Nilai terbesar dan terkecil dari fungsi kontinu memiliki ekstrem pada titik maka pada titik ini setiap turunan parsial dan u hilang atau tidak ada. Misalkan fungsi z = f(x) y) memiliki ekstrem di titik M0(x0, y0). Mari kita beri variabel y nilai yo. Maka fungsi z = /(x, y) akan menjadi fungsi dari satu variabel x\ Karena pada x = xo memiliki ekstrem (maksimum atau minimum, Gambar 20), maka turunannya terhadap x = “o, | (*o,l>)" Sama dengan nol, atau tidak ada. Demikian pula, kami memverifikasi bahwa) atau sama dengan nol, atau tidak ada. Titik di mana = 0 dan u = 0 atau tidak ada disebut titik kritis fungsi z = Dx, y) Titik di mana $£ = u = 0 juga disebut titik stasioner dari fungsi Teorema 11 hanya menyatakan kondisi yang diperlukan untuk ekstrem, yang tidak cukup. 18 Gbr.20 turunan immt yang hilang pada. Namun fungsi ini agak tipis pada imvat “straumum. Memang, fungsinya sama dengan nol pada titik 0(0, 0) dan mengambil titik M(x, y), sedekat mungkin dengan titik 0(0, 0) sesuka Anda, kkk nilai positif dan negatif. Untuk itu, maka pada titik-titik di titik (0,y) untuk sembarang titik kecil, titik 0(0, 0) jenis ini disebut titik mini-max (Gbr. 21). Kondisi yang cukup untuk ekstrem dari fungsi dua variabel dinyatakan oleh teorema berikut. Teorema 12 (kondisi yang cukup untuk ekstrem dari variabel fuzzy). Biarkan titik Mo(xo, y0) menjadi titik stasioner dari fungsi f(x, y), dan di beberapa lingkungan dari titik / termasuk titik Mo itu sendiri, fungsi f(r, y) memiliki turunan parsial kontinu ke atas untuk orde kedua inklusif. Maka "1) di titik Mq(xq, V0) fungsi f(x, y) maksimum jika determinannya ada di titik ini 2) di titik Mo(x0, V0) fungsi f(x, y) memiliki minimum jika di titik Mo(xo, yo) fungsi f(x, y) tidak memiliki ekstrem jika D(xo, yo)< 0. Если же то в точке Мо(жо> Wo) ekstrem dari fungsi f(x, y) mungkin atau mungkin tidak. Dalam hal ini, diperlukan penelitian lebih lanjut. Kami membatasi diri untuk membuktikan pernyataan 1) dan 2) dari teorema. Mari kita tulis rumus Taylor dari orde kedua untuk fungsi /(i, y): di mana. Dengan asumsi, dari mana jelas bahwa tanda kenaikan D/ ditentukan oleh tanda trinomial di sisi kanan (1), yaitu tanda diferensial kedua d2f. Mari kita tunjukkan untuk singkatnya. Maka persamaan (l) dapat ditulis sebagai berikut: Misalkan pada titik MQ(jadi, y0) kita mempunyai tetangga dari titik M0(s0,yo). Jika kondisi (di titik A/0) terpenuhi, dan, karena kontinuitas, turunan /,z(s, y) akan mempertahankan tandanya di beberapa lingkungan dari titik Af0. Di wilayah di mana A 0, kita memiliki 0 di beberapa lingkungan titik M0(x0) y0), maka tanda trinomial AAx2 -I- 2BAxAy + CDy2 bertepatan dengan tanda A di titik C tidak dapat memiliki tanda yang berbeda). Karena tanda jumlah AAs2 + 2BAxAy + CAy2 di titik (s0 + $ Ax, yo + 0 Dy) menentukan tanda selisih, kita sampai pada kesimpulan berikut: jika fungsi f(s, y) pada titik titik stasioner (s0, yo) memenuhi syarat, maka untuk cukup kecil || ketidaksetaraan akan bertahan. Jadi, pada titik (sq, y0) fungsi /(s, y) memiliki maksimum. Tetapi jika kondisi terpenuhi pada titik stasioner (s0, yo), maka untuk semua |Ar| . cukup kecil dan |Lakukan| pertidaksamaan benar, yang berarti bahwa fungsi /(s, y) memiliki minimum pada titik (so, yo). Contoh. 1. Selidiki fungsi 4 untuk ekstrem Menggunakan kondisi yang diperlukan untuk ekstrem, kami mencari titik stasioner dari fungsi. Untuk melakukan ini, kami menemukan turunan parsial, u dan menyamakannya dengan nol. Kami mendapatkan sistem persamaan dari mana - titik stasioner. Mari kita gunakan Teorema 12. Oleh karena itu, ada ekstrem di titik Ml. Karena ini minimal. Jika kita mengubah fungsi g ke dalam bentuk, maka mudah untuk melihat bahwa ruas kanan (")" akan menjadi minimal bila merupakan nilai minimum absolut dari fungsi ini. 2. Selidiki fungsi untuk suatu ekstrem Kami menemukan titik-titik stasioner dari fungsi tersebut, yang untuknya kami menyusun sistem persamaan Dari sini sehingga titik tersebut stasioner. Karena, berdasarkan Teorema 12, tidak ada ekstrem di titik M. * 3. Menyelidiki fungsi untuk suatu ekstrem Temukan titik-titik stasioner dari fungsi tersebut. Dari sistem persamaan diperoleh bahwa, sehingga titik tersebut stasioner. Selanjutnya, kita memiliki sehingga Teorema 12 tidak memberikan jawaban atas pertanyaan ada atau tidak adanya ekstrem. Mari kita lakukan dengan cara ini. Untuk fungsi tentang semua titik selain titik sehingga, menurut definisi, pada titik A/o(0,0) fungsi r memiliki minimum absolut. Dengan pengeringan analog, kami menetapkan bahwa fungsi memiliki maksimum pada titik, tetapi fungsi tidak memiliki ekstrem pada titik. Misalkan suatu fungsi dari variabel bebas terdiferensialkan pada suatu titik.Titik Mo disebut titik stasioner dari fungsi tersebut jika Teorema 13 (kondisi cukup untuk suatu ekstrem). Biarkan fungsi didefinisikan dan memiliki turunan parsial kontinu dari orde kedua di beberapa lingkungan dari garis halus Mc(xi..., yang merupakan fungsi halus stasioner, jika bentuk kuadrat (diferensial kedua dari fungsi f di denda titik adalah pasti-positif (negatif-pasti), titik minimum (masing-masing, maksimum halus) dari fungsi f baik-baik saja Jika bentuk kuadrat (4) bolak-balik tanda, maka tidak ada ekstrem dalam halus LG0. extremum Sejauh ini, kita telah memperhatikan pencarian ekstrem lokal dari suatu fungsi di seluruh domain definisinya, ketika argumen fungsi tidak terikat oleh kondisi tambahan apa pun. Biarkan fungsi z \u003d / (x, y) didefinisikan di wilayah D. Mari kita asumsikan bahwa kurva L diberikan di wilayah ini, dan perlu untuk menemukan ekstrem dari fungsi f (x> y) saja di antara nilai-nilainya yang sesuai dengan titik-titik kurva L. Ekstrem yang sama disebut ekstrem bersyarat dari fungsi z = f(x) y) pada kurva L. Definisi Dikatakan bahwa pada suatu titik terletak pada kurva L, fungsi f(x, y) memiliki kondisi maksimum (minimum) jika pertidaksamaan dipenuhi, masing-masing, di semua titik M (s, y) kurva L milik beberapa lingkungan dari titik M0 (x0, Yo) dan berbeda dari titik M0 (Jika kurva L diberikan oleh persamaan, maka masalah menemukan ekstrem bersyarat dari fungsi r - f (x, y) pada kurva! dapat dirumuskan sebagai berikut: cari ekstrema fungsi x = /(z, y) di daerah D, asalkan Jadi, ketika menemukan ekstrem bersyarat dari fungsi z = y), argumen zn tidak dapat dipertimbangkan lagi sebagai variabel independen: mereka saling berhubungan oleh hubungan y ) = 0, yang disebut persamaan kendala. Untuk memperjelas perbedaan antara m «* D y sebagai ekstrem bersyarat dan bersyarat, mari kita lihat contoh lain, fungsi maksimum tanpa syarat (Gbr. 23) sama dengan satu dan dicapai pada titik (0,0). Ini sesuai dengan tepat M - simpul dari pvvboloid Mari kita tambahkan persamaan kendala y = j. Maka maksimum bersyarat jelas akan sama, dicapai pada titik (o, |), dan sesuai dengan titik Afj pvvboloid, yaitu garis perpotongan pvvboloid dengan bidang y = j. Dalam kasus s minimum tak bersyarat, kita memiliki aplikasi terkecil di antara semua eksplisit permukaan * = 1 - n;2 ~ y1; slumvv conditional - hanya di antara titik vllkvt pvrboloidv, sesuai dengan titik * dari garis lurus y = j bukan dari bidang xOy. Salah satu metode untuk menemukan ekstrem bersyarat dari suatu fungsi di hadapan dan koneksi adalah sebagai berikut. Biarkan persamaan koneksi y)-0 mendefinisikan y sebagai fungsi terdiferensiasi bernilai tunggal dari argumen x: Substitusikan fungsi, bukan y ke dalam fungsi, kita memperoleh fungsi dari satu argumen di mana kondisi koneksi telah diperhitungkan . Ekstrem (tanpa syarat) dari fungsi adalah ekstrem bersyarat yang diinginkan. Contoh. Menemukan ekstrem dari suatu fungsi di bawah kondisi Ekstrem dari fungsi beberapa variabel Konsep ekstrem dari fungsi beberapa variabel. Kondisi yang diperlukan dan cukup untuk ekstrem Ekstrem bersyarat Nilai terbesar dan terkecil dari fungsi kontinu A \u003d 1 - titik kritis;, sehingga menghasilkan minimum bersyarat dari fungsi r (Gbr. 24). Mari kita tunjukkan cara lain untuk menyelesaikannya masalah ekstrem bersyarat, yang disebut metode pengali Lagrange. Biarkan ada titik ekstrem bersyarat dari fungsi di hadapan koneksi. Mari kita asumsikan bahwa persamaan koneksi mendefinisikan fungsi terdiferensiasi kontinu yang unik di beberapa lingkungan titik xi Dengan asumsi bahwa kita memperoleh turunan terhadap x dari fungsi /(r, ip(x)) pada titik xq harus sama dengan nol atau, yang setara dengan ini, diferensial dari f (x, y ) di titik Mo "O) Dari persamaan koneksi yang kita miliki (5) Kemudian, karena kesewenang-wenangan dx, kami memperoleh Persamaan (6) dan (7) menyatakan kondisi yang diperlukan untuk ekstrem tak bersyarat pada titik fungsi yang disebut fungsi Lagrange. Jadi, titik ekstrem bersyarat dari fungsi / (x, y), jika, tentu saja merupakan titik stasioner dari fungsi Lagrange di mana A adalah beberapa koefisien numerik. Dari sini kita memperoleh aturan untuk menemukan ekstrem bersyarat: untuk menemukan titik yang dapat menjadi titik ekstrem absolut suatu fungsi dengan adanya koneksi, 1) kita membuat fungsi Lagrange, 2) menyamakan turunan dan W dari fungsi ini ke nol dan menambahkan persamaan koneksi ke persamaan yang dihasilkan, kami memperoleh sistem tiga persamaan dari mana kami menemukan nilai A dan koordinat x, y dari titik ekstrem yang mungkin. Pertanyaan tentang keberadaan dan sifat ekstrem bersyarat diselesaikan berdasarkan mempelajari tanda diferensial kedua dari fungsi Lagrange untuk sistem nilai yang dipertimbangkan x0, Yo, A, diperoleh dari (8) di bawah kondisi bahwa Jika, maka pada titik (x0, Yo) fungsi f(x, y ) memiliki maksimum bersyarat; jika d2F > 0 - maka minimum bersyarat. Khususnya, jika pada titik stasioner (xo, J/o) determinan D untuk fungsi F(x, y) positif, maka pada titik (®o, V0) terdapat kondisi maksimum fungsi /( x, y) jika, dan minimum bersyarat dari fungsi /(x, y), jika Contoh. Mari kita kembali ke kondisi contoh sebelumnya: temukan ekstrem dari fungsi asalkan x + y = 1. Kami akan menyelesaikan masalah menggunakan metode pengali Lagrange. Fungsi Lagrange dalam hal ini berbentuk Untuk mencari titik stasioner, kita buat sistem Dari dua persamaan pertama sistem, kita peroleh bahwa x = y. Kemudian dari persamaan ketiga sistem (persamaan kopling) kita menemukan bahwa x - y = j - koordinat titik dari kemungkinan ekstrem. Dalam hal ini (ditunjukkan bahwa A \u003d -1. Dengan demikian, fungsi Lagrange. adalah titik minimum bersyarat dari fungsi * \u003d x2 + y2 di bawah kondisi bahwa tidak ada ekstrem tanpa syarat untuk fungsi Lagrangian. P ( x, y) belum berarti tidak adanya ekstrem bersyarat untuk fungsi /(x, y) dengan adanya koneksi Contoh: Temukan ekstrem dari fungsi di bawah kondisi y 4 Kami menyusun fungsi Lagrange dan menulis sistem untuk menentukan A dan koordinat titik ekstrem yang mungkin: Dari dua persamaan pertama kita peroleh x + y = 0 dan sampai pada sistem y = A = 0. Jadi, fungsi Lagrange yang sesuai memiliki bentuk Di titik (0 , 0), fungsi F(x, y; 0) tidak memiliki ekstrem bersyarat, tetapi ekstrem bersyarat dari fungsi r = xy. Ketika y = x, ada "Memang, dalam hal ini r = x2. Dari di sini jelas bahwa pada titik (0,0) ada minimum bersyarat. persamaan koneksi Sostaalyaem fungsi Lagrange di mana A|, Az,..., A„, - not faktor konstan tertentu. Menyamakan nol semua turunan parsial dari orde pertama fungsi F dan menambahkan ke persamaan yang diperoleh persamaan sambungan (9), kita memperoleh sistem persamaan n + m, dari mana kita menentukan Ab A3|..., Am dan koordinat x\) x2) . » xn titik yang mungkin dari ekstrem bersyarat. Pertanyaan apakah titik-titik yang ditemukan dengan metode Lagrange benar-benar titik ekstrem bersyarat seringkali dapat diselesaikan berdasarkan pertimbangan yang bersifat fisis atau geometris. 15.3. Nilai maksimum dan minimum dari fungsi kontinu Membiarkan diperlukan untuk menemukan nilai maksimum (terkecil) dari suatu fungsi z = /(x, y) kontinu dalam beberapa domain terbatas yang diperluas D. Berdasarkan Teorema 3, pada daerah ini terdapat sebuah titik (xo, V0) dimana fungsi tersebut mengambil nilai terbesar (terkecil). Jika titik (xo, y0) terletak di dalam domain D, maka fungsi / memiliki maksimum (minimum) di dalamnya, sehingga dalam hal ini titik yang kita minati terdapat di antara titik-titik kritis fungsi /(x , y). Namun, fungsi /(x,y) juga dapat mencapai nilai maksimum (terkecil) pada batas wilayah. Oleh karena itu, untuk mencari nilai terbesar (terkecil) yang diambil oleh fungsi z = /(x, y) di daerah tertutup terbatas 2), perlu untuk menemukan semua maksimum (minimum) dari fungsi yang dicapai di dalam daerah ini , serta nilai fungsi terbesar (terkecil) pada batas wilayah ini. Yang terbesar (terkecil) dari semua bilangan ini akan menjadi nilai maksimum (terkecil) yang diinginkan dari fungsi z = /(x, y) di daerah 27. Mari kita tunjukkan bagaimana hal ini dilakukan dalam kasus fungsi terdiferensiasi. Prmr. Temukan nilai terbesar dan terkecil dari fungsi area 4. Kami menemukan titik kritis fungsi di dalam area D. Untuk melakukan ini, kami membuat sistem persamaan Dari sini kami mendapatkan x \u003d y \u003e 0 , sehingga titik 0 (0,0) adalah titik kritis fungsi x. Sejak Mari kita sekarang menemukan nilai terbesar dan terkecil dari fungsi pada batas wilayah D. Pada bagian dari batas yang kita miliki sehingga y \u003d 0 adalah titik kritis, dan karena \u003d maka pada saat ini titik fungsi z \u003d 1 + y2 memiliki minimum sama dengan satu. Di ujung segmen G", pada titik (, ​​kami miliki. Dengan menggunakan pertimbangan simetri, kami memperoleh hasil yang sama untuk bagian lain dari batas. Akhirnya, kami memperoleh: nilai terkecil dari fungsi z \u003d x2 + y2 dalam daerah "B" sama dengan nol dan dicapai pada area titik interior 0( 0, 0), dan nilai maksimum fungsi ini, sama dengan dua, dicapai pada empat titik batas (Gbr.25) Gbr.25 Latihan fungsi: Menemukan turunan parsial dari fungsi dan diferensial totalnya: Menemukan turunan dari fungsi kompleks: 3 Menemukan J. Ekstrem dari suatu fungsi dari beberapa variabel Konsep ekstrem dari suatu fungsi dari beberapa variabel Kondisi yang diperlukan dan cukup untuk an extremum Conditional extremum Nilai terbesar dan terkecil dari fungsi kontinu 34. Menggunakan rumus turunan fungsi kompleks dua variabel, cari dan fungsi: 35. Menggunakan rumus turunan fungsi kompleks dalam dua variabel, cari |J dan fungsi: Temukan jj fungsi implisit: 40. Temukan kemiringan kurva singgung di titik perpotongan dengan garis lurus x = 3. 41. Temukan titik-titik di mana garis singgung kurva-x sejajar dengan sumbu-x. . Dalam tugas-tugas berikut, temukan dan Z: Tulis persamaan bidang singgung dan normal permukaan: 49. Tulis persamaan bidang singgung permukaan x2 + 2y2 + Zr2 \u003d 21, sejajar dengan bidang x + 4y + 6z \u003d 0. Temukan tiga hingga empat suku pertama dari ekspansi menggunakan rumus Taylor : 50. y di sekitar titik (0, 0). Dengan menggunakan definisi ekstrem suatu fungsi, selidiki fungsi ekstrem berikut ini :). Dengan menggunakan kondisi yang cukup untuk ekstrem dari fungsi dua variabel, selidiki ekstrem dari fungsi: 84. Temukan nilai terbesar dan terkecil dari fungsi z \u003d x2 - y2 dalam lingkaran tertutup 85. Temukan yang terbesar dan terkecil nilai fungsi * \u003d x2y (4-x-y) dalam segitiga yang dibatasi oleh garis x \u003d 0, y = 0, x + y = b. 88. Tentukan dimensi kolam terbuka persegi panjang dengan permukaan terkecil, asalkan volumenya sama dengan V. 87. Temukan dimensi persegi panjang paralelepiped dengan total permukaan yang diberikan 5 volume maksimum. Jawaban 1. dan | Persegi yang dibentuk oleh ruas garis x termasuk sisi-sisinya. 3. Keluarga cincin konsentris 2= 0,1,2,... .4. Seluruh bidang kecuali titik-titik garis lurus y. Bagian dari bidang yang terletak di atas parabola y \u003d -x?. 8. Lingkari titik x. Seluruh bidang kecuali garis lurus x Ekspresi radikal adalah non-negatif dalam dua kasus j * ^ atau j x ^ ^ yang masing-masing setara dengan deret pertidaksamaan tak hingga Domain definisi adalah kuadrat berbayang (Gbr. 26) ; l yang ekivalen dengan deret tak hingga. Fungsi didefinisikan di titik. a) Garis sejajar dengan garis x b) Lingkaran konsentris berpusat di titik asal. 10. a) parabola y) parabola y a) parabola b) hiperbola | .Pesawat xc. 13.Prim - hiperboloid satu rongga revolusi di sekitar sumbu Oz; untuk dan merupakan hiperboloid revolusi dua lapis di sekitar sumbu Oz, kedua keluarga permukaan dipisahkan oleh kerucut; Tidak ada limit, b) 0. 18. Misalkan y = kxt maka z lim z = -2, sehingga fungsi yang diberikan pada titik (0,0) tidak memiliki limit. 19. a) Poin (0.0); b) titik (0,0). 20. a) Garis putus - lingkaran x2 + y2 = 1; b) garis putus adalah garis lurus y \u003d x. 21. a) Garis putus - sumbu koordinat Ox dan Oy; b) 0 (set kosong). 22. Semua titik (m, n), di mana dan n adalah bilangan bulat

EKSTRIM KONDISI

Nilai minimum atau maksimum yang dicapai oleh fungsi tertentu (atau fungsional) asalkan beberapa fungsi lain (fungsional) mengambil nilai dari himpunan yang dapat diterima. Jika tidak ada kondisi yang membatasi perubahan dalam variabel independen (fungsi) dalam arti yang ditunjukkan, maka seseorang berbicara tentang ekstrem tanpa syarat.
Klasik tugas untuk W. e. adalah masalah menentukan minimum suatu fungsi dari beberapa variabel

Asalkan beberapa fungsi lain mengambil nilai yang diberikan:

Dalam masalah ini G, di mana nilai-nilai fungsi vektor g=(g 1 , ..., g m), termasuk dalam kondisi tambahan (2) adalah titik tetap c=(c 1 , ..., dengan t) dalam ruang Euclidean m-dimensi
Jika pada (2) bersama dengan tanda sama dengan, tanda pertidaksamaan diperbolehkan

Ini mengarah ke masalah pemrograman non-linier(tigabelas). Dalam masalah (1), (3), himpunan G dari nilai-nilai yang dapat diterima dari fungsi vektor g adalah lengkung tertentu , milik (n-m 1)-dimensi permukaan hiper yang didefinisikan oleh m 1 , m 1 kondisi tipe kesetaraan (3). Batas-batas polihedron lengkung yang ditentukan dibangun dengan mempertimbangkan pm 1 ketidaksetaraan termasuk dalam (3).
Kasus khusus masalah (1), (3) pada U.v. adalah tugas pemrograman linier, di mana semua fungsi yang dipertimbangkan f dan gi linier dalam x l , ... , x hal. Dalam masalah pemrograman linier, himpunan G dari nilai yang mungkin dari fungsi vektor g, termasuk dalam kondisi yang membatasi rentang variabel x 1 , .....xn , adalah , yang termasuk dalam hyperplane dimensi (n-t 1) yang didefinisikan oleh m 1 kondisi tipe kesetaraan dalam (3).
Demikian pula, sebagian besar masalah optimasi untuk fungsi yang mewakili praktis bunga, dikurangi menjadi tugas di U. e. (cm. Masalah isoperimetri, Masalah dering, Masalah Lagrange, Masalah cara). Sama seperti dalam matematika. pemrograman, masalah utama kalkulus variasi dan teori kontrol optimal adalah masalah cembung e.
Saat memecahkan masalah di U. e., terutama saat mempertimbangkan teoretis. pertanyaan yang berkaitan dengan masalah pada C. e., ternyata sangat berguna untuk menggunakan indefinite pengganda Lagrangian, memungkinkan untuk mengurangi masalah ke U. e. untuk masalah pada kondisi tanpa syarat dan menyederhanakan kondisi optimalitas yang diperlukan. Penggunaan pengganda Lagrange mendasari sebagian besar klasik metode untuk memecahkan masalah di U. e.

menyala.: Hadley J., Nonlinier dan , trans. dari bahasa Inggris, M., 1967; Bliss G.A., Ceramah tentang kalkulus variasi, trans. dari bahasa Inggris, M., 1950; Pontryagin L. S. [et al.], Proses Optimal Matematika, 2nd ed., M., 1969.
I.B.Vapnyarsky.

ensiklopedia matematika. - M.: Ensiklopedia Soviet. I.M. Vinogradov. 1977-1985.

Lihat apa itu "CONDITIONAL EXTREME" di kamus lain:

Ekstrem relatif, ekstrem dari fungsi f (x1,..., xn + m) dari n + m variabel, dengan asumsi bahwa variabel-variabel ini tunduk pada m lebih banyak persamaan (kondisi): k (x1,..., xn + m) = 0, 1≤ k m (*) (lihat Ekstrem).… …

Biarkan himpunan terbuka dan pada diberikan fungsi. Biarkan. Persamaan ini disebut persamaan kendala (terminologi dipinjam dari mekanika). Biarkan suatu fungsi didefinisikan pada G ... Wikipedia

- (dari bahasa Latin ekstrem ekstrem) nilai fungsi kontinu f (x), yang merupakan maksimum atau minimum. Lebih tepatnya: suatu fungsi f(x) kontinu di titik x0 memiliki maksimum (minimum) di x0 jika ada lingkungan (x0 + , x0 ) dari titik ini, ... ... Ensiklopedia Besar Soviet

Istilah ini memiliki arti lain, lihat Ekstrim (makna). Ekstrem (Latin extremum extreme) dalam matematika adalah nilai maksimum atau minimum suatu fungsi pada suatu himpunan tertentu. Titik di mana ekstrem tercapai adalah ... ... Wikipedia

Sebuah fungsi yang digunakan dalam memecahkan masalah untuk fungsi ekstrem bersyarat dari beberapa variabel dan fungsi. Dengan bantuan L. f. kondisi optimalitas yang diperlukan ditulis dalam masalah untuk ekstrem bersyarat. Tidak perlu hanya mengekspresikan variabel ... Ensiklopedia Matematika

Suatu disiplin matematika yang dikhususkan untuk menemukan nilai ekstrem (maksimum dan minimum) dari fungsi variabel tergantung pada pilihan satu atau lebih fungsi. Di dan. adalah perkembangan alami dari bab itu ... ... Ensiklopedia Besar Soviet

Variabel, dengan bantuan yang fungsi Lagrange dibangun dalam studi masalah untuk ekstrem bersyarat. Penggunaan L.m. dan fungsi Lagrange memungkinkan untuk memperoleh kondisi optimalitas yang diperlukan dengan cara yang seragam dalam masalah untuk ekstrem bersyarat ... Ensiklopedia Matematika

Kalkulus variasi adalah cabang dari analisis fungsional yang mempelajari variasi fungsi. Tugas paling umum dari kalkulus variasi adalah menemukan fungsi di mana fungsi tertentu mencapai ... ... Wikipedia

Bagian matematika yang dikhususkan untuk mempelajari metode untuk menemukan fungsi ekstrem yang bergantung pada pilihan satu atau lebih fungsi di bawah berbagai jenis pembatasan (fase, diferensial, integral, dll.) yang dikenakan pada ini ... ... Ensiklopedia Matematika

Kalkulus variasi adalah cabang matematika yang mempelajari variasi fungsi. Tugas yang paling umum dari kalkulus variasi adalah untuk menemukan fungsi di mana fungsional mencapai nilai ekstrim. Metode ... ... Wikipedia

Buku

• Kuliah teori kontrol. Volume 2. Kontrol Optimal, V. Boss. Masalah klasik dari teori kontrol optimal dipertimbangkan. Presentasi dimulai dengan konsep dasar optimasi dalam ruang berdimensi hingga: ekstrem bersyarat dan tak bersyarat, ...

Mari kita perhatikan dulu kasus fungsi dua variabel. Ekstrem bersyarat dari fungsi $z=f(x,y)$ pada titik $M_0(x_0;y_0)$ adalah ekstrem dari fungsi ini, dicapai dengan syarat bahwa variabel $x$ dan $y$ dalam sekitar titik ini memenuhi persamaan kendala $\ varphi(x,y)=0$.

Nama ekstrem "bersyarat" adalah karena fakta bahwa kondisi tambahan $\varphi(x,y)=0$ dikenakan pada variabel. Jika dimungkinkan untuk menyatakan satu variabel dalam bentuk variabel lain dari persamaan koneksi, maka masalah menentukan ekstrem bersyarat direduksi menjadi masalah ekstrem biasa dari fungsi satu variabel. Misalnya, jika $y=\psi(x)$ mengikuti persamaan kendala, kemudian mensubstitusikan $y=\psi(x)$ ke $z=f(x,y)$, kita mendapatkan fungsi satu variabel $ z=f\kiri (x,\psi(x)\kanan)$. Namun, dalam kasus umum, metode ini tidak banyak digunakan, sehingga diperlukan algoritma baru.

Metode pengganda Lagrange untuk fungsi dua variabel.

Metode pengali Lagrange adalah untuk mencari ekstrem bersyarat, fungsi Lagrange disusun: $F(x,y)=f(x,y)+\lambda\varphi(x,y)$ (parameter $\lambda $ disebut pengali Lagrange). Kondisi ekstrem yang diperlukan diberikan oleh sistem persamaan dari mana titik-titik stasioner ditentukan:

$$ \left \( \begin(aligned) & \frac(\partial F)(\partial x)=0;\\ & \frac(\partial F)(\partial y)=0;\\ & \varphi (x,y)=0.\end(sejajar)\kanan.$$

Tanda $d^2 F=F_(xx)^("")dx^2+2F_(xy)^("")dxdy+F_(yy)^("" )dy^2$. Jika pada titik stasioner $d^2F > 0$, maka fungsi $z=f(x,y)$ memiliki kondisi minimum pada titik ini, tetapi jika $d^2F< 0$, то условный максимум.

Ada cara lain untuk menentukan sifat ekstrem. Dari persamaan kendala kita mendapatkan: $\varphi_(x)^(")dx+\varphi_(y)^(")dy=0$, $dy=-\frac(\varphi_(x)^("))( \varphi_ (y)^("))dx$, jadi pada setiap titik stasioner kita memiliki:

$$d^2 F=F_(xx)^("")dx^2+2F_(xy)^("")dxdy+F_(yy)^("")dy^2=F_(xx)^( "")dx^2+2F_(xy)^("")dx\left(-\frac(\varphi_(x)^("))(\varphi_(y)^("))dx\right)+ F_(yy)^("")\left(-\frac(\varphi_(x)^("))(\varphi_(y)^("))dx\right)^2=\\ =-\frac (dx^2)(\left(\varphi_(y)^(") \right)^2)\cdot\left(-(\varphi_(y)^("))^2 F_(xx)^(" ")+2\varphi_(x)^(")\varphi_(y)^(")F_(xy)^("")-(\varphi_(x)^("))^2 F_(yy)^ ("")\kanan)$$

Faktor kedua (terletak dalam tanda kurung) dapat direpresentasikan dalam bentuk ini:

Elemen $\left| \begin(array) (cc) F_(xx)^("") & F_(xy)^("") \\ F_(xy)^("") & F_(yy)^("") \end (array) \right|$ yang merupakan Hessian dari fungsi Lagrange. Jika $H > 0$ maka $d^2F< 0$, что указывает на условный максимум. Аналогично, при $H < 0$ имеем $d^2F >$0, yaitu kita memiliki minimum bersyarat dari fungsi $z=f(x,y)$.

Perhatikan bentuk determinan $H$. tunjukan Sembunyikan

$$ H=-\left|\begin(array) (ccc) 0 & \varphi_(x)^(") & \varphi_(y)^(")\\ \varphi_(x)^(") & F_ (xx)^("") & F_(xy)^("") \\ \varphi_(y)^(") & F_(xy)^("") & F_(yy)^("") \ akhir(array) \kanan| $$

Dalam situasi ini, aturan yang dirumuskan di atas berubah sebagai berikut: jika $H > 0$, maka fungsi tersebut memiliki minimum bersyarat, dan untuk $H< 0$ получим условный максимум функции $z=f(x,y)$. При решении задач следует учитывать такие нюансы.

Algoritma untuk mempelajari fungsi dua variabel untuk ekstrem bersyarat

1. Buat fungsi Lagrange $F(x,y)=f(x,y)+\lambda\varphi(x,y)$
2. Memecahkan sistem $ \left \( \begin(aligned) & \frac(\partial F)(\partial x)=0;\\ & \frac(\partial F)(\partial y)=0;\\ & \ varphi(x,y)=0.\end(aligned)\right.$
3. Tentukan sifat ekstrem pada setiap titik stasioner yang ditemukan pada paragraf sebelumnya. Untuk melakukannya, gunakan salah satu metode berikut:
   • Buatlah determinan $H$ dan cari tahu tandanya
   • Dengan mempertimbangkan persamaan kendala, hitung tanda $d^2F$

Metode pengali Lagrange untuk fungsi n variabel

Misalkan kita memiliki fungsi dari variabel $n$ $z=f(x_1,x_2,\ldots,x_n)$ dan $m$ persamaan kendala ($n > m$):

$$\varphi_1(x_1,x_2,\ldots,x_n)=0; \; \varphi_2(x_1,x_2,\ldots,x_n)=0,\ldots,\varphi_m(x_1,x_2,\ldots,x_n)=0.$$

Dengan menyatakan pengali Lagrange sebagai $\lambda_1,\lambda_2,\ldots,\lambda_m$, kita menyusun fungsi Lagrange:

$$F(x_1,x_2,\ldots,x_n,\lambda_1,\lambda_2,\ldots,\lambda_m)=f+\lambda_1\varphi_1+\lambda_2\varphi_2+\ldots+\lambda_m\varphi_m$$

Kondisi yang diperlukan untuk keberadaan ekstrem bersyarat diberikan oleh sistem persamaan dari mana koordinat titik stasioner dan nilai pengali Lagrange ditemukan:

$$\left\(\begin(aligned) & \frac(\partial F)(\partial x_i)=0; (i=\overline(1,n))\\ & \varphi_j=0; (j=\ overline(1,m)) \end(aligned) \right.$$

Dimungkinkan untuk mengetahui apakah suatu fungsi memiliki minimum bersyarat atau maksimum bersyarat pada titik yang ditemukan, seperti sebelumnya, menggunakan tanda $d^2F$. Jika pada titik yang ditemukan $d^2F > 0$, maka fungsi tersebut memiliki minimum bersyarat, tetapi jika $d^2F< 0$, - то условный максимум. Можно пойти иным путем, рассмотрев следующую матрицу:

Penentu matriks $\left| \begin(array) (ccccc) \frac(\partial^2F)(\partial x_(1)^(2)) & \frac(\partial^2F)(\partial x_(1)\partial x_(2) ) & \frac(\parsial^2F)(\parsial x_(1)\parsial x_(3)) &\ldots & \frac(\parsial^2F)(\parsial x_(1)\parsial x_(n)) \\ \frac(\parsial^2F)(\parsial x_(2)\parsial x_1) & \frac(\parsial^2F)(\parsial x_(2)^(2)) & \frac(\parsial^2F )(\parsial x_(2)\parsial x_(3)) &\ldots & \frac(\parsial^2F)(\parsial x_(2)\parsial x_(n))\\ \frac(\parsial^2F )(\parsial x_(3) \parsial x_(1)) & \frac(\parsial^2F)(\parsial x_(3)\parsial x_(2)) & \frac(\parsial^2F)(\parsial x_(3)^(2)) &\ldots & \frac(\partial^2F)(\partial x_(3)\partial x_(n))\\ \ldots & \ldots & \ldots &\ldots & \ ldots\\ \frac(\parsial^2F)(\parsial x_(n)\parsial x_(1)) & \frac(\parsial^2F)(\parsial x_(n)\parsial x_(2)) & \ frac(\parsial^2F)(\parsial x_(n)\parsial x_(3)) &\ldots & \frac(\parsial^2F)(\parsial x_(n)^(2))\\ \end( array) \right|$ yang disorot dengan warna merah dalam matriks $L$ adalah fungsi Hessian dari Lagrange. Kami menggunakan aturan berikut:

• Jika tanda sudut di bawah umur adalah $H_(2m+1),\; H_(2m+2),\ldots,H_(m+n)$ matriks $L$ berimpit dengan tanda $(-1)^m$, maka titik stasioner yang diteliti adalah titik minimum bersyarat dari fungsi $z =f(x_1,x_2 ,x_3,\ldots,x_n)$.
• Jika tanda sudut di bawah umur adalah $H_(2m+1),\; H_(2m+2),\ldots,H_(m+n)$ bergantian, dan tanda minor $H_(2m+1)$ bertepatan dengan tanda bilangan $(-1)^(m+1 )$, maka titik stasioner yang dipelajari adalah titik maksimum bersyarat dari fungsi $z=f(x_1,x_2,x_3,\ldots,x_n)$.

Contoh 1

Temukan ekstrem bersyarat dari fungsi $z(x,y)=x+3y$ pada kondisi $x^2+y^2=10$.

Interpretasi geometris dari masalah ini adalah sebagai berikut: diperlukan untuk menemukan nilai terbesar dan terkecil dari aplikasi pesawat $z=x+3y$ untuk titik-titik perpotongannya dengan silinder $x^2+y^2 = $10.

Agak sulit untuk menyatakan satu variabel dalam bentuk variabel lain dari persamaan kendala dan mensubstitusikannya ke dalam fungsi $z(x,y)=x+3y$, jadi kita akan menggunakan metode Lagrange.

Menunjukkan $\varphi(x,y)=x^2+y^2-10$, kami membuat fungsi Lagrange:

$$ F(x,y)=z(x,y)+\lambda \varphi(x,y)=x+3y+\lambda(x^2+y^2-10);\\ \frac(\partial F)(\parsial x)=1+2\lambda x; \frac(\partial F)(\partial y)=3+2\lambda y. $$

Mari kita tuliskan sistem persamaan untuk menentukan titik stasioner dari fungsi Lagrange:

$$ \left \( \begin(aligned) & 1+2\lambda x=0;\\ & 3+2\lambda y=0;\\ & x^2+y^2-10=0. \end (selaras)\kanan.$$

Jika kita asumsikan $\lambda=0$, maka persamaan pertama menjadi: $1=0$. Kontradiksi yang dihasilkan mengatakan bahwa $\lambda\neq 0$. Pada kondisi $\lambda\neq 0$, dari persamaan pertama dan kedua kita mendapatkan: $x=-\frac(1)(2\lambda)$, $y=-\frac(3)(2\lambda) $. Mengganti nilai yang diperoleh ke dalam persamaan ketiga, kita mendapatkan:

$$ \left(-\frac(1)(2\lambda) \right)^2+\left(-\frac(3)(2\lambda) \right)^2-10=0;\\ \frac (1)(4\lambda^2)+\frac(9)(4\lambda^2)=10; \lambda^2=\frac(1)(4); \left[ \begin(aligned) & \lambda_1=-\frac(1)(2);\\ & \lambda_2=\frac(1)(2). \end(aligned) \right.\\ \begin(aligned) & \lambda_1=-\frac(1)(2); \; x_1=-\frac(1)(2\lambda_1)=1; \; y_1=-\frac(3)(2\lambda_1)=3;\\ & \lambda_2=\frac(1)(2); \; x_2=-\frac(1)(2\lambda_2)=-1; \; y_2=-\frac(3)(2\lambda_2)=-3.\end(selaras) $$

Jadi, sistem memiliki dua solusi: $x_1=1;\; y_1=3;\; \lambda_1=-\frac(1)(2)$ dan $x_2=-1;\; y_2=-3;\; \lambda_2=\frac(1)(2)$. Mari kita cari tahu sifat ekstrem pada setiap titik stasioner: $M_1(1;3)$ dan $M_2(-1;-3)$. Untuk melakukan ini, kami menghitung determinan $H$ di setiap titik.

$$ \varphi_(x)^(")=2x;\; \varphi_(y)^(")=2y;\; F_(xx)^("")=2\lambda;\; F_(xy)^("")=0;\; F_(yy)^("")=2\lambda.\\ H=\kiri| \begin(array) (ccc) 0 & \varphi_(x)^(") & \varphi_(y)^(")\\ \varphi_(x)^(") & F_(xx)^("") & F_(xy)^("") \\ \varphi_(y)^(") & F_(xy)^("") & F_(yy)^("") \end(array) \right|= \kiri| \begin(array) (ccc) 0 & 2x & 2th\\ 2x & 2\lambda & 0 \\ 2th & 0 & 2\lambda \end(array) \right|= 8\cdot\left| \begin(array) (ccc) 0 & x & y\\ x & \lambda & 0 \\ y & 0 & \lambda \end(array) \right| $$

Pada titik $M_1(1;3)$ kita mendapatkan: $H=8\cdot\left| \begin(array) (ccc) 0 & x & y\\ x & \lambda & 0 \\ y & 0 & \lambda \end(array) \right|= 8\cdot\left| \begin(array) (ccc) 0 & 1 & 3\\ 1 & -1/2 & 0 \\ 3 & 0 & -1/2 \end(array) \right|=40 > 0$, jadi pada titik $M_1(1;3)$ fungsi $z(x,y)=x+3y$ memiliki maksimum bersyarat, $z_(\max)=z(1;3)=10$.

Demikian pula, pada titik $M_2(-1;-3)$ kita menemukan: $H=8\cdot\left| \begin(array) (ccc) 0 & x & y\\ x & \lambda & 0 \\ y & 0 & \lambda \end(array) \right|= 8\cdot\left| \begin(array) (ccc) 0 & -1 & -3\\ -1 & 1/2 & 0 \\ -3 & 0 & 1/2 \end(array) \right|=-40$. Sejak $H< 0$, то в точке $M_2(-1;-3)$ имеем условный минимум функции $z(x,y)=x+3y$, а именно: $z_{\min}=z(-1;-3)=-10$.

Saya perhatikan bahwa alih-alih menghitung nilai determinan $H$ pada setiap titik, jauh lebih mudah untuk membukanya secara umum. Agar tidak mengacaukan teks dengan detail, saya akan menyembunyikan metode ini di bawah catatan.

Notasi determinan $H$ dalam bentuk umum. tunjukan Sembunyikan

$$ H=8\cdot\left|\begin(array)(ccc)0&x&y\\x&\lambda&0\\y&0&\lambda\end(array)\right| =8\cdot\left(-\lambda(y^2)-\lambda(x^2)\right) =-8\lambda\cdot\left(y^2+x^2\kanan). $$

Pada prinsipnya, sudah jelas tanda $H$ yang mana. Karena tidak ada titik $M_1$ atau $M_2$ yang bertepatan dengan titik asal, maka $y^2+x^2>0$. Oleh karena itu, tanda $H$ berlawanan dengan tanda $\lambda$. Anda juga dapat menyelesaikan perhitungan:

$$ \begin(aligned) &H(M_1)=-8\cdot\left(-\frac(1)(2)\right)\cdot\left(3^2+1^2\right)=40;\ \ &H(M_2)=-8\cdot\frac(1)(2)\cdot\left((-3)^2+(-1)^2\kanan)=-40. \end(selaras) $$

Pertanyaan tentang sifat ekstrem pada titik-titik stasioner $M_1(1;3)$ dan $M_2(-1;-3)$ dapat diselesaikan tanpa menggunakan determinan $H$. Temukan tanda $d^2F$ pada setiap titik stasioner:

$$ d^2 F=F_(xx)^("")dx^2+2F_(xy)^("")dxdy+F_(yy)^("")dy^2=2\lambda \left( dx^2+dy^2\kanan) $$

Saya perhatikan bahwa notasi $dx^2$ berarti persis $dx$ dinaikkan ke pangkat kedua, yaitu. $\kiri(dx\kanan)^2$. Karenanya kita memiliki: $dx^2+dy^2>0$, jadi untuk $\lambda_1=-\frac(1)(2)$ kita mendapatkan $d^2F< 0$. Следовательно, функция имеет в точке $M_1(1;3)$ условный максимум. Аналогично, в точке $M_2(-1;-3)$ получим условный минимум функции $z(x,y)=x+3y$. Отметим, что для определения знака $d^2F$ не пришлось учитывать связь между $dx$ и $dy$, ибо знак $d^2F$ очевиден без дополнительных преобразований. В следующем примере для определения знака $d^2F$ уже будет необходимо учесть связь между $dx$ и $dy$.

Menjawab: pada titik $(-1;-3)$ fungsi memiliki minimum bersyarat, $z_(\min)=-10$. Pada titik $(1;3)$ fungsi memiliki maksimum bersyarat, $z_(\max)=10$

Contoh #2

Temukan ekstrem bersyarat dari fungsi $z(x,y)=3y^3+4x^2-xy$ pada kondisi $x+y=0$.

Cara pertama (metode pengganda Lagrange)

Menunjukkan $\varphi(x,y)=x+y$ kita membuat fungsi Lagrange: $F(x,y)=z(x,y)+\lambda \varphi(x,y)=3y^3+4x ^2 -xy+\lambda(x+y)$.

$$ \frac(\parsial F)(\parsial x)=8x-y+\lambda; \; \frac(\partial F)(\partial y)=9y^2-x+\lambda.\\ \left \( \begin(aligned) & 8x-y+\lambda=0;\\ & 9y^2-x+\ lambda=0;\\&x+y=0.\end(aligned)\right.$$

Memecahkan sistem, kita mendapatkan: $x_1=0$, $y_1=0$, $\lambda_1=0$ dan $x_2=\frac(10)(9)$, $y_2=-\frac(10)(9 )$ , $\lambda_2=-10$. Kami memiliki dua titik stasioner: $M_1(0;0)$ dan $M_2 \left(\frac(10)(9);-\frac(10)(9) \right)$. Mari kita cari tahu sifat ekstrem di setiap titik stasioner menggunakan determinan $H$.

$$ H=\kiri| \begin(array) (ccc) 0 & \varphi_(x)^(") & \varphi_(y)^(")\\ \varphi_(x)^(") & F_(xx)^("") & F_(xy)^("") \\ \varphi_(y)^(") & F_(xy)^("") & F_(yy)^("") \end(array) \right|= \kiri| \begin(array) (ccc) 0 & 1 & 1\\ 1 & 8 & -1 \\ 1 & -1 & 18th \end(array) \right|=-10-18y $$

Pada titik $M_1(0;0)$ $H=-10-18\cdot 0=-10< 0$, поэтому $M_1(0;0)$ есть точка условного минимума функции $z(x,y)=3y^3+4x^2-xy$, $z_{\min}=0$. В точке $M_2\left(\frac{10}{9};-\frac{10}{9}\right)$ $H=10 >0$, jadi pada titik ini fungsi memiliki maksimum bersyarat, $z_(\max)=\frac(500)(243)$.

Kami menyelidiki sifat ekstrem di setiap titik dengan metode yang berbeda, berdasarkan tanda $d^2F$:

$$ d^2 F=F_(xx)^("")dx^2+2F_(xy)^("")dxdy+F_(yy)^("")dy^2=8dx^2-2dxdy+ 18ydy ^2 $$

Dari persamaan kendala $x+y=0$ kita mendapatkan: $d(x+y)=0$, $dx+dy=0$, $dy=-dx$.

$$ d^2 F=8dx^2-2dxdy+18ydy^2=8dx^2-2dx(-dx)+18y(-dx)^2=(10+18y)dx^2 $$

Karena $ d^2F \Bigr|_(M_1)=10 dx^2 > 0$, maka $M_1(0;0)$ adalah titik minimum bersyarat dari fungsi $z(x,y)=3y^3+ 4x^ 2-xy$. Demikian pula, $d^2F \Bigr|_(M_2)=-10 dx^2< 0$, т.е. $M_2\left(\frac{10}{9}; -\frac{10}{9} \right)$ - точка условного максимума.

Cara kedua

Dari persamaan kendala $x+y=0$ kita peroleh: $y=-x$. Substitusikan $y=-x$ ke dalam fungsi $z(x,y)=3y^3+4x^2-xy$, kita peroleh beberapa fungsi dari variabel $x$. Mari kita nyatakan fungsi ini sebagai $u(x)$:

$$ u(x)=z(x,-x)=3\cdot(-x)^3+4x^2-x\cdot(-x)=-3x^3+5x^2. $$

Jadi, kami mengurangi masalah menemukan ekstrem bersyarat fungsi dua variabel menjadi masalah menentukan ekstrem fungsi satu variabel.

$$ u_(x)^(")=-9x^2+10x;\\ -9x^2+10x=0; \; x\cdot(-9x+10)=0;\\ x_1=0; \ ;y_1=-x_1=0;\\ x_2=\frac(10)(9);\;y_2=-x_2=-\frac(10)(9).$$

Dapat poin $M_1(0;0)$ dan $M_2\left(\frac(10)(9); -\frac(10)(9)\right)$. Penelitian selanjutnya diketahui dari mata kuliah kalkulus diferensial fungsi satu variabel. Menyelidiki tanda $u_(xx)^("")$ pada setiap titik stasioner atau memeriksa perubahan tanda $u_(x)^(")$ pada titik-titik yang ditemukan, kita mendapatkan kesimpulan yang sama seperti ketika menyelesaikan yang pertama metode. Misalnya, centang tanda $u_(xx)^("")$:

$$u_(xx)^("")=-18x+10;\\ u_(xx)^("")(M_1)=10;\;u_(xx)^("")(M_2)=- 10.$$

Karena $u_(xx)^("")(M_1)>0$, maka $M_1$ adalah titik minimum dari fungsi $u(x)$, sedangkan $u_(\min)=u(0)=0 $ . Sejak $u_(xx)^("")(M_2)<0$, то $M_2$ - точка максимума функции $u(x)$, причём $u_{\max}=u\left(\frac{10}{9}\right)=\frac{500}{243}$.

Nilai fungsi $u(x)$ di bawah kondisi koneksi yang diberikan bertepatan dengan nilai fungsi $z(x,y)$, mis. ekstrem yang ditemukan dari fungsi $u(x)$ adalah ekstrem bersyarat yang diinginkan dari fungsi $z(x,y)$.

Menjawab: pada titik $(0;0)$ fungsi memiliki minimum bersyarat, $z_(\min)=0$. Pada titik $\left(\frac(10)(9); -\frac(10)(9) \right)$ fungsi memiliki maksimum bersyarat, $z_(\max)=\frac(500)(243 )$.

Mari kita perhatikan satu contoh lagi, di mana kita mengetahui sifat ekstrem dengan menentukan tanda $d^2F$.

Contoh #3

Temukan nilai maksimum dan minimum dari fungsi $z=5xy-4$ jika variabel $x$ dan $y$ positif dan memenuhi persamaan kendala $\frac(x^2)(8)+\frac( y^2)(2) -1=0$.

Buat fungsi Lagrange: $F=5xy-4+\lambda \left(\frac(x^2)(8)+\frac(y^2)(2)-1 \right)$. Temukan titik stasioner dari fungsi Lagrange:

$$ F_(x)^(")=5y+\frac(\lambda x)(4); \; F_(y)^(")=5x+\lambda y.\\ \left \( \begin(aligned) & 5y+\frac(\lambda x)(4)=0;\\ & 5x+\lambda y=0;\\ & \frac(x^2)(8)+\frac(y^2)(2)- 1=0;\\ & x > 0; \; y > 0. \end(sejajar) \kanan.$$

Semua transformasi lebih lanjut dilakukan dengan mempertimbangkan $x > 0; \; y > 0$ (ini ditetapkan dalam kondisi masalah). Dari persamaan kedua, kita ekspresikan $\lambda=-\frac(5x)(y)$ dan substitusikan nilai yang ditemukan ke persamaan pertama: $5y-\frac(5x)(y)\cdot \frac(x)( 4)=0$ , $4y^2-x^2=0$, $x=2y$. Substitusikan $x=2y$ ke persamaan ketiga, kita dapatkan: $\frac(4y^2)(8)+\frac(y^2)(2)-1=0$, $y^2=1$, $y=1$.

Karena $y=1$, maka $x=2$, $\lambda=-10$. Sifat ekstrem pada titik $(2;1)$ ditentukan dari tanda $d^2F$.

$$ F_(xx)^("")=\frac(\lambda)(4); \; F_(xy)^("")=5; \; F_(yy)^("")=\lambda. $$

Karena $\frac(x^2)(8)+\frac(y^2)(2)-1=0$, maka:

$$ d\left(\frac(x^2)(8)+\frac(y^2)(2)-1\kanan)=0; \; d\kiri(\frac(x^2)(8) \kanan)+d\kiri(\frac(y^2)(2) \kanan)=0; \; \frac(x)(4)dx+ydy=0; \; dy=-\frac(xdx)(4y). $$

Pada prinsipnya, di sini Anda dapat langsung mengganti koordinat titik stasioner $x=2$, $y=1$ dan parameter $\lambda=-10$, sehingga diperoleh:

$$ F_(xx)^("")=\frac(-5)(2); \; F_(xy)^("")=-10; \; dy=-\frac(dx)(2).\\ d^2 F=F_(xx)^("")dx^2+2F_(xy)^("")dxdy+F_(yy)^(" ")dy^2=-\frac(5)(2)dx^2+10dx\cdot \left(-\frac(dx)(2) \right)-10\cdot \left(-\frac(dx) (2) \kanan)^2=\\ =-\frac(5)(2)dx^2-5dx^2-\frac(5)(2)dx^2=-10dx^2. $$

Namun, dalam masalah lain untuk ekstrem bersyarat, mungkin ada beberapa titik stasioner. Dalam kasus seperti itu, lebih baik untuk merepresentasikan $d^2F$ dalam bentuk umum, dan kemudian mengganti koordinat setiap titik stasioner yang ditemukan ke dalam ekspresi yang dihasilkan:

$$ d^2 F=F_(xx)^("")dx^2+2F_(xy)^("")dxdy+F_(yy)^("")dy^2=\frac(\lambda) (4)dx^2+10\cdot dx\cdot \frac(-xdx)(4y) +\lambda\cdot \left(-\frac(xdx)(4y) \right)^2=\\ =\frac (\lambda)(4)dx^2-\frac(5x)(2y)dx^2+\lambda \cdot \frac(x^2dx^2)(16y^2)=\left(\frac(\lambda )(4)-\frac(5x)(2y)+\frac(\lambda \cdot x^2)(16y^2) \kanan)\cdot dx^2 $$

Substitusikan $x=2$, $y=1$, $\lambda=-10$, kita peroleh:

$$ d^2 F=\left(\frac(-10)(4)-\frac(10)(2)-\frac(10 \cdot 4)(16) \right)\cdot dx^2=- 10dx^2. $$

Karena $d^2F=-10\cdot dx^2< 0$, то точка $(2;1)$ есть точкой условного максимума функции $z=5xy-4$, причём $z_{\max}=10-4=6$.

Menjawab: pada titik $(2;1)$ fungsi memiliki maksimum bersyarat, $z_(\max)=6$.

Pada bagian selanjutnya, kita akan mempertimbangkan penerapan metode Lagrange untuk fungsi dari sejumlah besar variabel.