Inegalitatea este două numere sau expresii matematice, legat de unul dintre semnele: > (mai mult, în caz inegalități stricte), < (меньше, в случае строгих неравенств), ≥ (больше или равно, в случае нестрогих неравенств), ≤ (меньше или равно, в случае нестрогих неравенств).

inegalitatea este liniarîn aceleaşi condiţii ca o ecuaţie: conţine variabile doar până la gradul I şi nu conţine produse ale variabilelor.

Decizie inegalități liniare iar sistemele de inegalități liniare este indisolubil legată de lor sens geometric: soluția unei inegalități liniare este un anumit semiplan, în care întregul plan este împărțit printr-o dreaptă, a cărei ecuație este dată de o inegalitate liniară. Acest semiplan și, în cazul unui sistem de inegalități liniare, o parte a planului mărginită de mai multe drepte, trebuie găsite în desen.

La rezolvarea sistemelor de inegalități liniare cu un numar mare multe variabile sunt reduse sarcini economice, în special, probleme de programare liniară, în care se solicită găsirea maximului sau minimului unei funcții.

Rezolvarea sistemelor de inegalități liniare cu orice număr de necunoscute

Să analizăm mai întâi inegalitățile liniare în plan. Se consideră o inegalitate cu două variabile și:

,

unde sunt coeficienții variabilelor (unele numere), este termenul liber (și un număr).

O inegalitate cu două necunoscute, ca o ecuație, are un număr infinit de soluții. O soluție a acestei inegalități este o pereche de numere care satisfac această inegalitate. Din punct de vedere geometric, setul de soluții ale inegalității este reprezentat ca un semiplan delimitat de o linie dreaptă

,

pe care o vom numi linia de hotar.

Pasul 1. Construiți o dreaptă care mărginește mulțimea soluțiilor inegalității liniare

Pentru a face acest lucru, trebuie să cunoașteți oricare două puncte ale acestei linii. Să găsim punctele de intersecție cu axele de coordonate. ordonata de intersectie A este zero (Figura 1). Valorile numerice de pe axele din această figură se referă la exemplul 1, pe care îl vom analiza imediat după această digresiune teoretică.

Găsim abscisa rezolvând ca sistem ecuația unei drepte cu ecuația axei.

Să găsim intersecția cu axa:

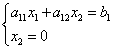
Înlocuind valoarea în prima ecuație, obținem

Unde .

Astfel, am găsit abscisa punctului A .

Să găsim coordonatele punctului de intersecție cu axa.

Punct de abscisă B este egal cu zero. Să rezolvăm ecuația liniei de limită cu ecuația axei de coordonate:

,

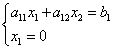
de unde coordonatele punctului B: .

Pasul 2. Desenați o linie care delimitează setul de soluții ale inegalității. Cunoscând punctele Ași B intersectia liniei de limita cu axele de coordonate, putem trasa aceasta linie. Linia dreaptă (din nou figura 1) împarte întregul plan în două părți situate la dreapta și la stânga (deasupra și dedesubt) acestei linii drepte.

Pasul 3. Determinați care dintre semiplanuri este soluția acestei inegalități. Pentru a face acest lucru, trebuie să înlocuim originea coordonatelor (0; 0) în această inegalitate. Dacă coordonatele originii satisfac inegalitatea, atunci soluția inegalității este semiplanul în care se află originea. Dacă coordonatele nu satisfac inegalitatea, atunci soluția inegalității este un semiplan care nu conține originea. Semiplanul soluției inegalității va fi notat cu linii din dreapta din interiorul semiplanului, ca în Figura 1.

Dacă rezolvăm sistemul de inegalități liniare, apoi fiecare pas este efectuat pentru fiecare dintre inegalitățile sistemului.

Exemplul 1 Rezolvați inegalitatea

Decizie. Să tragem o linie dreaptă

Înlocuind o linie dreaptă în ecuație, obținem, iar înlocuind, obținem. Prin urmare, coordonatele punctelor de intersecție cu axele vor fi A(3; 0) , B(0; 2). Desenați o linie dreaptă prin aceste puncte (din nou, Figura 1).

Alegem un semiplan de soluții ale inegalității. Pentru a face acest lucru, înlocuim coordonatele începutului (0; 0) în inegalitatea:

obținem , adică coordonatele originii satisfac această inegalitate. Prin urmare, soluția inegalității este un semiplan care conține originea, adică semiplanul stâng (sau inferior).

Dacă această inegalitate ar fi strictă, adică ar avea forma

atunci punctele liniei de frontieră nu ar fi o soluție, deoarece nu satisfac inegalitatea.

Acum luați în considerare un sistem de inegalități liniare cu două necunoscute:

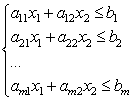
Fiecare dintre inegalitățile acestui sistem pe plan definește un semiplan. Un sistem de inegalități liniare se numește consistent dacă are cel puțin o soluție și inconsecvent dacă nu are soluții. O soluție a unui sistem de inegalități liniare este orice pereche de numere () care satisface toate inegalitățile acestui sistem.

Geometric, soluția unui sistem de inegalități liniare este mulțimea de puncte care satisfac toate inegalitățile sistemului, adică partea comună a semiplanurilor rezultate. Prin urmare, geometric caz general soluția poate fi descrisă ca un anumit poligon, într-un caz particular poate fi o linie, un segment și chiar un punct. Dacă sistemul de inegalități liniare este inconsecvent, atunci nu există un singur punct pe plan care să satisfacă toate inegalitățile sistemului.

Exemplul 2

Decizie. Deci, este necesar să se găsească un poligon de soluții ale acestui sistem de inegalități. Să construim o linie de limită pentru prima inegalitate, adică o linie, și o linie de limită pentru a doua inegalitate, adică o linie.

Facem acest lucru pas cu pas, așa cum s-a arătat în referința teoretică și în exemplul 1, mai ales că în exemplul 1 a fost construită o linie de frontieră pentru inegalitate, care este prima din acest sistem.

Semiplanurile soluției corespunzătoare inegalităților acestui sistem sunt umbrite în interior în Figura 2. o parte comună soluțiile semiplane este un unghi deschis ABC. Aceasta înseamnă că setul de puncte din plan care formează unghiul deschis ABC, este o soluție atât pentru prima cât și pentru a doua inegalități ale sistemului, adică este o soluție pentru un sistem de două inegalități liniare. Cu alte cuvinte, coordonatele oricărui punct din această mulțime satisfac ambele inegalități ale sistemului.

Exemplul 3 Rezolvați un sistem de inegalități liniare

Decizie. Să construim liniile de limită corespunzătoare inegalităților sistemului. Facem acest lucru urmând pașii dați în contextul teoretic pentru fiecare inegalitate. Acum definim semiplanurile soluțiilor pentru fiecare inegalitate (Figura 3).

Semiplanurile soluției corespunzătoare inegalităților sistemului dat sunt umbrite spre interior. Intersecția semiplanurilor soluțiilor este reprezentată, așa cum se arată în figură, sub forma unui patrulater. ABCE. Am constatat că poligonul soluție al unui sistem de inegalități liniare cu două variabile este un patrulater ABCE .

Tot ceea ce este descris mai sus despre sistemele de inegalități liniare cu două necunoscute se aplică și unui sistem de inegalități cu orice număr de necunoscute, cu singura diferență că soluția unei inegalități cu n necunoscutul va fi totalitatea n numere () care satisfac toate inegalitățile, iar în locul liniei de graniță va exista un hiperplan de graniță n-spațiul dimensional. Soluția va fi un poliedru soluție (simplex) mărginit de hiperplane.

Rezolvarea unei inegalități cu două variabile, și cu atât mai mult sisteme de inegalităţi cu două variabile, pare a fi destul de o provocare. Cu toate acestea, există un algoritm simplu care ajută ușor și fără eforturi deosebite decide la prima vedere sarcini provocatoare de asemenea fel. Să încercăm să ne dăm seama.

Să presupunem că avem o inegalitate cu două variabile de unul dintre următoarele tipuri:

y > f(x); y ≥ f(x); y< f(x); y ≤ f(x).

Pentru a descrie setul de soluții ale unei astfel de inegalități pe plan de coordonate procedați după cum urmează:

1. Construim un grafic al funcției y = f(x), care împarte planul în două regiuni.

2. Alegem oricare dintre zonele obținute și luăm în considerare în ea punct arbitrar. Verificăm satisfacabilitatea inegalității originale pentru acest punct. Dacă rezultatul testului este corect inegalitatea numerică, apoi concluzionăm că inegalitatea inițială este satisfăcută în întreaga regiune căreia îi aparține punctul selectat. Astfel, setul de soluții ale inegalității este aria căreia îi aparține punctul selectat. Dacă în urma verificării se obține o inegalitate numerică incorectă, atunci setul de soluții ale inegalității va fi a doua regiune, căreia nu îi aparține punctul selectat.

3. Dacă inegalitatea este strictă, atunci limitele regiunii, adică punctele graficului funcției y = f(x), nu sunt incluse în mulțimea de soluții, iar granița este prezentată ca o linie punctată. Dacă inegalitatea nu este strictă, atunci granițele regiunii, adică punctele graficului funcției y = f (x), sunt incluse în mulțimea soluțiilor acestei inegalități, iar granița în acest caz este înfățișat linie solida.
Acum să ne uităm la câteva probleme pe acest subiect.

Sarcina 1.

Ce set de puncte este dat de inegalitatea x · y ≤ 4?

Decizie.

1) Construim un grafic al ecuației x · y = 4. Pentru a face acest lucru, îl transformăm mai întâi. Este evident că x în acest caz nu se transformă în 0, deoarece altfel am avea 0 · y = 4, ceea ce nu este adevărat. Deci ne putem împărți ecuația la x. Se obține: y = 4/x. Graficul acestei funcții este o hiperbolă. Împarte întregul plan în două regiuni: cea dintre cele două ramuri ale hiperbolei și cea din afara acestora.

2) Alegem un punct arbitrar din prima regiune, fie punctul (4; 2).
Verificarea inegalității: 4 2 ≤ 4 este falsă.

Aceasta înseamnă că punctele acestei regiuni nu satisfac inegalitatea inițială. Apoi putem concluziona că setul de soluții ale inegalității va fi a doua regiune, căreia nu îi aparține punctul selectat.

3) Deoarece inegalitatea nu este strictă, trasăm cu linie continuă punctele de limită, adică punctele graficului funcției y = 4/x.

Să colorăm setul de puncte care definește inegalitatea inițială, galben (Fig. 1).

Sarcina 2.

Desenați aria definită pe planul de coordonate de către sistem
( y > x 2 + 2;
(y + x > 1;
( x 2 + y 2 ≤ 9.

Decizie.

Construirea grafică pentru a începe următoarele funcții (Fig. 2):

y \u003d x 2 + 2 - parabolă,

y + x = 1 - linie dreaptă

x 2 + y 2 \u003d 9 este un cerc.

1) y > x 2 + 2.

Luăm punctul (0; 5), care se află deasupra graficului funcției.
Verificarea inegalității: 5 > 0 2 + 2 este corectă.

Prin urmare, toate punctele situate deasupra parabolei date y = x 2 + 2 satisfac prima inegalitate a sistemului. Să le colorăm în galben.

2) y + x > 1.

Luăm punctul (0; 3), care se află deasupra graficului funcției.
Verificarea inegalității: 3 + 0 > 1 este adevărat.

Prin urmare, toate punctele situate deasupra dreptei y + x = 1 satisfac cea de-a doua inegalitate a sistemului. Să le colorăm în verde.

3) x2 + y2 ≤ 9.

Luăm un punct (0; -4), care se află în afara cercului x 2 + y 2 = 9.
Verificarea inegalității: 0 2 + (-4) 2 ≤ 9 este greșită.

Prin urmare, toate punctele aflate în afara cercului x 2 + y 2 = 9, nu satisfac a treia inegalitate a sistemului. Apoi putem concluziona că toate punctele aflate în interiorul cercului x 2 + y 2 = 9 satisfac a treia inegalitate a sistemului. Să le pictăm cu umbrire violet.

Nu uitați că, dacă inegalitatea este strictă, atunci linia de delimitare corespunzătoare trebuie trasă cu o linie punctată. Obținem următoarea imagine (Fig. 3).

(Fig. 4).

Sarcina 3.

Desenați aria definită pe planul de coordonate de către sistem:
(x 2 + y 2 ≤ 16;
(x ≥ -y;
(x 2 + y 2 ≥ 4.

Decizie.

Pentru început, construim grafice ale următoarelor funcții:

x 2 + y 2 \u003d 16 - cerc,

x \u003d -y - drept

x 2 + y 2 \u003d 4 - cerc (Fig. 5).

Acum ne ocupăm de fiecare inegalitate separat.

1) x2 + y2 ≤ 16.

Luăm punctul (0; 0), care se află în interiorul cercului x 2 + y 2 = 16.
Verificarea inegalității: 0 2 + (0) 2 ≤ 16 este corectă.

Prin urmare, toate punctele aflate în interiorul cercului x 2 + y 2 = 16 satisfac prima inegalitate a sistemului.
Să le colorăm în roșu.

Luăm punctul (1; 1), care se află deasupra graficului funcției.
Verificăm inegalitatea: 1 ≥ -1 - adevărat.

Prin urmare, toate punctele situate deasupra dreptei x = -y satisfac cea de-a doua inegalitate a sistemului. Să le colorăm în albastru.

3) x2 + y2 ≥ 4.

Luăm punctul (0; 5), care se află în afara cercului x 2 + y 2 = 4.
Verificăm inegalitatea: 0 2 + 5 2 ≥ 4 este adevărată.

Prin urmare, toate punctele din afara cercului x 2 + y 2 = 4 satisfac a treia inegalitate a sistemului. Să le colorăm în albastru.

În această problemă, toate inegalitățile nu sunt stricte, ceea ce înseamnă că trasăm toate limitele cu o linie continuă. Obținem următoarea imagine (Fig. 6).

Zona de interes este zona în care toate cele trei zone colorate se intersectează. (fig 7).

Aveti vreo intrebare? Nu sunteți sigur cum să rezolvați un sistem de inegalități cu două variabile?
Pentru a primi ajutor de la un tutor -.
Prima lecție este gratuită!

blog.site, cu copierea integrală sau parțială a materialului, este necesar un link către sursă.

Adesea este necesar să se înfățișeze pe planul de coordonate mulțimea soluțiilor unei inegalități cu două variabile. O soluție la o inegalitate cu două variabile este o pereche de valori ale acestor variabile care transformă inegalitatea dată într-o inegalitate numerică adevărată.

2 ani+ Zx< 6.

Să tragem mai întâi o linie dreaptă. Pentru a face acest lucru, scriem inegalitatea ca o ecuație 2 ani+ Zx = 6 si exprima y. Astfel, obținem: y=(6-3x)/2.

Această linie împarte setul tuturor punctelor planului de coordonate în puncte de deasupra lui și puncte de sub el.

Luați un meme din fiecare zonă punct de control, de exemplu A (1; 1) și B (1; 3)

Coordonatele punctului A satisfac inegalitatea dată 2y + 3x< 6, т. е. 2 . 1 + 3 . 1 < 6.

Coordonatele punctului B nu satisface această inegalitate 2∙3 + 3∙1< 6.

Deoarece această inegalitate poate schimba semnul pe dreapta 2y + Zx = 6, atunci inegalitatea satisface mulțimea de puncte a zonei în care se află punctul A. Să umbrim această zonă.

Astfel, am descris setul de soluții ale inegalității 2y + Zx< 6.

Exemplu

Prezentăm mulțimea de soluții la inegalitatea x 2 + 2x + y 2 - 4y + 1 > 0 pe planul de coordonate.

Mai întâi, construim un grafic al ecuației x 2 + 2x + y 2 - 4y + 1 \u003d 0. Împărțim ecuația cercului în această ecuație: (x 2 + 2x + 1) + (y 2 - 4y + 4) \u003d 4 sau (x + 1) 2 + (y - 2) 2 \u003d 2 2.

Aceasta este ecuația unui cerc centrat în punctul 0 (-1; 2) și raza R = 2. Să construim acest cerc.

Deoarece această inegalitate este strictă și punctele aflate pe cerc în sine nu satisfac inegalitatea, construim cercul cu o linie punctată.

Este ușor de verificat că coordonatele centrului O al cercului nu satisfac această inegalitate. Expresia x 2 + 2x + y 2 - 4y + 1 își schimbă semnul pe cercul construit. Atunci inegalitatea este satisfăcută de punctele situate în afara cercului. Aceste puncte sunt umbrite.

Exemplu

Să descriem pe planul de coordonate mulțimea soluțiilor inegalității

(y - x 2) (y - x - 3)< 0.

Mai întâi, să reprezentăm ecuația (y - x 2) (y - x - 3) = 0. Sunt parabola y \u003d x 2 și linia dreaptă y \u003d x + 3. Să construim aceste linii și să observăm că modificarea semnului expresiei (y - x 2) (y - x - 3) are loc numai pe aceste linii. Pentru punctul A (0; 5), determinăm semnul acestei expresii: (5-3) > 0 (adică această inegalitate nu este satisfăcută). Acum este ușor să marcați setul de puncte pentru care această inegalitate este satisfăcută (aceste zone sunt umbrite).

Algoritm pentru rezolvarea inegalităților cu două variabile

1. Reducem inegalitatea la forma f (x; y)< 0 (f (х; у) >0; f (x; y) ≤ 0; f (x; y) ≥ 0;)

2. Scriem egalitatea f (x; y) = 0

3. Recunoașteți graficele înregistrate în partea stângă.

4. Construim aceste grafice. Dacă inegalitatea este strictă (f (x; y)< 0 или f (х; у) >0), atunci - cu linii, dacă inegalitatea nu este strictă (f (x; y) ≤ 0 sau f (x; y) ≥ 0), atunci - cu o linie continuă.

5. Determinați câte părți ale graficului sunt împărțite în planul de coordonate

6. Selectați un punct de control într-una dintre aceste părți. Determinați semnul expresiei f (x; y)

7. Aranjam semne in alte parti ale planului, tinand cont de alternanta (ca prin metoda intervalelor)

8. Selectăm părțile de care avem nevoie în funcție de semnul inegalității pe care o rezolvăm și aplicăm hașura

Lasă dat ecuație cu două variabile F(x; y). Ați învățat deja cum să rezolvați astfel de ecuații analitic. Mulțimea soluțiilor unor astfel de ecuații poate fi reprezentată și sub forma unui grafic.

Graficul ecuației F(x; y) este mulțimea de puncte ale planului de coordonate xOy ale căror coordonate satisfac ecuația.

Pentru a reprezenta o ecuație cu două variabile, mai întâi exprimați variabila y în termenii variabilei x din ecuație.

Cu siguranță știți deja cum să construiți diverse grafice de ecuații cu două variabile: ax + b \u003d c este o linie dreaptă, yx \u003d k este o hiperbolă, (x - a) 2 + (y - b) 2 \u003d R 2 este un cerc a cărui rază este R, iar centrul este în punctul O(a; b).

Exemplul 1

Trasează ecuația x 2 - 9y 2 = 0.

Decizie.

Să factorizăm partea stângă a ecuației.

(x - 3y)(x+ 3y) = 0, adică y = x/3 sau y = -x/3.

Răspuns: figura 1.

Un loc aparte îl ocupă alocarea figurilor pe plan prin ecuații care conțin semnul valoare absolută, despre care vom discuta în detaliu. Luați în considerare etapele de reprezentare a ecuațiilor de forma |y| = f(x) și |y| = |f(x)|.

Prima ecuație este echivalentă cu sistemul

(f(x) ≥ 0,
(y = f(x) sau y = -f(x).

Adică, graficul său este format din grafice cu două funcții: y = f(x) și y = -f(x), unde f(x) ≥ 0.

Pentru a reprezenta graficul celei de-a doua ecuații, sunt reprezentate grafice a două funcții: y = f(x) și y = -f(x).

Exemplul 2

Trasează ecuația |y| = 2 + x.

Decizie.

Ecuația dată este echivalentă cu sistemul

(x + 2 ≥ 0,
(y = x + 2 sau y = -x - 2.

Construim un set de puncte.

Răspuns: figura 2.

Exemplul 3

Trasează ecuația |y – x| = 1.

Decizie.

Dacă y ≥ x, atunci y = x + 1, dacă y ≤ x, atunci y = x - 1.

Răspuns: figura 3.

Când construiți grafice ale ecuațiilor care conțin o variabilă sub semnul modulului, este convenabil și rațional să utilizați metoda zonei, bazat pe împărțirea planului de coordonate în părți în care fiecare expresie de submodul își păstrează semnul.

Exemplul 4

Trasează ecuația x + |x| + y + |y| = 2.

Decizie.

LA acest exemplu semnul fiecărei expresii submodulului depinde de sfert de coordonate.

1) În primul cadran de coordonate x ≥ 0 și y ≥ 0. După extinderea modulului ecuația dată va arata ca:

2x + 2y = 2, iar după simplificare x + y = 1.

2) În al doilea trimestru, unde x< 0, а y ≥ 0, уравнение будет иметь вид: 0 + 2y = 2 или y = 1.

3) În trimestrul al treilea x< 0, y < 0 будем иметь: x – x + y – y = 2. Перепишем этот результат в виде уравнения 0 · x + 0 · y = 2.

4) În al patrulea trimestru, pentru x ≥ 0 și y< 0 получим, что x = 1.

Programa ecuația dată Vom construi în sferturi.

Răspuns: figura 4.

Exemplul 5

Desenați o mulțime de puncte ale căror coordonate satisfac egalitatea |x – 1| + |y – 1| = 1.

Decizie.

Zerourile expresiilor submodulului x = 1 și y = 1 împart planul de coordonate în patru regiuni. Să defalcăm modulele pe regiune. Să punem asta sub forma unui tabel.

Regiune	Semnul expresiei submodulului	Ecuația rezultată după extinderea modulului
eu	x ≥ 1 și y ≥ 1	x + y = 3
II	X< 1 и y ≥ 1	-x+y=1
III	X< 1 и y < 1	x + y = 1
IV	x ≥ 1 și y< 1	x – y = 1

Răspuns: figura 5.

Pe planul de coordonate pot fi specificate cifre și inegalităților.

Graficul inegalității cu două variabile este mulțimea tuturor punctelor planului de coordonate ale căror coordonate sunt soluții ale acestei inegalități.

Considera algoritm pentru construirea unui model pentru rezolvarea unei inegalități cu două variabile:

1. Notați ecuația corespunzătoare inegalității.
2. Trasează ecuația de la pasul 1.
3. Alegeți un punct arbitrar într-unul dintre semiplanuri. Verificați dacă coordonatele punctului selectat satisfac inegalitatea dată.
4. Desenați grafic mulțimea tuturor soluțiilor inegalității.

Luați în considerare, în primul rând, inegalitatea ax + bx + c > 0. Ecuația ax + bx + c = 0 definește o dreaptă care împarte planul în două semiplane. În fiecare dintre ele, funcția f(x) = ax + bx + c este păstrătoare de semne. Pentru a determina acest semn, este suficient să luați orice punct aparținând semiplanului și să calculați valoarea funcției în acest punct. Dacă semnul funcției coincide cu semnul inegalității, atunci acest semiplan va fi soluția inegalității.

Luați în considerare exemple de soluții grafice pentru cele mai comune inegalități cu două variabile.

1) ax + bx + c ≥ 0. Figura 6.

2) |x| ≤ a, a > 0. Figura 7.

3) x 2 + y 2 ≤ a, a > 0. Figura 8.

4) y ≥ x2. Figura 9

5) xy ≤ 1. Figura 10.

Dacă aveți întrebări sau doriți să exersați desenarea pe planul modelului a mulțimilor tuturor soluțiilor inegalităților din două variabile folosind modelare matematică, poți cheltui sesiune gratuită de 25 de minute cu tutore online dupa ce te inregistrezi. Pentru munca in continuare cu un profesor, vei avea ocazia sa alegi planul tarifar care ti se potriveste.

Aveti vreo intrebare? Nu știi cum să desenezi o figură pe planul de coordonate?
Pentru a obține ajutorul unui tutore - înregistrați-vă.
Prima lecție este gratuită!

site, cu copierea integrală sau parțială a materialului, este necesară un link către sursă.