Este un patrulater ale cărui laturi opuse sunt paralele pe perechi.

Proprietatea 1 . Orice diagonală a unui paralelogram îl împarte în două triunghiuri egale.

Dovada . Conform semnului II (colțuri încrucișate și o latură comună).

Teoremă demonstrată.

Proprietatea 2 . Într-un paralelogram, laturile opuse sunt egale, iar unghiurile opuse sunt egale.

Dovada .
De asemenea,

Teoremă demonstrată.

Proprietatea 3. Într-un paralelogram diagonal, punctul de intersecție este împărțit la jumătate.

Dovada .

Teoremă demonstrată.

Proprietatea 4 . Bisectoarea unghiului unui paralelogram, care intersectează latura opusă, îl împarte într-un triunghi isoscel și un trapez. (Ch. cuvânt - sus - doi isoscele? -ka).

Dovada .

Teoremă demonstrată.

Proprietatea 5 . Într-un paralelogram, un segment cu capete pe laturi opuse, care trece prin punctul de intersecție al diagonalelor, este tăiat în două de acest punct.

Dovada .

Teoremă demonstrată.

Proprietatea 6 . Unghiul dintre înălțimile coborâte de la vârful unghiului obtuz al paralelogramului este egal cu unghiul ascuțit al paralelogramului.

Dovada .

Teoremă demonstrată.

Proprietatea 7 . Suma unghiurilor unui paralelogram adiacent unei laturi este de 180°.

Dovada .

Teoremă demonstrată.

Construcția bisectoarei unui unghi. Proprietățile bisectoarei unui triunghi.

1) Construiți o rază arbitrară DE.

2) Pe o rază dată, construiți un cerc arbitrar cu un centru la vârf și același
centrat la începutul razei construite.

3) F și G - punctele de intersecție ale cercului cu laturile unghiului dat, H - punctul de intersecție al cercului cu raza construită

Construiți un cerc cu centrul în punctul H și raza egală cu FG.

5) I - punctul de intersecție al cercurilor grinzii construite.

6) Desenați o linie prin vârf și I.

IDH - unghi necesar.
)

Proprietatea 1 . Bisectoarea unghiului unui triunghi împarte latura opusă proporțional cu laturile adiacente.

Dovada . Fie x, y segmente ale laturii c. Continuăm raza BC. Pe raza BC, trasăm un segment CK din C egal cu AC.

Dovada

Să desenăm mai întâi diagonala AC. Se obțin două triunghiuri: ABC și ADC.

Deoarece ABCD este un paralelogram, este adevărat:

AD || BC \Rightarrow \angle 1 = \angle 2 ca întins peste cap.

AB || CD \Rightarrow \angle3 = \angle 4 ca întins peste cap.

Prin urmare, \triangle ABC = \triangle ADC (prin a doua caracteristică: iar AC este comun).

Și, prin urmare, \triangle ABC = \triangle ADC , apoi AB = CD și AD = BC .

Dovedit!

2. Unghiurile opuse sunt identice.

Dovada

Conform dovezii proprietăți 1 Noi stim aia \angle 1 = \angle 2, \angle 3 = \angle 4. Deci suma unghiurilor opuse este: \angle 1 + \angle 3 = \angle 2 + \angle 4. Considerând că \triangle ABC = \triangle ADC obținem \angle A = \angle C , \angle B = \angle D .

Dovedit!

3. Diagonalele sunt tăiate în două de punctul de intersecție.

Dovada

Să desenăm o altă diagonală.

De proprietatea 1știm că laturile opuse sunt identice: AB = CD . Încă o dată observăm unghiurile egale situate transversal.

Astfel, se poate observa că \triangle AOB = \triangle COD după al doilea semn de egalitate a triunghiurilor (două unghiuri și o latură între ele). Adică BO = OD (opus \angle 2 și \angle 1 ) și AO = OC (opus \angle 3 și respectiv \angle 4).

Dovedit!

Caracteristicile paralelogramului

Dacă în problema dvs. este prezent un singur semn, atunci figura este un paralelogram și puteți utiliza toate proprietățile acestei figuri.

Pentru o mai bună memorare, rețineți că semnul paralelogramului va răspunde la următoarea întrebare − "cum sa aflu?". Adică, cum să afli că o cifră dată este un paralelogram.

1. Un paralelogram este un patrulater ale cărui două laturi sunt egale și paralele.

AB=CD; AB || CD \Rightarrow ABCD este un paralelogram.

Dovada

Să luăm în considerare mai detaliat. De ce AD ​​|| BC?

\triunghi ABC = \triunghi ADC de proprietatea 1: AB = CD , AC este comun și \angle 1 = \angle 2 ca transversal cu AB și CD paralel și secant AC .

Dar dacă \triangle ABC = \triangle ADC , atunci \angle 3 = \angle 4 (se află vizavi de AB și, respectiv, CD). Și prin urmare AD || BC (\angle 3 și \angle 4 - întins în față sunt de asemenea egale).

Primul semn este corect.

2. Un paralelogram este un patrulater ale cărui laturi opuse sunt egale.

AB = CD , AD = BC \Rightarrow ABCD este un paralelogram.

Dovada

Să luăm în considerare această caracteristică. Să desenăm din nou diagonala AC.

De proprietatea 1\triangle ABC = \triangle ACD .

Rezultă că: \angle 1 = \angle 2 \Rightarrow AD || î.Hrși \angle 3 = \angle 4 \Rightarrow AB || CD, adică ABCD este un paralelogram.

Al doilea semn este corect.

3. Un paralelogram este un patrulater ale cărui unghiuri opuse sunt egale.

\angle A = \angle C , \angle B = \angle D \Rightarrow ABCD- paralelogram.

Dovada

2 \alpha + 2 \beta = 360^(\circ)(deoarece ABCD este un patrulater, iar \angle A = \angle C , \angle B = \angle D prin convenție).

Deci \alpha + \beta = 180^(\circ) . Dar \alpha și \beta sunt interne unilaterale la secanta AB .

Și faptul că \alpha + \beta = 180^(\circ) înseamnă și că AD || î.Hr.

În același timp, \alpha și \beta sunt interne unilaterale cu un AD secant . Și asta înseamnă AB || CD.

Al treilea semn este corect.

4. Un paralelogram este un patrulater ale cărui diagonale sunt tăiate în două de punctul de intersecție.

AO=OC; BO = OD \Rightarrow paralelogram.

Dovada

BO=OD; AO = OC , \angle 1 = \angle 2 ca verticală \Rightarrow \triangle AOB = \triangle COD, \Rightarrow \angle 3 = \angle 4și \Rightarrow AB || CD.

În mod similar BO = OD ; AO=OC, \angle 5 = \angle 6 \Rightarrow \triangle AOD = \triangle BOC \Rightarrow \angle 7 = \angle 8și \Rightarrow AD || î.Hr.

Al patrulea semn este corect.

Subiectul lecției

• Proprietățile diagonalelor unui paralelogram.

Obiectivele lecției

• Familiarizați-vă cu noi definiții și amintiți-vă unele deja studiate.
• Formulați și demonstrați proprietatea diagonalelor unui paralelogram.
• Învață să aplici proprietățile formelor în rezolvarea problemelor.
• Dezvoltarea - pentru a dezvolta atenția elevilor, perseverența, perseverența, gândirea logică, vorbirea matematică.
• Educativ - prin lecție de a cultiva o atitudine atentă unul față de celălalt, de a insufla capacitatea de ascultare a camarazilor, asistență reciprocă, independență.

Obiectivele lecției

• Verificați capacitatea elevilor de a rezolva probleme.

Planul lecției

1. Introducere.
2. Repetarea materialului învățat anterior.
3. Paralelogramul, proprietățile și semnele sale.
4. Exemple de sarcini.
5. Verificare personală.

Introducere

„O descoperire științifică majoră oferă o soluție la o problemă majoră, dar în soluționarea oricărei probleme există un sâmbure de descoperire.”

Proprietățile laturilor opuse ale unui paralelogram

Un paralelogram are laturile opuse egale.

Dovada.

Fie ABCD un paralelogram dat. Și lăsați diagonalele sale să se intersecteze în punctul O.
Deoarece Δ ​​AOB = Δ COD prin primul semn de egalitate al triunghiurilor (∠ AOB = ∠ COD, ca verticale, AO=OC, DO=OB, prin proprietatea diagonalelor paralelogramelor), atunci AB=CD. În mod similar, din egalitatea triunghiurilor BOC și DOA rezultă că BC=DA. Teorema a fost demonstrată.

Proprietatea unghiurilor opuse ale unui paralelogram

Un paralelogram are unghiuri opuse.

Dovada.

Fie ABCD un paralelogram dat. Și lăsați diagonalele sale să se intersecteze în punctul O.
Din proprietățile laturilor opuse ale unui paralelogram demonstrate în teorema pe Δ ABC = Δ CDA pe trei laturi (AB=CD, BC=DA din dovedit, AC este general). Din egalitatea triunghiurilor rezultă că ∠ABC = ∠CDA.
De asemenea, se demonstrează că ∠ DAB = ∠ BCD, care rezultă din ∠ ABD = ∠ CDB. Teorema a fost demonstrată.

Proprietatea diagonalelor unui paralelogram

Diagonalele unui paralelogram se intersectează, iar punctul de intersecție este bisectat.

Dovada.

Fie ABCD un paralelogram dat. Să desenăm diagonala AC. Marcam pe el mijlocul O. Pe continuarea segmentului DO, punem deoparte segmentul OB 1 egal cu DO.
După teorema anterioară, AB 1 CD este un paralelogram. Prin urmare, linia AB 1 este paralelă cu DC. Dar prin punctul A, o singură linie poate fi trasată paralelă cu DC. Prin urmare, linia AB 1 coincide cu dreapta AB.
De asemenea, se dovedește că BC 1 coincide cu BC. Deci punctul C coincide cu C 1 . paralelogramul ABCD coincide cu paralelogramul AB 1 CD. Prin urmare, diagonalele paralelogramului se intersectează și punctul de intersecție este bisectat. Teorema a fost demonstrată.

În manualele pentru școlile obișnuite (de exemplu, la Pogorelov), se demonstrează astfel: diagonalele împart paralelogramul în 4 triunghiuri. Luați în considerare o pereche și aflați - sunt egale: bazele lor sunt laturi opuse, unghiurile corespunzătoare adiacente acesteia sunt egale ca verticale cu linii paralele. Adică, segmentele diagonalelor sunt egale pe perechi. Tot.

Asta-i tot?
S-a dovedit mai sus că punctul de intersecție traversează diagonalele - dacă există. Raționamentul de mai sus nu dovedește în niciun fel existența sa. Adică, partea din teorema „diagonalele paralelogramelor se intersectează” rămâne nedovedită.

Este amuzant că această parte este mult mai greu de demonstrat. Apropo, asta rezultă dintr-un rezultat mai general: pentru orice patrulater convex, diagonalele se vor intersecta, pentru orice neconvex, nu.

Pe egalitatea triunghiurilor de-a lungul laturii și a două unghiuri adiacente acesteia (al doilea semn al egalității triunghiurilor) și altele.

Teorema privind egalitatea a două triunghiuri de-a lungul unei laturi și a două unghiuri adiacente acesteia, Thales a găsit o aplicație practică importantă. În portul Milet a fost construit un telemetru, care determină distanța până la navă pe mare. Acesta a constat din trei chei antrenate A, B și C (AB = BC) și o linie dreaptă marcată SK, perpendiculară pe CA. Când nava a apărut pe linia dreaptă SC, s-a găsit un punct D astfel încât punctele D, .B și E se aflau pe aceeași linie dreaptă. După cum reiese din desen, distanța CD la sol este distanța dorită până la navă.

Întrebări

1. Diagonalele unui pătrat sunt încrucișate de punctul de intersecție?
   
2. Diagonalele unui paralelogram sunt egale?
3. Sunt unghiurile opuse ale unui paralelogram egale?
4. Care este definiția unui paralelogram?
5. Câte caracteristici ale unui paralelogram?
   
6. Poate un romb să fie un paralelogram?
   

Lista surselor utilizate

1. Kuznetsov A. V., profesor de matematică (clasele 5-9), Kiev
2. „Examen unificat de stat 2006. Matematică. Materiale educaționale și de instruire pentru pregătirea studenților / Rosobrnadzor, ISOP - M .: Intellect-Center, 2006 "
3. Mazur K. I. „Rezolvarea principalelor probleme competitive de matematică ale colecției editate de M. I. Scanavi”
4. L. S. Atanasyan, V. F. Butuzov, S. B. Kadomtsev, E. G. Poznyak, I. I. Yudina „Geometrie, 7 - 9: un manual pentru instituțiile de învățământ”

Lucrând la lecție

Kuznetsov A.V.

Poturnak S.A.

Evgheni Petrov

Puteți ridica o întrebare despre educația modernă, puteți exprima o idee sau rezolva o problemă urgentă la Forumul Educației unde se întrunește la nivel internațional un consiliu educațional de gândire și acțiune proaspătă. După ce a creat blog, Nu numai că îți vei îmbunătăți statutul de profesor competent, ci vei aduce și o contribuție semnificativă la dezvoltarea școlii viitorului. Breasla Liderilor Educației deschide porțile specialiștilor de top și vă invită să cooperați în direcția creării celor mai bune școli din lume.

Subiecte > Matematică > Matematică Clasa a 8-a

Un paralelogram este un patrulater ale cărui laturi opuse sunt paralele, adică. se află pe linii paralele

Proprietățile paralelogramului:
Teorema 22. Laturile opuse ale unui paralelogram sunt egale.
Dovada. Desenați o diagonală AC într-un paralelogram ABCD. Triunghiurile ACD și ACB sunt congruente ca având o latură comună AC și două perechi de unghiuri egale. adiacent acestuia: ∠ CAB=∠ ACD, ∠ ASV=∠ DAC (ca unghiuri încrucișate cu drepte paralele AD și BC). Prin urmare, AB=CD și BC=AD ca laturi corespunzătoare ale triunghiurilor egale etc. Egalitatea acestor triunghiuri implică și egalitatea unghiurilor corespunzătoare ale triunghiurilor:
Teorema 23. Unghiurile opuse ale unui paralelogram sunt: ​​∠ A=∠ C și ∠ B=∠ D.
Egalitatea primei perechi provine din egalitatea triunghiurilor ABD și CBD, iar a doua - ABC și ACD.
Teorema 24. Colțurile învecinate ale unui paralelogram, de ex. unghiurile adiacente unei laturi se adaugă până la 180 de grade.
Acest lucru se datorează faptului că sunt colțuri interioare unilaterale.
Teorema 25. Diagonalele unui paralelogram se bisectează în punctul de intersecție.
Dovada. Luați în considerare triunghiurile BOC și AOD. Conform primei proprietăți, AD=BC ∠ ОАD=∠ OSV și ∠ ОDA=∠ ОВС ca fiind situate peste drepte paralele AD și BC. Prin urmare, triunghiurile BOC și AOD sunt egale ca latură și unghiuri adiacente acestuia. Prin urmare, BO=OD și AO=OC, ca laturile corespunzătoare ale triunghiurilor egale etc.

Caracteristicile paralelogramului
Teorema 26. Dacă laturile opuse ale unui patrulater sunt egale în perechi, atunci acesta este un paralelogram.
Dovada. Fie patrulaterul ABCD să aibă laturile AD și BC, AB și, respectiv, CD, egale (Fig. 2). Să desenăm diagonala AC. Triunghiul ABC și ACD au trei laturi egale. Atunci unghiurile BAC și DCA sunt egale și, prin urmare, AB este paralel cu CD. Paralelismul laturilor BC și AD rezultă din egalitatea unghiurilor CAD și DIA.
Teorema 27. Dacă unghiurile opuse ale unui patrulater sunt egale în perechi, atunci acesta este un paralelogram.
Fie ∠ A=∠ C și ∠ B=∠ D. ∠ A+∠ B+∠ C+∠ D=360 o, atunci ∠ A+∠ B=180 o iar laturile AD și BC sunt paralele (pe baza dreptelor paralele). De asemenea, dovedim paralelismul laturilor AB și CD și concluzionăm că ABCD este un paralelogram prin definiție.
Teorema 28. Dacă colțurile adiacente ale patrulaterului, i.e. unghiurile adiacente unei laturi se adaugă până la 180 de grade, atunci este un paralelogram.
Dacă unghiurile interioare unilaterale se adună până la 180 de grade, atunci liniile sunt paralele. Aceasta înseamnă că AB este o pereche de CD și BC este o pereche de AD. Un patrulater se dovedește a fi un paralelogram prin definiție.
Teorema 29. Dacă diagonalele unui patrulater sunt împărțite reciproc în punctul de intersecție în jumătate, atunci patrulaterul este un paralelogram.
Dovada. Dacă AO=OC, BO=OD, atunci triunghiurile AOD și BOC sunt egale, ca având unghiuri egale (verticale) la vârful O, închise între perechi de laturi egale. Din egalitatea triunghiurilor concluzionăm că AD și BC sunt egale. Laturile AB și CD sunt, de asemenea, egale, iar patrulaterul se dovedește a fi un paralelogram conform caracteristicii 1.
Teorema 30. Dacă un patrulater are o pereche de laturi egale, paralele, atunci este un paralelogram.
Fie laturile AB și CD paralele și egale în patrulaterul ABCD. Desenați diagonalele AC și BD. Din paralelismul acestor drepte rezultă egalitatea unghiurilor încrucișate ABO=CDO și BAO=OCD. Triunghiurile ABO și CDO sunt egale în laturi și unghiuri adiacente. Prin urmare, AO=OC, BO=OD, i.e. diagonalele punctului de intersecție sunt împărțite în jumătate și patrulaterul se dovedește a fi un paralelogram conform caracteristicii 4.

În geometrie, sunt luate în considerare cazuri speciale de paralelogram.

Conceptul de paralelogram

Definiția 1

Paralelogram este un patrulater în care laturile opuse sunt paralele între ele (Fig. 1).

Poza 1.

Un paralelogram are două proprietăți principale. Să le luăm în considerare fără dovezi.

Proprietatea 1: Laturile și unghiurile opuse ale unui paralelogram sunt, respectiv, egale între ele.

Proprietatea 2: Diagonalele desenate într-un paralelogram sunt tăiate în două de punctul lor de intersecție.

Caracteristicile paralelogramului

Luați în considerare trei caracteristici ale unui paralelogram și prezentați-le sub formă de teoreme.

Teorema 1

Dacă două laturi ale unui patrulater sunt egale între ele și, de asemenea, paralele, atunci acest patrulater va fi un paralelogram.

Dovada.

Să ni se dea un patrulater $ABCD$. În care $AB||CD$ și $AB=CD$ Să desenăm în ea o diagonală $AC$ (Fig. 2).

Figura 2.

Luați în considerare liniile paralele $AB$ și $CD$ și secantele lor $AC$. Apoi

\[\angle CAB=\angle DCA\]

ca niște colțuri transversale.

Conform criteriului $I$ pentru egalitatea triunghiurilor,

deoarece $AC$ este partea lor comună și $AB=CD$ prin presupunere. Mijloace

\[\angle DAC=\angle ACB\]

Se consideră dreptele $AD$ și $CB$ și secantele lor $AC$; prin ultima egalitate a unghiurilor încrucișate, obținem că $AD||CB$.) Prin urmare, prin definiția lui $1$, acest patrulater este un paralelogram.

Teorema a fost demonstrată.

Teorema 2

Dacă laturile opuse ale unui patrulater sunt egale, atunci acesta este un paralelogram.

Dovada.

Să ni se dea un patrulater $ABCD$. În care $AD=BC$ și $AB=CD$. Să desenăm în ea o diagonală $AC$ (Fig. 3).

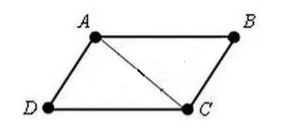
Figura 3

Deoarece $AD=BC$, $AB=CD$ și $AC$ este o latură comună, atunci prin testul de egalitate triunghi $III$,

\[\triunghi DAC=\triunghi ACB\]

\[\angle DAC=\angle ACB\]

Luați în considerare liniile $AD$ și $CB$ și secantele lor $AC$, prin ultima egalitate a unghiurilor încrucișate obținem acel $AD||CB$. Prin urmare, după definiția lui $1$, acest patrulater este un paralelogram.

\[\angle DCA=\angle CAB\]

Luați în considerare liniile $AB$ și $CD$ și secantele lor $AC$, prin ultima egalitate a unghiurilor încrucișate obținem acel $AB||CD$. Prin urmare, după Definiția 1, acest patrulater este un paralelogram.

Teorema a fost demonstrată.

Teorema 3

Dacă diagonalele desenate într-un patrulater sunt împărțite în două părți egale prin punctul lor de intersecție, atunci acest patrulater este un paralelogram.

Dovada.

Să ni se dea un patrulater $ABCD$. Să desenăm în ea diagonalele $AC$ și $BD$. Lasă-le să se intersecteze în punctul $O$ (Fig. 4).

Figura 4

Deoarece, după condiția $BO=OD,\ AO=OC$, și unghiurile $\angle COB=\angle DOA$ sunt verticale, atunci, prin testul de egalitate triunghi $I$,

\[\triunghi BOC=\triunghi AOD\]

\[\angle DBC=\angle BDA\]

Luați în considerare liniile $BC$ și $AD$ și secantele lor $BD$, prin ultima egalitate a unghiurilor încrucișate obținem acel $BC||AD$. De asemenea, $BC=AD$. Prin urmare, după teorema $1$, acest patrulater este un paralelogram.