Solution of logarithmic equations. Part 1.
Logarithmic equation called an equation in which the unknown is contained under the sign of the logarithm (in particular, in the base of the logarithm).
Protozoa logarithmic equation looks like:
Solving any logarithmic equation involves the transition from logarithms to expressions under the sign of logarithms. However, this action expands the scope allowed values equations and can lead to the appearance extraneous roots. To avoid the appearance of extraneous roots you can do it in one of three ways:
1. Make an equivalent transition from the original equation to a system including


depending on which inequality or easier.
If the equation contains an unknown at the base of the logarithm:
then we go to the system:

2. Separately find the range of admissible values of the equation, then solve the equation and check if the solutions found satisfy the equation.
3. Solve the equation, and then do a check: substitute the found solutions into the original equation, and check if we get the correct equality.
A logarithmic equation of any level of complexity always eventually reduces to the simplest logarithmic equation.
All logarithmic equations can be divided into four types:
1 . Equations that contain logarithms to the first power only. With the help of transformations and use, they are reduced to the form
Example. Let's solve the equation:
Equate the expressions under the sign of the logarithm:
Let's check if our root of the equation satisfies:
Yes, it satisfies.
Answer: x=5
2 . Equations that contain logarithms to a power other than 1 (in particular, in the denominator of a fraction). These equations are solved using introducing a change of variable.
Example. Let's solve the equation:
Let's find the ODZ equation:
The equation contains logarithms squared, so it is solved using a change of variable.
Important! Before introducing a replacement, you need to "pull" the logarithms that are part of the equation into "bricks" using the properties of logarithms.
When "pulling" logarithms, it is important to apply the properties of logarithms very carefully:
In addition, there is one more subtle place here, and in order to avoid a common mistake, we will use an intermediate equality: we write the degree of the logarithm in this form:
Likewise,
We substitute the obtained expressions into the original equation. We get:
Now we see that the unknown is contained in the equation as part of . We introduce the replacement: . Since it can take any real value, we do not impose any restrictions on the variable.
The final videos of a long series of lessons on solving logarithmic equations. This time we will work primarily with the logarithm ODZ - it is precisely because of the incorrect accounting (or even ignoring) of the domain of definition that most errors occur when solving such problems.
In this short video tutorial, we will analyze the application of the addition and subtraction formulas for logarithms, as well as deal with fractional rational equations, which many students also have problems with.
What will be discussed? Main formula, which I would like to deal with, looks like this:
log a (f g ) = log a f + log a g
This is the standard transition from the product to the sum of logarithms and vice versa. You probably know this formula from the very beginning of the study of logarithms. However, there is one hitch here.
As long as the variables a , f and g are ordinary numbers, there are no problems. This formula works great.
However, as soon as functions appear instead of f and g, the problem of expanding or narrowing the domain of definition arises, depending on which way to convert. Judge for yourself: in the logarithm written on the left, the domain of definition is as follows:
fg > 0
But in the sum written on the right, the domain of definition is already somewhat different:
f > 0
g > 0
This set of requirements is more stringent than the original one. In the first case, we will be satisfied with the option f< 0, g < 0 (ведь их произведение положительное, поэтому неравенство fg >0 is being executed).
Thus, when passing from the left construction to the right one, the domain of definition becomes narrower. If at first we had a sum, and we rewrite it as a product, then the domain of definition is expanded.
In other words, in the first case, we could lose roots, and in the second, we could get extra ones. This must be taken into account when solving real logarithmic equations.
So the first task is:
 [Figure caption]
[Figure caption] On the left we see the sum of the logarithms in the same base. Therefore, these logarithms can be added:
 [Figure caption]
[Figure caption] As you can see, on the right we have replaced zero by the formula:
a = log b b a
Let's rearrange our equation a little more:
log 4 (x − 5) 2 = log 4 1
Before us is the canonical form of the logarithmic equation, we can cross out the log sign and equate the arguments:
(x − 5) 2 = 1
|x−5| = 1
Pay attention: where did the module come from? Let me remind you that the root of the exact square is exactly equal to the modulus:
Then we decide classical equation with module:
|f| = g (g > 0) ⇒f = ±g
x − 5 = ±1 ⇒ x 1 = 5 − 1 = 4; x 2 = 5 + 1 = 6
Here are two candidates for the answer. Are they solutions to the original logarithmic equation? No way!
We have no right to leave everything just like that and write down the answer. Take a look at the step where we replace the sum of the logarithms with one logarithm of the product of the arguments. The problem is that in the original expressions we have functions. Therefore, it should be required:
x(x − 5) > 0; (x − 5)/x > 0.
When we transformed the product, getting an exact square, the requirements changed:
(x − 5) 2 > 0
When is this requirement met? Yes, almost always! Except for the case when x − 5 = 0. That is, the inequality will be reduced to one punctured point:
x − 5 ≠ 0 ⇒ x ≠ 5
As you can see, there has been an expansion of the domain of definition, which we talked about at the very beginning of the lesson. Therefore, extra roots may also appear.
How to prevent the emergence of these extra roots? It's very simple: we look at our obtained roots and compare them with the domain of the original equation. Let's count:
x (x − 5) > 0
We will solve using the interval method:
x (x − 5) = 0 ⇒ x = 0; x = 5
We mark the received numbers on a straight line. All points are punctured because the inequality is strict. We take any number greater than 5 and substitute:
 [Figure caption]
[Figure caption] We are interested in the intervals (−∞; 0) ∪ (5; ∞). If we mark our roots on the segment, we will see that x = 4 does not suit us, because this root lies outside the domain of the original logarithmic equation.
We return to the population, cross out the root x \u003d 4 and write down the answer: x \u003d 6. This is the final answer to the original logarithmic equation. Everything, the task is solved.
We pass to the second logarithmic equation:
 [Figure caption]
[Figure caption] We solve it. Note that the first term is a fraction, and the second is the same fraction, but inverted. Don't be intimidated by the lgx expression - it's simple decimal logarithm, we can write:
lgx = log 10 x
Since we have two inverted fractions, I propose to introduce a new variable:
 [Figure caption]
[Figure caption] Therefore, our equation can be rewritten as follows:
t + 1/t = 2;
t + 1/t − 2 = 0;
(t 2 − 2t + 1)/t = 0;
(t − 1) 2 /t = 0.
As you can see, the numerator of the fraction is an exact square. A fraction is zero when its numerator zero, and the denominator is different from zero:
(t − 1) 2 = 0; t ≠ 0
We solve the first equation:
t − 1 = 0;
t = 1.
This value satisfies the second requirement. Therefore, it can be argued that we have completely solved our equation, but only with respect to the variable t . Now let's remember what t is:
[Figure caption]We got the ratio:
lgx = 2 lgx + 1
2 lgx − lgx = −1
logx = −1
We bring this equation to the canonical form:
lgx = lg 10 −1
x = 10 −1 = 0.1
As a result, we got the only root, which, in theory, is the solution to the original equation. However, let's still play it safe and write out the domain of the original equation:
 [Figure caption]
[Figure caption] Therefore, our root satisfies all the requirements. We have found a solution to the original logarithmic equation. Answer: x = 0.1. Problem solved.
There is only one key point in today's lesson: when using the formula for the transition from product to sum and vice versa, be sure to keep in mind that the domain of definition can narrow or expand depending on which direction the transition is made.
How to understand what is happening: contraction or expansion? Very simple. If before function were together, and now they have become separate, then there has been a narrowing of the scope of definition (because there are more requirements). If at first the functions were separate, and now they are together, then the domain of definition is expanded (less requirements are imposed on the product than on individual factors).
In view of this remark, I would like to note that the second logarithmic equation does not require these transformations at all, i.e. we do not add or multiply the arguments anywhere. However, here I would like to draw your attention to another wonderful trick that allows you to significantly simplify the solution. It's about changing a variable.
However, remember that no substitution does not free us from the scope. That is why after all the roots were found, we were not too lazy and returned to the original equation to find its ODZ.
Often when changing a variable, an annoying mistake occurs when students find the value of t and think that the solution is over. No way!
When you have found the value of t , you need to return to the original equation and see what exactly we denoted by this letter. As a result, we have to solve one more equation, which, however, will be much simpler than the original one.
This is precisely the point of introducing a new variable. We split the original equation into two intermediate ones, each of which is solved much easier.
How to solve "nested" logarithmic equations
Today we continue to study logarithmic equations and analyze constructions when one logarithm is under the sign of another logarithm. We will solve both equations using the canonical form.
Today we continue to study logarithmic equations and analyze constructions when one logarithm is under the sign of another. We will solve both equations using the canonical form. Let me remind you that if we have the simplest logarithmic equation of the form log a f (x) \u003d b, then to solve such an equation we perform next steps. First of all, we need to replace the number b :
b = log a a b
Note that a b is an argument. Similarly, in the original equation, the argument is the function f(x). Then we rewrite the equation and get this construction:
log a f(x) = log a a b
After that, we can perform the third step - get rid of the sign of the logarithm and simply write:
f(x) = a b
As a result, we get a new equation. In this case, no restrictions are imposed on the function f(x). For example, in its place can also stand logarithmic function. And then we again get a logarithmic equation, which we again reduce to the simplest and solve through the canonical form.
But enough of the lyrics. Let's solve the real problem. So task number 1:
log 2 (1 + 3 log 2 x ) = 2
As you can see, we have a simple logarithmic equation. The role of f (x) is the construction 1 + 3 log 2 x, and the number b is the number 2 (the role of a is also two). Let's rewrite this two as follows:
It is important to understand that the first two deuces came to us from the base of the logarithm, that is, if there were 5 in the original equation, then we would get that 2 = log 5 5 2. In general, the base depends solely on the logarithm, which is initially given in the problem. And in our case this number is 2.
So, we rewrite our logarithmic equation, taking into account the fact that the two, which is on the right, is actually also a logarithm. We get:
log 2 (1 + 3 log 2 x ) = log 2 4
We pass to the last step of our scheme - we get rid of the canonical form. We can say, just cross out the signs of log. However, from the point of view of mathematics, it is impossible to “cross out log” - it is more correct to say that we simply simply equate the arguments:
1 + 3 log 2 x = 4
From here it is easy to find 3 log 2 x :
3 log 2 x = 3
log 2 x = 1
We again got the simplest logarithmic equation, let's bring it back to the canonical form. To do this, we need to make the following changes:
1 = log 2 2 1 = log 2 2
Why is there a deuce at the base? Because in our canonical equation on the left is the logarithm exactly to the base 2. We rewrite the problem taking into account this fact:
log 2 x = log 2 2
Again, we get rid of the sign of the logarithm, i.e., we simply equate the arguments. We have the right to do this, because the bases are the same, and no more additional actions were performed either on the right or on the left:
That's all! Problem solved. We have found a solution to the logarithmic equation.
Note! Although the variable x is in the argument (that is, there are requirements for the domain of definition), we will not make any additional requirements.
As I said above, this check is redundant if the variable occurs in only one argument of only one logarithm. In our case, x really is only in the argument and only under one log sign. Therefore, no additional checks are required.
However, if you do not trust this method, then you can easily verify that x = 2 is indeed a root. It is enough to substitute this number into the original equation.
Let's move on to the second equation, it's a little more interesting:
log 2 (log 1/2 (2x − 1) + log 2 4) = 1
If we denote the expression inside the large logarithm by the function f (x), we get the simplest logarithmic equation with which we started today's video lesson. Therefore, it is possible to apply the canonical form, for which it is necessary to represent the unit in the form log 2 2 1 = log 2 2.
Rewriting our big equation:
log 2 (log 1/2 (2x − 1) + log 2 4) = log 2 2
We get rid of the sign of the logarithm, equating the arguments. We have the right to do this, because the bases are the same on the left and on the right. Also, note that log 2 4 = 2:
log 1/2 (2x − 1) + 2 = 2
log 1/2 (2x − 1) = 0
Before us again is the simplest logarithmic equation of the form log a f (x) \u003d b. We pass to the canonical form, i.e. we represent zero in the form log 1/2 (1/2)0 = log 1/2 1.
We rewrite our equation and get rid of the log sign by equating the arguments:
log 1/2 (2x − 1) = log 1/2 1
2x − 1 = 1
Again, we received an immediate response. No additional checks are required, because in the original equation, only one logarithm contains the function in the argument.
Therefore, no additional checks are required. We can safely say that x = 1 is the only root of this equation.
But if in the second logarithm instead of four there would be some function of x (or 2x would not be in the argument, but in the base) - then it would be necessary to check the domain of definition. Otherwise, there is a great chance of running into extra roots.
Where do these extra roots come from? This point needs to be understood very clearly. Look at the original equations: everywhere the function x is under the sign of the logarithm. Therefore, since we have written log 2 x , we automatically set the requirement x > 0. Otherwise, this record simply does not make sense.
However, as we solve the logarithmic equation, we get rid of all the signs of log and get simple constructions. There are no more restrictions here, because linear function defined for any value of x.
It is this problem, when the final function is defined everywhere and always, and the initial one is by no means everywhere and not always, that is the reason why extra roots very often appear in the solution of logarithmic equations.
But I repeat once again: this happens only in a situation where the function is either in several logarithms, or at the base of one of them. In the problems that we are considering today, there are in principle no problems with expanding the domain of definition.
Cases of different grounds
This lesson is dedicated to complex structures. The logarithms in today's equations will no longer be solved "blank" - first you need to perform some transformations.
We start solving logarithmic equations with completely different bases, which are not exact powers of each other. Don't be intimidated by such tasks - they are no more difficult to solve than the most simple designs which we have discussed above.
But before proceeding directly to the problems, let me remind you of the formula for solving the simplest logarithmic equations using the canonical form. Consider a problem like this:
log a f(x) = b
It is important that the function f (x) is just a function, and the numbers a and b should be exactly the numbers (without any variables x). Of course, literally in a minute we will also consider such cases when instead of variables a and b there are functions, but this is not about that now.
As we remember, the number b must be replaced by a logarithm in the same base a, which is on the left. This is done very simply:
b = log a a b
Of course, the words "any number b" and "any number a" mean such values that satisfy the domain of definition. In particular, in given equation we are talking only the base a > 0 and a ≠ 1.
However this requirement is performed automatically, because in the original problem there is already a logarithm in base a - it will certainly be greater than 0 and not equal to 1. Therefore, we continue the solution of the logarithmic equation:
log a f(x) = log a a b
Such a notation is called the canonical form. Its convenience is that we can immediately get rid of the log sign by equating the arguments:
f(x) = a b
It is this technique that we will now use to solve logarithmic equations with variable base. So let's go!
log 2 (x 2 + 4x + 11) = log 0.5 0.125
What's next? Someone will now say that you need to calculate the right logarithm, or reduce them to one base, or something else. And indeed, now you need to bring both bases to the same form - either 2 or 0.5. But let's learn the following rule once and for all:
If the logarithmic equation contains decimals, be sure to convert these fractions from decimal notation into the usual. Such a transformation can significantly simplify the solution.
Such a transition must be performed immediately, even before any actions and transformations are performed. Let's get a look:
log 2 (x 2 + 4x + 11) = log 1/2 1/8
What does such a record give us? We can represent 1/2 and 1/8 as a power with negative indicator:
 [Figure caption]
[Figure caption] We have the canonical form. Equate the arguments and get the classical quadratic equation:
x 2 + 4x + 11 = 8
x 2 + 4x + 3 = 0
Before us is the given quadratic equation, which is easily solved using the Vieta formulas. You should see similar calculations in high school literally orally:
(x + 3)(x + 1) = 0
x 1 = -3
x 2 = -1
That's all! The original logarithmic equation is solved. We have two roots.
Let me remind you that to define the scope in this case is not required, since the function with variable x is present in only one argument. Therefore, the scope is performed automatically.
So the first equation is solved. Let's move on to the second one:
log 0.5 (5x 2 + 9x + 2) = log 3 1/9
log 1/2 (5x 2 + 9x + 2) = log 3 9 −1
And now note that the argument of the first logarithm can also be written as a power with a negative exponent: 1/2 = 2 −1. Then you can take out the powers on both sides of the equation and divide everything by −1:
 [Figure caption]
[Figure caption] And now we have done very important step in solving a logarithmic equation. Perhaps someone did not notice something, so let me explain.
Take a look at our equation: log is on the left and right, but the base 2 logarithm is on the left, and the base 3 logarithm is on the right. whole degree two and vice versa: it is impossible to write that 2 is 3 to the integer power.
Therefore, these are logarithms with different bases, which are not reduced to each other by simple exponentiation. The only way solving such problems is to get rid of one of these logarithms. In this case, since we are still considering quite simple tasks, the logarithm on the right was simply calculated, and we got the simplest equation - exactly the one we talked about at the very beginning of today's lesson.
Let's represent the number 2, which is on the right, as log 2 2 2 = log 2 4. And then get rid of the sign of the logarithm, after which we are left with just a quadratic equation:
log 2 (5x 2 + 9x + 2) = log 2 4
5x2 + 9x + 2 = 4
5x2 + 9x − 2 = 0
Before us is the usual quadratic equation, but it is not reduced, because the coefficient at x 2 is different from unity. Therefore, we will solve it using the discriminant:
D = 81 − 4 5 (−2) = 81 + 40 = 121
x 1 = (−9 + 11)/10 = 2/10 = 1/5
x 2 \u003d (−9 - 11) / 10 \u003d -2
That's all! We found both roots, which means we got the solution to the original logarithmic equation. Indeed, in the original problem, the function with the variable x is present in only one argument. Consequently, no additional checks on the domain of definition are required - both roots that we have found certainly meet all possible restrictions.
This could be the end of today's video tutorial, but in conclusion I would like to say again: be sure to convert all decimal fractions to ordinary ones when solving logarithmic equations. In most cases, this greatly simplifies their solution.
Rarely, very rarely, there are problems in which getting rid of decimal fractions only complicates the calculations. However, in such equations, as a rule, it is initially clear that it is not necessary to get rid of decimal fractions.
In most other cases (especially if you are just starting to train in solving logarithmic equations), feel free to get rid of decimal fractions and translate them into ordinary ones. Because practice shows that in this way you will greatly simplify the subsequent solution and calculations.
Subtleties and tricks of the solution
Today we move on to more complex tasks and we will solve a logarithmic equation, which is based not on a number, but on a function.
And even if this function is linear, you will have to add to the solution scheme minor changes, the meaning of which is additional requirements superimposed on the domain of the logarithm.
Difficult tasks
This lesson will be quite long. In it, we will analyze two rather serious logarithmic equations, in the solution of which many students make mistakes. During my practice as a tutor in mathematics, I constantly encountered two types of errors:
- The appearance of extra roots due to the expansion of the domain of definition of logarithms. To avoid making such offensive mistakes, just keep a close eye on each transformation;
- Loss of roots due to the fact that the student forgot to consider some "subtle" cases - it is on such situations that we will focus today.
This last lesson dedicated to logarithmic equations. It will be long, we will analyze complex logarithmic equations. Make yourself comfortable, make yourself some tea, and we'll begin.
The first equation looks quite standard:
log x + 1 (x - 0.5) = log x - 0.5 (x + 1)
Immediately, we note that both logarithms are inverted copies of each other. Let's remember the wonderful formula:
log a b = 1/log b a
However, this formula has a number of limitations that arise if instead of the numbers a and b there are functions of the variable x:
b > 0
1 ≠ a > 0
These requirements are imposed on the base of the logarithm. On the other hand, in a fraction, we are required to have 1 ≠ a > 0, since not only is the variable a in the argument of the logarithm (hence, a > 0), but the logarithm itself is in the denominator of the fraction. But log b 1 = 0, and the denominator must be non-zero, so a ≠ 1.
So, the restrictions on the variable a are preserved. But what happens to the variable b ? On the one hand, b > 0 follows from the base, on the other hand, the variable b ≠ 1, because the base of the logarithm must be different from 1. In total, it follows from the right side of the formula that 1 ≠ b > 0.
But here's the problem: the second requirement (b ≠ 1) is missing from the first inequality on the left logarithm. In other words, when performing this transformation, we must check separately that the argument b is different from one!
Here, let's check it out. Let's apply our formula:
 [Figure caption]
[Figure caption] 1 ≠ x - 0.5 > 0; 1 ≠ x + 1 > 0
So we got that already from the original logarithmic equation it follows that both a and b must be greater than 0 and not equal to 1. So, we can easily flip the logarithmic equation:

I propose to introduce a new variable:
log x + 1 (x − 0.5) = t
In this case, our construction will be rewritten as follows:
(t 2 − 1)/t = 0
Note that in the numerator we have the difference of squares. We reveal the difference of squares using the abbreviated multiplication formula:
(t − 1)(t + 1)/t = 0
A fraction is zero when its numerator is zero and its denominator is non-zero. But the numerator contains the product, so we equate each factor to zero:
t1 = 1;
t2 = −1;
t ≠ 0.
As you can see, both values of the variable t suit us. However, the solution does not end there, because we need to find not t , but the value of x . We return to the logarithm and get:
log x + 1 (x − 0.5) = 1;
log x + 1 (x − 0.5) = −1.
Let's bring each of these equations to canonical form:
log x + 1 (x − 0.5) = log x + 1 (x + 1) 1
log x + 1 (x − 0.5) = log x + 1 (x + 1) −1
We get rid of the sign of the logarithm in the first case and equate the arguments:
x − 0.5 = x + 1;
x - x \u003d 1 + 0.5;
Such an equation has no roots, therefore, the first logarithmic equation also has no roots. But with the second equation, everything is much more interesting:
(x − 0.5)/1 = 1/(x + 1)
We solve the proportion - we get:
(x − 0.5)(x + 1) = 1
I remind you that when solving logarithmic equations, it is much more convenient to give all common decimal fractions, so let's rewrite our equation as follows:
(x − 1/2)(x + 1) = 1;
x 2 + x - 1/2x - 1/2 - 1 = 0;
x 2 + 1/2x - 3/2 = 0.
Before us is the given quadratic equation, it is easily solved using the Vieta formulas:
(x + 3/2) (x − 1) = 0;
x 1 \u003d -1.5;
x2 = 1.
We got two roots - they are candidates for solving the original logarithmic equation. In order to understand what roots will really go into the answer, let's go back to the original problem. Now we'll check each of our roots to see if they match the scope:
1.5 ≠ x > 0.5; 0 ≠ x > −1.
These requirements are tantamount to a double inequality:
1 ≠ x > 0.5
From here we immediately see that the root x = −1.5 does not suit us, but x = 1 is quite satisfied. Therefore x \u003d 1 - final decision logarithmic equation.
Let's move on to the second task:
log x 25 + log 125 x 5 = log 25 x 625
At first glance, it may seem that all logarithms different grounds and various arguments. What to do with such structures? First of all, note that the numbers 25, 5, and 625 are powers of 5:
25 = 5 2 ; 625 = 5 4
And now we will use the remarkable property of the logarithm. The fact is that you can take out the degrees from the argument in the form of factors:
log a b n = n ∙ log a b
On given transformation restrictions are also imposed in the case when there is a function in place of b. But with us b is just a number, and no additional restrictions arise. Let's rewrite our equation:
2 ∙ log x 5 + log 125 x 5 = 4 ∙ log 25 x 5
We got an equation with three terms containing the log sign. Moreover, the arguments of all three logarithms are equal.
It's time to flip the logarithms to bring them to the same base - 5. Since the variable b is a constant, there is no change in the scope. We just rewrite:
 [Figure caption]
[Figure caption] As expected, the same logarithms “crawled out” in the denominator. I suggest changing the variable:
log 5 x = t
In this case, our equation will be rewritten as follows:

Let's write out the numerator and open the brackets:
2 (t + 3) (t + 2) + t (t + 2) - 4t (t + 3) = 2 (t 2 + 5t + 6) + t 2 + 2t - 4t 2 - 12t = 2t 2 + 10t + 12 + t 2 + 2t − 4t 2 − 12t = −t 2 + 12
We return to our fraction. The numerator must be zero:
 [Figure caption]
[Figure caption] And the denominator is different from zero:
t ≠ 0; t ≠ −3; t ≠ −2
The last requirements are fulfilled automatically, since they are all "tied" to integers, and all answers are irrational.
So, fractional rational equation solved, the values of the variable t are found. We return to the solution of the logarithmic equation and remember what t is:
We bring this equation to the canonical form, we get a number with irrational degree. Don't let this confuse you - even such arguments can be equated:
 [Figure caption]
[Figure caption] We have two roots. More precisely, two candidates for answers - let's check them for compliance with the scope. Since the base of the logarithm is the variable x, we require the following:
1 ≠ x > 0;
With the same success, we assert that x ≠ 1/125, otherwise the base of the second logarithm will turn into one. Finally, x ≠ 1/25 for the third logarithm.
In total, we got four restrictions:
1 ≠ x > 0; x ≠ 1/125; x ≠ 1/25
Now the question is: do our roots meet these requirements? Certainly satisfied! Because 5 to any power will be greater than zero, and the requirement x > 0 is automatically fulfilled.
On the other hand, 1 = 5 0 , 1/25 = 5 −2 , 1/125 = 5 −3 , which means that these restrictions for our roots (which, let me remind you, have irrational number) are also satisfied, and both answers are solutions to the problem.
So we've got the final answer. Key Points There are two tasks in this one:
- Be careful when reversing the logarithm when the argument and base are reversed. Such transformations impose unnecessary restrictions on the domain of definition.
- Do not be afraid to convert logarithms: you can not only flip them, but also open them according to the sum formula and generally change them according to any formulas that you studied when solving logarithmic expressions. However, always remember that some transformations expand the scope, and some narrow it down.
As you know, when multiplying expressions with powers, their exponents always add up (a b * a c = a b + c). This mathematical law was derived by Archimedes, and later, in the 8th century, the mathematician Virasen created a table of integer indicators. It was they who served for the further discovery of logarithms. Examples of using this function can be found almost everywhere where it is required to simplify cumbersome multiplication to simple addition. If you spend 10 minutes reading this article, we will explain to you what logarithms are and how to work with them. Simple and accessible language.
Definition in mathematics
The logarithm is an expression of the following form: log a b=c, that is, the logarithm of any non-negative number(i.e. any positive) "b" to its base "a" is considered the power of "c" to which the base "a" must be raised in order to finally get the value "b". Let's analyze the logarithm using examples, let's say there is an expression log 2 8. How to find the answer? It's very simple, you need to find such a degree that from 2 to the required degree you get 8. Having done some calculations in your mind, we get the number 3! And rightly so, because 2 to the power of 3 gives the number 8 in the answer.
Varieties of logarithms
For many pupils and students, this topic seems complicated and incomprehensible, but in fact, logarithms are not so scary, the main thing is to understand their general meaning and remember their properties and some rules. There are three certain types logarithmic expressions:
- Natural logarithm ln a, where the base is the Euler number (e = 2.7).
- Decimal a, where the base is 10.
- The logarithm of any number b to the base a>1.
Each of them is decided in a standard way, which includes simplification, reduction and subsequent reduction to one logarithm using logarithmic theorems. For getting correct values logarithms, you should remember their properties and the sequence of actions in their decisions.
Rules and some restrictions
In mathematics, there are several rules-limitations that are accepted as an axiom, that is, they are not subject to discussion and are true. For example, you cannot divide numbers by zero, and it is also impossible to extract the root even degree from negative numbers. Logarithms also have their own rules, following which you can easily learn how to work even with long and capacious logarithmic expressions:
- the base "a" must always be greater than zero, and at the same time not be equal to 1, otherwise the expression will lose its meaning, because "1" and "0" to any degree are always equal to their values;
- if a > 0, then a b > 0, it turns out that "c" must be greater than zero.
How to solve logarithms?
For example, the task was given to find the answer to the equation 10 x \u003d 100. It is very easy, you need to choose such a power, raising the number ten to which we get 100. This, of course, is 10 2 \u003d 100.
Now let's imagine given expression in logarithmic form. We get log 10 100 = 2. When solving logarithms, all actions practically converge to finding the degree to which the base of the logarithm must be entered in order to obtain a given number.
For an error-free determination of the value unknown degree you need to learn how to work with a table of degrees. It looks like this:

As you can see, some exponents can be guessed intuitively if you have a technical mindset and knowledge of the multiplication table. However, for large values you need a table of degrees. It can be used even by those who do not understand anything at all in complex mathematical topics. The left column contains numbers (base a), the top row of numbers is the value of the power c, to which the number a is raised. At the intersection in the cells, the values of the numbers are determined, which are the answer (a c =b). Let's take, for example, the very first cell with the number 10 and square it, we get the value 100, which is indicated at the intersection of our two cells. Everything is so simple and easy that even the most real humanist will understand!
Equations and inequalities
It turns out that under certain conditions, the exponent is the logarithm. Therefore, any mathematical numerical expressions can be written as a logarithmic equation. For example, 3 4 =81 can be written as the logarithm of 81 to base 3, which is four (log 3 81 = 4). For negative powers the rules are the same: 2 -5 \u003d 1/32 we write in the form of a logarithm, we get log 2 (1/32) \u003d -5. One of the most fascinating sections of mathematics is the topic of "logarithms". We will consider examples and solutions of equations a little lower, immediately after studying their properties. Now let's look at what inequalities look like and how to distinguish them from equations.

An expression of the following form is given: log 2 (x-1) > 3 - it is logarithmic inequality, since the unknown value "x" is under the sign of the logarithm. And also in the expression two quantities are compared: the logarithm of the desired number in base two is greater than the number three.
The most important difference between logarithmic equations and inequalities is that equations with logarithms (for example, the logarithm of 2 x = √9) imply one or more specific numerical values, while when solving the inequality, both the range of admissible values and the discontinuity points of this function are determined. As a consequence, the answer is not a simple set individual numbers as in the answer of the equation, and a continuous series or a set of numbers.

Basic theorems about logarithms
When solving primitive tasks on finding the values of the logarithm, its properties may not be known. However, when it comes to logarithmic equations or inequalities, first of all, it is necessary to clearly understand and apply in practice all the basic properties of logarithms. We will get acquainted with examples of equations later, let's first analyze each property in more detail.
- The basic identity looks like this: a logaB =B. It only applies if a is greater than 0, not equal to one, and B is greater than zero.
- The logarithm of the product can be represented in the following formula: log d (s 1 *s 2) = log d s 1 + log d s 2. Moreover, prerequisite is: d, s 1 and s 2 > 0; a≠1. You can give a proof for this formula of logarithms, with examples and a solution. Let log a s 1 = f 1 and log a s 2 = f 2 , then a f1 = s 1 , a f2 = s 2. We get that s 1 *s 2 = a f1 *a f2 = a f1+f2 (degree properties ), and further by definition: log a (s 1 *s 2)= f 1 + f 2 = log a s1 + log a s 2, which was to be proved.
- The logarithm of the quotient looks like this: log a (s 1 / s 2) = log a s 1 - log a s 2.
- The theorem in the form of a formula acquires next view: log a q b n = n/q log a b.
This formula is called "property of the degree of the logarithm". It resembles the properties of ordinary degrees, and it is not surprising, because all mathematics rests on regular postulates. Let's look at the proof.
Let log a b \u003d t, it turns out a t \u003d b. If you raise both parts to the power m: a tn = b n ;
but since a tn = (a q) nt/q = b n , hence log a q b n = (n*t)/t, then log a q b n = n/q log a b. The theorem has been proven.
Examples of problems and inequalities
The most common types of logarithm problems are examples of equations and inequalities. They are found in almost all problem books, and are also included in obligatory part math exams. For admission to the university or passing entrance examinations in mathematics, you need to know how to solve such problems correctly.

Unfortunately, there is no single plan or scheme for solving and determining the unknown value of the logarithm, however, for each mathematical inequality or the logarithmic equation can be applied certain rules. First of all, you should find out whether the expression can be simplified or reduced to general view. Simplify long logarithmic expressions You can, if you use their properties correctly. Let's get to know them soon.
When solving logarithmic equations, it is necessary to determine what kind of logarithm we have before us: an example of an expression may contain a natural logarithm or a decimal one.
Here are examples ln100, ln1026. Their solution boils down to the fact that you need to determine the degree to which the base 10 will be equal to 100 and 1026, respectively. For solutions natural logarithms need to apply logarithmic identities or their properties. Let's take a look at the solution with examples. logarithmic problems different type.

How to Use Logarithm Formulas: With Examples and Solutions
So, let's look at examples of using the main theorems on logarithms.
- The property of the logarithm of the product can be used in tasks where it is necessary to expand great importance numbers b into simpler factors. For example, log 2 4 + log 2 128 = log 2 (4*128) = log 2 512. The answer is 9.
- log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1.5 - as you can see, using the fourth property of the degree of the logarithm, we managed to solve at first glance a complex and unsolvable expression. It is only necessary to factorize the base and then take the exponent values out of the sign of the logarithm.

Tasks from the exam
Logarithms are often found in entrance exams, especially a lot of logarithmic problems in the exam ( State exam for all high school graduates). Usually these tasks are present not only in part A (the easiest test part exam), but also in part C (the most difficult and voluminous tasks). The exam implies an accurate and perfect knowledge of the topic "Natural logarithms".
Examples and problem solutions are taken from official USE options. Let's see how such tasks are solved.
Given log 2 (2x-1) = 4. Solution:
let's rewrite the expression, simplifying it a little log 2 (2x-1) = 2 2 , by the definition of the logarithm we get that 2x-1 = 2 4 , therefore 2x = 17; x = 8.5.
- All logarithms are best reduced to the same base so that the solution is not cumbersome and confusing.
- All expressions under the sign of the logarithm are indicated as positive, therefore, when taking out the exponent of the exponent of the expression, which is under the sign of the logarithm and as its base, the expression remaining under the logarithm must be positive.
Your privacy is important to us. For this reason, we have developed a Privacy Policy that describes how we use and store your information. Please read our privacy policy and let us know if you have any questions.
Collection and use of personal information
Personal information refers to data that can be used to identify or contact a specific person.
You may be asked to provide your personal information at any time when you contact us.
The following are some examples of the types of personal information we may collect and how we may use such information.
What personal information we collect:
- When you submit an application on the site, we may collect various information, including your name, phone number, address Email etc.
How we use your personal information:
- Collected by us personal information allows us to contact you and inform you about unique offers, promotions and other events and upcoming events.
- From time to time, we may use your personal information to send you important notices and communications.
- We may also use personal information for internal purposes such as auditing, data analysis and various studies to improve the services we provide and to provide you with recommendations regarding our services.
- If you enter a prize draw, contest or similar incentive, we may use the information you provide to administer such programs.
Disclosure to third parties
We do not disclose information received from you to third parties.
Exceptions:
- If necessary - in accordance with the law, judicial order, in legal proceedings, and / or based on public requests or requests from government agencies on the territory of the Russian Federation - disclose your personal information. We may also disclose information about you if we determine that such disclosure is necessary or appropriate for security, law enforcement, or other public important occasions.
- In the event of a reorganization, merger or sale, we may transfer the personal information we collect to the relevant third party successor.
Protection of personal information
We take precautions - including administrative, technical and physical - to protect your personal information from loss, theft, and misuse, as well as from unauthorized access, disclosure, alteration and destruction.
Maintaining your privacy at the company level
To ensure that your personal information is secure, we communicate privacy and security practices to our employees and strictly enforce privacy practices.
Logarithmic expressions, solution of examples. In this article, we will consider problems related to solving logarithms. The tasks raise the question of finding the value of the expression. It should be noted that the concept of the logarithm is used in many tasks and it is extremely important to understand its meaning. As for the USE, the logarithm is used when solving equations, in applied tasks, also in tasks related to the study of functions.
Here are examples to understand the very meaning of the logarithm:
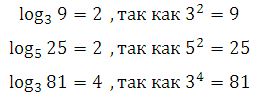

Basic logarithmic identity:

Properties of logarithms that you must always remember:

*Logarithm of the product is equal to the sum the logarithms of the factors.
* * *

* The logarithm of the quotient (fraction) is equal to the difference of the logarithms of the factors.
* * *
![]()
*Logarithm of degree is equal to the product exponent to the logarithm of its base.
* * *

*Transition to new base
* * *
More properties:

* * *
Computing logarithms is closely related to using the properties of exponents.
We list some of them:
essence given property is that when transferring the numerator to the denominator and vice versa, the sign of the exponent changes to the opposite. For example:

Consequence of this property:
* * *
![]()
When raising a power to a power, the base remains the same, but the exponents are multiplied.
* * *
As you can see, the very concept of the logarithm is simple. The main thing is what is needed good practice, which gives a certain skill. Certainly knowledge of formulas is obligatory. If the skill in the transformation of elementary logarithms is not formed, then when solving simple tasks it is easy to make a mistake.
Practice, solve the simplest examples from the math course first, then move on to more complex ones. In the future, I will definitely show how the “ugly” logarithms are solved, there will be no such ones at the exam, but they are of interest, do not miss it!
That's all! Good luck to you!
Sincerely, Alexander Krutitskikh
P.S: I would be grateful if you tell about the site in social networks.
