Types of numbers. Naturals, integers, rationals, and reals. Number is an abstraction used for quantitative characteristics objects. Numbers originated in primitive society in connection with the need of people to count objects. Over time, with the development of science, the number has become the most important mathematical concept.

For problem solving and proof various theorems you need to understand what types of numbers are. The main types of numbers include: natural numbers, integers, rational numbers, real numbers.

Integers- these are the numbers obtained with the natural counting of objects, or rather, with their numbering ("first", "second", "third" ...). A bunch of natural numbers denoted Latin letter N(can be remembered based on English word natural). It can be said that N ={1,2,3,....}

Whole numbers are numbers from the set (0, 1, -1, 2, -2, ....). This set consists of three parts - natural numbers, negative integers (the opposite of natural numbers) and the number 0 (zero). Integers are denoted by a Latin letter Z. It can be said that Z={...,-3,-2,-1,0,1,2,3,....}.

Rational numbers are numbers that can be represented as a fraction, where m is an integer and n is a natural number. In this case, the number m is called numerator, and the number n - denominator fractions. Such a fraction should be understood as the result of dividing m by n, even if it cannot be completely divided. The Latin letter is used to denote rational numbers Q. Q={... ;-3;-2,5;-2;-1;0; ;1;2;3;3,5....}. All natural and integer numbers are rational. Also, as examples of rational numbers, you can give: , , . AT real life rational numbers are used to count the parts of some whole but divisible objects, such as cakes or other foods that are cut into several pieces, or to roughly estimate the spatial relationships of extended objects.

Real (real) numbers are the numbers used to measure continuous quantities. A bunch of real numbers denoted by the Latin letter R. Real numbers include rational numbers and irrational numbers. Irrational numbers- these are numbers that are obtained as a result of performing various operations with rational numbers (for example, extracting a root, calculating logarithms), but are not rational. Examples of irrational numbers are , , .

Any real number can be displayed on the number line:

For the sets of numbers listed above, the following statement is true:

That is, the set of natural numbers is included in the set of integers. The set of integers is included in the set of rational numbers. And the set of rational numbers is included in the set of real numbers. This statement can be illustrated using Euler circles.

Natural numbers definition are integers positive numbers. Natural numbers are used to count objects and for many other purposes. These numbers are: 1; 2; 3; 4;...

This is a natural series of numbers.
Zero is a natural number? No, zero is not a natural number.
How many natural numbers are there? Exist infinite set natural numbers.
What is the smallest natural number? One is the smallest natural number.
What is the largest natural number? It cannot be specified, because there is an infinite set of natural numbers.

The sum of natural numbers is a natural number. So, the addition of natural numbers a and b:

The product of natural numbers is a natural number. So, the product of natural numbers a and b:

c is always a natural number.

Difference of natural numbers There is not always a natural number. If the minuend is greater than the subtrahend, then the difference of natural numbers is a natural number, otherwise it is not.

The quotient of natural numbers There is not always a natural number. If for natural numbers a and b

where c is a natural number, it means that a is evenly divisible by b. In this example, a is the dividend, b is the divisor, c is the quotient.

The divisor of a natural number is the natural number by which the first number is evenly divisible.

Every natural number is divisible by 1 and itself.

Simple natural numbers are only divisible by 1 and themselves. Here, it means that they are completely divided. Example, numbers 2; 3; 5; 7 is only divisible by 1 and itself. These are simple natural numbers.

One is not considered a prime number.

Numbers that are greater than one and that are not prime are called composite numbers. Examples composite numbers: 4; 6; 8; 9; 10

One is not considered a composite number.

The set of natural numbers is one, prime numbers and composite numbers.

The set of natural numbers is denoted by the Latin letter N.

Properties of addition and multiplication of natural numbers:

commutative property of addition

associative property additions

(a + b) + c = a + (b + c);

commutative property of multiplication

associative property of multiplication

(ab)c = a(bc);

distributive property multiplication

a (b + c) = ab + ac;

Whole numbers

Integers are natural numbers, zero and the opposite of natural numbers.

Numbers that are opposite to natural numbers are integers. negative numbers, for example: -1; -2; -3; -4;...

The set of integers is denoted by the Latin letter Z.

Rational numbers

Rational numbers are integers and fractions.

Any rational number can be represented as a periodic fraction. Examples: -1,(0); 3,(6); 0,(0);...

From the examples it is clear that any integer is periodic fraction with period zero.

Any rational number can be represented as a fraction m/n, where m integer,n natural number. Let's represent the number 3,(6) from the previous example as such a fraction: 22/6 = 3,(6);

Another example: the rational number 9 can be represented as a simple fraction as 18/2 or as 36/4.

Another example: the rational number -9 can be represented as a simple fraction as -18/2 or as -72/8.

The set of rational numbers is denoted by the Latin letter Q.

Irrational numbers

Irrational numbers are infinite non-recurring decimals.

Examples: pi = 3.141592... e = 2.718281...

Real numbers

Real numbers are all rational and all irrational numbers.

The set of real numbers is denoted by the Latin letter R.

Purpose: To know what a natural, integer, rational number, a periodic fraction is; be able to write endless decimal in the form of an ordinary, be able to perform actions with decimal and ordinary fractions.

1. To consolidate the studied material, changing the types of work, on this topic “Integer and rational numbers”.
2. Develop skills and abilities in performing actions with decimal and ordinary fractions, develop logical thinking, correct and competent mathematical speech, development of independence and confidence in their knowledge and skills when performing different types works.
3. Raise interest in mathematics by introducing different types of consolidation of the material: oral work, work with a textbook, work at the blackboard, answering questions and the ability to do introspection, independent work; stimulating and encouraging the activities of students.

I. Organizing time.
II. New topic:
"Integers and Rational Numbers".
1.Theoretical part.
2. Practical part.
3. Work according to the textbook and at the blackboard.
4. Independent work by options.
III. Outcome.
1. For questions.
IV. Homework.

During the classes

I. Organizational moment.

Emotional mood and readiness of the teacher and students for the lesson. Communication of goals and objectives.

II. New topic: “Integers and rational numbers”:

Theoretical part.

1. Initially, the number was understood only as natural numbers. Which is enough to count individual items.

Set N = (1; 2; 3...) natural numbers is closed under the operations of addition and multiplication. This means that the sum and product of natural numbers are natural numbers.

2. However, the difference of two natural numbers is no longer always a natural number.

(Give examples: 5 - 5 = 0; 5 - 7 = - 2, the numbers 0 and - 2 are not natural).

Thus, the result of subtracting two identical natural numbers leads to the concept of zero and the introduction sets of non-negative integers

Z0 = (0; 1; 2;...).

3. To make the subtraction operation feasible, enter negative integers, that is, numbers opposite to natural ones. Thus, a set of integers is obtained Z={...; -3; -2; -1; 0; 1; 2;...}.

To make the operation of division by any number not equal to zero feasible, it is necessary to add to the set of all integers the set of all positive and negative fractions. The result is set of rational numbers Q=.

When doing four arithmetic operations(except division by zero) over rational numbers, rational numbers are always obtained.

4. Every rational number can be represented as a periodic decimal fraction.

Let's remember what is periodic fraction. This is an infinite decimal fraction, in which, starting from a certain decimal place, the same digit or several digits are repeated - the period of the fraction. For example, 0.3333…= 0,(3);

1,057373…=1,05(73).

These fractions are read like this: “0 whole and 3 in the period”, “1 whole, 5 hundredths and 73 in the period”.

We write rational numbers as an infinite periodic decimal fraction:

natural number 25 = 25.00…= 25,(0);

integer -7 = -7.00…= -7,(0);

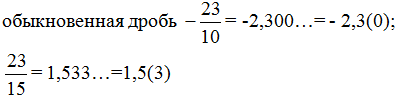
(we use the corner division algorithm).

5. The converse statement is also true: every infinite periodic decimal fraction is rational number, since it can be represented as a fraction, where m is an integer, n is a natural number.

Consider an example:

1) Let x \u003d 0.2 (18) multiplying by 10, we get 10x \u003d 2.1818 ... (You need to multiply the fraction by 10 n, where n is the number of decimal places contained in the record of this fraction up to the period: x10 n).

2) Multiplying both sides of the last equality by 100, we find

1000x = 218.1818…(Multiplying by 10 k , where k is the number of digits in the period x10 n 10 k = x10 n+k).

3) Subtracting from equality (2) equality (1), we obtain 990x = 216, x = .

Practical part.

1. Write as a decimal fraction:

1) - on the board;

3) - at the blackboard one student writes down the decision, the rest decide on the ground, then check each other;

4) - under dictation, everyone performs the task, and one speaks out loud.

2. Perform actions and write the result as a decimal fraction:

1) - on the board;

3) - under dictation, everyone performs the task, and one speaks out loud;

5) - independently with subsequent verification.

3. Write as common fraction infinite decimal:

6) -2.3(82) - the teacher shows the solution on the board, based on the algorithm.