ეს სტატია აგრძელებს სიბრტყეზე სწორი ხაზის განტოლების თემას: განიხილეთ განტოლების ისეთი ტიპი, როგორიცაა სწორი ხაზის ზოგადი განტოლება. განვსაზღვროთ თეორემა და დავამტკიცოთ იგი; მოდით გავარკვიოთ, რა არის სწორი ხაზის არასრული ზოგადი განტოლება და როგორ განვახორციელოთ გადასვლები ზოგადი განტოლებიდან სხვა ტიპის სწორი ხაზის განტოლებაზე. ჩვენ გავაერთიანებთ მთელ თეორიას ილუსტრაციებით და პრაქტიკული პრობლემების გადაწყვეტით.

Yandex.RTB R-A-339285-1

სიბრტყეზე მოცემული იყოს მართკუთხა კოორდინატთა სისტემა O x y.

თეორემა 1

პირველი ხარისხის ნებისმიერი განტოლება, რომელსაც აქვს ფორმა A x + B y + C \u003d 0, სადაც A, B, C არის რამდენიმე რეალური რიცხვი (A და B ერთდროულად არ არის ნულის ტოლი) განსაზღვრავს სწორ ხაზს მართკუთხა კოორდინატთა სისტემა სიბრტყეზე. თავის მხრივ, სიბრტყეზე მართკუთხა კოორდინატთა სისტემის ნებისმიერი ხაზი განისაზღვრება განტოლებით, რომელსაც აქვს ფორმა A x + B y + C = 0 მნიშვნელობების გარკვეული ნაკრებისთვის A, B, C.

მტკიცებულება

ეს თეორემა ორი წერტილისგან შედგება, თითოეულ მათგანს დავამტკიცებთ.

1. დავამტკიცოთ, რომ განტოლება A x + B y + C = 0 განსაზღვრავს წრფეს სიბრტყეზე.

იყოს რაღაც წერტილი M 0 (x 0 , y 0), რომლის კოორდინატები შეესაბამება A x + B y + C = 0 განტოლებას. ამრიგად: A x 0 + B y 0 + C = 0. გამოვაკლოთ განტოლებების მარცხენა და მარჯვენა მხარეებს A x + B y + C \u003d 0 განტოლების მარცხენა და მარჯვენა მხარეები A x 0 + B y 0 + C \u003d 0, მივიღებთ ახალ განტოლებას, რომელიც ჰგავს A-ს. (x - x 0) + B (y - y 0) = 0 . ის უდრის A x + B y + C = 0-ს.

მიღებული განტოლება A (x - x 0) + B (y - y 0) = 0 არის აუცილებელი და საკმარისი პირობა n → = (A, B) და M 0 M → = (x - x ვექტორების პერპენდიკულარულობისთვის. 0, y - y 0). ამრიგად, M (x, y) წერტილების სიმრავლე განსაზღვრავს მართკუთხა კოორდინატულ სისტემაში n → = (A, B) ვექტორის მიმართულების პერპენდიკულარულ სწორ ხაზს. შეგვიძლია ვივარაუდოთ, რომ ეს ასე არ არის, მაგრამ მაშინ ვექტორები n → = (A, B) და M 0 M → = (x - x 0, y - y 0) არ იქნება პერპენდიკულარული და ტოლობა A (x - x 0 ) + B (y - y 0) = 0 არ იქნება მართალი.

მაშასადამე, განტოლება A (x - x 0) + B (y - y 0) \u003d 0 განსაზღვრავს გარკვეულ ხაზს მართკუთხა კოორდინატთა სისტემაში სიბრტყეზე და, შესაბამისად, ექვივალენტური განტოლება A x + B y + C \u003d 0 განსაზღვრავს იგივე ხაზი. ამრიგად, ჩვენ დავამტკიცეთ თეორემის პირველი ნაწილი.

1. დავამტკიცოთ, რომ სიბრტყეზე მართკუთხა კოორდინატთა სისტემის ნებისმიერი სწორი ხაზი შეიძლება მივიღოთ პირველი ხარისხის A x + B y + C = 0 განტოლებით.

სიბრტყეზე მართკუთხა კოორდინატულ სისტემაში დავსახოთ სწორი ხაზი a; წერტილი M 0 (x 0 , y 0), რომლითაც გადის ეს წრფე, ისევე როგორც ამ წრფის ნორმალური ვექტორი n → = (A , B) .

ასევე არსებობდეს M (x, y) წერტილი - წრფის მცურავი წერტილი. ამ შემთხვევაში ვექტორები n → = (A , B) და M 0 M → = (x - x 0 , y - y 0) ერთმანეთის პერპენდიკულარულია და მათი სკალარული ნამრავლი არის ნული:

n → , M 0 M → = A (x - x 0) + B (y - y 0) = 0

გადავწეროთ განტოლება A x + B y - A x 0 - B y 0 = 0 , განვსაზღვროთ C: C = - A x 0 - B y 0 და ბოლოს მივიღოთ განტოლება A x + B y + C = 0 .

ასე რომ, ჩვენ დავამტკიცეთ თეორემის მეორე ნაწილი და დავამტკიცეთ მთელი თეორემა მთლიანობაში.

განმარტება 1

განტოლება, რომელიც ჰგავს A x + B y + C = 0 - ეს სწორი ხაზის ზოგადი განტოლებამართკუთხა კოორდინატულ სისტემაში სიბრტყეზეO x y.

დადასტურებული თეორემის საფუძველზე შეგვიძლია დავასკვნათ, რომ მართკუთხა კოორდინატთა სისტემაში მოცემული სწორი ხაზი და მისი ზოგადი განტოლება განუყოფლად არის დაკავშირებული. სხვა სიტყვებით რომ ვთქვათ, თავდაპირველი ხაზი შეესაბამება მის ზოგად განტოლებას; სწორი ხაზის ზოგადი განტოლება შეესაბამება მოცემულ სწორ ხაზს.

თეორემის დადასტურებიდან ასევე გამომდინარეობს, რომ კოეფიციენტები A და B x და y ცვლადებისთვის არის სწორი ხაზის ნორმალური ვექტორის კოორდინატები, რომელიც მოცემულია A x + B y + სწორი ხაზის ზოგადი განტოლებით. C = 0.

განვიხილოთ სწორი ხაზის ზოგადი განტოლების კონკრეტული მაგალითი.

მოცემული იყოს განტოლება 2 x + 3 y - 2 = 0, რომელიც შეესაბამება სწორ ხაზს მოცემულ მართკუთხა კოორდინატულ სისტემაში. ამ ხაზის ნორმალური ვექტორი არის ვექტორი n → = (2, 3). დახაზეთ მოცემული სწორი ხაზი ნახაზზე.

ასევე შეიძლება ვიკამათოთ: სწორი ხაზი, რომელსაც ნახატზე ვხედავთ, განისაზღვრება ზოგადი განტოლებით 2 x + 3 y - 2 = 0, ვინაიდან მოცემული სწორი ხაზის ყველა წერტილის კოორდინატები შეესაბამება ამ განტოლებას.

ჩვენ შეგვიძლია მივიღოთ განტოლება λ · A x + λ · B y + λ · C = 0 ზოგადი სწორი ხაზის განტოლების ორივე მხარის არანულოვანი რიცხვით λ-ზე გამრავლებით. შედეგად მიღებული განტოლება ორიგინალური ზოგადი განტოლების ექვივალენტურია, შესაბამისად, იგი აღწერს იმავე ხაზს სიბრტყეში.

განმარტება 2

სწორი ხაზის სრული ზოგადი განტოლება- A x + B y + C \u003d 0 წრფის ასეთი ზოგადი განტოლება, რომელშიც რიცხვები A, B, C არ არის ნულოვანი. წინააღმდეგ შემთხვევაში, განტოლება არის არასრული.

მოდით გავაანალიზოთ სწორი ხაზის არასრული ზოგადი განტოლების ყველა ვარიაცია.

1. როდესაც A \u003d 0, B ≠ 0, C ≠ 0, ზოგადი განტოლება ხდება B y + C \u003d 0. ასეთი არასრული ზოგადი განტოლება განსაზღვრავს სწორ ხაზს მართკუთხა კოორდინატულ სისტემაში O x y, რომელიც პარალელურია O x ღერძის, ვინაიდან x-ის ნებისმიერი რეალური მნიშვნელობისთვის, ცვლადი y მიიღებს მნიშვნელობას. - C B. სხვა სიტყვებით რომ ვთქვათ, A x + B y + C \u003d 0 წრფის ზოგადი განტოლება, როდესაც A \u003d 0, B ≠ 0, განსაზღვრავს წერტილების ადგილს (x, y), რომელთა კოორდინატები ტოლია იმავე რიცხვისა. - C B.
2. თუ A \u003d 0, B ≠ 0, C \u003d 0, ზოგადი განტოლება ხდება y \u003d 0. ასეთი არასრული განტოლება განსაზღვრავს x-ღერძს O x.
3. როდესაც A ≠ 0, B \u003d 0, C ≠ 0, ჩვენ ვიღებთ არასრულ ზოგად განტოლებას A x + C \u003d 0, რომელიც განსაზღვრავს y-ღერძის პარალელურ სწორ ხაზს.
4. მოდით A ≠ 0, B \u003d 0, C \u003d 0, მაშინ არასრული ზოგადი განტოლება მიიღებს x \u003d 0 ფორმას და ეს არის O y კოორდინატთა ხაზის განტოლება.
5. დაბოლოს, როდესაც A ≠ 0, B ≠ 0, C \u003d 0, არასრული ზოგადი განტოლება იღებს ფორმას A x + B y \u003d 0. და ეს განტოლება აღწერს სწორ ხაზს, რომელიც გადის საწყისზე. მართლაც, რიცხვების წყვილი (0, 0) შეესაბამება ტოლობას A x + B y = 0, ვინაიდან A · 0 + B · 0 = 0.

მოდით გრაფიკულად გამოვხატოთ სწორი ხაზის არასრული ზოგადი განტოლების ყველა ზემოთ ჩამოთვლილი ტიპი.

მაგალითი 1

ცნობილია, რომ მოცემული სწორი ხაზი y-ღერძის პარალელურია და გადის 2 7 , - 11 წერტილში. აუცილებელია მოცემული სწორი ხაზის ზოგადი განტოლების ჩაწერა.

გადაწყვეტილება

სწორი ხაზი y-ღერძის პარალელურად მოცემულია A x + C \u003d 0 ფორმის განტოლებით, რომელშიც A ≠ 0. პირობა ასევე განსაზღვრავს იმ წერტილის კოორდინატებს, რომლითაც გადის ხაზი და ამ წერტილის კოორდინატები შეესაბამება არასრული ზოგადი განტოლების პირობებს A x + C = 0, ე.ი. თანასწორობა სწორია:

A 2 7 + C = 0

მისგან C-ის დადგენა შესაძლებელია A-ს არა-ნულოვანი მნიშვნელობის მიცემით, მაგალითად, A = 7. ამ შემთხვევაში ვიღებთ: 7 2 7 + C \u003d 0 ⇔ C \u003d - 2. ჩვენ ვიცით ორივე კოეფიციენტი A და C, შევცვალოთ ისინი განტოლებაში A x + C = 0 და მივიღოთ წრფის საჭირო განტოლება: 7 x - 2 = 0.

პასუხი: 7 x - 2 = 0

მაგალითი 2

ნახატზე ნაჩვენებია სწორი ხაზი, აუცილებელია მისი განტოლების ჩაწერა.

გადაწყვეტილება

მოცემული ნახაზი საშუალებას გვაძლევს მარტივად ავიღოთ საწყისი მონაცემები პრობლემის გადასაჭრელად. ნახაზზე ვხედავთ, რომ მოცემული წრფე პარალელურია O x ღერძისა და გადის წერტილში (0, 3).

სწორი ხაზი, რომელიც აბსცისის პარალელურია, განისაზღვრება არასრული ზოგადი განტოლებით B y + С = 0. იპოვეთ B და C მნიშვნელობები. წერტილის კოორდინატები (0, 3), ვინაიდან მასში მოცემული სწორი ხაზი გადის, დააკმაყოფილებს B y + С = 0 სწორი ხაზის განტოლებას, მაშინ ტოლობა მოქმედებს: В · 3 + С = 0. მოდით დავაყენოთ B ნულის გარდა სხვა მნიშვნელობაზე. ვთქვათ B \u003d 1, ამ შემთხვევაში, B · 3 + C \u003d 0 ტოლობიდან შეგვიძლია ვიპოვოთ C: C \u003d - 3. B და C ცნობილი მნიშვნელობების გამოყენებით ვიღებთ სწორი ხაზის საჭირო განტოლებას: y - 3 = 0.

პასუხი: y - 3 = 0.

სიბრტყის მოცემულ წერტილში გამავალი სწორი ხაზის ზოგადი განტოლება

მოცემულმა წრფემ გაიაროს M 0 (x 0, y 0) წერტილი, მაშინ მისი კოორდინატები შეესაბამება წრფის ზოგად განტოლებას, ე.ი. ტოლობა მართალია: A x 0 + B y 0 + C = 0 . გამოვაკლოთ ამ განტოლების მარცხენა და მარჯვენა მხარეები სწორი ხაზის ზოგადი სრული განტოლების მარცხენა და მარჯვენა მხარეს. ვიღებთ: A (x - x 0) + B (y - y 0) + C \u003d 0, ეს განტოლება უდრის თავდაპირველ ზოგადს, გადის M 0 წერტილში (x 0, y 0) და აქვს ნორმალური ვექტორი n → \u003d (A, B) .

ჩვენ მიერ მიღებული შედეგი საშუალებას იძლევა დავწეროთ სწორი ხაზის ზოგადი განტოლება სწორი ხაზის ნორმალური ვექტორის ცნობილი კოორდინატებისთვის და ამ სწორი ხაზის გარკვეული წერტილის კოორდინატებისთვის.

მაგალითი 3

მოცემულია წერტილი M 0 (- 3, 4), რომლითაც გადის წრფე და ამ წრფის ნორმალური ვექტორი n → = (1 , - 2) . აუცილებელია მოცემული სწორი ხაზის განტოლების ჩაწერა.

გადაწყვეტილება

საწყისი პირობები საშუალებას გვაძლევს მივიღოთ განტოლების შედგენისთვის საჭირო მონაცემები: A \u003d 1, B \u003d - 2, x 0 \u003d - 3, y 0 \u003d 4. შემდეგ:

A (x - x 0) + B (y - y 0) = 0 ⇔ 1 (x - (- 3)) - 2 y (y - 4) = 0 ⇔ ⇔ x - 2 y + 22 = 0

პრობლემის სხვაგვარად გადაჭრა შეიძლებოდა. სწორი ხაზის ზოგად განტოლებას აქვს ფორმა A x + B y + C = 0. მოცემული ნორმალური ვექტორი საშუალებას გაძლევთ მიიღოთ A და B კოეფიციენტების მნიშვნელობები, შემდეგ:

A x + B y + C = 0 ⇔ 1 x - 2 y + C = 0 ⇔ x - 2 y + C = 0

ახლა ვიპოვოთ C-ის მნიშვნელობა ამოცანის პირობით მოცემული წერტილის M 0 (- 3, 4) გამოყენებით, რომლითაც გადის წრფე. ამ წერტილის კოორდინატები შეესაბამება განტოლებას x - 2 · y + C = 0, ე.ი. - 3 - 2 4 + C \u003d 0. აქედან გამომდინარე, C = 11. საჭირო სწორი ხაზის განტოლება იღებს ფორმას: x - 2 · y + 11 = 0 .

პასუხი: x - 2 y + 11 = 0.

მაგალითი 4

მოცემულია ხაზი 2 3 x - y - 1 2 = 0 და წერტილი M 0, რომელიც დევს ამ წრფეზე. ამ წერტილის მხოლოდ აბსციზაა ცნობილი და ის უდრის - 3-ს. აუცილებელია მოცემული პუნქტის ორდინატის განსაზღვრა.

გადაწყვეტილება

მოდით დავაყენოთ M 0 წერტილის კოორდინატების აღნიშვნა x 0 და y 0 . საწყისი მონაცემები მიუთითებს, რომ x 0 \u003d - 3. ვინაიდან წერტილი მიეკუთვნება მოცემულ წრფეს, მაშინ მისი კოორდინატები შეესაბამება ამ წრფის ზოგად განტოლებას. მაშინ შემდეგი თანასწორობა იქნება ჭეშმარიტი:

2 3 x 0 - y 0 - 1 2 = 0

განსაზღვრეთ y 0: 2 3 (- 3) - y 0 - 1 2 = 0 ⇔ - 5 2 - y 0 = 0 ⇔ y 0 = - 5 2

პასუხი: - 5 2

სწორი ხაზის ზოგადი განტოლებიდან გადასვლა სწორი ხაზის განტოლებათა სხვა ტიპებზე და პირიქით

როგორც ვიცით, სიბრტყეში ერთი და იგივე სწორი ხაზის განტოლების რამდენიმე ტიპი არსებობს. განტოლების ტიპის არჩევანი დამოკიდებულია პრობლემის პირობებზე; შესაძლებელია აირჩიოს ის, რომელიც უფრო მოსახერხებელია მისი გადაწყვეტისთვის. სწორედ აქ გამოდგება ერთი სახის განტოლების სხვა სახის განტოლებად გადაქცევის უნარი.

ჯერ განვიხილოთ A x + B y + C = 0 ფორმის ზოგადი განტოლებიდან გადასვლა კანონიკურ განტოლებაზე x - x 1 a x = y - y 1 a y .

თუ A ≠ 0, მაშინ B y ტერმინს გადავიტანთ ზოგადი განტოლების მარჯვენა მხარეს. მარცხენა მხარეს ვიღებთ A-ს ფრჩხილებიდან. შედეგად მივიღებთ: A x + C A = - B y .

ეს ტოლობა შეიძლება დაიწეროს პროპორციულად: x + C A - B = y A .

თუ B ≠ 0, ზოგადი განტოლების მარცხენა მხარეს ვტოვებთ მხოლოდ ტერმინს A x, დანარჩენებს გადავიტანთ მარჯვენა მხარეს, მივიღებთ: A x \u003d - B y - C. ფრჩხილებიდან ამოვიღებთ - B, შემდეგ: A x \u003d - B y + C B.

გადავიწეროთ ტოლობა პროპორციულად: x - B = y + C B A .

რა თქმა უნდა, არ არის საჭირო მიღებული ფორმულების დამახსოვრება. საკმარისია ვიცოდეთ მოქმედებების ალგორითმი ზოგადი განტოლებიდან კანონიკურზე გადასვლისას.

მაგალითი 5

მოცემულია 3 y - 4 = 0 წრფის ზოგადი განტოლება. ის უნდა გარდაიქმნას კანონიკურ განტოლებად.

გადაწყვეტილება

ჩვენ ვწერთ თავდაპირველ განტოლებას, როგორც 3 y - 4 = 0. შემდეგი, ჩვენ ვმოქმედებთ ალგორითმის მიხედვით: ტერმინი 0 x რჩება მარცხენა მხარეს; ხოლო მარჯვენა მხარეს ამოვიღებთ - 3 ფრჩხილიდან; ვიღებთ: 0 x = - 3 y - 4 3 .

მიღებული ტოლობა ჩავწეროთ პროპორციულად: x - 3 = y - 4 3 0 . ამრიგად, ჩვენ მივიღეთ კანონიკური ფორმის განტოლება.

პასუხი: x - 3 = y - 4 3 0.

სწორი ხაზის ზოგადი განტოლების პარამეტრულებად გადაქცევისთვის, ჯერ ხდება კანონიკურ ფორმაზე გადასვლა, შემდეგ კი სწორი ხაზის კანონიკური განტოლებიდან პარამეტრულ განტოლებაზე გადასვლა.

მაგალითი 6

სწორი ხაზი მოცემულია განტოლებით 2 x - 5 y - 1 = 0. ჩაწერეთ ამ წრფის პარამეტრული განტოლებები.

გადაწყვეტილება

მოდით გადავიდეთ ზოგადი განტოლებიდან კანონიკურზე:

2 x - 5 y - 1 = 0 ⇔ 2 x = 5 y + 1 ⇔ 2 x = 5 y + 1 5 ⇔ x 5 = y + 1 5 2

ახლა ავიღოთ მიღებული კანონიკური განტოლების ორივე ნაწილი λ-ის ტოლი, მაშინ:

x 5 = λ y + 1 5 2 = λ ⇔ x = 5 λ y = - 1 5 + 2 λ , λ ∈ R

პასუხი:x = 5 λ y = - 1 5 + 2 λ , λ ∈ R

ზოგადი განტოლება შეიძლება გარდაიქმნას სწორი ხაზის განტოლებაში y \u003d k x + b დახრილობით, მაგრამ მხოლოდ მაშინ, როდესაც B ≠ 0. მარცხენა მხარეს გადასასვლელად ვტოვებთ ტერმინს B y, დანარჩენი გადადის მარჯვნივ. ვიღებთ: B y = - A x - C . მიღებული ტოლობის ორივე ნაწილი გავყოთ B-ზე, რომელიც განსხვავდება ნულისაგან: y = - A B x - C B .

მაგალითი 7

სწორი ხაზის ზოგადი განტოლება მოცემულია: 2 x + 7 y = 0 . თქვენ უნდა გადაიყვანოთ ეს განტოლება დახრილობის განტოლებად.

გადაწყვეტილება

შევასრულოთ საჭირო მოქმედებები ალგორითმის მიხედვით:

2 x + 7 y = 0 ⇔ 7 y - 2 x ⇔ y = - 2 7 x

პასუხი: y = - 2 7 x .

სწორი ხაზის ზოგადი განტოლებიდან საკმარისია უბრალოდ მივიღოთ განტოლება x a + y b \u003d 1 ფორმის სეგმენტებში. ასეთი გადასვლისთვის გადავიტანთ C რიცხვს ტოლობის მარჯვენა მხარეს, ვყოფთ მიღებული ტოლობის ორივე ნაწილს - С-ზე და ბოლოს, x და y ცვლადების კოეფიციენტებს გადავცემთ მნიშვნელებს:

A x + B y + C = 0 ⇔ A x + B y = - C ⇔ ⇔ A - C x + B - C y = 1 ⇔ x - C A + y - C B = 1

მაგალითი 8

აუცილებელია სწორი ხაზის ზოგადი განტოლება x - 7 y + 1 2 = 0 გადავიტანოთ სწორი ხაზის განტოლებად სეგმენტებში.

გადაწყვეტილება

გადავიტანოთ 1 2 მარჯვენა მხარეს: x - 7 y + 1 2 = 0 ⇔ x - 7 y = - 1 2 .

გაყავით -1/2-ზე განტოლების ორივე მხარე: x - 7 y = - 1 2 ⇔ 1 - 1 2 x - 7 - 1 2 y = 1 .

პასუხი: x - 1 2 + y 1 14 = 1.

ზოგადად, საპირისპირო გადასვლა ასევე მარტივია: სხვა ტიპის განტოლებიდან ზოგადზე.

სწორი ხაზის განტოლება სეგმენტებში და განტოლება ფერდობთან შეიძლება ადვილად გარდაიქმნას ზოგად განტოლების მარცხენა მხარეს ყველა ტერმინის უბრალოდ შეგროვებით:

x a + y b ⇔ 1 a x + 1 b y - 1 = 0 ⇔ A x + B y + C = 0 y = k x + b ⇔ y - k x - b = 0 ⇔ A x + B y + C = 0

კანონიკური განტოლება გარდაიქმნება ზოგადში შემდეგი სქემის მიხედვით:

x - x 1 a x = y - y 1 a y ⇔ a y (x - x 1) = a x (y - y 1) ⇔ ⇔ a y x - a x y - a y x 1 + a x y 1 = 0 ⇔ A x + B y + C = 0

პარამეტრულიდან გადასასვლელად ჯერ ხდება კანონიკურზე გადასვლა, შემდეგ კი ზოგადზე:

x = x 1 + a x λ y = y 1 + a y λ ⇔ x - x 1 a x = y - y 1 a y ⇔ A x + B y + C = 0

მაგალითი 9

მოცემულია x = - 1 + 2 · λ y = 4 სწორი წრფის პარამეტრული განტოლებები. აუცილებელია ამ ხაზის ზოგადი განტოლების ჩაწერა.

გადაწყვეტილება

მოდით გადავიდეთ პარამეტრული განტოლებიდან კანონიკურზე:

x = - 1 + 2 λ y = 4 ⇔ x = - 1 + 2 λ y = 4 + 0 λ ⇔ λ = x + 1 2 λ = y - 4 0 ⇔ x + 1 2 = y - 4 0

გადავიდეთ კანონიკურიდან ზოგადზე:

x + 1 2 = y - 4 0 ⇔ 0 (x + 1) = 2 (y - 4) ⇔ y - 4 = 0

პასუხი: y - 4 = 0

მაგალითი 10

სწორი ხაზის განტოლება სეგმენტებში x 3 + y 1 2 = 1 მოცემულია. აუცილებელია განტოლების ზოგად ფორმაზე გადასვლა.

გადაწყვეტილება:

მოდით, უბრალოდ გადავიწეროთ განტოლება საჭირო ფორმით:

x 3 + y 1 2 = 1 ⇔ 1 3 x + 2 y - 1 = 0

პასუხი: 1 3 x + 2 y - 1 = 0.

სწორი ხაზის ზოგადი განტოლების შედგენა

ზემოთ ვთქვით, რომ ზოგადი განტოლება შეიძლება დაიწეროს ნორმალური ვექტორის ცნობილი კოორდინატებით და იმ წერტილის კოორდინატებით, რომლითაც გადის წრფე. ასეთი სწორი ხაზი განისაზღვრება განტოლებით A (x - x 0) + B (y - y 0) = 0 . იმავე ადგილას გავაანალიზეთ შესაბამისი მაგალითი.

ახლა მოდით შევხედოთ უფრო რთულ მაგალითებს, რომლებშიც, პირველ რიგში, აუცილებელია ნორმალური ვექტორის კოორდინატების დადგენა.

მაგალითი 11

მოცემულია წრფე პარალელურად 2 x - 3 y + 3 3 = 0 . ასევე ცნობილია წერტილი M 0 (4 , 1), რომლითაც გადის მოცემული წრფე. აუცილებელია მოცემული სწორი ხაზის განტოლების ჩაწერა.

გადაწყვეტილება

საწყისი პირობები გვეუბნება, რომ წრფეები პარალელურია, მაშინ როცა, როგორც წრფის ნორმალური ვექტორი, რომლის განტოლებაც უნდა დაიწეროს, ვიღებთ n წრფის მიმართულ ვექტორს → \u003d (2, - 3) : 2 x - 3 y + 3 3 \u003d 0. ახლა ჩვენ ვიცით ყველა საჭირო მონაცემი სწორი ხაზის ზოგადი განტოლების შესაქმნელად:

A (x - x 0) + B (y - y 0) = 0 ⇔ 2 (x - 4) - 3 (y - 1) = 0 ⇔ 2 x - 3 y - 5 = 0

პასუხი: 2 x - 3 y - 5 = 0.

მაგალითი 12

მოცემული წრფე გადის x - 2 3 = y + 4 5 წრფის პერპენდიკულარულ საწყისზე. აუცილებელია მოცემული სწორი ხაზის ზოგადი განტოლების დაწერა.

გადაწყვეტილება

მოცემული წრფის ნორმალური ვექტორი იქნება x - 2 3 = y + 4 5 წრფის ვექტორი.

შემდეგ n → = (3 , 5) . სწორი ხაზი გადის საწყისზე, ე.ი. O წერტილის გავლით (0, 0). მოდით შევადგინოთ მოცემული სწორი ხაზის ზოგადი განტოლება:

A (x - x 0) + B (y - y 0) = 0 ⇔ 3 (x - 0) + 5 (y - 0) = 0 ⇔ 3 x + 5 y = 0

უპასუხე: 3 x + 5 y = 0 .

თუ შეამჩნევთ შეცდომას ტექსტში, მონიშნეთ იგი და დააჭირეთ Ctrl+Enter

ხშირ შემთხვევაში, ფუნქციის დახატვა უფრო ადვილია, თუ პირველად დახაზავთ მრუდის ასიმპტოტებს.

განმარტება 1. ასიმპტოტებს უწოდებენ ისეთ ხაზებს, რომლებსაც ფუნქციის გრაფიკი უახლოვდება ისე, როგორც სასურველია, როდესაც ცვლადი მიდრეკილია პლუს უსასრულობისკენ ან მინუს უსასრულობისკენ.

განმარტება 2. სწორ ხაზს ეწოდება ფუნქციის გრაფიკის ასიმპტოტი, თუ მანძილი ცვლადი წერტილიდან მამ ხაზამდე ფუნქციის გრაფიკი ნულისკენ მიისწრაფვის, რადგან წერტილი განუსაზღვრელი დროით შორდება მკოორდინატების წარმოშობიდან ფუნქციის გრაფიკის რომელიმე ტოტის გასწვრივ.

არსებობს სამი სახის ასიმპტოტები: ვერტიკალური, ჰორიზონტალური და ირიბი.

ვერტიკალური ასიმპტოტები

განმარტება. პირდაპირ x = აარის ფუნქციის გრაფიკის ვერტიკალური ასიმპტოტა თუ წერტილი x = აარის მეორე ტიპის რღვევის წერტილიამ მახასიათებლისთვის.

განმარტებიდან გამომდინარეობს, რომ ხაზი x = აარის ფუნქციის გრაფიკის ვერტიკალური ასიმპტოტი ვ(x) თუ დაკმაყოფილებულია ქვემოთ ჩამოთვლილი პირობებიდან ერთი მაინც:

ამავე დროს, ფუნქცია ვ(x) შეიძლება საერთოდ არ იყოს განსაზღვრული, შესაბამისად, ამისთვის x ≥ ადა x ≤ ა .

კომენტარი:

მაგალითი 1ფუნქციის გრაფიკი წ= ლნ xაქვს ვერტიკალური ასიმპტოტი x= 0 (ანუ ემთხვევა ღერძს ოი) განსაზღვრების დომენის საზღვარზე, ვინაიდან ფუნქციის ზღვარი, როდესაც x მარჯვნივ იხრება ნულისკენ, უდრის მინუს უსასრულობას:

(ნახ. ზემოთ).

დამოუკიდებლად და შემდეგ იხილეთ გადაწყვეტილებები

მაგალითი 2იპოვეთ ფუნქციის გრაფიკის ასიმპტოტები.

მაგალითი 3იპოვეთ ფუნქციის გრაფიკის ასიმპტოტები

ჰორიზონტალური ასიმპტოტები

თუ (ფუნქციის ზღვარი, როდესაც არგუმენტი მიდრეკილია პლუს ან მინუს უსასრულობისკენ, უდრის გარკვეულ მნიშვნელობას ბ), შემდეგ წ = ბ – ჰორიზონტალური ასიმპტოტი მრუდე წ = ვ(x ) (მარჯვნივ, როცა x მიდრეკილია პლუს უსასრულობისკენ, მარცხნივ, როცა x მიდრეკილია მინუს უსასრულობისკენ და ორმხრივი, თუ ზღვრები, როდესაც x მიდრეკილია პლუს ან მინუს უსასრულობისკენ, ტოლია).

მაგალითი 5ფუნქციის გრაფიკი

ზე ა> 1-ს აქვს მარცხენა ჰორიზონტალური ასიმპტოტა წ= 0 (ანუ ემთხვევა ღერძს ოქსი), რადგან ფუნქციის ზღვარი, როდესაც "x" მიდრეკილია მინუს უსასრულობისკენ, ნულის ტოლია:

მრუდს არ აქვს მარჯვენა ჰორიზონტალური ასიმპტოტა, რადგან ფუნქციის ზღვარი, როდესაც x მიდრეკილია პლუს უსასრულობისკენ, უდრის უსასრულობას:

ირიბი ასიმპტოტები

ვერტიკალური და ჰორიზონტალური ასიმპტოტები, რომლებიც ზემოთ განვიხილეთ, კოორდინატთა ღერძების პარალელურია, ამიტომ, მათი ასაგებად, დაგვჭირდა მხოლოდ გარკვეული რიცხვი - წერტილი აბსცისაზე ან ორდინატულ ღერძზე, რომლითაც გადის ასიმპტოტი. მეტია საჭირო ირიბი ასიმპტოტისთვის - ფერდობზე კ, რომელიც გვიჩვენებს სწორი ხაზის დახრილობის კუთხეს და კვეთას ბ, რომელიც გვიჩვენებს რამდენად არის ხაზი საწყისის ზემოთ ან ქვემოთ. მათ, ვისაც არ ჰქონდა დრო დაივიწყოს ანალიტიკური გეომეტრია და მისგან - სწორი ხაზის განტოლებები, შეამჩნევს, რომ ირიბი ასიმპტოტისთვის ისინი პოულობენ ფერდობის განტოლება. ირიბი ასიმპტოტის არსებობა განისაზღვრება შემდეგი თეორემით, რომლის საფუძველზეც გვხვდება ახლად დასახელებული კოეფიციენტები.

თეორემა.მოსახვევის გასაკეთებლად წ = ვ(x) ჰქონდა ასიმპტოტი წ = kx + ბ , აუცილებელია და საკმარისია სასრული საზღვრების არსებობა კდა ბგანსახილველი ფუნქციის, როგორც ცვლადის ტენდენცია xპლუს უსასრულობას და მინუს უსასრულობას:

(1)

(2)

ამგვარად ნაპოვნი ნომრები კდა ბდა არის ირიბი ასიმპტოტის კოეფიციენტები.

პირველ შემთხვევაში (როცა x მიდრეკილია პლუს უსასრულობისკენ), მიიღება მარჯვენა ირიბი ასიმპტოტი, მეორეში (როცა x მიდრეკილია მინუს უსასრულობისკენ) მიიღება მარცხენა ასიმპტოტი. მარჯვენა ირიბი ასიმპტოტი ნაჩვენებია ნახ. ქვემოდან.

ირიბი ასიმპტოტის განტოლების პოვნისას აუცილებელია გავითვალისწინოთ x-ის ტენდენცია როგორც პლუს უსასრულობის, ასევე მინუს უსასრულობისკენ. ზოგიერთი ფუნქციისთვის, მაგალითად, წილადი რაციონალებისთვის, ეს საზღვრები ემთხვევა, მაგრამ ბევრი ფუნქციისთვის ეს ლიმიტები განსხვავებულია და მათგან მხოლოდ ერთი შეიძლება არსებობდეს.

თუ საზღვრები ემთხვევა x მიდრეკილებას პლუს უსასრულობისკენ და მინუს უსასრულობისკენ, სწორი ხაზი წ = kx + ბ არის მრუდის ორმხრივი ასიმპტოტი.

თუ ასიმპტოტის განმსაზღვრელი ზღვრებიდან ერთი მაინც წ = kx + ბ , არ არსებობს, მაშინ ფუნქციის გრაფიკს არ აქვს ირიბი ასიმპტოტი (მაგრამ შეიძლება ჰქონდეს ვერტიკალური).

ჰორიზონტალური ასიმპტოტის დანახვა ადვილია წ = ბირიბის განსაკუთრებული შემთხვევაა წ = kx + ბზე კ = 0 .

მაშასადამე, თუ მრუდს აქვს ჰორიზონტალური ასიმპტოტა რომელიმე მიმართულებით, მაშინ არ არსებობს ირიბი ასიმპტოტა ამ მიმართულებით და პირიქით.

მაგალითი 6იპოვეთ ფუნქციის გრაფიკის ასიმპტოტები

გადაწყვეტილება. ფუნქცია განსაზღვრულია მთელ რიცხვით ხაზზე გარდა x= 0, ე.ი.

მაშასადამე, რღვევის წერტილში x= 0 მრუდს შეიძლება ჰქონდეს ვერტიკალური ასიმპტოტი. მართლაც, ფუნქციის ზღვარი, როდესაც x მარცხნიდან ნულისკენ მიისწრაფვის, არის პლუს უსასრულობა:

აქედან გამომდინარე, x= 0 არის ამ ფუნქციის გრაფიკის ვერტიკალური ასიმპტოტა.

ამ ფუნქციის გრაფიკს არ აქვს ჰორიზონტალური ასიმპტოტი, რადგან ფუნქციის ზღვარი, როდესაც x მიდრეკილია პლუს უსასრულობისკენ, უდრის პლუს უსასრულობას:

მოდით გავარკვიოთ ირიბი ასიმპტოტის არსებობა:

მიიღეთ სასრული საზღვრები კ= 2 და ბ= 0. პირდაპირ წ = 2xარის ამ ფუნქციის გრაფიკის ორმხრივი ირიბი ასიმპტოტი (ნახ. მაგალითის შიგნით).

მაგალითი 7იპოვეთ ფუნქციის გრაფიკის ასიმპტოტები

გადაწყვეტილება. ფუნქციას აქვს ერთი შესვენების წერტილი x= −1. მოდით გამოვთვალოთ ცალმხრივი ლიმიტები და განვსაზღვროთ შეწყვეტის ტიპი:

დასკვნა: x= −1 არის მეორე სახის უწყვეტობის წერტილი, ამიტომ წრფე x= −1 არის ამ ფუნქციის გრაფიკის ვერტიკალური ასიმპტოტა.

ვეძებთ ირიბი ასიმპტოტებს. ვინაიდან ეს ფუნქცია ფრაქციულად რაციონალურია, ამისთვის და for-ის საზღვრები დაემთხვევა. ამრიგად, ჩვენ ვპოულობთ კოეფიციენტებს სწორი ხაზის - ირიბი ასიმპტოტის განტოლებაში ჩანაცვლებისთვის:

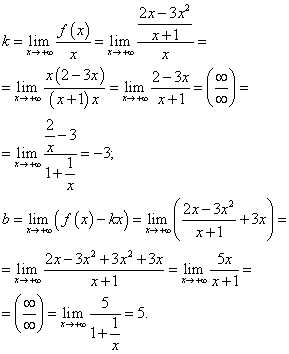
ნაპოვნი კოეფიციენტების ჩანაცვლებით სწორი ხაზის განტოლებაში დახრილობით, მივიღებთ ირიბი ასიმპტოტის განტოლებას:

წ = −3x + 5 .

ნახატზე ფუნქციის გრაფიკი მონიშნულია შინდისფრად, ასიმპტოტები კი შავით.

მაგალითი 8იპოვეთ ფუნქციის გრაფიკის ასიმპტოტები

გადაწყვეტილება. ვინაიდან ეს ფუნქცია უწყვეტია, მის გრაფიკს არ აქვს ვერტიკალური ასიმპტოტები. ჩვენ ვეძებთ ირიბი ასიმპტოტებს:

.

ამრიგად, ამ ფუნქციის გრაფიკს აქვს ასიმპტოტი წ= 0 at და არ აქვს ასიმპტოტა at.

მაგალითი 9იპოვეთ ფუნქციის გრაფიკის ასიმპტოტები

გადაწყვეტილება. პირველ რიგში, ჩვენ ვეძებთ ვერტიკალურ ასიმპტოტებს. ამისათვის ჩვენ ვპოულობთ ფუნქციის დომენს. ფუნქცია განისაზღვრება, როდესაც უტოლობა მოქმედებს და . ცვლადი ნიშანი xშეესაბამება ნიშანს. ამიტომ, განიხილეთ ეკვივალენტური უტოლობა. აქედან ვიღებთ ფუნქციის ფარგლებს: . ვერტიკალური ასიმპტოტი შეიძლება იყოს მხოლოდ ფუნქციის დომენის საზღვარზე. მაგრამ x= 0 არ შეიძლება იყოს ვერტიკალური ასიმპტოტი, რადგან ფუნქცია განსაზღვრულია x = 0 .

განვიხილოთ მარჯვენა ლიმიტი at (მარცხენა ლიმიტი არ არსებობს):

.

Წერტილი x= 2 არის მეორე სახის შეწყვეტის წერტილი, ამიტომ ხაზი x= 2 - ამ ფუნქციის გრაფიკის ვერტიკალური ასიმპტოტი.

ჩვენ ვეძებთ ირიბი ასიმპტოტებს:

Ისე, წ = x+ 1 - ამ ფუნქციის გრაფიკის ირიბი ასიმპტოტი at . ჩვენ ვეძებთ ირიბი ასიმპტოტას:

Ისე, წ = −x − 1 - oblique asymptote at .

მაგალითი 10იპოვეთ ფუნქციის გრაფიკის ასიმპტოტები

გადაწყვეტილება. ფუნქციას აქვს ფარგლები . ვინაიდან ამ ფუნქციის გრაფიკის ვერტიკალური ასიმპტოტი შეიძლება იყოს მხოლოდ განსაზღვრების დომენის საზღვარზე, ჩვენ ვიპოვით ფუნქციის ცალმხრივ საზღვრებს.

სწორი ხაზის თვისებები ევკლიდეს გეომეტრიაში.

არსებობს უსასრულოდ ბევრი ხაზი, რომელიც შეიძლება გაივლოს ნებისმიერ წერტილში.

ნებისმიერი ორი არათანაბარი წერტილის გავლით მხოლოდ ერთი სწორი ხაზია.

სიბრტყეში ორი შეუსაბამო ხაზი ან იკვეთება ერთ წერტილში, ან არის

პარალელურად (მოჰყვება წინა).

სამგანზომილებიან სივრცეში ორი ხაზის შედარებითი პოზიციის სამი ვარიანტია:

• ხაზები იკვეთება;

• სწორი ხაზები პარალელურია;

• სწორი ხაზები იკვეთება.

პირდაპირ ხაზი- პირველი რიგის ალგებრული მრუდი: დეკარტის კოორდინატულ სისტემაში სწორი ხაზი

სიბრტყეზე მოცემულია პირველი ხარისხის განტოლებით (წრფივი განტოლება).

სწორი ხაზის ზოგადი განტოლება.

განმარტება. სიბრტყეში ნებისმიერი ხაზი შეიძლება იყოს მოცემული პირველი რიგის განტოლებით

Ah + Wu + C = 0,

და მუდმივი A, Bერთდროულად ნულის ტოლი არ არის. ეს პირველი რიგის განტოლება ეწოდება გენერალი

სწორი ხაზის განტოლება.მუდმივების მნიშვნელობებიდან გამომდინარე A, Bდა თანშესაძლებელია შემდეგი განსაკუთრებული შემთხვევები:

. C = 0, A ≠ 0, B ≠ 0- ხაზი გადის საწყისზე

. A = 0, B ≠0, C ≠0 ( By + C = 0)- სწორი ხაზი ღერძის პარალელურად ოჰ

. B = 0, A ≠ 0, C ≠ 0 ( Ax + C = 0)- სწორი ხაზი ღერძის პარალელურად OU

. B = C = 0, A ≠ 0- ხაზი ემთხვევა ღერძს OU

. A = C = 0, B ≠ 0- ხაზი ემთხვევა ღერძს ოჰ

სწორი ხაზის განტოლება შეიძლება წარმოდგენილი იყოს სხვადასხვა ფორმით, რაც დამოკიდებულია ნებისმიერ მოცემულობაზე

საწყისი პირობები.

სწორი ხაზის განტოლება წერტილით და ნორმალური ვექტორით.

განმარტება. დეკარტის მართკუთხა კოორდინატულ სისტემაში ვექტორი კომპონენტებით (A, B)

განტოლებით მოცემული წრფის პერპენდიკულარული

Ah + Wu + C = 0.

მაგალითი. იპოვნეთ წერტილის გავლის სწორი ხაზის განტოლება A(1, 2)ვექტორზე პერპენდიკულარული (3, -1).

გადაწყვეტილება. მოდით შევადგინოთ A \u003d 3 და B \u003d -1 სწორი ხაზის განტოლება: 3x - y + C \u003d 0. ვიპოვოთ კოეფიციენტი C

მოცემული A წერტილის კოორდინატებს ვცვლით მიღებულ გამოსახულებაში ვიღებთ: 3 - 2 + C = 0, შესაბამისად

C = -1. სულ: სასურველი განტოლება: 3x - y - 1 \u003d 0.

ორ წერტილში გამავალი სწორი ხაზის განტოლება.

ორი ქულა იყოს მოცემული სივრცეში M 1 (x 1 , y 1 , z 1)და M2 (x 2, y 2, z 2),მაშინ სწორი ხაზის განტოლება,

გადის ამ წერტილებში:

თუ რომელიმე მნიშვნელი ნულის ტოლია, შესაბამისი მრიცხველი ნულის ტოლი უნდა იყოს. Ზე

სიბრტყეზე, ზემოთ დაწერილი სწორი ხაზის განტოლება გამარტივებულია:

თუ x 1 ≠ x 2და x = x 1, თუ x 1 = x 2 .

ფრაქცია = კდაურეკა ფერდობის ფაქტორი სწორი.

მაგალითი. იპოვეთ A(1, 2) და B(3, 4) წერტილებზე გამავალი სწორი ხაზის განტოლება.

გადაწყვეტილება. ზემოაღნიშნული ფორმულის გამოყენებით მივიღებთ:

სწორი ხაზის განტოლება წერტილით და დახრილობით.

თუ სწორი ხაზის ზოგადი განტოლება Ah + Wu + C = 0მიიტანეთ ფორმაში:

და დანიშნეთ , მაშინ მიღებული განტოლება ეწოდება

სწორი ხაზის განტოლება დახრილობით k.

სწორი ხაზის განტოლება წერტილზე და მიმართულ ვექტორზე.

ნორმალური ვექტორის გავლით სწორი ხაზის განტოლების გათვალისწინებით წერტილის ანალოგიით, შეგიძლიათ შეიყვანოთ დავალება

სწორი ხაზი წერტილის გავლით და სწორი ხაზის მიმართულების ვექტორი.

განმარტება. ყოველი არანულოვანი ვექტორი (α 1 , α 2), რომლის კომპონენტები აკმაყოფილებს პირობას

Aα 1 + Bα 2 = 0დაურეკა სწორი ხაზის მიმართულების ვექტორი.

Ah + Wu + C = 0.

მაგალითი. იპოვეთ სწორი ხაზის განტოლება მიმართულების ვექტორთან (1, -1) და A(1, 2) წერტილში გავლისას.

გადაწყვეტილება. ჩვენ ვეძებთ სასურველი სწორი ხაზის განტოლებას სახით: Axe + By + C = 0.განმარტების მიხედვით,

კოეფიციენტები უნდა აკმაყოფილებდეს პირობებს:

1 * A + (-1) * B = 0, ე.ი. A = B.

მაშინ სწორი ხაზის განტოლებას აქვს ფორმა: Ax + Ay + C = 0,ან x + y + C / A = 0.

ზე x=1, y=2ვიღებთ C/A = -3, ე.ი. სასურველი განტოლება:

x + y - 3 = 0

სწორი ხაზის განტოლება სეგმენტებში.

თუ სწორი ხაზის ზოგად განტოლებაში Ah + Wu + C = 0 C≠0, მაშინ -C-ზე გაყოფით მივიღებთ:

ან სად

კოეფიციენტების გეომეტრიული მნიშვნელობა არის ის, რომ კოეფიციენტი a არის გადაკვეთის წერტილის კოორდინატი.

სწორი ღერძით ოჰ,ა ბ- ღერძთან წრფის გადაკვეთის წერტილის კოორდინატი OU.

მაგალითი. მოცემულია სწორი ხაზის ზოგადი განტოლება x - y + 1 = 0.იპოვეთ ამ სწორი ხაზის განტოლება მონაკვეთებში.

C \u003d 1, , a \u003d -1, b \u003d 1.

სწორი ხაზის ნორმალური განტოლება.

თუ განტოლების ორივე მხარე Ah + Wu + C = 0რიცხვით გაყოფა , რომელსაც ქვია

ნორმალიზების ფაქტორი, შემდეგ მივიღებთ

xcosφ + ysinφ - p = 0 -სწორი ხაზის ნორმალური განტოლება.

ნორმალიზების ფაქტორის ნიშანი ± უნდა შეირჩეს ისე, რომ μ * C< 0.

რ- პერპენდიკულარულის სიგრძე დაეცა საწყისიდან ხაზამდე,

ა φ - ამ პერპენდიკულარით წარმოქმნილი კუთხე ღერძის დადებითი მიმართულებით ოჰ.

მაგალითი. მოცემულია სწორი ხაზის ზოგადი განტოლება 12x - 5y - 65 = 0. საჭიროა სხვადასხვა ტიპის განტოლებების დასაწერად

ეს სწორი ხაზი.

ამ სწორი ხაზის განტოლება სეგმენტებში:

ამ ხაზის განტოლება დახრილობასთან: (გაყოფა 5-ზე)

სწორი ხაზის განტოლება:

cos φ = 12/13; sin φ= -5/13; p=5.

უნდა აღინიშნოს, რომ ყველა სწორი ხაზი არ შეიძლება იყოს წარმოდგენილი განტოლებით სეგმენტებში, მაგალითად, სწორი ხაზებით,

ცულების პარალელურად ან საწყისზე გავლისას.

კუთხე ხაზებს შორის სიბრტყეზე.

განმარტება. თუ მოცემულია ორი ხაზი y \u003d k 1 x + b 1, y \u003d k 2 x + b 2, შემდეგ ამ ხაზებს შორის მწვავე კუთხე

განისაზღვრება როგორც

ორი წრფე პარალელურია თუ k 1 = k 2. ორი ხაზი პერპენდიკულარულია

თუ k 1 \u003d -1 / k 2 .

თეორემა.

პირდაპირი Ah + Wu + C = 0და A 1 x + B 1 y + C 1 \u003d 0პარალელურია, როდესაც კოეფიციენტები პროპორციულია

A 1 \u003d λA, B 1 \u003d λB. თუ ასევე С 1 \u003d λС, შემდეგ ხაზები ემთხვევა. ორი წრფის გადაკვეთის წერტილის კოორდინატები

გვხვდება ამ წრფეების განტოლებათა სისტემის ამონახსნის სახით.

მოცემულ წერტილში გამავალი წრფის განტოლება მოცემული წრფის პერპენდიკულარულია.

განმარტება. ხაზი, რომელიც გადის წერტილს M 1 (x 1, y 1)და ხაზის პერპენდიკულარული y = kx + b

წარმოდგენილია განტოლებით:

მანძილი წერტილიდან ხაზამდე.

თეორემა. თუ ქულა მიენიჭება M(x 0, y 0),შემდეგ მანძილი ხაზამდე Ah + Wu + C = 0განისაზღვრება როგორც:

მტკიცებულება. დაუშვით წერტილი M 1 (x 1, y 1)- წერტილიდან ჩამოვარდა პერპენდიკულურის ფუძე მმოცემულისთვის

პირდაპირი. შემდეგ მანძილი წერტილებს შორის მდა M 1:

(1)

კოორდინატები x 1და 1შეიძლება მოიძებნოს, როგორც განტოლებათა სისტემის ამონახსნი:

სისტემის მეორე განტოლება არის სწორი ხაზის განტოლება, რომელიც გადის მოცემულ წერტილში M 0 პერპენდიკულურად.

მოცემული ხაზი. თუ სისტემის პირველ განტოლებას გადავიყვანთ ფორმაში:

A(x - x 0) + B(y - y 0) + Ax 0 + By 0 + C = 0,

შემდეგ, ამოხსნით, მივიღებთ:

ამ გამონათქვამების (1) განტოლებით ჩანაცვლებით, ჩვენ ვპოულობთ:

თეორემა დადასტურდა.

განტოლება

Ah+Wu+C=0

(სად A, B, Cშეიძლება ჰქონდეს ნებისმიერი მნიშვნელობა, რამდენადაც კოეფიციენტები A, Bარ იყო ნული ორივე ერთდროულად) წარმოადგენს სწორი ხაზი. ნებისმიერი სწორი ხაზი შეიძლება წარმოდგენილი იყოს ამ ტიპის განტოლებით. ამიტომ მას უწოდებენ სწორი ხაზის ზოგადი განტოლება.

Თუ მაგრამ X x-ღერძის პარალელურად.

Თუ AT=0, ანუ განტოლება არ შეიცავს ზე, მაშინ ის წარმოადგენს ხაზს, OY ღერძის პარალელურად.

კოღლა ATარ არის ნულის ტოლი, მაშინ სწორი ხაზის ზოგადი განტოლება შეიძლება იყოს გადაწყვეტა ორდინატთან შედარებითზე , შემდეგ ის გარდაიქმნება ფორმაში

(სად a=-A/B; b=-C/B).

ანალოგიურად, როდესაც მაგრამნულისაგან განსხვავებული, სწორი ხაზის ზოგადი განტოლება შეიძლება ამოხსნას მიმართ X.

Თუ თან=0, ანუ სწორი ხაზის ზოგადი განტოლება არ შეიცავს თავისუფალ წევრს, მაშინ იგი წარმოადგენს სწორ ხაზს, რომელიც გადის საწყისზე.

5.

მოცემულ წერტილში გამავალი წრფის განტოლება ა(x 1 , წ 1) მოცემული მიმართულებით, განსაზღვრული ფერდობზე კ,

წ - წ 1 = კ(x - x 1). (1)

ეს განტოლება განსაზღვრავს ხაზების ფანქარს, რომელიც გადის წერტილში ა(x 1 , წ 1), რომელსაც სხივის ცენტრს უწოდებენ.

. სწორი ხაზის განტოლება, რომელიც გადის ორ წერტილში: ა(x 1 , წ 1) და ბ(x 2 , წ 2) ასე წერია:

ორ მოცემულ წერტილში გამავალი სწორი ხაზის დახრილობა განისაზღვრება ფორმულით

7 სწორი ხაზის განტოლება მონაკვეთებში

თუ წრფის ზოგად განტოლებაში, მაშინ (1)-ზე გაყოფით მივიღებთ წრფის განტოლებას სეგმენტებში.

სად,. ხაზი კვეთს ღერძს წერტილში , ღერძს წერტილში .

8 ფორმულა: კუთხე ხაზებს შორის სიბრტყეზე

ზე მიზანი α ორ სწორ ხაზს შორის, რომლებიც მოცემულია განტოლებებით: y=k 1 x+b 1 (პირველი ხაზი) ​​და y=k 2 x+b 2 (მეორე ხაზი), შეიძლება გამოითვალოს ფორმულით (კუთხე იზომება 1-ლი ხაზიდან მე-2-მდე საათის საწინააღმდეგოდ ):

tg(α)=(კ 2 -კ 1 )/(1+კ 1 კ 2 )

9 სიბრტყეზე ორი სწორი ხაზის ურთიერთგანლაგება.

მოდით ახლა ორივე განტოლებებისწორი ხაზები იწერება ზოგადი ფორმით.

თეორემა. დაე იყოს

- გენერალი განტოლებებიორი სწორი ხაზი კოორდინაცია Oxy თვითმფრინავი. მაშინ

1) თუ, მაშინ სწორიდა ემთხვევა;

2) თუ , მაშინ ხაზები და

პარალელურად;

3) თუ, მაშინ სწორიიკვეთება.

მტკიცებულება. მდგომარეობა ნორმალურის კოლინარობის ტოლფასია ვექტორებიპირდაპირი მონაცემები:

ამიტომ, თუ, მაშინ სწორიიკვეთება.

თუ , შემდეგ , , და განტოლება სწორიიღებს ფორმას:

ან , ე.ი. სწორიმატჩი. გაითვალისწინეთ, რომ პროპორციულობის კოეფიციენტი, წინააღმდეგ შემთხვევაში, ჯამის ყველა კოეფიციენტი განტოლებებიიქნება ნული, რაც შეუძლებელია.

თუ სწორიარ ემთხვევა და არ იკვეთება, მაშინ საქმე რჩება, ე.ი. სწორიპარალელურები არიან.

თეორემა დადასტურდა.

წერტილიდან წრფემდე მანძილის დასადგენად, თქვენ უნდა იცოდეთ წრფის განტოლებები და წერტილის კოორდინატები დეკარტის კოორდინატთა სისტემაში. მანძილი წერტილიდან ხაზამდე არის პერპენდიკულური, რომელიც შედგენილია ამ წერტილიდან ხაზამდე.

ინსტრუქცია

სწორი ხაზის ზოგადი განტოლება დეკარტის კოორდინატებში არის Ax+By+C=0, სადაც A, B და C ცნობილი რიცხვებია. დაე, O წერტილს ჰქონდეს კოორდინატები (x1, y1) დეკარტის კოორდინატთა სისტემაში.

ამ შემთხვევაში, ამ წერტილის გადახრა სწორი ხაზიდან არის δ=(Ax1+By1+C)/sqrt((A^2)+(B^2)), თუ C<0, и δ=(Ax1+By1+C)/(-sqrt((A^2)+(B^2))), если C>0.

მანძილი წერტილიდან წრფემდე არის წერტილის აბსოლუტური გადახრა წრფედან, ანუ r=|(Ax1+By1+C)/sqrt((A^2)+(B^2))|, თუ C<0, и δ=|(Ax1+By1+C)/(-sqrt((A^2)+(B^2)))|, если C>0.

მოდით, წერტილი კოორდინატებით (x1, y1, z1) იყოს მოცემული სამგანზომილებიან სივრცეში. სწორი ხაზი შეიძლება განისაზღვროს პარამეტრულად, სამი განტოლების სისტემით: x = x0+ta, y = y0+tb, z = z0+tc, სადაც t არის რეალური რიცხვი. მანძილი წერტილიდან ხაზამდე შეიძლება მოიძებნოს როგორც მინიმალური მანძილი ამ წერტილიდან ხაზის თვითნებურ წერტილამდე. ამ წერტილის კოეფიციენტი t არის tmin=(a(x1-x0)+b(y1-y0)+c(z1-z0))/((a^2)+(b^2)+(c^2) )

მანძილი წერტილიდან (x1, y1) სწორ ხაზამდე ასევე შეიძლება გამოითვალოს, თუ სწორი ხაზი მოცემულია დახრილობის მქონე განტოლებით: y = kx+b. მაშინ მასზე პერპენდიკულარული სწორი წრფის განტოლება ასე გამოიყურება: y = (-1/k)x+a. შემდეგი, თქვენ უნდა გაითვალისწინოთ, რომ ეს ხაზი უნდა გაიაროს წერტილი (x1, y1). აქედან არის რიცხვი a. გარდაქმნების შემდეგ აღმოჩენილია მანძილი წერტილისა და წრფეს შორის.

31 . დაფუძნებულია თვითმფრინავზე და სივრცეში

განმარტება. ბაზა თვითმფრინავზენებისმიერი ორი წრფივად დამოუკიდებელი ვექტორი ეწოდება.

ნებისმიერი ორი არასწორხაზოვანი ვექტორი ქმნის საფუძველს. დაე იყოს ანებისმიერი ვექტორი სიბრტყეზე და ვექტორები ბდა გსაფუძველს ქმნის. ვინაიდან ნებისმიერი სამი ვექტორი წრფივად არის დამოკიდებული სიბრტყეზე, ვექტორზე აწრფივად არის გამოხატული საბაზისო ვექტორების, ანუ მიმართებაში

განმარტება. საფუძველი სივრცეშინებისმიერი სამი წრფივად დამოუკიდებელი ვექტორი ეწოდება. ნებისმიერი სამი არათანაბარი ვექტორი ქმნის საფუძველს. როგორც თვითმფრინავის შემთხვევაში, დადგენილია, რომ ნებისმიერი ვექტორი აიშლება ვექტორებად ბ, გდა დ

ზოგადი განმარტება (ყველასთვის გასაგებად) სიბრტყეზე (სივრცეში) საფუძველს წარმოადგენს არასწორხაზოვანი (არათანაბარწონიანი) ვექტორების მოწესრიგებული წყვილი (სამმაგი). ნებისმიერი ვექტორი შეიძლება ცალსახად გაფართოვდეს საფუძვლის თვალსაზრისით. გაფართოების კოეფიციენტებს უწოდებენ ამ ვექტორის კოორდინატებს მოცემულ საფუძველთან მიმართებაში. ვექტორები ქმნიან საფუძველს დეკარტის კოორდინატთა სივრცეში Oxyz.