ეს არის ოთხკუთხედი, რომლის მოპირდაპირე გვერდები წყვილად პარალელურია.

საკუთრება 1 . პარალელოგრამის ნებისმიერი დიაგონალი მას ორ ტოლ სამკუთხედად ყოფს.

მტკიცებულება . II ნიშნის მიხედვით (ჯვარედინი კუთხეები და საერთო მხარე).

დადასტურებული თეორემა.

საკუთრება 2 . პარალელოგრამში მოპირდაპირე გვერდები ტოლია და მოპირდაპირე კუთხეები ტოლია.

მტკიცებულება .
ანალოგიურად,

დადასტურებული თეორემა.

თვისება 3. დიაგონალურ პარალელოგრამში გადაკვეთის წერტილი იყოფა შუაზე.

მტკიცებულება .

დადასტურებული თეორემა.

საკუთრება 4 . პარალელოგრამის კუთხის ბისექტორი, რომელიც კვეთს მოპირდაპირე მხარეს, ყოფს მას ტოლფერდა სამკუთხედად და ტრაპეციად. (ჩ. სიტყვა - ზედა - ორი ტოლფერდა? -კა).

მტკიცებულება .

დადასტურებული თეორემა.

საკუთრება 5 . პარალელოგრამში, მონაკვეთი, რომელსაც ბოლოები აქვს მოპირდაპირე მხარეს, რომელიც გადის დიაგონალების გადაკვეთის წერტილში, ორად არის გაყოფილი ამ წერტილით.

მტკიცებულება .

დადასტურებული თეორემა.

საკუთრება 6 . პარალელოგრამის ბლაგვი კუთხის წვეროდან ჩამოშვებულ სიმაღლეებს შორის კუთხე უდრის პარალელოგრამის მახვილ კუთხეს.

მტკიცებულება .

დადასტურებული თეორემა.

საკუთრება 7 . ერთი მხარის მიმდებარე პარალელოგრამის კუთხეების ჯამი არის 180°.

მტკიცებულება .

დადასტურებული თეორემა.

კუთხის ბისექტრის აგება. სამკუთხედის კუთხის ბისექტრის თვისებები.

1) ააშენეთ თვითნებური სხივი DE.

2) მოცემულ სხივზე ააგეთ თვითნებური წრე, ცენტრით წვეროზე და იგივე
კონცენტრირებულია აშენებული სხივის დასაწყისში.

3) F და G - წრის გადაკვეთის წერტილები მოცემული კუთხის გვერდებთან, H - წრის გადაკვეთის წერტილი აგებულ სხივთან.

ააგეთ წრე H წერტილში ცენტრით და რადიუსით FG-ის ტოლი.

5) I - აგებული სხივის წრეების გადაკვეთის წერტილი.

6) დახაზეთ ხაზი წვეროზე და I.

IDH - საჭირო კუთხე.
)

საკუთრება 1 . სამკუთხედის კუთხის ბისექტორი ყოფს მოპირდაპირე მხარეს მიმდებარე გვერდების პროპორციულად.

მტკიცებულება . მოდით x, y იყოს c გვერდის სეგმენტები. ვაგრძელებთ სხივს ძვ.წ. BC სხივზე გამოვსახავთ CK სეგმენტს C-დან AC-ის ტოლი.

მტკიცებულება

ჯერ დავხატოთ AC დიაგონალი. მიიღება ორი სამკუთხედი: ABC და ADC.

ვინაიდან ABCD არის პარალელოგრამი, მართებულია შემდეგი:

AD || BC \მარჯვენა ისარი \კუთხე 1 = \კუთხე 2ისევე როგორც წევს.

AB || CD \Rightarrow \angle3 = \angle 4ისევე როგორც წევს.

ამიტომ, \სამკუთხედი ABC = \სამკუთხედი ADC (მეორე მახასიათებლის მიხედვით: და AC საერთოა).

და, შესაბამისად, \სამკუთხედი ABC = \სამკუთხედი ADC, შემდეგ AB = CD და AD = BC.

დადასტურებული!

2. მოპირდაპირე კუთხეები იდენტურია.

მტკიცებულება

მტკიცებულების მიხედვით თვისებები 1ჩვენ ეს ვიცით \ კუთხე 1 = \კუთხე 2, \კუთხე 3 = \კუთხე 4. ასე რომ, საპირისპირო კუთხეების ჯამი არის: \კუთხე 1 + \კუთხე 3 = \კუთხე 2 + \კუთხე 4. იმის გათვალისწინებით, რომ \სამკუთხედი ABC = \სამკუთხედი ADC მივიღებთ \კუთხე A = \კუთხე C , \კუთხე B = \კუთხე D .

დადასტურებული!

3. დიაგონალები იკვეთება გადაკვეთის წერტილით.

მტკიცებულება

დავხატოთ კიდევ ერთი დიაგონალი.

ავტორი ქონება 1ჩვენ ვიცით, რომ მოპირდაპირე მხარეები იდენტურია: AB = CD . კიდევ ერთხელ აღვნიშნავთ თანაბარ კუთხეებს ჯვარედინად.

ამრიგად, ჩანს, რომ \სამკუთხედი AOB = \სამკუთხედი COD სამკუთხედების ტოლობის მეორე ნიშნით (ორი კუთხე და გვერდი მათ შორის). ანუ, BO = OD (პირდაპირი \კუთხე 2 და \კუთხე 1 ) და AO = OC (საპირისპირო \კუთხე 3 და \კუთხე 4 შესაბამისად).

დადასტურებული!

პარალელოგრამის მახასიათებლები

თუ თქვენს პრობლემაში მხოლოდ ერთი ნიშანია, მაშინ ფიგურა არის პარალელოგრამი და შეგიძლიათ გამოიყენოთ ამ ფიგურის ყველა თვისება.

უკეთესი დასამახსოვრებლად, გაითვალისწინეთ, რომ პარალელოგრამის ნიშანი უპასუხებს შემდეგ კითხვას − "როგორ გავარკვიოთ?". ანუ როგორ გავარკვიოთ, რომ მოცემული ფიგურა პარალელოგრამია.

1. პარალელოგრამი არის ოთხკუთხედი, რომლის ორი გვერდი ტოლია და პარალელურია.

AB=CD; AB || CD \Rightarrow ABCD არის პარალელოგრამი.

მტკიცებულება

განვიხილოთ უფრო დეტალურად. რატომ AD || ძვ.წ.

\სამკუთხედი ABC = \სამკუთხედი ADC მიერ ქონება 1: AB = CD , AC არის საერთო და \კუთხე 1 = \კუთხე 2 ჯვარედინად AB და CD პარალელურად და სეკანტური AC .

მაგრამ თუ \სამკუთხედი ABC = \სამკუთხედი ADC , მაშინ \კუთხე 3 = \კუთხე 4 (ისინი დევს შესაბამისად AB და CD საპირისპიროდ). და ამიტომ AD || BC (\კუთხე 3 და \კუთხე 4 - განლაგებული ასევე ტოლია).

პირველი ნიშანი სწორია.

2. პარალელოგრამი არის ოთხკუთხედი, რომლის მოპირდაპირე გვერდები ტოლია.

AB = CD , AD = BC \Rightarrow ABCD არის პარალელოგრამი.

მტკიცებულება

განვიხილოთ ეს თვისება. ისევ დავხატოთ AC დიაგონალი.

ავტორი ქონება 1\სამკუთხედი ABC = \სამკუთხედი ACD.

Აქედან გამომდინარეობს, რომ: \კუთხე 1 = \კუთხე 2 \Rightarrow AD || ძვ.წდა \კუთხე 3 = \კუთხე 4 \Rightarrow AB || CD, ანუ ABCD არის პარალელოგრამი.

მეორე ნიშანი სწორია.

3. პარალელოგრამი არის ოთხკუთხედი, რომლის მოპირდაპირე კუთხეები ტოლია.

\ კუთხე A = \ კუთხე C, \ კუთხე B = \ კუთხე D \ მარჯვენა ისარი ABCD- პარალელოგრამი.

მტკიცებულება

2 \ალფა + 2 \ბეტა = 360^(\circ)(რადგან ABCD არის ოთხკუთხედი და \კუთხე A = \კუთხე C , \კუთხე B = \კუთხე D კონვენციით).

ასე რომ, \alpha + \beta = 180^(\circ) . მაგრამ \alpha და \beta არის შიდა ცალმხრივი სეკანტურ AB-ზე.

და ის ფაქტი, რომ \alpha + \beta = 180^(\circ) ასევე ნიშნავს, რომ AD || ძვ.წ.

ამავდროულად, \alpha და \beta არის შიდა ცალმხრივი სეკანტური AD . და ეს ნიშნავს AB || CD.

მესამე ნიშანი სწორია.

4. პარალელოგრამი არის ოთხკუთხედი, რომლის დიაგონალები იკვეთება გადაკვეთის წერტილით.

AO=OC; BO = OD \მარჯვენა პარალელოგრამი.

მტკიცებულება

BO=OD; AO = OC, \კუთხე 1 = \კუთხე 2 ვერტიკალურად \მარჯვენა ისარი \სამკუთხედი AOB = \სამკუთხედი COD, \მარჯვენა ისარი \კუთხე 3 = \კუთხე 4და \Rightarrow AB || CD.

ანალოგიურად BO = OD; AO=OC, \ კუთხე 5 = \კუთხე 6 \მარჯვენა ისარი \სამკუთხედი AOD = \სამკუთხედი BOC \მარჯვენა ისარი \კუთხე 7 = \კუთხე 8, და \Rightarrow AD || ძვ.წ.

მეოთხე ნიშანი სწორია.

გაკვეთილის თემა

• პარალელოგრამის დიაგონალების თვისებები.

გაკვეთილის მიზნები

• გაეცანით ახალ განმარტებებს და გაიხსენეთ უკვე შესწავლილი.
• ჩამოაყალიბეთ და დაამტკიცეთ პარალელოგრამის დიაგონალების თვისება.
• ისწავლეთ ფორმების თვისებების გამოყენება ამოცანების ამოხსნისას.
• განმავითარებელი - მოსწავლეთა ყურადღების განვითარება, შეუპოვრობა, შეუპოვრობა, ლოგიკური აზროვნება, მათემატიკური მეტყველება.
• საგანმანათლებლო - გაკვეთილის საშუალებით, ერთმანეთის მიმართ ყურადღებიანი დამოკიდებულების ჩამოყალიბება, ამხანაგების მოსმენის უნარის, ურთიერთდახმარების, დამოუკიდებლობის ჩამოყალიბება.

გაკვეთილის მიზნები

• შეამოწმეთ მოსწავლეთა პრობლემების გადაჭრის უნარი.

Გაკვეთილის გეგმა

1. შესავალი.
2. ადრე ნასწავლი მასალის გამეორება.
3. პარალელოგრამი, მისი თვისებები და ნიშნები.
4. დავალების მაგალითები.
5. Თვითშემოწმება.

შესავალი

”მთავარი მეცნიერული აღმოჩენა იძლევა ძირითადი პრობლემის გადაწყვეტას, მაგრამ ნებისმიერი პრობლემის გადაჭრაში არის აღმოჩენის მარცვალი.”

პარალელოგრამის მოპირდაპირე გვერდების თვისებები

პარალელოგრამს მოპირდაპირე გვერდები ტოლი აქვს.

მტკიცებულება.

ABCD იყოს მოცემული პარალელოგრამი. და დაე, მისი დიაგონალები იკვეთოს O წერტილში.
ვინაიდან Δ AOB = Δ COD სამკუთხედების ტოლობის პირველი ნიშნით (∠ AOB = ∠ COD, როგორც ვერტიკალურად, AO=OC, DO=OB, პარალელოგრამის დიაგონალების თვისებით), მაშინ AB=CD. ანალოგიურად, BOC და DOA სამკუთხედების ტოლობიდან გამომდინარეობს, რომ BC=DA. თეორემა დადასტურდა.

პარალელოგრამის საპირისპირო კუთხეების თვისება

პარალელოგრამს აქვს საპირისპირო კუთხეები.

მტკიცებულება.

ABCD იყოს მოცემული პარალელოგრამი. და დაე, მისი დიაგონალები იკვეთოს O წერტილში.
პარალელოგრამის მოპირდაპირე გვერდების თვისებებიდან დადასტურებული თეორემაში Δ ABC = Δ CDA სამ მხარეს (AB=CD, BC=DA დადასტურებულიდან, AC ზოგადია). სამკუთხედების ტოლობიდან გამომდინარეობს, რომ ∠ABC = ∠CDA.
ასევე დადასტურებულია, რომ ∠ DAB = ∠ BCD, რომელიც გამომდინარეობს ∠ ABD = ∠ CDB-დან. თეორემა დადასტურდა.

პარალელოგრამის დიაგონალების თვისება

პარალელოგრამის დიაგონალები იკვეთება და გადაკვეთის წერტილი ორად იკვეთება.

მტკიცებულება.

ABCD იყოს მოცემული პარალელოგრამი. დავხატოთ AC დიაგონალი. მასზე ვნიშნავთ შუა O-ს. DO სეგმენტის გაგრძელებაზე ვდებთ DO-ს ტოლი OB 1 სეგმენტს.
წინა თეორემით AB 1 CD არის პარალელოგრამი. მაშასადამე, AB 1 ხაზი DC-ის პარალელურია. მაგრამ A წერტილის გავლით DC-ის პარალელურად მხოლოდ ერთი ხაზის გაყვანა შეიძლება. აქედან გამომდინარე, ხაზი AB 1 ემთხვევა AB ხაზს.
ასევე დასტურდება, რომ ძვ.წ 1 ემთხვევა ძვ.წ. ასე რომ C წერტილი ემთხვევა C 1-ს. პარალელოგრამი ABCD ემთხვევა პარალელოგრამს AB 1 CD. ამრიგად, პარალელოგრამის დიაგონალები იკვეთება და გადაკვეთის წერტილი ორად იკვეთება. თეორემა დადასტურდა.

ჩვეულებრივი სკოლების სახელმძღვანელოებში (მაგალითად, პოგორელოვში) ასეა დადასტურებული: დიაგონალები ყოფენ პარალელოგრამს 4 სამკუთხედად. განვიხილოთ ერთი წყვილი და გაარკვიეთ - ისინი ტოლია: მათი ფუძეები მოპირდაპირე მხარეებია, მის მიმდებარედ შესაბამისი კუთხეები ტოლია, როგორც ვერტიკალური პარალელური ხაზებით. ანუ დიაგონალების სეგმენტები წყვილში ტოლია. ყველაფერი.

Სულ ეს არის?
ზემოთ დადასტურდა, რომ გადაკვეთის წერტილი ყოფს დიაგონალებს - თუ ის არსებობს. ზემოაღნიშნული მსჯელობა არანაირად არ ადასტურებს მის არსებობას. ანუ თეორემის ნაწილი „პარალელოგრამის დიაგონალები იკვეთება“ რჩება დაუმტკიცებელი.

სასაცილოა, რამდენად რთულია ამ ნაწილის დამტკიცება. სხვათა შორის, ეს უფრო ზოგადი შედეგიდან გამომდინარეობს: ნებისმიერი ამოზნექილი ოთხკუთხედისთვის დიაგონალები იკვეთება, ნებისმიერი არაამოზნექილისთვის - არა.

გვერდის გასწვრივ სამკუთხედების და მის მიმდებარე ორი კუთხის ტოლობის შესახებ (სამკუთხედების ტოლობის მეორე ნიშანი) და სხვა.

თეორემა გვერდის გასწვრივ ორი ​​სამკუთხედის და მის მიმდებარე ორი კუთხის ტოლობის შესახებ, თალესმა იპოვა მნიშვნელოვანი პრაქტიკული გამოყენება. მილეტის ნავსადგურში აშენდა დიაპაზონი, რომელიც განსაზღვრავს მანძილს ზღვაზე გემამდე. იგი შედგებოდა სამი ამოძრავებული სამაგრი A, B და C (AB = BC) და მონიშნული სწორი ხაზი SK, პერპენდიკულარული CA. როდესაც გემი გამოჩნდა SC სწორ ხაზზე, აღმოჩნდა D წერტილი ისეთი, რომ D, .B და E წერტილები იმავე სწორ ხაზზე იყო. როგორც ნახატიდან ირკვევა, CD მანძილი ადგილზე არის სასურველი მანძილი გემამდე.

კითხვები

1. კვადრატის დიაგონალები იკვეთება გადაკვეთის წერტილით?
   
2. პარალელოგრამის დიაგონალები ტოლია?
3. პარალელოგრამის საპირისპირო კუთხეები ტოლია?
4. რა არის პარალელოგრამის განმარტება?
5. პარალელოგრამის რამდენი თვისებაა?
   
6. შეიძლება რომბი იყოს პარალელოგრამი?
   

გამოყენებული წყაროების სია

1. კუზნეცოვი A.V., მათემატიკის მასწავლებელი (5-9 კლასები), კიევი
2. „ერთიანი სახელმწიფო გამოცდა 2006წ. მათემატიკა. საგანმანათლებლო და სასწავლო მასალები სტუდენტების მოსამზადებლად / Rosobrnadzor, ISOP - M .: Intellect-Center, 2006 "
3. Mazur K. I. "მ.ი. სკანავის რედაქტორული კრებულის ძირითადი საკონკურსო ამოცანების ამოხსნა მათემატიკაში"
4. ლ.

გაკვეთილზე მუშაობა

კუზნეცოვი A.V.

Poturnak S.A.

ევგენი პეტროვი

თქვენ შეგიძლიათ დასვათ შეკითხვა თანამედროვე განათლების შესახებ, გამოხატოთ აზრი ან გადაწყვიტოთ გადაუდებელი პრობლემა განათლების ფორუმისადაც ახალი აზრისა და მოქმედების საგანმანათლებლო საბჭო იკრიბება საერთაშორისო დონეზე. რომელმაც შექმნა ბლოგი,თქვენ არა მხოლოდ გააუმჯობესებთ კომპეტენტური მასწავლებლის სტატუსს, არამედ მნიშვნელოვან წვლილს შეიტანთ მომავლის სკოლის განვითარებაში. განათლების ლიდერთა გილდიაკარს უხსნის უმაღლესი რანგის სპეციალისტებს და გიწვევთ თანამშრომლობისთვის მსოფლიოში საუკეთესო სკოლების შექმნის მიმართულებით.

საგნები > მათემატიკა > მათემატიკა მე-8 კლასი

პარალელოგრამი არის ოთხკუთხედი, რომლის მოპირდაპირე გვერდები პარალელურია, ე.ი. დაწექი პარალელურ ხაზებზე

პარალელოგრამის თვისებები:
თეორემა 22. პარალელოგრამის მოპირდაპირე მხარეები ტოლია.
მტკიცებულება. დახაზეთ AC დიაგონალი ABCD პარალელოგრამზე. სამკუთხედები ACD და ACB თანმიმდევრულია, რადგან აქვთ საერთო გვერდი AC და ორი წყვილი თანაბარი კუთხე. მის მიმდებარედ: ∠ CAB=∠ ACD, ∠ ASV=∠ DAC (როგორც ჯვარედინი კუთხეები AD და BC პარალელური ხაზებით). აქედან გამომდინარე, AB=CD და BC=AD, როგორც ტოლი სამკუთხედების შესაბამისი გვერდები და ა.შ. ამ სამკუთხედების ტოლობა ასევე გულისხმობს სამკუთხედების შესაბამისი კუთხეების ტოლობას:
თეორემა 23. პარალელოგრამის საპირისპირო კუთხეებია: ∠ A=∠ C და ∠ B=∠ D.
პირველი წყვილის ტოლობა მოდის ABD და CBD სამკუთხედების ტოლობიდან, ხოლო მეორე - ABC და ACD.
თეორემა 24. პარალელოგრამის მეზობელი კუთხეები, ე.ი. ერთი მხარის მიმდებარე კუთხეები ემატება 180 გრადუსს.
ეს იმიტომ ხდება, რომ ისინი შიდა ცალმხრივი კუთხეებია.
თეორემა 25. პარალელოგრამის დიაგონალები ერთმანეთს კვეთენ მათი გადაკვეთის წერტილში.
მტკიცებულება. განვიხილოთ სამკუთხედები BOC და AOD. პირველი თვისების მიხედვით, AD=BC ∠ ОАD=∠ OSV და ∠ ОDA=∠ ОВС, როგორც AD და BC პარალელური წრფეების გასწვრივ. მაშასადამე, BOC და AOD სამკუთხედები ტოლია გვერდით და მის მიმდებარე კუთხეებით. აქედან გამომდინარე, BO=OD და AO=OC, როგორც ტოლი სამკუთხედების შესაბამისი გვერდები და ა.შ.

პარალელოგრამის მახასიათებლები
თეორემა 26. თუ ოთხკუთხედის მოპირდაპირე მხარეები წყვილებში ტოლია, მაშინ ის პარალელოგრამია.
მტკიცებულება. დაე, ოთხკუთხედს ABCD ჰქონდეს გვერდები AD და BC, AB და CD, შესაბამისად, ტოლები (ნახ. 2). დავხატოთ AC დიაგონალი. სამკუთხედს ABC და ACD აქვს სამი თანაბარი გვერდი. მაშინ კუთხეები BAC და DCA ტოლია და ამიტომ AB არის CD-ის პარალელურად. BC და AD გვერდების პარალელიზმი გამომდინარეობს CAD და DIA კუთხეების ტოლობიდან.
თეორემა 27. თუ ოთხკუთხედის საპირისპირო კუთხეები წყვილებში ტოლია, მაშინ ის პარალელოგრამია.
მოდით ∠ A=∠ C და ∠ B=∠ D. ∠ A+∠ B+∠ C+∠ D=360 o, შემდეგ ∠ A+∠ B=180 o და AD და BC გვერდები პარალელურია (პარალელური წრფეების საფუძველზე). ჩვენ ასევე ვამტკიცებთ AB და CD გვერდების პარალელიზმს და დავასკვნით, რომ ABCD განსაზღვრებით პარალელოგრამია.
თეორემა 28. თუ ოთხკუთხედის მიმდებარე კუთხეები, ე.ი. ერთი მხარის მიმდებარე კუთხეები ემატება 180 გრადუსს, მაშინ ეს არის პარალელოგრამი.
თუ შიდა ცალმხრივი კუთხეები ემატება 180 გრადუსს, მაშინ ხაზები პარალელურია. ეს ნიშნავს, რომ AB არის წყვილი CD და BC არის წყვილი AD. ოთხკუთხედი გამოდის პარალელოგრამი განსაზღვრებით.
თეორემა 29. თუ ოთხკუთხედის დიაგონალები გადაკვეთის ადგილას ორმხრივ იყოფა შუაზე, მაშინ ოთხკუთხედი პარალელოგრამია.
მტკიცებულება. თუ AO=OC, BO=OD, მაშინ სამკუთხედები AOD და BOC ტოლია, რადგან აქვთ თანაბარი კუთხეები (ვერტიკალური) O წვეროზე, ჩასმული ტოლ გვერდებს შორის. სამკუთხედების ტოლობიდან ვასკვნით, რომ AD და BC ტოლია. გვერდები AB და CD ასევე ტოლია და ოთხკუთხედი აღმოჩნდება პარალელოგრამი 1-ლი მახასიათებლის მიხედვით.
თეორემა 30. თუ ოთხკუთხედს აქვს წყვილი თანაბარი, პარალელური გვერდი, მაშინ ის პარალელოგრამია.
მოდით, AB და CD გვერდები იყოს პარალელური და ტოლი ოთხკუთხედში ABCD. დახაზეთ დიაგონალები AC და BD. ამ წრფეების პარალელიზმიდან გამომდინარეობს ჯვარედინ დაწოლის კუთხეების ტოლობა ABO=CDO და BAO=OCD. სამკუთხედები ABO და CDO ტოლია გვერდით და მიმდებარე კუთხით. ამიტომ, AO=OC, BO=OD, ე.ი. გადაკვეთის წერტილის დიაგონალები იყოფა ნახევრად და ოთხკუთხედი აღმოჩნდება პარალელოგრამი 4-ის მიხედვით.

გეომეტრიაში განიხილება პარალელოგრამის განსაკუთრებული შემთხვევები.

პარალელოგრამის ცნება

განმარტება 1

პარალელოგრამიარის ოთხკუთხედი, რომელშიც მოპირდაპირე გვერდები ერთმანეთის პარალელურია (ნახ. 1).

სურათი 1.

პარალელოგრამს აქვს ორი ძირითადი თვისება. განვიხილოთ ისინი მტკიცებულების გარეშე.

საკუთრება 1: პარალელოგრამის საპირისპირო გვერდები და კუთხეები, შესაბამისად, ერთმანეთის ტოლია.

საკუთრება 2: პარალელოგრამზე დახატული დიაგონალები იკვეთება მათი გადაკვეთის წერტილით.

პარალელოგრამის მახასიათებლები

განვიხილოთ პარალელოგრამის სამი მახასიათებელი და წარმოადგინეთ ისინი თეორემების სახით.

თეორემა 1

თუ ოთხკუთხედის ორი გვერდი ერთმანეთის ტოლია და ასევე პარალელურია, მაშინ ეს ოთხკუთხედი პარალელოგრამი იქნება.

მტკიცებულება.

მოდით, მოგვცეს ოთხკუთხედი $ABCD$. რომელშიც $AB||CD$ და $AB=CD$ მოდით დავხატოთ მასში $AC$ დიაგონალი (ნახ. 2).

სურათი 2.

განვიხილოთ პარალელური ხაზები $AB$ და $CD$ და მათი სეკანტი $AC$. მერე

\[\კუთხე CAB=\კუთხე DCA\]

როგორც ჯვარედინი კუთხეები.

სამკუთხედების ტოლობის $I$ კრიტერიუმის მიხედვით,

ვინაიდან $AC$ მათი საერთო მხარეა და $AB=CD$ ვარაუდით. ნიშნავს

\[\კუთხე DAC=\კუთხე ACB\]

განვიხილოთ $AD$ და $CB$ წრფეები და მათი სეკანტი $AC$; ჯვარედინი კუთხეების ბოლო ტოლობით მივიღებთ $AD||CB$.) ამიტომ, $1$-ის განმარტებით, ეს ოთხკუთხედი არის პარალელოგრამი.

თეორემა დადასტურდა.

თეორემა 2

თუ ოთხკუთხედის მოპირდაპირე მხარეები ტოლია, მაშინ ის პარალელოგრამია.

მტკიცებულება.

მოდით, მოგვცეს ოთხკუთხედი $ABCD$. რომელშიც $AD=BC$ და $AB=CD$. მოდით დავხატოთ მასში $AC$ დიაგონალი (ნახ. 3).

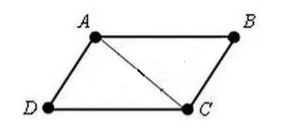
სურათი 3

ვინაიდან $AD=BC$, $AB=CD$ და $AC$ არის საერთო გვერდი, მაშინ $III$ სამკუთხედის თანასწორობის ტესტით,

\[\სამკუთხედი DAC=\სამკუთხედი ACB\]

\[\კუთხე DAC=\კუთხე ACB\]

განვიხილოთ $AD$ და $CB$ წრფეები და მათი სეკანტი $AC$, ჯვარედინი კუთხის ბოლო თანასწორობით მივიღებთ $AD||CB$. ამიტომ, $1$-ის განმარტებით, ეს ოთხკუთხედი არის პარალელოგრამი.

\[\კუთხე DCA=\კუთხე CAB\]

განვიხილოთ $AB$ და $CD$ წრფეები და მათი სეკანტი $AC$, ჯვარედინი კუთხეების ბოლო თანასწორობით მივიღებთ $AB||CD$. ამიტომ, განმარტებით 1, ეს ოთხკუთხედი არის პარალელოგრამი.

თეორემა დადასტურდა.

თეორემა 3

თუ ოთხკუთხედში დახატული დიაგონალები მათი გადაკვეთის წერტილით იყოფა ორ ტოლ ნაწილად, მაშინ ეს ოთხკუთხედი პარალელოგრამია.

მტკიცებულება.

მოდით, მოგვცეს ოთხკუთხედი $ABCD$. მოდით დავხატოთ მასში $AC$ და $BD$ დიაგონალები. დაე, ისინი გადაიკვეთონ $O$ წერტილში (ნახ. 4).

სურათი 4

ვინაიდან $BO=OD,\ AO=OC$ პირობით, და კუთხეები $\კუთხე COB=\კუთხე DOA$ ვერტიკალურია, მაშინ $I$ სამკუთხედის თანასწორობის ტესტით,

\[\სამკუთხედი BOC=\სამკუთხედი AOD\]

\[\კუთხე DBC=\კუთხე BDA\]

განვიხილოთ $BC$ და $AD$ წრფეები და მათი სეკანტი $BD$, ჯვარედინი დაწოლის კუთხეების ბოლო თანასწორობით მივიღებთ $BC||AD$-ს. ასევე $BC=AD$. მაშასადამე, $1$ თეორემის მიხედვით, ეს ოთხკუთხედი არის პარალელოგრამი.