អនុគមន៍ y=f(x) ត្រូវបានគេហៅថាខុសគ្នាត្រង់ចំនុចខ្លះ x 0 ប្រសិនបើវាមានដេរីវេច្បាស់លាស់នៅចំណុចនោះ ឧ. ប្រសិនបើដែនកំណត់នៃទំនាក់ទំនងមាន ហើយមានកំណត់។

ប្រសិនបើមុខងារអាចខុសគ្នានៅគ្រប់ចំណុចនៃផ្នែកខ្លះ [a; b] ឬចន្លោះពេល (a; b) បន្ទាប់មកវាត្រូវបានគេនិយាយថាអាចខុសគ្នានៅលើផ្នែក [a; b] ឬរៀងគ្នាក្នុងចន្លោះពេល (a; b) ។

ទ្រឹស្តីបទខាងក្រោមមានសុពលភាព ដែលបង្កើតការតភ្ជាប់រវាងមុខងារផ្សេងគ្នា និងបន្ត។

ទ្រឹស្តីបទ។ ប្រសិនបើអនុគមន៍ y=f(x) អាចខុសគ្នាត្រង់ចំនុចណាមួយ x 0 នោះវាបន្តនៅចំណុចនោះ។

ដូច្នេះភាពខុសគ្នានៃមុខងារបង្កប់ន័យបន្តរបស់វា។

ភស្តុតាង. បើអញ្ចឹង

ដែល b ជា​តម្លៃ​គ្មាន​ដែន​កំណត់ i.e. បរិមាណទំនោរទៅសូន្យនៅ Ax>0។ ប៉ុន្តែ​បន្ទាប់មក

Dy=f "(x 0) Dx+bDx=> Dy>0 សម្រាប់ Dx>0, i.e. f(x) - f(x 0)>0 សម្រាប់ x>x 0,

ហើយនេះមានន័យថាអនុគមន៍ f(x) បន្តនៅចំណុច x 0 ។ Q.E.D.

ដូច្នេះ នៅចំនុចដាច់ មុខងារមិនអាចមានដេរីវេទេ។ សេចក្តីថ្លែងការសន្ទនាគឺមិនពិតទេ៖ មានមុខងារបន្តដែលមិនមានភាពខុសគ្នានៅចំណុចមួយចំនួន (នោះគឺពួកគេមិនមានដេរីវេនៅចំណុចទាំងនេះទេ)។

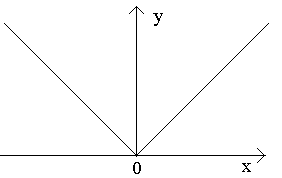
ពិចារណាចំណុច a, b, c ក្នុងរូប។

នៅចំណុច a នៅពេលដែល Dx>0 ទំនាក់ទំនងមិនមានដែនកំណត់ទេ (ព្រោះដែនកំណត់ម្ខាងគឺខុសគ្នាសម្រាប់ Dx>0-0 និង Dx>0+0)។ មិនមានតង់សង់ដែលបានកំណត់នៅចំណុច A នៅលើក្រាហ្វនោះទេ ប៉ុន្តែមានតង់សង់ម្ខាងពីរផ្សេងគ្នាដែលមានជម្រាល 1 និង 2 ។ ចំណុចប្រភេទនេះត្រូវបានគេហៅថា ចំណុចជ្រុង។

នៅចំណុច b សម្រាប់ Dx> 0 សមាមាត្រគឺជាតម្លៃថេរនៃសញ្ញា។ អនុគមន៍មានដេរីវេគ្មានកំណត់។ នៅចំណុចនេះ ក្រាហ្វមានតង់សង់បញ្ឈរ។ ប្រភេទចំណុច - "ចំណុចបញ្ឆេះ" ដែលមានតង់សង់បញ្ឈរ។

នៅចំណុច គ និស្សន្ទវត្ថុម្ខាងគឺមានចំនួនច្រើនគ្មានកំណត់នៃសញ្ញាផ្សេងគ្នា។ នៅចំណុចនេះ ក្រាហ្វមានតង់ហ្សង់បញ្ឈរពីររួមបញ្ចូលគ្នា។ ប្រភេទ - "cusp" ជាមួយតង់សង់បញ្ឈរ - ករណីពិសេសនៃចំណុចជ្រុង។

1. ពិចារណាអនុគមន៍ y=|x|។ មុខងារនេះគឺបន្តនៅចំណុច

ចូរយើងបង្ហាញថាវាមិនមានដេរីវេនៅចំណុចនេះទេ។

f(0+Dx) = f(Dx) = |Dx| ។ ដូច្នេះ Dy = f(Dx) - f(0) = |Dx|

ប៉ុន្តែបន្ទាប់មកសម្រាប់ Dx< 0 (т.е. при Дx стремящемся к 0 слева)

ហើយនៅពេលដែល Dx > 0

ដូច្នេះទំនាក់ទំនងសម្រាប់ Dx> 0 មានដែនកំណត់ផ្សេងគ្នានៅខាងស្តាំនិងខាងឆ្វេងដែលមានន័យថាទំនាក់ទំនងមិនមានដែនកំណត់ទេ i.e. ដេរីវេនៃអនុគមន៍ y=|x| នៅចំណុច x = 0 មិនមានទេ។ តាមធរណីមាត្រ នេះមានន័យថានៅចំណុច x=0 "ខ្សែកោង" នេះមិនមានតង់ហ្សង់ច្បាស់លាស់ទេ (មានពីរចំណុចនេះ)។

2. មុខងារត្រូវបានកំណត់ និងបន្តនៅលើបន្ទាត់ពិតទាំងមូល។ ចូរយើងស្វែងយល់ថាតើអនុគមន៍នេះមានដេរីវេនៅ x=0។

ដូច្នេះ អនុគមន៍​ដែល​កំពុង​ពិចារណា​គឺ​មិន​អាច​ខុស​គ្នា​នៅ​ចំណុច x= 0។ តង់សង់​ទៅ​ខ្សែ​កោង​ត្រង់​ចំណុច​នេះ​បង្កើត​ជា​មុំ p/2 ជាមួយ​អ័ក្ស x ឧ. ស្របគ្នានឹងអ័ក្ស y ។

3 និយមន័យនៃដេរីវេនៃអនុគមន៍នៅចំណុចមួយ ចូរឱ្យអនុគមន៍ f(x) ត្រូវបានកំណត់នៅក្នុងសង្កាត់មួយចំនួននៃចំនុច x 0។ និយមន័យ។ ប្រសិនបើមានដែនកំណត់ (កំណត់) នៃទំនាក់ទំនង នោះ f (x) ត្រូវបានគេហៅថា ចំណុចផ្សេងគ្នា x 0 ហើយដែនកំណត់ខ្លួនវាត្រូវបានគេហៅថាដេរីវេនៃអនុគមន៍ f (x) នៅចំណុច x 0 ហើយត្រូវបានតាងដោយ f "(x 0) នោះគឺយើងសម្គាល់ x \u003d x - x 0 គឺជាការកើនឡើងនៃអាគុយម៉ង់នៅពេលផ្លាស់ទីពីចំណុច x 0 ទៅចំណុច x និង y \u003d f (x 0 + x) - f (x 0 ។ ) គឺជាការកើនឡើងដែលត្រូវគ្នានៃអនុគមន៍ បន្ទាប់មកដេរីវេនៃអនុគមន៍ f (x) នៅចំណុច x 0 គឺជាដែនកំណត់នៃសមាមាត្រនៃការកើនឡើងនៃអនុគមន៍ទៅនឹងការកើនឡើងនៃអាគុយម៉ង់ដែលបណ្តាលឱ្យវានៅពេលដែលការកើនឡើងនៃ អាគុយម៉ង់មាននិន្នាការទៅសូន្យ។

4 ឧទាហរណ៍ 1. ចូរយើងផ្តល់ឧទាហរណ៍នៃការគណនាដេរីវេនៃអនុគមន៍បឋមសាមញ្ញមួយចំនួន ដោយផ្អែកលើនិយមន័យនៃដេរីវេ។ y = a x (0 0. ពិចារណាថា | x | 0 គឺជាចំណុចបំពាន បន្ទាប់មក 0. ពិចារណាថា | x | 0 ជា​ចំណុច​បំពាន​មួយ​បន្ទាប់​មក ">

0. ពិចារណាថា | x | 0 គឺជាចំណុចបំពាន បន្ទាប់មកឧទាហរណ៍ 4. y = sinx, x R. យក x 0 R ហើយគណនាចំនួនបន្ថែមនៃអនុគមន៍នៅចំណុចនេះ៖ ដូច្នេះ (sinx) = cosx, x R" title=" 5 ឧទាហរណ៍ 3. ចូរយើងយក x 0 > 0. ពិចារណាថា | x | 0 គឺជាចំនុចបំពាន បន្ទាប់មក ឧទាហរណ៍ 4. y = sinx, x R. ចូរយើងយក x 0 R ហើយគណនាចំនួនបន្ថែមនៃអនុគមន៍នៅចំណុចនេះ៖ ដូច្នេះ (sinx) = cosx, x R ។" class="link_thumb"> 5 !} 5 ឧទាហរណ៍ 3. យក x 0 > 0. ពិចារណាថា | x | 0 គឺជាចំនុចដែលបំពាន បន្ទាប់មកឧទាហរណ៍ 4. y = sinx, x R. ចូរយើងយក x 0 R ហើយគណនាចំនួនបន្ថែមនៃអនុគមន៍នៅចំណុចនេះ៖ ដូច្នេះ (sinx) = cosx, x R ។ 0. ពិចារណាថា | x | 0 ជាចំនុចអតិផរណា បន្ទាប់មក ឧទាហរណ៍ 4. y = sinx, x R. យក x 0 R ហើយគណនាចំនួនបន្ថែមនៃអនុគមន៍នៅចំណុចនេះ៖ ដូច្នេះ (sinx) = cosx, x R."> 0. ពិចារណាថា |x | 0 - ចំណុចបំពាន បន្ទាប់មកឧទាហរណ៍ 4. y \u003d sinx, x R. យក x 0 R ហើយគណនាការបង្កើនមុខងារនៅចំណុចនេះ៖ ដូច្នេះ (sinx) \u003d cosx, x R."> 0. ពិចារណាថា | x | 0 គឺជាចំណុចបំពាន បន្ទាប់មកឧទាហរណ៍ 4. y = sinx, x R. យក x 0 R ហើយគណនាចំនួនបន្ថែមនៃអនុគមន៍នៅចំណុចនេះ៖ ដូច្នេះ (sinx) = cosx, x R" title=" 5 ឧទាហរណ៍ 3. ចូរយើងយក x 0 > 0. ពិចារណាថា | x | 0 គឺជាចំនុចបំពាន បន្ទាប់មក ឧទាហរណ៍ 4. y = sinx, x R. ចូរយើងយក x 0 R ហើយគណនាចំនួនបន្ថែមនៃអនុគមន៍នៅចំណុចនេះ៖ ដូច្នេះ (sinx) = cosx, x R ។"> title="5 ឧទាហរណ៍ 3. យក x 0 > 0. ពិចារណាថា | x | 0 គឺជាចំនុចដែលបំពាន បន្ទាប់មកឧទាហរណ៍ 4. y = sinx, x R. ចូរយើងយក x 0 R ហើយគណនាចំនួនបន្ថែមនៃអនុគមន៍នៅចំណុចនេះ៖ ដូច្នេះ (sinx) = cosx, x R ។"> !}

៦ ទ្រឹស្តីបទ។ ប្រសិនបើមុខងារ f(x) អាចខុសគ្នាត្រង់ចំនុច x 0 នោះវានឹងបន្តនៅចំណុចនោះ។ ភស្តុតាង។ អនុញ្ញាតឱ្យវាមាន បន្ទាប់មកពីទីនេះយើងទទួលបាន f (x) - f (x 0) \u003d f "(x 0) (x - x 0) + (x - x 0) α (x) សម្រាប់ x x 0 ។ , f ( x) គឺបន្តនៅចំណុច x 0 ។ ការបន្តនៃអនុគមន៍ផ្សេងគ្នា (1)

7 ចំណាំ។ ការបន្តនៃអនុគមន៍នៅចំណុចមួយមិនមែនជាលក្ខខណ្ឌគ្រប់គ្រាន់សម្រាប់អត្ថិភាពនៃដេរីវេនៅចំណុចនេះទេ។ ឧទាហរណ៍ 5. f (x) \u003d x ។ យើងស៊ើបអង្កេតឥរិយាបទរបស់ f (x) នៅជិត x 0 = 0 ។ នៅទីនេះ និង f (x) f (0) = 0 សម្រាប់ x 0 ។ អនុគមន៍គឺបន្តនៅចំណុច x 0 \u003d 0 ។ ពិចារណា x y 0 ដែនកំណត់មិនមានទេ ព្រោះដូច្នេះ អនុគមន៍ f (x) \u003d x មិនមានដេរីវេនៅចំណុច x \u003d 0 ទោះបីជាវាមាន បន្តនៅចំណុចនេះ។

8 ឧទាហរណ៍ x y 0 at x 0. at x 0. I.e. f (x) គឺបន្តនៅ x = 0 ។ f(x) មិនមានដេរីវេនៅ x = 0 ទេ ដូច្នេះហើយវាមិនខុសគ្នាត្រង់ចំណុចនោះទេ។ យើងស៊ើបអង្កេតឥរិយាបទនៃ f (x) នៅក្នុងបរិវេណនៃចំនុច x = 0 ។

9 អនុញ្ញាតឱ្យអនុគមន៍ y \u003d f (x) ខុសគ្នាត្រង់ចំនុច x 0។ បន្ទាប់មកយោងទៅតាម (1) ការបង្កើនរបស់វានៅចំណុច x 0 អាចត្រូវបានសរសេរជា y \u003d f (x 0 + x) - f (x 0) \u003d f ( x 0) x + o(x) នៅ x ។ ឌីផេរ៉ង់ស្យែលនៃអនុគមន៍ f (x 0) x - ផ្នែកលីនេអ៊ែរសំខាន់នៃការបង្កើនមុខងារ y \u003d f (x) នៅចំណុច x 0 លីនេអ៊ែរទាក់ទងនឹង x ត្រូវបានគេហៅថាឌីផេរ៉ង់ស្យែលនៃអនុគមន៍នៅ ចំណុច x 0 នៅក្នុងការបង្កើន x និងត្រូវបានតំណាង df (x 0; x) ឬ df (x 0) ឬ df ឬ dу ។ y \u003d f (x 0 + x) - f (x 0) \u003d df (x 0; x) + o (x) នៅ x ។ និយមន័យ។ ផ្នែកសំខាន់នៃការកើនឡើង, លីនេអ៊ែរក្នុង x ។ លំដាប់​ខ្ពស់​ជាង x ។ ឥឡូវនេះការបង្កើនមុខងារអាចត្រូវបានសរសេរដូចនេះ៖

10 ចំណាំ។ ការកើនឡើង x ជារឿយៗត្រូវបានតាងដោយនិមិត្តសញ្ញា dx ហើយត្រូវបានគេហៅថាឌីផេរ៉ង់ស្យែលនៃអថេរឯករាជ្យ។ ដូច្នេះឌីផេរ៉ង់ស្យែលនៃអនុគមន៍នៅចំណុច x 0 អាចត្រូវបានសរសេរជា df (x 0) \u003d f "(x 0) dx ។ ប្រសិនបើអនុគមន៍អាចខុសគ្នានៅចំណុចនីមួយៗនៃចន្លោះពេលជាក់លាក់មួយ នោះឌីផេរ៉ង់ស្យែលរបស់វាគឺ មុខងារនៃ x និង dx៖ dy \u003d f "(x)dx ។ ពីទីនេះជាពិសេស កន្សោមសម្រាប់ដេរីវេត្រូវបានទទួល នោះមានន័យថា ដេរីវេអាចត្រូវបានចាត់ទុកថាជាសមាមាត្រនៃឌីផេរ៉ង់ស្យែលនៃអនុគមន៍ទៅនឹងឌីផេរ៉ង់ស្យែលនៃអថេរឯករាជ្យ។

11 អត្ថន័យធរណីមាត្រនៃដេរីវេ និងឌីផេរ៉ង់ស្យែល អនុញ្ញាតឱ្យអនុគមន៍ y \u003d f (x) ត្រូវបានកំណត់ក្នុង U (x 0) និងអាចខុសគ្នាត្រង់ចំនុច x 0. M0M0 M x0x0 x 0 + x y x y = f (x) y0y0 y 0 + y 0 L គឺជាសេកនៃ L 0 - តង់សង់ x y \u003d f (x 0 + x) - f (x 0) នៅ x ដោយសារការបន្តនៃអនុគមន៍។ តង់សង់ទៅក្រាហ្វនៃអនុគមន៍ y \u003d f (x) នៅចំណុច M 0 គឺជាទីតាំងកំណត់នៃសេកង់ L នៅ x ។ y ប្រសិនបើមុខងារអាចខុសគ្នាត្រង់ចំនុច x 0 នោះនៅក្នុងសមីការ secant y / x f (x 0) at x ហើយសមីការតង់សង់មានទម្រង់ y \u003d y 0 + f (x 0) (x - x 0) .

12 M0M0 M x0x0 x 0 + x dy = df(x 0; x) = f (x 0) x x y = f(x) f(x0)f(x0) f(x 0 + x) 0 x y F E EM = o (x) នៅ x 0 L0L0 tg \u003d f (x 0) ប្រសិនបើ y / x នៅ x នោះបន្ទាត់ត្រង់ x \u003d x 0 ដែលកើតចេញពីសមីការនិមិត្ត ត្រូវបានគេហៅថាតង់ហ្សង់បញ្ឈរទៅក្រាហ្វនៃអនុគមន៍នៅ ចំនុច M 0. ពីសមីការតង់សង់យើងទទួលបាន y - y 0 \u003d f (x 0) (x - x 0) \u003d df (x 0) - ការកើនឡើងនៃតង់សង់តង់សង់នៅពេលផ្លាស់ទីពីចំនុច x 0 ទៅចំនុច x . ធម្មតាទៅនឹងក្រាហ្វនៃអនុគមន៍នៅចំណុច M 0 គឺជាបន្ទាត់ត្រង់កាត់កែងទៅនឹងតង់សង់ដែលឆ្លងកាត់ចំណុច M 0 ។ សមីការរបស់វាមានទម្រង់ y \u003d y 0 - 1 / f (x 0) (x - x 0). L 1 - ធម្មតា។

13 កម្មវិធីរូបវិទ្យានៃដេរីវេ និងឌីផេរ៉ង់ស្យែល ប្រសិនបើ S (t) គឺជាផ្លូវដែលធ្វើដំណើរដោយចំណុចសម្ភារៈក្នុងពេលវេលា t នោះ S "(t) គឺជាល្បឿនភ្លាមៗនៃចំណុចសម្ភារៈ ហើយ dS \u003d S "(t) dt គឺជាចម្ងាយដែលចំណុចសម្ភារៈនឹងធ្វើដំណើរក្នុងរយៈពេលពី t ដល់ t + dt ប្រសិនបើវាផ្លាស់ទីក្នុងល្បឿនស្មើនឹងល្បឿនភ្លាមៗនៅពេល t ។ ប្រសិនបើ Q (t) គឺជាបរិមាណនៃចរន្តអគ្គិសនីដែលហូរកាត់ផ្នែកឆ្លងកាត់នៃ conductor នៅពេល t នោះ Q "(t) \u003d I គឺជាកម្លាំងបច្ចុប្បន្ន។ ប្រសិនបើ N (t) គឺជាបរិមាណនៃសារធាតុដែលបានបង្កើតឡើងនៅពេល t ។ ក្នុងអំឡុងពេលប្រតិកម្មគីមីបន្ទាប់មក N "(t) - អត្រានៃប្រតិកម្មគីមីមួយ។

ប្រសិនបើមុខងារ y = f(x) អាចខុសគ្នាត្រង់ចំណុចខ្លះ x = x 0 បន្ទាប់មកវាបន្តនៅចំណុចនេះ។

ដូច្នេះ នៅចំនុចដាច់ មុខងារមិនអាចមានដេរីវេទេ។ ការសន្និដ្ឋាននៃការសន្ទនាគឺមិនពិត, i.e. ពីការពិតដែលថានៅចំណុចណាមួយ។ x = x 0 មុខងារ y = f(x) គឺបន្ត វាមិនធ្វើតាមថាវាខុសគ្នាត្រង់ចំណុចនេះទេ។ ឧទាហរណ៍មុខងារ y = |x| បន្តសម្រាប់ទាំងអស់គ្នា x (–< X < ), но в точке x= 0 មិនមានដេរីវេទេ។ ត្រង់​ចំណុច​នេះ មិន​មាន​តង់សង់​ទៅ​នឹង​ក្រាហ្វ​ទេ។ មានតង់សង់ខាងស្តាំ និងតង់សង់ខាងឆ្វេង ប៉ុន្តែវាមិនត្រូវគ្នាទេ។

21 ការស្វែងរកច្បាប់។ ផលិតផល បរិមាណ

វិធាន 1ប្រសិនបើអនុគមន៍ y \u003d f (x) និង y \u003d g (x) មានដេរីវេនៅចំណុច x នោះផលបូករបស់ពួកគេក៏មានដេរីវេនៅចំណុច x ហើយដេរីវេនៃផលបូកគឺស្មើនឹងផលបូកនៃ និស្សន្ទវត្ថុ៖
(f (x) + 8 (x))" \u003d f (x) + (x) ។
នៅក្នុងការអនុវត្ត ច្បាប់នេះត្រូវបានបង្កើតតាមរបៀបខ្លីជាងនេះ៖ ដេរីវេនៃផលបូកគឺស្មើនឹងផលបូកនៃនិស្សន្ទវត្ថុ។
ឧទាហរណ៍,
ក្បួនទី 2ប្រសិនបើអនុគមន៍ y \u003d f (x) មានដេរីវេនៅចំណុច x នោះអនុគមន៍ y \u003d kf (x) មានដេរីវេនៅចំណុច x និង៖

នៅក្នុងការអនុវត្តច្បាប់នេះត្រូវបានបង្កើតតាមរបៀបខ្លីជាងនេះ: កត្តាថេរអាចត្រូវបានយកចេញពីសញ្ញានៃដេរីវេ។ ឧទាហរណ៍,

វិធាន 3ប្រសិនបើមុខងារ y \u003d f (x) និង y \u003d g (x) មានដេរីវេនៅចំណុច x នោះផលិតផលរបស់ពួកគេក៏មានដេរីវេនៅចំនុច x ហើយ៖

នៅក្នុងការអនុវត្ត ច្បាប់នេះត្រូវបានបង្កើតដូចខាងក្រោមៈ ដេរីវេនៃផលនៃអនុគមន៍ពីរគឺស្មើនឹងផលបូកនៃពាក្យពីរ។ ពាក្យទីមួយគឺជាផលនៃដេរីវេនៃអនុគមន៍ទីមួយ និងអនុគមន៍ទីពីរ ហើយពាក្យទីពីរគឺជាផលគុណនៃអនុគមន៍ទីមួយ និងដេរីវេនៃអនុគមន៍ទីពីរ។
ឧទាហរណ៍:
ក្បួនទី 4ប្រសិនបើមុខងារ y \u003d f (x) និង y \u003d g (x) មានដេរីវេនៅពេលនោះ ហើយកូតាមានដេរីវេនៅចំណុច x លើសពីនេះទៀត៖

តារាងនៃនិស្សន្ទវត្ថុស្មុគស្មាញ

22 ភាពខុសគ្នា។ funkt ។ នៅចំណុច

មុខងារ y=f(x) ត្រូវបានគេហៅថាខុសគ្នានៅចំណុចមួយ។ x 0 ប្រសិនបើការកើនឡើងរបស់វា Δ y(x 0,Δ x) អាចត្រូវបានតំណាងជា

Δ y(x 0,Δ x)=កΔ x+o(Δ x).

ផ្នែកលីនេអ៊ែរសំខាន់ កΔ xការកើនឡើង Δ yត្រូវបានគេហៅថាឌីផេរ៉ង់ស្យែលនៃមុខងារនេះនៅចំណុច x 0 ដែលត្រូវគ្នានឹងការកើនឡើង Δ xនិងត្រូវបានតំណាងដោយនិមិត្តសញ្ញា ឌី(x 0,Δ x).

ដើម្បីឱ្យមុខងារ y=f(x) គឺខុសគ្នាត្រង់ចំណុច x 0, វាចាំបាច់ និងគ្រប់គ្រាន់ដែលដេរីវេ f′( x 0) ខណៈពេលដែលសមភាព ក=f′( x 0).

កន្សោមសម្រាប់ឌីផេរ៉ង់ស្យែលមានទម្រង់

ឌី(x 0,dx)=f′( x 0)dx,

កន្លែងណា dx=Δ x.

២៣ ផលិត។ ភាពខុសគ្នា មុខងារ

ដេរីវេនៃមុខងារស្មុគស្មាញ។ ដេរីវេនៃអនុគមន៍ដែលបានកំណត់តាមប៉ារ៉ាម៉ែត្រ

អនុញ្ញាតឱ្យ y - មុខងារស្មុគស្មាញ x, i.e. y = f(យូ), យូ = g(x) ឬ

ប្រសិនបើ g(x) និង f(យូ) គឺជាមុខងារផ្សេងគ្នានៃអាគុយម៉ង់របស់ពួកគេរៀងៗខ្លួននៅចំណុច xនិង យូ = g(x), បន្ទាប់មកមុខងារស្មុគ្រស្មាញក៏ខុសគ្នាត្រង់ចំណុចដែរ។ x ហើយត្រូវបានរកឃើញដោយរូបមន្ត

ដេរីវេនៃអនុគមន៍ដែលបានផ្តល់ឱ្យតាមប៉ារ៉ាម៉ែត្រ។

24 Prod. និងភាពខុសគ្នា។ លំដាប់ខ្ពស់ជាង

ឥឡូវ​នេះ និស្សន្ទវត្ថុ​លំដាប់​ទី ត្រូវ​បាន​កំណត់​ក្នុង​សង្កាត់​មួយ​ចំនួន​នៃ​ចំណុច ហើយ​អាច​ខុសគ្នា។ បន្ទាប់មក

ប្រសិនបើអនុគមន៍មាននិស្សន្ទវត្ថុដោយផ្នែកទាក់ទងនឹងអថេរមួយនៅក្នុងដែន D មួយចំនួននោះ និស្សន្ទវត្ថុដែលមានឈ្មោះជាមុខងាររបស់ អាចមាននិស្សន្ទវត្ថុដោយផ្នែកទាក់ទងនឹងអថេរដូចគ្នា ឬអថេរផ្សេងទៀតនៅចំណុចណាមួយ។ សម្រាប់អនុគមន៍ដើម និស្សន្ទវត្ថុទាំងនេះនឹងជានិស្សន្ទវត្ថុផ្នែកទីពីរ (ឬនិស្សន្ទវត្ថុផ្នែកទីពីរ)។

ដេរីវេមួយផ្នែកនៃលំដាប់ទីពីរ ឬខ្ពស់ជាងនេះ ដែលធ្វើឡើងទាក់ទងនឹងអថេរផ្សេងៗត្រូវបានគេហៅថា ដេរីវេភាគចម្រុះ។ ឧទាហរណ៍,

លំដាប់ឌីផេរ៉ង់ស្យែល ន, កន្លែងណា n > 1នៃអនុគមន៍នៅចំណុចមួយចំនួនត្រូវបានគេហៅថាឌីផេរ៉ង់ស្យែលនៅចំណុចនៃឌីផេរ៉ង់ស្យែលលំដាប់នេះ។ (n - 1)នោះគឺ

សម្រាប់មុខងារដែលអាស្រ័យលើអថេរមួយ ឌីផេរ៉ង់ស្យែលទីពីរ និងទីបីមើលទៅដូចនេះ៖

ពីនេះយើងអាចទាញយកទម្រង់ទូទៅនៃឌីផេរ៉ង់ស្យែល ន- លំដាប់ពីមុខងារ៖

25 ទ្រឹស្តីបទ Fermat, Rolle, Langrage

v ទ្រឹស្តីបទ Fermat៖អនុញ្ញាតឱ្យមុខងារមួយត្រូវបានកំណត់នៅលើ និងឈានដល់តម្លៃអតិបរមា និងអប្បបរមារបស់វា ( មនិង ម) នៅក្នុងមួយចំនួន។ ប្រសិនបើមានដេរីវេនៅក្នុង នោះវាចាំបាច់ស្មើនឹង 0។

ភស្តុតាង៖ មាន។ ករណីពីរអាចធ្វើទៅបាន៖

1) , => , => .

2) , => , => .

ពី 1) និង 2) វាធ្វើតាមនោះ។

v ទ្រឹស្តីបទរបស់ Rolle (អំពីឫសនៃដេរីវេ)៖អនុញ្ញាតឱ្យអនុគមន៍បន្តនៅលើ និងខុសគ្នានៅលើ ហើយយកតម្លៃដូចគ្នានៅចុងបញ្ចប់នៃផ្នែក៖ . បន្ទាប់មក យ៉ាងហោចណាស់មានចំណុចមួយនៅក្នុង ដែលដេរីវេគឺ .

v ភ័ស្តុតាង៖ ការឈានទៅដល់ជាបន្តបន្ទាប់ មនិង ម. បន្ទាប់មកករណីពីរអាចធ្វើទៅបាន៖

2) តម្លៃធំបំផុតត្រូវបានសម្រេចក្នុងចន្លោះពេលយោងទៅតាមទ្រឹស្តីបទរបស់ Fermat ។

v ទ្រឹស្តីបទរបស់ Langage (អំពីការកើនឡើងកំណត់)៖អនុញ្ញាតឱ្យមុខងារបន្ត និងអាចបែងចែកបាននៅលើ . បន្ទាប់មក មានយ៉ាងហោចណាស់មួយ ដែលសមភាពខាងក្រោមទទួលបាន៖ .

ភស្តុតាង៖ ចូរយើងណែនាំមុខងារ។ (បន្តនិងអាចខុសគ្នានៅលើ) ។

អនុគមន៍បំពេញទ្រឹស្តីបទរបស់ Rolle ដែលមាន៖ , , , .

មុខងារត្រូវបានគេហៅថា កើនឡើងយ៉ាងតឹងរ៉ឹងនៅលើប្រសិនបើ

មុខងារត្រូវបានគេហៅថា ថយចុះនៅលើប្រសិនបើ

មុខងារត្រូវបានគេហៅថា ថយចុះយ៉ាងតឹងរ៉ឹងនៅលើប្រសិនបើ

និយមន័យ៖ ដេរីវេនៃអនុគមន៍នៅចំណុចមួយគឺជាដែនកំណត់ដែលសមាមាត្រនៃការកើនឡើងរបស់វានៅចំណុចនោះទៅនឹងការកើនឡើងដែលត្រូវគ្នានៃអាគុយម៉ង់នៅពេលក្រោយមានទំនោរទៅសូន្យ៖

នោះ​គឺ​ប្រសិន​បើ​បាន​កំណត់​នៅ​ក្នុង​នោះ​

ទ្រឹស្តីបទ ១៖

ក្រាហ្វនៃអនុគមន៍មួយមានតង់ហ្សង់មិនបញ្ឈរ ប្រសិនបើនិងមានតែតម្លៃកំណត់នៃដេរីវេនៃអនុគមន៍នេះនៅចំណុចដែលបានផ្តល់ឱ្យ។

ភស្តុតាង៖

អនុញ្ញាតឱ្យមានតម្លៃ f'()-finite បន្ទាប់មក

សូមឱ្យមានតង់សង់មិនបញ្ឈរ => មាន - កំណត់។

សេកមានទំនោរទៅរកតង់សង់។

ទ្រឹស្តីបទត្រូវបានបញ្ជាក់។

សំបុត្រទី 2 ការបន្តនៃអនុគមន៍ដែលមានដេរីវេ។

អនុគមន៍ f (x) ដែលកំណត់នៅក្នុងសង្កាត់មួយចំនួននៃចំណុច a ត្រូវបានគេហៅថាបន្តនៅចំណុចនេះ ប្រសិនបើ

ទ្រឹស្តីបទ៖ (លក្ខខណ្ឌចាំបាច់សម្រាប់អត្ថិភាពនៃដេរីវេ)

ប្រសិនបើមុខងារមានចំនុចកំណត់ នោះវាបន្តនៅចំណុច។

ភស្តុតាង៖

ដូច្នេះ - គឺបន្តនៅចំណុចមួយ។

ទ្រឹស្តីបទត្រូវបានបញ្ជាក់។

មតិយោបល់ : converse មិនពិតទេ ប្រសិនបើអនុគមន៍បន្តនៅចំណុចមួយ នោះវាមិនធ្វើតាមថាវាមានដេរីវេនៅចំណុចនោះទេ។

សេចក្តីថ្លែងការណ៍ : ប្រសិនបើអនុគមន៍មួយមានដេរីវេទីវខាងស្តាំ និងខាងឆ្វេងនៅចំណុចមួយ នោះវាបន្តទាំងនៅខាងស្តាំ និងខាងឆ្វេង។

សំបុត្រ ៣

ដេរីវេនៃផលបូក, ផលិតផល, កូតា។

ដេរីវេនៃមុខងារបញ្ច្រាស។

និយមន័យនៃមុខងារដែលអាចបែងចែកបាន។ លក្ខខណ្ឌចាំបាច់ និងគ្រប់គ្រាន់សម្រាប់ភាពខុសគ្នា។

អនុញ្ញាតឱ្យអនុគមន៍មានដេរីវេនៅចំណុចមួយ (ចុងក្រោយ)៖ .

បន្ទាប់មក សម្រាប់ទំហំតូចល្មម យើងអាចសរសេរជាផលបូកនៃអនុគមន៍មួយចំនួន ដែលយើងសម្គាល់ដោយ វាមានទំនោរទៅសូន្យ រួមជាមួយនឹង៖,

ហើយការកើនឡើងនៅចំណុចមួយអាចត្រូវបានសរសេរជា:

ឬ (1) ,

សម្រាប់​កន្សោម​ត្រូវ​បាន​គេ​យល់​ថា​ជា​មុខងារ​មួយ​ដែល​សមាមាត្រ​របស់​វា​មាន​ទំនោរ​ទៅ​សូន្យ​រួម​ជាមួយ។

ការពន្យល់៖

និយមន័យ .

អនុគមន៍​ត្រូវ​បាន​គេ​ហៅ​ថា​ខុស​គ្នា​នៅ​ចំណុច​មួយ ប្រសិន​បើ​ការ​បង្កើន​របស់​វា​អាច​ត្រូវ​បាន​តំណាង​ជា៖ (2),

ដែល A មិនអាស្រ័យលើ ប៉ុន្តែជាទូទៅអាស្រ័យលើ .

ទ្រឹស្តីបទ ១៖

ដើម្បីឱ្យមុខងារអាចខុសគ្នាត្រង់ចំណុចមួយ វាចាំបាច់ និងគ្រប់គ្រាន់ដែលវាមានដេរីវេទីកំណត់នៅចំណុចនោះ។

ភស្តុតាង៖

ភាពគ្រប់គ្រាន់នៃលក្ខខណ្ឌ បានបង្ហាញខាងលើ៖ អត្ថិភាពនៃនិស្សន្ទវត្ថុកំណត់បានបង្ហាញពីលទ្ធភាពនៃការតំណាងក្នុងទម្រង់ (1) ដែលមនុស្សម្នាក់អាចកំណត់

លក្ខខណ្ឌចាំបាច់ . អនុញ្ញាតឱ្យមុខងារមានភាពខុសប្លែកគ្នានៅចំណុចមួយ។ បន្ទាប់មកពី (2) សន្មតថាយើងទទួលបាន។

ដែនកំណត់នៃផ្នែកខាងស្តាំសម្រាប់មានហើយស្មើនឹង A: ។

នេះមានន័យថាមានដេរីវេ។ ទ្រឹស្តីបទត្រូវបានបញ្ជាក់។

សំបុត្រ 6 ឌីផេរ៉ង់ស្យែលនៃមុខងារមួយ អត្ថន័យធរណីមាត្ររបស់វា។

ប្រសិនបើមុខងារ fមានដេរីវេ f΄(x o ) នៅចំណុច x oបន្ទាប់មកមានដែនកំណត់ ដែល Δ f=f(x o + Δ x)-f(x o ) ,, ឬកន្លែងណា A=f΄(x o ) .

និយមន័យ៖

មុខងារ fខុសគ្នាត្រង់ចំណុចមួយ។ x oប្រសិនបើការកើនឡើងរបស់វាអាចត្រូវបានតំណាងជា៖

កន្លែងណា កΔ x=df. (*)

ឌីផេរ៉ង់ស្យែលគឺជាផ្នែកលីនេអ៊ែរសំខាន់នៃការបង្កើនមុខងារ។

ប្រសិនបើមាននិស្សន្ទវត្ថុកំណត់ f΄(x o ) នៅចំណុច x oបន្ទាប់មកមុខងារ f(x)ត្រង់ចំណុចនេះ គឺអាចខុសគ្នា។

ការសន្ទនាក៏ពិតដែរ៖ ប្រសិនបើមុខងារ fខុសគ្នាត្រង់ចំណុចមួយ។ x o, i.e. ការកើនឡើងរបស់វាអាចត្រូវបានតំណាងជា (*) បន្ទាប់មកវាមានដេរីវេនៅចំណុច x oស្មើនឹង ក:

អត្ថន័យធរណីមាត្រនៃឌីផេរ៉ង់ស្យែល៖

កនិង ខ- ចំណុចក្រាហ្វិក f(x)ដែលត្រូវគ្នានឹងតម្លៃ x oនិង (x o + Δ x)អថេរឯករាជ្យ។ ចំណុចបញ្ជា កនិង ខស្មើគ្នា f(x o ) និង f(x o + Δ x). ការបង្កើនមុខងារ Δ f=f(x o + Δ x)-f(x o ) នៅចំណុច x oស្មើនឹងប្រវែងនៃផ្នែក BDហើយអាចត្រូវបានតំណាងជាផលបូក Δ f=BD=DC+CB, កន្លែងណា DC = tgaΔ x=f΄(x o ) Δ xនិង α គឺជាមុំរវាងតង់សង់នៅចំណុច កទៅក្រាហ្វនិងទិសដៅវិជ្ជមាននៃអ័ក្ស x. ពីទីនេះវាច្បាស់ណាស់។ ឌី.ស៊ីគឺជាឌីផេរ៉ង់ស្យែលនៃមុខងារ fនៅចំណុច x o :

DC=df=f΄(x o ) Δ x.

ទន្ទឹមនឹងនេះចំណែកនៃសមាជិកទីពីរ ស៊ី.ប៊ីការកើនឡើង Δ fគណនាទំហំ។ តម្លៃនេះ Δ xប្រហែលជាច្រើនជាងពាក្យសំខាន់ ប៉ុន្តែវាជាលំដាប់ខ្ពស់ជាង Δ xនៅពេលដែល Δ x → 0.

លក្ខណសម្បត្តិនៃមុខងារបន្តក្នុងចន្លោះពេល

អនុញ្ញាតឱ្យយើងពិចារណាលក្ខណៈសម្បត្តិមួយចំនួននៃមុខងារបន្តនៅចន្លោះពេលមួយ។ យើងបង្ហាញលក្ខណៈសម្បត្តិទាំងនេះដោយគ្មានភស្តុតាង។

មុខងារ y = f(x)ហៅ បន្តនៅលើផ្នែក [ក, ខ] ប្រសិនបើវាបន្តនៅគ្រប់ចំណុចខាងក្នុងនៃផ្នែកនេះ ហើយនៅចុងបញ្ចប់របស់វា i.e. នៅចំណុច កនិង ខគឺបន្តនៅខាងស្តាំ និងខាងឆ្វេង រៀងគ្នា។

ទ្រឹស្តីបទ ១.មុខងារបន្តនៅលើផ្នែក [ ក, ខ] យ៉ាងហោចណាស់នៅចំណុចមួយនៃផ្នែកនេះយកតម្លៃធំបំផុត ហើយយ៉ាងហោចណាស់នៅចំណុចមួយ - តូចបំផុត។

ទ្រឹស្តីបទចែងថាប្រសិនបើមុខងារ y = f(x)បន្តនៅលើផ្នែក [ ក, ខ] បន្ទាប់មកយ៉ាងហោចណាស់មានចំណុចមួយ។ x ១ Î [ ក, ខ] ដូចនេះតម្លៃនៃមុខងារ f(x)នៅចំណុចនេះនឹងជាតម្លៃធំបំផុតនៃតម្លៃទាំងអស់របស់វានៅលើផ្នែកនេះ៖ f(x1) ≥ f(x). ដូចគ្នានេះដែរមានចំណុចបែបនេះ x2ដែលក្នុងនោះតម្លៃនៃអនុគមន៍នឹងតូចបំផុតនៃតម្លៃទាំងអស់នៅលើផ្នែក៖ f(x 1) ≤ f(x).

វាច្បាស់ណាស់ថាវាអាចមានចំណុចបែបនេះជាច្រើនឧទាហរណ៍តួលេខបង្ហាញថាមុខងារ f(x)យកតម្លៃតូចបំផុតនៅពីរចំណុច x2និង x 2 ".

មតិយោបល់. សេចក្តីថ្លែងការណ៍នៃទ្រឹស្តីបទអាចក្លាយទៅជាមិនពិត ប្រសិនបើយើងពិចារណាតម្លៃនៃអនុគមន៍នៅលើចន្លោះពេល ( ក, ខ) ជាការពិតប្រសិនបើយើងពិចារណាមុខងារ y=xនៅលើ (0, 2) បន្ទាប់មកវាបន្តនៅលើចន្លោះពេលនេះ ប៉ុន្តែមិនឈានដល់តម្លៃអតិបរមា ឬអប្បបរមារបស់វានៅក្នុងវាទេ៖ វាឈានដល់តម្លៃទាំងនេះនៅចុងបញ្ចប់នៃចន្លោះពេល ប៉ុន្តែចុងបញ្ចប់មិនមែនជារបស់យើងទេ។ តំបន់។

ដូចគ្នានេះផងដែរ ទ្រឹស្តីបទឈប់ជាការពិតសម្រាប់មុខងារមិនបន្ត។ ផ្តល់ឧទាហរណ៍មួយ។

ផលវិបាក។ប្រសិនបើមុខងារ f(x)បន្ត​នៅ [ ក, ខ] បន្ទាប់មកវាត្រូវបានកំណត់នៅលើចន្លោះពេលនេះ។

ទ្រឹស្តីបទ ២.អនុញ្ញាតឱ្យមុខងារ y = f(x)បន្តនៅលើផ្នែក [ ក, ខ] ហើយយកតម្លៃនៃសញ្ញាផ្សេងគ្នានៅចុងផ្នែកនេះ បន្ទាប់មកមានយ៉ាងហោចណាស់មួយចំណុចនៅខាងក្នុងផ្នែក x=Cកន្លែងដែលមុខងារបាត់៖ f(C)= 0 ដែល ក< C< b

ទ្រឹស្តីបទនេះមានអត្ថន័យធរណីមាត្រសាមញ្ញ៖ ប្រសិនបើចំនុចនៃក្រាហ្វនៃអនុគមន៍បន្ត y = f(x)ដែលត្រូវគ្នាទៅនឹងចុងបញ្ចប់នៃផ្នែក [ ក, ខ] ដេកនៅលើជ្រុងម្ខាងនៃអ័ក្ស គោបន្ទាប់មកក្រាហ្វនេះយ៉ាងហោចណាស់នៅចំណុចមួយនៃផ្នែកកាត់អ័ក្ស គោ. មុខងារមិនបន្តអាចមិនមានទ្រព្យសម្បត្តិនេះទេ។

ទ្រឹស្តីបទនេះទទួលយកការទូទៅដូចខាងក្រោម។

ទ្រឹស្តីបទ ៣ (ទ្រឹស្តីបទស្តីពីតម្លៃមធ្យម)។អនុញ្ញាតឱ្យមុខងារ y = f(x)បន្តនៅលើផ្នែក [ ក, ខ] និង f(a) = ក, f (b) = ខ. បន្ទាប់មកសម្រាប់លេខណាមួយ។ គរវាង កនិង ខមានចំណុចបែបនេះនៅក្នុងផ្នែកនេះ។ គÎ [ ក, ខ] អ្វី f (c) = គ.

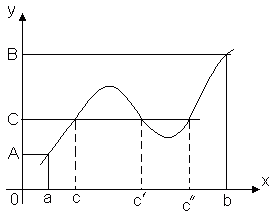
ទ្រឹស្តីបទនេះគឺជាក់ស្តែងតាមធរណីមាត្រ។ ពិចារណាក្រាហ្វនៃមុខងារ y = f(x). អនុញ្ញាតឱ្យ f(a) = ក, f (b) = ខ. បន្ទាប់មកបន្ទាត់ណាមួយ។ y=C, កន្លែងណា គ- លេខណាមួយរវាង កនិង ខ, ប្រសព្វក្រាហ្វនៃអនុគមន៍យ៉ាងហោចណាស់នៅចំណុចមួយ។ abscissa នៃចំនុចប្រសព្វនឹងជាតម្លៃនោះ។ x=Cនៅឯណា f (c) = គ.

ដូច្នេះ មុខងារបន្តដែលឆ្លងកាត់ពីតម្លៃមួយរបស់វាទៅតម្លៃមួយទៀត ចាំបាច់ឆ្លងកាត់តម្លៃមធ្យមទាំងអស់។ ជាពិសេស:

ផលវិបាក។ប្រសិនបើមុខងារ y = f(x)គឺបន្តនៅចន្លោះពេលខ្លះ ហើយទទួលយកតម្លៃធំបំផុត និងតូចបំផុត បន្ទាប់មកនៅចន្លោះពេលនេះ វាត្រូវចំណាយពេលយ៉ាងហោចណាស់ម្តង តម្លៃណាមួយរវាងតម្លៃតូចបំផុត និងធំបំផុតរបស់វា។

ដេរីវេ និងកម្មវិធីរបស់វា។ និយមន័យដេរីវេ

តោះមានមុខងារខ្លះ y=f(x),កំណត់នៅចន្លោះពេលខ្លះ។ សម្រាប់តម្លៃអាគុយម៉ង់នីមួយៗ xពីចន្លោះពេលនេះមុខងារ y=f(x)មានអត្ថន័យជាក់លាក់។

ពិចារណាតម្លៃអាគុយម៉ង់ពីរ៖ ដំបូង x 0 និងថ្មី។ x.

ភាពខុសគ្នា x–x 0 ត្រូវបានគេហៅថា ការបង្កើនអាគុយម៉ង់ xនៅចំណុច x 0 និងតំណាង Δx. ដូច្នេះ ∆x = x − x 0 (ការបង្កើនអាគុយម៉ង់អាចជាវិជ្ជមាន ឬអវិជ្ជមាន)។ ពីសមភាពនេះវាធ្វើតាមនោះ។ x=x 0 +Δx, i.e. តម្លៃដំបូងនៃអថេរបានទទួលការបន្ថែមមួយចំនួន។ បន្ទាប់មកប្រសិនបើនៅចំណុច x 0 តម្លៃមុខងារគឺ f(x 0 ), បន្ទាប់មកនៅចំណុចថ្មី។ xមុខងារនឹងយកតម្លៃ f(x) = f(x 0 +∆x).

ភាពខុសគ្នា y-y 0 = f(x) – f(x 0 ) ហៅ ការបង្កើនមុខងារ y = f(x)នៅចំណុច x 0 និងត្រូវបានតំណាងដោយនិមិត្តសញ្ញា Δy. ដូច្នេះ

Δy = f(x) – f(x 0 ) = f(x 0 +Δx) - f(x 0 ) .

(1)

ជាធម្មតាតម្លៃដំបូងនៃអាគុយម៉ង់ x 0 ត្រូវបានចាត់ទុកថាថេរ និងតម្លៃថ្មី។ x- អថេរ។ បន្ទាប់មក y 0 = f(x 0 ) ប្រែទៅជាថេរនិង y = f(x)- អថេរ។ ការកើនឡើង Δyនិង Δxក៏នឹងក្លាយជាអថេរ ហើយរូបមន្ត (1) បង្ហាញថា ឌីគឺជាមុខងារនៃអថេរ Δx.

ផ្សំសមាមាត្រនៃការកើនឡើងនៃអនុគមន៍ទៅនឹងការកើនឡើងនៃអាគុយម៉ង់

អនុញ្ញាតឱ្យយើងរកឃើញដែនកំណត់នៃទំនាក់ទំនងនេះនៅ Δx→0. ប្រសិនបើដែនកំណត់នេះមាន នោះវាត្រូវបានគេហៅថាដេរីវេនៃមុខងារនេះ។ f(x)នៅចំណុច x 0 និងសម្គាល់ f "(x 0). ដូច្នេះ

ដេរីវេមុខងារនេះ។ y = f(x)នៅចំណុច x 0 ត្រូវបានគេហៅថាដែនកំណត់នៃសមាមាត្របង្កើននៃអនុគមន៍Δ yដល់ការកើនឡើងនៃអាគុយម៉ង់ Δ xនៅពេលក្រោយមានទំនោរទៅសូន្យតាមអំពើចិត្ត។

ចំណាំថាសម្រាប់មុខងារដូចគ្នា ដេរីវេនៅចំណុចផ្សេងគ្នា xអាចទទួលយកតម្លៃផ្សេងគ្នា, i.e. ដេរីវេអាចត្រូវបានគិតថាជាមុខងារនៃអាគុយម៉ង់ x. មុខងារនេះត្រូវបានសម្គាល់ f "(x)

ដេរីវេត្រូវបានតំណាងដោយនិមិត្តសញ្ញា f "(x), y", . តម្លៃជាក់លាក់នៃដេរីវេនៅ x = កតំណាង f "(ក) ឬ y "| x=a.

ប្រតិបត្តិការនៃការស្វែងរកដេរីវេនៃអនុគមន៍មួយ។ f(x)ត្រូវបានគេហៅថាភាពខុសគ្នានៃមុខងារនេះ។

ដើម្បីស្វែងរកដោយផ្ទាល់នូវដេរីវេតាមនិយមន័យ អ្នកអាចអនុវត្តដូចខាងក្រោម ច្បាប់​នៃ​មេដៃ:

ឧទាហរណ៍។

អត្ថន័យមេកានិកនៃដេរីវេ

វាត្រូវបានគេស្គាល់ពីរូបវិទ្យាថាច្បាប់នៃចលនាឯកសណ្ឋានមានទម្រង់ s = v t, កន្លែងណា ស- ផ្លូវបានធ្វើដំណើរដល់ចំណុចទាន់ពេលវេលា t, vគឺជាល្បឿននៃចលនាឯកសណ្ឋាន។

ទោះយ៉ាងណាក៏ដោយចាប់តាំងពី ភាគច្រើននៃចលនាដែលកើតឡើងនៅក្នុងធម្មជាតិគឺមិនស្មើគ្នា បន្ទាប់មកក្នុងករណីទូទៅ ល្បឿន ហើយជាលទ្ធផល ចម្ងាយ សនឹងអាស្រ័យលើពេលវេលា t, i.e. នឹងជាមុខងារនៃពេលវេលា។

ដូច្នេះ សូម​ឲ្យ​ចំណុច​សម្ភារៈ​ផ្លាស់ទី​ក្នុង​បន្ទាត់​ត្រង់​ក្នុង​ទិស​មួយ​ស្រប​តាម​ច្បាប់ s=s(t)។

ចំណាំមួយភ្លែតនៅក្នុងពេលវេលា t 0. ដោយចំណុចនេះចំណុចបានឆ្លងកាត់ផ្លូវ s=s(t 0 ). ចូរយើងកំណត់ល្បឿន vចំណុចសម្ភារៈនៅពេល t 0 .

ដើម្បី​ធ្វើ​បែប​នេះ សូម​ពិចារណា​ពេល​វេលា​ផ្សេង​ទៀត។ t 0 + Δ t. វា​ត្រូវ​នឹង​ចម្ងាយ​ដែល​បាន​ធ្វើ​ដំណើរ s =s(t 0 + Δ t) បន្ទាប់មកសម្រាប់ចន្លោះពេល Δ tចំណុចបានធ្វើដំណើរតាមផ្លូវ Δs =s(t 0 + Δ t)–s(t)

ចូរយើងពិចារណាទំនាក់ទំនង។ វាត្រូវបានគេហៅថាល្បឿនមធ្យមក្នុងចន្លោះពេល Δ t. ល្បឿនមធ្យមមិនអាចកំណត់លក្ខណៈល្បឿននៃចលនានៃចំណុចណាមួយបានត្រឹមត្រូវទេនៅពេលនេះ t 0 (ដោយសារតែចលនាមិនស្មើគ្នា) ។ ដើម្បីបង្ហាញឱ្យកាន់តែច្បាស់នូវល្បឿនពិតនេះដោយប្រើល្បឿនមធ្យម អ្នកត្រូវប្រើចន្លោះពេលតិចជាង Δ t.

ដូច្នេះល្បឿននៃចលនានៅពេលកំណត់ t 0 (ល្បឿនភ្លាមៗ) គឺជាដែនកំណត់នៃល្បឿនមធ្យមក្នុងចន្លោះពេលពី t 0 ទៅ t 0 +Δ tនៅពេលដែល Δ t→0:

,

ទាំងនោះ។ ល្បឿននៃចលនាមិនស្មើគ្នាគឺជាដេរីវេនៃចម្ងាយធ្វើដំណើរដោយគោរពតាមពេលវេលា។

អត្ថន័យធរណីមាត្រនៃដេរីវេ

ចូរយើងណែនាំនិយមន័យនៃតង់សង់ទៅខ្សែកោងនៅចំណុចដែលបានផ្តល់ឱ្យ។

សូមឱ្យយើងមានខ្សែកោងនិងចំណុចថេរនៅលើវា។ ម ០(សូមមើលរូប) សូមពិចារណាចំណុចមួយទៀត មខ្សែកោង​នេះ​ហើយ​គូរ​វិនាទី ម 0 ម. ប្រសិនបើចំណុច មចាប់ផ្តើមផ្លាស់ទីតាមខ្សែកោង និងចំណុច ម ០នៅ​តែ​ស្ថិត​នៅ​ក្នុង​ស្ថាន​ភាព, secant ផ្លាស់​ប្តូ​រ​ទីតាំង​របស់​ខ្លួន​។ ប្រសិនបើជាមួយនឹងការប៉ាន់ស្មានគ្មានដែនកំណត់នៃចំណុច មកោងទៅចំណុច ម ០នៅផ្នែកម្ខាងៗ សេកមានទំនោរទៅរកទីតាំងនៃបន្ទាត់ត្រង់ជាក់លាក់មួយ។ ម 0 ធបន្ទាប់មកបន្ទាត់ត្រង់ ម 0 ធត្រូវបានគេហៅថាតង់សង់ទៅខ្សែកោងនៅចំណុចដែលបានផ្តល់ឱ្យ ម ០.

នោះ., តង់សង់ទៅខ្សែកោងនៅចំណុចដែលបានផ្តល់ឱ្យ ម ០ហៅថាទីតាំងកំណត់នៃសេកាន ម 0 មនៅពេលដែលចំណុច មទំនោរតាមបណ្តោយខ្សែកោងទៅចំណុចមួយ។ ម ០.

ឥឡូវពិចារណាមុខងារបន្ត y=f(x)និងខ្សែកោងដែលត្រូវគ្នានឹងមុខងារនេះ។ សម្រាប់តម្លៃមួយចំនួន Xមុខងារ 0 យកតម្លៃមួយ។ y0=f(x0)។តម្លៃទាំងនេះ x 0 និង y 0 នៅលើខ្សែកោងត្រូវគ្នាទៅនឹងចំណុចមួយ។ M 0 (x 0; y 0) ។ចូរយើងផ្តល់អំណះអំណាង x0បង្កើន Δ X. តម្លៃថ្មីនៃអាគុយម៉ង់ត្រូវគ្នាទៅនឹងតម្លៃបន្ថែមនៃអនុគមន៍ y 0 +Δ y=f(x 0 –Δ x). យើងទទួលបានចំណុចមួយ។ M(x 0+Δ x; y ០+Δ y)តោះ​គូរ​ឃ្លា ម 0 មនិងសម្គាល់ដោយφមុំដែលបង្កើតឡើងដោយសេកង់ជាមួយនឹងទិសដៅវិជ្ជមាននៃអ័ក្ស គោ. ចូរ​យើង​បង្កើត​ទំនាក់​ទំនង​មួយ ហើយ​កត់​សម្គាល់។

ប្រសិនបើឥឡូវនេះ Δ x→ 0 បន្ទាប់មកដោយសារតែការបន្តនៃអនុគមន៍ Δ នៅ→0 ហើយ​ដូច្នេះ​ចំណុច មផ្លាស់ទីតាមខ្សែកោង ចូលទៅជិតចំណុចមិនកំណត់ ម ០. បន្ទាប់មកសេក ម 0 មទំនោរនឹងយកទីតាំងនៃតង់សង់ទៅខ្សែកោងនៅចំណុច ម ០, និងមុំφ→αនៅΔ x→0 ដែល α បង្ហាញពីមុំរវាងតង់សង់ និងទិសដៅវិជ្ជមាននៃអ័ក្ស គោ. ដោយសារអនុគមន៍ tg φ បន្តអាស្រ័យលើφនៅφ≠π/2 បន្ទាប់មកនៅφ→α tg φ→ tg α ហើយដូច្នេះជម្រាលនៃតង់សង់នឹងមានៈ

ទាំងនោះ។ f"(x)= tgα ។

ដូច្នេះធរណីមាត្រ y "(x 0)តំណាងឱ្យជម្រាលនៃតង់សង់ទៅក្រាហ្វនៃអនុគមន៍នេះនៅចំណុច x0, i.e. សម្រាប់តម្លៃដែលបានផ្តល់ឱ្យនៃអាគុយម៉ង់ xដេរីវេគឺស្មើនឹងតង់ហ្សង់នៃមុំដែលបង្កើតឡើងដោយតង់សង់ទៅក្រាហ្វនៃអនុគមន៍ f(x)នៅចំណុចដែលត្រូវគ្នា។ M 0 (x; y)ជាមួយនឹងទិសដៅអ័ក្សវិជ្ជមាន គោ។

ឧទាហរណ៍។ស្វែងរកជម្រាលនៃតង់សង់ទៅខ្សែកោង y = x 2 នៅចំណុច ម(-1; 1).

យើងបានឃើញរួចហើយថា ( x 2)" = 2X. ប៉ុន្តែជម្រាលនៃតង់សង់ទៅខ្សែកោងគឺ tg α = y"|x=-1=-2 ។

ភាពខុសគ្នានៃមុខងារ។ ការបន្តនៃមុខងារដែលអាចផ្លាស់ប្តូរបាន។

មុខងារ y=f(x)ហៅ ខុសគ្នានៅចំណុចណាមួយ។ x 0 ប្រសិនបើវាមានដេរីវេជាក់លាក់នៅចំណុចនេះ i.e. ប្រសិនបើដែនកំណត់នៃទំនាក់ទំនងមាន ហើយមានកំណត់។

ប្រសិនបើមុខងារអាចខុសគ្នានៅគ្រប់ចំណុចនៃផ្នែកខ្លះ [ ក; ខ] ឬចន្លោះពេល ( ក; ខ) បន្ទាប់មកពួកគេនិយាយថាវា។ ខុសគ្នានៅលើផ្នែក [ ក; ខ] ឬរៀងគ្នាក្នុងចន្លោះពេល ( ក; ខ).

ទ្រឹស្តីបទខាងក្រោមមានសុពលភាព ដែលបង្កើតការតភ្ជាប់រវាងមុខងារផ្សេងគ្នា និងបន្ត។

ទ្រឹស្តីបទ។ប្រសិនបើមុខងារ y=f(x)ខុសគ្នាត្រង់ចំណុចណាមួយ។ x0បន្ទាប់មកវាបន្តនៅចំណុចនេះ។

ដូច្នេះភាពខុសគ្នានៃមុខងារបង្កប់ន័យបន្តរបស់វា។

ភស្តុតាង. ប្រសិនបើ , នោះ។

,

ដែល α គឺជាតម្លៃគ្មានកំណត់ ពោលគឺឧ។ បរិមាណទំនោរទៅសូន្យនៅ Δ x→0. ប៉ុន្តែ​បន្ទាប់មក

Δ y=f "(x0) Δ x+αΔ x=> Δ y→ 0 នៅ Δ x→ 0, ឧ។ f(x) - f(x0)→ 0 នៅ x→x 0 ដែលមានន័យថាមុខងារ f(x)បន្តនៅចំណុច x 0. Q.E.D.

ដូច្នេះ នៅចំនុចដាច់ មុខងារមិនអាចមានដេរីវេទេ។ សេចក្តីថ្លែងការសន្ទនាគឺមិនពិតទេ៖ មានមុខងារបន្តដែលមិនមានភាពខុសគ្នានៅចំណុចមួយចំនួន (នោះគឺពួកគេមិនមានដេរីវេនៅចំណុចទាំងនេះទេ)។

ពិចារណាចំណុចនៅក្នុងរូបភាព ក, ខ, គ។

នៅចំណុច កនៅ Δ x→0 ទំនាក់ទំនងមិនមានដែនកំណត់ទេ (ព្រោះដែនកំណត់ម្ខាងគឺខុសគ្នាសម្រាប់Δ x→ 0–0 និង Δ x→0+0)។ នៅចំណុច កក្រាហ្វមិនមានតង់សង់ដែលបានកំណត់ទេ ប៉ុន្តែមានតង់សង់ម្ខាងពីរផ្សេងគ្នាដែលមានជម្រាល ទៅ 1 និង ទៅ២. ចំណុចប្រភេទនេះត្រូវបានគេហៅថា ចំណុចជ្រុង។

នៅចំណុច ខនៅ Δ x→ 0 សមាមាត្រគឺជាសញ្ញាថេរ តម្លៃដ៏ធំគ្មានកំណត់។ អនុគមន៍មានដេរីវេគ្មានកំណត់។ នៅចំណុចនេះ ក្រាហ្វមានតង់សង់បញ្ឈរ។ ប្រភេទចំណុច - "ចំណុចបញ្ឆេះ" ដែលមានតង់សង់បញ្ឈរ។

នៅចំណុច គនិស្សន្ទវត្ថុម្ខាងគឺមានចំនួនច្រើនឥតកំណត់នៃសញ្ញាផ្សេងគ្នា។ នៅចំណុចនេះ ក្រាហ្វមានតង់ហ្សង់បញ្ឈរពីររួមបញ្ចូលគ្នា។ ប្រភេទ - "cusp" ជាមួយតង់សង់បញ្ឈរ - ករណីពិសេសនៃចំណុចជ្រុង។