O princípio da menor ação, declarado explicitamente pela primeira vez por Jacobi, é semelhante ao princípio de Hamilton, mas menos geral e mais difícil de provar. Este princípio é aplicável apenas no caso em que as conexões e a função de força não dependem do tempo e quando, portanto, há uma integral da força viva.
Esta integral se parece com:
O princípio de Hamilton afirmado acima afirma que a variação da integral

é igual a zero quando o movimento real passa para qualquer outro movimento infinitamente próximo que leve o sistema da mesma posição inicial para a mesma posição final no mesmo intervalo de tempo.
O princípio de Jacobi, ao contrário, expressa uma propriedade, movimento, que não depende do tempo. Jacobi considera a integral
ação definidora. O princípio que ele estabeleceu afirma que a variação dessa integral é zero quando comparamos o movimento real do sistema com qualquer outro movimento infinitamente próximo que leve o sistema da mesma posição inicial para a mesma posição final. Nesse caso, não prestamos atenção ao intervalo de tempo gasto, mas observamos a equação (1), ou seja, a equação da mão de obra com o mesmo valor da constante h do movimento real.
Essa condição extrema necessária leva, de modo geral, ao mínimo da integral (2), de onde vem o nome do princípio da menor ação. A condição mínima parece ser a mais natural, pois o valor de T é essencialmente positivo e, portanto, a integral (2) deve necessariamente ter um mínimo. A existência de um mínimo só pode ser rigorosamente comprovada se o intervalo de tempo for suficientemente pequeno. A prova desta proposição pode ser encontrada no conhecido curso de Darboux sobre a teoria das superfícies. No entanto, não a apresentaremos aqui e nos limitaremos a derivar a condição
432. Prova do princípio da menor ação.
Na computação real encontramos uma dificuldade que não está presente na prova do teorema de Hamilton. A variável t não permanece mais independente da variação; então as variações de q i e q. estão relacionados com a variação de t por uma relação complexa que segue da Eq. (1). A maneira mais fácil de contornar essa dificuldade é alterar a variável independente para uma cujos valores estejam entre limites constantes independentes do tempo. Seja k uma nova variável independente cujos limites são considerados independentes de t. Ao mover o sistema, os parâmetros e t serão funções desta variável
Deixe que as letras q denotam as derivadas dos parâmetros q em relação ao tempo.
Como as ligações são consideradas independentes do tempo, as coordenadas cartesianas x, y, z são funções de q que não contêm tempo. Portanto suas derivadas serão funções homogêneas lineares de q e 7 serão uma forma quadrática homogênea de q cujos coeficientes são funções de q. Nós temos
![]()
Para distinguir as derivadas temporais de q, denotamos entre parênteses, (q), as derivadas de q, tomadas em relação a e colocadas de acordo com esta
![]()
então teremos
![]()
e a integral (2), expressa através da nova variável independente A, terá a forma;

A derivada pode ser eliminada usando o teorema da força viva. De fato, a integral da força viva será
![]()
![]()
Substituindo esta expressão na fórmula para , trazemos a integral (2) para a forma

A integral que define a ação tomou assim a forma final (3). O integrando é a raiz quadrada da forma quadrática das quantidades
Mostremos que as equações diferenciais dos extremos da integral (3) são exatamente as equações de Lagrange. As equações extremas, baseadas nas fórmulas gerais do cálculo das variações, serão:

Multiplicamos as equações por 2 e realizamos diferenciações parciais, levando em conta que não contém então obtemos, se não escrevermos o índice ,
Estas são as equações extremas expressas em termos da variável independente. A tarefa agora é retornar à variável independente
Como Г é uma função homogênea de segundo grau de e é uma função homogênea de primeiro grau, temos
Por outro lado, aos fatores de derivadas nas equações de extremais, pode-se aplicar o teorema da força viva, o que leva, como vimos acima, à substituição
![]()
Como resultado de todas as substituições, as equações extremas são reduzidas à forma
![]()
![]()
Chegamos assim às equações de Lagrange.
433. O caso quando não há forças motrizes.
No caso em que não há forças motrizes, há uma equação para mão de obra e temos

A condição de que a integral seja mínima é, neste caso, que o valor correspondente de -10 seja o menor. Assim, quando não há forças motrizes, então entre todos os movimentos em que a força viva mantém o mesmo valor dado, o movimento real é aquele que leva o sistema da sua posição inicial à sua posição final no menor tempo.
Se o sistema é reduzido a um único ponto movendo-se ao longo de uma superfície fixa, então o movimento real, entre todos os movimentos ao longo da superfície, realizados com a mesma velocidade, é um movimento no qual o ponto passa de sua posição inicial para a posição final. para o mais curto
intervalo de tempo. Em outras palavras, um ponto descreve na superfície a linha mais curta entre suas duas posições, ou seja, uma linha geodésica.
434. Observação.
O princípio da menor ação pressupõe que o sistema tenha vários graus de liberdade, pois se houvesse apenas um grau de liberdade, uma equação seria suficiente para determinar o movimento. Como o movimento pode, neste caso, ser completamente determinado pela equação da força viva, o movimento real será o único que satisfaz essa equação e, portanto, não pode ser comparado com nenhum outro movimento.

Em revisamos brevemente um dos princípios físicos mais notáveis - o princípio da menor ação, e estabelecemos um exemplo que pareceria contradizê-lo. Neste artigo, examinaremos mais de perto esse princípio e veremos o que acontece neste exemplo.
Desta vez, precisamos de um pouco mais de matemática. No entanto, tentarei novamente apresentar a parte principal do artigo em um nível elementar. Pontos um pouco mais rígidos e complexos que destacarei em cores, podem ser omitidos sem prejuízo do entendimento principal do artigo.
Condições de fronteira
Vamos começar com o objeto mais simples - uma bola se movendo livremente no espaço, que não é afetada por nenhuma força. Tal bola, como se sabe, se move uniforme e retilínea. Para simplificar, vamos supor que ele se mova ao longo do eixo:
Para descrever com precisão seu movimento, como regra, são dadas as condições iniciais. Por exemplo, especifica-se que no momento inicial a bola estava no ponto com a coordenada e tinha velocidade . Ao definir as condições iniciais desta forma, determinamos exclusivamente o movimento adicional da bola - ela se moverá a uma velocidade constante e sua posição no momento será igual à posição inicial mais a velocidade multiplicada pelo tempo decorrido : . Esta forma de definir as condições iniciais é muito natural e intuitivamente familiar. Fornecemos todas as informações necessárias sobre o movimento da bola no momento inicial, e então seu movimento é determinado pelas leis de Newton.
No entanto, esta não é a única maneira de especificar o movimento da bola. Outra forma alternativa é especificar a posição da bola em dois tempos diferentes e . Aqueles. defina isso:
1) no momento em que a bola estava em um ponto (com coordenada );
2) no momento em que a bola estava em um ponto (com coordenada ).
A expressão "estava no ponto" não significa que a bola estava em repouso no ponto. No momento, poderia voar através do ponto. Isso significa que sua posição no momento coincidiu com o ponto. O mesmo vale para o ponto.
Essas duas condições também determinam exclusivamente o movimento da bola. Seu movimento é fácil de calcular. Para satisfazer ambas as condições, a velocidade da bola deve ser obviamente . A posição da bola no momento será novamente igual à posição inicial mais a velocidade multiplicada pelo tempo decorrido:
Observe que nas condições do problema, não precisamos definir a velocidade inicial. Foi determinado exclusivamente a partir das condições 1) e 2).
Definir as condições da segunda maneira parece incomum. Talvez não esteja claro por que pode ser necessário defini-los dessa forma. No entanto, no princípio de menor ação, são as condições na forma 1) e 2) que são usadas, e não na forma de especificar a posição inicial e a velocidade inicial.
Trajetória com menos ação
Agora vamos desviar um pouco do movimento livre real da bola e considerar o seguinte problema puramente matemático. Digamos que temos uma bola que podemos mover manualmente da maneira que quisermos. Neste caso, precisamos satisfazer as condições 1) e 2). Aqueles. no intervalo de tempo entre e temos que movê-lo de ponto a ponto. Isso pode ser feito de maneiras completamente diferentes. Cada uma dessas formas chamaremos a trajetória da bola e pode ser descrita como uma função da posição da bola no tempo. Vamos traçar várias dessas trajetórias no gráfico da posição da bola em função do tempo:
Por exemplo, podemos mover a bola com a mesma velocidade igual a (trajetória verde). Ou podemos mantê-lo no ponto metade do tempo e depois movê-lo para o ponto em velocidade dupla (caminho azul). Você pode primeiro movê-lo na direção oposta e depois movê-lo para (caminho marrom). Você pode movê-lo para frente e para trás (caminho vermelho). Em geral, você pode movê-lo como quiser, desde que as condições 1) e 2) sejam atendidas.
Para cada trajetória, podemos combinar um número. Em nosso exemplo, ou seja, na ausência de quaisquer forças agindo sobre a bola, esse número é igual à energia cinética total acumulada durante todo o tempo de seu movimento no intervalo de tempo entre e e é chamado de ação.
Nesse caso, a palavra energia cinética "acumulada" não transmite com precisão o significado. Na realidade, a energia cinética não se acumula em nenhum lugar, a acumulação é usada apenas para calcular a ação da trajetória. Em matemática, existe um conceito muito bom para tal acumulação - a integral:Como exemplo, vamos pegar uma bola de 1 kg, definir algumas condições de contorno e calcular a ação para duas trajetórias diferentes. Deixe o ponto estar a uma distância de 1 metro do ponto , e o tempo está a 1 segundo do tempo. Aqueles. devemos mover a bola, que no momento inicial estava no ponto, em um segundo a uma distância de 1 m ao longo do eixo.A ação geralmente é indicada pela letra . O símbolo significa energia cinética. Essa integral significa que a ação é igual à energia cinética acumulada da bola no intervalo de tempo de até .
No primeiro exemplo (trajetória verde), movemos a bola uniformemente, ou seja, com a mesma velocidade, que, obviamente, deve ser igual a: m/s. A energia cinética da bola em cada momento é: = 1/2 J. Em um segundo, 1/2 J de energia cinética se acumulará. Aqueles. ação para tal trajetória é: J s.
Agora, não vamos transferir imediatamente a bola de um ponto a outro, mas segure-a no ponto por meio segundo e, então, pelo tempo restante, transfira-a uniformemente para o ponto. No primeiro meio segundo, a bola está em repouso e sua energia cinética é zero. Portanto, a contribuição para a ação desta parte da trajetória também é igual a zero. No segundo meio segundo, movemos a bola com velocidade dupla: m/s. A energia cinética neste caso será igual a = 2 J. A contribuição deste intervalo de tempo para a ação será igual a 2 J multiplicado por meio segundo, ou seja, 1J. Portanto, a ação total para tal trajetória é igual a J s.
Da mesma forma, qualquer outra trajetória com as condições de contorno 1) e 2) dadas por nós corresponde a algum número igual à ação para essa trajetória. Entre todas essas trajetórias, há uma trajetória com a menor ação. Pode-se provar que esta trajetória é uma trajetória verde, ou seja, movimento uniforme da bola. Para qualquer outra trajetória, por mais complicada que seja, a ação será maior que 1/2.
Em matemática, essa comparação para cada função de um determinado número é chamada de funcional. Muitas vezes, em física e matemática, há problemas semelhantes aos nossos, ou seja, encontrar tal função para a qual o valor de um determinado funcional seja mínimo. Por exemplo, um dos problemas que teve grande significado histórico para o desenvolvimento da matemática é o problema da bachistocrona. Aqueles. Encontrar a curva ao longo da qual a bola rola mais rápido. Novamente, cada curva pode ser representada pela função h(x), e cada função pode receber um número, neste caso, o tempo que a bola rola. Novamente, o problema se reduz a encontrar uma função para a qual o valor do funcional seja mínimo. O ramo da matemática que lida com esses problemas é chamado de cálculo de variações.
Princípio da menor ação
Nos exemplos discutidos acima, temos duas trajetórias especiais obtidas de duas maneiras diferentes.A primeira trajetória é obtida a partir das leis da física e corresponde à trajetória real de uma bola livre, que não é afetada por nenhuma força e para a qual as condições de contorno são definidas nas formas 1) e 2).
A segunda trajetória é obtida a partir do problema matemático de encontrar uma trajetória com determinadas condições de contorno 1) e 2) para as quais a ação é mínima.
O princípio da menor ação afirma que esses dois caminhos devem coincidir. Em outras palavras, se é sabido que a bola se moveu de tal forma que as condições de contorno 1) e 2) foram satisfeitas, então ela necessariamente se moveu ao longo de uma trajetória para a qual a ação é mínima em comparação com qualquer outra trajetória com as mesmas condições de contorno. .
Isso pode ser considerado uma mera coincidência. Você nunca conhece os problemas em que aparecem trajetórias uniformes e linhas retas. No entanto, o princípio da menor ação acaba sendo um princípio muito geral, que também é válido em outras situações, por exemplo, para o movimento de uma bola em um campo gravitacional uniforme. Para fazer isso, você só precisa substituir a energia cinética pela diferença entre as energias cinética e potencial. Essa diferença é chamada de função Lagrangiana ou Lagrange e a ação agora se torna igual à Lagrangiana total acumulada. De fato, a função Lagrange contém todas as informações necessárias sobre as propriedades dinâmicas do sistema.
Se lançarmos uma bola em um campo gravitacional uniforme de tal forma que ela passe por um ponto no tempo e chegue a um ponto no tempo , então ela, de acordo com as leis de Newton, voará ao longo de uma parábola. É esta parábola que coincidirá com as trajetórias para as quais a ação será mínima.
Assim, para um corpo se movendo em um campo potencial, por exemplo, no campo gravitacional da Terra, a função de Lagrange é: . A energia cinética depende da velocidade do corpo, e a energia potencial depende de sua posição, ou seja, coordenadas. Na mecânica analítica, todo o conjunto de coordenadas que determinam a posição do sistema geralmente é denotado por uma letra. Para uma bola movendo-se livremente no campo gravitacional, significa as coordenadas , e .Para indicar a taxa de variação de uma quantidade, em física é muito comum simplesmente colocar um ponto sobre essa quantidade. Por exemplo, denota a taxa de variação da coordenada , ou, em outras palavras, a velocidade do corpo na direção . Usando essas convenções, a velocidade de nossa bola em mecânica analítica é denotada como . Aqueles. significa componentes de velocidade.
Como a função de Lagrange depende da velocidade e das coordenadas, e também pode depender explicitamente do tempo (depende explicitamente do tempo, o que significa que o valor é diferente em tempos diferentes, para as mesmas velocidades e posições da bola), então a ação em geral é escrito como
Nem sempre mínimo
No entanto, no final da parte anterior, consideramos um exemplo em que o princípio da menor ação claramente não funciona. Para fazer isso, pegamos novamente uma bola livre, na qual nenhuma força atua, e colocamos uma parede elástica ao lado dela.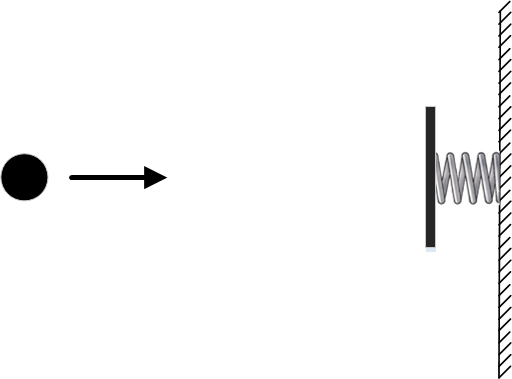
Definimos as condições de contorno de modo que os pontos e coincidam. Aqueles. e no momento do tempo e no momento do tempo a bola deve estar no mesmo ponto. Uma das trajetórias possíveis será a bola parada. Aqueles. todo o intervalo de tempo entre e ele ficará no ponto . A energia cinética e potencial neste caso será igual a zero, então a ação para tal trajetória também será igual a zero.
Estritamente falando, a energia potencial pode ser considerada igual não a zero, mas a qualquer número, já que a diferença de energia potencial em diferentes pontos no espaço é importante. No entanto, uma mudança no valor da energia potencial não afeta a busca por uma trajetória com ação mínima. É só que para todas as trajetórias o valor da ação mudará no mesmo número, e a trajetória com a ação mínima permanecerá a trajetória com a ação mínima. Por conveniência, para nossa bola vamos escolher a energia potencial igual a zero.Outra trajetória física possível com as mesmas condições de contorno seria a trajetória em que a bola primeiro voa para a direita, passando pelo ponto no tempo. Então ele colide com a mola, comprime-a, a mola, endireitando-se, empurra a bola para trás e ela novamente passa pelo ponto. Você pode escolher a velocidade da bola para que, depois de quicar na parede, ela voe sobre o ponto exatamente no momento. A ação em tal trajetória será basicamente igual à energia cinética acumulada durante o voo entre o ponto e a parede e volta. Haverá algum período de tempo em que a bola comprime a mola e sua energia potencial aumenta, e durante esse período de tempo a energia potencial fará uma contribuição negativa para a ação. Mas esse período de tempo não será muito grande e não reduzirá muito o efeito.

A figura mostra ambas as trajetórias fisicamente possíveis da bola. A trajetória verde corresponde a uma bola em repouso, enquanto a azul corresponde a uma bola quicando em uma parede elástica.
No entanto, apenas um deles tem um efeito mínimo, ou seja, o primeiro! A segunda trajetória tem mais ação. Acontece que neste problema existem duas trajetórias fisicamente possíveis e apenas uma com ação mínima. Aqueles. Nesse caso, o princípio da menor ação não funciona.
Pontos estacionários
Para entender o que está acontecendo aqui, vamos divagar por enquanto do princípio da menor ação e lidar com funções comuns. Vamos pegar alguma função e desenhar seu gráfico:
No gráfico, marquei quatro pontos especiais em verde. O que é comum para esses pontos? Imagine que o gráfico de uma função é um escorregador real ao longo do qual uma bola pode rolar. Os quatro pontos designados são especiais, pois se você colocar a bola exatamente neste ponto, ela não rolará para nenhum lugar. Em todos os outros pontos, por exemplo, ponto E, ele não conseguirá ficar parado e começará a deslizar para baixo. Tais pontos são chamados de estacionários. Encontrar tais pontos é uma tarefa útil, pois qualquer máximo ou mínimo de uma função, se não tiver quebras acentuadas, deve necessariamente ser um ponto estacionário.
Se classificarmos esses pontos com mais precisão, então o ponto A é o mínimo absoluto da função, ou seja, seu valor é menor do que qualquer outro valor de função. O ponto B não é máximo nem mínimo e é chamado de ponto de sela. O ponto C é chamado de máximo local, ou seja, o valor nele é maior do que nos pontos vizinhos da função. E o ponto D é um mínimo local, ou seja. o valor nele é menor do que nos pontos vizinhos da função.
O ramo da matemática chamado cálculo está engajado na busca de tais pontos. De outra forma, às vezes também é chamada de análise infinitesimal, pois pode trabalhar com quantidades infinitesimais. Do ponto de vista da análise matemática, os pontos estacionários têm uma propriedade especial, devido à qual são encontrados. Para entender o que é essa propriedade, precisamos entender como a função se parece a distâncias muito pequenas desses pontos. Para fazer isso, pegamos um microscópio e o examinamos em nossos pontos. A figura mostra como a função se parece nas proximidades de vários pontos em várias ampliações.

Pode-se ver que em uma ampliação muito alta (ou seja, para desvios muito pequenos de x), os pontos estacionários parecem exatamente os mesmos e são muito diferentes do ponto não estacionário. É fácil entender qual é essa diferença - o gráfico de uma função em um ponto estacionário torna-se uma linha estritamente horizontal com um aumento e em um ponto não estacionário torna-se inclinada. É por isso que a bola, instalada em um ponto estacionário, não rolará.
A horizontalidade de uma função em um ponto estacionário pode ser expressa de outra forma: uma função em um ponto estacionário praticamente não muda com uma mudança muito pequena em seu argumento, mesmo em comparação com a mudança no próprio argumento. A função em um ponto não estacionário com uma pequena mudança muda proporcionalmente à mudança. E quanto maior a inclinação da função, mais a função muda quando . De fato, à medida que a função aumenta, ela se torna cada vez mais uma tangente ao gráfico no ponto em questão.
Em linguagem matemática estrita, a expressão "função praticamente não muda em um ponto com uma mudança muito pequena" significa que a razão entre a mudança na função e a mudança em seu argumento tende a 0 como tende a 0:$$display$$\lim_(∆x \to 0) \frac (∆y(x_0))(∆x) = \lim_(x \to 0) \frac (y(x_0+∆x)-y(x_0) )(∆x) = 0$$exibir$$
Para um ponto não estacionário, esta razão tende a um número diferente de zero, que é igual à tangente da inclinação da função neste ponto. O mesmo número é chamado de derivada da função em um determinado ponto. A derivada de uma função mostra a rapidez com que uma função muda em torno de um determinado ponto com uma pequena mudança em seu argumento. Assim, pontos estacionários são pontos nos quais a derivada de uma função é 0.
Trajetórias estacionárias
Por analogia com pontos estacionários, podemos introduzir o conceito de trajetórias estacionárias. Lembre-se que para cada trajetória temos um certo valor da ação, ou seja, algum número. Então pode haver uma trajetória que para trajetórias próximas a ela com as mesmas condições de contorno, os valores correspondentes da ação praticamente não diferirão da ação para a trajetória mais estacionária. Tal trajetória é chamada de estacionária. Em outras palavras, qualquer trajetória próxima a estacionária terá um valor de ação muito pouco diferente da ação para aquela trajetória estacionária.Novamente, em linguagem matemática, "ligeiramente diferente" tem o seguinte significado preciso. Vamos supor que temos um funcional para funções com as condições de contorno exigidas 1) e 2), ou seja. e . Suponhamos que a trajetória seja estacionária.Podemos pegar qualquer outra função de tal forma que assuma valores zero nas extremidades, ou seja, = = 0. Pegue também uma variável , que tornaremos cada vez menor. A partir dessas duas funções e de uma variável, podemos compor uma terceira função que também satisfará as condições de contorno e . À medida que diminui, a trajetória correspondente à função se aproximará cada vez mais da trajetória .
Neste caso, para trajetórias estacionárias para pequenas, o valor do funcional para as trajetórias diferirá muito pouco do valor do funcional para mesmo comparado a . Aqueles.
$$display$$\lim_(ε \to 0) \frac (S(x"(t))-S(x(t)))ε=\lim_(ε \to 0) \frac (S(x( t)+εg(t))-S(x(t)))ε = 0$$exibir$$
Além disso, isso deve ser verdade para qualquer trajetória que satisfaça as condições de contorno = = 0.A mudança no funcional com uma pequena mudança na função (mais precisamente, a parte linear da mudança no funcional, proporcional à mudança na função) é chamada de variação do funcional e é denotada por . Do termo "variação" vem o nome "cálculo de variações".
Para trajetórias estacionárias, a variação do funcional .
O método de encontrar funções estacionárias (não apenas para o princípio da menor ação, mas também para muitos outros problemas) foi encontrado por dois matemáticos - Euler e Lagrange. Acontece que uma função estacionária cujo funcional é expresso por uma integral como a integral de ação deve satisfazer uma certa equação, agora chamada de equação de Euler-Lagrange.
Princípio da ação estacionária
A situação com o mínimo de ação para trajetórias é semelhante à situação com o mínimo para funções. Para uma trajetória ter a menor ação, ela deve ser uma trajetória estacionária. No entanto, nem todas as trajetórias estacionárias são trajetórias com ação mínima. Por exemplo, uma trajetória estacionária pode ter uma ação mínima localmente. Aqueles. terá menos ação do que qualquer outra trajetória vizinha. No entanto, em algum lugar distante pode haver outras trajetórias para as quais a ação será ainda menor.Acontece que corpos reais podem não necessariamente se mover ao longo de trajetórias com o mínimo de ação. Eles podem se mover ao longo de um conjunto mais amplo de trajetórias especiais, ou seja, trajetórias estacionárias. Aqueles. a trajetória real do corpo será sempre estacionária. Portanto, o princípio da menor ação é mais corretamente chamado de princípio da ação estacionária. No entanto, de acordo com a tradição estabelecida, muitas vezes é chamado de princípio da menor ação, implicando não apenas a minimalidade, mas também a estacionaridade das trajetórias.
Agora podemos escrever o princípio da ação estacionária em linguagem matemática, como geralmente é escrito em livros didáticos:.Se voltarmos ao exemplo com uma bola e uma parede elástica, a explicação desta situação torna-se muito simples agora. Sob as condições de contorno dadas em que a bola deve estar no ponto tanto no momento quanto no momento, existem duas trajetórias estacionárias. E a bola pode realmente se mover ao longo de qualquer uma dessas trajetórias. Para escolher explicitamente uma das trajetórias, você pode impor uma condição adicional ao movimento da bola. Por exemplo, digamos que a bola deve quicar na parede. Então a trajetória será determinada de forma inequívoca.Aqui, são coordenadas generalizadas, ou seja. um conjunto de variáveis que especificam exclusivamente a posição do sistema.
- a taxa de mudança de coordenadas generalizadas.
- Função de Lagrange, que depende das coordenadas generalizadas, das suas velocidades e, eventualmente, do tempo.
- uma ação que depende da trajetória específica do sistema (ou seja, de).As trajetórias reais do sistema são estacionárias, ou seja, para eles, uma variação da ação.
Do princípio da ação mínima (mais precisamente, estacionária), seguem-se algumas consequências notáveis, que discutiremos na próxima seção.
Quando aprendi pela primeira vez sobre esse princípio, tive uma sensação de algum tipo de misticismo. Parece que a natureza misteriosamente classifica todas as formas possíveis de movimento do sistema e escolhe a melhor delas.
Hoje quero falar um pouco sobre um dos princípios físicos mais notáveis - o princípio da menor ação.
fundo
Desde a época de Galileu, sabe-se que os corpos que não sofrem a ação de nenhuma força se movem em linhas retas, isto é, ao longo do caminho mais curto. Os raios de luz também viajam em linhas retas.Quando refletida, a luz também se move de forma a ir de um ponto a outro pelo caminho mais curto. Na figura, o caminho mais curto será o caminho verde, no qual o ângulo de incidência é igual ao ângulo de reflexão. Qualquer outro caminho, como o vermelho, será mais longo.

Isso é fácil de provar simplesmente refletindo os caminhos dos raios para o lado oposto do espelho. Eles são mostrados em linhas pontilhadas na imagem.

Pode-se ver que o caminho verde ACB se transforma em uma linha reta ACB'. E o caminho vermelho se transforma em uma linha quebrada ADB ', que, é claro, é mais longa que a verde.
Em 1662, Pierre Fermat sugeriu que a velocidade da luz em uma substância densa, como o vidro, é menor do que no ar. Antes disso, a versão geralmente aceita era Descartes, segundo a qual a velocidade da luz na matéria deve ser maior que no ar para obter a lei de refração correta. Para Fermat, a suposição de que a luz poderia se mover mais rápido em um meio mais denso do que em um rarefeito parecia antinatural. Portanto, ele assumiu que tudo é exatamente o oposto e provou uma coisa incrível - sob essa suposição, a luz é refratada para chegar ao seu destino no tempo mínimo.

Na figura novamente, a cor verde mostra o caminho que o feixe de luz realmente percorre. O caminho marcado em vermelho é o mais curto, mas não o mais rápido, pois a luz tem um caminho mais longo para percorrer no vidro, e sua velocidade é menor nele. O mais rápido é o caminho real do feixe de luz.
Todos esses fatos sugeriam que a natureza age de alguma forma racional, a luz e os corpos se movem da maneira mais otimizada possível, gastando o mínimo de esforço possível. Mas quais eram esses esforços e como calculá-los permanecia um mistério.
Em 1744, Maupertuis introduziu o conceito de "ação" e formulou o princípio segundo o qual a verdadeira trajetória de uma partícula difere de qualquer outra, pois a ação para ela é mínima. No entanto, o próprio Maupertuis não conseguiu dar uma definição clara do que é essa ação. Uma formulação matemática rigorosa do princípio da menor ação foi desenvolvida por outros matemáticos - Euler, Lagrange, e finalmente foi dada por William Hamilton:

Em linguagem matemática, o princípio da menor ação é formulado de forma bastante resumida, mas nem todos os leitores podem entender o significado da notação usada. Quero tentar explicar este princípio de forma mais clara e em termos mais simples.
corpo solto
Então, imagine que você está sentado em um carro em um ponto e em um ponto no tempo você recebe uma tarefa simples: no ponto no tempo você precisa dirigir um carro até o ponto .
O combustível para o carro é caro e, claro, você quer gastá-lo o mínimo possível. Seu carro é feito usando as mais recentes supertecnologias e pode acelerar ou desacelerar tão rápido quanto você quiser. No entanto, ele é projetado de tal forma que quanto mais rápido ele for, mais combustível ele consumirá. Além disso, o consumo de combustível é proporcional ao quadrado da velocidade. Se você dirigir duas vezes mais rápido, consumirá 4 vezes mais combustível no mesmo período de tempo. Além da velocidade, o consumo de combustível, é claro, é afetado pela massa do carro. Quanto mais pesado nosso carro, mais combustível ele consome. O consumo de combustível do nosso carro em cada momento é , ou seja, é exatamente igual à energia cinética do carro.
Então, como você precisa dirigir para chegar ao ponto a tempo e usar o mínimo de combustível possível? É claro que você precisa ir em linha reta. Com um aumento na distância percorrida, o combustível será consumido exatamente não menos. E então você pode escolher táticas diferentes. Por exemplo, você pode chegar rapidamente ao ponto com antecedência e apenas sentar, esperar a hora chegar. A velocidade de condução e, portanto, o consumo de combustível em cada momento, será elevada, mas o tempo de condução também será reduzido. Talvez o consumo geral de combustível neste caso não seja tão grande. Ou você pode ir uniformemente, com a mesma velocidade, de modo que, sem pressa, chegue exatamente no momento. Ou parte do caminho para ir rápido e parte mais devagar. Qual é a melhor maneira de ir?
Acontece que a maneira mais otimizada e econômica de dirigir é dirigir a uma velocidade constante, como estar no ponto exatamente na hora marcada. Qualquer outra opção usará mais combustível. Você pode verificar por si mesmo com alguns exemplos. A razão é que o consumo de combustível aumenta com o quadrado da velocidade. Portanto, à medida que a velocidade aumenta, o consumo de combustível aumenta mais rapidamente do que o tempo de condução diminui e o consumo geral de combustível também aumenta.
Então, descobrimos que, se um carro consome combustível em um determinado momento em proporção à sua energia cinética, então a maneira mais econômica de ir de um ponto a outro exatamente no momento designado é dirigir uniformemente e em linha reta, assim como um corpo se move na ausência de forças agindo sobre ele. Qualquer outra forma de condução resultará em um maior consumo geral de combustível.
No campo da gravidade
Agora vamos melhorar um pouco nosso carro. Vamos anexar motores a jato para que ele possa voar livremente em qualquer direção. Em geral, o design permaneceu o mesmo, então o consumo de combustível permaneceu estritamente proporcional à energia cinética do carro. Se a tarefa agora é partir de um ponto no tempo e chegar a um ponto no tempo t, então a maneira mais econômica, como antes, é claro, voará uniformemente e em linha reta para chegar ao ponto exatamente hora designada t. Isso novamente corresponde ao movimento livre do corpo no espaço tridimensional.
No entanto, um dispositivo incomum foi instalado no modelo mais recente do carro. Esta unidade é capaz de produzir combustível literalmente do nada. Mas o design é tal que quanto mais alto o carro, mais combustível o dispositivo produz a qualquer momento. A saída de combustível é diretamente proporcional à altura em que o veículo está atualmente localizado. Além disso, quanto mais pesado o carro, mais potente o dispositivo está instalado nele e mais combustível ele produz, e a saída é diretamente proporcional à massa do carro. O aparelho acabou sendo tal que a saída de combustível é exatamente igual a (onde é a aceleração de queda livre), ou seja, energia potencial do carro.
O consumo de combustível em cada momento é igual à energia cinética menos a energia potencial do carro (menos a energia potencial, pois o veículo instalado produz combustível e não gasta). Agora nossa tarefa é o movimento mais econômico do carro entre os pontos e fica mais difícil. O movimento uniforme retilíneo neste caso não é o mais eficaz. Acontece que é mais ideal subir um pouco, ficar lá por um tempo, tendo desenvolvido mais combustível e depois descer até o ponto. Com a trajetória de voo correta, o consumo total de combustível devido à subida cobrirá os custos adicionais de combustível para aumentar o comprimento da trajetória e aumentar a velocidade. Se calculado com cuidado, a forma mais econômica de um carro seria voar em uma parábola, exatamente na mesma trajetória e exatamente na mesma velocidade que uma pedra voaria no campo gravitacional da Terra.

Aqui vale a pena fazer uma explicação. Claro, é possível atirar uma pedra de um ponto de muitas maneiras diferentes para que ela atinja o ponto. Mas você precisa jogá-lo de tal maneira que, tendo saído de um ponto no tempo, ele atinja um ponto exatamente no tempo. É esse movimento que será o mais econômico para o nosso carro.
A função de Lagrange e o princípio da menor ação
Agora podemos transferir esta analogia para corpos físicos reais. Um análogo da intensidade do consumo de combustível para corpos é chamado de função Lagrange ou Lagrange (em homenagem a Lagrange) e é denotado pela letra . O Lagrangiano mostra quanto "combustível" o corpo consome em um determinado momento. Para um corpo se movendo em um campo potencial, a Lagrangiana é igual à sua energia cinética menos sua energia potencial.Um análogo da quantidade total de combustível consumido durante todo o tempo de movimento, ou seja, o valor do Lagrangiano acumulado durante todo o tempo de movimento é chamado de "ação".
O princípio da menor ação é que o corpo se move de tal forma que a ação (que depende da trajetória do movimento) é mínima. Neste caso, não se deve esquecer que as condições iniciais e finais são dadas, ou seja, onde o corpo está no tempo e no tempo.
Nesse caso, o corpo não precisa se mover em um campo gravitacional uniforme, que consideramos para nosso carro. Você pode considerar situações completamente diferentes. Um corpo pode oscilar em um elástico, balançar em um pêndulo ou voar em torno do Sol, em todos esses casos ele se move de forma a minimizar o "consumo total de combustível", ou seja, açao.
Se o sistema consiste em vários corpos, então a Lagrangiana de tal sistema será igual à energia cinética total de todos os corpos menos a energia potencial total de todos os corpos. E, novamente, todos os corpos se moverão em conjunto para que o efeito de todo o sistema durante esse movimento seja mínimo.
Não tão simples
Na verdade, eu trapaceei um pouco dizendo que os corpos sempre se movem de forma a minimizar a ação. Embora em muitos casos isso seja verdade, é possível pensar em situações em que a ação claramente não é mínima.Por exemplo, vamos pegar uma bola e colocá-la em um espaço vazio. A alguma distância dele, colocamos uma parede elástica. Digamos que queremos que a bola acabe no mesmo lugar depois de algum tempo. Sob essas condições, a bola pode se mover de duas maneiras diferentes. Primeiro, ele pode simplesmente ficar parado. Em segundo lugar, você pode empurrá-lo em direção à parede. A bola vai atingir a parede, ricochetear e voltar. É claro que você pode empurrá-lo com tanta velocidade que ele retornará exatamente no momento certo.

Ambas as variantes do movimento da bola são possíveis, mas a ação no segundo caso será maior, porque todo esse tempo a bola se moverá com energia cinética diferente de zero.
Como o princípio da menor ação pode ser salvo para que seja verdadeiro em tais situações? Falaremos sobre isso em.
Eles obedecem a ele, em conexão com o qual este princípio é uma das principais disposições da física moderna. As equações de movimento obtidas com sua ajuda são chamadas de equações de Euler-Lagrange.
A primeira formulação do princípio foi dada por P. Maupertuis em 1999, apontando desde logo o seu carácter universal, considerando-o aplicável à óptica e à mecânica. A partir deste princípio, ele derivou as leis de reflexão e refração da luz.
História
Maupertuis chegou a esse princípio a partir do sentimento de que a perfeição do universo requer uma certa economia da natureza e é contrária a qualquer gasto inútil de energia. O movimento natural deve ser tal que torne alguma quantidade um mínimo. Bastou encontrar esse valor, o que ele continuou fazendo. Era o produto da duração (tempo) do movimento dentro do sistema pelo dobro da quantidade, que agora chamamos de energia cinética do sistema.
Euler (em "Reflexions sur quelques loix generales de la nature", 1748) adota o princípio da menor ação, chamando a ação de "esforço". Sua expressão em estática corresponde ao que chamaríamos agora de energia potencial, de modo que sua afirmação de menor ação em estática é equivalente à condição de energia potencial mínima para a configuração de equilíbrio.
Na mecânica clássica
O princípio da menor ação serve como base fundamental e padrão para as formulações lagrangeanas e hamiltonianas da mecânica.
Vamos primeiro considerar a construção de tal forma mecânica lagrangeana. Usando o exemplo de um sistema físico com um grau de liberdade, lembramos que uma ação é um funcional em relação a coordenadas (generalizadas) (no caso de um grau de liberdade - uma coordenada), ou seja, é expressa através de que cada versão concebível da função está associada a um determinado número - uma ação (neste sentido, podemos dizer que uma ação como funcional é uma regra que permite, para qualquer função, calcular um número bem definido - também chamado de ação). A ação se parece com:
onde é a Lagrangiana do sistema dependendo da coordenada generalizada , sua primeira derivada em relação ao tempo , e também, possivelmente, explicitamente no tempo . Se o sistema tem mais graus de liberdade, então a Lagrangiana depende de um número maior de coordenadas generalizadas e suas derivadas de primeira vez. Assim, a ação é um funcional escalar dependendo da trajetória do corpo.
O fato de a ação ser escalar facilita a escrita em qualquer coordenada generalizada, o principal é que a posição (configuração) do sistema é caracterizada exclusivamente por elas (por exemplo, em vez de coordenadas cartesianas, elas podem ser polares coordenadas, distâncias entre pontos do sistema, ângulos ou suas funções, etc. d.).
A ação pode ser calculada para uma trajetória completamente arbitrária, não importa quão "selvagem" e "não natural" possa ser. No entanto, na mecânica clássica, entre todo o conjunto de trajetórias possíveis, há apenas uma ao longo da qual o corpo realmente irá. O princípio da estacionaridade da ação apenas dá a resposta à questão de como o corpo realmente se moverá:
Isso significa que, se o Lagrangiano do sistema for dado, então, usando o cálculo de variações, podemos estabelecer exatamente como o corpo se moverá, primeiro obtendo as equações de movimento - as equações de Euler-Lagrange e depois resolvendo-as. Isso permite não apenas generalizar seriamente a formulação da mecânica, mas também escolher as coordenadas mais convenientes para cada problema específico, não se limitando às cartesianas, o que pode ser muito útil para obter as equações mais simples e fáceis de resolver.
onde é a função de Hamilton do sistema dado; - coordenadas (generalizadas), - impulsos conjugados (generalizados), caracterizando juntos em cada momento dado o estado dinâmico do sistema e, sendo cada um uma função do tempo, caracterizando assim a evolução (movimento) do sistema. Neste caso, para obter as equações de movimento do sistema na forma de equações canônicas de Hamilton, é necessário variar a ação escrita desta forma independentemente para todos e .
Deve-se notar que, se é possível, em princípio, encontrar a lei do movimento a partir das condições do problema, isso é automaticamente não significa que é possível construir um funcional que assume um valor estacionário durante o movimento real. Um exemplo é o movimento conjunto de cargas elétricas e monopolos - cargas magnéticas - em um campo eletromagnético. Suas equações de movimento não podem ser derivadas do princípio da estacionaridade da ação. Da mesma forma, alguns sistemas hamiltonianos têm equações de movimento que não seguem esse princípio.
Exemplos
Exemplos triviais ajudam a avaliar o uso do princípio de funcionamento através das equações de Euler-Lagrange. Partícula livre (massa m e velocidade v) no espaço euclidiano se move em linha reta. Usando as equações de Euler-Lagrange, isso pode ser mostrado em coordenadas polares como segue. Na ausência de potencial, a função de Lagrange é simplesmente igual à energia cinética
em um sistema de coordenadas ortogonais.
Em coordenadas polares, a energia cinética e, portanto, a função de Lagrange, torna-se
As componentes radial e angular das equações se tornam, respectivamente:
Resolvendo essas duas equações
Aqui, é um registro condicional de integração funcional de dobras infinitas sobre todas as trajetórias x(t), e é a constante de Planck. Ressaltamos que, em princípio, a ação no exponencial aparece (ou pode aparecer) em si, ao estudar o operador evolução em mecânica quântica, porém, para sistemas que possuem um análogo clássico exato (não quântico), é exatamente igual a a ação clássica usual.
A análise matemática desta expressão no limite clássico - para suficientemente grande , ou seja, para oscilações muito rápidas do expoente imaginário - mostra que a grande maioria de todas as trajetórias possíveis nesta integral se cancelam no limite (formalmente, em ) . Para quase qualquer caminho, existe um caminho no qual a incursão de fase será exatamente oposta, e eles somarão contribuição zero. Apenas aquelas trajetórias para as quais a ação está próxima do valor extremo (para a maioria dos sistemas - o mínimo) não são reduzidas. Este é um fato puramente matemático da teoria das funções de uma variável complexa; por exemplo, o método da fase estacionária é baseado nele.
Como resultado, a partícula, em total conformidade com as leis da mecânica quântica, se move ao longo de todas as trajetórias simultaneamente, mas em condições normais, apenas trajetórias próximas ao estacionário (ou seja, clássicas) contribuem para os valores observados. Como a mecânica quântica se torna clássica no limite de altas energias, podemos supor que isso é - derivação mecânica quântica do princípio clássico da estacionaridade da ação.
Na teoria quântica de campos
Na teoria quântica de campos, o princípio da estacionaridade da ação também é aplicado com sucesso. A densidade Lagrangiana aqui inclui os operadores dos campos quânticos correspondentes. Embora seja mais correto aqui (com exceção do limite clássico e parcialmente semiclássico) falar não do princípio da estacionaridade da ação, mas da integração de Feynman sobre trajetórias na configuração ou espaço de fase desses campos - usando a densidade Lagrangiana acabei de mencionar.
Generalizações adicionais
Mais amplamente, uma ação é entendida como um funcional que define um mapeamento do espaço de configuração para o conjunto dos números reais e, em geral, não precisa ser uma integral, pois ações não locais são, em princípio, possíveis, pelo menos teoricamente. Além disso, um espaço de configuração não é necessariamente um espaço de função porque pode ter uma geometria não comutativa.
2.2. Princípio da menor ação
No século XVIII, ocorreu uma maior acumulação e sistematização de resultados científicos, marcados por uma tendência de combinar realizações científicas individuais em uma imagem estritamente ordenada e coerente do mundo através da aplicação sistemática de métodos de análise matemática ao estudo de fenômenos físicos. O trabalho de muitas mentes brilhantes nessa direção levou à criação da teoria básica de um programa de pesquisa mecanicista - a mecânica analítica, com base na qual várias teorias fundamentais foram criadas que descrevem uma classe particular de componentes.
fenômenos: hidrodinâmica, teoria da elasticidade, aerodinâmica, etc. Um dos resultados mais importantes da mecânica analítica é o princípio da menor ação (princípio variacional), importante para a compreensão dos processos que ocorrem na física no final do século XX.
As raízes do surgimento de princípios variacionais na ciência remontam à Grécia Antiga e estão associadas ao nome de Heron de Alexandria. A ideia de qualquer princípio variacional é variar (alterar) um determinado valor que caracteriza um determinado processo, e selecionar de todos os processos possíveis aquele para o qual esse valor assume um valor extremo (máximo ou mínimo). Heron tentou explicar as leis da reflexão da luz variando o valor que caracteriza o comprimento do caminho percorrido por um feixe de luz de uma fonte para um observador quando é refletido por um espelho. Ele chegou à conclusão de que de todos os caminhos possíveis, um raio de luz escolhe o mais curto (de todos geometricamente possíveis).
No século XVII, dois mil anos depois, o matemático francês Fermat chamou a atenção para o princípio de Heron, estendeu-o a meios com diferentes índices de refração e, portanto, reformulou-o em termos de tempo. O princípio de Fermat afirma que em um meio refrativo, cujas propriedades não dependem do tempo, um feixe de luz que passa por dois pontos escolhe um caminho para si mesmo, de modo que o tempo que leva para viajar do primeiro ponto ao segundo seja mínimo. O princípio de Heron é um caso especial do princípio de Fermat para meios com índice de refração constante.
O princípio de Fermat atraiu a atenção dos contemporâneos. Por um lado, ele era a melhor evidência do "princípio da economia" na natureza, do plano divino racional realizado na estrutura do mundo, por outro, ele contradizia a teoria corpuscular da luz de Newton. De acordo com Newton, descobriu-se que em meios mais densos a velocidade da luz deveria ser maior, enquanto seguia do princípio de Fermat de que em tais meios a velocidade da luz se torna menor.
Em 1740, o matemático Pierre Louis Moreau de Maupertuis, analisando criticamente o princípio de Fermat e seguindo o
motivos lógicos sobre a perfeição e o dispositivo mais econômico do Universo, proclamado na obra “Sobre as várias leis da natureza que pareciam incompatíveis” o princípio da menor ação. Maupertuis abandonou o menor tempo de Fermat e introduziu um novo conceito - ação. A ação é igual ao produto do momento do corpo (momento Р = mV) e o caminho percorrido pelo corpo. O tempo não tem vantagem sobre o espaço e vice-versa. Portanto, a luz não escolhe o caminho mais curto e nem o menor tempo para percorrê-lo, mas, segundo Maupertuis, “escolhe o caminho que dá uma economia mais real: o caminho que ela percorre é o caminho em que a magnitude da ação é mínima.” O princípio da menor ação foi desenvolvido nas obras de Euler e Lagrange; ele foi a base sobre a qual Lagrange desenvolveu uma nova área de análise matemática - o cálculo de variações. Este princípio foi generalizado e completado nos trabalhos de Hamilton. De forma generalizada, o princípio da menor ação usa o conceito de ação expresso não em termos de momento, mas em termos da função de Lagrange. Para o caso de uma partícula se movendo em algum campo potencial, a função de Lagrange pode ser representada como a diferença da cinética ![]() e energia potencial:
e energia potencial:
(O conceito de "energia" é discutido em detalhes no Capítulo 3 desta seção.)
O produto é chamado de ação elementar. A ação total é a soma de todos os valores ao longo de todo o intervalo de tempo considerado, ou seja, a ação total A:

As equações de movimento de uma partícula podem ser obtidas usando o princípio da menor ação, segundo o qual o movimento real ocorre de tal forma que a ação se torna extrema, ou seja, sua variação passa a 0:
![]()
O princípio variacional de Lagrange-Hamilton permite facilmente a extensão a sistemas que consistem em
quantas (muitas) partículas. O movimento de tais sistemas é geralmente considerado em um espaço abstrato (uma técnica matemática conveniente) de um grande número de dimensões. Digamos, para N pontos, algum espaço abstrato de 3N coordenadas de N partículas é introduzido, formando um sistema chamado espaço de configuração. A sequência de diferentes estados do sistema é representada por uma curva neste espaço de configuração - uma trajetória. Considerando todas as trajetórias possíveis conectando dois pontos dados desse espaço tridimensional, pode-se ter certeza de que o movimento real do sistema ocorre de acordo com o princípio da menor ação: dentre todas as trajetórias possíveis, aquela para a qual a ação é extrema todo o intervalo de tempo do movimento é realizado.
Ao minimizar a ação na mecânica clássica, obtêm-se as equações de Euler-Lagrange, cuja conexão com as leis de Newton é bem conhecida. As equações de Euler-Lagrange para a Lagrangiana do campo eletromagnético clássico são as equações de Maxwell. Assim, vemos que o uso da Lagrangiana e do princípio de menor ação permite definir a dinâmica das partículas. No entanto, o Lagrangiano tem mais uma característica importante, que fez do formalismo Lagrangiano o principal na resolução de quase todos os problemas da física moderna. O fato é que junto com a mecânica newtoniana na física, já no século XIX, foram formuladas leis de conservação para algumas grandezas físicas: a lei da conservação da energia, a lei da conservação do momento, a lei da conservação do momento angular, a lei de conservação da carga elétrica. O número de leis de conservação em conexão com o desenvolvimento da física quântica e da física de partículas elementares em nosso século tornou-se ainda maior. Surge a questão de como encontrar uma base comum para escrever tanto as equações do movimento (digamos, as leis de Newton ou as equações de Maxwell) quanto as quantidades conservadas no tempo. Descobriu-se que tal base é o uso do formalismo lagrangeano, pois o lagrangeano de uma determinada teoria acaba sendo invariante (inalterado) em relação às transformações correspondentes ao espaço abstrato específico considerado nesta teoria, o que resulta na conservação leis. Essas características da Lagrangiana
não levou à conveniência de formular teorias físicas na linguagem dos lagrangianos. A percepção dessa circunstância veio para a física devido ao surgimento da teoria da relatividade de Einstein.
| " |
