Solução gráfica de uma equação quadrática Consolidar a capacidade de construir gráficos de várias funções; Formar a capacidade de resolver equações do segundo grau graficamente. Projeto sobre o tema "Transformação de gráficos de uma função"

Solução gráfica de uma equação quadrática Consolidar a capacidade de construir gráficos de várias funções; Formar a capacidade de resolver equações do segundo grau graficamente. Brdsk 2009 Instituição educacional municipal - Liceu Econômico Lição de generalização sobre o tema "Função quadrática", professor de álgebra da 8ª série Fedoseeva T.M.

Traçar uma função quadrática Determine a direção dos ramos: a>0 ramos para cima; uma 0 ramos para cima; a"> 0 ramos para cima; a"> 0 ramos para cima; a" title="(!LANG:Plotagem de uma função quadrática Determinar a direção do desvio: a>0 desvios para cima; a"> title="Traçar uma função quadrática Determine a direção dos ramos: a>0 ramos para cima; uma"> !}

0 ramos são direcionados para cima; 2) vértice y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - o eixo da parábola Pontos de controle: (0: -3), (3) ; 0) e simétrico a eles em torno do eixo x = 1 Construímos uma parábola. Encontre o ponto "title="(!LANG: Vamos construir um gráfico da função y=x 2 -2x-3 usando o algoritmo: 1) a=1>0 os ramos são direcionados para cima; 2) vértice y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - o eixo da parábola Pontos de controle: (0: -3), (3) ; 0) e simétrico a eles em torno do eixo x = 1 Construímos uma parábola. Encontrando um ponto" class="link_thumb"> 3 !} Vamos construir um gráfico da função y=x 2 -2x-3 usando o algoritmo: 1) a=1>0 ramos são direcionados para cima; 2) vértice y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - o eixo da parábola Pontos de controle: (0: -3), (3) ; 0) e simétrico a eles em torno do eixo x = 1 Construímos uma parábola. Encontramos os pontos de interseção com o eixo OX: x 1 \u003d -1; x 2 \u003d 3 1 maneira de resolver a equação x 2 -2x-3 \u003d 0 y x Resolva a equação x 2 +2x-3 \u003d 0 0 ramos são direcionados para cima; 2) vértice y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - o eixo da parábola Pontos de controle: (0: -3), (3) ; 0) e simétrico a eles em torno do eixo x = 1 Construímos uma parábola. Encontramos o ponto "\u003e 0 os ramos são direcionados para cima; 2) o topo y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - o eixo da parábola Pontos de controle: (0: -3) , (3; 0) e simétrico em torno do eixo x = 1 Construímos uma parábola.Encontre os pontos de interseção com o eixo OX: x 1 \u003d -1; x 2 \u003d 3 1 maneira de resolver a equação x 2 -2x-3 \u003d 0 y x 0 1 - 4 23 Resolva a equação x 2 + 2x-3 \u003d 0 "\u003e 0 ramos são direcionados para cima; 2) vértice y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - o eixo da parábola Pontos de controle: (0: -3), (3) ; 0) e simétrico a eles em torno do eixo x = 1 Construímos uma parábola. Encontre o ponto "title="(!LANG: Vamos construir um gráfico da função y=x 2 -2x-3 usando o algoritmo: 1) a=1>0 os ramos são direcionados para cima; 2) vértice y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - o eixo da parábola Pontos de controle: (0: -3), (3) ; 0) e simétrico a eles em torno do eixo x = 1 Construímos uma parábola. Encontrando um ponto"> title="Vamos construir um gráfico da função y=x 2 -2x-3 usando o algoritmo: 1) a=1>0 ramos são direcionados para cima; 2) vértice y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - o eixo da parábola Pontos de controle: (0: -3), (3) ; 0) e simétrico a eles em torno do eixo x = 1 Construímos uma parábola. Encontrando um ponto"> !}

A segunda maneira: a). Vamos dividir a equação x 2 -2x-3=0 em partes x 2 = 2x+3 Vamos escrever duas funções y= x 2 ; y \u003d 2x + 3 Construímos gráficos dessas funções em um sistema de coordenadas. As abcissas dos pontos de interseção são as raízes da equação. 0 1 x y Resolva a equação x 2 +2x-3=0

A terceira maneira: x 2 -3 \u003d 2x y \u003d x 2 -3; y=2x Construímos gráficos dessas funções em um sistema de coordenadas. As abcissas dos pontos de interseção são as raízes da equação. 0 1 x y Resolva a equação x 2 +2x-3=0

Solução gráfica de equações

Ei, 2009

Introdução

A necessidade de resolver equações quadráticas na antiguidade foi causada pela necessidade de resolver problemas relacionados à localização das áreas de terrenos e terraplenagem de natureza militar, bem como o desenvolvimento da astronomia e da própria matemática. Os babilônios sabiam como resolver equações quadráticas por volta de 2.000 aC. A regra para resolver essas equações, indicada nos textos babilônicos, coincide essencialmente com as modernas, mas não se sabe como os babilônios chegaram a essa regra.

Fórmulas para resolver equações quadráticas na Europa foram estabelecidas pela primeira vez no Livro do Ábaco, escrito em 1202 pelo matemático italiano Leonardo Fibonacci. Seu livro contribuiu para a difusão do conhecimento algébrico não apenas na Itália, mas também na Alemanha, França e outros países europeus.

Mas a regra geral para resolver equações quadráticas, com todas as combinações possíveis dos coeficientes b e c, foi formulada na Europa apenas em 1544 por M. Stiefel.

Em 1591 François Viet introduziu fórmulas para resolver equações quadráticas.

Alguns tipos de equações quadráticas podiam ser resolvidas na antiga Babilônia.

Diofanto de Alexandria e Euclides , Al-Khwarizmi e Omar Khayyam equações resolvidas em formas geométricas e gráficas.

Na 7ª série estudamos funções y \u003d C, y= kx , e = kx + m , e = x 2 ,y = - x 2 , na 8ª série - y = √ x , e = |x |, y= machado 2 + bx + c , e = k / x. No livro de álgebra do 9º ano, vi funções que ainda não eram conhecidas por mim: y= x 3 , y= x 4 ,y= x 2n, y= x - 2n, y= 3 √x , ( x – uma ) 2 + (s- b ) 2 = r 2 e outros. Existem regras para a construção de gráficos dessas funções. Eu queria saber se existem outras funções que obedecem a essas regras.

Meu trabalho é estudar gráficos de funções e resolver equações graficamente.

1. Quais são as funções

O gráfico de uma função é o conjunto de todos os pontos do plano de coordenadas, cujas abcissas são iguais aos valores dos argumentos, e as ordenadas são iguais aos valores correspondentes da função.

A função linear é dada pela equação y= kx + b, Onde k e b- alguns números. O gráfico desta função é uma linha reta.

Função Proporcional Inversa y= k / x, onde k¹ 0. O gráfico desta função é chamado de hipérbole.

Função ( x – uma ) 2 + (s – b ) 2 = r 2 , Onde uma , b e r- alguns números. O gráfico desta função é um círculo de raio r centrado no ponto A ( uma , b).

função quadrática y = machado 2 + bx + c Onde uma, b , com- alguns números e uma¹ 0. O gráfico desta função é uma parábola.

A equação e 2 ( uma – x ) = x 2 ( uma + x ) . O gráfico desta equação será uma curva chamada estrofóide.

A equação ( x 2 + y 2 ) 2 = uma ( x 2 – y 2 ) . O gráfico desta equação é chamado de lemniscata de Bernoulli.

A equação. O gráfico desta equação é chamado de astroide.

Curva (x 2 y 2 - 2 a x) 2 \u003d 4 a 2 (x 2 + y 2). Essa curva é chamada de cardióide.

Funções: y= x 3 - parábola cúbica, y= x 4 , y = 1/ x 2 .

2. O conceito de uma equação, sua solução gráfica

A equaçãoé uma expressão que contém uma variável.

resolva a equação- isso significa encontrar todas as suas raízes, ou provar que elas não existem.

Raiz da equaçãoé um número que, quando substituído na equação, produz a igualdade numérica correta.

Resolvendo equações graficamente permite encontrar o valor exato ou aproximado das raízes, permite encontrar o número de raízes da equação.

Ao plotar gráficos e resolver equações, as propriedades de uma função são usadas, então o método é frequentemente chamado de gráfico funcional.

Para resolver a equação, nós a “dividimos” em duas partes, introduzimos duas funções, construímos seus gráficos, encontramos as coordenadas dos pontos de interseção dos gráficos. As abcissas desses pontos são as raízes da equação.

3. Algoritmo para construir um gráfico de uma função

Conhecendo o gráfico da função y= f ( x ) , você pode plotar funções y= f ( x + m ) ,y= f ( x )+ eu e y= f ( x + m )+ eu. Todos esses gráficos são obtidos a partir do gráfico da função y= f ( x ) usando a transformação de tradução paralela: em │ m │ unidades de escala para a direita ou esquerda ao longo do eixo x e em │ eu │ unidades de escala para cima ou para baixo ao longo do eixo y .

4. Solução gráfica da equação quadrática

Usando o exemplo de uma função quadrática, vamos considerar uma solução gráfica de uma equação quadrática. O gráfico de uma função quadrática é uma parábola.

O que os antigos gregos sabiam sobre a parábola?

O simbolismo matemático moderno originou-se no século XVI.

Os antigos matemáticos gregos não tinham o método das coordenadas nem o conceito de função. No entanto, as propriedades da parábola foram estudadas por eles em detalhes. A inventividade dos matemáticos antigos é simplesmente incrível, porque eles só podiam usar desenhos e descrições verbais de dependências.

A maioria explorou a parábola, a hipérbole e a elipse Apolônio de Perga, que viveu no século 3 aC. Ele também deu nomes a essas curvas e indicou quais condições os pontos situados em uma determinada curva satisfazem (afinal, não havia fórmulas!).

Existe um algoritmo para construir uma parábola:

Encontramos as coordenadas do vértice da parábola A (x 0; y 0): x0 =- b /2 uma ;

Y 0 \u003d ax cerca de 2 + em 0 + c;

Encontramos o eixo de simetria da parábola (linha reta x \u003d x 0);

Compilar uma tabela de valores para construir pontos de controle;

Construímos os pontos obtidos e construímos pontos simétricos a eles em relação ao eixo de simetria.

1. Vamos construir uma parábola de acordo com o algoritmo y = x 2 – 2 x – 3 . Abscissas dos pontos de intersecção com o eixo x e são as raízes da equação quadrática x 2 – 2 x – 3 = 0.

Existem cinco maneiras de resolver graficamente esta equação.

2. Vamos quebrar a equação em duas funções: y = x 2 e y = 2 x + 3

3. Vamos quebrar a equação em duas funções: y = x 2 –3 e y =2 x. As raízes da equação são as abcissas dos pontos de interseção da parábola com a reta.

4. Transforme a equação x 2 – 2 x – 3 = 0 selecionando o quadrado completo na função: y = ( x –1) 2 e y =4. As raízes da equação são as abcissas dos pontos de interseção da parábola com a reta.

5. Dividimos termo por termo ambas as partes da equação x 2 – 2 x – 3 = 0 no x, Nós temos x – 2 – 3/ x = 0 Vamos dividir esta equação em duas funções: y = x – 2, y = 3/ x . As raízes da equação são as abcissas dos pontos de interseção da reta e da hipérbole.

5. Solução gráfica de equações de grau n

Exemplo 1 resolva a equação x 5 = 3 – 2 x .

y = x 5 , y = 3 – 2 x .

Responda: x = 1.

Exemplo 2 resolva a equação 3 √ x = 10 – x .

As raízes desta equação é a abscissa do ponto de intersecção dos gráficos de duas funções: y = 3 √ x , y = 10 – x .

Responda: x=8.

Conclusão

Considerando os gráficos da função: y= machado 2 + bx + c , e = k / x , y = √ x , e = |x |, y= x 3 , y= x 4 ,y= 3 √x , Percebi que todos esses gráficos são construídos de acordo com a regra da tradução paralela em relação aos eixos x e y .

Usando o exemplo de resolução de uma equação quadrática, podemos concluir que o método gráfico também é aplicável a equações de grau n.

Os métodos gráficos para resolver equações são bonitos e compreensíveis, mas não garantem 100% de resolução de qualquer equação. As abcissas dos pontos de interseção dos gráficos podem ser aproximadas.

No 9º ano e nas turmas seniores, ainda vou conhecer outras funções. Estou interessado em saber se essas funções obedecem às regras de tradução paralela ao traçar seus gráficos.

No próximo ano também quero considerar as questões de solução gráfica de sistemas de equações e desigualdades.

Literatura

1. Álgebra. 7 ª série. Parte 1. Livro didático para instituições de ensino / A.G. Mordkovich. Moscou: Mnemosyne, 2007.

2. Álgebra. 8 ª série. Parte 1. Livro didático para instituições de ensino / A.G. Mordkovich. Moscou: Mnemosyne, 2007.

3. Álgebra. 9º ano Parte 1. Livro didático para instituições de ensino / A.G. Mordkovich. Moscou: Mnemosyne, 2007.

4. Glazer G.I. História da matemática na escola. Classes VII-VIII. – M.: Iluminismo, 1982.

5. Revista Matemática №5 2009; Nº 8 2007; Nº 23 2008.

6. Solução gráfica de equações Sites da Internet: Tol WIKI; stimul.biz/pt; wiki.iot.ru/images; berdsk.edu; página 3–6.htm.

Solução gráfica de equações

Ei, 2009

Introdução

Mas a regra geral para resolver equações quadráticas, com todas as combinações possíveis dos coeficientes b e c, foi formulada na Europa apenas em 1544 por M. Stiefel.

Em 1591 François Viet introduziu fórmulas para resolver equações quadráticas.

Alguns tipos de equações quadráticas podiam ser resolvidas na antiga Babilônia.

Diofanto de Alexandria e Euclides, Al-Khwarizmi e Omar Khayyam equações resolvidas em formas geométricas e gráficas.

Na 7ª série estudamos funções y \u003d C, y=kx, e =kx+ m, e =x 2,y = -x 2, na 8ª série - y = √x, e =|x|, y=machado2 + bx+ c, e =k/ x. No livro de álgebra do 9º ano, vi funções que ainda não eram conhecidas por mim: y=x 3, y=x 4,y=x 2n, y=x- 2n, y= 3√x, (x– uma) 2 + (s-b) 2 = r 2 e outros. Existem regras para a construção de gráficos dessas funções. Eu queria saber se existem outras funções que obedecem a essas regras.

Meu trabalho é estudar gráficos de funções e resolver equações graficamente.

1. Quais são as funções

A função linear é dada pela equação y=kx+ b, Onde k e b- alguns números. O gráfico desta função é uma linha reta.

Função Proporcional Inversa y=k/ x, onde k ¹ 0. O gráfico desta função é chamado de hipérbole.

Função (x– uma) 2 + (s-b) 2 = r2 , Onde uma, b e r- alguns números. O gráfico desta função é um círculo de raio r centrado no ponto A ( uma, b).

função quadrática y= machado2 + bx+ c Onde uma,b, com- alguns números e uma¹ 0. O gráfico desta função é uma parábola.

A equação no2 (uma– x) = x2 (uma+ x) . O gráfico desta equação será uma curva chamada estrofóide.

/>Equação (x2 + y2 ) 2 = uma(x2 – y2 ) . O gráfico desta equação é chamado de lemniscata de Bernoulli.

A equação. O gráfico desta equação é chamado de astroide.

Curva (x2 y2 – 2x)2 =4 a2 (x2 +y2 ) . Essa curva é chamada de cardióide.

Funções: y=x 3 - parábola cúbica, y=x 4, y = 1/x 2.

2. O conceito de uma equação, sua solução gráfica

A equaçãoé uma expressão que contém uma variável.

resolva a equação- isso significa encontrar todas as suas raízes, ou provar que elas não existem.

Raiz da equaçãoé um número que, quando substituído na equação, produz a igualdade numérica correta.

Resolvendo equações graficamente permite encontrar o valor exato ou aproximado das raízes, permite encontrar o número de raízes da equação.

Ao plotar gráficos e resolver equações, as propriedades de uma função são usadas, então o método é frequentemente chamado de gráfico funcional.

3. Algoritmo para construir um gráfico de uma função

Conhecendo o gráfico da função y=f(x) , você pode plotar funções y=f(x+ m) ,y=f(x)+ eu e y=f(x+ m)+ eu. Todos esses gráficos são obtidos a partir do gráfico da função y=f(x) usando a transformação de tradução paralela: em │ m│ unidades de escala para a direita ou esquerda ao longo do eixo x e em │ eu│ unidades de escala para cima ou para baixo ao longo do eixo y.

4. Solução gráfica da equação quadrática

Usando o exemplo de uma função quadrática, vamos considerar uma solução gráfica de uma equação quadrática. O gráfico de uma função quadrática é uma parábola.

O que os antigos gregos sabiam sobre a parábola?

O simbolismo matemático moderno originou-se no século XVI.

Existe um algoritmo para construir uma parábola:

Encontre as coordenadas do vértice da parábola A (x0; y0): X=- b/2 uma;

y0=aho2+in0+s;

Encontre o eixo de simetria da parábola (reta x=x0);

QUEBRA DE PÁGINA--

Compilar uma tabela de valores para construir pontos de controle;

Construímos os pontos obtidos e construímos pontos simétricos a eles em relação ao eixo de simetria.

1. Vamos construir uma parábola de acordo com o algoritmo y= x2 – 2 x– 3 . Abscissas dos pontos de intersecção com o eixo x e são as raízes da equação quadrática x2 – 2 x– 3 = 0.

Existem cinco maneiras de resolver graficamente esta equação.

2. Vamos quebrar a equação em duas funções: y= x2 e y= 2 x+ 3

3. Vamos quebrar a equação em duas funções: y= x2 –3 e y=2 x. As raízes da equação são as abcissas dos pontos de interseção da parábola com a reta.

4. Transforme a equação x2 – 2 x– 3 = 0 selecionando o quadrado completo na função: y= (x–1) 2 e y=4. As raízes da equação são as abcissas dos pontos de interseção da parábola com a reta.

5. Dividimos termo por termo ambas as partes da equação x2 – 2 x– 3 = 0 no x, Nós temos x– 2 – 3/ x= 0 Vamos dividir esta equação em duas funções: y= x– 2, y= 3/ x. As raízes da equação são as abcissas dos pontos de interseção da reta e da hipérbole.

5. Solução gráfica de equações de graun

Exemplo 1 resolva a equação x5 = 3 – 2 x.

y= x5 , y= 3 – 2 x.

Responda: x = 1.

Exemplo 2 resolva a equação 3 √ x= 10 – x.

As raízes desta equação é a abscissa do ponto de intersecção dos gráficos de duas funções: y= 3 √ x, y= 10 – x.

Responda: x=8.

Conclusão

Considerando os gráficos da função: y=machado2 + bx+ c, e =k/ x, y = √x, e =|x|, y=x 3, y=x 4,y= 3√x, Percebi que todos esses gráficos são construídos de acordo com a regra da tradução paralela em relação aos eixos x e y.

Usando o exemplo de resolução de uma equação quadrática, podemos concluir que o método gráfico também é aplicável a equações de grau n.

No 9º ano e nas turmas seniores, ainda vou conhecer outras funções. Estou interessado em saber se essas funções obedecem às regras de tradução paralela ao traçar seus gráficos.

No próximo ano também quero considerar as questões de solução gráfica de sistemas de equações e desigualdades.

Literatura

1. Álgebra. 7 ª série. Parte 1. Livro didático para instituições de ensino / A.G. Mordkovich. Moscou: Mnemosyne, 2007.

2. Álgebra. 8 ª série. Parte 1. Livro didático para instituições de ensino / A.G. Mordkovich. Moscou: Mnemosyne, 2007.

3. Álgebra. 9º ano Parte 1. Livro didático para instituições de ensino / A.G. Mordkovich. Moscou: Mnemosyne, 2007.

4. Glazer G.I. História da matemática na escola. Classes VII-VIII. – M.: Iluminismo, 1982.

5. Revista Matemática №5 2009; Nº 8 2007; Nº 23 2008.

6. Solução gráfica de equações Sites da Internet: Tol WIKI; stimul.biz/pt; wiki.iot.ru/images; berdsk.edu; página 3–6.htm.

Nesta vídeo-aula, o tópico “Função y \u003d x 2. Solução gráfica de equações. Durante esta aula, os alunos poderão familiarizar-se com uma nova forma de resolver equações - gráfica, que se baseia no conhecimento das propriedades dos gráficos de funções. O professor mostrará como resolver graficamente a função y=x 2 .

Sujeito:Função

Lição:Função. Solução gráfica de equações

A solução gráfica de equações é baseada no conhecimento de gráficos de funções e suas propriedades. Listamos as funções cujos gráficos conhecemos:

1), o gráfico é uma linha reta paralela ao eixo x, passando por um ponto no eixo y. Considere um exemplo: y=1:

Para valores diferentes, obtemos uma família de linhas retas paralelas ao eixo x.

2) Função de proporcionalidade direta o gráfico desta função é uma linha reta que passa pela origem. Considere um exemplo:

Já construímos esses gráficos em lições anteriores, lembre-se que para construir cada linha, você precisa selecionar um ponto que a satisfaça e tomar a origem como o segundo ponto.

Lembre-se do papel do coeficiente k: à medida que a função aumenta, o ângulo entre a linha e a direção positiva do eixo x é agudo; quando a função diminui, o ângulo entre a linha reta e a direção positiva do eixo x é obtuso. Além disso, existe a seguinte relação entre dois parâmetros k de mesmo sinal: para k positivo, quanto maior, mais rápido a função aumenta, e para negativo, a função diminui mais rapidamente para valores grandes de k módulo.

3) Função linear. Quando - obtemos o ponto de interseção com o eixo y e todas as linhas desse tipo passam pelo ponto (0; m). Além disso, à medida que a função aumenta, o ângulo entre a linha e a direção positiva do eixo x é agudo; quando a função diminui, o ângulo entre a linha reta e a direção positiva do eixo x é obtuso. E, claro, o valor de k afeta a taxa de variação do valor da função.

4). O gráfico desta função é uma parábola.

Considere exemplos.

Exemplo 1 - resolva graficamente a equação:

Não conhecemos funções desse tipo, então precisamos transformar a equação dada para trabalhar com funções conhecidas:

Temos funções familiares em ambas as partes da equação:

Vamos construir gráficos de funções:

Os gráficos possuem dois pontos de interseção: (-1; 1); (2; 4)

Vamos verificar se a solução foi encontrada corretamente, substitua as coordenadas na equação:

O primeiro ponto foi encontrado corretamente.

, , , , , ,

O segundo ponto também é encontrado corretamente.

Então, as soluções da equação são e

Agimos de maneira semelhante ao exemplo anterior: transformamos a equação dada nas funções conhecidas por nós, traçamos seus gráficos, encontramos as correntes de interseção e, a partir daqui, indicamos as soluções.

Obtemos duas funções:

Vamos construir gráficos:

Esses gráficos não têm pontos de interseção, o que significa que a equação dada não tem soluções

Conclusão: nesta lição, revisamos as funções conhecidas por nós e seus gráficos, lembramos suas propriedades e consideramos uma maneira gráfica de resolver equações.

1. Dorofeev G.V., Suvorova S.B., Bunimovich E.A. et al.Álgebra 7. 6ª edição. M.: Iluminismo. 2010

2. Merzlyak A.G., Polonsky V.B., Yakir M.S. Álgebra 7. M.: VENTANA-GRAF

3. Kolyagin Yu.M., Tkacheva M.V., Fedorova N.E. e outros Álgebra 7 .M .: Educação. 2006

Tarefa 1: Makarychev Yu.N., Mindyuk N.G., Neshkov K.I. et ai, Algebra 7, nº 494, página 110;

Tarefa 2: Makarychev Yu.N., Mindyuk N.G., Neshkov K.I. e outros Álgebra 7, nº 495, item 110;

Tarefa 3: Makarychev Yu.N., Mindyuk N.G., Neshkov K.I. et ai, Algebra 7, nº 496, página 110;

INSTITUTO DO DAGESTÃO PARA O DESENVOLVIMENTO PROFISSIONAL

EQUIPE PEDAGÓGICA

DEPARTAMENTO DE EDUCAÇÃO FÍSICA E MATEMÁTICA E TIC

Projeto

sobre o tema:

« Construção e p reformas

gráficos de função

na escola matemática »

Rabadanova P.A.

professor de matemática

MBOU "Escola secundária de Kochubey"

distrito de Tarumovsky

2015

1. Introdução………………………………………………………………….….3

2. Capítulo EU. Revisão da literatura sobre o tema do projeto………………………….….5

3. Capítulo II. Parte empírica:

3.1. Métodos básicos para converter gráficos de funções……….….7

3.2. Traçar um parefunções ímpares…………….. 10

3.3. Traçando uma função inversa………………………… 11

3.4. Deformação (compressão e tensão) de gráficos………………….12

3.5. Combinação de transferência, reflexão e deformação………………......13

4. Tarefas para solução independente…………………………………14

5. Conclusão…………………………………………………………………15

6. Conclusões………………………………………………………………………17

INTRODUÇÃO

A transformação de gráficos de funções é um dos conceitos matemáticos fundamentais diretamente relacionados às atividades práticas. Os gráficos refletem a variabilidade e o dinamismo do mundo real, as relações mútuas de objetos e fenômenos reais.

A linha funcional é o tema básico abordado nos Exames Estaduais Básico e Unificado.Além disso, muitos conceitos matemáticos são considerados por métodos gráficos. Por exemplo, paraquadráticoa função é introduzida e estudada em estreita conexão com equações e desigualdades quadráticas.Daí segue queensinar os alunos a construir e transformar gráficos de uma função é uma das principais tarefas do ensino de matemática na escola.

O estudo da função permite encontrar cerca dedomínio de definição e escopo da função, escopoTaxas decrescentes ou crescentes, assíntotas, intervalosconstância do sinal, etc. No entanto, para construir um gráficokov muitas funções podem serusar vários métodostorne isso fácilprédio. Assim, os alunos devem ter competência para construir gráficos de acordo com esquemas metodológicos.

O acima definerelevância Tópicos de pesquisa.

Objeto de estudo é o estudo da transformação de gráficos de linhas funcionais na matemática escolar.

Objeto de estudo - o processo de construção e transformação de gráficos de funções em uma escola secundária.

Objetivo do estudo: educacional - consiste em identificar um esquema metodológico para construção e conversão de gráficos de uma função;em desenvolvimento - desenvolvimento do pensamento abstrato, algorítmico, lógico, imaginação espacial;educacional - educação da cultura gráfica dos escolares, a formação de habilidades mentais.

Os objetivos levaram à decisão dos seguintestarefas:

1. Analisar as vertentes pedagógica e metodológica sobre o problema em estudo.

2. Identificar esquemas metodológicostransformação de gráficos de funções no curso escolar de matemática.

3. Selecione os métodos e meios mais eficazesconstrução e transformação de gráficos de funções em uma escola secundáriacontribuindo para: assimilação significativa do material educativo; aumentar a atividade cognitiva dos alunos; desenvolvimento de suas habilidades criativas.

HIPÓTESE pesquisar: a formação de habilidades gráficas no processo de estudo das funções e a educação da cultura gráfica dos alunos eficaz se os alunos tiverem um esquema metódico para construir e transformar gráficos de funções em um curso de matemática escolar.

CAPÍTULO EU . REVISÃO DA LITERATURA SOBRE O TEMA DO PROJETO.

Em preparação para o projeto, estudamos a seguinte literatura:

Sivashinsky, I. Kh. Teoremas e problemas em álgebra, funções elementares - M., 2002. - 115 p.

Gelfand, I. M., Glagoleva, E. G., Shnol, E. E. Funções e gráficos (técnicas básicas) - M., 1985. - 120 s

V.Z.Zaitsev, V.V. Ryzhkov, M.I. Scanavi. Matemática Elementar - M., 2010 (reedição). - 590 p.

Kuzmin, M. K. Construção de um gráfico de uma função - J. Matemática na escola. - 2003. - Nº 5. - S. 61-62.

Shilov G. E. Como construir gráficos? - M., 1982.

Isaac Tanatar. Transformações geométricas de gráficos de funções - MTsNMO, 2012

NONota-se que a capacidade de “ler” o comportamento de uma função em um determinado conjunto usando um gráfico é utilizada não apenas no curso de matemática, mas também em qualquer atividade humana prática na qual ele tenha que lidar com certas representações gráficas de dependências. Portanto, os alunos devem ser capazes de determinar algumas de suas propriedades a partir do gráfico de uma função.

O material teórico para a transformação de gráficos é estritamente indicado em. A técnica é acompanhada por ilustrações com desenhos, exemplos de complexidade variável e suas soluções, o que possibilita aprofundar conhecimentos e traçar funções complexas.

Representa um curso de treinamento eletrônico, cujo volume e conteúdo atendem aos requisitos de um curso de matemática do ensino médio. O material teórico é apoiado por ilustrações de animação gráfica que dão uma representação visual do tema em estudo. O curso inclui três módulos: um módulo de estudo de material teórico, um módulo de auto-exame e um módulo de controle de conhecimento.

De , , esquemas de gráficos metódicos, exemplos de trabalho independente foram usados para a parte empírica do projeto.

Conclusões do capítulo 1

O estudo da literatura educacional e metódica permitiu:

1. Identificar esquema metodológicoestudar, construir e transformar gráficos de uma função em um curso de matemática escolar.

2. Selecione os métodos e meios mais eficazesconstrução e transformação de gráficos de funções na matemática escolar,contribuindo:

assimilação significativa do material educativo;

aumentar a atividade cognitiva dos alunos;

desenvolvimento de suas habilidades criativas.

3. mostre que a linha funcional tem um impacto significativo no estudo de vários conceitos em matemática.

Capítulo 2. PARTE EMPÍRICA

Neste capítulo, consideraremos os principais métodos para transformar gráficos de funções e forneceremos esquemas metodológicos para construir várias combinações de gráficos para várias funções.

2.1. TÉCNICAS BÁSICAS PARA CONVERSÃO DE GRÁFICOS DE FUNÇÕES

Translação ao longo do eixo y

f ( x ) f ( x )+ b .

Porplotando uma funçãoy = f( x) + bvestígioem:

1. construir um gráfico de funçãoy= f( x)

2. mover o eixoabscissa em| b| unidades atéb>0 ou em| b| comerprostrar-se emb < 0. Obtido no novo sistemagráfico dinat é o gráfico de uma funçãoy = f( x) + b.

2. Transferência junto eixos abscissa

f ( x ) f ( x + uma ) .

y = f( x+ uma) vestígioem:

3. Traçando uma função da forma y = f (- x )

f (x ) f (- x ).

Para plotar uma funçãoy = f( - x) segue:

plotar uma funçãoy = f( x)

reflita de voltaem relação ao eixo y

o gráfico resultante égráfico de funçãoy = f( - X).

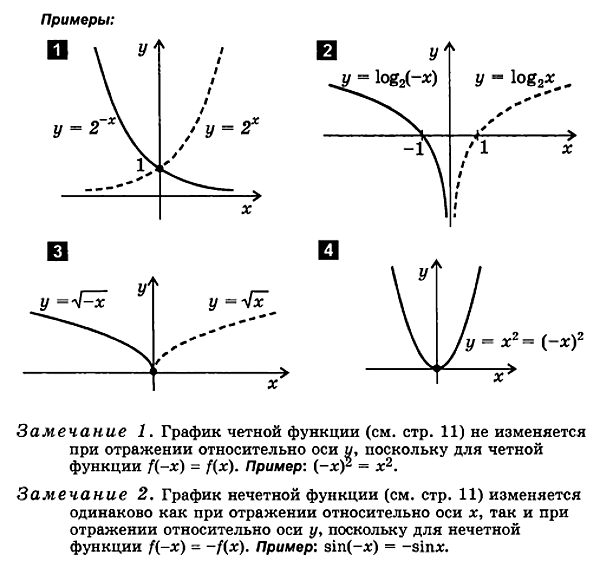
4. Traçando uma função da forma y= - f ( x )

f ( x ) - f ( x )

- f( x) segue:

plotar uma funçãoy= f( x)

reflita sobre o eixo x

2.2. Traçar um par e características estranhas

Ao plotarPara funções pares e ímpares, é conveniente usar as seguintes propriedades:

1. Gráfico de uma função par simmetarroz em relação ao eixo y.

2. O gráfico de uma função ímpar é simétrico em relação à origem.

Para construir gráficos de funções pares e ímpares, basta traçar apenas o ramo direito do gráfico para valores positivos do argumento. O ramo esquerdo é completado simetricamente em torno da origem para uma função ímpar e em torno do eixo y para uma função par.

Para plotar uma função par y = f ( x ) depois dueto:

construir um ramo do gráfico desta função apenas emintervalo de valores positivos do argumento x≥0.

Otrace este ramo em torno do eixo y

Para plotar uma função ímpar y = f ( x ) segue:

construir um ramo gráfico desta função apenas emárea de valores positivos do argumento (х≥0).

Orastrear este ramo em relação à origempara a região de valores negativos de x.

2.3. Plotando a função inversa

Como já mencionado, as funções direta e inversamostrar a mesma relação entre as variáveisx e y, com a única diferença de que na função inversa estesvariáveis mudaram de função, o que equivale a mudarnotação dos eixos coordenados. Portanto, o cronogramaa função inversa é simétrica ao gráfico da função diretasobre a bissetrizEUeIIIângulos coordenados,ou seja, relativamente retoy = x. Assim, obtemospróxima regra.

Para plotar a função y = (x) inversa à funçãoy = f( x), deve ser construídocronogramay = f( x) e refleti-lo em relação à linha reta y = x.

2.4. Deformação (compressão e tensão) de gráficos

1. Compressão (expansão) do gráfico ao longo do eixo y

f ( x ) UMA ∙ f ( x ).

Para plotar uma funçãoy= UMA∙ f( x) segue:

8. Compressão (expansão) do gráfico ao longo do eixo x

f( x)

Para plotar a função y= f( x) segue:

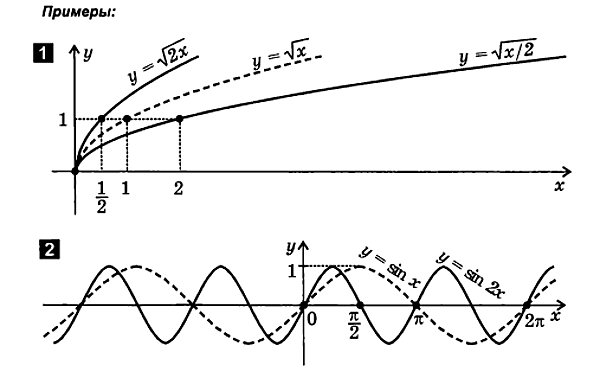
2.5. Combinação de translação, reflexão e deformação

Muitas vezes, ao traçar gráficos de funções paramude a combinação.

Aplicação consistente de várias dessas técnicas de posturapermite simplificar significativamente a construção de um gráfico usandofunção em execução e muitas vezes reduzi-la no final paraconstrução de uma das funções elementares mais simplesções. Considere como, em vista do exposto, segueconstruir gráficos de funções.

Notemos que é horaé aconselhável realizar a doca de simplificação no próximo sucessorness.

Usando paridade ouestranheza da função.

Transferência de eixos.

Reflexão e deformação.

A construção do gráfico é realizada na ordem inversa.

Exemplo. Plotar uma função

A construção será realizada nas seguintes etapas:

1. plote o logaritmo natural:

2. apertarpara o eixoOY2 vezes:;
3. exibir simetricamentesobre o eixoOY: ;
4. mova-se ao longo do eixoBOIno(!!!) Para a direita::

5. exibir simetricamente em torno do eixoBOI: ;
6. moverao longo do eixoOY3 unidades acima::

EXEMPLOS DE CONSTRUÇÃO E CONVERSÃO DE GRÁFICOS DE FUNÇÃO

Exemplo 1 Plotar uma função.

Primeiro, desenhe um gráfico seno, seu período é igual a:

gráfico de funçãoobtido comprimindo o gráficoduas vezes ao eixo y. registro .

Plotar uma funçãono = 2 porqueX.

Plotar uma funçãoy = pecadox .

CONCLUSÃO

Durante o trabalho de projeto, foram analisadas várias literaturas pedagógicas e metodológicas sobre esta temática. Os resultados do estudo permitiram identificar os aspectos positivos mais característicos do estudo, construção e transformação de gráficos de uma função em um curso de matemática escolar

O principal objetivo do projeto é desenvolver habilidades e habilidades dos alunos na leitura e no desenho de desenhos, na formação de métodos racionais de atividade independente.

A necessidade de melhorar a educação gráfica como um todo é ditada não apenas pelos requisitos modernos de produção, mas também pelo papel dos gráficos no desenvolvimento do pensamento técnico e das habilidades cognitivas dos alunos. A capacidade de uma pessoa de processar informações gráficas é um dos indicadores de seu desenvolvimento mental. Portanto, a formação gráfica deve tornar-se um elemento integrante da formação educacional geral.

descobertas

Assim, o projeto desenvolvido "Construção e transformação de grafos de funções", dedicado a um dos conceitos centrais da matemática - dependência funcional, tem como foco a sistematização e ampliação do conhecimento dos alunos. O estudo de métodos específicos para transformar gráficos de funções é realizado de forma analítica e gráfica de acordo com esquemas metodológicos rigorosos. O material coletado pode ser utilizado em sala de aula e para autoformação dos alunos. Uma variedade de formas e métodos de organização e treinamento podem ser usados para conduzir as aulas.

Portal para o aluno. Autotreinamento

ARTIGOS RELACIONADOS