Sivu 1

Pienjännitepiirin värähtelyprosessi pysähtyy jo korkeataajuisten värähtelyjen ensimmäisen jakson aikana, koska näiden värähtelyjaksojen toisella puoliskolla virran suunta muuttuu päinvastaiseksi tehopiirin virran kanssa. Generaattorin kipinän kirkkauden lisäämiseksi on mahdollista lisätä kapasitanssia edelleen.

Värähtelyprosessit kattavat laajan kirjon ilmiöitä, joille on tunnusomaista niiden ominaisuuksien toistuminen tietyin väliajoin aika.

Värähtelyprosessi tapahtuu järjestelmässä, kun sen tasapainosta poistuvan voiman ohella on myös palauttava (palauttava) voima. Mitä tapahtuu, jos palautusvoima vaikuttaa järjestelmään jatkuvalla viiveellä. Lisäksi, jos tällainen epävakaus, joka liittyy viiveen vaikutuksiin, on haitallista aluksen stabilointimekanismeille, se on hyödyllinen elektronisten generaattoreiden kehittämisessä.

Värähtelyprosessit, jotka määrittävät tankoihin kohdistuvien dynaamisten kuormien suuruuden, määräävät olennaisesti dynamogrammien muodon, jotka on tallennettu lähelle kiillotettua sauvaa.

Värähtelyprosessi piirissä tapahtuu nollasta poikkeavissa alkuolosuhteissa. Alkuvirta induktanssissa x määritetään seuraavien näkökohtien perusteella. Kytkin B katkaisee piirin, kun virta tB - i0 - ic kulkee nollan läpi.

Värähtelyprosesseja voi esiintyä myös sähkökoneissa ja muissa sähköasennuksissa, joissa on merkittävä induktanssi ja pyörivä massa, päälle, pois ja päälle. äkillisiä muutoksia toimintatila. Tietyissä olosuhteissa ei esiinny vaimennettuja, mutta heiluvia värähtelyjä. Tällaiset vaihtelut voivat johtaa vakavia rikkomuksia sähkölaitteiden toimintaa ja jopa onnettomuuksia. Siksi sähkökoneiden ja muiden asennuksien ohjausjärjestelmiä kehitettäessä joissakin tapauksissa on tarpeen soveltaa erityistoimenpiteitä värähtelyprosessien nopeimman vaimentamiseksi (syöttää vastukset niiden piireihin jne.).

Värähtelevät prosessit ja värähtelevät stabiilisuuden rajat eri epälineaariset järjestelmät voidaan usein määrittää harmoninen linearisointi, jonka käsite on annettu edellä. On myös muita menetelmiä. Tehokkaimpia tässä ovat numeeris-graafiset menetelmät transienttiprosessien konstruoimiseksi sekä erityisesti sähköisen simuloinnin menetelmät jatkuvan ja diskreetin toiminnan matemaattisilla koneilla.

Erilaisten epälineaaristen järjestelmien värähtelyprosessit ja stabiilisuuden värähtelyrajat voidaan usein määrittää harmonisen linearisoinnin menetelmällä, jonka käsite on annettu edellä.

Värähtelyprosessit ovat yleisiä luonnossa ja tekniikassa. Kellon heilurin heilahdus, aallot vedessä, vaihtovirta, valo, ääni ovat esimerkkejä erilaisten värähtelyistä. fyysisiä määriä. Heilurin liikkuessa sen painopisteen koordinaatti vaihtelee. Kun vaihtovirta jännite ja virta vaihtelevat piirissä. Nämä kaksi prosessia ovat laadullisesti täysin erilaisia fyysinen luonne. Näiden prosessien määrällisillä säännönmukaisuuksilla on kuitenkin paljon yhteistä.

Tankojen värähtelyprosessit eivät aiheudu pelkästään pintalaitteiden toiminnasta, vaan myös männän liikkeestä. Tässä synkroniset värähtelyt ovat toivottavampia, koska in Tämä tapaus ne eivät aiheuta ylikuormitusta.

Värähtelyprosessit ovat yleisiä luonnossa ja tekniikassa. Kellon heilurin heilautus, aallot vedessä, vaihtovirta, valo, ääni ovat esimerkkejä erilaisten fysikaalisten suureiden värähtelystä. Heilurin liikkuessa sen painopisteen koordinaatti vaihtelee. Vaihtovirran tapauksessa piirin jännite ja virta vaihtelevat. Nämä kaksi prosessia ovat laadullisesti täysin erilaisia ​​fysikaalisesti. Näiden prosessien määrällisillä säännönmukaisuuksilla on kuitenkin paljon yhteistä.

Vapaa värinä piirissä.

Edellisissä osissa käsitellyt AC-piirit viittaavat siihen, että elementtipari - kondensaattori ja induktori muodostavat eräänlaisen värähtelevän järjestelmän. Nyt näytämme, että näin todellakin on, vain näistä elementeistä koostuvassa piirissä (kuva 669) jopa vapaat värähtelyt ovat mahdollisia, eli ilman ulkoinen lähde EMF.

riisi. 669
Siksi kutsutaan piiriä (tai toisen piirin osaa), joka koostuu kondensaattorista ja induktorista värähtelevä piiri.
Varataan kondensaattori lataukseen qo ja sitten siihen kytketty induktori. Tällainen menettely voidaan helposti suorittaa käyttämällä piiriä, jonka kaavio on esitetty kuvassa. 670: ensin avain suljetaan asentoon 1 , kun taas kondensaattori ladataan jännitteeseen, joka on yhtä suuri kuin lähde emf, jonka jälkeen avain heitetään asentoihin 2 , jonka jälkeen kondensaattorin purkautuminen kelan läpi alkaa.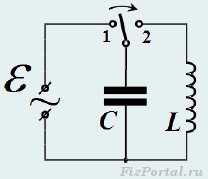

riisi. 670
Määrittää kondensaattorin varauksen riippuvuus ajasta q(t) sovelletaan Ohmin lakia, jonka mukaan jännite kondensaattorin yli U C = q/C on yhtä suuri EMF-itseinduktio, joka syntyy kelassa

tässä "alkuluku" tarkoittaa johdannaista ajan suhteen.
Siten yhtälö osoittautuu päteväksi

Tämä yhtälö sisältää kaksi tuntematonta funktiota - riippuvuuden latausajasta q(t) ja nykyinen Se), joten sitä ei voida ratkaista. Virran voimakkuus on kuitenkin johdannainen kondensaattorin varauksesta q / (t) = I (t), joten virranvoimakkuuden derivaatta on varauksen toinen derivaatta

Tämän suhteen huomioon ottaen kirjoitamme yhtälön (1) uudelleen muotoon

Yllättäen tämä yhtälö osuu täysin yhteen hyvin tutkitun harmonisten värähtelyjen yhtälön kanssa (tuntemattoman funktion toinen derivaatta on verrannollinen itse tähän funktioon negatiivisella suhteellisuuskertoimella x // = −ω o 2 x)! Siksi tämän yhtälön ratkaisu on harmoninen funktio

pyöreällä taajuudella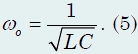

Tämä kaava määrittelee värähtelypiirin luonnollinen taajuus. Vastaavasti kondensaattorin varauksen värähtelyjakso (ja piirin virranvoimakkuus) on yhtä suuri kuin

Tuloksena olevaa värähtelyjakson lauseketta kutsutaan J. Thompsonin kaava.
Kuten tavallista, mielivaltaisten parametrien määrittämiseen A, φ sisään yhteinen päätös(4) on tarpeen asettaa alkuehdot - varaus ja virran voimakkuus sisään alkuhetki aika. Erityisesti kuvion 2 piirin tarkasteltavalle esimerkille. 670, alkuehdot ovat muotoa: at t = 0, q = qo, I = 0, joten funktio kuvaa kondensaattorin varauksen riippuvuutta ajasta

ja virran voimakkuus muuttuu ajan myötä lain mukaan

Yllä oleva värähtelypiirin huomio on likimääräinen - jokaisella todellisella piirillä on aktiivinen vastus (kytkentäjohdot ja kelan käämit).

riisi. 671
Siksi yhtälössä (1) tämän aktiivisen resistanssin yli oleva jännitehäviö tulisi ottaa huomioon, joten tämä yhtälö saa muodon

joka varauksen ja virran voimakkuuden välinen suhde huomioon ottaen muunnetaan muotoon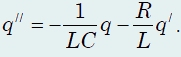

Tämä yhtälö on myös meille tuttu - tämä on vaimennettujen värähtelyjen yhtälö

ja vaimennuskerroin, kuten odotettiin, on verrannollinen piirin aktiiviseen resistanssiin β = R/L.
Vuonna tapahtuvat prosessit värähtelevä piiri, voidaan myös kuvata käyttämällä energian säilymisen lakia. Jos jätämme huomiotta piirin aktiivisen resistanssin, niin energioiden summa sähkökenttä kondensaattori ja magneettikenttä kela pysyy vakiona, mikä ilmaistaan ​​yhtälöllä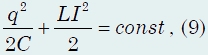

joka on myös harmonisten värähtelyjen yhtälö kaavan (5) taajuudella. Tämä yhtälö vastaa muodoltaan myös mekaanisten värähtelyjen aikana energian säilymisen laista seuraavien yhtälöiden kanssa. Koska yhtälöt kuvaavat värähtelyjä sähkövaraus kondensaattorit ovat samanlaisia ​​kuin kuvatut yhtälöt mekaanisia tärinöitä, niin voimme vetää analogian värähtelypiirissä tapahtuvien prosessien ja missä tahansa prosessien välillä mekaaninen järjestelmä. Kuvassa 672 tällainen analogia on vedetty värähtelyille matemaattinen heiluri. Tässä tapauksessa analogit ovat "kondensaattorin varaus q(t)− heilurin taipumakulma φ(t)" ja "nykyinen I(t) = q / (t)− heilurin nopeus V(t)».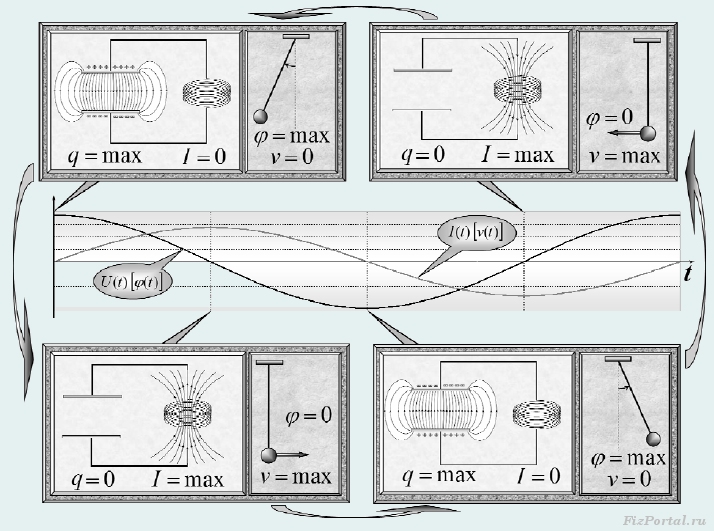



riisi. 672
Käyttämällä tätä analogiaa kuvaamme kvalitatiivisesti varausvärähtelyprosessia ja sähkövirtaääriviivassa. Alkuhetkellä kondensaattori latautuu, sähkövirran voimakkuus on nolla, kaikki energia sisältyy kondensaattorin sähkökentän energiaan (joka on samanlainen kuin heilurin maksimipoikkeama tasapainosta asema). Sitten kondensaattori alkaa purkautua, virran voimakkuus kasvaa, kun taas itseinduktio-EMF tapahtuu kelassa, mikä estää virran lisääntymisen; kondensaattorin energia pienenee muuttuen käämin magneettikentän energiaksi (analogia - heiluri liikkuu kohti alakohta nopeuden kasvaessa). Kun kondensaattorin varaus muuttuu nolla, virran voimakkuus saavuttaa maksimiarvonsa, kun taas kaikki energia muuttuu magneettikentän energiaksi (heiluri on saavuttanut alimmansa, sen nopeus on suurin). Sitten magneettikenttä alkaa pienentyä, kun taas itseinduktio-EMF ylläpitää virtaa samaan suuntaan, kun taas kondensaattori alkaa latautua, ja kondensaattorilevyjen varausten merkit ovat vastakkaisia ​​alkuperäisen jakautumisen kanssa (analogi - heiluri siirtyy vastakkaiseen alkuperäiseen maksimipoikkeamaan). Sitten virta piirissä pysähtyy, kun taas kondensaattorin varauksesta tulee jälleen maksimi, mutta vastakkainen etumerkillä (heiluri on saavuttanut suurimman poikkeamansa), minkä jälkeen prosessi toistetaan vastakkaiseen suuntaan.

LUENTO #8

Mekaniikka

vaihtelut

värähtelevä liike. Värähtelevän liikkeen kinemaattiset ja dynaamiset ominaisuudet. Matemaattinen, fysikaalinen ja jousiheiluri.

Elämme maailmassa, jossa värähtelyprosessit ovat olennainen osa maailmaamme ja niitä löytyy kaikkialta.

Värähtelyprosessi tai värähtely on prosessi, joka eroaa toiston asteelta.

Jos värähtelevä suure toistaa arvonsa säännöllisin väliajoin, tällaisia ​​värähtelyjä kutsutaan jaksollisiksi ja näitä ajanjaksoja kutsutaan värähtelyjaksoiksi.

Ilmiön fysikaalisesta luonteesta riippuen erotetaan värähtelyt: mekaaniset, sähkömekaaniset, sähkömagneettiset jne.

Vaihtelut ovat yleisiä luonnossa ja tekniikassa. Värähtelyprosessit ovat joidenkin mekaniikan haarojen taustalla. Tällä luentokurssilla puhumme vain mekaanisista tärinöistä.

Värähtelyjärjestelmään kohdistuvan vaikutuksen luonteesta riippuen värähtelyt erotetaan: 1. Vapaat tai luonnolliset, 2. Pakotetut värähtelyt, 3. Itsevärähtelyt, 4. Parametriset värähtelyt.

Vapaita värähtelyjä kutsutaan värähtelyiksi, jotka tapahtuvat ilman ulkoista vaikutusta ja jotka aiheutuvat alkuperäisestä "työntöstä".

Pakotettuja tärinöitä esiintyy jaksoittaisen ulkoisen voiman vaikutuksesta

Itsevärähtelyjä suoritetaan myös ulkoisen voiman vaikutuksesta, mutta voiman vaikutuksen systeemiin hetken määrää värähtelyjärjestelmä itse.

Ulkoisista vaikutuksista johtuvilla parametrisilla värähtelyillä tapahtuu säännöllistä muutosta järjestelmän parametreissa, mikä aiheuttaa tämän tyyppisen värähtelyn.

Yksinkertaisin muoto on harmonisia värähtelyjä

Harmoniset värähtelyt ovat lain mukaan tapahtuvia värähtelyjäsynti taicos . Esimerkki harmonisista värähtelyistä on matemaattisen heilurin värähtely

Värähtelevän suuren maksimipoikkeamaa värähtelyprosessissa kutsutaan värähtelyn amplitudi(MUTTA) . Aikaa, joka kuluu yhden täydellisen värähtelyn suorittamiseen, kutsutaan värähtelyjakso(T) . Värähtelyjakson käänteislukua kutsutaan värähtelytaajuus(). Usein kutsutaan vaihtelua kerrottuna 2:llä syklinen taajuus(). Siten harmonisia värähtelyjä kuvataan lausekkeella

Tässä ( t+  0 ) värähtelyvaihe ja  0 - alkuvaihe

Yksinkertaisimmat mekaaniset värähtelyjärjestelmät ovat ns.: matemaattiset, jousi- ja fyysiset heilurit. Katsotaanpa tarkemmin näitä heilurit.

8.1. Matemaattinen heiluri

Matemaattinen heiluri on värähtelevä järjestelmä, joka koostuu massiivisesta pisterungosta, joka on ripustettu painovoimakentässä venymättömään, painottomaan langaan.

Pohjapisteessä heilurin potentiaalienergia on minimissään. Taivutetaan heiluri kulmassa  . Massiivisen pistekappaleen painopiste nousee korkealle  h ja tässä tapauksessa heilurin potentiaalienergia kasvaa arvolla mg h. Lisäksi taipuneessa asennossa painoon vaikuttavat painovoima ja langan kireys. Näiden voimien toimintalinjat eivät täsmää, ja resultanttivoima vaikuttaa kuormaan pyrkien palauttamaan sen tasapainoasentoon. Jos kuormaa ei pidetä, tämän voiman vaikutuksesta se alkaa siirtyä alkuperäiseen tasapainoasentoon, sen kineettinen energia kasvaa nopeuden lisääntymisen vuoksi, kun taas potentiaalinen energia pienenee. Kun tasapainopiste saavutetaan, resultanttivoima ei enää vaikuta kehoon (painovoima tässä kohdassa kompensoituu langan kireyden voimalla). Kehon potentiaalinen energia tässä vaiheessa on minimaalinen, ja kineettisellä energialla on päinvastoin omansa enimmäisarvo. Inertialla liikkuva kappale ohittaa tasapainoasennon ja alkaa siirtyä siitä pois, mikä johtaa tuloksena (jännityksestä ja painovoimasta) muodostuvan voiman syntymiseen, joka kohdistuu kehon liikettä vastaan ​​hidastaen sitä alas. Tästä alkaa lasku kineettinen energia rahti ja sen lisäys Mahdollinen energia. Tämä prosessi jatkuu, kunnes kineettiset energiavarat ovat loppuneet ja siirtyvät potentiaaliseen energiaan. Tässä tapauksessa kuorman poikkeama tasapainoasennosta saavuttaa maksimiarvon ja prosessi toistetaan. Jos järjestelmässä ei ole kitkaa, kuorma värähtelee loputtomasti.

Siten värähteleville mekaanisille järjestelmille on tunnusomaista se, että kun ne poikkeavat tasapainoasennosta, järjestelmään syntyy palautusvoima, joka pyrkii palauttamaan järjestelmän tasapainoasentoon. Tässä tapauksessa tapahtuu värähtelyjä, joihin liittyy järjestelmän potentiaalisen energian ajoittainen siirtyminen sen kineettiseksi energiaksi ja päinvastoin.

Laskea värähtelevä prosessi. Voimien hetki M heiluriin vaikuttaminen on ilmeisesti yhtä suuri kuin - mglsin Miinusmerkki kuvastaa sitä tosiasiaa, että voimien momentilla on taipumus palauttaa kuorma tasapainoasentoon. Toisaalta peruslain mukaan pyörivä liike M=ID 2  / dt 2 . Siten saamme tasa-arvon

B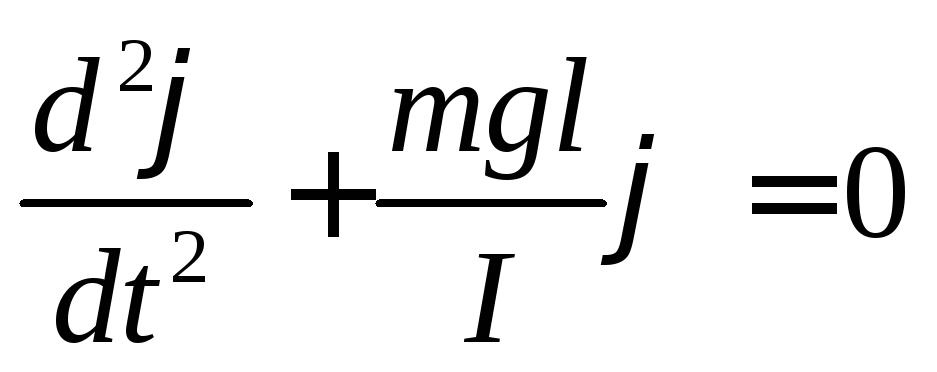

Tarkastellaan vain pieniä heilurin poikkeamakulmia tasapainoasennosta. Sitten synti ≈  . Ja tasa-arvomme tulee muotoon:

D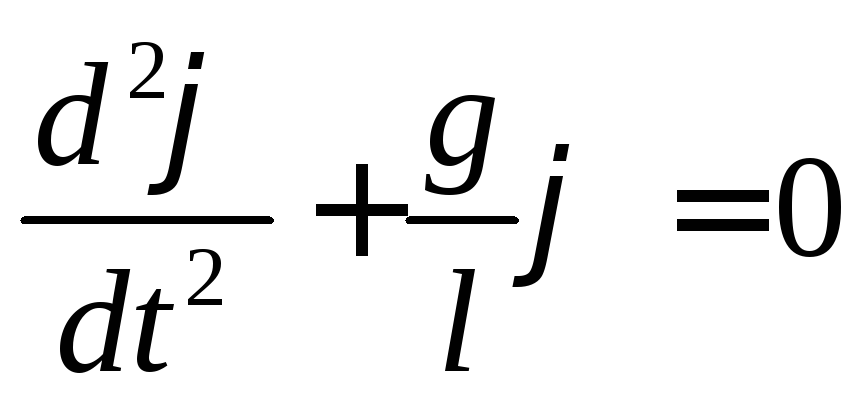

matemaattiselle heilurille se on totta minä= ml 2 . Korvaamalla tämän yhtälön tuloksena olevaan lausekkeeseen, saadaan yhtälö, joka kuvaa matemaattisen heilurin värähtelyprosessia:

Tämä differentiaaliyhtälö kuvaa värähtelyprosessia. Ratkaisu tähän yhtälöön on harmoniset funktiot synti( t+  0 ) tai cos ( t+  0 ) Todellakin, korvaamme minkä tahansa näistä funktioista yhtälöön ja saamme:  2 = g/ l. Siten, jos tämä ehto täyttyy, funktiot synti( t+  0 ) tai cos( t+  0 ) muuttaa värähtelyjen differentiaaliyhtälö identiteetiksi.

O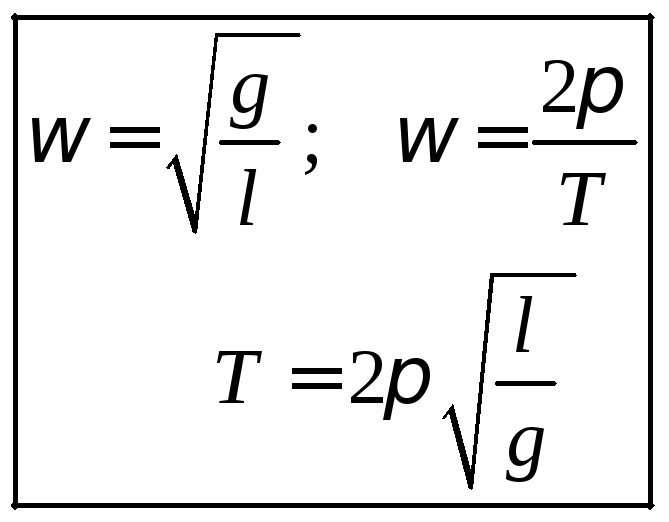

tässä harmonisen heilurin syklinen taajuus ja värähtelyjakso ilmaistaan ​​seuraavasti:

Värähtelyn amplitudi löydetään ongelman alkuolosuhteista.

Kuten näette, matemaattisen heilurin värähtelytaajuus ja -jakso eivät riipu kuorman massasta ja riippuvat vain painovoiman kiihtyvyydestä ja ripustuslangan pituudesta, mikä mahdollistaa heilurin käytön yksinkertaisena mutta erittäin tarkka laite painovoiman kiihtyvyyden määrittämiseen.

Toinen heilurityyppi on mikä tahansa fyysinen keho, joka on ripustettu mistä tahansa kehon kohdasta ja jolla on kyky suorittaa värähtelevää liikettä.

8.2. fyysinen heiluri

AT Otetaan mielivaltainen kappale, lävistetään se jossain pisteessä akselilla, joka ei ole sama kuin sen massakeskipiste, jonka ympäri kappale voi vapaasti pyöriä. Ripusta kappale tälle akselille ja poikkea se tasapainoasennosta jonkin kulman verran  .

T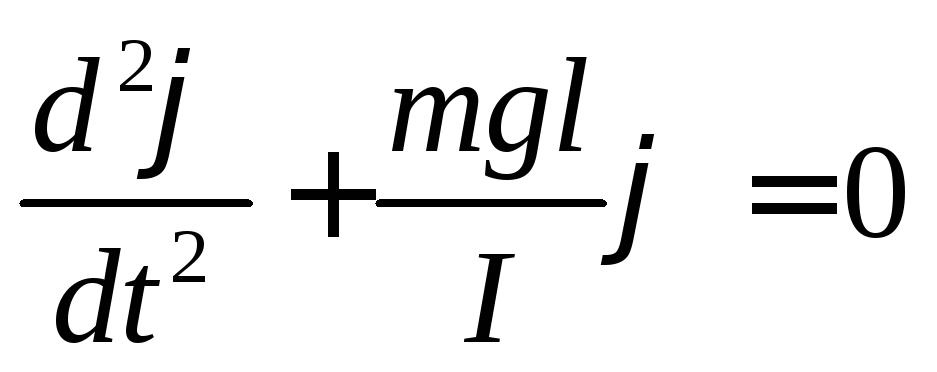

ollessaan keholla, jolla on hitausmomentti minä akselin suhteen O tasapainoasentoon palaamisen hetki vaikuttaa M = - mglsin ja fysikaalisen heilurin värähtelyt sekä matemaattisen heilurin värähtelyt kuvataan differentiaaliyhtälöllä:

Koska eri fysikaalisilla heilureilla hitausmomentti ilmaistaan ​​eri tavalla, emme kuvaile sitä kuten matemaattisen heilurin tapauksessa. Tämä yhtälö on myös värähtelyyhtälön muotoinen, jonka ratkaisu on harmonisia värähtelyjä kuvaavia funktioita. Tässä tapauksessa syklinen taajuus ( ) , värähtelyjakso (T) määritelty:

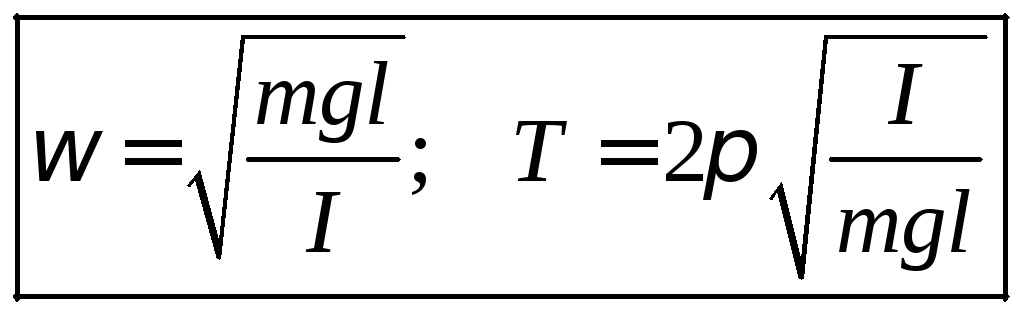
Näemme, että fysikaalisen heilurin tapauksessa värähtelyjakso riippuu heilurikappaleen geometriasta, ei sen massasta, kuten matemaattisen heilurin tapauksessa. Itse asiassa hitausmomentin lauseke sisältää heilurin massan ensimmäiseen potenssiin. Värähtelyjakson lausekkeen hitausmomentti on osoittajassa, kun taas heilurin massa on mukana nimittäjässä ja myös ensimmäisessä asteessa. Joten osoittajan massa kumoutuu nimittäjässä olevan massan kanssa.

Fyysisellä heilurilla on vielä yksi ominaisuus - pienentynyt pituus.

Fysikaalisen heilurin lyhennetty pituus on matemaattisen heilurin pituus, jonka jakso osuu yhteen fyysisen heilurin jakson kanssa.

Tämän määritelmän avulla on helppo määrittää lauseke pienennetylle pituudelle.

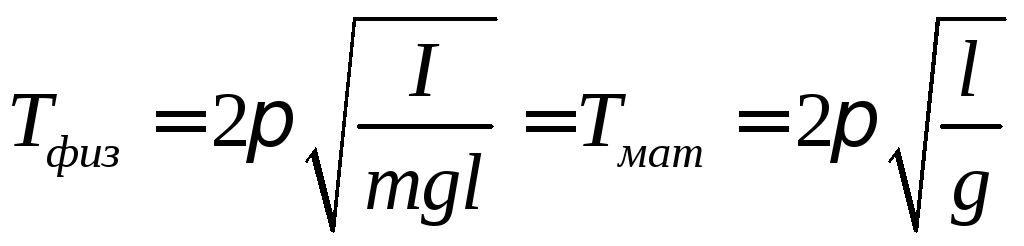
Vertaamalla näitä ilmaisuja saamme

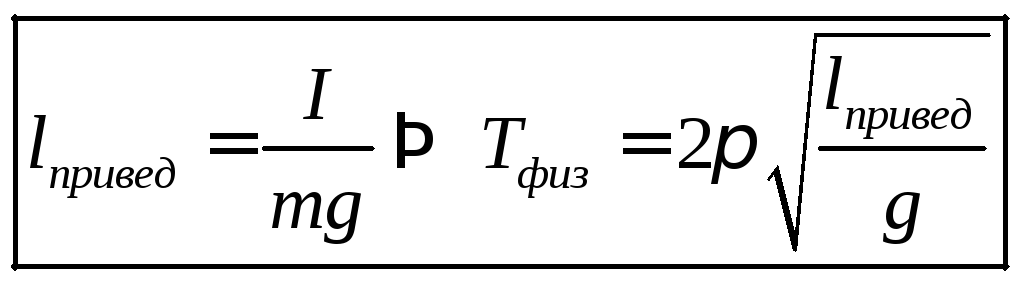
Jos ripustuspisteestä fyysisen heilurin massakeskipisteen läpi vedetylle viivalla piirretään (ripustuspisteestä alkaen) fyysisen heilurin pienentynyt pituus, niin tämän segmentin lopussa on piste, joka on merkittävä ominaisuus. Jos fyysinen heiluri ripustetaan tästä pisteestä, sen värähtelyjakso on sama kuin heilurin ripustettaessa edellisessä ripustuspisteessä. Näitä pisteitä kutsutaan fyysisen heilurin kääntökeskuksiksi.

Harkitse toista yksinkertaista värähtelyjärjestelmää, joka suorittaa harmonisia värähtelyjä

8.3 Jousi heiluri

P 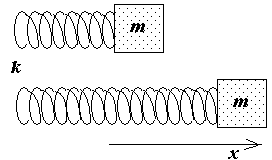kuvittele, että jousen loppuun mennessä jäykkyyskertoimella k paino kiinni m.

Jos liikutamme kuormaa x-akselia pitkin jousta venyttämällä, niin tasapainoasentoon palaava voima vaikuttaa kuormaan F palata = - kx. Jos kuorma vapautetaan, tämä voima aiheuttaa kiihtyvyyttä d 2 x / dt 2 . Newtonin toisen lain mukaan saamme:

md 2 x / dt 2 = - kx tästä yhtälöstä saadaan yhtälö jousen kuorman värähtelylle sen lopullisessa muodossa: d 2 x / dt 2 + (k/ m) x = 0

E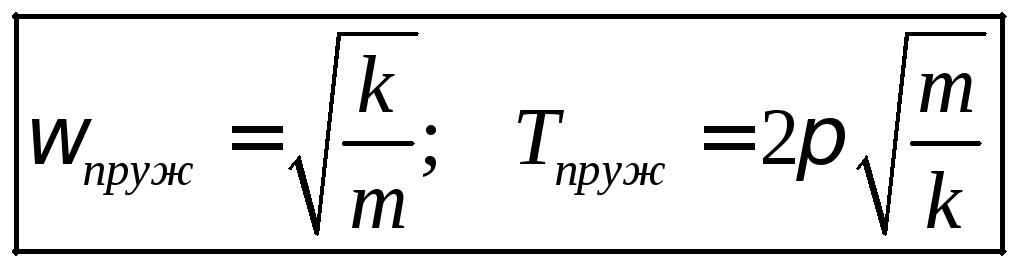

silloin värähtelyyhtälöllä on sama muoto kuin värähtelyyhtälöillä jo tarkasteluissa tapauksissa, mikä tarkoittaa, että tämän yhtälön ratkaisu on samat harmoniset funktiot. Värähtelyn taajuus ja jakso ovat vastaavasti samat

Lisäksi painovoima ei millään tavalla vaikuta jousiheilurin värähtelyihin. Koska tässä tapauksessa se on jatkuvasti vaikuttava tekijä, joka toimii koko ajan yhteen suuntaan ja jolla ei ole mitään tekemistä palauttavan voiman kanssa.

Näin ollen, kuten näemme värähtelyprosessin mekaanisessa värähtelyjärjestelmässä, sille on ominaista ensisijaisesti läsnäolo järjestelmässä palauttava voima vaikuttavat järjestelmään, ja itse värähtelyille on ominaista: vaihteluiden amplitudi niiden ajanjakson, taajuuden ja vaihteluvaiheen mukaan.