Typy čísel. Prirodzené, celé čísla, racionálne a reálne čísla. Číslo je abstrakcia používaná pre kvantitatívne charakteristiky predmety. Čísla vznikli v r primitívna spoločnosť v súvislosti s potrebou ľudí počítať predmety. Postupom času, s rozvojom vedy, sa číslo stalo najdôležitejším matematickým pojmom.

Ak chcete vyriešiť problémy a dokázať rôzne vety, musíte pochopiť, aké typy čísel sú. Medzi hlavné typy čísel patria: celé čísla, celé čísla, racionálne čísla, reálne čísla.

Celé čísla- to sú čísla získané prirodzeným počítaním predmetov, alebo skôr ich číslovaním ("prvý", "druhý", "tretí" ...). Množina prirodzených čísel je označená latinské písmeno N(dá sa zapamätať na základe anglické slovo prirodzené). Dá sa to povedať N ={1,2,3,....}

Celé čísla sú čísla z množiny (0, 1, -1, 2, -2, ....). Táto množina sa skladá z troch častí – prirodzených čísel, záporných celých čísel (opak prirodzených čísel) a čísla 0 (nula). Celé čísla sú označené latinkou Z. Dá sa to povedať Z={...,-3,-2,-1,0,1,2,3,....}.

Racionálne čísla sú čísla, ktoré možno znázorniť ako zlomok, kde m je celé číslo a n je prirodzené číslo. V tomto prípade sa volá číslo m čitateľ a číslo n - menovateľ zlomky. Takýto zlomok by sa mal chápať ako výsledok delenia m n, aj keď sa nedá úplne rozdeliť. Označiť racionálne čísla používa sa latinské písmeno Q. Q={... ;-3;-2,5;-2;-1;0; ;1;2;3;3,5....}. Všetky prirodzené a celé čísla sú racionálne. Ako príklady racionálnych čísel môžete uviesť: , , . AT skutočný život racionálne čísla sa používajú na počítanie častí niektorých celých, ale deliteľných predmetov, ako sú koláče alebo iné potraviny, ktoré sú nakrájané na niekoľko kusov, alebo na hrubý odhad priestorových vzťahov rozšírených predmetov.

Reálne (skutočné) čísla sú čísla používané na meranie spojité množstvá. Kopa reálne čísla označujeme latinským písmenom R. Reálne čísla zahŕňajú racionálne čísla a iracionálne čísla. Iracionálne čísla- sú to čísla, ktoré sa získajú v dôsledku vykonávania rôznych operácií s racionálnymi číslami (napríklad extrakcia koreňa, výpočet logaritmov), ale nie sú racionálne. Príklady iracionálnych čísel sú , , .

Na číselnej osi môže byť zobrazené akékoľvek reálne číslo:

Pre vyššie uvedené množiny čísel platí nasledujúce tvrdenie:

To znamená, že množina prirodzených čísel je zahrnutá do množiny celých čísel. Množina celých čísel je zahrnutá do množiny racionálnych čísel. A množina racionálnych čísel je zahrnutá do množiny reálnych čísel. Toto tvrdenie možno ilustrovať pomocou Eulerových kruhov.

Účel: Vedieť, aké prirodzené, celé číslo, racionálne číslo, periodický zlomok; vedieť písať donekonečna desiatkový vo forme obyčajného, ​​byť schopný vykonávať akcie s desatinnými a obyčajnými zlomkami.

1. Upevniť študovaný materiál, zmeniť typy práce, na túto tému „Celé a racionálne čísla“.
2. Rozvíjajte zručnosti a schopnosti pri vykonávaní akcií s desatinnými a obyčajnými zlomkami, rozvíjajte sa logické myslenie, správny a kompetentný matematický prejav, rozvoj samostatnosti a dôvery vo svoje vedomosti a zručnosti pri výkone odlišné typy Tvorba.
3. Zvýšte záujem o matematiku zavedením rôznych typov konsolidácie materiálu: ústna práca, práca s učebnicou, práca pri tabuli, odpovedanie na otázky a schopnosť introspekcie, samostatná práca; stimulovanie a povzbudzovanie aktivít žiakov.

ja Organizácia času.
II. Nová téma:
"Celé čísla a racionálne čísla".
1.Teoretická časť.
2. Praktická časť.
3. Pracujte podľa učebnice a pri tabuli.
4. Samostatná práca podľa možností.
III. Výsledok.
1. Na otázky.
IV. Domáca úloha.

Počas vyučovania

I. Organizačný moment.

Emocionálna nálada a pripravenosť učiteľa a žiakov na vyučovaciu hodinu. Komunikácia cieľov a zámerov.

II. Nová téma: „Celé čísla a racionálne čísla“:

Teoretická časť.

1. Spočiatku sa číslo chápalo len ako prirodzené čísla. Čo stačí na počítanie jednotlivých položiek.

Sada N = (1; 2; 3...) prirodzené čísla je uzavretá pod operáciami sčítania a násobenia. To znamená, že súčet a súčin prirodzených čísel sú prirodzené čísla.

2. Rozdiel dvoch prirodzených čísel však už nie je vždy prirodzeným číslom.

(Uveďte príklady: 5 - 5 = 0; 5 - 7 = - 2, čísla 0 a - 2 nie sú prirodzené).

Výsledok odčítania dvoch rovnakých prirodzených čísel teda vedie k pojmu nula a úvodu množiny nezáporných celých čísel

Zo = (0; 1; 2;...).

3. Aby bola operácia odčítania uskutočniteľná, zadajte záporné celé čísla, teda čísla opačné k prirodzeným. Takto sa získa množina celých čísel Z={...; -3; -2; -1; 0; 1; 2;...}.

Aby bolo možné vykonať delenie ľubovoľným číslom, ktoré sa nerovná nule, je potrebné pridať k množine všetkých celých čísel množinu všetkých kladných a záporné zlomky. Výsledkom je množina racionálnych čísel Q=.

Keď robíte štyri aritmetické operácie(okrem delenia nulou) nad racionálnymi číslami sa vždy získajú racionálne čísla.

4. Každé racionálne číslo možno znázorniť ako periodický desatinný zlomok.

Pripomeňme si, čo je periodický zlomok. Toto je nekonečný desatinný zlomok, v ktorom sa od určitého desatinného miesta opakuje rovnaká číslica alebo niekoľko číslic - perióda zlomku. Napríklad 0,3333...= 0,(3);

1,057373…=1,05(73).

Tieto zlomky sa čítajú takto: „0 celých a 3 v období“, „1 celý, 5 stotín a 73 v období“.

Racionálne čísla zapisujeme ako nekonečný periodický desatinný zlomok:

prirodzené číslo 25 = 25,00…= 25,(0);

celé číslo -7 = -7,00…= -7,(0);

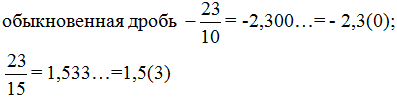
(používame algoritmus rohového delenia).

5. Platí aj opačné tvrdenie: každý nekonečný periodický desatinný zlomok je racionálne číslo, pretože ho možno znázorniť ako zlomok, kde m je celé číslo, n je prirodzené číslo.

Zvážte príklad:

1) Nech x \u003d 0,2 (18) vynásobíme 10, dostaneme 10x \u003d 2,1818 ... (Musíte vynásobiť zlomok 10 n, kde n je počet desatinných miest obsiahnutých v zázname tohto zlomku nahor do obdobia: x10 n).

2) Vynásobením oboch strán poslednej rovnosti 100 zistíme

1000x = 218,1818…(Vynásobenie 10 k , kde k je počet číslic v perióde x10 n 10 k = x10 n+k).

3) Odčítaním od rovnosti (2) rovnosti (1) dostaneme 990x = 216, x = .

Praktická časť.

1. Napíšte ako desatinný zlomok:

1) - na doske;

3) - pri tabuli jeden žiak zapíše rozhodnutie, ostatní rozhodnú na zemi, potom sa navzájom kontrolujú;

4) - pod diktátom každý vykonáva úlohu a jeden hovorí nahlas.

2. Vykonajte akcie a zapíšte výsledok ako desatinný zlomok:

1) - na doske;

3) - pod diktátom každý vykonáva úlohu a jeden hovorí nahlas;

5) - nezávisle s následným overením.

3. Napíšte ako spoločný zlomok nekonečné desatinné číslo:

6) -2,3(82) - učiteľ ukáže riešenie na tabuli podľa algoritmu.

Definícia prirodzených čísel sú celé čísla kladné čísla. Prirodzené čísla sa používajú na počítanie predmetov a na mnohé iné účely. Tieto čísla sú: 1; 2; 3; 4;...

Toto je prirodzený rad čísel.
Nula je prirodzené číslo? Nie, nula nie je prirodzené číslo.
Koľko prirodzených čísel existuje? Existuje nekonečná množina prirodzených čísel.
Aké je najmenšie prirodzené číslo? Jedna je najmenšie prirodzené číslo.
Aké je najväčšie prirodzené číslo? Nedá sa to špecifikovať, pretože existuje nekonečná množina prirodzených čísel.

Súčet prirodzených čísel je prirodzené číslo. Takže sčítanie prirodzených čísel a a b:

Súčin prirodzených čísel je prirodzené číslo. Takže súčin prirodzených čísel a a b:

c je vždy prirodzené číslo.

Rozdiel prirodzených čísel Nie vždy existuje prirodzené číslo. Ak je minuend väčší ako subtrahend, potom rozdiel prirodzených čísel je prirodzené číslo, inak nie je.

Podiel prirodzených čísel Nie vždy existuje prirodzené číslo. Ak pre prirodzené čísla a a b

kde c je prirodzené číslo, znamená to, že a je rovnomerne deliteľné b. V tomto príklade a je dividenda, b je deliteľ, c je kvocient.

Deliteľ prirodzeného čísla je prirodzené číslo, ktorým je prvé číslo rovnomerne deliteľné.

Každé prirodzené číslo je deliteľné 1 a samo sebou.

Jednoduché prirodzené čísla sú deliteľné iba 1 a samy sebou. Tu to znamená, že sú úplne rozdelené. Príklad, čísla 2; 3; 5; 7 je deliteľné iba 1 a sebou samým. Sú to jednoduché prirodzené čísla.

Jedna sa nepovažuje za prvočíslo.

Čísla, ktoré sú väčšie ako jedna a nie sú prvočísla, sa nazývajú zložené čísla. Príklady zložené čísla: 4; 6; 8; 9; 10

Jedna sa nepovažuje za zložené číslo.

Množina prirodzených čísel je jedna, základné čísla a zložené čísla.

Množinu prirodzených čísel označujeme latinským písmenom N.

Vlastnosti sčítania a násobenia prirodzených čísel:

komutatívna vlastnosť sčítania

asociatívna vlastnosť prílohy

(a + b) + c = a + (b + c);

komutatívna vlastnosť násobenia

asociatívna vlastnosť násobenia

(ab)c = a(bc);

distribučný majetok násobenie

a (b + c) = ab + ac;

Celé čísla

Celé čísla sú prirodzené čísla, nula a opak prirodzených čísel.

Čísla, ktoré sú opačné ako prirodzené čísla, sú celé čísla. záporné čísla napríklad: -1; -2; -3; -4;...

Množina celých čísel je označená latinským písmenom Z.

Racionálne čísla

Racionálne čísla sú celé čísla a zlomky.

Akékoľvek racionálne číslo môže byť reprezentované ako periodický zlomok. Príklady: -1,(0); 3,(6); 0,(0);...

Z príkladov je zrejmé, že akékoľvek celé číslo je periodický zlomok s periódou nula.

Akékoľvek racionálne číslo môže byť vyjadrené ako zlomok m/n, kde m celé číslo, n prirodzené číslo. Predstavme si číslo 3,(6) z predchádzajúceho príkladu ako taký zlomok: 22/6 = 3,(6);

Ďalší príklad: racionálne číslo 9 môže byť reprezentované ako jednoduchý zlomok ako 18/2 alebo ako 36/4.

Ďalší príklad: racionálne číslo -9 môže byť reprezentované ako jednoduchý zlomok ako -18/2 alebo ako -72/8.

Množina racionálnych čísel sa označuje latinským písmenom Q.

Iracionálne čísla

Iracionálne čísla sú nekonečné neopakujúce sa desatinné miesta.

Príklady: pi = 3,141592... e = 2,718281...

Reálne čísla

Reálne čísla sú všetky racionálne a všetky iracionálne čísla.

Množina reálnych čísel je označená latinským písmenom R.