Bernoullin yhtälön johtamiseen käytämme mekaniikasta hyvin tunnettua muutokseen liittyvää lausetta kineettinen energia. Muista, että tämä lause kuuluu seuraavasti: tarkasteltavana olevan kappaleen liike-energian 2 muutos jossain sen siirtymäkohdassa on yhtä suuri kuin kaikkien voimien (ulkoisten ja sisäisten) työn summa. tämä ruumis, samalla siirrolla.

Otetaan virran alkeisvirtaus (kuva 3-20). Valitse osat 1-1 ja 2-2 jokin valulokero AB. Merkitään z 1:llä ja z 2:lla osien ylimäärät 1 -1 Ja 2 -2 vertailutason yläpuolella Vai niin, läpi - virran asuinosien alueet osissa 1-1i 2 -2.

Oletamme, että aikana AB suihkut siirtyvät paikoilleen A"B" tässä tapauksessa virran osio 1-1 siirtyy etäisyydelle ja osio 2 -2 valuu - kaukaisuudessa . huomaa, että

Missä ja 1 Ja Ja 2 - nopeudet osissa 1-1i 2 -2.

Väittäen, kuten § 3-9, voimme osoittaa, että tihkumisen alkeisosastojen tilavuudet AA" Ja BB" ovat tasa-arvoisia, ts.

äänenvoimakkuutta (AA")= tilavuus (BB") =(nimitys),

missä on nesteen virtausnopeus suihkulle.

Merkitään alkeistilavuuden massa seuraavasti:

missä on nesteen tiheys.

Etsitään nyt osaston liike-energian muutos AB kun siirrät sen asentoon A"B" ja tähän osastoon kohdistettujen voimien työ määritellyllä siirtymällä.

1°. Osaston kineettisen energian muutos AB kun siirrät sen asentoon A "B". Merkitään mainittu kineettisen energian muutos (CE) b:n kautta (CE). Sitten voit kirjoittaa (katso kuva 3-20):

(KE) \u003d KE (A "B") - KE (AB) \u003d KE (A "B -f BB") -

KE (AA "+ A" B) \u003d KE (BB ") - KE (AA"),

tai annettu (3-55),

Riisi. 3-20. Yhtälön (3-60) johtamiseen

2°. Voimien työ osastoa liikutettaessa AB paikalleen A "B". Ilmoitetulla siirtymällä saamme seuraavien voimien työn.

1. Painovoiman työ. Kuten voidaan nähdä, painovoiman toiminnan vaikutus ilmeni ikään kuin siinä, että osasto AA" siirretty asentoon BB" (a lokero A "B jäi paikallaan). Käyttämällä tällaista ehdollista järjestelmää painovoiman työ (PCT) saamme muotoon

Oikeudenmukaisuus (3-57) voidaan perustella tiukemmin. Rikomme lokeron A "B perusosastoihin, joissa on tilavuus . Sitten haluttu painovoimatyö voidaan esittää seuraavasti:

Missä z", z", z",. . ., z(n) - korkeudet tason yläpuolella 00 alkeistilavuuksia erottavat rajaosat .

2. Hydrodynaamisen paineen voimien työ,
toimii päätyosissa 1 -1 Ja 2 -2 lokero
AB(setä ympäröivän nesteen puolelta). Tämä työ

missä ja ovat hydrodynaamiset paineet, vastaavasti, osissa 1 -1 ja 2-2.

3. Työ ulkoiset voimat ympäröivän nesteen paine luuhun sivupinta lokero AB. Tämä työ on yhtä suuri kuin nolla, koska voimat suunnataan kohtisuoraan osaston sivupintaa pitkin liikkuvien nestehiukkasten siirtymiin AB.

4. Työ sisäisiä voimia paine ( normaaleja voimia tilavuuden muodostavien yksittäisten nestehiukkasten vuorovaikutus AB).

Nämä voimat ovat pareittain (vastakkain suunnattu) samojen siirtymien kanssa. Heidän työnsä summa on nolla.

5. Ulkoisten ja sisäisten kitkavoimien työ on yhtä suuri kuin nolla (kitkavoimat ihanteellinen neste poissa).

3°. Lopullinen johtopäätös. Kineettisen energian muutoslauseen avulla voimme kirjoittaa:

Jaetaan tämä lauseke , eli viittaamme sen nestetilavuuden yksikköpainoon, joka kulkee ajassa b / läpi selkeä jakso valuu. Tässä tapauksessa edustamme tuloksena olevaa yhtälöä muodossa

Jaksoista lähtien 1-1 Ja 2 -2 suunniteltiin mielivaltaisesti, niin (3-59) voidaan myös kirjoittaa uudelleen muotoon:

Yhtälöä (3-59) tai (3-60) kutsutaan Bernoullin yhtälöksi. Sen hankki Daniil Bernoulli vuonna 1738. Tämä yhtälö pätee vain ihanteellisen nesteen alkuainevirtaan.

Kiinnitämme huomiota myös seuraaviin:

1) Bernoullin yhtälö suhteuttaa suureet z, p ja;

2) kuten (3-60) voidaan nähdä, ideaalisen nesteen tapauksessa kolmen termin summa z,, on vakio pitkin tarkasteltua valua;

3) jos ilmoitettu vakioarvo tietylle valumalle on yhtä suuri kuin Alt silloin naapuritihkulle edellä olevien kolmen termin summa on yhtä suuri A 2, ja sisään " yleinen tapaus A 1 ≠ A 2 ;

4) Tietäen tietyn valumisen vakioarvo A, ja myös tietäen kolmen suuren suihkun tietylle poikkileikkaukselle ( z, minä, p) mistä tahansa kahdesta suuresta, voimme Bernoullin yhtälön avulla löytää kolmannen tuntematon määrä suihkun kyseiselle osalle.

Yhtälö (3-60) voidaan saada myös integroimalla Eulerin differentiaaliyhtälöt (katso § 3-3) mille tahansa nesteeseen vaikuttaville kehon voimille, joilla on potentiaali (katso § 9-2). Yhtälö (3-60) viittaa tiettyyn virtaviivaan (tarkemmin sanottuna: alkeisvirtaukseen tiettyä virtaviivaa pitkin). Tätä yhtälöä kutsutaan usein Bernoullin integraaliksi.

Lisää yksityiskohtaista pohdintaa tästä asiasta osoittaa, että Bernoullin yhtälö (Bernoulli-integraali) osoittautuu päteväksi sekä ihanteellisen nesteen irrotaatio- (potentiaalinen) tasaiselle liikkeelle että pyörteen tasaiselle liikkeelle, edellyttäen kuitenkin, että nesteeseen vaikuttavilla kehon voimilla on potentiaali ( erityisesti painovoima, jonka pidimme edellä). Kun tarkastellaan ihanteellisen nesteen tasaista pyörreliikettä nopeudella, joka sisältyy Bernoullin yhtälöön, seuraa ymmärrä (niin sama kuten irrotaatioliikkeen tapauksessa) nopeus suhteessa todellinen vektorikenttä, joka heijastaa tarkasteltavana olevan nesteen liikettä (liikkeen jakautumista kolmeen tyyppiin, joka on selitetty kappaleissa 3-4, ei tule käsitellä tässä).

Voidaan myös osoittaa, että kun: a) ihanteellisen nesteen ilman pyörteistä (potentiaalista) liikettä ja b) nesteeseen vaikuttavia kehon voimia, joilla on potentiaali, arvo A, josta keskusteltiin edellä, on sama kaikille virtauksen muodostaville virtalinjoille: A 1 \u003d A 2 \u003d A 3 \u003d --- Tässä tapauksessa yhtälö (3-60) osoittautuu voimassa koko miehitetylle alueelle nesteen kautta, eikä vain tietyille virtalinjoille.

Yllä on saatu ihanteellisen nesteen liikkeen differentiaaliyhtälöt ja liikkeen jatkuvuuden yhtälö, jotka muodostavat suljetun yhtälöjärjestelmän. Tiettyjen teknisten ongelmien ratkaisemiseksi on välttämätöntä pystyä löytämään näiden yhtälöiden integraalit.

Ennen kuin siirrymme ihanteellisen nesteen liikeyhtälöiden integrointiin, hyväksymme seuraavat lisäehdot:

Kehon voiman kiihtyvyyden projektiot (in Tämä tapaus painovoima) ottaa seuraavat arvot, kun se valitaan; koordinaattiakselien suunta:

X = 0; Y = 0; Z = -g.

Muutoksen jälkeen saamme:

Jakamalla g:llä saamme:

Integroimalla tämän differentiaaliyhtälön kokonaiserot, saamme seuraavan tuloksen:

Tätä yhtälöä kutsutaan D. Bernoullin yhtälöksi, se pätee ihanteellisen nesteen tasainen liike.

Alkeisvirran kahdelle mielivaltaiselle osalle:

Tämä on D. Bernoullin yhtälö.

Geometrinen ja energinen merkitysyhtälöt

D. Bernoulli

Kaikilla D. Bernoullin yhtälöön sisältyvillä termeillä on lineaarinen ulottuvuus, joten niitä kutsutaan yleensä korkeuksiksi. Näin ollen seuraavat jäsenten nimet ovat yleisesti hyväksyttyjä:

z - geometrinen tai geodeettinen korkeus;

Pietsometrinen korkeus tai painekorkeus;

- dynaaminen tai nopeuspää;

Seuraava on helppo nähdä geometrinen merkitys D. Bernoullin yhtälö, joka on se ihanteellisen nesteen tasaisessa liikkeessä kolmen summakorkeudet (geometriset, pietsometriset ja nopeus) eivät olevaihtelee tietyn perusvirran mukaan. Tämä tilanne näkyy selvästi kuvassa. 1.

On mahdollista tulkita yhtälön yksittäisten termien merkitys

Bernoulli on erilainen. Edellä on esitetty summa

Edustaa nesteen ominaisenergiaa. Näin ollen voimme olettaa, että:

z - on paikan ominaisenergia;

paine energia;

On olemassa tiettyä kineettistä energiaa.

Bernoullin yhtälön energinen merkitys on se ihanteellisen nesteen tasaisessa liikkeessäasennon, paineen ja kineettisten spesifisten energioiden summa ei muutu tietyssä alkeissuihkussa.

Riisi. 1

Kokonaisominaisenergia (eli potentiaali + kineettinen) kutsutaan hydrodynaamiseksi pääksi ja on merkitty . Siten Bernoullin yhtälö osoittaa, että tietylle virralle ihanteellisen nesteen tasaisessa liikkeessä hydrodynaaminen korkeus on vakioarvo. Kaaviossa hydrodynaaminen päälinja on kuvattu vaakaviivana.

D. Bernoullin yhtälö alkeisvirralle oikeaa nestettä. Pietsometrinen ja hydraulinenrinteet.

Kun todellinen neste liikkuu vierekkäisten virtojen välillä, syntyy kitkavoimia, joiden voittamiseksi osa nesteen energiasta kuluu. Siksi nesteen ominaisenergia perussuihkun poikkileikkauksessa 2 -2 on pienempi kuin nesteen ominaisenergia poikkileikkauksessa 1-1 jonkin verran , jota kutsutaan menetetyksi korkeudeksi tai menetetyksi ominaisenergiaksi, joka kuluu hydraulisen vastuksen voittamiseksi. Analyyttisesti tämä tilanne voidaan kirjoittaa seuraavasti:

Siten, todellisen nesteen tasaisessa liikkeessäneljän korkeuden luun summa (geometrinen, pietsometrinentaivas, nopea ja kadonnut) tai, mikä on sama, summaneljä erityistä energiaa (sijainti, paine, kineettinen ja hävinnyt) eivät muutu annetussa alkuainevirrassa.

Bernoullin yhtälö on helppo esittää graafisesti tarkasteltavalle tapaukselle. Tätä varten, kun olet valinnut mielivaltaisen vaakasuuntaisen vertailutason, aseta siihen jokaiseen osaan korkeus ; ; ; Ja . Segmenttien z päät, jotka on yhdistetty tasaisella käyrällä, näyttävät valun akselin sijainnin. Yhdistämällä tasaisen käyrän segmenttien päät saadaan ns. pietsometrinen viiva. Asettamalla kuhunkin osioon pietsometrisistä linjasegmenteistä ylöspäin nopeuspaineita vastaavat segmentit ja yhdistämällä niiden päät tasaisella käyrällä, saadaan hydrodynaaminen päälinja tai, kuten sitä usein kutsutaan, hydraulinen linja (kuva 2). segmentit, yhtä suuri kuin etäisyydet pystysuunnassa hydraulilinjasta vaakatasoon, joka kulkee vertailutason yläpuolella korkeudella, joka on yhtä suuri kuin alkuperäisen ominaisenergian, edustavat hydraulisen vastuksen energiahäviötä osassa alustasta tarkasteltavaan osaan.

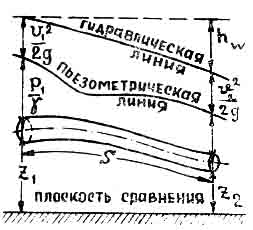
Riisi. 2

Kutsukaamme hydraulilinjan putoamista alkeisvirran pituusyksikköä kohti hydraulinen kaltevuusminä:

Hydraulinen kaltevuus (kuva 3) on aina positiivinen arvo, koska nesteen liikkuvan osan kokonaisominaisenergia pienenee vähitellen liikkuessaan alkuainevirtaa pitkin, kuluen kitkavoimien voittamiseen, muuttuen lämpöenergia ja sirottelu.

Riisi. 3

Tasaisesti muuttuvan (hitaasti muuttuvan) nesteliikkeen käsite

Yleisessä tapauksessa tasaisella liikkeellä nestevirtaus voidaan esittää sarjana perussuihkuja, joilla on erilaisia ​​merkityksiä niiden erottelukulmat ja erilaiset kaarevuussäteet. erikoistapaus dvivirtaus, jossa se kokee pienen muodonmuutoksenioni, niin että alkuainefilamentit pysyvät samansuuntaisinatai melkein samansuuntaisesti toistensa kanssa (), ja niiden kaarevuussäteet ovat hyvin suuria arvoja (), kutsutaan sujuvasti muuttuvaksi tai hitaasti muuttuvaksi liikkeeksi.

SISÄÄN virtauksen vapaan osan taso tasaisesti muuttuvallahydrodynaamiset paineet jakautuvat hydrostaattisten lakien mukaan, mikä tarkoittaa sitä tietyssä elävässä osassa minkä tahansa hiukkasen ominaispotentiaalienergia on vakioarvo:

D. Bernoullin yhtälö todellisen nesteen virtaukselle.

Yhtälön sovellettavuuden ehdot D. Bernoulli.

Laajennetaan Bernoullin yhtälö todellisen nesteen tasaiseen virtaukseen. Tätä varten valitsemme virtauksen heikosti epämuodostuneelta osalta vapaan osan, jonka lähellä liikettä voidaan pitää sujuvasti muuttuvana.

Tämän osion kautta jokainen alkeissuihku ajaa dt syötetään energiaa, joka yllä olevan mukaisesti osoittautuu yhtä suureksi kuin:

Poistetaan suluista läpi kulkevan nesteen paino poikkileikkaus nokka per;aika dt, yhtä suuri , kirjoita tämä lauseke uudelleen seuraavaa lomaketta:

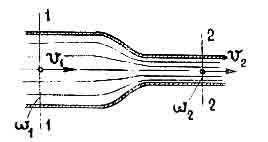
Riisi. 4

Selvitetään vapaan osan 1 läpi nestevirtauksen kuljettama kokonaisenergia - 1. Tätä varten on ilmeisesti tarpeen summata tuloksena oleva lauseke tietyn vapaan poikkileikkauksen kaikkien virtojen osalta. Sitten saamme:

Kokonaisenergia siis osoittautuu yhtä suuri kuin summa kaksi integraalia, jotka edustavat vastaavasti virtauksen potentiaalista ja kineettistä energiaa.

Kirjoitamme toisen integraalin seuraavassa muodossa:

Tämä integraali edustaa, kuten jo mainittiin, kineettistä energiaa, jonka virtaus kuljettaa osan 1-1 läpi ajan kuluessa. dt. Sen laskemiseksi on tarpeen tietää, kuinka nestehiukkasten nopeudet jakautuvat elävän osan yli. Jos laskemme virtauksen kineettisen energian olettaen, että nämä nopeudet ovat vakioita (toisin sanoen keskimääräisen virtausnopeuden mukaan tietyssä elävässä osassa ), sitten saamme:

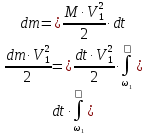
Tämä lauseke on aina suuruudeltaan pienempi kuin todellisista nopeuksista laskettu todellinen kineettinen energia. Merkitään näiden kahden määrän suhdetta:

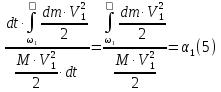
Koska virtausosassa osien 1-1 välillä ja 2-2 osa virtausenergiasta kuluu hydraulisen vastuksen voittamiseksi ja muuttuu palautumattomasti lämpöenergiaksi, . On myös selvää, että. Näiden spesifisten energioiden välinen ero ilmaisee virtauksen ominaisenergian häviämisen tarkasteltavassa liikeosuudessa:

Integroinnin ja korvaamisen jälkeen saamme:

Kerroin kutsutaan kineettiseksi kertoimeksivirtausenergia ja on suhde todelliseenvirtauksen kineettinen energia liike-energiaan, sinänumeerinen olettaen, että nopeudet vapaan osan kaikissa kohdissa ovat yhtä suuret kuin keskimääräinen virtausnopeus. Se on selvää tämä kerroin on aina suurempi kuin yksi.

Tuloksena oleva yhtälö on D. Bernoullin yhtälö todellisen nesteen tasaiselle virtaukselle.

Luento numero 8.

hydraulinen vastus.

Hydraulisen vastuksen ja painehäviön luokitus.

Kun todellinen neste liikkuu, osa virtausenergiasta kuluu hydraulisten vastusten voittamiseen, jotka jaetaan kahteen tyyppiin:

1) vastus virtauksen pituudella;

2) paikallinen vastus.

Virtauksen pituudella olevat vastukset ovat kitkavoimien aiheuttamia ja virtauksen pituudesta riippuvia vastuksia.

Paikalliset vastukset ovat sellaisia, jotka johtuvat nopeuden suunnan tai suuruuden muutoksesta virtauksen eri osissa. Nämä vastukset johtuvat hanoista, sulkuventtiileistä, putkien venttiileistä, virtauksen äkillisestä laajenemisesta tai supistumisesta jne.

Osaa virtausenergiasta, joka kuluu hydraulisen vastuksen voittamiseksi, kutsutaan painehäviöksi tai energiahäviöksi.

Painehäviöt jaetaan myös kahteen tyyppiin:

1) painehäviö virtauksen pituudella, joka johtuu hydraulisesta vastuksesta virtauksen pituudella ( h f);

2) paikallisista painehäviöistä, jotka johtuvat paikallisesta hydraulivastuksesta ( h i). Tappiot yhteensä pää:

h ω = . (1)

Pään menetys riippuu merkittävästi nesteen liikkumistavasta.

Laminaari ja myrskyisä järjestelmä s nestemäistä liikettä.

Nesteen liikettä on kaksi: laminaarinen ja turbulenttinen.

Laminaarisessa liiketilassa nestehiukkaset liikkuvat erillisinä suihkuina, jotka eivät sekoitu keskenään. Esimerkkejä laminaarista liikettä ovat: pohjaveden liike, korkean viskositeetin nesteiden liikkuminen putkistojen läpi (polttoöljy, öljy jne.), veren liikkuminen verisuonissa.

Turbulenttisessa liiketilassa yksittäiset virrat sekoittuvat keskenään. Turbulenttia liikettä havaitaan luonnossa paljon useammin kuin laminaarista liikettä. Esimerkki pyörteisestä liikkeestä on veden liikkuminen joissa, kanavissa, vesiputkissa jne.

Sana "laminaari" tulee latinan sanasta lamina - levy, nauha, kerros; Sana "turbulentti" tulee latinan sanasta turbulentus - arvaamaton.

Kahden nesteliikkeen olemassaolon luonnossa huomautti ensimmäisenä erinomainen venäläinen tiedemies professori D. I. Mendeleev vuonna 1880 teoksessaan "Nesteen vastus ja ilmailu".

Englantilainen tiedemies O. Reynolds suoritti liiketilojen kokeellisen tutkimuksen vuonna 1883.

Kokemus alkaa putkilipulla D nesteitä alhaisilla nopeuksilla. Samanaikaisesti maali syötetään säiliöstä KANSSA. Tällöin saadaan seuraava kuva (kuva 1b): sävytetty virta on suoran vaakaviivan muotoinen, kun taas muu liikkuvan nesteen massa jää värittömäksi. Näin ollen tässä tapauksessa sävytetyn virran hiukkaset eivät sekoitu muun nesteen kanssa, ja nesteen liiketapa putkessa D laminaarinen.

Putken nopeuden asteittaisella lisäyksellä D tulee hetki, jolloin sävytetty virta katoaa ja koko liikkuva neste värjäytyy tasaisesti. Tämä osoittaa, että virtauksen nesteen hiukkaset ovat sekoittuneet, eli putkessa D tapahtuu turbulenttinen järjestelmä (kuvio 1c).

Riisi. 1

Nopeutta, jolla yksi liiketapa vaihtuu toiseen kutsutaan kriittinen. On olemassa kaksi kriittistä nopeutta: ylempi kriittinen nopeus V VC , jossa laminaarinen liiketapa muuttuu turbulentiksi ja alempi kriittinen nopeus V nk - käänteisen siirtymän aikana.

O. Reynolds antoi liikemuotojen kokeellisen tutkimuksen perusteella kriteerin yhden tai toisen liiketavan määrittämiseksi.

Nesteen liiketavan määrittämisen kriteeri on ns Reynoldsin numero, joka on merkitty Re ja se saadaan kaavalla:

Missä V on keskinopeus virtausliikkeet;

L on virtauksen avoimen osan ominainen geometrinen koko;

on viskositeetin kinemaattinen kerroin.

Ylempää kriittistä nopeutta vastaavaa Reynoldsin lukua kutsutaan ylemmäksi kriittiseksi Reynolds-luvuksi ja sitä merkitään Re vk , tällä Reynoldsin numerolla laminaarivirtaus muuttuu turbulentiksi.

Alempaa kriittistä nopeutta vastaavaa Reynoldsin lukua kutsutaan alemmaksi kriittiseksi Reynolds-luvuksi ja se merkitään Re nk ; tällä Reynoldsin numerolla turbulenttisesta järjestelmästä tulee laminaarinen.

Putkilinjojen paineliikkeelle on tehty seuraavat kokeet: numeerisia arvoja kriittinen Reynoldsin luku:

Re d (nk) = 2000 2320;

Re d (VC) = 10000 13000.

Oikealla nesteellä on viskositeetti, ja kun se liikkuu, syntyy liikevastus. Liikevastus johtuu voimien esiintymisestä sisäinen kitka. Kun todellisen nesteen virta liikkuu, virran sisältämä mekaaninen energia vähenee sitä pitkin, koska osa siitä kuluu vastuksen voittamiseen, .

Tämä energia kuluu johonkin peruuttamattomaan työhön, ts. kitkavoimien työhön, ja se muuttuu lämmöksi, joka haihtuu.

Mitä pidempi virta, sitä enemmän energiaa kuluu liikevastuksen voittamiseksi.

Energiaa kului kitkavoimien työstä, - mekaaninen energiahäviö virtoja, jotka muuttuvat lämmöksi. Nesteen yksikköpainoon liittyviä energiahäviöitä sen liikkuessa alkuainevirtaa pitkin kutsutaan hydraulihäviöiksi (ominaisenergiahäviöiksi).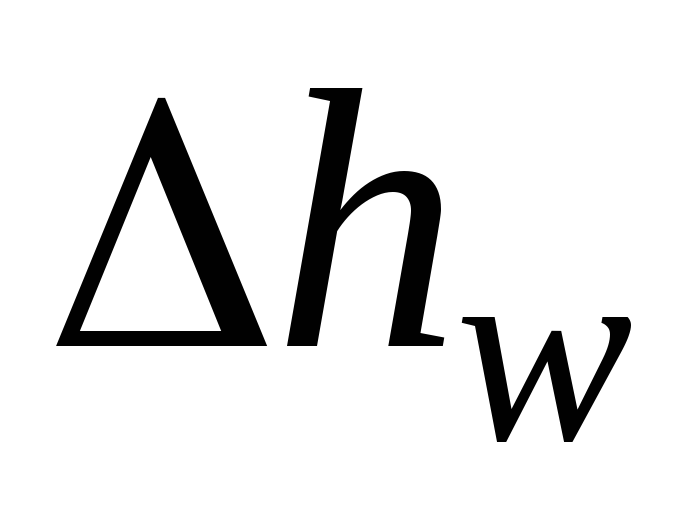

.

Tarkastellaan todellisen nesteen tihkumista tasaisella liikkeellä (kuva 3.8).

Riisi. 3.8. Bernoullin yhtälöön todellisen nesteen valumiselle

Todellisen valumisen mekaaninen kokonaisenergia sen elävissä osissa 1-1 ja 2-2 on

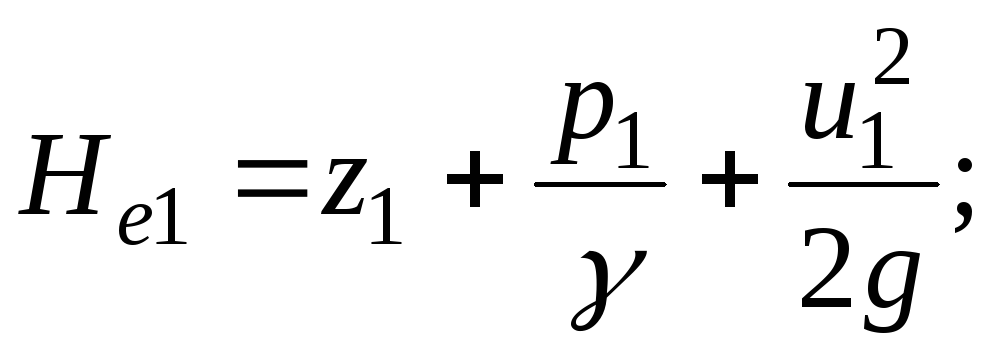
Ominaismekaanisen energian menetykset kitkan vuoksi asuinosien 1-1 ja 2-2 alueella

(3.45)

Siten Bernoullin yhtälö todellisen nesteen perusvirtaukselle tasaisen liikkeen tapauksessa voidaan esittää

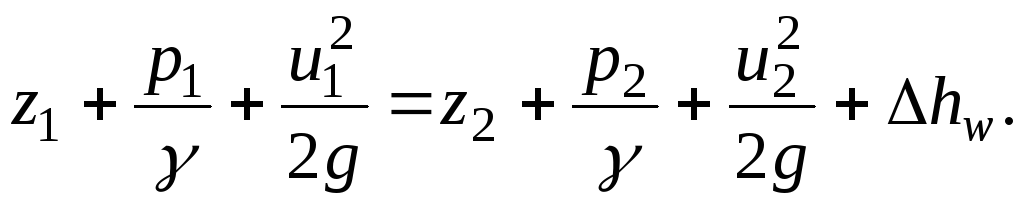(3.47)

Nesteen liikkeen ominaisuus on pietsometristen ja hydraulisten kaltevuuden käsite.

Kuvassa 3.8 esittää Bernoullin yhtälölle ominaisia ​​käyriä. Pietsometrisen korkeuden arvoa vastaavien pisteiden läpi kulkeva viiva jännitteissä osissa 1-1 ja 2-2 on pietsometrinen viiva.

Pietsometrinen kaltevuus on nesteen hydrostaattisen korkeuden muutos virtaa pitkin pituusyksikköä kohti. Viron osassa, jonka pituus on 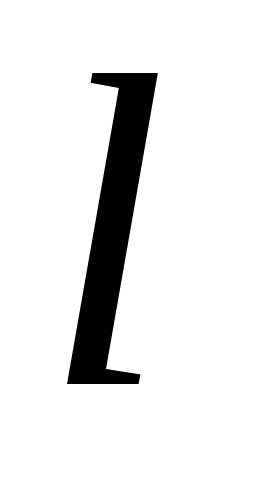osien 1-1 ja 2-2 pietsometrinen kaltevuus

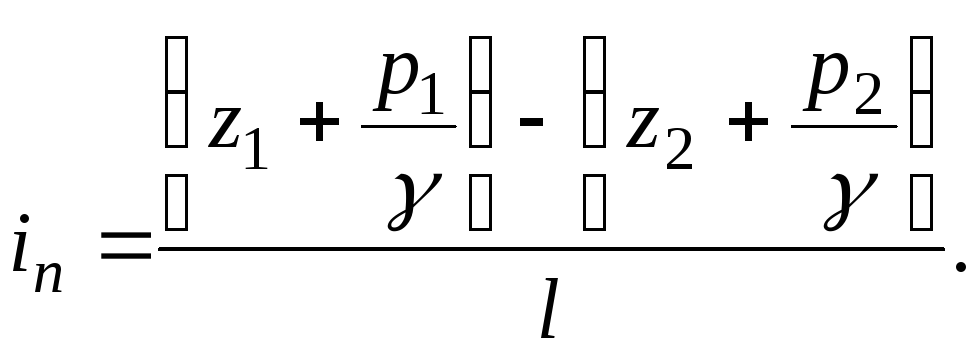(3.48)

Pietsometrinen kaltevuus, joka vastaa äärettömän pientä pituutta

(at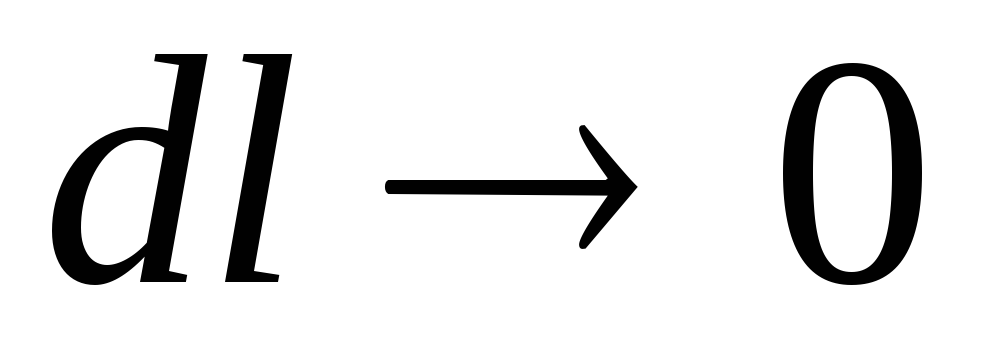

), - pisteen kaltevuus:

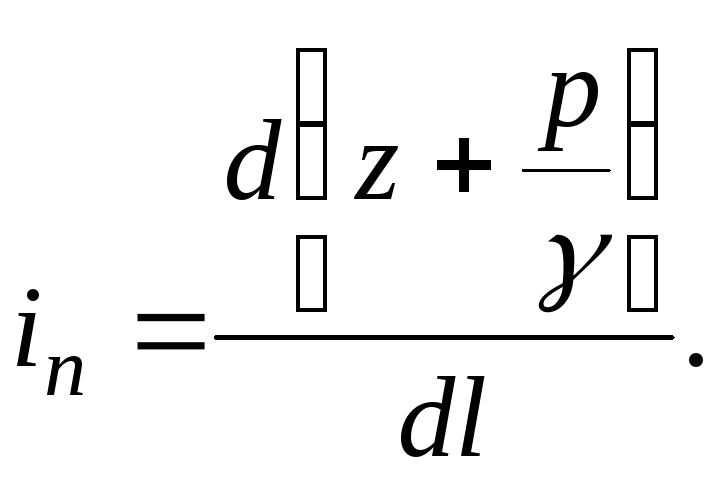(3.49)

Hehkulangan elävien osien spesifisten mekaanisten energioiden arvopisteiden läpi kulkeva viiva on painelinja(täysi painejohto). Hydraulinen kaltevuus on mekaanisen kokonaisenergian väheneminen hehkulangan pituutta kohti:

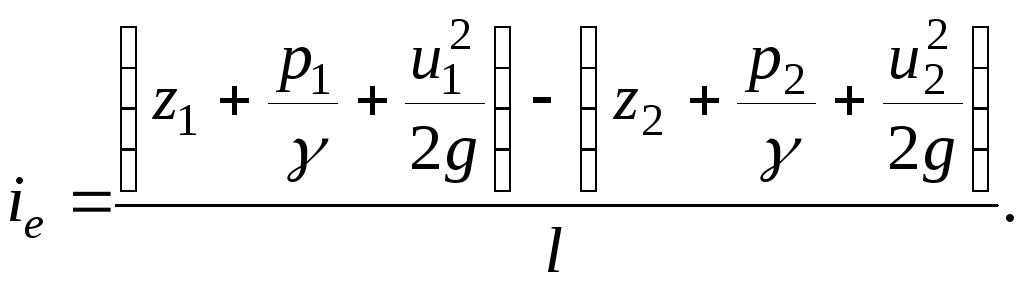(3.50)

Alkuperäisellä ominaisenergian laskulla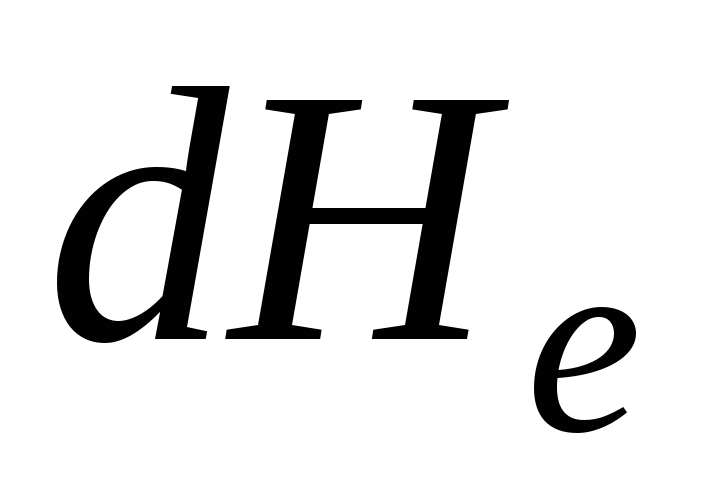

äärettömän pienellä alueella

hydraulinen kaltevuus

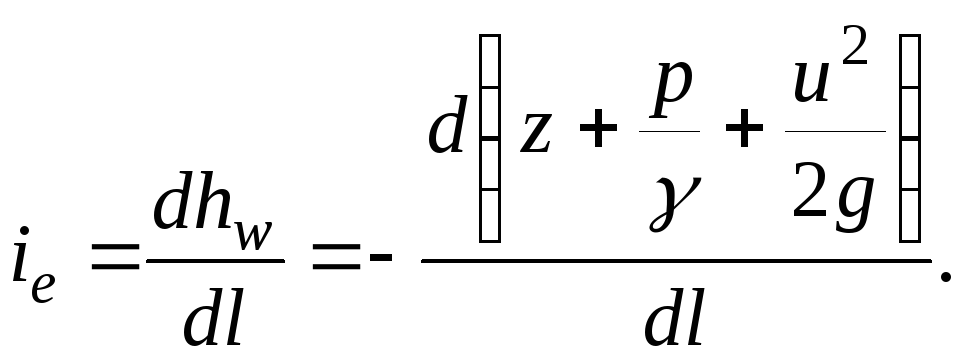(3.51)

Koska kokonaispään käyrä pienenee valun pituudella, etumerkki lausekkeessa (3.51) miinus [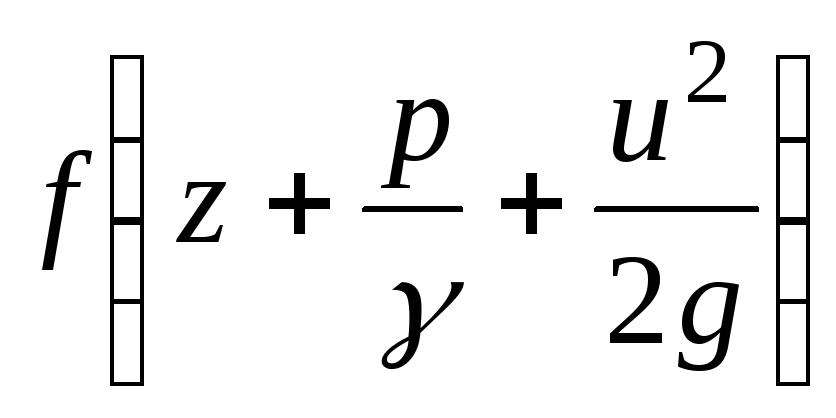

- laskeva toiminto].

Jos elävät osat ovat pysyviä pitkin suihkun pituutta, pietsometrinen viiva ja kokonaispaineviiva ovat yhdensuuntaiset.

3.9. Ihanteellisen nesteen liikkeen differentiaaliyhtälöt (Eulerin yhtälö)

Tilassa, joka on täynnä liikkuvaa ihanteellinen nestetiheys , valitse alkeissuuntaissärmiö, jonka reunoilla on sivut

, ,

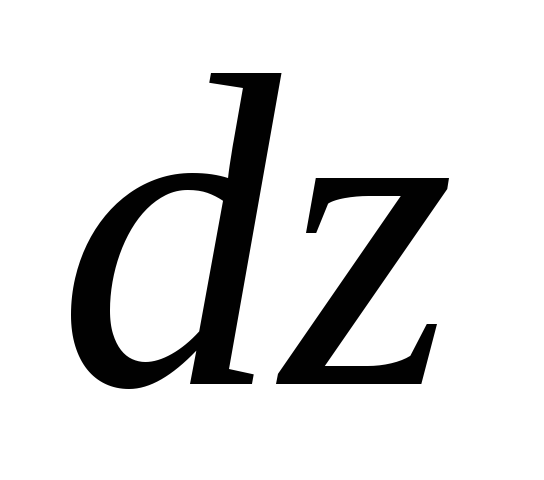yhdensuuntainen koordinaattiakselien kanssa (kuva 3.9). Kun ihanteellinen neste liikkuu, sisäisiä kitkavoimia ei ole. Suuntaissärmiössä oleva alkeistilavuus liikkuu absoluuttisella nopeudella . Tämän nopeuden komponentit koordinaattiakseleita pitkin ovat , , .

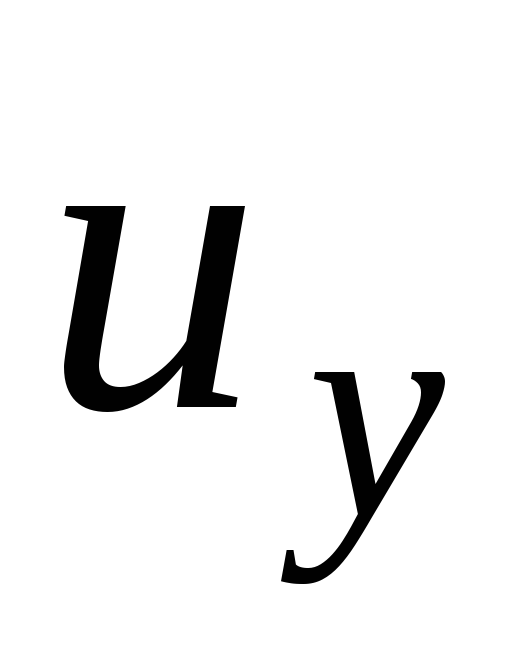Massa- ja pintavoimat vaikuttavat alkuainetilavuuteen. Kitkavoimat suuntaissärmiön liikkeen aikana ovat nolla.

Nesteen massa suuntaissärmiön alkutilavuudessa

(3.52)

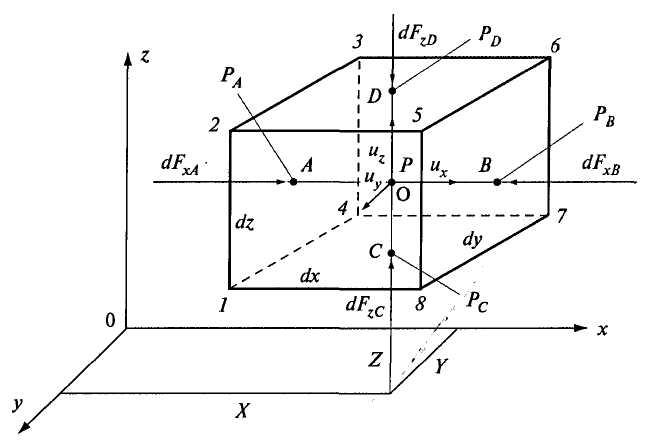
Riisi. 3.9. Eulerin liikeyhtälön johtamiseen

Massavoimien projektiot suunnassa koordinaattiakselit:

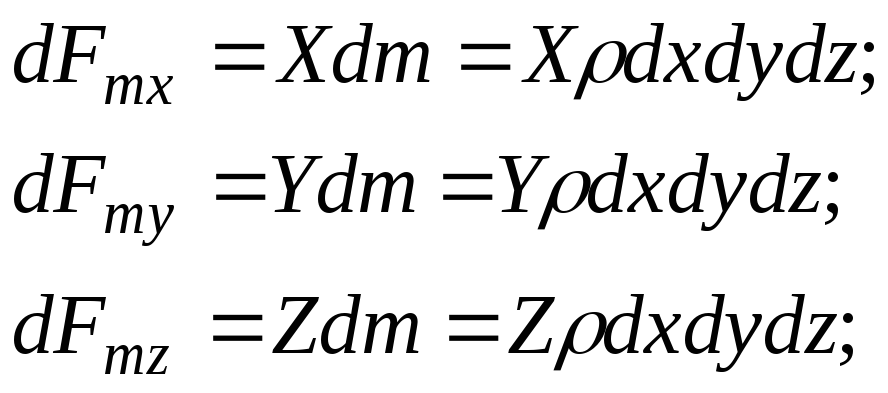(3.53)

Missä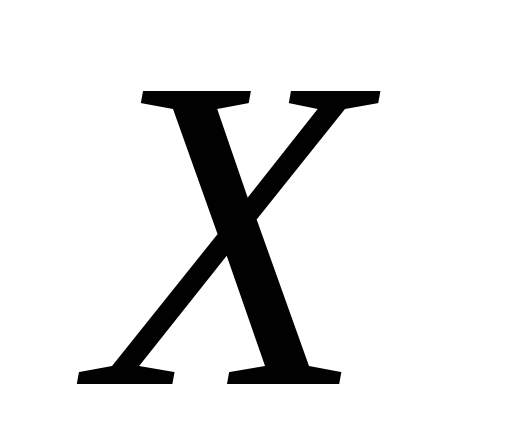

, , - yksikön runkovoimien komponentit suhteessa akseleihin , , (näiden voimien kiihtyvyyden ennusteet).

Pintavoimat määräytyvät suuntaissärmiön pintoihin kohdistuvan paineen perusteella.

Olkoon hydrostaattinen paine suuntaissärmiön painopisteessä (piste O). 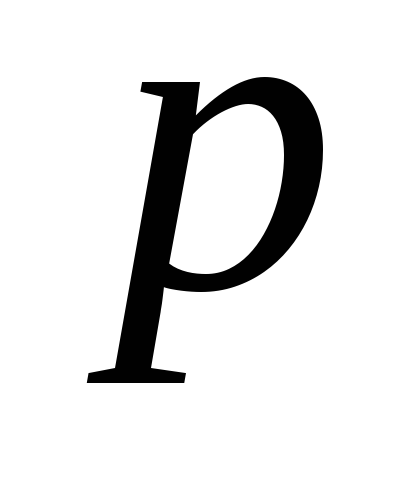, tämän pisteen koordinaatit , , .Liikenopeus tässä vaiheessa . Tämän nopeuden komponentit koordinaattiakseleita pitkin ovat , , .

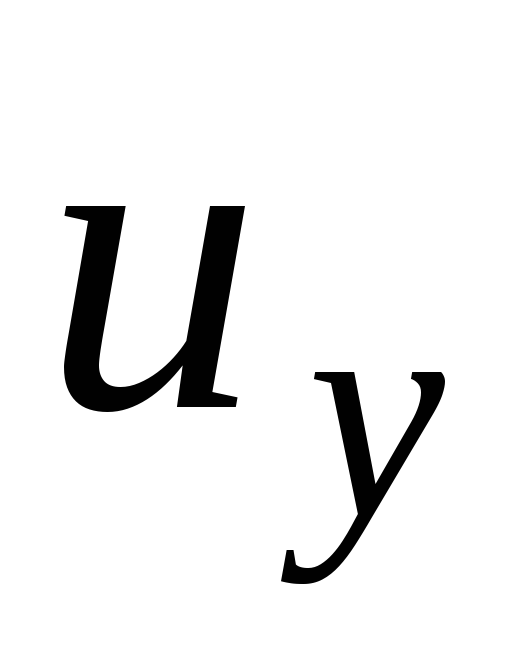Piirretään t:n läpi. Noin akselin suuntainen vaakaviiva . Leikkauspisteet laatikon A (pinta 1234), B (pinta 5678) pintojen kanssa. Paine näissä kohdissa akselia pitkin

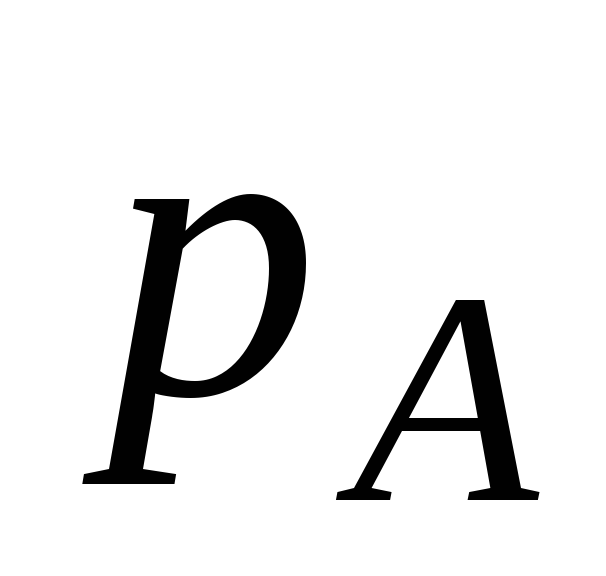Ja

.

Nestemäisessä jatkuvassa väliaineessa paine pisteessä ilmaistaan ​​jatkuvalla jatkuvalla funktiolla pisteen sijainnin avaruudessa koordinaateista: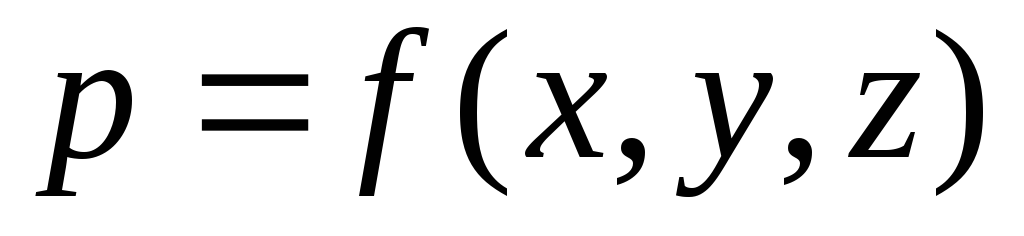

. Hydrostaattinen paine muuttuu jatkuvasti lineaarisesti ja paineen lisäys alkiopituusyksikköä kohti

-

-



-

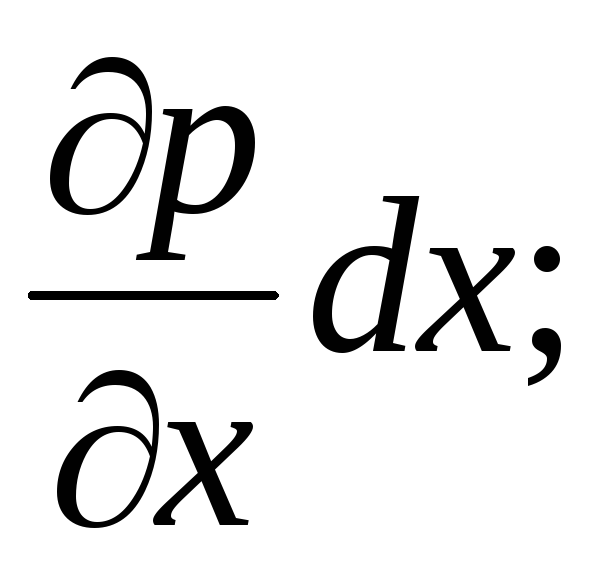
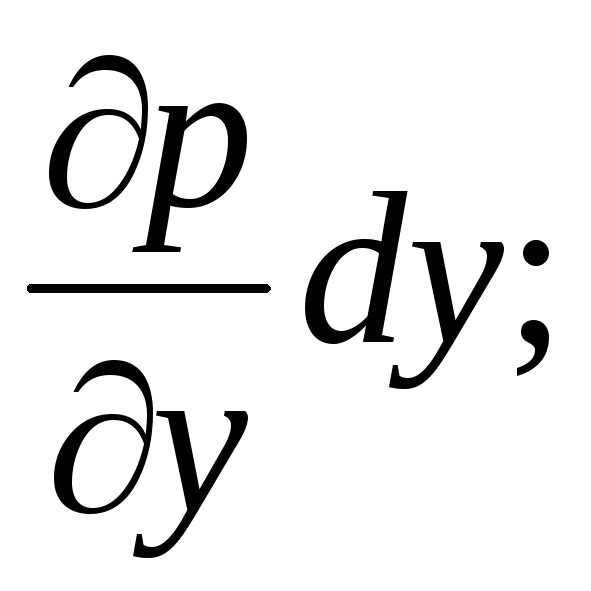
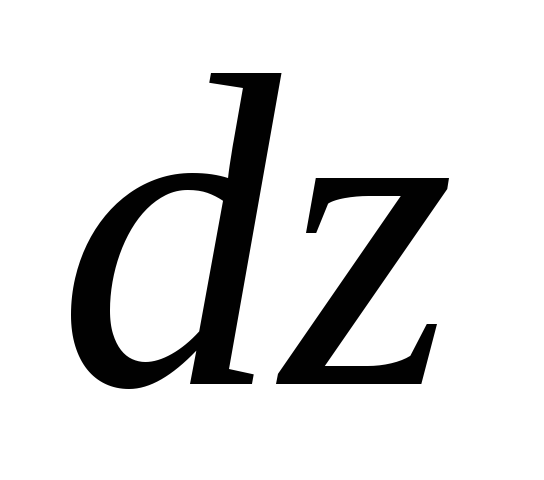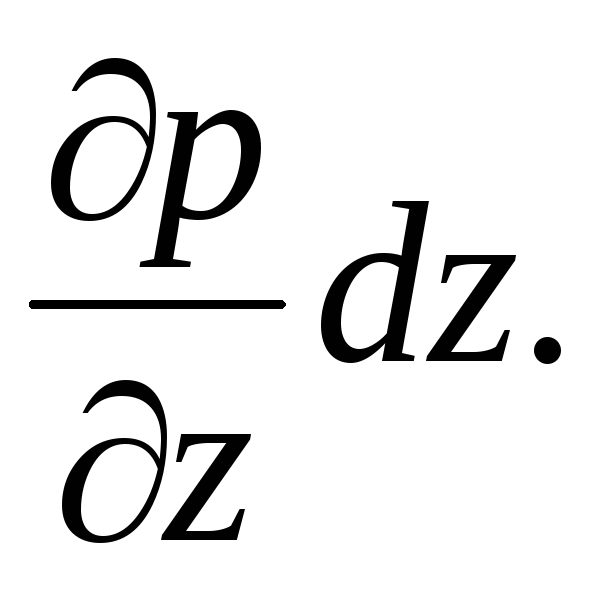
Näin ollen paineet pisteissä A ja B eroavat toisistaan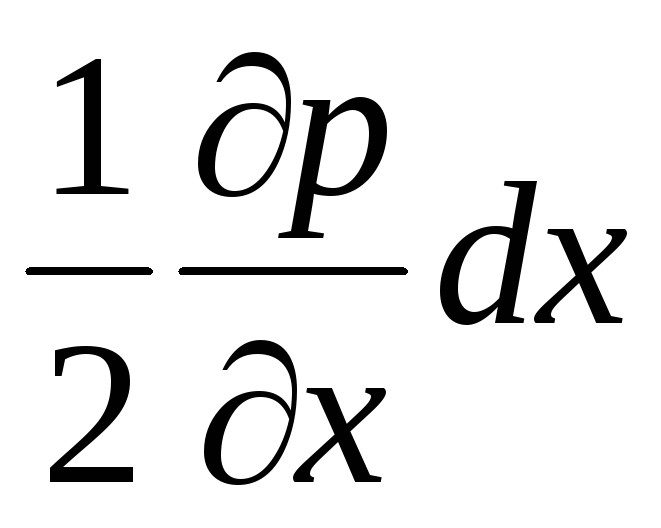

.

Ilmaisemme paineet pisteissä A ja B seuraavassa muodossa:

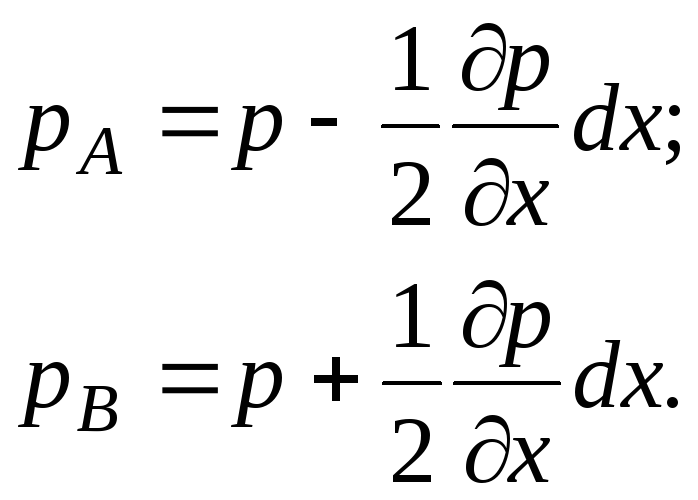(3.54)

Kasvojen pienen alueen vuoksi voimme olettaa, että paineet

Ja

ovat keskimääräisiä hydrostaattisia paineita, jotka vaikuttavat pintoihin 1234 ja 5678. Pintapainevoimat näillä pinnoilla akselin suuntaisesti yhtä suuri kuin kasvojen alueelle kohdistuvan paineen tulo:

(3.55)

Samoin pintapainevoimat pinnoille z-akselilla (pinnat 1478 ja 2365):

(3.56)

Voit myös määrittää pinnan pintavoimat akselin suuntaisesti .

Tarkastellaan suuntaissärmiön tasapainoa liikkuvassa nesteessä käyttämällä d'Alembertin periaate.

D'Alembertin periaatteen mukaan liikeyhtälöä voidaan pitää tasapainoyhtälönä, jos otetaan käyttöön hitausvoimat. Oletetaan, että suuntaissärmiö, jolla on massa

liikkuu nopeudella , tämän nopeuden komponentit , , .

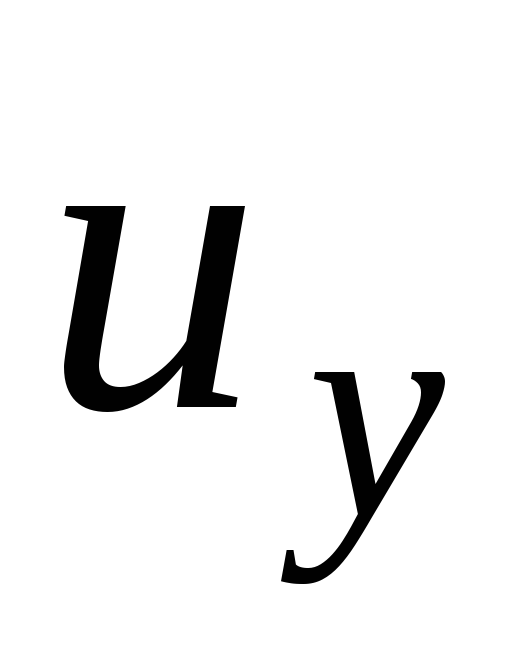hitausvoima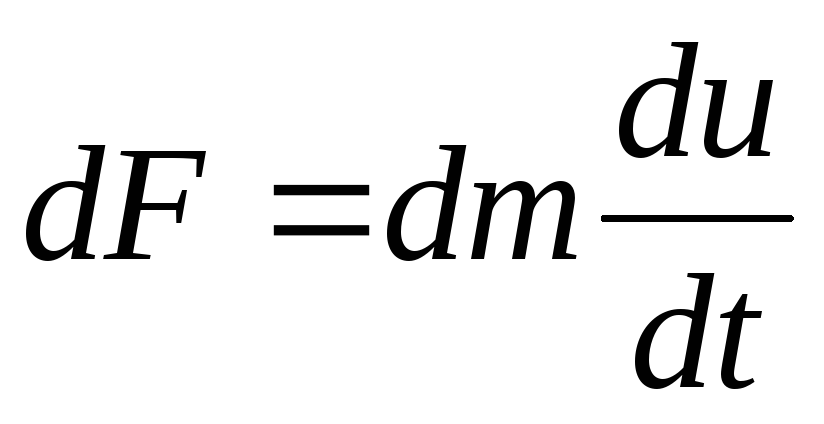

(- kiihtyvyys).

Inertiavoiman projektiot vastaaville koordinaattiakseleille:

(3.57)

Missä 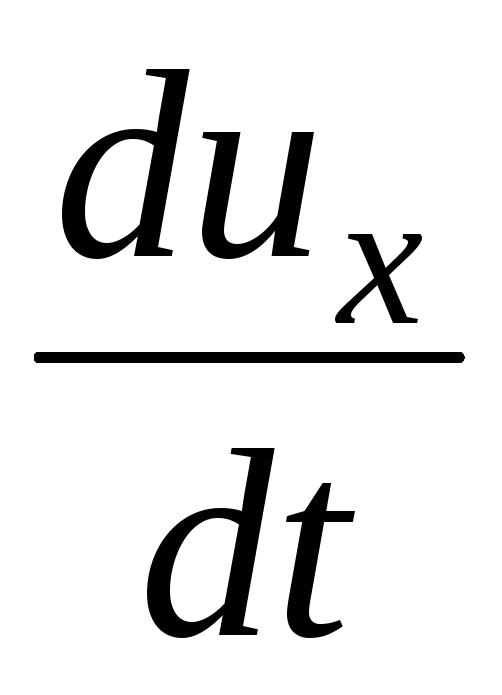,,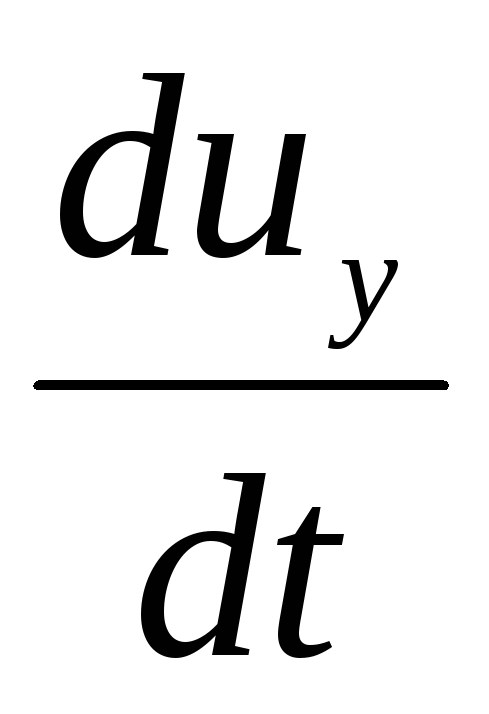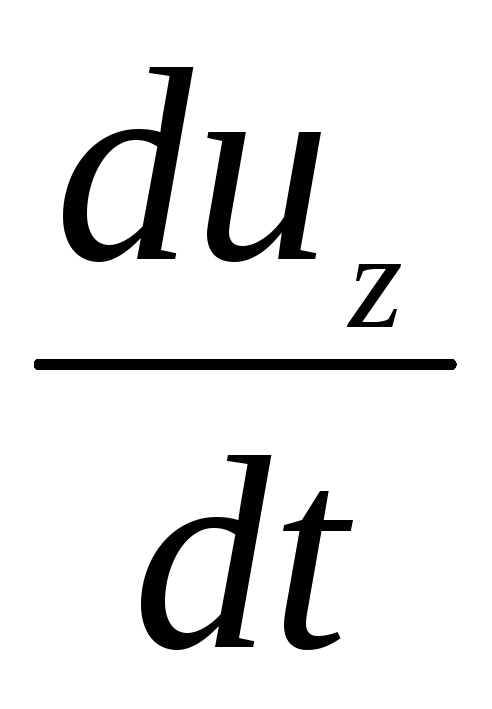- kiihtyvyyden projektiot akselilla , , .

Muodostetaan tasapainoyhtälö tarkasteltavana olevaan nestemäiseen suuntaissärmiöön vaikuttaville voimille ottaen huomioon akseleita pitkin kulkeva hitausvoima Ja :

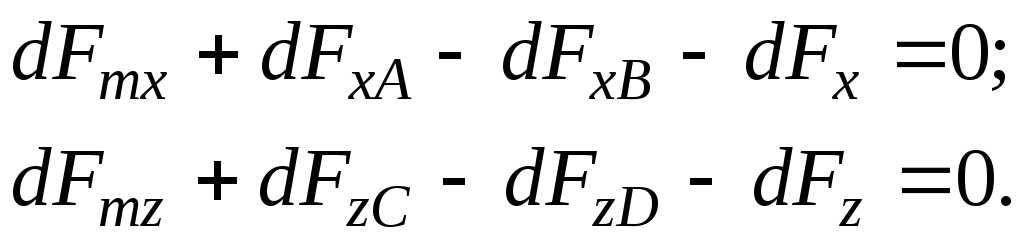(3.58)

Korvaamalla (3.58) aiemmin saadut riippuvuudet (3.53), (3.55), (3.56) ja (3.57) saadaan seuraavat yhtälöt

Avaa sulut ja jaa yllä saadut yhtälöt arvolla

, kirjoittaa

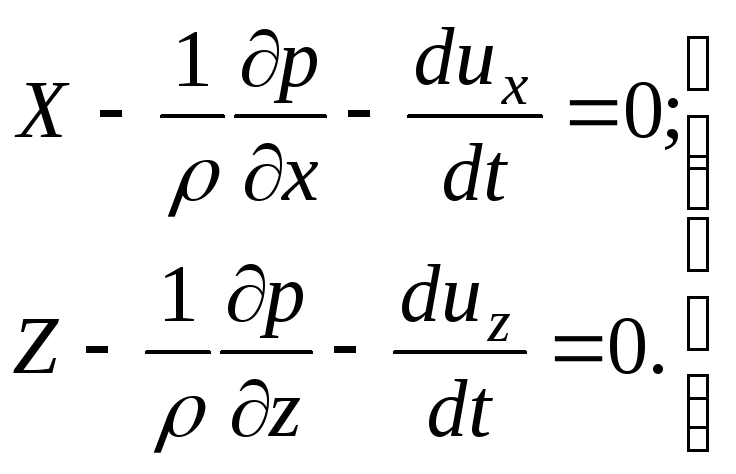(3.59)

Samalla tavalla voit saada y-akselin yhtälön:

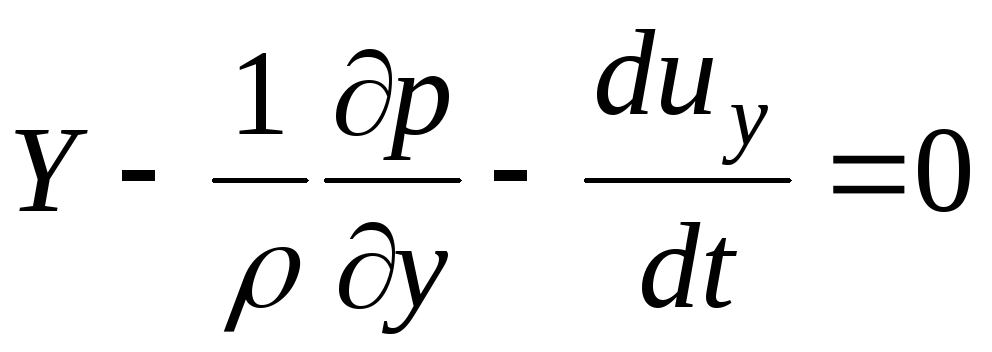(3.60)

Yhtälöt (3.59) ja (3.60) voidaan kirjoittaa yhtälöjärjestelmäksi:

(3.61)

Yleisessä tapauksessa määrät , , 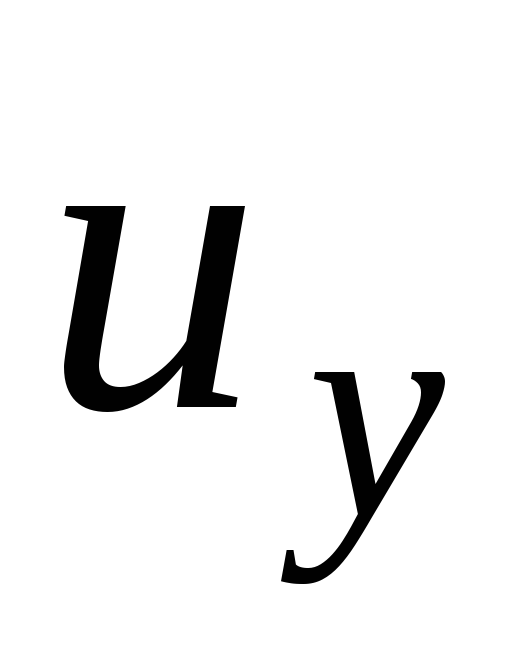ovat koordinaattien funktio , , , samoin kuin aika . Siksi kokonaisnopeusero tahtoa

Kiihtyvyys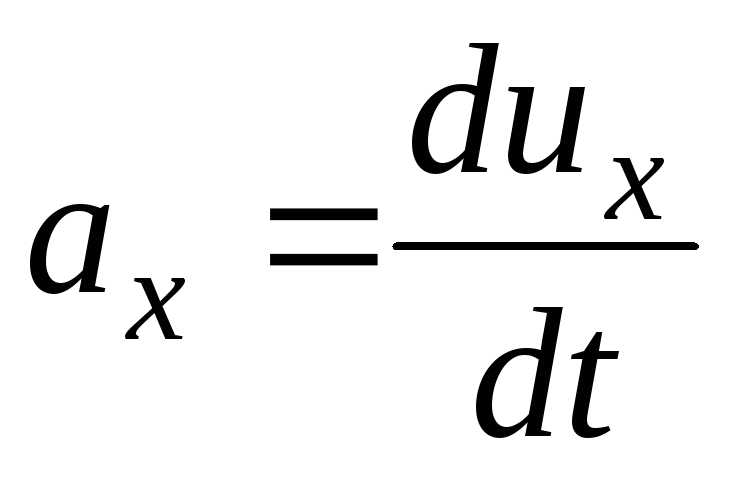

;

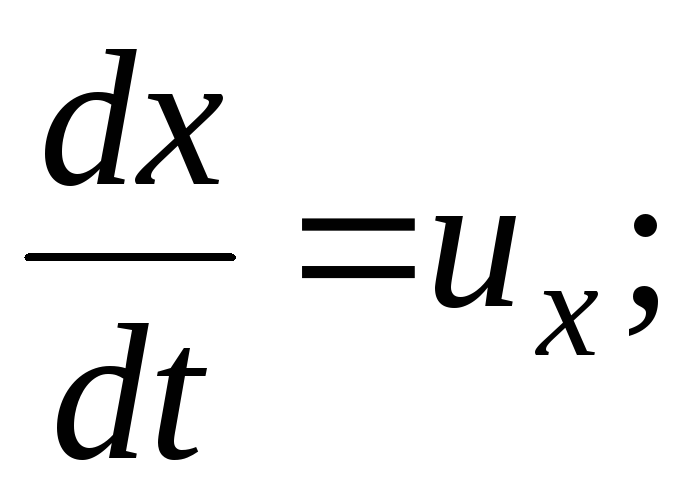
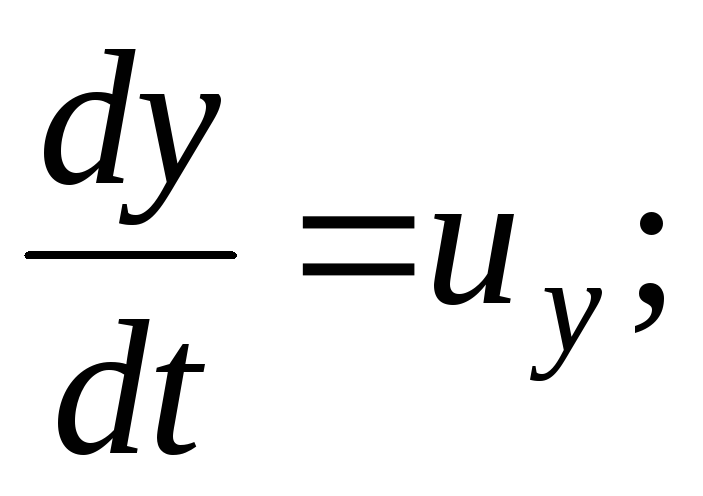
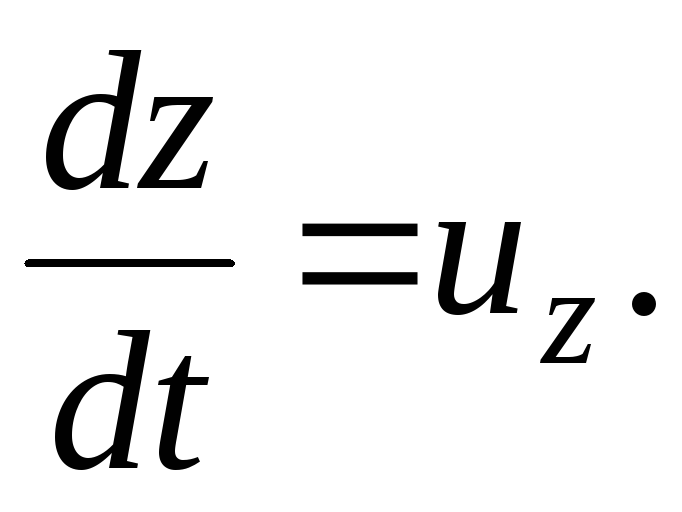
(3.64)

Samalla tavalla voit saada nopeuserot ,.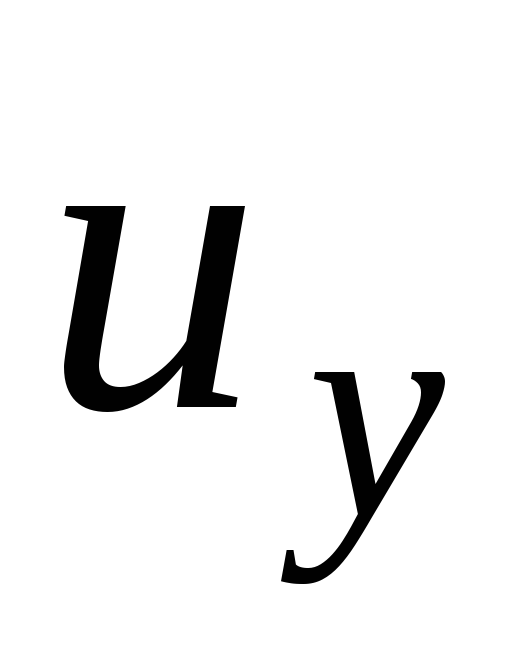

Lisättyään yhtälöjärjestelmään (3.61) nopeuserot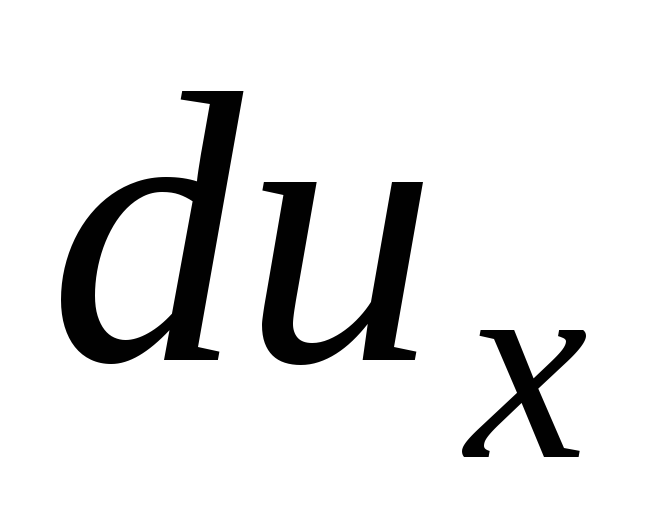

,

Ja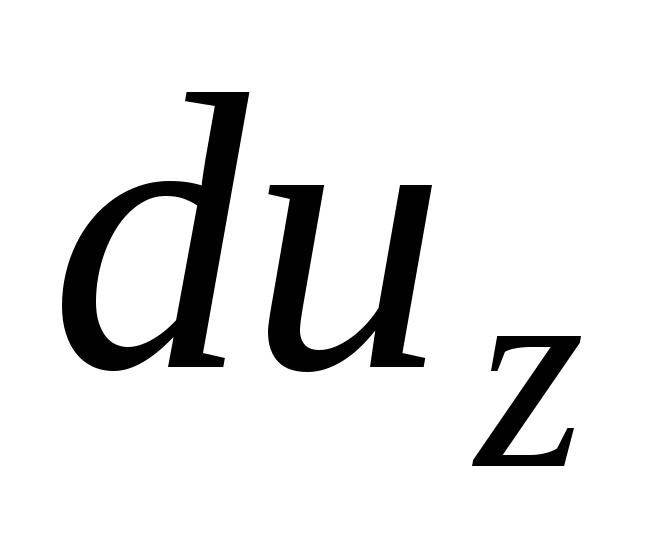

hän tulee katsomaan

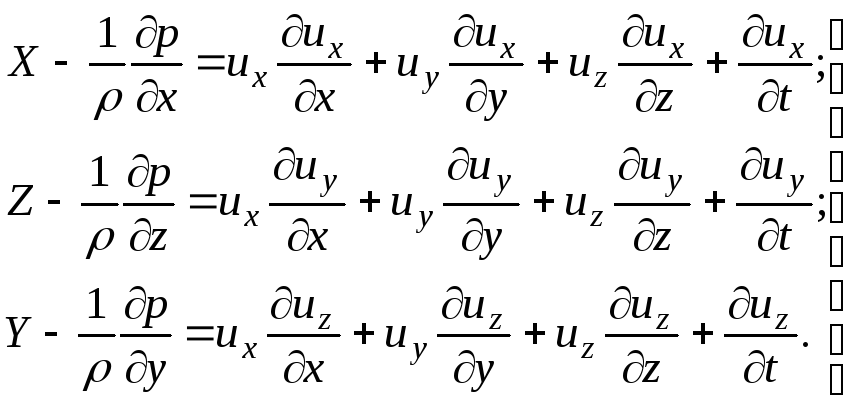(3.65)

Tasaisen liikkeen tapauksessa

;

;

. (3.66)

Yhtälöt (3.65) ovat ihanteellisen (ei-viskoosisen) nesteen liikkeen differentiaaliyhtälöt - Eulerin yhtälöt. Euler laati nämä yhtälöt vuonna 1775.

Eulerin yhtälöt ilmaisevat vaikuttavien voimien, nopeuksien, paineen ja nesteen tiheyden projektioiden välisen suhteen. Eulerin yhtälöt ovat erittäin tärkeitä nesteen liikkeen tutkimuksessa.

Nestettä levossa meillä on

Eulerin differentiaaliyhtälöt ovat seuraavassa muodossa:

(3.67)

Differentiaaliyhtälöjärjestelmä on nesteen tasapainoyhtälö.

Tasapainoyhtälöstä saadaan hydrostaattisen perusyhtälö (2.2) (ks. liite).

Eulerin liikeyhtälön integrointi. Bernoullin integraali

Harkitse ihanteellisen nesteen tasaista liikettä. Esitämme Eulerin yhtälöt muodossa (3.61). Kerro ensimmäinen yhtälö luvulla

, toinen - päällä ja kolmanneksi

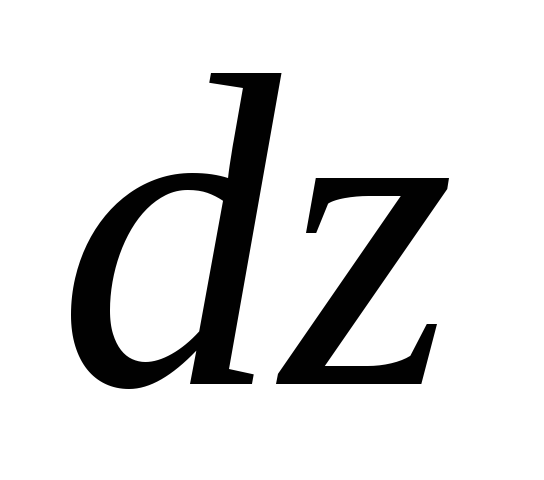, saamme

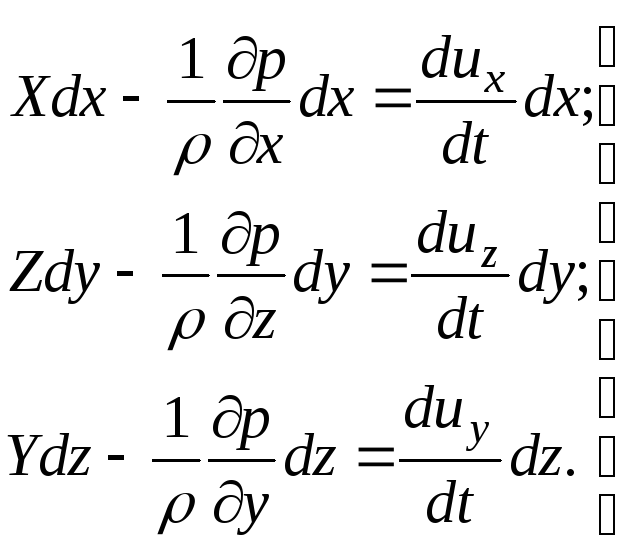(3.68)

Lisäämme termi kerrallaan järjestelmän kaikki kolme yhtälöä:

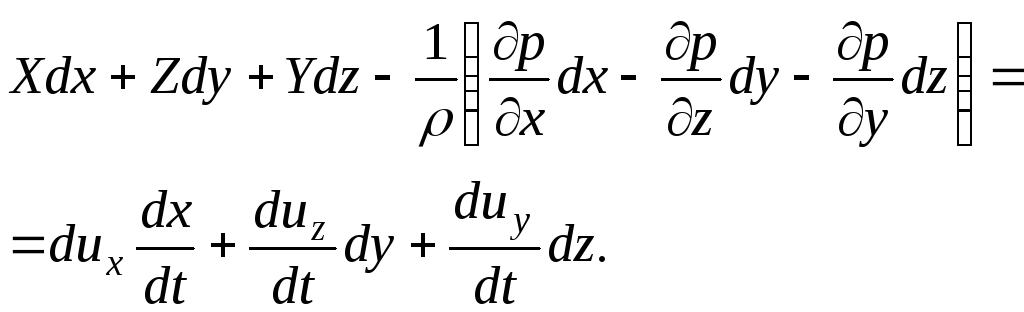(3.69)

Tasaista liikettä varten paine 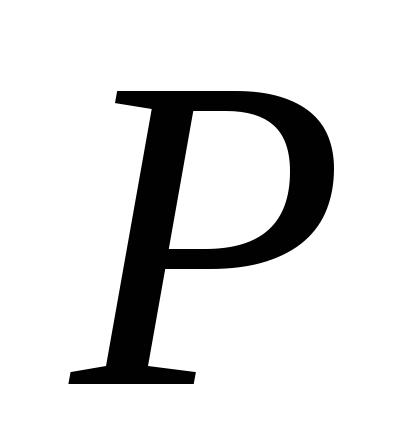pisteessä on sen koordinaattien funktio, eikä se riipu ajasta. Siksi paine-ero ilmaistaan ​​osittaisina derivaattaina:

.

Koska

;

Ja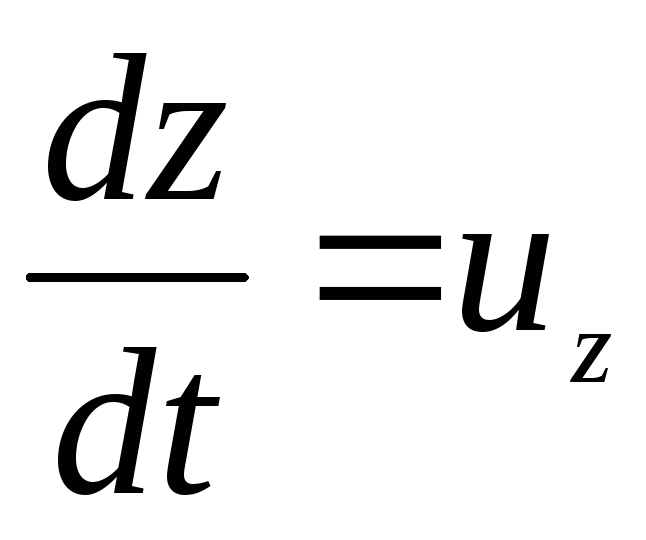

, sitten yhtälön (3.69) viimeinen termi

sitä paitsi

;

;

.

Näin ollen yhtälön (3.69) oikea puoli saa muodon

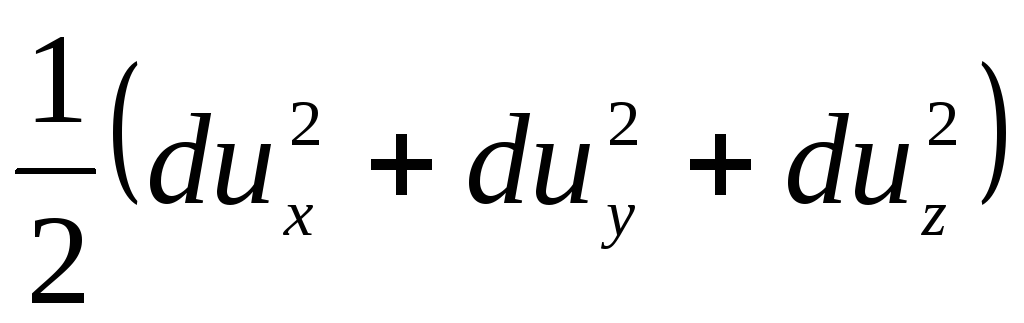. (3.71)

Täysi (absoluuttinen) nopeus ja ilmaistaan ​​kautta , , :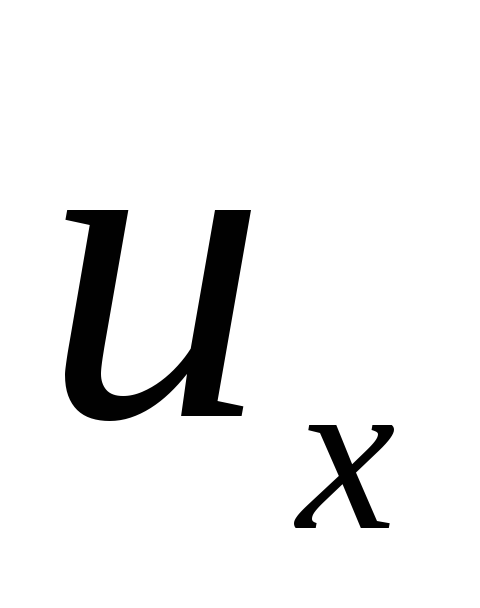

.

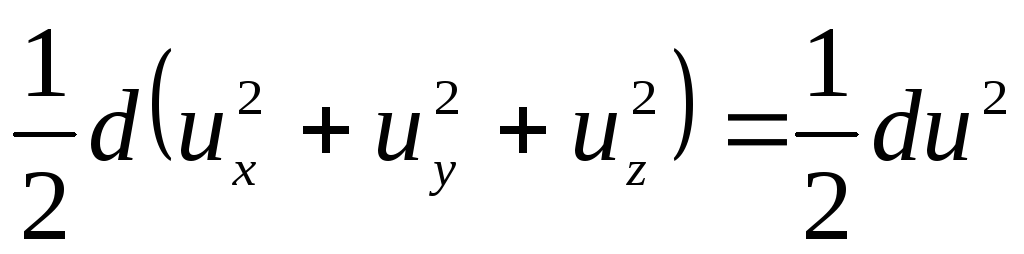. (3.72)

Yhtälö (3.69) muunnoksen jälkeen voidaan kirjoittaa uudelleen seuraavaan muotoon:

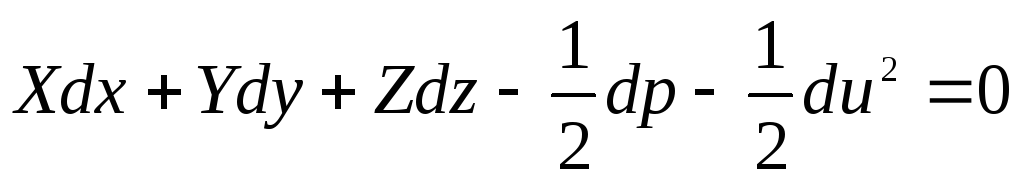. (3.73)

Tämän yhtälön kolme ensimmäistä lauseketta ovat voima- (potentiaali)funktion kokonaisdifferentiaali :

Siten yhtälö (3.74) saa muodon

. (3.75)

Integroimalla yhtälön (3.75), saamme

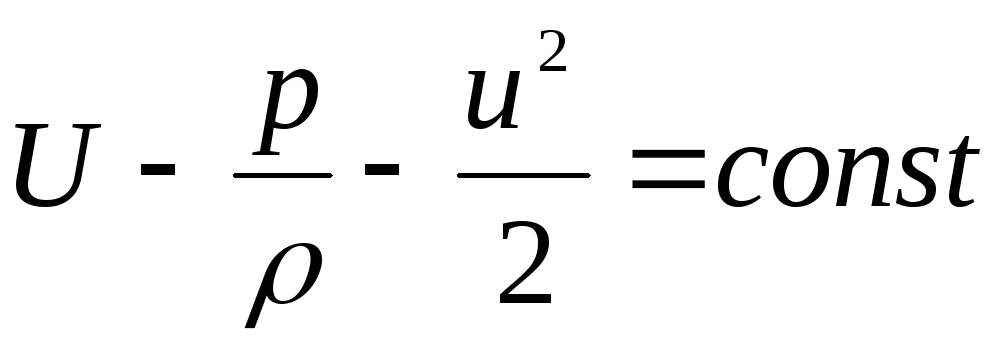. (3.76)

Tätä lauseketta kutsutaan Bernoulli-Euler-integraaliksi.

Tuloksena oleva trinomi - yhtälö pysyy muuttumattomana virtaviivaa pitkin.

Siinä tapauksessa, että liike tapahtuu vain yhden massavoiman - painovoiman - vaikutuksesta, niin yksikkömassavoimat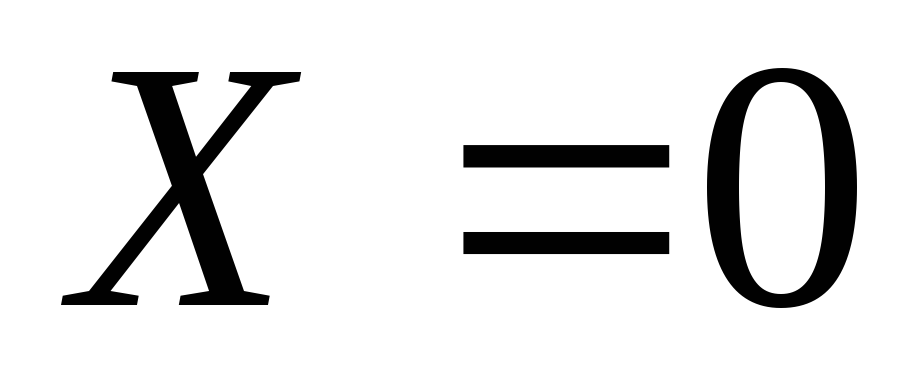

,

,

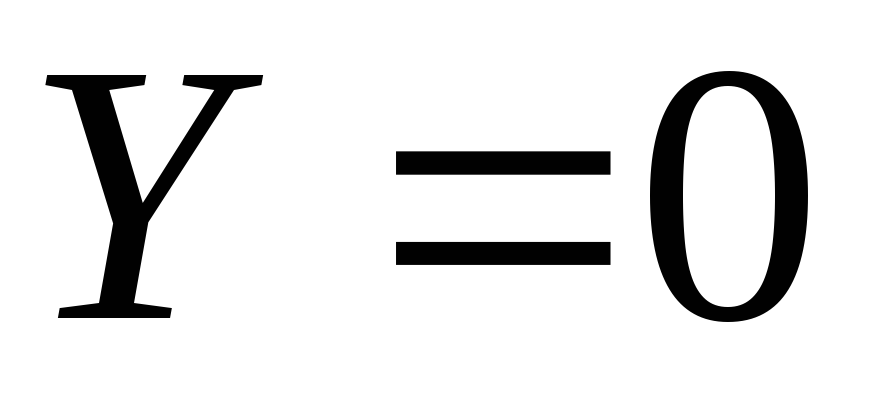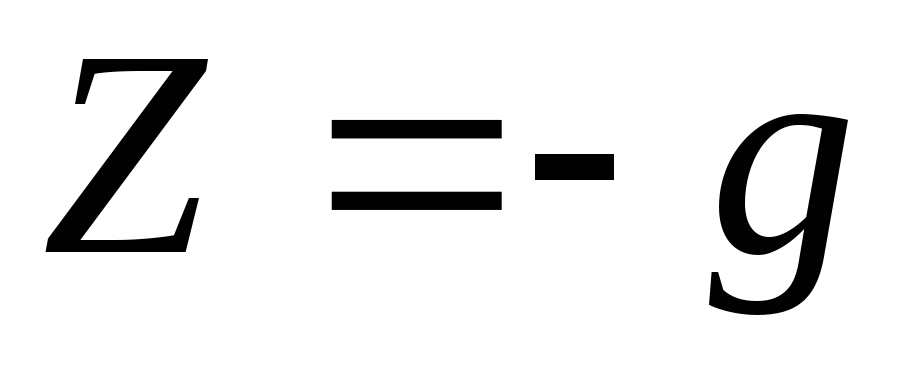(akseli suunnattu pystysuoraan ylöspäin). Voimatoimintojen erotus

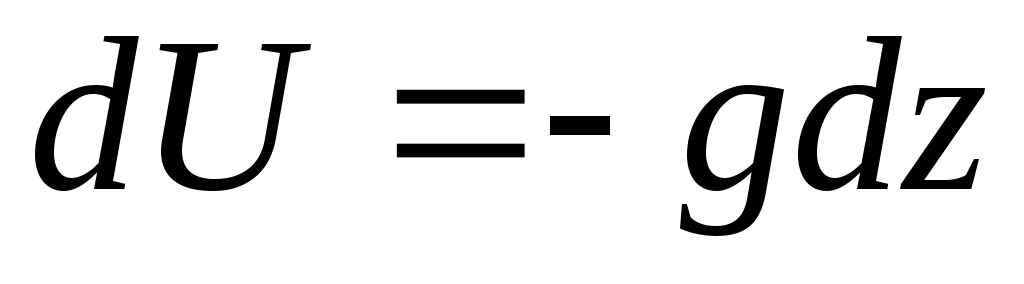. (3.77)

Yhtälö (3.75) voidaan kirjoittaa seuraavassa muodossa:

. (3.78)

Jaamme kaikki yhtälön ehdot vapaan pudotuksen kiihtyvyydellä , sitten saamme

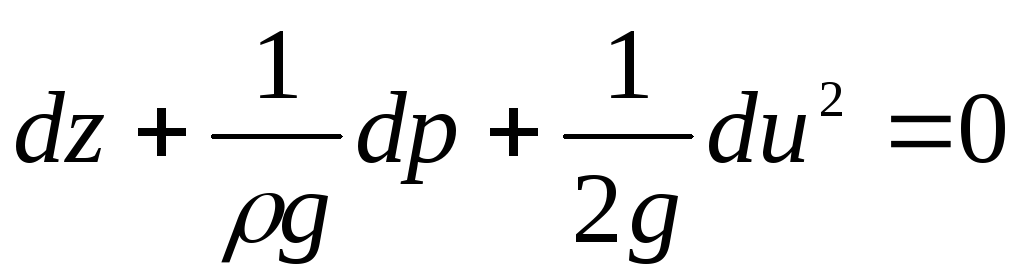. (3 79)

Tämän yhtälön kaikkien kolmen ehdon summan lisäys virtaviivaa pitkin liikuttaessa on yhtä suuri kuin nolla.

Integroimalla differentiaaliyhtälön (3.79) saadaan

. (3.80)

Kaikkien termien summa nesteen virtaviivalla on vakioarvo, ja näin ollen se on vakio myös ideaalialkuainevirralla.

Yhtälö (3.80), joka on saatu käyttämällä Eulerin liikeyhtälöä tasaiselle liikkeelle, on Bernoullin yhtälö. Sama yhtälö saatiin aikaisemmin eri tavalla käyttäen kineettisen energian teoreemaa (3.43).

Yhtälö (3.80), joka on kirjoitettu kahdelle elävälle nokan osalle, saa aiemmin tunnetun muodon

.
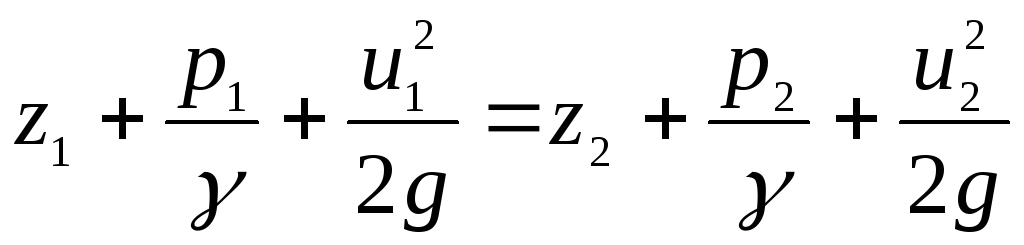