Untuk menurunkan persamaan Bernoulli, kami menggunakan teorema terkenal dari mekanika mengenai perubahan energi kinetik. Ingatlah bahwa teorema ini berbunyi sebagai berikut: perubahan energi kinetik 2 benda yang dipertimbangkan pada beberapa perpindahannya sama dengan jumlah kerja semua gaya (eksternal dan internal) yang diterapkan pada tubuh ini, pada perpindahan yang sama.

Mari kita ambil aliran dasar sungai (Gbr. 3-20). Pilih bagian 1-1 dan 2-2 beberapa kompartemen tetesan AB. Dilambangkan dengan z 1 dan z 2 kelebihan bagian 1 -1 dan 2 -2 di atas bidang perbandingan Oh, melalui - daerah bagian hidup sungai di bagian 1-1i 2 -2.

Kami berasumsi bahwa selama ini AB jet akan pindah ke posisi A"B" dalam hal ini, bagian 1-1 dari aliran akan bergerak ke kejauhan dan bagian 2 -2 menetes - di kejauhan . perhatikan itu

di mana dan 1 dan dan 2 - kecepatan di bagian 1-1i 2 -2.

Berdebat, seperti pada 3-9, kita dapat menunjukkan bahwa volume kompartemen dasar tetesan A A" dan bb" adalah setara, yaitu

volume (A A")= volume (BB") =(penamaan),

di mana adalah laju aliran fluida untuk jet.

Mari kita nyatakan massa volume dasar melalui:

dimana adalah densitas cairan.

Mari kita cari perubahan energi kinetik kompartemen AB saat memindahkannya ke posisi A"B" dan kerja gaya yang diterapkan pada kompartemen ini pada perpindahan yang ditentukan.

1°. Perubahan energi kinetik kompartemen AB saat memindahkannya ke posisi A"B". Mari kita tunjukkan perubahan energi kinetik yang disebutkan (CE) melalui b (CE). Kemudian Anda dapat menulis (lihat Gambar 3-20):

(KE) \u003d KE (A "B") - KE (AB) \u003d KE (A "B -f BB") -

KE (AA "+ A" B) \u003d KE (BB ") - KE (AA"),

atau, diberikan (3-55),

Beras. 3-20. Ke turunan persamaan (3-60)

2°. Kerja gaya saat memindahkan kompartemen AB ke posisi A"B". Dengan perpindahan yang ditunjukkan, kami memperoleh pekerjaan gaya-gaya berikut.

1. Kerja gravitasi. Seperti yang dapat dilihat, efek aksi gravitasi memanifestasikan dirinya, seolah-olah, dalam kenyataan bahwa kompartemen A A" pindah ke posisi BB" (a kompartemen A "B tinggal di tempat). Menggunakan skema bersyarat seperti itu, pekerjaan gravitasi (PCT) kita dapatkan dalam bentuk

Keadilan (3-57) dapat dibenarkan dengan lebih ketat. Kami memecahkan kompartemen A "B menjadi kompartemen dasar dengan volume . Maka kerja gravitasi yang diinginkan dapat direpresentasikan sebagai:

di mana z", z", z",. . ., z(n) - ketinggian di atas bidang 00 bagian batas yang memisahkan volume dasar .

2. Kerja gaya tekanan hidrodinamik,
bertindak pada bagian akhir 1 -1 dan 2 -2 kompartemen
AB(dari sisi cairan yang mengelilinginya). Pekerjaan ini

di mana dan adalah tekanan hidrodinamik, masing-masing, di bagian 1 -1 dan 2-2.

3. Bekerja kekuatan luar tekanan cairan di sekitarnya pada tulang permukaan samping kompartemen AB. Usaha ini sama dengan nol, karena gaya-gaya diarahkan tegak lurus terhadap perpindahan partikel-partikel cair yang bergerak di sepanjang permukaan sisi kompartemen. AB.

4. Bekerja kekuatan internal tekanan ( kekuatan normal interaksi partikel cairan individu yang membentuk volume AB).

Gaya-gaya ini dipasangkan (berarah berlawanan) dengan perpindahan yang sama. Jumlah pekerjaan mereka adalah nol.

5. Usaha gaya gesekan luar dan dalam sama dengan nol (gaya gesekan pada cairan ideal absen).

3°. Kesimpulan akhir. Dengan menggunakan teorema perubahan energi kinetik, kita dapat menulis:

Mari kita bagi ekspresi ini menjadi , yaitu, kami akan merujuknya ke satuan berat volume cairan yang lewat dalam waktu b / melalui bagian yang jelas menetes. Dalam hal ini, kami mewakili persamaan yang dihasilkan dalam bentuk

Sejak bagian 1-1 dan 2 -2 direncanakan secara sewenang-wenang, maka (3-59) juga dapat ditulis ulang dalam bentuk:

Persamaan (3-59) atau (3-60) disebut persamaan Bernoulli. Itu diperoleh oleh Daniil Bernoulli pada tahun 1738. Persamaan ini hanya berlaku untuk aliran dasar dari cairan ideal.

Mari kita perhatikan juga hal-hal berikut:

1) persamaan Bernoulli menghubungkan kuantitas z, p, dan;

2) seperti yang dapat dilihat dari (3-60), dalam kasus fluida ideal, jumlah dari tiga suku z,, adalah konstanta sepanjang tetesan yang dipertimbangkan;

3) jika nilai konstanta yang ditunjukkan untuk tetesan tertentu sama dengan Alt maka untuk tetesan tetangga jumlah ketiga suku di atas sama dengan A2 , dan masuk " kasus umum A 1 A 2 ;

4) mengetahui tetesan tertentu nilai konstan TETAPI, dan juga mengetahui untuk penampang tertentu dari jet tiga kuantitas ( z, aku p) dua kuantitas apa pun, kita dapat, menggunakan persamaan Bernoulli, menemukan yang ketiga jumlah yang tidak diketahui untuk bagian jet yang dipertimbangkan.

Persamaan (3-60) juga dapat diperoleh dengan mengintegrasikan persamaan diferensial Euler (lihat 3-3) untuk setiap sistem gaya benda yang bekerja pada fluida dan memiliki potensial (lihat 9-2). Persamaan (3-60) mengacu pada garis arus tertentu (lebih tepatnya: tetesan dasar di sepanjang garis arus tertentu). Persamaan ini sering disebut integral Bernoulli.

Lagi pertimbangan rinci masalah ini menunjukkan bahwa persamaan Bernoulli (integral Bernoulli) ternyata valid baik untuk gerak tunak irotasional (potensial) dan untuk gerakan tunak vortex dari fluida ideal, asalkan gaya-gaya benda yang bekerja pada fluida memiliki potensial ( khususnya, gravitasi, yang kami pikirkan di atas). Ketika mempertimbangkan gerakan pusaran stabil dari fluida ideal dengan kecepatan dan termasuk dalam persamaan Bernoulli, berikut: mengerti (jadi sama seperti dalam kasus gerak irotasional) kecepatan yang berhubungan dengan medan vektor nyata yang mencerminkan gerakan fluida yang sedang dipertimbangkan (di sini tidak perlu merujuk pada penguraian gerakan menjadi tiga jenisnya, dijelaskan dalam 3-4).

Juga dapat ditunjukkan bahwa dalam kasus: a) tanpa gerakan pusaran (potensial) fluida ideal dan b) gaya-gaya tubuh yang bekerja pada fluida, yang memiliki potensial, nilai TETAPI, yang dibahas di atas, adalah sama untuk semua garis arus yang membentuk aliran: A 1 \u003d A 2 \u003d A 3 \u003d --- Dalam hal ini, persamaan (3-60) ternyata valid untuk seluruh area yang ditempati oleh cairan, dan bukan hanya untuk garis arus tertentu.

Di atas, diperoleh persamaan diferensial gerak fluida ideal dan persamaan kontinuitas gerak, yang membentuk sistem persamaan tertutup. Untuk memecahkan masalah teknik tertentu, perlu untuk dapat menemukan integral dari persamaan ini.

Sebelum melanjutkan ke integrasi persamaan gerak fluida ideal, kita menerima kondisi tambahan berikut:

Proyeksi percepatan gaya tubuh (dalam kasus ini gravitasi) akan mengambil nilai berikut saat dipilih; arah sumbu koordinat:

X=0; Y=0; Z=-g.

Setelah transformasi kita mendapatkan:

Membagi dengan g, kita mendapatkan:

Integrasikan persamaan diferensial ini ke dalam diferensial total, kita sampai pada hasil berikut:

Persamaan ini disebut persamaan D. Bernoulli, berlaku untuk gerak tetap dari fluida ideal.

Untuk dua bagian sembarang dari aliran elementer:

Ini adalah persamaan D. Bernoulli.

Arti geometris dan energikpersamaan

D. Bernoulli

Semua suku yang termasuk dalam persamaan D. Bernoulli memiliki dimensi linier, sehingga biasanya disebut ketinggian. Dengan demikian, nama-nama berikut untuk anggota ini diterima secara umum:

z - ketinggian geometris atau geodetik;

Tinggi piezometrik atau tinggi tekanan;

- kepala dinamis atau kecepatan;

Sangat mudah untuk melihat yang berikutnya pengertian geometris Persamaan D. Bernoulli, yaitu dalam gerak tetap fluida ideal, jumlah dari tigaketinggian (geometris, piezometrik dan kecepatan) tidakbervariasi sepanjang aliran dasar tertentu. Situasi ini diilustrasikan dengan jelas pada Gambar. satu.

Dimungkinkan untuk menafsirkan arti istilah individu dari persamaan

Bernoulli berbeda. Di atas ditunjukkan bahwa jumlah

Melambangkan energi spesifik dari fluida. Dengan demikian, kita dapat berasumsi bahwa:

z - adalah energi spesifik dari posisi;

energi tekanan;

Ada energi kinetik spesifik.

Arti energik dari persamaan Bernoulli adalah bahwa dalam gerak tetap dari fluida idealjumlah energi spesifik posisi, tekanan, dan kinetik tidak berubah sepanjang pancaran elementer tertentu.

Beras. satu

Total energi spesifik (yaitu potensial + kinetik) disebut kepala hidrodinamik dan dilambangkan . Dengan demikian, persamaan Bernoulli menunjukkan bahwa dalam gerakan tunak dari fluida ideal untuk aliran tertentu, head hidrodinamika adalah konstan. Pada grafik, garis kepala hidrodinamik digambarkan sebagai garis horizontal.

D. Persamaan Bernoulli untuk aliran elementer cairan nyata. Pizometrik dan hidroliklereng.

Ketika fluida nyata bergerak di antara aliran yang berdekatan, gaya gesekan muncul, untuk mengatasi sebagian energi fluida yang dikeluarkan. Oleh karena itu, energi spesifik cairan pada penampang pancaran elementer 2 -2 akan kurang dari energi spesifik cairan di penampang 1-1 dengan jumlah tertentu , yang disebut ketinggian yang hilang atau energi spesifik yang hilang yang dikeluarkan untuk mengatasi hambatan hidrolik. Secara analitik, situasi ini dapat ditulis sebagai berikut:

Karena itu, dalam gerakan stabil dari cairan nyatajumlah tulang dari empat ketinggian (geometris, piezometriklangit, kecepatan tinggi dan hilang) atau, apa yang sama, jumlahempat energi spesifik (posisi, tekanan, kinetik, dan hilang) tidak berubah sepanjang aliran dasar yang diberikan.

Persamaan Bernoulli untuk kasus yang sedang dibahas dapat dengan mudah direpresentasikan secara grafis. Untuk melakukan ini, setelah memilih bidang perbandingan horizontal sewenang-wenang, letakkan di setiap bagian ketinggian ; ; ; dan . Ujung segmen z, dihubungkan oleh kurva halus, akan menunjukkan posisi sumbu tetesan. Menghubungkan ujung segmen kurva halus, kita mendapatkan apa yang disebut garis piezometrik. Menempatkan di setiap bagian dari segmen garis piezometrik sama dengan tekanan kecepatan, dan menghubungkan ujungnya dengan kurva halus, kita mendapatkan garis kepala hidrodinamik atau, seperti yang sering disebut, garis hidrolik (Gbr. 2). segmen, sama dengan jarak vertikal dari garis hidraulik ke bidang horizontal yang lewat di atas bidang pembanding pada ketinggian yang sama dengan energi spesifik awal, mewakili kehilangan energi untuk tahanan hidraulik pada penampang dari awal ke penampang yang dipertimbangkan.

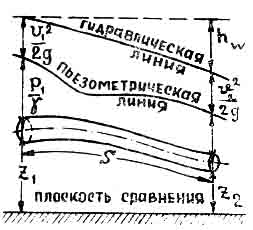
Beras. 2

Mari kita sebut jatuhnya saluran hidrolik per satuan panjang dari aliran dasar kemiringan hidrolikSaya:

Kemiringan hidrolik (Gbr. 3) selalu bernilai positif, karena energi spesifik total dari bagian yang bergerak dari cairan secara bertahap berkurang saat bergerak di sepanjang aliran dasar, dihabiskan untuk mengatasi gaya gesekan, berubah menjadi energi termal dan hamburan.

Beras. 3

Konsep gerakan fluida yang berubah dengan lancar (berubah perlahan)

Dalam kasus umum, dengan gerakan tetap, aliran fluida dapat direpresentasikan sebagai satu set pancaran elementer yang memiliki: berbagai arti sudut divergensi dan jari-jari kelengkungan yang berbeda. kasus spesial dvialiran di mana ia mengalami sedikit deformasiion, sehingga filamen dasar tetap sejajaratau hampir sejajar satu sama lain (), dan jari-jari kelengkungannya sangat nilai-nilai besar (), disebut gerak berubah halus atau gerak lambat berubah.

PADA bidang bagian bebas aliran dengan perubahan yang mulustekanan hidrodinamik didistribusikan sesuai dengan hukum hidrostatika, yang berarti bahwa di bagian hidup tertentu, energi potensial spesifik dari setiap partikel adalah nilai konstan:

D. Persamaan Bernoulli untuk aliran fluida nyata.

Kondisi penerapan persamaan D. Bernoulli.

Mari kita perpanjang persamaan Bernoulli ke aliran tunak dari fluida nyata. Untuk melakukan ini, kami memilih bagian bebas pada bagian aliran yang terdeformasi lemah, di dekat mana gerakan dapat dianggap berubah dengan lancar.

Melalui bagian ini, setiap jet dasar dalam waktu dt energi diperkenalkan, yang, sesuai dengan hal di atas, ternyata sama dengan:

Mengambil dari tanda kurung berat cairan yang melewati bagian melintang tetesan per; waktu dt, setara , tulis ulang ekspresi ini di bentuk berikut:

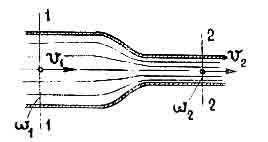
Beras. 4

Mari kita cari energi total yang dibawa oleh aliran fluida melalui bagian bebas 1 - 1. Untuk melakukan ini, tentu saja, perlu untuk menjumlahkan ekspresi yang dihasilkan atas semua aliran dari penampang bebas yang diberikan. Kemudian kita mendapatkan:

Jadi energi totalnya ternyata sama dengan jumlah dua integral mewakili, masing-masing, energi potensial dan kinetik aliran.

Kami menulis integral kedua dalam bentuk berikut:

Integral ini mewakili, seperti yang telah disebutkan, energi kinetik yang dibawa oleh aliran melalui bagian 1-1 selama waktu dt. Untuk menghitungnya, perlu diketahui bagaimana kecepatan partikel fluida didistribusikan di atas bagian hidup. Jika kita menghitung energi kinetik aliran dengan asumsi bahwa kecepatan ini konstan (dengan kata lain, menurut kecepatan aliran rata-rata di bagian hidup yang diberikan ), maka kita mendapatkan:

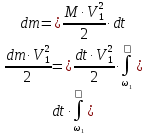
Ekspresi ini selalu lebih kecil besarnya daripada energi kinetik aktual yang dihitung dari kecepatan aktual. Mari kita tunjukkan rasio dari dua kuantitas ini:

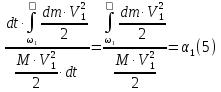
Karena di bagian aliran antara bagian 1-1 dan 2-2 bagian dari energi aliran dihabiskan untuk mengatasi hambatan hidrolik dan diubah secara ireversibel menjadi energi panas, . Hal ini juga jelas bahwa . Perbedaan antara energi spesifik ini akan mengungkapkan hilangnya energi spesifik aliran di bagian gerak yang dipertimbangkan:

Setelah integrasi dan substitusi, kita mendapatkan:

Koefisien disebut koefisien kinetikaenergi aliran dan merupakan rasio realenergi kinetik dari aliran ke energi kinetik, Andanumerik dengan asumsi bahwa kecepatan di semua titik bagian bebas sama dengan kecepatan aliran rata-rata. Jelas bahwa koefisien ini selalu lebih besar dari satu.

Persamaan yang dihasilkan adalah persamaan D. Bernoulli untuk aliran tunak dari fluida nyata.

Kuliah nomor 8.

resistensi hidrolik.

Klasifikasi tahanan hidrolik dan kehilangan tekanan.

Ketika fluida nyata bergerak, sebagian energi aliran dihabiskan untuk mengatasi hambatan hidrolik, yang dibagi menjadi dua jenis:

1) hambatan sepanjang aliran;

2) resistensi lokal.

Tahanan sepanjang aliran adalah tahanan yang disebabkan oleh gaya gesekan dan bergantung pada panjang aliran.

Hambatan lokal adalah hambatan yang disebabkan oleh perubahan arah atau besarnya kecepatan pada bagian aliran yang berbeda. Hambatan ini disebabkan oleh keran, katup gerbang, katup pada pipa, ekspansi atau kontraksi aliran yang tiba-tiba, dll.

Bagian dari energi aliran yang dikeluarkan untuk mengatasi hambatan hidrolik disebut head loss atau kehilangan energi.

Kehilangan tekanan juga dibagi menjadi dua jenis:

1) head loss sepanjang aliran, yang disebabkan oleh tahanan hidrolik sepanjang aliran ( h f);

2) kehilangan tekanan lokal, yang disebabkan oleh tahanan hidrolik lokal ( h saya). Total kerugian kepala:

h ω = . (1)

Kehilangan head pada dasarnya tergantung pada mode gerakan cairan.

Laminar dan rezim yang bergejolak s gerakan fluida.

Ada dua mode gerak fluida: laminar dan turbulen.

Dalam mode gerak laminar, partikel fluida bergerak dalam pancaran terpisah yang tidak bercampur satu sama lain. Contoh gerak laminer adalah: pergerakan air tanah, pergerakan cairan dengan viskositas tinggi melalui pipa (bahan bakar minyak, minyak, dll), pergerakan darah di pembuluh darah.

Dalam mode gerak turbulen, aliran individu bercampur satu sama lain. Gerak turbulen diamati di alam jauh lebih sering daripada gerak laminer. Contoh pergerakan turbulen adalah pergerakan air di sungai, kanal, pipa air, dll.

Kata "laminar" berasal dari kata Latin lamina - pelat, strip, lapisan; Kata "turbulen" berasal dari kata Latin turbulentus - tidak menentu.

Keberadaan dua mode gerak fluida di alam pertama kali ditunjukkan oleh orang Rusia yang luar biasa profesor ilmuwan D. I. Mendeleev pada tahun 1880 dalam karyanya "On fluid resistance and aeronautics".

Sebuah studi eksperimental mode gerak dilakukan oleh ilmuwan Inggris O. Reynolds pada tahun 1883.

Pengalaman dimulai dengan pass pipa D cairan dengan kecepatan rendah. Pada saat yang sama cat disuplai dari tangki DENGAN. Dalam hal ini, diperoleh gambar berikut (Gbr. 1b): aliran berwarna berbentuk garis horizontal lurus, sedangkan sisa massa cairan yang bergerak tetap tidak berwarna. Akibatnya, dalam hal ini, partikel aliran berwarna tidak bercampur dengan cairan lainnya, dan mode gerakan cairan di dalam pipa D berlapis-lapis.

Dengan peningkatan kecepatan secara bertahap di dalam pipa D ada saatnya ketika aliran berwarna menghilang dan seluruh cairan yang bergerak menjadi berwarna seragam. Hal ini menunjukkan bahwa partikel-partikel cairan dalam aliran bercampur, yaitu di dalam pipa D rezim turbulen terjadi (Gbr. 1c).

Beras. satu

Kecepatan di mana satu mode gerak berubah ke yang lain disebut kritis. Ada dua kecepatan kritis: kecepatan kritis atas V VK , di mana rezim gerak laminar masuk ke turbulen, dan kecepatan kritis yang lebih rendah V nk - selama transisi terbalik.

Atas dasar studi eksperimental mode gerak, O. Reynolds memberikan kriteria untuk menetapkan satu atau lain mode gerak.

Kriteria untuk menentukan mode gerak fluida adalah apa yang disebut bilangan Reynolds, yang dilambangkan dengan Ulang dan diberikan oleh rumus:

Dimana V adalah kecepatan rata-rata gerakan aliran;

L adalah ukuran geometris karakteristik dari bagian terbuka aliran;

adalah koefisien kinematik viskositas.

Bilangan Reynolds yang sesuai dengan kecepatan kritis atas disebut bilangan Reynolds kritis atas dan dilambangkan Re vk , pada bilangan Reynolds ini, aliran laminar menjadi turbulen.

Bilangan Reynolds yang sesuai dengan kecepatan kritis yang lebih rendah disebut bilangan Reynolds kritis yang lebih rendah dan dilambangkan Ulang nk ; pada bilangan Reynolds ini, rezim turbulen menjadi laminar.

Untuk pergerakan tekanan dalam pipa, percobaan berikut telah dilakukan: nilai numerik bilangan Reynolds kritis:

Ulang d (nk) = 2000 2320;

Ulang d (VK) = 10000 13000.

Cairan nyata memiliki viskositas, dan ketika bergerak, resistensi terhadap gerakan muncul. Perlawanan gerakan disebabkan oleh munculnya kekuatan friksi internal. Ketika aliran cairan nyata bergerak, energi mekanik yang terkandung dalam aliran akan berkurang di sepanjang aliran itu, karena sebagian darinya akan dihabiskan untuk mengatasi hambatan, .

Energi ini dikeluarkan untuk beberapa pekerjaan ireversibel, mis. untuk pekerjaan gaya gesekan, dan itu berubah menjadi panas, yang dihamburkan.

Semakin lama alirannya, semakin banyak energi yang akan dikeluarkan untuk mengatasi hambatan gerakan.

Energi yang dihabiskan untuk kerja gaya gesekan, - kehilangan energi mekanik aliran yang berubah menjadi panas. Kehilangan energi yang berhubungan dengan berat satuan cairan ketika bergerak sepanjang aliran dasar disebut kerugian hidrolik (kehilangan energi spesifik)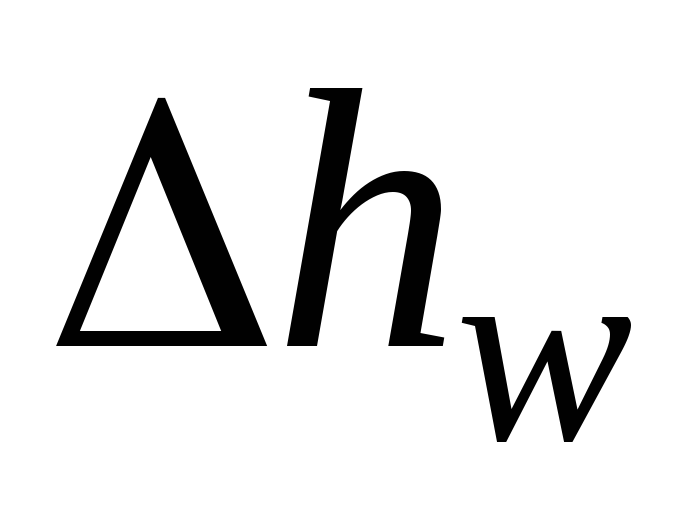

.

Pertimbangkan tetesan cairan nyata dengan gerakan tetap (Gbr. 3.8).

Beras. 3.8. Untuk persamaan Bernoulli untuk tetesan cairan nyata

Energi mekanik spesifik total dari tetesan nyata di bagian hidup 1-1 dan 2-2 akan menjadi

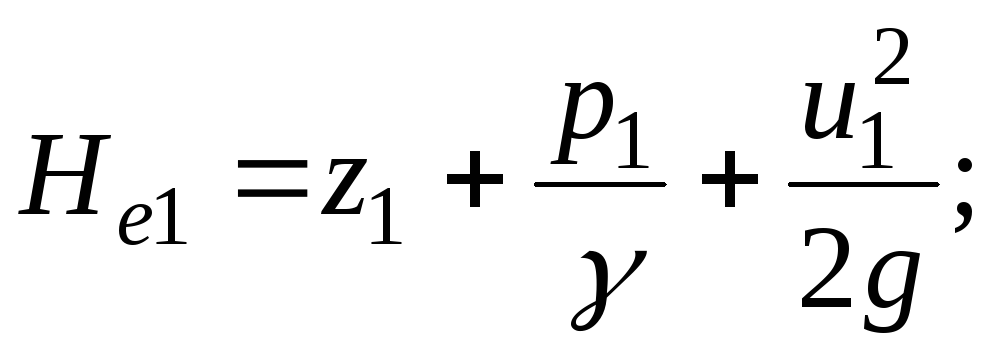
Kehilangan energi mekanik spesifik karena gesekan di area bagian hidup 1-1 dan 2-2

(3.45)

Dengan demikian, persamaan Bernoulli untuk aliran elementer dari cairan nyata dalam kasus gerak tetap dapat direpresentasikan sebagai:

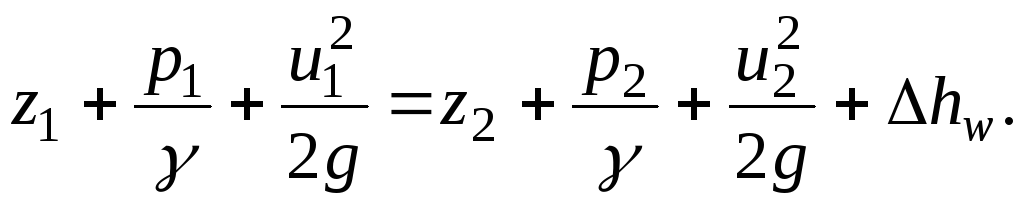(3.47)

Salah satu ciri gerak fluida adalah konsep piezometrik dan lereng hidrolik.

pada gambar. 3.8 menunjukkan kurva yang mencirikan persamaan Bernoulli. Garis yang melalui titik-titik yang sesuai dengan nilai tinggi piezometrik pada penampang hidup 1-1 dan 2-2 adalah garis piezometrik.

Kemiringan piezometrik adalah perubahan tinggi hidrostatik cairan di sepanjang aliran, per satuan panjang. Di bagian sungai dengan panjang 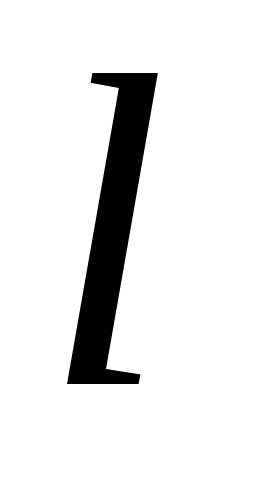antara bagian 1-1 dan 2-2 kemiringan piezometrik

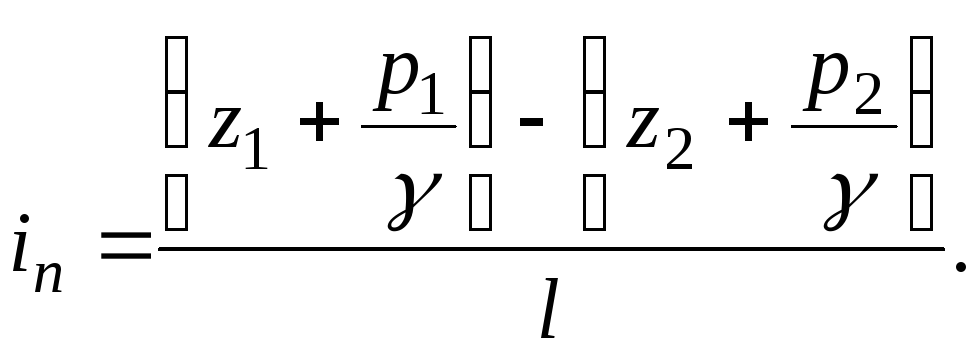(3.48)

Kemiringan piezometrik yang sesuai dengan panjang yang sangat kecil

(pada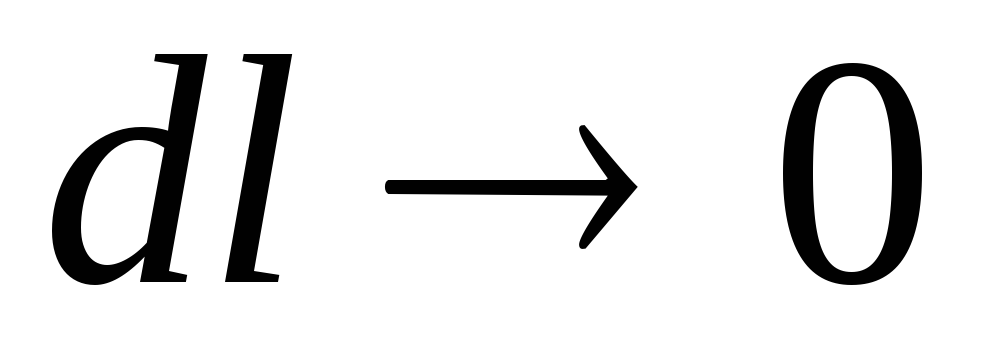

), - kemiringan pada titik:

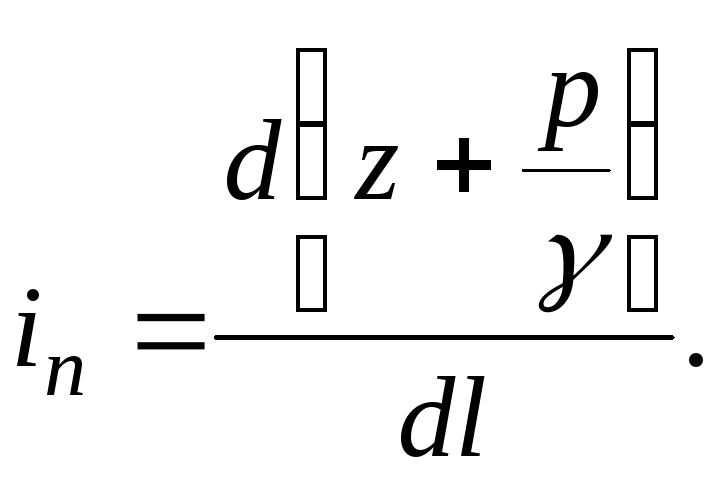(3.49)

Garis yang melewati titik-titik nilai energi mekanik spesifik di bagian hidup filamen adalah tekanangaris(garis tekanan penuh). Kemiringan hidrolik adalah penurunan total energi mekanik spesifik sepanjang filamen per satuan panjang:

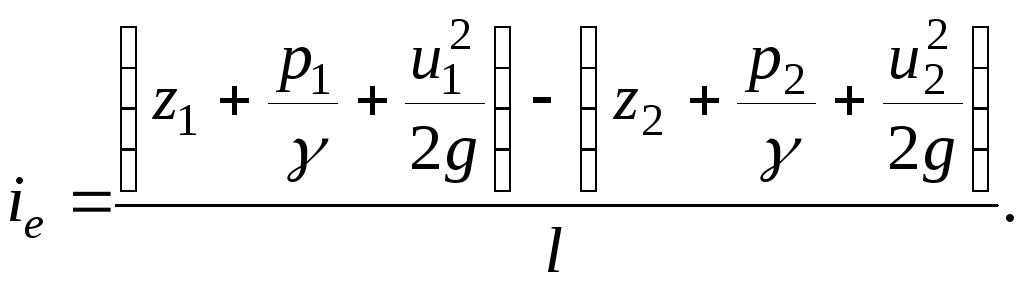(3.50)

Dengan penurunan dasar dalam energi spesifik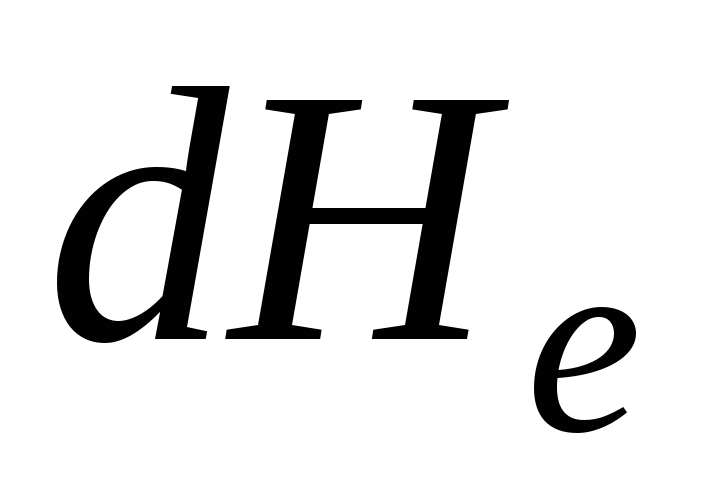

pada area yang sangat kecil

kemiringan hidrolik

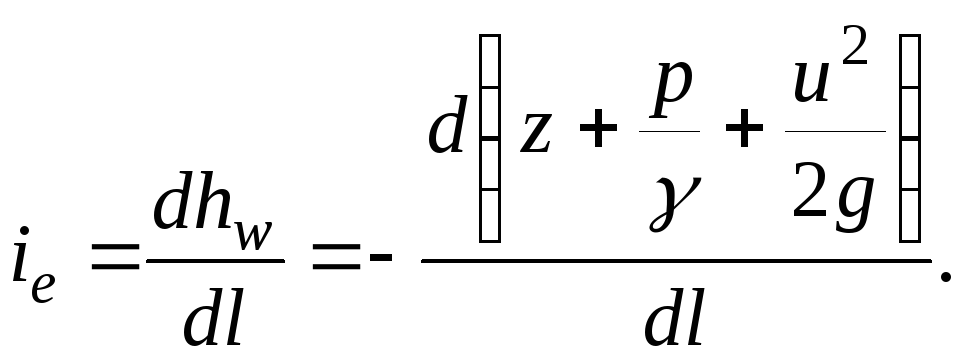(3.51)

Karena kurva kepala total menurun sepanjang tetesan, tanda dalam ekspresi (3.51) dikurangi [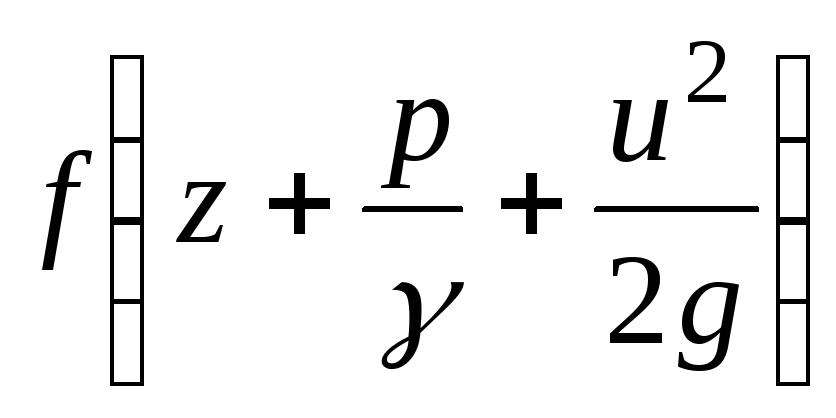

- fungsi menurun].

Dalam hal keteguhan bagian hidup di sepanjang pancaran, garis piezometrik dan garis tekanan total adalah paralel.

3.9. Persamaan Diferensial Gerak Fluida Ideal (Persamaan Euler)

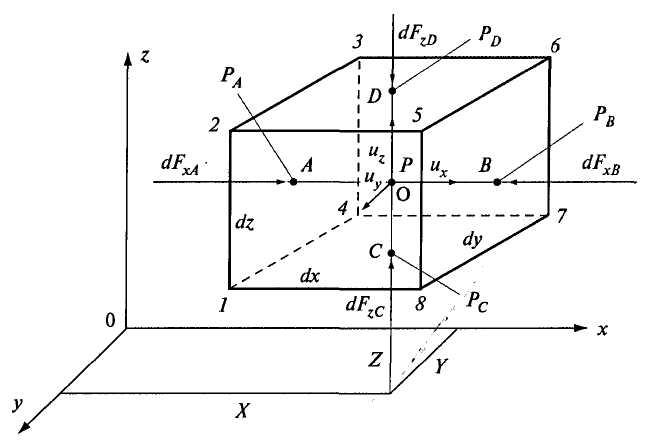
Dalam ruang yang diisi dengan massa jenis fluida ideal yang bergerak , pilih parallelepiped dasar yang ujung-ujungnya dengan sisi

, ,

sejajar dengan sumbu koordinat (Gbr. 3.9). Ketika fluida ideal bergerak, tidak ada gaya gesekan internal. Volume dasar yang terletak di paralelepiped bergerak dengan kecepatan absolut . Komponen kecepatan ini di sepanjang sumbu koordinat adalah: , , .

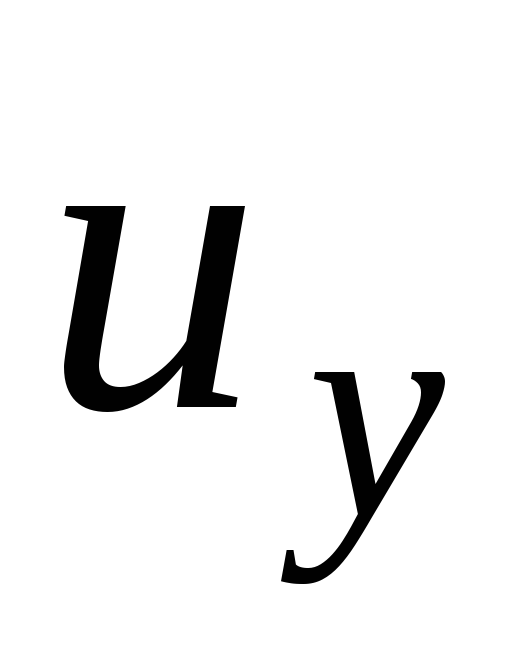Massa dan gaya permukaan akan bekerja pada volume dasar. Gaya gesekan selama pergerakan paralelepiped sama dengan nol.

Massa cairan dalam volume dasar paralelepiped

(3.52)

Beras. 3.9. Untuk turunan persamaan gerak Euler

Proyeksi gaya massa ke arah sumbu koordinat:

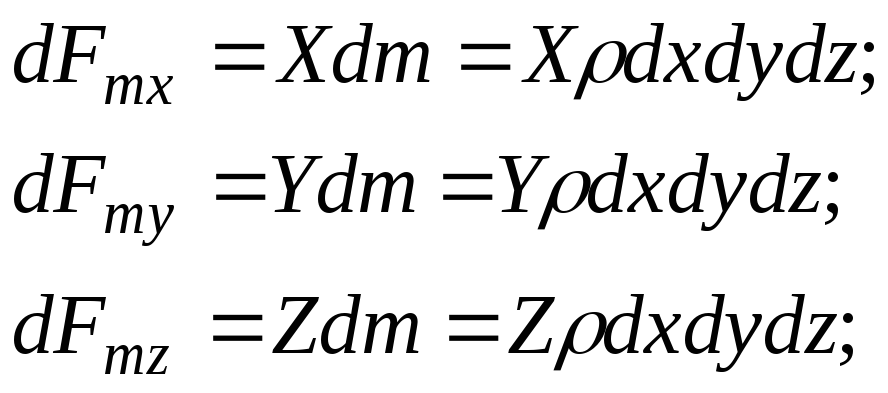(3.53)

di mana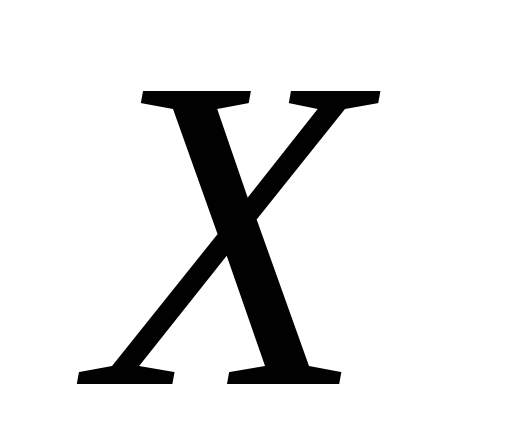

, , - komponen kekuatan tubuh unit sehubungan dengan sumbu , , (proyeksi percepatan gaya-gaya ini).

Gaya permukaan ditentukan oleh tekanan pada permukaan parallelepiped.

Biarkan tekanan hidrostatik di pusat gravitasi paralelepiped (titik O) menjadi 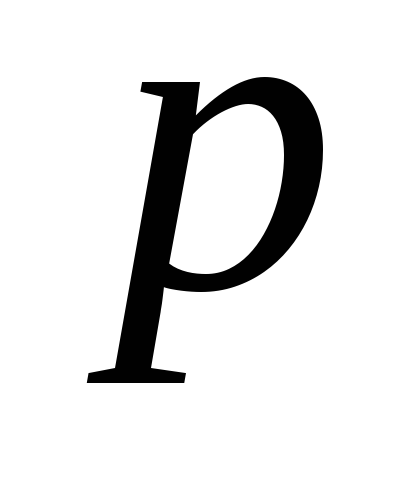, koordinat titik ini , , .Kecepatan gerakan pada titik ini . Komponen kecepatan sepanjang sumbu koordinat adalah , , .

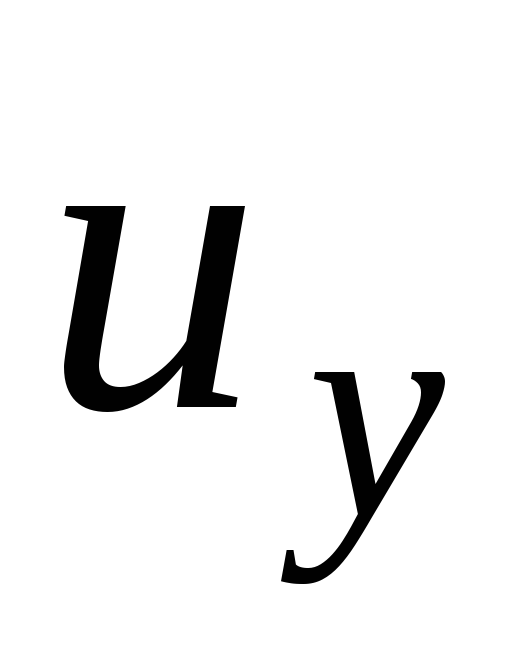Mari kita menggambar melalui t. Tentang garis horizontal yang sejajar dengan sumbu . Titik potong dengan muka kotak A (muka 1234), B (muka 5678). Tekanan pada titik-titik ini di sepanjang sumbu

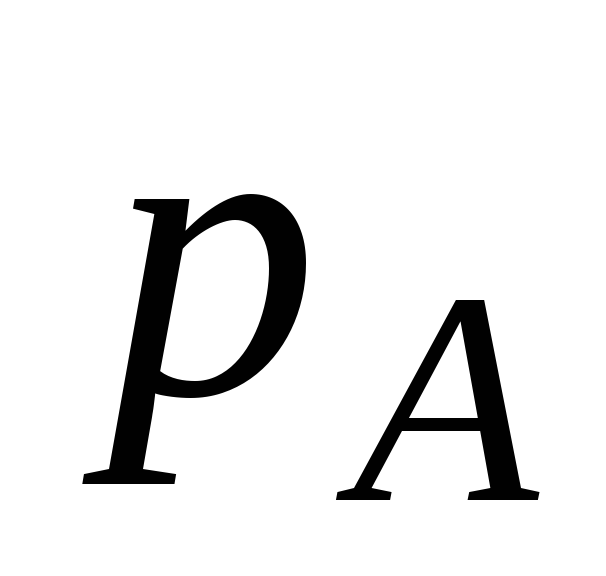dan

.

Dalam media kontinu cair, tekanan pada suatu titik dinyatakan oleh fungsi kontinu kontinu dari koordinat lokasi titik dalam ruang: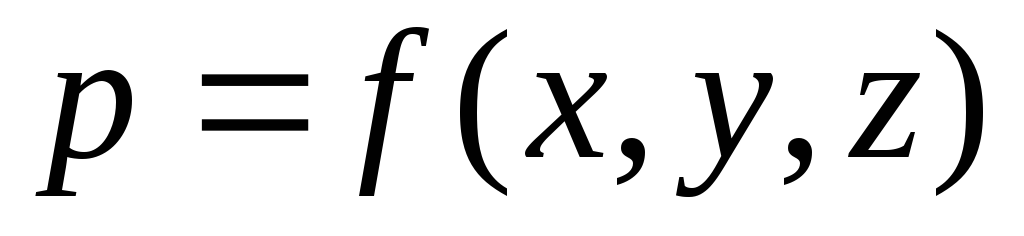

. Tekanan hidrostatik berubah terus menerus secara linier, dan kenaikan tekanan per satuan panjang dasar

-

-



-

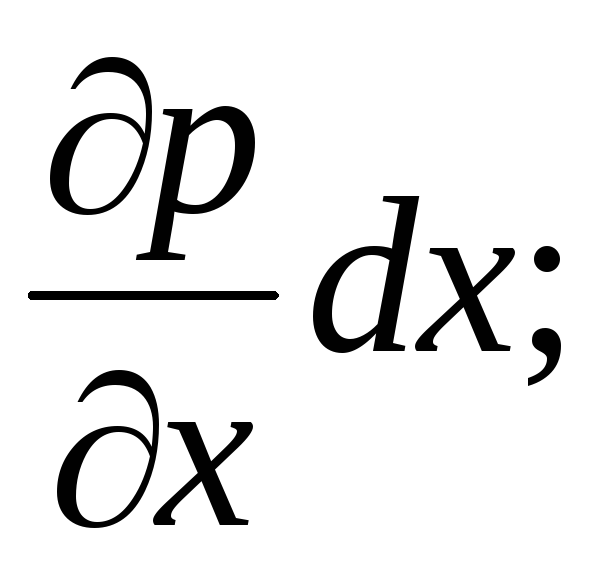
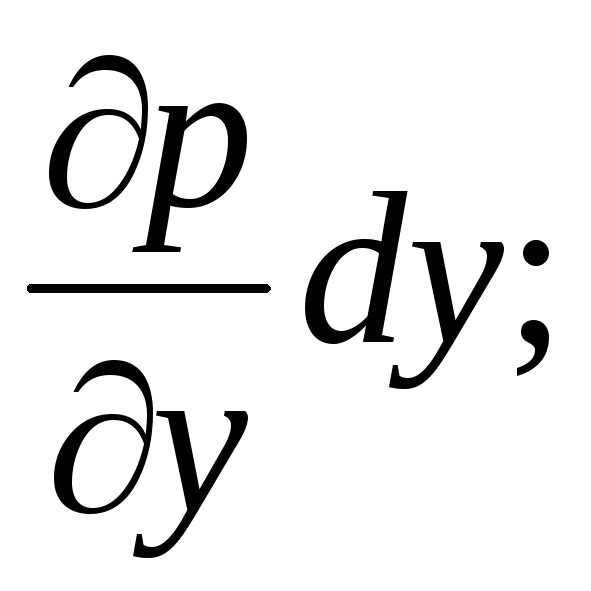
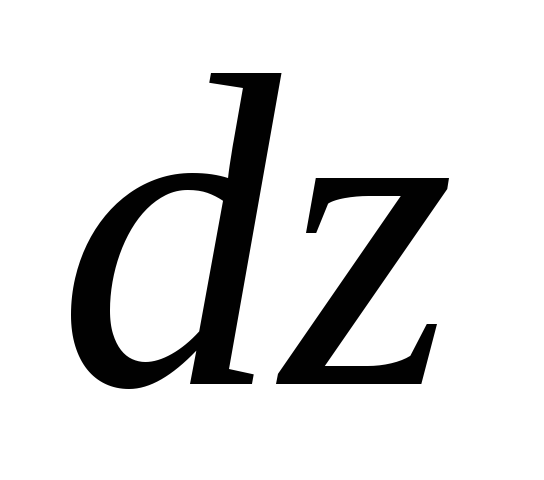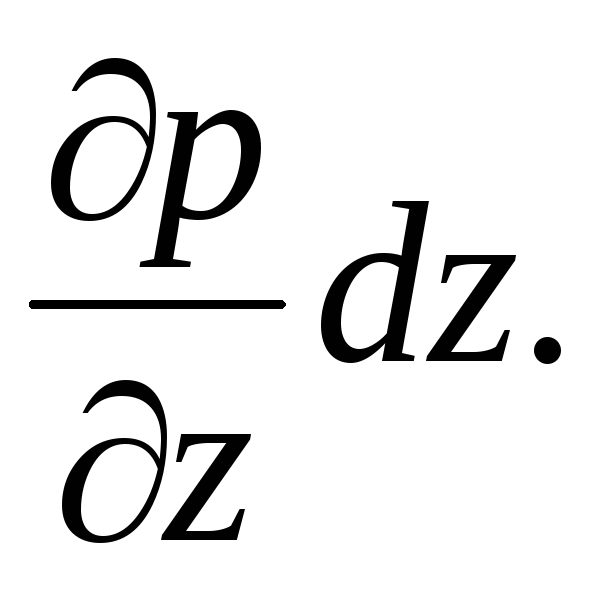
Akibatnya, tekanan di titik A dan B akan berbeda sebesar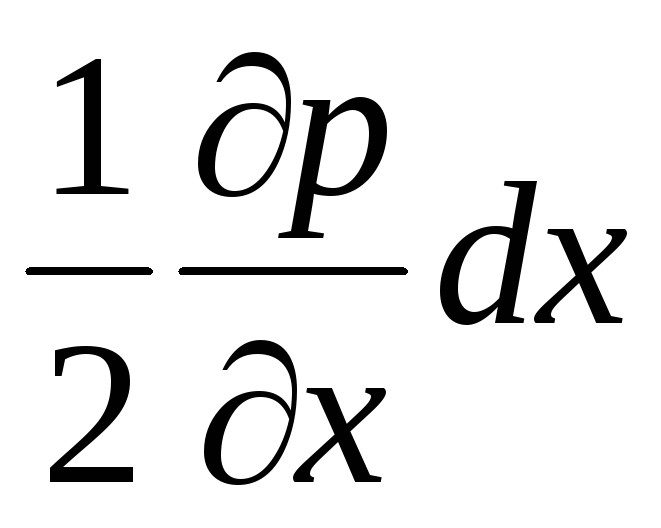

.

Kami menyatakan tekanan di titik A dan B dalam bentuk berikut:

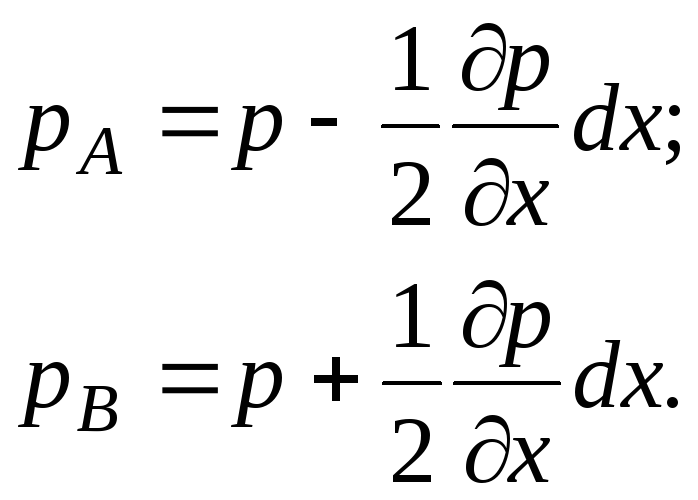(3.54)

Karena area wajah yang kecil, kita dapat mengasumsikan bahwa tekanan

dan

adalah tekanan hidrostatik rata-rata yang bekerja pada permukaan 1234 dan 5678. Gaya tekanan permukaan pada permukaan ini sepanjang sumbu sama dengan produk dari tekanan pada area wajah:

(3.55)

Demikian pula, gaya tekanan permukaan pada permukaan sepanjang sumbu z (permukaan 1478 dan 2365):

(3.56)

Anda juga dapat menentukan gaya permukaan pada wajah di sepanjang sumbu .

Pertimbangkan keseimbangan paralelepiped dalam cairan bergerak menggunakan prinsip d'Alembert.

Menurut prinsip d'Alembert, persamaan gerak dapat dianggap sebagai persamaan kesetimbangan jika kita memperkenalkan gaya inersia. Kami berasumsi bahwa paralelepiped dengan massa

bergerak dengan kecepatan , komponen kecepatan ini , , .

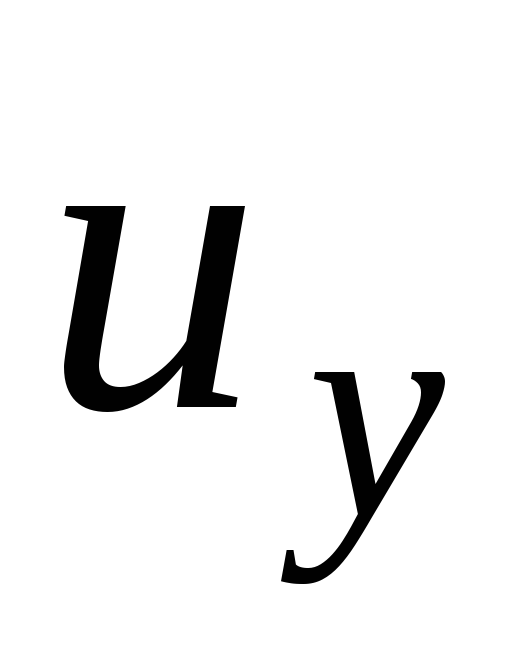gaya inersia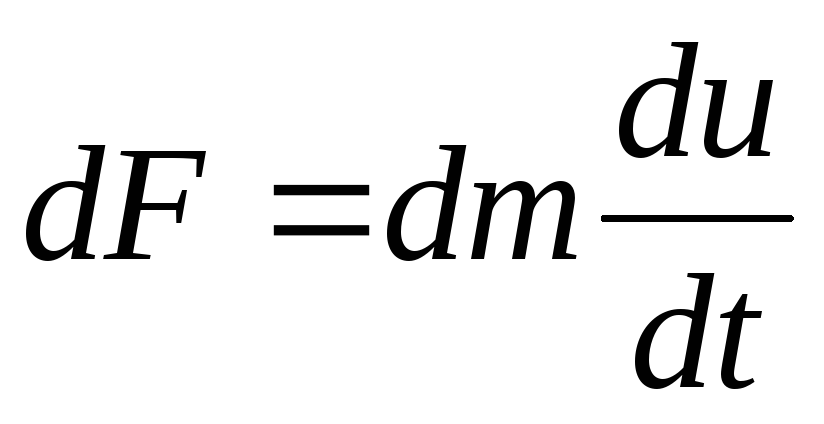

(- percepatan).

Proyeksi gaya inersia pada sumbu koordinat yang sesuai:

(3.57)

di mana 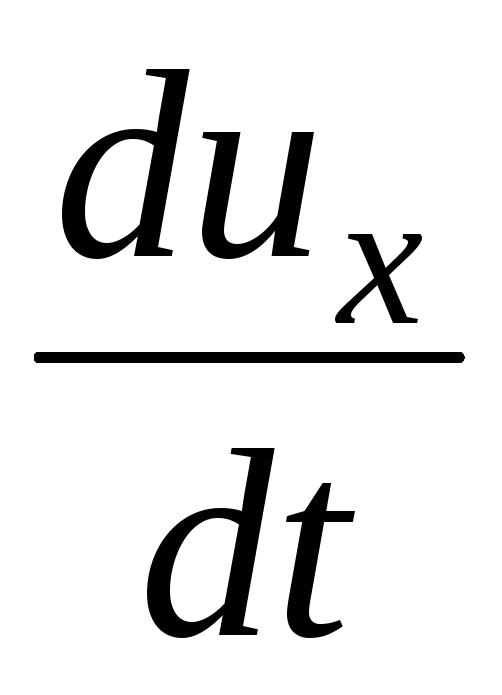,,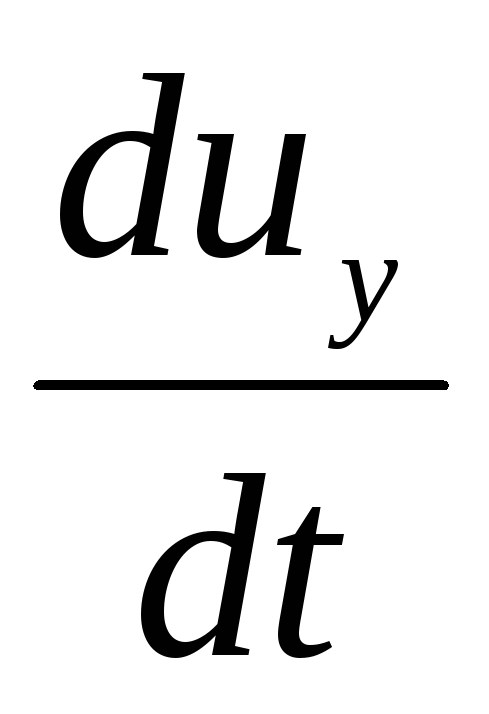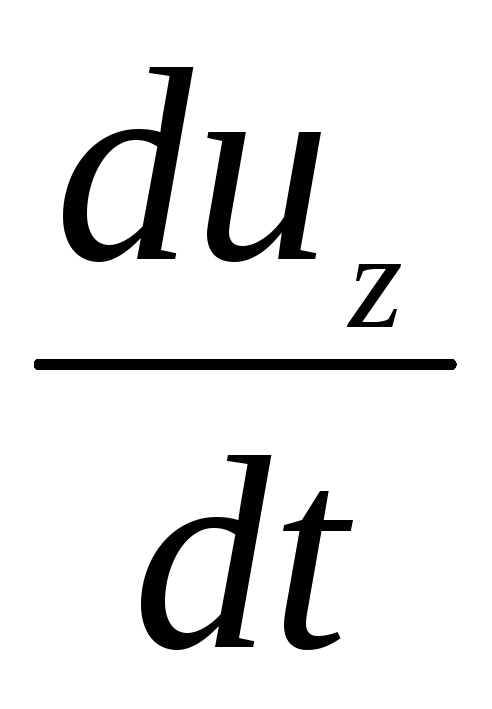- proyeksi percepatan pada sumbu , , .

Mari kita buat persamaan keseimbangan untuk gaya-gaya yang bekerja pada fluida paralelepiped yang sedang dipertimbangkan, dengan mempertimbangkan gaya inersia sepanjang sumbu dan :

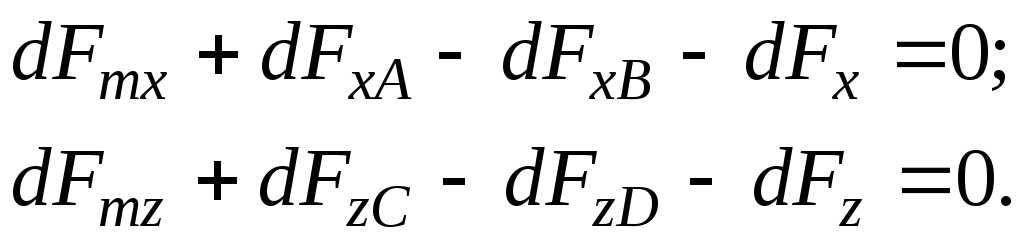(3.58)

Substitusi ke (3.58) ketergantungan yang diperoleh sebelumnya (3,53), (3,55), (3,56) dan (3,57), kita memperoleh persamaan berikut

Buka kurung dan bagi persamaan yang diperoleh di atas dengan

, menulis

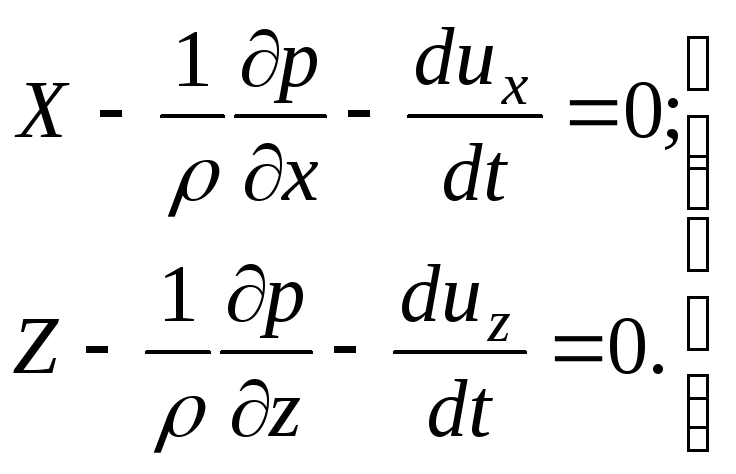(3.59)

Demikian pula, Anda bisa mendapatkan persamaan untuk sumbu y:

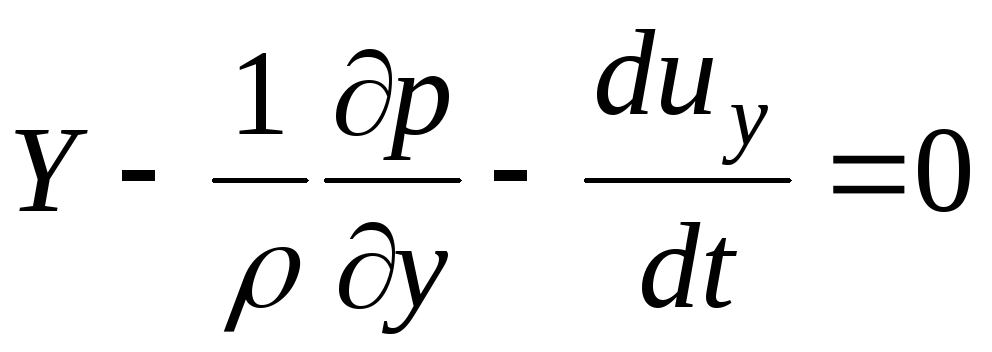(3.60)

Persamaan (3.59) dan (3.60) dapat ditulis sebagai sistem persamaan:

(3.61)

Dalam kasus umum, jumlah , , 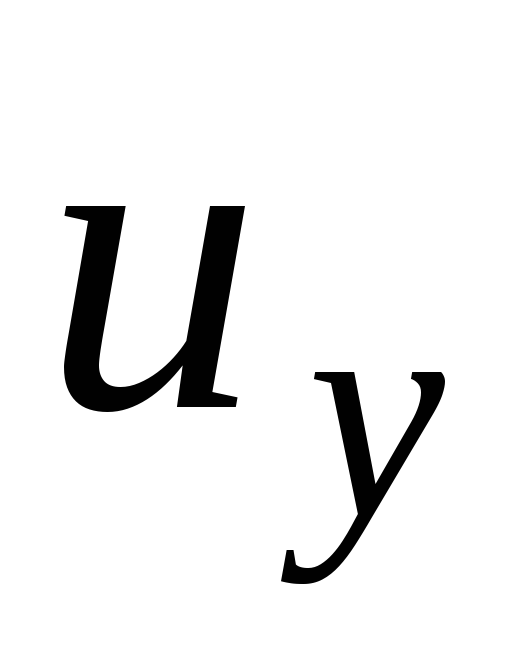adalah fungsi dari koordinat , , , serta waktu . Oleh karena itu, perbedaan kecepatan total akan

Percepatan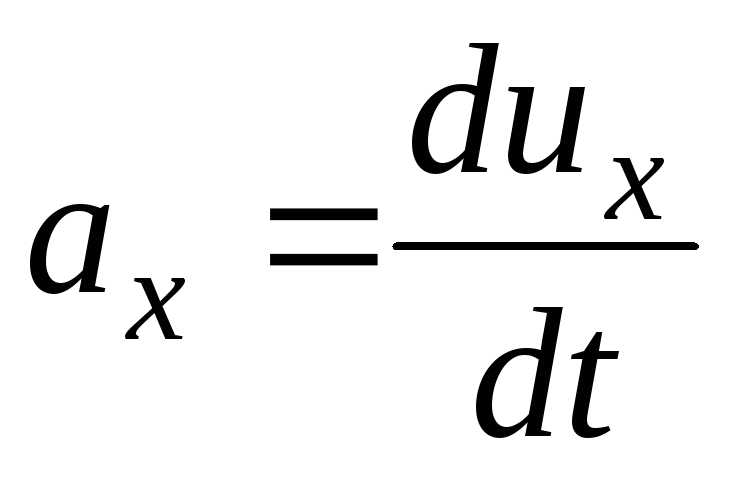

;

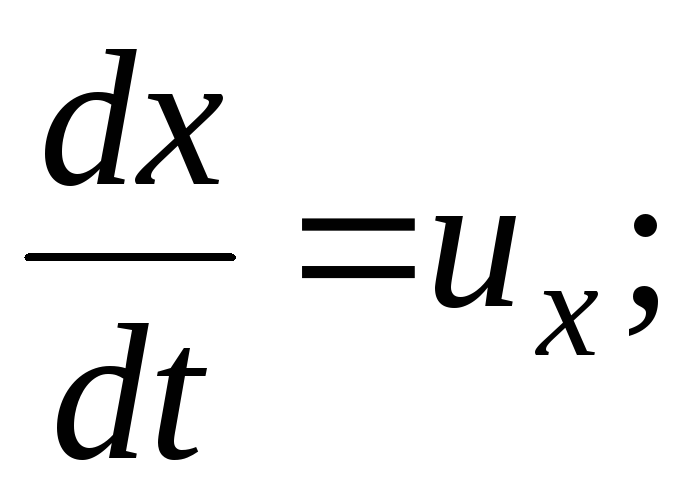
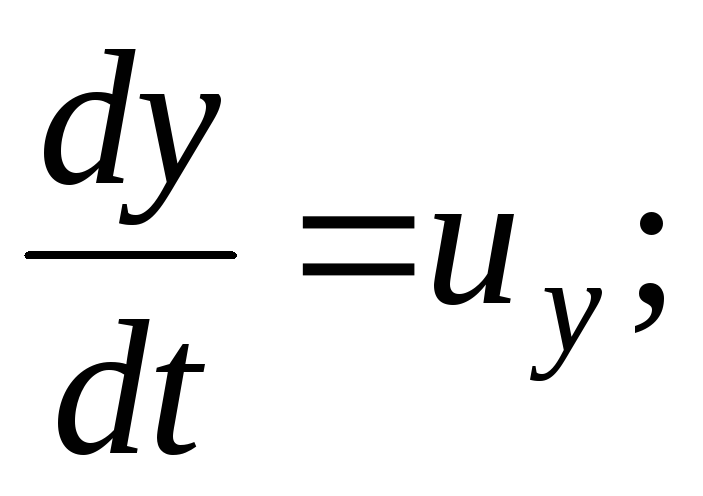
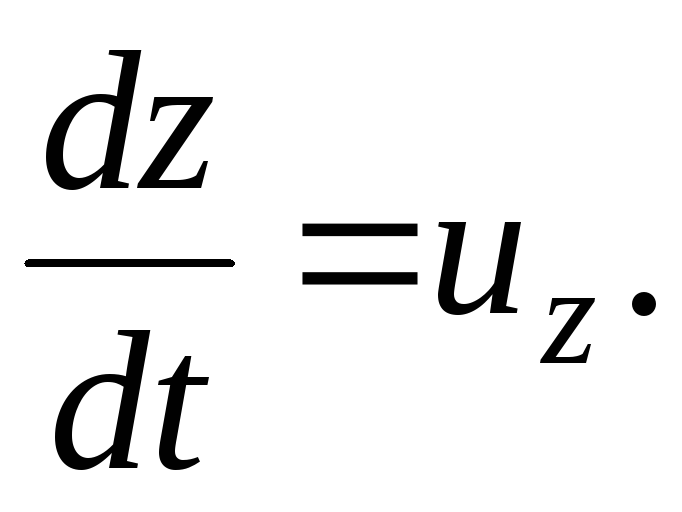
(3.64)

Demikian pula, Anda bisa mendapatkan perbedaan kecepatan ,.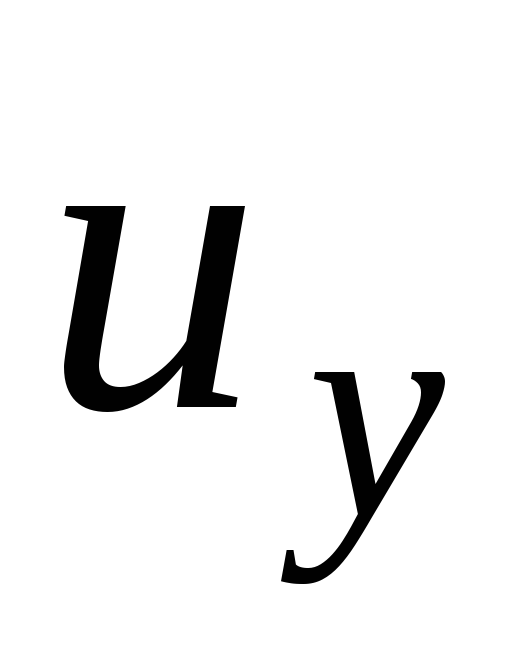

Setelah dimasukkan ke dalam sistem persamaan (3.61), perbedaan kecepat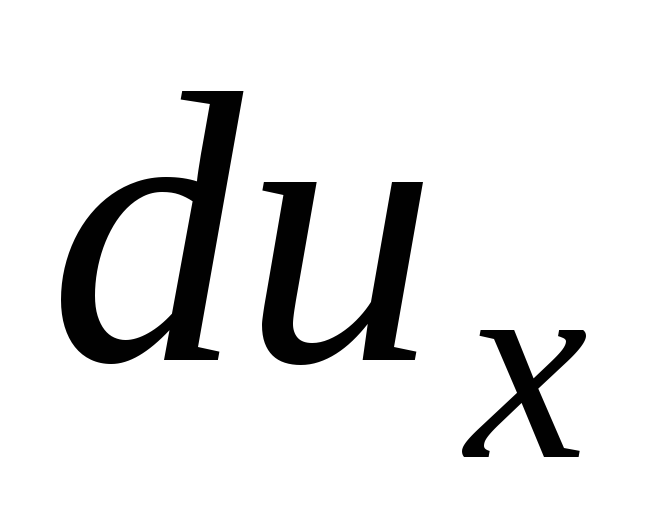an

,

dan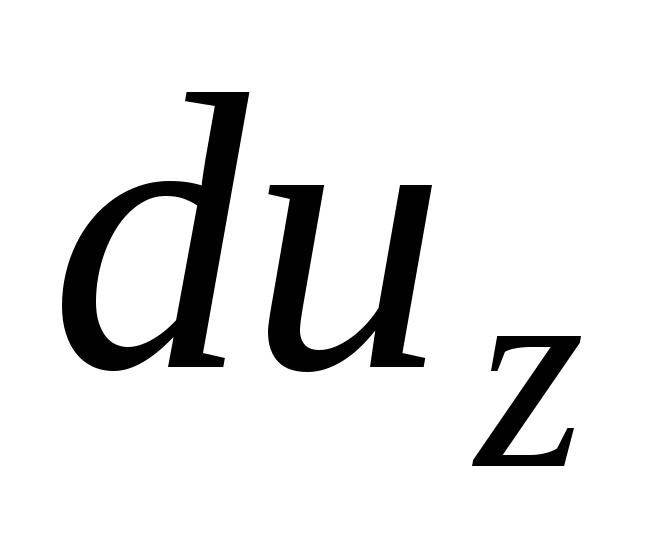

dia akan terlihat

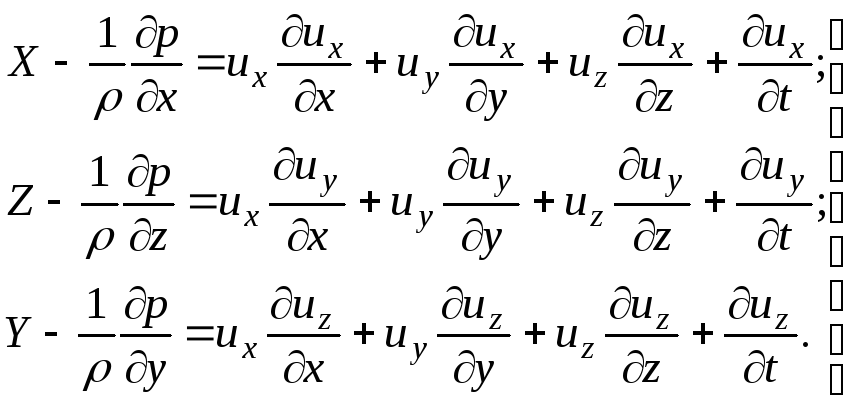(3.65)

Dalam kasus gerakan stabil

;

;

. (3.66)

Persamaan (3.65) adalah persamaan diferensial gerak fluida ideal (tidak kental) - persamaan Euler. Persamaan ini diperoleh oleh Euler pada tahun 1775.

Persamaan Euler menyatakan hubungan antara proyeksi gaya yang bekerja, kecepatan, tekanan, dan densitas fluida. Persamaan Euler sangat penting dalam mempelajari gerak fluida.

Untuk fluida dalam keadaan diam, kita memiliki

Persamaan diferensial Euler mengambil bentuk berikut:

(3.67)

Sistem persamaan diferensial adalah persamaan kesetimbangan fluida.

Dari persamaan kesetimbangan dapat diperoleh persamaan dasar hidrostatika (2.2) (lihat Lampiran).

Integrasi persamaan gerak Euler. integral Bernoulli

Pertimbangkan gerakan tetap dari fluida ideal. Kami mewakili persamaan Euler dalam bentuk (3.61). Kalikan persamaan pertama dengan

, yang kedua - aktif dan ketiga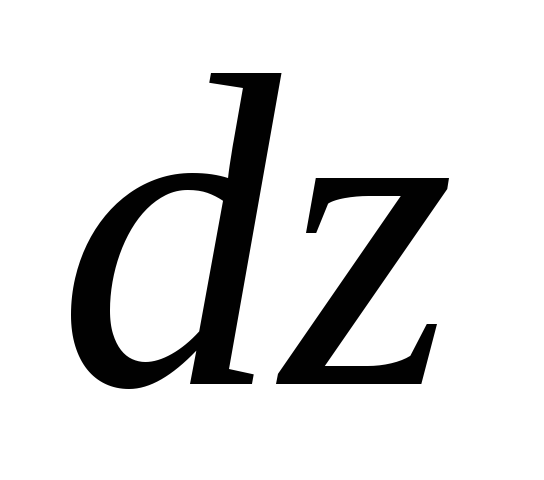

, kita mendapatkan

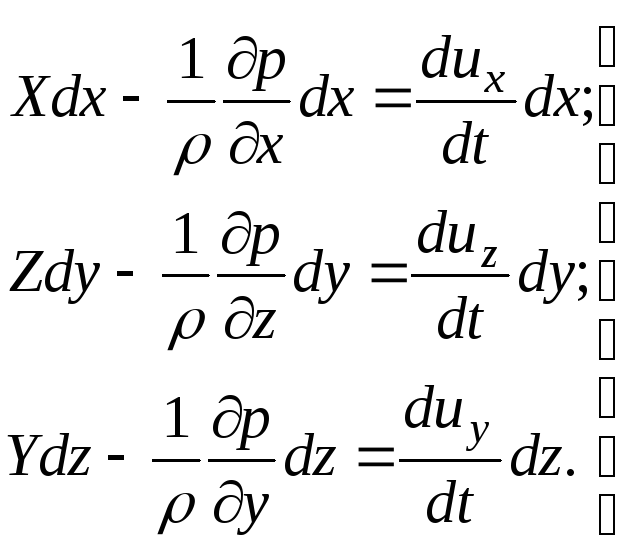(3.68)

Kami menambahkan istilah demi istilah ketiga persamaan sistem:

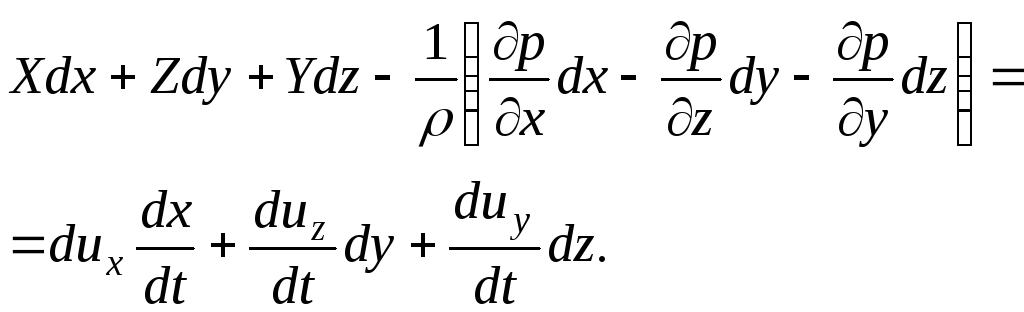(3.69)

Untuk gerakan tetap, tekanan 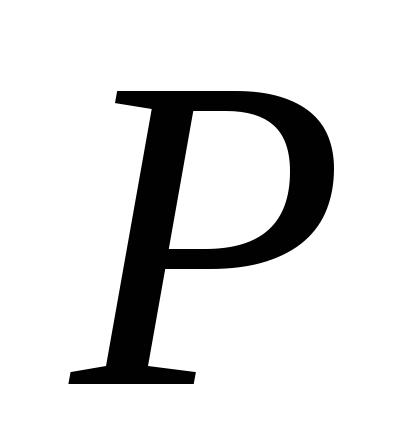pada suatu titik merupakan fungsi dari koordinatnya dan tidak bergantung pada waktu. Oleh karena itu, perbedaan tekanan dinyatakan dalam turunan parsial:

.

Sebagai

;

dan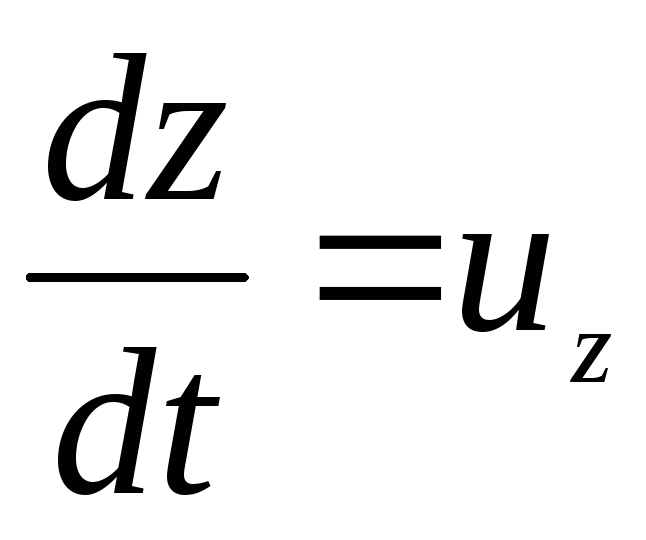

, maka suku terakhir persamaan (3.69)

di samping itu

;

;

.

Akibatnya, ruas kanan persamaan (3.69) berbentuk

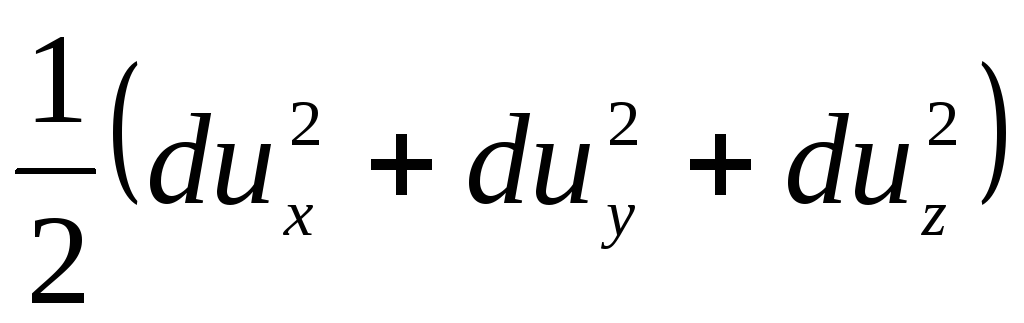. (3.71)

Kecepatan penuh (mutlak) dan dinyatakan melalui , , :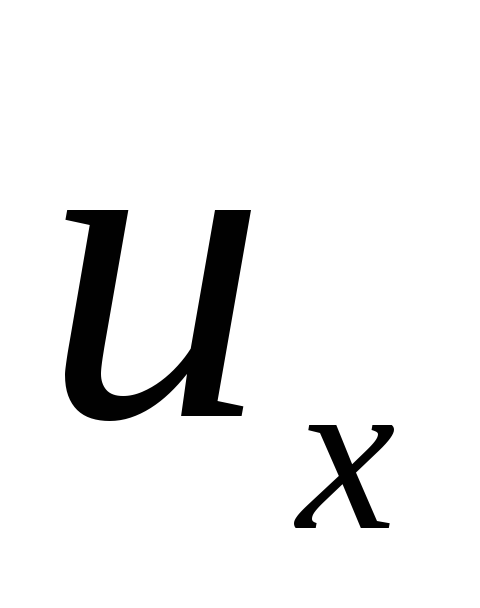

.

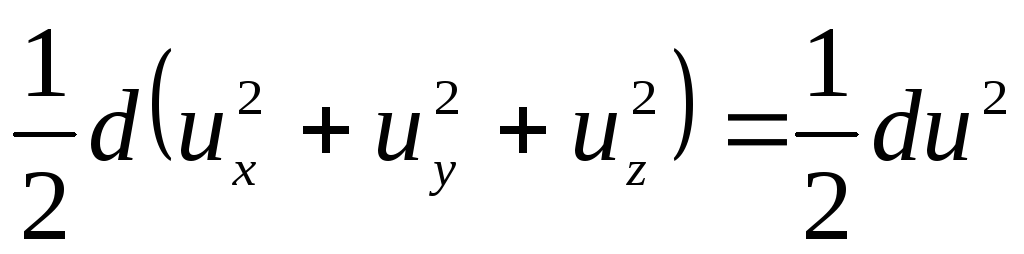. (3.72)

Persamaan (3.69) setelah transformasi dapat ditulis ulang dalam bentuk berikut:

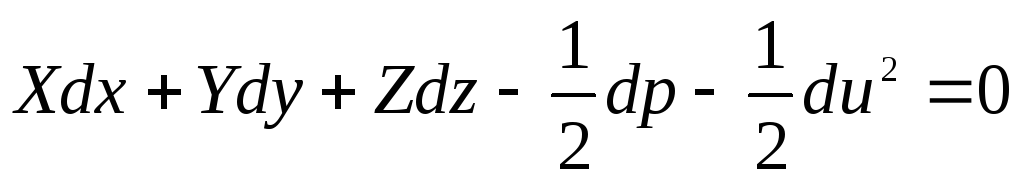. (3.73)

Tiga ekspresi pertama dalam persamaan ini adalah diferensial total dari fungsi gaya (potensial) :

Jadi, persamaan (3.74) mengambil bentuk

. (3.75)

Mengintegrasikan persamaan (3,75), kami memperoleh

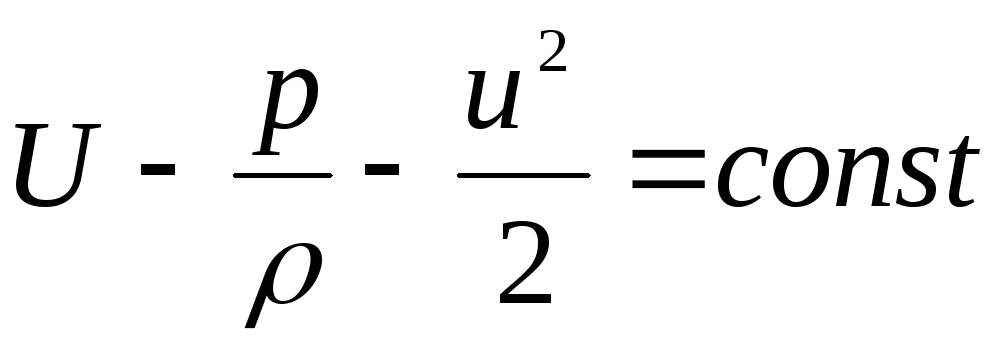. (3.76)

Persamaan ini disebut integral Bernoulli-Euler.

Trinomial yang dihasilkan - persamaan tetap tidak berubah di sepanjang garis arus.

Dalam kasus ketika gerakan terjadi di bawah aksi hanya satu gaya massa - gaya gravitasi, maka gaya massa satuan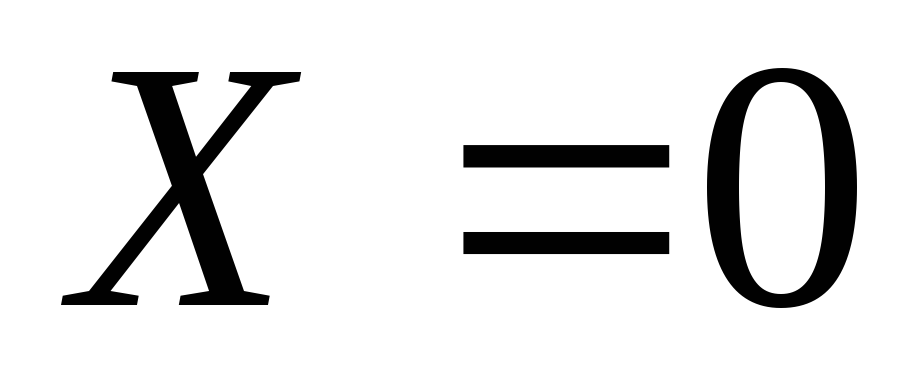

,

,

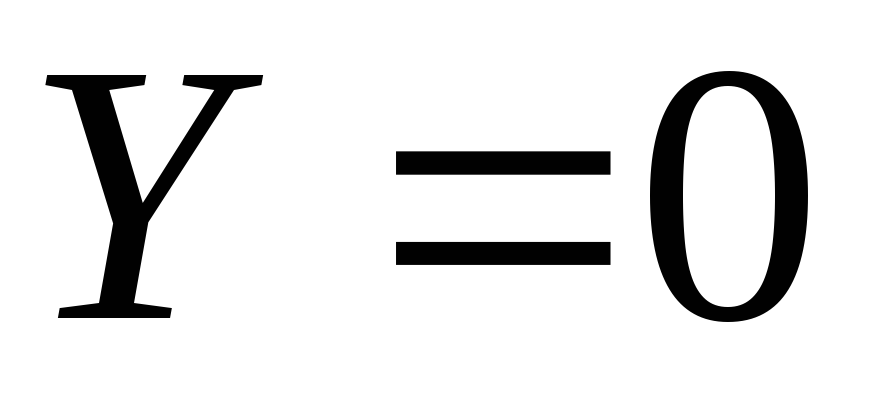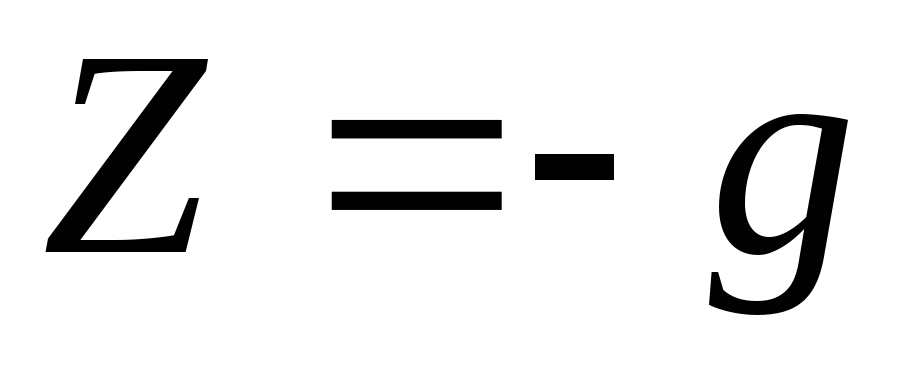(sumbu diarahkan vertikal ke atas). Diferensial fungsi gaya

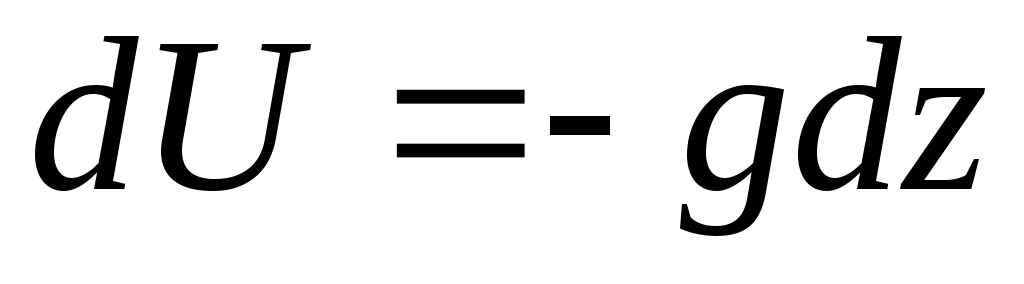. (3.77)

Persamaan (3.75) dapat ditulis dalam bentuk berikut:

. (3.78)

Kami membagi semua istilah persamaan dengan percepatan jatuh bebas , maka kita dapatkan

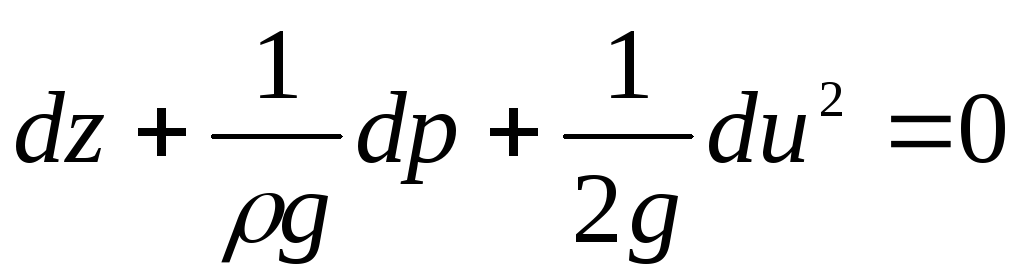. (3 79)

Pertambahan jumlah ketiga suku persamaan ini ketika bergerak sepanjang garis arus sama dengan nol.

Mengintegrasikan persamaan diferensial (3.79), kita memperoleh

. (3.80)

Jumlah semua suku di sepanjang garis arus zat cair adalah nilai konstan, dan, akibatnya, juga konstan di sepanjang aliran elementer ideal.

Persamaan (3.80), diperoleh dengan menggunakan persamaan gerak Euler, untuk gerak tetap adalah persamaan Bernoulli. Persamaan identik diperoleh sebelumnya dengan cara yang berbeda menggunakan teorema energi kinetik (3.43).

Persamaan (3.80), ditulis untuk dua bagian yang hidup dari tetesan, memperoleh bentuk yang diketahui sebelumnya

.
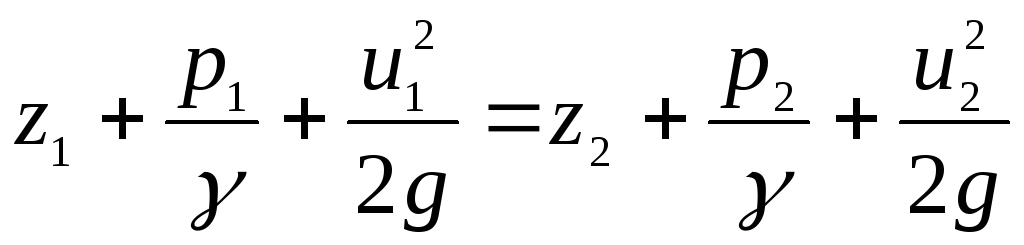