Arten von Zahlen. Naturals, Integers, Rationals und Reals. Number ist eine Abstraktion, für die verwendet wird quantitative Merkmale Objekte. Nummern entstanden in Urgesellschaft im Zusammenhang mit dem Bedürfnis des Menschen, Gegenstände zu zählen. Mit der Entwicklung der Wissenschaft ist die Zahl im Laufe der Zeit zum wichtigsten mathematischen Konzept geworden.

Zur Problemlösung und Beweisführung verschiedene Theoreme Sie müssen verstehen, welche Arten von Zahlen es gibt. Die wichtigsten Arten von Zahlen sind: natürliche Zahlen, ganze Zahlen, rationale Zahlen, reelle Zahlen.

Ganze Zahlen- Dies sind die Zahlen, die durch das natürliche Zählen von Objekten oder vielmehr durch ihre Nummerierung ("erster", "zweiter", "dritter" ...) erhalten werden. Ein Haufen natürliche Zahlen bezeichnet Lateinischer Buchstabe N(kann erinnert werden basierend auf englisches Wort natürlich). Das kann man sagen N ={1,2,3,....}

Ganze Zahlen sind Zahlen aus der Menge (0, 1, -1, 2, -2, ....). Dieses Set besteht aus drei Teilen - natürliche Zahlen, negative ganze Zahlen (das Gegenteil von natürlichen Zahlen) und die Zahl 0 (Null). Ganze Zahlen werden mit einem lateinischen Buchstaben bezeichnet Z. Das kann man sagen Z={...,-3,-2,-1,0,1,2,3,....}.

Rationale Zahlen sind Zahlen, die als Bruch dargestellt werden können, wobei m eine ganze Zahl und n eine natürliche Zahl ist. In diesem Fall wird die Nummer m aufgerufen Zähler, und die Zahl n - Nenner Brüche. Ein solcher Bruch ist als Ergebnis einer Division von m durch n zu verstehen, auch wenn er nicht vollständig dividierbar ist. Der lateinische Buchstabe wird verwendet, um rationale Zahlen zu bezeichnen Q. Q={... ;-3;-2,5;-2;-1;0; ;1;2;3;3,5....}. Alle natürlichen und ganzen Zahlen sind rational. Als Beispiele für rationale Zahlen können Sie auch angeben: , , . BEIM wahres Leben Rationale Zahlen werden verwendet, um die Teile einiger ganzer, aber teilbarer Objekte zu zählen, wie z. B. Kuchen oder andere Lebensmittel, die in mehrere Stücke geschnitten werden, oder um die räumlichen Beziehungen ausgedehnter Objekte grob abzuschätzen.

Reelle (reelle) Zahlen sind die Zahlen, die zum Messen verwendet werden kontinuierliche Mengen. Ein Haufen reale Nummern mit dem lateinischen Buchstaben R bezeichnet. Reelle Zahlen umfassen rationale Zahlen und irrationale Zahlen. Irrationale Zahlen- Dies sind Zahlen, die durch verschiedene Operationen mit rationalen Zahlen erhalten werden (z. B. Wurzel ziehen, Logarithmen berechnen), aber nicht rational sind. Beispiele für irrationale Zahlen sind , , .

Jede reelle Zahl kann auf dem Zahlenstrahl dargestellt werden:

Für die oben aufgeführten Zahlenmengen gilt die folgende Aussage:

Das heißt, die Menge der natürlichen Zahlen ist in der Menge der ganzen Zahlen enthalten. Die Menge der ganzen Zahlen ist in der Menge der rationalen Zahlen enthalten. Und die Menge der rationalen Zahlen ist in der Menge der reellen Zahlen enthalten. Diese Aussage lässt sich mit Eulerkreisen veranschaulichen.

Die Definition natürlicher Zahlen sind ganze Zahlen positive Zahlen. Natürliche Zahlen werden zum Zählen von Objekten und für viele andere Zwecke verwendet. Diese Zahlen sind: 1; 2; 3; 4;...

Das ist eine natürliche Zahlenreihe.
Null ist eine natürliche Zahl? Nein, Null ist keine natürliche Zahl.
Wie viele natürliche Zahlen gibt es? Existieren unendlicher Satz natürliche Zahlen.
Was ist die kleinste natürliche Zahl? Eins ist die kleinste natürliche Zahl.
Was ist die größte natürliche Zahl? Sie kann nicht angegeben werden, da es eine unendliche Menge natürlicher Zahlen gibt.

Die Summe natürlicher Zahlen ist eine natürliche Zahl. Also die Addition der natürlichen Zahlen a und b:

Das Produkt natürlicher Zahlen ist eine natürliche Zahl. Also das Produkt der natürlichen Zahlen a und b:

c ist immer eine natürliche Zahl.

Unterschied natürlicher Zahlen Nicht immer gibt es eine natürliche Zahl. Ist der Minuend größer als der Subtrahend, dann ist die Differenz natürlicher Zahlen eine natürliche Zahl, sonst nicht.

Der Quotient natürlicher Zahlen Es gibt nicht immer eine natürliche Zahl. Wenn für die natürlichen Zahlen a und b

wobei c eine natürliche Zahl ist, bedeutet dies, dass a durch b teilbar ist. In diesem Beispiel ist a der Dividende, b der Divisor, c der Quotient.

Der Teiler einer natürlichen Zahl ist die natürliche Zahl, durch die die erste Zahl ohne Restzahl teilbar ist.

Jede natürliche Zahl ist durch 1 und sich selbst teilbar.

Einfache natürliche Zahlen sind nur durch 1 und sich selbst teilbar. Hier bedeutet es, dass sie vollständig geteilt sind. Beispiel, Zahlen 2; 3; 5; 7 ist nur durch 1 und sich selbst teilbar. Das sind einfache natürliche Zahlen.

Eins gilt nicht als Primzahl.

Zahlen, die größer als eins und keine Primzahlen sind, heißen zusammengesetzte Zahlen. Beispiele Zusammengesetzte Zahlen: 4; 6; 8; 9; 10

Eins gilt nicht als zusammengesetzte Zahl.

Die Menge der natürlichen Zahlen ist eins, Primzahlen und zusammengesetzte Zahlen.

Die Menge der natürlichen Zahlen wird mit dem lateinischen Buchstaben N bezeichnet.

Eigenschaften der Addition und Multiplikation natürlicher Zahlen:

Kommutative Eigenschaft der Addition

assoziative Eigenschaft Ergänzungen

(a + b) + c = a + (b + c);

Kommutativgesetz der Multiplikation

Assoziativgesetz der Multiplikation

(ab)c = a(bc);

Verteilungseigenschaft Multiplikation

a (b + c) = ab + ac;

Ganze Zahlen

Ganze Zahlen sind natürliche Zahlen, Null und das Gegenteil von natürlichen Zahlen.

Zahlen, die natürlichen Zahlen entgegengesetzt sind, sind ganze Zahlen. negative Zahlen, zum Beispiel: -1; -2; -3; -4;...

Die Menge der ganzen Zahlen wird mit dem lateinischen Buchstaben Z bezeichnet.

Rationale Zahlen

Rationale Zahlen sind ganze Zahlen und Brüche.

Jede rationale Zahl kann als periodischer Bruch dargestellt werden. Beispiele: -1,(0); 3, (6); 0,(0);...

Aus den Beispielen wird deutlich, dass jede ganze Zahl ist periodischer Bruch mit Periode Null.

Jede rationale Zahl kann als Bruch m/n dargestellt werden, wobei m ganze Zahl,n natürliche Zahl. Stellen wir die Zahl 3,(6) aus dem vorigen Beispiel als solchen Bruch dar: 22/6 = 3,(6);

Ein weiteres Beispiel: Die rationale Zahl 9 kann als einfacher Bruch als 18/2 oder als 36/4 dargestellt werden.

Ein weiteres Beispiel: Die rationale Zahl -9 kann als einfacher Bruch als -18/2 oder als -72/8 dargestellt werden.

Die Menge der rationalen Zahlen wird mit dem lateinischen Buchstaben Q bezeichnet.

Irrationale Zahlen

Irrationale Zahlen sind unendliche, nicht wiederkehrende Dezimalzahlen.

Beispiele: pi = 3,141592... e = 2,718281...

Reale Nummern

Reelle Zahlen sind alle rationale und alle irrationalen Zahlen.

Die Menge der reellen Zahlen wird mit dem lateinischen Buchstaben R bezeichnet.

Zweck: Zu wissen, was eine natürliche, ganzzahlige, rationale Zahl, ein periodischer Bruch ist; endlos schreiben können Dezimal in Form eines gewöhnlichen, in der Lage sein, Aktionen mit Dezimal- und gewöhnlichen Brüchen auszuführen.

1. Konsolidierung des studierten Materials, Änderung der Arbeitstypen zu diesem Thema „Ganze Zahlen und rationale Zahlen“.
2. Entwickeln Sie Fähigkeiten und Fertigkeiten bei der Durchführung von Aktionen mit Dezimal- und gewöhnlichen Brüchen logisches Denken, korrektes und kompetentes mathematisches Sprechen, Entwicklung von Selbständigkeit und Vertrauen in ihr Wissen und ihre Fähigkeiten bei der Durchführung verschiedene Typen funktioniert.
3. Wecken Sie das Interesse an Mathematik, indem Sie verschiedene Arten der Vertiefung des Materials einführen: mündliche Arbeit, Arbeit mit einem Lehrbuch, Arbeit an der Tafel, Beantwortung von Fragen und Fähigkeit zur Selbstbeobachtung, selbstständiges Arbeiten; Aktivitäten der Schüler anregen und fördern.

ICH. Zeit organisieren.
II. Neues Thema:
"Ganzzahlen und rationale Zahlen".
1. Theoretischer Teil.
2. Praktischer Teil.
3. Arbeite nach Lehrbuch und an der Tafel.
4. Selbstständige Arbeit nach Optionen.
III. Ergebnis.
1. Für Fragen.
IV. Hausaufgaben.

Während des Unterrichts

I. Organisatorischer Moment.

Emotionale Stimmung und Bereitschaft des Lehrers und der Schüler für den Unterricht. Kommunikation von Zielen und Zielen.

II. Neues Thema: „Ganze Zahlen und rationale Zahlen“:

Theoretischer Teil.

1. Anfangs wurde die Zahl nur als natürliche Zahl verstanden. Was ausreicht, um einzelne Artikel zu zählen.

Setze N = (1; 2; 3...) natürliche Zahlen ist unter den Operationen Addition und Multiplikation abgeschlossen. Das bedeutet, dass Summe und Produkt natürlicher Zahlen natürliche Zahlen sind.

2. Die Differenz zweier natürlicher Zahlen ist aber nicht mehr immer eine natürliche Zahl.

(Geben Sie Beispiele: 5 - 5 = 0; 5 - 7 = - 2, die Zahlen 0 und - 2 sind nicht natürlich).

Somit führt das Ergebnis der Subtraktion zweier identischer natürlicher Zahlen zum Konzept der Null und der Einführung Mengen von nicht negativen ganzen Zahlen

Z0 = (0; 1; 2;...).

3. Um die Subtraktionsoperation durchführbar zu machen, geben Sie negative Ganzzahlen ein, d. h. Zahlen, die den natürlichen Zahlen entgegengesetzt sind. Somit wird ein Satz von ganzen Zahlen erhalten Z={...; -3; -2; -1; 0; 1; 2;...}.

Um die Operation der Division durch eine beliebige Zahl ungleich Null durchführbar zu machen, ist es notwendig, der Menge aller ganzen Zahlen die Menge aller positiven und hinzuzufügen negative Brüche. Das Ergebnis ist Menge rationaler Zahlen Q=.

Wenn du vier machst Rechenoperationen(außer bei Division durch Null) über rationale Zahlen erhält man immer rationale Zahlen.

4. Jede rationale Zahl kann als periodischer Dezimalbruch dargestellt werden.

Erinnern wir uns, was ist periodischer Bruch. Dies ist ein unendlicher Dezimalbruch, bei dem sich ab einer bestimmten Dezimalstelle dieselbe Ziffer oder mehrere Ziffern wiederholen - die Periode des Bruchs. Zum Beispiel 0,3333…= 0,(3);

1,057373…=1,05(73).

Diese Brüche werden so gelesen: „0 ganze und 3 im Punkt“, „1 ganze, 5 Hundertstel und 73 im Punkt“.

Wir schreiben rationale Zahlen als unendlich periodischen Dezimalbruch:

natürliche Zahl 25 = 25,00…= 25,(0);

ganze Zahl -7 = -7,00…= -7,(0);

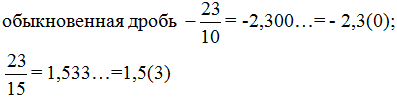
(Wir verwenden den Eckenteilungsalgorithmus).

5. Auch die Umkehrung gilt: Jeder unendliche periodische Dezimalbruch ist Rationale Zahl, da es als Bruch dargestellt werden kann, wobei m eine ganze Zahl ist, ist n eine natürliche Zahl.

Betrachten Sie ein Beispiel:

1) Wenn x \u003d 0,2 (18) mit 10 multipliziert wird, erhalten wir 10x \u003d 2,1818 ... (Sie müssen den Bruch mit 10 n multiplizieren, wobei n die Anzahl der Dezimalstellen ist, die in der Aufzeichnung dieses Bruchs enthalten sind zum Zeitraum: x10 n).

2) Wir multiplizieren beide Seiten der letzten Gleichheit mit 100, finden wir

1000x = 218,1818…(Multiplikation mit 10 k , wobei k die Anzahl der Ziffern in der Periode x10 n 10 k = x10 n+k ist).

3) Subtrahieren wir von Gleichheit (2) Gleichheit (1), erhalten wir 990x = 216, x = .

Praktischer Teil.

1. Schreiben Sie als Dezimalbruch:

1) - auf dem Brett;

3) - an der Tafel schreibt ein Schüler die Entscheidung auf, die anderen entscheiden auf dem Boden, dann kontrollieren sie sich gegenseitig;

4) - Unter Diktat führt jeder die Aufgabe aus und einer spricht laut.

2. Führen Sie Aktionen aus und schreiben Sie das Ergebnis als Dezimalbruch:

1) - auf dem Brett;

3) - Unter Diktat führt jeder die Aufgabe aus und einer spricht laut;

5) - selbstständig mit anschließender Prüfung.

3. Schreiben Sie als gemeinsamer Bruchteil unendlich dezimal:

6) -2.3(82) - Der Lehrer zeigt die Lösung auf der Tafel, basierend auf dem Algorithmus.