FOLIE 4

Dokumentinhalt anzeigen
"Wie man Wahrscheinlichkeitsprobleme löst"

Mitrofanova Snezhana Viktorovna, MBOU „Werchowskaja-Schule“ Oblast Wologda

Gegenstand: Workshop zur Lösung Probleme.

FOLIE 1

Wie löse ich Wahrscheinlichkeitsprobleme?

Wahrscheinlichkeit. Was ist das?

FOLIE 2

Wahrscheinlichkeitstheorie, wie der Name schon sagt, beschäftigt sich mit Wahrscheinlichkeiten. Wir sind von vielen Dingen und Phänomenen umgeben, über die es unmöglich ist, genaue Vorhersagen zu treffen, egal wie fortgeschritten die Wissenschaft ist. Wir wissen nicht, welche Karte wir zufällig aus dem Stapel ziehen oder wie viele Tage es im Mai regnen wird, aber wir haben einige Weitere Informationen können wir Vorhersagen treffen und die Wahrscheinlichkeiten dieser zufälligen Ereignisse berechnen.

Damit stehen wir vor dem Grundkonzept Zufälliges Ereignis - es handelt sich um Phänomene, deren Verhalten nicht vorhergesagt werden kann, oder es handelt sich um ein Experiment, dessen Ergebnis nicht im Voraus berechnet werden kann usw. Es sind die Wahrscheinlichkeiten von Ereignissen, die eingerechnet werden typische Aufgaben BENUTZEN.

FOLIE 2 (WIEDER EINS)

Wahrscheinlichkeit- Dies ist streng genommen eine Funktion, die Werte von 0 bis 1 annimmt und ein bestimmtes zufälliges Ereignis charakterisiert.

Dann verwenden wir Beispieldiagramm, die verwendet werden sollte, um den Standard zu lösen Lernziele um die Wahrscheinlichkeit eines zufälligen Ereignisses zu berechnen,

FOLIE 3

und dann unten mit Beispielen werde ich seine Anwendung veranschaulichen.

Finden Sie die Hauptfrage der Aufgabe (finden Sie heraus, was das Ergebnis der Aufgabe ist, finden Sie günstige Ergebnisse.)

Wählen Sie eine Formel (oder mehrere) für die Lösung aus.

FOLIE 4

WARUM LESEN WIR AUFGABEN SORGFÄLTIG?

Von den 20 in der Prüfung angebotenen Tickets kann der Student nur 17 beantworten. Wie groß ist die Wahrscheinlichkeit, dass der Student das zufällig ausgewählte Ticket beantworten kann?

Von den 20 in der Prüfung angebotenen Tickets kann der Student nur 17 beantworten. Wie groß ist die Wahrscheinlichkeit, dass der Student das zufällig ausgewählte Ticket nicht beantworten kann?

FOLIE 5,6,7

FOLIE 8.9

FOLIE 10

Aufgabe 1.

FOLIE 11

Entscheidung.

FOLIE 12

0,5 0,25 = 0,125

FOLIE 13

Aufgabe 2.

FOLIE 14

Entscheidung.

P(M)=P(ABD)+P(ABE)+P(ACF)

FOLIE 15

FOLIE 16

FOLIE 17

FOLIE 18

FOLIE 19, 20

Aufgabe 4.

Präsentationsinhalte anzeigen
"Präsentation"

Wie man Probleme löst

auf Wahrscheinlichkeit?

Mitrofanova Snezhana Viktorovna,

Mathematiklehrer

MBOU "Werchowskaja-Schule"

Region Wologda

Wahrscheinlichkeit Was ist das? ?

Wahrscheinlichkeit ist eine Funktion, die Werte von 0 bis 1 annimmt.

Ungefähres Schema , die verwendet werden sollten, um pädagogische Standardaufgaben zur Berechnung der Wahrscheinlichkeit zu lösen:

Finden Sie die Hauptfrage des Problems

Die Formel (oder mehrere) für die Lösung wird ausgewählt.

Von den 20 in der Prüfung angebotenen Tickets kann der Student nur 17 beantworten. Wie groß ist die Wahrscheinlichkeit, dass der Student das zufällig ausgewählte Ticket beantworten kann?

Von den 20 in der Prüfung angebotenen Tickets kann der Student nur 17 beantworten. Wie groß ist die Wahrscheinlichkeit, dass der Student das zufällig ausgewählte Ticket nicht beantworten kann?

Wahrscheinlichkeit Veranstaltungen ist das Verhältnis der Anzahl der Ergebnisse, die sein Eintreten begünstigen, zur Anzahl aller Ergebnisse (inkompatibel, einzig möglich und gleichermaßen möglich):

Probleme, die durch Konstruktion eines Wahrscheinlichkeitsbaums gelöst werden.

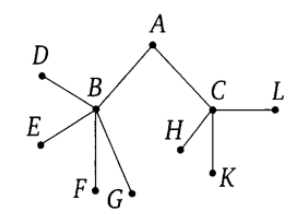
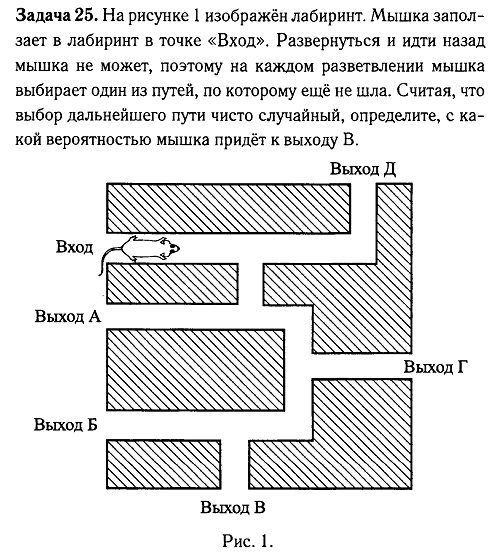
Aufgabe 1. Pavel Ivanovich macht einen Spaziergang von Punkt A entlang der Wege des Parks. An jeder Gabelung wählt er zufällig die nächste Spur, ohne zurückzugehen.Das Gleisdiagramm ist in der Abbildung dargestellt. Berechnen Sie die Wahrscheinlichkeit, dass Pavel Ivanovich Punkt G trifft.

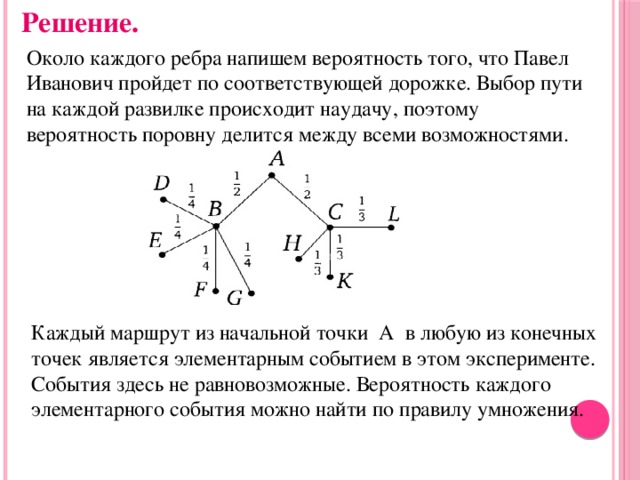
Entscheidung.

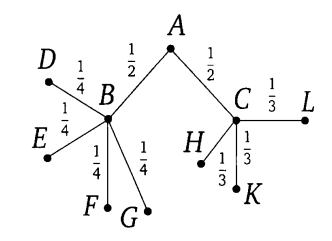
Schreiben Sie neben jede Kante die Wahrscheinlichkeit, dass Pavel Ivanovic wird passen entlang der entsprechenden Spur. Die Wahl des Weges an jeder Gabelung erfolgt zufällig, sodass die Wahrscheinlichkeit gleichmäßig auf alle Möglichkeiten aufgeteilt wird.

Jeder Weg vom Startpunkt A zu einem der Endpunkte ist ein elementares Ereignis in diesem Experiment. Ereignisse hier sind nicht gleich wahrscheinlich. Die Wahrscheinlichkeit jedes elementaren Ereignisses kann durch die Multiplikationsregel gefunden werden.

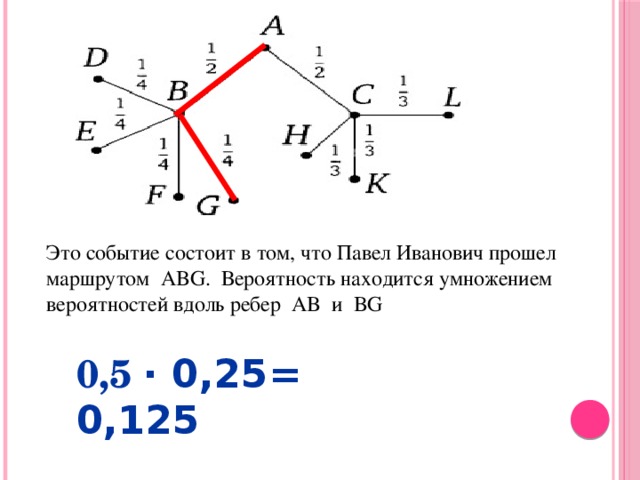
Dieses Ereignis besteht darin, dass Pavel Ivanovich die ABG-Route passiert hat. Die Wahrscheinlichkeit wird ermittelt, indem die Wahrscheinlichkeiten entlang der Kanten AB und BG multipliziert werden

0,5 0,25 = 0,125

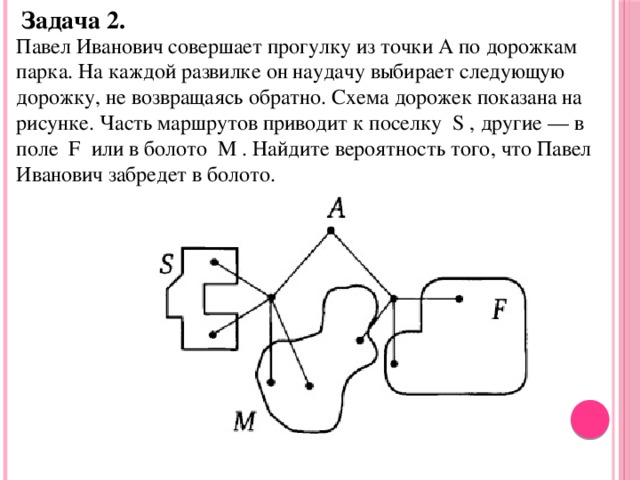
Aufgabe 2.

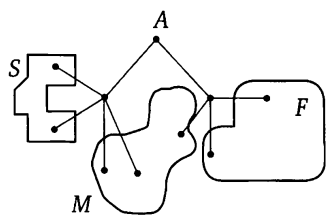
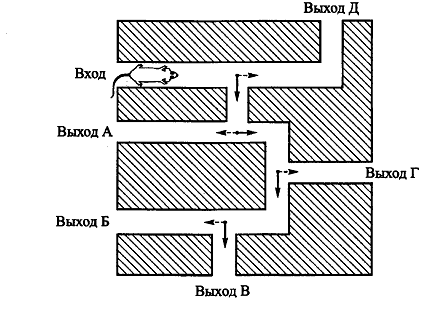
Pavel Ivanovich macht einen Spaziergang von Punkt A entlang der Wege des Parks. An jeder Gabelung wählt er zufällig den nächsten Weg, ohne zurückzugehen. Das Gleisbild ist in der Abbildung dargestellt. Einige der Routen führen zum Dorf S, andere zum Feld F oder zum Sumpf M. Finden Sie die Wahrscheinlichkeit heraus, dass Pavel Ivanovich in den Sumpf wandert.

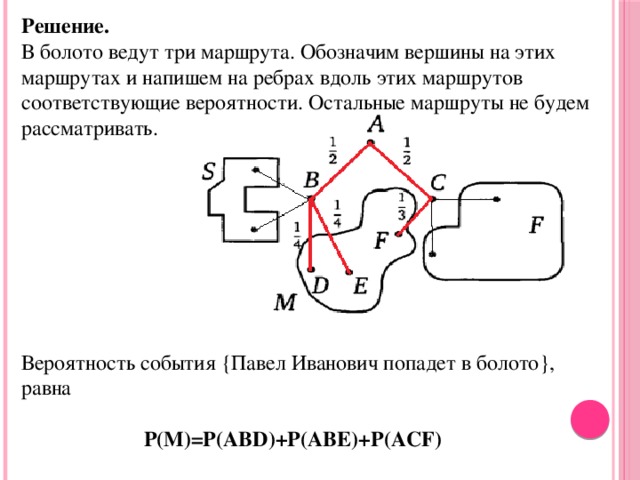
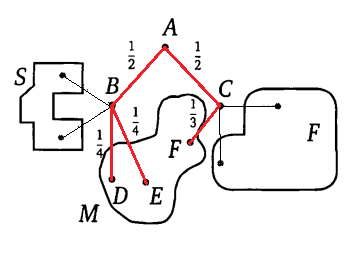
Entscheidung. Drei Wege führen in den Sumpf. Wir bezeichnen die Knoten auf diesen Routen und schreiben die entsprechenden Wahrscheinlichkeiten auf die Kanten entlang dieser Routen. Andere Strecken werden nicht berücksichtigt.

Die Wahrscheinlichkeit eines Ereignisses (Pavel Ivanovich wird in einen Sumpf fallen) ist gleich

P(M)=P(ABD)+P(ABE)+P(ACF)

Antworten: 0,125

Aufgabe 4. Zwei Fabriken derselben Firma stellen dieselben Mobiltelefone her.

Die erste Fabrik produziert 30% aller Telefone dieser Marke und die zweite - den Rest der Telefone.

Es ist bekannt, dass 1 % aller von der ersten Fabrik hergestellten Telefone versteckte Mängel aufweisen und 1,5 % aller von der zweiten Fabrik hergestellten Telefone.

Finden Sie die Wahrscheinlichkeit heraus, dass ein in einem Geschäft gekauftes Telefon dieser Marke einen versteckten Defekt hat.

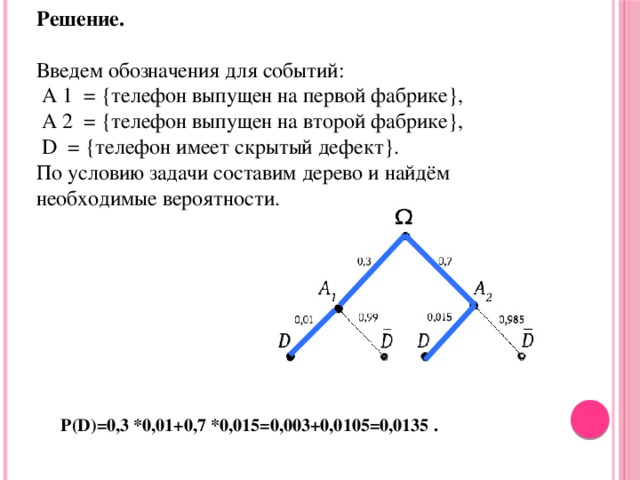
Entscheidung. Lassen Sie uns die Notation für die Ereignisse einführen: A 1 = (das Telefon wird in der ersten Fabrik freigegeben), A 2 = (das Telefon wird in der zweiten Fabrik freigegeben), D = (das Telefon hat einen versteckten Defekt). Entsprechend der Bedingung des Problems werden wir einen Baum erstellen und die notwendigen Wahrscheinlichkeiten finden.

P(D)=0,3*0,01+0,7*0,015=0,003+0,0105=0,0135 .

USE TEST - 2017 IN MATHEMATIK

PROFILSTUFE

MÖGLICHKEIT 4

Teil 1

1. Durch Tarifplan Unternehmen „Just Like Day“. zellulare Kommunikation zieht jeden Abend 18 Rubel vom Konto des Abonnenten ab. Wenn auf dem Konto weniger als 18 Rubel übrig sind, wird die Nummer am nächsten Morgen gesperrt, bis das Konto wieder aufgefüllt ist. Heute Morgen hatte Lisa 500 Rubel auf ihrem Konto. Wie viele Tage (einschließlich heute) kann sie ihr Telefon benutzen, ohne ihr Konto aufzuladen?

2. Wenn die Taschenlampe eingeschaltet ist, wird die Batterie allmählich entladen und die Spannung eingespeist elektrische Schaltung die Taschenlampe fällt. Die Abbildung zeigt die Abhängigkeit der Spannung im Stromkreis von der Betriebszeit der Taschenlampe. Auf der horizontale Achse zeigt die Betriebszeit der Taschenlampe in Stunden an, vertikale Achse- Spannung in Volt. Bestimmen Sie anhand der Abbildung, welche Spannung nach 15 Betriebsstunden der Taschenlampe im Stromkreis vorhanden sein wird. Geben Sie Ihre Antwort in Volt an.

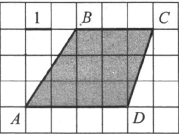
3. Finden Sie den Bereich Trapez ABCD gezeigt auf kariertes Papier mit einer Zellengröße von 1 x 1 (siehe Abb.).

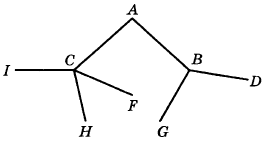
4. Pavel Ivanovich macht einen Spaziergang von Punkt A entlang der Wege des Parks. An jeder Gabelung wählt er zufällig den nächsten Weg, ohne zurückzugehen. Das Gleisbild ist in der Abbildung dargestellt. Berechnen Sie die Wahrscheinlichkeit, dass Pavel Ivanovich Punkt G trifft.

5. Finde die Wurzel der Gleichung

6. Das Viereck ABCD ist in einen Kreis eingeschrieben. Der Winkel ABC beträgt 132°, der Winkel ABD 61°. Finden Sie den Winkel CAD. Geben Sie Ihre Antwort in Grad an.

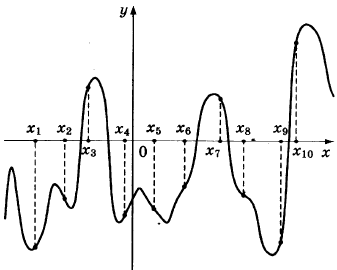
7. Die Abbildung zeigt ein Diagramm der Funktion y \u003d f (x) und zehn Punkte auf der x-Achse: x 1, x 2, x 3, ..., x 10. An wie vielen dieser Punkte ist die Ableitung f"(x) der Funktion f(x) positiv?

8. Eine Betonkugel wiegt 0,5 Tonnen, wie viele Tonnen wiegt die Kugel zweimal? größerer Radius aus dem gleichen Beton?

Teil 2

9. Suchen Sie den Wert des Ausdrucks

10. Verhältnis nützliche Aktion ein Motor wird durch die Formel bestimmt

Bei welchem ​​Wert der Heizungstemperatur T 1 (in Grad Kelvin) beträgt der Wirkungsgrad dieses Motors 80 %, wenn die Kühlschranktemperatur T 2 = 200 K ist?

11. Hosen sind 30 % teurer als ein Hemd und 22 % billiger als eine Jacke. Um wie viel Prozent ist das Hemd billiger als die Jacke?

12. Finden Höchster Wert Funktionen

y \u003d 13x - 13tg x - 18

auf dem Segment.

13. a) Lösen Sie die Gleichung

b) Finden Sie alle Wurzeln dieser Gleichung, Zugehörigkeit zum Segment [−3; 1].

14. Rechts dreieckiges Prisma ABCA 1 B 1 C 1 Basisseite AB = 7√3, und Seitenrippe AA 1 = 8.

a) Beweisen Sie, dass die Ebene BCA 1 senkrecht zu der Ebene steht, die durch die Kante AA 1 und den Mittelpunkt der Kante B 1 C 1 verläuft.

b) Finden Sie die Tangente des Winkels zwischen den Ebenen BCA 1 und BB 1 C 1.

15. Lösen Sie die Ungleichung

16. Auf AC- und BC-Seiten Dreieck ABC die Quadrate ACDE und BFKC werden außerhalb des Dreiecks konstruiert. Punkt M ist der Mittelpunkt der Seite AB.

a) Beweisen Sie, dass CM = 1/2 DK.

b) Finden Sie den Abstand von Punkt M zu den Mittelpunkten der Quadrate, wenn AC = 14, BC = 16 und Winkel ACB = 150°.

17. In zwei Regionen gibt es jeweils 50 Arbeiter, von denen jeder bereit ist, 10 Stunden am Tag in der Gewinnung von Aluminium oder Nickel zu arbeiten. In der ersten Region produziert ein Arbeiter 0,2 kg Aluminium oder 0,1 kg Nickel pro Stunde. Im zweiten Abbaugebiet X kg Aluminium pro Tag erfordert x 2 Arbeitsstunden und für die Extraktion beim kg Nickel pro Tag werden für 2 Arbeitsstunden benötigt.

Beide Regionen liefern das geförderte Metall an das Werk, in dem eine Legierung aus Aluminium und Nickel für den Bedarf der Industrie hergestellt wird, in der 1 kg Aluminium 2 kg Nickel entspricht. Gleichzeitig vereinbaren die Regionen untereinander, Metalle abzubauen, damit das Werk produzieren kann die größte Zahl Legierung. Wie viele Kilogramm Legierung kann die Anlage unter solchen Bedingungen täglich produzieren?

"Punktfluktuation" - Zwischensituation. Die Bewegung ist gedämpft und aperiodisch. 5. Lineare Schwingungen. 7. Freie Schwingungen mit viskosem Widerstand. Allgemeine Lösung = gemeinsame Entscheidung+ private Lösung homogen heterogen. 1. Beispiele für Schwingungen. Harmonische treibende Kraft. Freie Schwingungen, die durch eine treibende Kraft verursacht werden.

"Die Ableitung der Funktion an einem Punkt" - Was ist der Wert der Ableitung der Funktion y \u003d f (x) an Punkt B? Die Abbildung zeigt einen Graphen der Ableitung y= f‘(x) der Funktion f(x), die auf dem Intervall (-3;3) definiert ist. Welchen Wert nimmt die Ableitung der Funktionen y= f(x) im Punkt A an? Welchen Winkel bildet die Tangente an den Funktionsgraphen mit der positiven Richtung der x-Achse?

"Kritische Punkte der Funktion" - Unter den kritischen Punkten gibt es Extrempunkte. Notwendige Bedingung extrem. Kritische Punkte Funktionen Extrempunkte. Definition. Extrempunkte (Wiederholung). Aber wenn f "(x0) = 0, dann ist es nicht notwendig, dass der Punkt x0 ein Extremumpunkt sein wird. Beispiele. Kritische Punkte.

"Punktkoordinaten" - Symmetrie des Punktes um die Abszissenachse (Ox). Der Körper der Eidechse ist symmetrisch zu einer geraden Linie. Der menschliche Körper hat eine Symmetrieachse. Auch in der Natur gehorcht der Aufbau tierischer Körper den Gesetzen der Symmetrie. Punkt B (3; 6) ist symmetrisch zu Punkt B (3; - 6), der sich unterhalb der x-Achse befindet. Fazit: Semirichnik ist eine seltene Pflanze, aber die sieben Blütenblätter der Blume haben bilaterale Symmetrie.

"Südafrikanische Nationalparks" - "Reise nach Republik von südafrika". In der Nähe befindet sich der berühmte Wasserfall Tugela (948 m) mit fünf Kaskaden. Der dritte Tag Nationalparks und Reserven. Erster Tag Die Hauptstadt von Südafrika. Die Kosten für Hotelzimmer beginnen bei 400 $. Ein Regenbogen leuchtet in einer Wasserstaubwolke, die 100 Meter hoch aufsteigt.

"Vier bemerkenswerte Punkte des Dreiecks" - Die Senkrechte, die von der Spitze des Dreiecks auf die Linie fällt, die die gegenüberliegende Seite enthält, wird genannt. Höhe. Der Median eines Dreiecks. Problem Nummer 1. Die Höhe des Dreiecks. Segment AN ist eine Senkrechte, die von Punkt A auf Linie a fällt, wenn. Ein Liniensegment, das einen Scheitelpunkt mit einem Mittelpunkt verbindet gegenüberliegende Seite, wird genannt.

Der Rentner geht auf den Wegen des Parks spazieren. An jeder Gabelung wählt er zufällig den nächsten Weg, ohne zurückzugehen. Das Gleisbild ist in der Abbildung dargestellt. Der Rentner beginnt bei Punkt A zu laufen. Berechnen Sie die Wahrscheinlichkeit, dass er zu Punkt F kommt.

Die Lösung des Problems

BEIM diese Lektion Es wird ein Beispiel für die Lösung des Problems mithilfe der Wahrscheinlichkeitstheorie gezeigt. Für erfolgreiche Lösung Problem, müssen Sie wissen, dass die Wahrscheinlichkeit der Wahrscheinlichkeitsgrad des Eintretens eines Ereignisses oder das Verhältnis der Anzahl günstiger Ergebnisse zur Gesamtzahl möglicher Ergebnisse ist. Somit wird die Lösung des Problems auf die Anwendung der Formel der Wahrscheinlichkeitstheorie reduziert: , wobei eine günstige Anzahl von Ergebnissen ist, und - Gesamtzahl Ergebnisse. Die Lösung des Problems ist in Stufen unterteilt. Zuerst wird die Wahrscheinlichkeit bestimmt, dass der Rentner den Spaziergang genau vom Pfad aus beginnt, während Dann wird die Wahrscheinlichkeit berechnet, dass der Spaziergang entlang der Route fortgesetzt wird, während Durch den Wahrscheinlichkeitsmultiplikationssatz: die Wahrscheinlichkeit, mehrere Ereignisse zu erzeugen, gleich dem ist Produkt der Wahrscheinlichkeiten dieser Ereignisse und der Wahrscheinlichkeit jedes folgenden Ereignisses. Die Reihenfolge des Ereignisses wird unter der Annahme berechnet, dass alle vorherigen Ereignisse stattgefunden haben. Somit ist das Ergebnis der Produktberechnung die gewünschte Antwort.

Diese Aufgabe ähnelt Aufgaben des Typs B6, kann also erfolgreich als Vorbereitung auf die Prüfung in Mathematik eingesetzt werden.