Power-Funktion, seine Eigenschaften und Diagramm Demomaterial Unterrichtsvortrag Funktionsbegriff. Funktionseigenschaften. Potenzfunktion, ihre Eigenschaften und ihr Diagramm. Klasse 10 Alle Rechte vorbehalten. Urheberrecht mit Urheberrecht mit

Unterrichtsfortschritt: Wiederholung. Funktion. Funktionseigenschaften. Neues Material lernen. 1. Definition einer Potenzfunktion Definition einer Potenzfunktion 2. Eigenschaften und Graphen von Potenzfunktionen Eigenschaften und Graphen von Potenzfunktionen. Konsolidierung des studierten Materials. Verbale Zählung. Verbale Zählung. Zusammenfassung der Lektion. Hausaufgaben Hausaufgaben.

Definitionsbereich und Wertebereich der Funktion Alle Werte der unabhängigen Variablen bilden den Definitionsbereich der Funktion x y=f(x) f Definitionsbereich der Funktion Definitionsbereich der Funktion Alle Werte, die die abhängige Variable annimmt, bilden den Definitionsbereich der Funktion Funktion. Funktionseigenschaften

Graph einer Funktion Gegeben sei eine Funktion mit xY y x.75 3 0,6 4 0,5 Der Graph einer Funktion ist die Menge aller Punkte der Koordinatenebene, deren Abszissen gleich den Werten des Arguments sind, und die Ordinaten sind gleich den entsprechenden Werten der Funktion. Funktion. Funktionseigenschaften

Y x Definitionsbereich und Bereich der Funktion 4 y=f(x) Definitionsbereich der Funktion: Definitionsbereich der Funktion: Funktion. Funktionseigenschaften

Gerade Funktion y x y=f(x) Graph gleiche Funktion symmetrisch zur y-Achse Die Funktion y=f(x) wird auch dann aufgerufen, wenn f(-x) = f(x) für beliebige x aus dem Definitionsbereich der Funktion Function. Funktionseigenschaften

Ungerade Funktion y x y=f(x) Graph komische Funktion symmetrisch zum Ursprung O(0;0) Die Funktion y=f(x) heißt ungerade, falls f(-x) = -f(x) für beliebige x aus dem Definitionsbereich der Funktion Function. Funktionseigenschaften

Definition einer Potenzfunktion Eine Funktion, bei der p eine gegebene reelle Zahl ist, heißt Potenzfunktion. p y \u003d x p P \u003d x y 0 Unterrichtsfortschritt

Potenzfunktion x y 1. Der Definitionsbereich und der Wertebereich von Potenzfunktionen der Form, wobei n ist natürliche Zahl, sind alles reelle Zahlen. 2. Diese Funktionen sind ungerade. Ihr Graph ist bezüglich des Ursprungs symmetrisch. Eigenschaften und Diagramme der Potenzfunktion

Potenzfunktionen mit einem rationalen positiven Exponenten Definitionsbereich - alle positive Zahlen und die Zahl 0. Der Funktionsumfang mit einem solchen Exponenten sind auch alle positiven Zahlen und die Zahl 0. Diese Funktionen sind weder gerade noch ungerade. y x Eigenschaften und Graphen der Potenzfunktion

Potenzfunktion mit rational negativer Indikator. Der Definitionsbereich und der Bereich solcher Funktionen sind alle positive Zahlen. Die Funktionen sind weder gerade noch ungerade. Solche Funktionen nehmen über ihren gesamten Definitionsbereich ab. y x Eigenschaften und Graphen der Potenzfunktion Unterrichtsfortschritt

1. Potenzfunktion, ihre Eigenschaften und ihr Diagramm;

2. Transformationen:

Parallelübertragung;

Symmetrie um die Koordinatenachsen;

Symmetrie um den Ursprung;

Symmetrie um die Gerade y = x;

Strecken und Schrumpfen entlang der Koordinatenachsen.

3. Eine Exponentialfunktion, ihre Eigenschaften und ihr Graph, ähnliche Transformationen;

4. Logarithmische Funktion, ihre Eigenschaften und ihr Diagramm;

5. Trigonometrische Funktion, ihre Eigenschaften und ihr Graph, ähnliche Transformationen (y = sin x; y = cos x; y = tg x);

Funktion: y = x\n - seine Eigenschaften und Graph.

Potenzfunktion, ihre Eigenschaften und ihr Diagramm

y \u003d x, y \u003d x 2, y \u003d x 3, y \u003d 1 / x etc. Alle diese Funktionen sind Sonderfälle der Potenzfunktion, also der Funktion y = xp, wobei p eine gegebene reelle Zahl ist.
Die Eigenschaften und der Verlauf einer Potenzfunktion hängen im Wesentlichen von den Eigenschaften einer Potenz mit reellem Exponenten ab, insbesondere von deren Werten x und p macht Sinn XP. Kommen wir zu einer ähnlichen Überlegung. verschiedene Anlässe abhängig von
Exponent p.

1. Indikator p = 2n ist eine gerade natürliche Zahl.

y=x2n, wo n ist eine natürliche Zahl und hat folgende Eigenschaften:

• der Definitionsbereich sind alle reellen Zahlen, dh die Menge R;
• Wertesatz - nicht negative Zahlen, d. h. y ist größer oder gleich 0;
• Funktion y=x2n sogar, weil x2n = (-x)2n
• Die Funktion nimmt im Intervall ab x< 0 und im Intervall ansteigend x > 0.

Funktionsgraph y=x2n hat die gleiche Form wie beispielsweise der Graph einer Funktion y=x4.

2. Anzeige p = 2n - 1- ungerade natürliche Zahl

In diesem Fall die Potenzfunktion y=x2n-1, wobei eine natürliche Zahl ist, hat die folgenden Eigenschaften:

• Definitionsbereich - Menge R;
• Wertesatz - R setzen;
• Funktion y=x2n-1 seltsam, weil (- x) 2n-1= x 2n-1 ;
• die Funktion nimmt auf der gesamten reellen Achse zu.

Funktionsgraph y=x2n-1 y=x3.

3. Anzeige p=-2n, wo n- natürliche Zahl.

In diesem Fall die Potenzfunktion y=x-2n=1/x2n hat folgende Eigenschaften:

• Wertesatz - positive Zahlen y>0;
• Funktion y = 1/x2n sogar, weil 1/(-x) 2n= 1/x2n;
• die Funktion wächst im Intervall x0.

Graph der Funktion y = 1/x2n hat die gleiche Form wie beispielsweise der Graph der Funktion y = 1/x2.

4. Anzeige p = -(2n-1), wo n- natürliche Zahl.
In diesem Fall die Potenzfunktion y=x-(2n-1) hat folgende Eigenschaften:

• der Definitionsbereich ist die Menge R, außer für x = 0;
• Wertesatz - R setzen, außer y = 0;
• Funktion y=x-(2n-1) seltsam, weil (- x)-(2n-1) = -x-(2n-1);
• Die Funktion nimmt in den Intervallen ab x< 0 und x > 0.

Funktionsgraph y=x-(2n-1) hat die gleiche Form wie zum Beispiel der Graph der Funktion y = 1/x3.

Das methodisches Material dient nur als Referenz und gilt für eine Vielzahl Themen. Der Artikel gibt einen Überblick über die Graphen der wichtigsten Elementarfunktionen und berücksichtigt die wichtigste Frage – wie man richtig und SCHNELL ein Diagramm erstellt. Während des Studiums höhere Mathematik Ohne die Graphen der elementaren Grundfunktionen zu kennen, wird es schwierig, daher ist es sehr wichtig, sich daran zu erinnern, wie die Graphen einer Parabel, Hyperbel, Sinus, Cosinus usw. aussehen, sich an einige Funktionswerte zu erinnern. Wir werden auch über einige Eigenschaften der Hauptfunktionen sprechen.

Ich erhebe keinen Anspruch auf Vollständigkeit und wissenschaftliche Gründlichkeit der Materialien, der Schwerpunkt wird in erster Linie auf die Praxis gelegt - die Dinge, mit denen man muss sich buchstäblich auf Schritt und Tritt stellen, in jedem Thema der höheren Mathematik. Charts für Dummies? Das können Sie sagen.

Von zahlreiche Anfragen Leser anklickbares Inhaltsverzeichnis:

Zusätzlich gibt es ein ultrakurzes Abstract zum Thema
– Meistere 16 Arten von Diagrammen, indem du SECHS Seiten studierst!

Im Ernst, sechs, sogar ich selbst war überrascht. Diese Zusammenfassung enthält verbesserte Grafiken und ist gegen eine geringe Gebühr erhältlich, eine Demoversion kann angezeigt werden. Es ist bequem, die Datei auszudrucken, damit die Grafiken immer zur Hand sind. Danke für die Unterstützung des Projekts!

Und wir fangen gleich an:

Wie baut man Koordinatenachsen richtig?

In der Praxis werden Tests fast immer von Studenten in separaten Notizbüchern erstellt, die in einem Käfig ausgekleidet sind. Warum brauchen Sie karierte Markierungen? Schließlich kann die Arbeit im Prinzip auf A4-Blättern erledigt werden. Und der Käfig ist nur für die hochwertige und genaue Gestaltung der Zeichnungen erforderlich.

Jede Zeichnung eines Funktionsgraphen beginnt mit Koordinatenachsen.

Zeichnungen sind zweidimensional und dreidimensional.

Betrachten wir zunächst den zweidimensionalen Fall Kartesisch rechteckiges System Koordinaten:

1) Wir zeichnen Koordinatenachsen. Die Achse wird aufgerufen x-Achse , und die Achse y-Achse . Wir versuchen immer, sie zu zeichnen sauber und nicht schief. Die Pfeile sollten auch nicht dem Bart von Papa Carlo ähneln.

2) Wir signieren die Achsen Großbuchstaben"x" und "y". Vergessen Sie nicht, die Äxte zu unterschreiben.

3) Stellen Sie die Skalierung entlang der Achsen ein: Ziehe null und zwei Einsen. Beim Zeichnen ist der bequemste und gebräuchlichste Maßstab: 1 Einheit = 2 Zellen (Zeichnung links) - halten Sie sich möglichst daran. Ab und zu kommt es aber vor, dass die Zeichnung nicht auf ein Notizbuchblatt passt – dann verkleinern wir den Maßstab: 1 Einheit = 1 Zelle (rechte Zeichnung). Selten, aber es kommt vor, dass der Maßstab der Zeichnung noch weiter verkleinert (oder vergrößert) werden muss

Kritzeln Sie NICHT mit einem Maschinengewehr ... -5, -4, -3, -1, 0, 1, 2, 3, 4, 5, .... Für Koordinatenebene ist kein Denkmal für Descartes, und der Student ist keine Taube. Wir stellen Null und zwei Einheiten entlang der Achsen. Manchmal anstatt Einheiten ist es praktisch, andere Werte zu „erfassen“, zum Beispiel „zwei“ auf der Abszissenachse und „drei“ auf der Ordinatenachse – und dieses System (0, 2 und 3) wird auch das Koordinatengitter eindeutig festlegen.

Es ist besser, die geschätzten Abmessungen der Zeichnung abzuschätzen, BEVOR die Zeichnung gezeichnet wird.. Wenn die Aufgabe beispielsweise das Zeichnen eines Dreiecks mit Eckpunkten , , erfordert, dann ist es ziemlich klar, dass der beliebte Maßstab 1 Einheit = 2 Zellen nicht funktioniert. Wieso den? Schauen wir uns den Punkt an - hier müssen Sie fünfzehn Zentimeter nach unten messen, und die Zeichnung passt offensichtlich nicht (oder kaum) auf ein Notizbuchblatt. Daher wählen wir sofort einen kleineren Maßstab 1 Einheit = 1 Zelle.

By the way, etwa Zentimeter und Notebook-Zellen. Stimmt es, dass in 30 Notebook-Zellen 15 Zentimeter Platz finden? Messen Sie in einem Notizbuch für Zinsen 15 Zentimeter mit einem Lineal. In der UdSSR war das vielleicht wahr ... Es ist interessant festzustellen, dass die Ergebnisse (in Zellen) unterschiedlich sind, wenn Sie dieselben Zentimeter horizontal und vertikal messen! Genau genommen sind moderne Notizbücher nicht kariert, sondern rechteckig. Es mag wie Unsinn erscheinen, aber in solchen Situationen zum Beispiel einen Kreis mit einem Kompass zu zeichnen, ist sehr unpraktisch. Um ehrlich zu sein, fängt man in solchen Momenten an, über die Richtigkeit von Genosse Stalin nachzudenken, der wegen Hackerarbeiten in der Produktion in Lager geschickt wurde, ganz zu schweigen von der heimischen Automobilindustrie, fallenden Flugzeugen oder explodierenden Kraftwerken.

Apropos Qualität, bzw kurze Empfehlung durch Briefpapier. Bis heute sind die meisten Notebooks im Angebot, böse Worte Ganz zu schweigen von der kompletten Scheiße. Aus dem Grund, dass sie nass werden, und zwar nicht nur von Gelstiften, sondern auch von Kugelschreibern! Papier sparen. Zur Freigabe Kontrolle funktioniert Ich empfehle die Verwendung der Notizbücher der Archangelsk Pulp and Paper Mill (18 Blatt, Käfig) oder Pyaterochka, obwohl dies teurer ist. Es ist ratsam, einen Gelschreiber zu wählen, selbst die billigste chinesische Gelmine ist viel besser als ein Kugelschreiber, der entweder Papier verschmiert oder zerreißt. Die einzige "Konkurrenz" Kugelschreiber in meiner Erinnerung ist "Erich Krause". Sie schreibt klar, schön und stabil – entweder mit vollem Vorbau oder mit fast leerem Vorbau.

Zusätzlich: ein rechtwinkliges Koordinatensystem mit den Augen sehen Analytische Geometrie im Artikel behandelt Lineare (Nicht-) Abhängigkeit von Vektoren. Vektorbasis, genaue InformationÜber Quartiere koordinieren finden Sie im zweiten Absatz der Lektion Lineare Ungleichungen.

3D-Fall

Hier ist es fast genauso.

1) Wir zeichnen Koordinatenachsen. Standard: Achse anwenden – nach oben gerichtet, Achse – nach rechts gerichtet, Achse – nach unten nach links streng in einem Winkel von 45 Grad.

2) Wir signieren die Achsen.

3) Stellen Sie die Skala entlang der Achsen ein. Maßstab entlang der Achse - zweimal kleiner als der Maßstab entlang der anderen Achsen. Beachten Sie auch, dass ich in der rechten Zeichnung eine nicht standardmäßige "Serife" entlang der Achse verwendet habe (diese Möglichkeit wurde oben bereits erwähnt). Aus meiner Sicht ist es genauer, schneller und ästhetischer – man muss nicht unter dem Mikroskop die Mitte der Zelle suchen und die Einheit bis zum Ursprung „modellieren“.

Wenn Sie erneut eine 3D-Zeichnung erstellen, geben Sie der Skalierung Priorität
1 Einheit = 2 Zellen (Zeichnung links).

Wozu all diese Regeln? Regeln sind dazu da, gebrochen zu werden. Was soll ich jetzt machen. Tatsache ist, dass die nachfolgenden Zeichnungen des Artikels von mir in Excel erstellt werden und die Koordinatenachsen aus der Sicht falsch aussehen richtige Gestaltung. Ich könnte alle Diagramme von Hand zeichnen, aber es ist wirklich beängstigend, sie zu zeichnen, da Excel zögert, sie viel genauer zu zeichnen.

Graphen und grundlegende Eigenschaften elementarer Funktionen

Die lineare Funktion ist durch die Gleichung gegeben. Linearer Funktionsgraph ist Direkte. Um eine Gerade zu konstruieren, genügt es, zwei Punkte zu kennen.

Beispiel 1

Zeichnen Sie die Funktion. Finden wir zwei Punkte. Es ist vorteilhaft, als einen der Punkte Null zu wählen.

Wenn, dann

Wir nehmen einen anderen Punkt, zum Beispiel 1.

Wenn, dann

Bei der Vorbereitung von Aufgaben werden die Koordinaten von Punkten normalerweise in einer Tabelle zusammengefasst:

Und die Werte selbst werden mündlich oder auf einem Entwurfsrechner berechnet.

Zwei Punkte werden gefunden, lasst uns zeichnen:

Bei der Erstellung einer Zeichnung unterzeichnen wir die Grafiken immer.

Es wird nicht überflüssig sein, sich an Spezialfälle einer linearen Funktion zu erinnern:

Beachten Sie, wie ich die Bildunterschriften platziert habe, Unterschriften sollten beim Studium der Zeichnung nicht mehrdeutig sein. BEIM dieser Fall Es war äußerst unerwünscht, neben dem Schnittpunkt der Linien oder unten rechts zwischen den Diagrammen eine Signatur anzubringen.

1) Eine lineare Funktion der Form () heißt direkte Proportionalität. Zum Beispiel, . Der direkte Proportionalitätsgraph geht immer durch den Ursprung. Dadurch wird die Konstruktion einer Geraden vereinfacht - es reicht aus, nur einen Punkt zu finden.

2) Eine Gleichung der Form definiert eine gerade Linie parallel zur Achse, insbesondere ist die Achse selbst durch die Gleichung gegeben. Der Graph der Funktion wird sofort aufgebaut, ohne irgendwelche Punkte zu finden. Das heißt, der Eintrag sollte wie folgt verstanden werden: "y ist immer gleich -4, für jeden Wert von x."

3) Eine Gleichung der Form definiert eine gerade Linie parallel zur Achse, insbesondere ist die Achse selbst durch die Gleichung gegeben. Der Graph der Funktion wird auch sofort aufgebaut. Der Eintrag ist wie folgt zu verstehen: "x ist für jeden Wert von y immer gleich 1."

Einige werden fragen, warum erinnern Sie sich an die 6. Klasse?! So ist es vielleicht, nur in den Jahren der Praxis habe ich ein gutes Dutzend Studenten kennengelernt, die von der Aufgabe, einen Graphen wie oder zu konstruieren, verblüfft waren.

Das Zeichnen einer geraden Linie ist die häufigste Aktion beim Erstellen von Zeichnungen.

Die gerade Linie wird im Verlauf der analytischen Geometrie ausführlich behandelt, und wer möchte, kann auf den Artikel verweisen Gleichung einer geraden Linie in einer Ebene.

Quadratischer Funktionsgraph, kubischer Funktionsgraph, Polynomgraph

Parabel. Plan quadratische Funktion () ist eine Parabel. Prüfen berühmter Fall:

Erinnern wir uns an einige Eigenschaften der Funktion.

Also, die Lösung unserer Gleichung: - An diesem Punkt befindet sich der Scheitelpunkt der Parabel. Warum das so ist, erfahren Sie aus dem theoretischen Artikel über die Ableitung und der Lektion über die Extrema der Funktion. In der Zwischenzeit berechnen wir den entsprechenden Wert von "y":

Der Scheitelpunkt ist also der Punkt

Jetzt finden wir andere Punkte, indem wir dreist die Symmetrie der Parabel nutzen. Zu beachten ist die Funktion – ist nicht einmal, aber trotzdem hat niemand die Symmetrie der Parabel aufgehoben.

In welcher Reihenfolge die verbleibenden Punkte zu finden sind, wird meiner Meinung nach am Final Table deutlich:

Dieser Algorithmus Konstruktion kann bildlich als „Shuttle“ oder das Prinzip „Hin und Her“ bei Anfisa Chekhova bezeichnet werden.

Machen wir eine Zeichnung:

Aus den betrachteten Grafiken fällt mir ein weiteres nützliches Feature ein:

Für eine quadratische Funktion () Folgendes gilt:

Wenn , dann sind die Äste der Parabel nach oben gerichtet.

Wenn , dann sind die Äste der Parabel nach unten gerichtet.

Vertiefte Kenntnisse der Kurve erhalten Sie in der Lektion Hyperbel und Parabel.

Die kubische Parabel ist durch die Funktion gegeben. Hier eine aus der Schule bekannte Zeichnung:

Wir listen die wichtigsten Eigenschaften der Funktion auf

Funktionsgraph

Es repräsentiert einen der Zweige der Parabel. Machen wir eine Zeichnung:

Die wichtigsten Eigenschaften der Funktion:

In diesem Fall ist die Achse vertikale Asymptote für den Hyperbelgraphen bei .

Es ist ein GROSSER Fehler, wenn Sie beim Erstellen einer Zeichnung fahrlässig zulassen, dass sich der Graph mit der Asymptote schneidet.

Auch einseitige Begrenzungen sagen uns das zu einer Übertreibung nicht von oben begrenzt und nicht von unten begrenzt.

Lassen Sie uns die Funktion im Unendlichen untersuchen: , das heißt, wenn wir anfangen, uns entlang der Achse nach links (oder rechts) bis ins Unendliche zu bewegen, dann werden die „Spiele“ ein schmaler Schritt sein unendlich nah nähern sich Null und dementsprechend die Äste der Hyperbel unendlich nah Annäherung an die Achse.

Die Achse ist also horizontale Asymptote für den Graphen der Funktion, wenn "x" gegen plus oder minus unendlich geht.

Die Funktion ist seltsam, was bedeutet, dass die Hyperbel bezüglich des Ursprungs symmetrisch ist. Dieser Fakt ist aus der Zeichnung ersichtlich, außerdem lässt sie sich leicht analytisch verifizieren: .

Der Graph einer Funktion der Form () repräsentiert zwei Zweige einer Hyperbel.

Wenn , dann befindet sich die Hyperbel im ersten und dritten Koordinatenquadranten(siehe Bild oben).

Wenn , dann befindet sich die Hyperbel im zweiten und vierten Koordinatenquadranten.

Es ist nicht schwierig, die angegebene Regelmäßigkeit des Wohnorts der Hyperbel vom Standpunkt geometrischer Transformationen von Graphen zu analysieren.

Beispiel 3

Konstruieren Sie den rechten Ast der Hyperbel

Wir verwenden die punktweise Konstruktionsmethode, wobei es vorteilhaft ist, die Werte so zu wählen, dass sie sich vollständig teilen:

Machen wir eine Zeichnung:

Es wird nicht schwierig sein, den linken Zweig der Hyperbel zu konstruieren, hier hilft nur die Seltsamkeit der Funktion. Grob gesagt fügen Sie in der punktweisen Konstruktionstabelle gedanklich ein Minus zu jeder Zahl hinzu, setzen Sie die entsprechenden Punkte und zeichnen Sie den zweiten Zweig.

Detaillierte geometrische Informationen zur betrachteten Linie finden Sie im Artikel Hyperbel und Parabel.

Graph einer Exponentialfunktion

BEIM diesen Absatz Ich werde gleich die Exponentialfunktion betrachten, da in den Problemen der höheren Mathematik in 95% der Fälle der Exponent vorkommt.

Ich erinnere Sie daran, dass dies der Fall ist irrationale Zahl: , dies wird beim Erstellen eines Diagramms erforderlich sein, das ich tatsächlich ohne Zeremonie erstellen werde. Drei Punkte wahrscheinlich genug:

Lassen wir den Graphen der Funktion erstmal in Ruhe, dazu später.

Die wichtigsten Eigenschaften der Funktion:

Grundsätzlich sehen die Graphen von Funktionen gleich aus usw.

Ich muss sagen, dass der zweite Fall in der Praxis weniger häufig ist, aber er kommt vor, weshalb ich es für notwendig hielt, ihn in diesen Artikel aufzunehmen.

Graph einer logarithmischen Funktion

Betrachten Sie eine Funktion mit natürlicher Logarithmus.
Machen wir eine Strichzeichnung:

Wenn Sie vergessen haben, was ein Logarithmus ist, schlagen Sie bitte in Schulbüchern nach.

Die wichtigsten Eigenschaften der Funktion:

Domain:

Wertebereich: .

Die Funktion wird von oben nicht eingeschränkt: , wenn auch langsam, aber der Zweig des Logarithmus geht bis ins Unendliche.
Betrachten wir rechts das Verhalten der Funktion nahe Null: . Die Achse ist also vertikale Asymptote für den Graphen der Funktion mit "x", das rechts gegen Null geht.

Achten Sie darauf, den typischen Wert des Logarithmus zu kennen und sich daran zu erinnern: .

Grundsätzlich sieht der Graph des Logarithmus zur Basis gleich aus: , , ( dezimaler Logarithmus in Basis 10) usw. Zur gleichen Zeit, als mehr Basis, desto flacher wird der Graph.

Wir werden den Fall nicht prüfen, ich erinnere mich nicht wann das letzte Mal baute einen Graphen mit einer solchen Basis. Ja, und der Logarithmus scheint ein sehr seltener Gast bei Problemen der höheren Mathematik zu sein.

Zum Abschluss des Absatzes möchte ich noch eine Tatsache sagen: Exponentialfunktion und Logarithmische Funktion sind zwei gegenseitig Umkehrfunktionen . Wenn Sie sich den Graphen des Logarithmus genau ansehen, können Sie sehen, dass dies derselbe Exponent ist, nur dass er etwas anders angeordnet ist.

Graphen trigonometrischer Funktionen

Wie beginnt trigonometrische Qual in der Schule? Korrekt. Vom Sinus

Zeichnen wir die Funktion

Diese Linie namens sinusförmig.

Ich erinnere Sie daran, dass „pi“ eine irrationale Zahl ist: und in der Trigonometrie blendet es in den Augen.

Die wichtigsten Eigenschaften der Funktion:

Diese Funktion ist ein Zeitschrift mit Periode. Was bedeutet das? Schauen wir uns den Schnitt an. Links und rechts davon wiederholt sich genau derselbe Teil des Diagramms endlos.

Domain: , das heißt, für jeden Wert von "x" gibt es einen Sinuswert.

Wertebereich: . Die Funktion ist begrenzt: , das heißt, alle „Spiele“ sitzen strikt im Segment .
Das passiert nicht, oder genauer gesagt, es passiert, aber diese Gleichungen haben keine Lösung.

Zur Vereinfachung der Betrachtung der Potenzfunktion betrachten wir 4 separate Fälle: eine Potenzfunktion mit natürlicher Indikator, Potenzfunktion mit ganzzahligem Exponenten, Potenzfunktion mit rationaler Indikator und Leistungsfunktion mit irrationaler Indikator.

Potenzfunktion mit natürlichem Exponenten

Zunächst führen wir den Begriff Grad mit natürlichem Exponenten ein.

Bestimmung 1

Die Potenz einer reellen Zahl $a$ mit natürlichem Exponenten $n$ ist die Zahl dem Produkt gleich$n$ Faktoren, von denen jeder gleich der Zahl $a$ ist.

Bild 1.

$a$ ist die Basis des Abschlusses.

$n$ - Exponent.

Betrachten Sie nun eine Potenzfunktion mit einem natürlichen Exponenten, ihre Eigenschaften und ihren Graphen.

Bestimmung 2

$f\left(x\right)=x^n$ ($n\in N)$ heißt Potenzfunktion mit natürlichem Exponenten.

Betrachten Sie der Einfachheit halber getrennt die Potenzfunktion mit geradem Exponenten $f\left(x\right)=x^(2n)$ und die Potenzfunktion mit ungeradem Exponenten $f\left(x\right)=x^(2n- 1)$ ($n\in N)$.

Eigenschaften einer Potenzfunktion mit natürlichem geraden Exponenten

$f\left(-x\right)=((-x))^(2n)=x^(2n)=f(x)$ ist eine gerade Funktion.

Geltungsbereich -- $ \

Die Funktion verringert sich als $x\in (-\infty ,0)$ und erhöht sich als $x\in (0,+\infty)$.

$f("")\left(x\right)=(\left(2n\cdot x^(2n-1)\right))"=2n(2n-1)\cdot x^(2(n-1 ))\ge 0$

Die Funktion ist im gesamten Definitionsbereich konvex.

Verhalten an den Enden des Bereichs:

\[(\mathop(lim)_(x\to -\infty ) x^(2n)\ )=+\infty \] \[(\mathop(lim)_(x\to +\infty ) x^( 2n)\ )=+\infty \]

Diagramm (Abb. 2).

Abbildung 2. Graph der Funktion $f\left(x\right)=x^(2n)$

Eigenschaften einer Potenzfunktion mit natürlichem ungeraden Exponenten

Der Definitionsbereich sind alle reellen Zahlen.

$f\left(-x\right)=((-x))^(2n-1)=(-x)^(2n)=-f(x)$ ist eine ungerade Funktion.

$f(x)$ ist stetig auf dem gesamten Definitionsbereich.

Der Bereich besteht ausschließlich aus reellen Zahlen.

$f"\left(x\right)=\left(x^(2n-1)\right)"=(2n-1)\cdot x^(2(n-1))\ge 0$

Die Funktion nimmt über den gesamten Definitionsbereich zu.

$f\left(x\right)0$, für $x\in (0,+\infty)$.

$f(""\links(x\rechts))=(\links(\links(2n-1\rechts)\cdot x^(2\links(n-1\rechts))\rechts))"=2 \left(2n-1\right)(n-1)\cdot x^(2n-3)$

\ \

Die Funktion ist konkav für $x\in (-\infty ,0)$ und konvex für $x\in (0,+\infty)$.

Diagramm (Abb. 3).

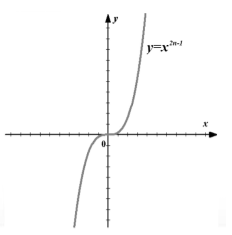
Abbildung 3. Graph der Funktion $f\left(x\right)=x^(2n-1)$

Potenzfunktion mit ganzzahligem Exponenten

Zunächst führen wir den Begriff Grad mit ganzzahligem Exponenten ein.

Bestimmung 3

Grad reelle Zahl$a$ mit ganzzahligem Index $n$ wird durch die Formel bestimmt:

Figur 4

Betrachten Sie nun eine Potenzfunktion mit einem ganzzahligen Exponenten, ihre Eigenschaften und ihren Graphen.

Bestimmung 4

$f\left(x\right)=x^n$ ($n\in Z)$ heißt Potenzfunktion mit ganzzahligem Exponenten.

Ist der Grad größer Null, dann liegt der Fall einer Potenzfunktion mit natürlichem Exponenten vor. Wir haben es oben bereits berücksichtigt. Für $n=0$ erhalten wir lineare Funktion$y=1$. Ihre Betrachtung überlassen wir dem Leser. Es bleibt noch, die Eigenschaften einer Potenzfunktion mit negativem ganzzahligen Exponenten zu betrachten

Eigenschaften einer Potenzfunktion mit einem negativen ganzzahligen Exponenten

Der Geltungsbereich ist $\left(-\infty ,0\right)(0,+\infty)$.

Wenn der Exponent gerade ist, dann ist die Funktion gerade, wenn er ungerade ist, dann ist die Funktion ungerade.

$f(x)$ ist stetig auf dem gesamten Definitionsbereich.

Wertebereich:

Wenn der Exponent gerade ist, dann $(0,+\infty)$, wenn er ungerade ist, dann $\left(-\infty ,0\right)(0,+\infty)$.

Wenn der Exponent ungerade ist, verringert sich die Funktion als $x\in \left(-\infty ,0\right)(0,+\infty)$. Bei einem geraden Exponenten nimmt die Funktion als $x\in (0,+\infty)$ ab. und erhöht sich als $x\in \left(-\infty ,0\right)$.

$f(x)\ge 0$ über die gesamte Domäne