Nerovnosť sú dve čísla resp matematické výrazy, spojené jedným zo znakov: > (viac, v prípade prísne nerovnosti), < (меньше, в случае строгих неравенств), ≥ (больше или равно, в случае нестрогих неравенств), ≤ (меньше или равно, в случае нестрогих неравенств).

nerovnosť je lineárne za rovnakých podmienok ako rovnica: obsahuje premenné len do prvého stupňa a neobsahuje súčin premenných.

Riešenie lineárne nerovnosti a sústav lineárnych nerovností je s nimi neoddeliteľne spojená geometrický zmysel: riešením lineárnej nerovnice je určitá polrovina, na ktorú je celá rovina rozdelená priamkou, ktorej rovnica je daná lineárnou nerovnicou. Túto polrovinu a v prípade sústavy lineárnych nerovností časť roviny ohraničenú niekoľkými priamkami treba nájsť na výkrese.

K riešeniu sústav lineárnych nerovníc s Vysoké číslo mnohé premenné sú znížené ekonomické úlohy, najmä problémy lineárneho programovania, v ktorých je potrebné nájsť maximum alebo minimum funkcie.

Riešenie sústav lineárnych nerovníc s ľubovoľným počtom neznámych

Najprv analyzujme lineárne nerovnosti v rovine. Zvážte jednu nerovnosť s dvoma premennými a:

,

kde sú koeficienty premenných (nejaké čísla), je voľný člen (aj nejaké číslo).

Jedna nerovnosť s dvoma neznámymi, podobne ako rovnica, má nekonečný počet riešení. Riešením tejto nerovnosti je dvojica čísel, ktorá túto nerovnosť spĺňa. Geometricky je množina riešení nerovnosti znázornená ako polrovina ohraničená priamkou

,

ktorú budeme nazývať hraničná čiara.

Krok 1. Zostrojte priamku ohraničujúcu množinu riešení lineárnej nerovnosti

Aby ste to dosiahli, musíte poznať akékoľvek dva body tejto čiary. Nájdite priesečníky so súradnicovými osami. Súradnica križovatky A je nula (obrázok 1). Číselné hodnoty na osiach na tomto obrázku sa vzťahujú na príklad 1, ktorý budeme analyzovať hneď po tejto teoretickej odbočke.

Úsečku nájdeme vyriešením sústavy rovnice priamky s rovnicou osi.

Nájdite priesečník s osou:

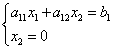
Dosadením hodnoty do prvej rovnice dostaneme

Kde .

Takto sme našli úsečku bodu A .

Nájdite súradnice priesečníka s osou.

Abscisový bod B rovná sa nule. Vyriešme rovnicu hraničnej čiary s rovnicou súradnicovej osi:

,

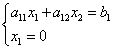
teda súradnice bodu B: .

Krok 2. Nakreslite čiaru, ktorá ohraničuje množinu riešení nerovnosti. Poznanie bodov A a B priesečník hraničnej čiary so súradnicovými osami, môžeme túto čiaru nakresliť. Priamka (opäť obrázok 1) rozdeľuje celú rovinu na dve časti ležiace vpravo a vľavo (nad a pod) tejto priamky.

Krok 3. Určte, ktorá z polrovín je riešením tejto nerovnosti. Aby sme to dosiahli, musíme do tejto nerovnosti dosadiť počiatok súradníc (0; 0). Ak súradnice počiatku vyhovujú nerovnosti, potom riešením nerovnosti je polrovina, v ktorej sa počiatok nachádza. Ak súradnice nerovnici nevyhovujú, tak riešením nerovnosti je polrovina, ktorá neobsahuje počiatok. Polrovinu riešenia nerovnice označíme ťahmi od priamky vo vnútri polroviny, ako na obrázku 1.

Ak riešime sústavu lineárnych nerovníc, potom sa každý krok vykoná pre každú z nerovností systému.

Príklad 1 Vyriešte nerovnosť

Riešenie. Nakreslíme rovnú čiaru

Dosadením priamky do rovnice dostaneme a dosadením dostaneme. Preto súradnice priesečníkov s osami budú A(3; 0) , B(0; 2). Cez tieto body nakreslite priamku (opäť obrázok 1).

Volíme polrovinu riešení nerovnosti. Za týmto účelom dosadíme súradnice začiatku (0; 0) do nerovnosti:

získame , t.j. súradnice pôvodu spĺňajú túto nerovnosť. V dôsledku toho je riešením nerovnosti polrovina obsahujúca počiatok, t.j. ľavá (alebo nižšia) polrovina.

Ak by bola táto nerovnosť prísna, teda mala by podobu

potom by body hraničnej čiary neboli riešením, keďže nespĺňajú nerovnosť.

Teraz zvážte systém lineárnych nerovností s dvoma neznámymi:

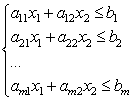
Každá z nerovností tohto systému v rovine definuje polrovinu. Systém lineárnych nerovností sa nazýva konzistentný, ak má aspoň jedno riešenie, a nekonzistentný, ak nemá žiadne riešenia. Riešením sústavy lineárnych nerovníc je ľubovoľná dvojica čísel (), ktorá spĺňa všetky nerovnosti tejto sústavy.

Geometricky je riešením sústavy lineárnych nerovníc množina bodov, ktoré spĺňajú všetky nerovnosti sústavy, teda spoločná časť výsledných polrovín. Preto geometricky všeobecný prípad riešenie môže byť znázornené ako určitý mnohouholník, v konkrétnom prípade to môže byť priamka, úsečka a dokonca aj bod. Ak je sústava lineárnych nerovností nekonzistentná, potom v rovine nie je jediný bod, ktorý by vyhovoval všetkým nerovnostiam sústavy.

Príklad 2

Riešenie. Preto je potrebné nájsť mnohouholník riešení tohto systému nerovníc. Zostrojme hraničnú čiaru pre prvú nerovnosť, teda priamku, a hraničnú čiaru pre druhú nerovnosť, teda priamku.

Robíme to krok za krokom, ako bolo ukázané v teoretickej referencii a v príklade 1, najmä preto, že v príklade 1 bola vytvorená hraničná čiara pre nerovnosť, ktorá je prvá v tomto systéme.

Polroviny riešenia zodpovedajúce nerovnostiam tohto systému sú na obrázku 2 vytieňované dovnútra. spoločná časť polrovinové riešenia je otvorený uhol ABC. To znamená, že množina bodov v rovine, ktoré tvoria otvorený uhol ABC, je riešením prvej aj druhej nerovnice sústavy, čiže je riešením sústavy dvoch lineárnych nerovníc. Inými slovami, súradnice ktoréhokoľvek bodu z tejto množiny spĺňajú obe nerovnosti systému.

Príklad 3 Vyriešte sústavu lineárnych nerovníc

Riešenie. Zostrojme hraničné čiary zodpovedajúce nerovniciam systému. Robíme to podľa krokov uvedených v teoretickom základe pre každú nerovnosť. Teraz definujeme polroviny riešení pre každú nerovnosť (obrázok 3).

Polroviny riešenia zodpovedajúce nerovniciam danej sústavy sú zatienené smerom dovnútra. Priesečník polrovín riešení je znázornený, ako je znázornené na obrázku, vo forme štvoruholníka ABCE. Zistili sme, že polygón riešenia sústavy lineárnych nerovníc s dvoma premennými je štvoruholník ABCE .

Všetko popísané vyššie o sústavách lineárnych nerovníc s dvoma neznámymi platí aj pre sústavu nerovníc s ľubovoľným počtom neznámych, len s tým rozdielom, že riešenie nerovnosti s n neznáma bude totalita nčísla () spĺňajúce všetky nerovnosti a namiesto hraničnej čiary bude hraničná nadrovina n-rozmerný priestor. Riešením bude mnohosten riešenia (simplex) ohraničený nadrovinami.

Riešenie nerovnosti s dvoma premennými, a ešte viac sústavy nerovností s dvoma premennými, sa zdá byť celkom výzvou. Existuje však jednoduchý algoritmus, ktorý pomáha ľahko a bez osobitné úsilie rozhodnúť na prvý pohľad náročné úlohy takéhoto druhu. Skúsme na to prísť.

Predpokladajme, že máme nerovnosť s dvoma premennými jedného z nasledujúcich typov:

y > f(x); y > f(x); r< f(x); y ≤ f(x).

Znázorniť množinu riešení takejto nerovnosti na súradnicová rovina postupujte nasledovne:

1. Zostrojíme graf funkcie y = f(x), ktorý rozdelí rovinu na dve oblasti.

2. Vyberieme si ktorúkoľvek zo získaných oblastí a uvažujeme v nej ľubovoľný bod. Pre tento bod skontrolujeme splniteľnosť pôvodnej nerovnosti. Ak je výsledok testu správny číselná nerovnosť, potom dospejeme k záveru, že pôvodná nerovnosť je splnená v celej oblasti, do ktorej patrí vybraný bod. Množina riešení nerovnosti je teda oblasť, do ktorej patrí vybraný bod. Ak sa v dôsledku kontroly získa nesprávna číselná nerovnosť, potom množina riešení nerovnosti bude druhou oblasťou, do ktorej vybraný bod nepatrí.

3. Ak je nerovnosť striktná, potom hranice oblasti, teda body grafu funkcie y = f(x), nie sú zahrnuté v množine riešení a hranica je znázornená bodkovanou čiarou. Ak nerovnosť nie je striktná, potom sú hranice oblasti, teda body grafu funkcie y = f (x), zahrnuté do množiny riešení tejto nerovnosti a hranica je v tomto prípade zobrazené plná čiara.
Teraz sa pozrime na niekoľko problémov na túto tému.

Úloha 1.

Aká množina bodov je daná nerovnicou x · y ≤ 4?

Riešenie.

1) Zostavíme graf rovnice x · y = 4. Aby sme to dosiahli, najprv ho transformujeme. Je zrejmé, že x in tento prípad sa neobráti na 0, pretože inak by sme mali 0 · y = 4, čo nie je pravda. Takže našu rovnicu môžeme rozdeliť x. Dostaneme: y = 4/x. Graf tejto funkcie je hyperbola. Rozdeľuje celú rovinu na dve oblasti: jednu medzi dvoma vetvami hyperboly a tú mimo nich.

2) Vyberieme si ľubovoľný bod z prvej oblasti, nech je to bod (4; 2).
Kontrola nerovnosti: 4 2 ≤ 4 je nepravda.

To znamená, že body tohto regiónu nespĺňajú pôvodnú nerovnosť. Potom môžeme konštatovať, že množina riešení nerovnice bude druhou oblasťou, do ktorej vybraný bod nepatrí.

3) Keďže nerovnosť nie je striktná, hraničné body, teda body grafu funkcie y = 4/x, nakreslíme plnou čiarou.

Vyfarbme množinu bodov, ktorá definuje pôvodnú nerovnosť, žltá (obr. 1).

Úloha 2.

Nakreslite oblasť definovanú v súradnicovej rovine systémom
(y > x 2 + 2;
(y + x > 1;
(x2 + y2 ≤ 9.

Riešenie.

Začnite vytvárať grafiku nasledujúce funkcie (obr. 2):

y \u003d x 2 + 2 - parabola,

y + x = 1 - priamka

x 2 + y 2 \u003d 9 je kruh.

1) y > x 2 + 2.

Zoberieme bod (0; 5), ktorý leží nad grafom funkcie.
Kontrola nerovnosti: 5 > 0 2 + 2 je pravda.

Preto všetky body ležiace nad danou parabolou y = x 2 + 2 vyhovujú prvej nerovnici sústavy. Zafarbíme ich na žlto.

2) y + x > 1.

Zoberieme bod (0; 3), ktorý leží nad grafom funkcie.
Kontrola nerovnosti: 3 + 0 > 1 je správne.

Preto všetky body ležiace nad priamkou y + x = 1 spĺňajú druhú nerovnosť sústavy. Vyfarbíme ich na zeleno.

3) x2 + y2 ≤ 9.

Zoberieme bod (0; -4), ktorý leží mimo kružnice x 2 + y 2 = 9.
Kontrola nerovnosti: 0 2 + (-4) 2 ≤ 9 je nesprávna.

Preto všetky body ležiace mimo kružnice x 2 + y 2 = 9, nespĺňajú tretiu nerovnosť systému. Potom môžeme konštatovať, že všetky body ležiace vo vnútri kruhu x 2 + y 2 = 9 spĺňajú tretiu nerovnosť systému. Namaľujeme ich fialovým tieňovaním.

Nezabudnite, že ak je nerovnosť prísna, potom by mala byť zodpovedajúca hraničná čiara nakreslená bodkovanou čiarou. Dostávame nasledujúci obrázok (obr. 3).

(obr. 4).

Úloha 3.

Nakreslite oblasť definovanú v súradnicovej rovine systémom:
(x2 + y2 < 16;
(x > -y;
(x 2 + y 2 ≥ 4.

Riešenie.

Na začiatok vytvoríme grafy nasledujúcich funkcií:

x 2 + y 2 \u003d 16 - kruh,

x \u003d -y - rovné

x 2 + y 2 \u003d 4 - kruh (obr. 5).

Teraz sa zaoberáme každou nerovnosťou samostatne.

1) x2 + y2 ≤ 16.

Zoberieme bod (0; 0), ktorý leží vo vnútri kruhu x 2 + y 2 = 16.
Kontrola nerovnosti: 0 2 + (0) 2 ≤ 16 je správne.

Preto všetky body ležiace vo vnútri kruhu x 2 + y 2 = 16 spĺňajú prvú nerovnosť systému.
Vyfarbíme ich na červeno.

Zoberieme bod (1; 1), ktorý leží nad grafom funkcie.
Skontrolujeme nerovnosť: 1 ≥ -1 - pravda.

Preto všetky body ležiace nad priamkou x = -y spĺňajú druhú nerovnosť sústavy. Vyfarbíme ich na modro.

3) x2 + y2 ≥ 4.

Zoberieme bod (0; 5), ktorý leží mimo kružnice x 2 + y 2 = 4.
Skontrolujeme nerovnosť: 0 2 + 5 2 ≥ 4 je správna.

Preto všetky body mimo kružnice x 2 + y 2 = 4 spĺňajú tretiu nerovnosť sústavy. Zafarbíme ich na modro.

V tomto probléme nie sú všetky nerovnosti striktné, čo znamená, že všetky hranice nakreslíme plnou čiarou. Dostávame nasledujúci obrázok (obr. 6).

Oblasť záujmu je oblasť, kde sa všetky tri farebné oblasti navzájom pretínajú. (obr. 7).

Máte nejaké otázky? Nie ste si istí, ako vyriešiť systém nerovností s dvoma premennými?
Ak chcete získať pomoc od tútora -.
Prvá lekcia je zadarmo!

blog.site, pri úplnom alebo čiastočnom skopírovaní materiálu je potrebný odkaz na zdroj.

Často je potrebné znázorniť na súradnicovej rovine množinu riešení nerovnosti s dvoma premennými. Riešením nerovnosti s dvoma premennými je dvojica hodnôt týchto premenných, ktorá premení danú nerovnosť na skutočnú číselnú nerovnosť.

2r+ Zx< 6.

Najprv nakreslíme rovnú čiaru. Aby sme to dosiahli, napíšeme nerovnosť ako rovnicu 2r+ Zx = 6 a vyjadriť r. Tak dostaneme: y=(6-3x)/2.

Táto čiara rozdeľuje množinu všetkých bodov súradnicovej roviny na body nad ňou a body pod ňou.

Vezmite si meme z každej oblasti kontrolný bod napríklad A (1; 1) a B (1; 3)

Súradnice bodu A vyhovujú danej nerovnici 2y + 3x< 6, т. е. 2 . 1 + 3 . 1 < 6.

Súradnice bodu B nie splniť túto nerovnosť 2∙3 + 3∙1< 6.

Keďže táto nerovnosť môže zmeniť znamienko na úsečke 2y + Zx = 6, potom nerovnosť vyhovuje množine bodov oblasti, kde sa nachádza bod A. Vytienime túto oblasť.

Takto sme zobrazili množinu riešení nerovnosti 2r + Zx< 6.

Príklad

Množinu riešení nerovnice x 2 + 2x + y 2 - 4y + 1 > 0 znázorníme na súradnicovej rovine.

Najprv zostrojíme graf rovnice x 2 + 2x + y 2 - 4y + 1 \u003d 0. Rovnicu kruhu rozdelíme do tejto rovnice: (x 2 + 2x + 1) + (y 2 - 4y + 4) \u003d 4 alebo (x + 1) 2 + (y - 2) 2 \u003d 2 2.

Toto je rovnica kružnice so stredom v bode 0 (-1; 2) a polomerom R = 2. Zostrojme túto kružnicu.

Keďže táto nerovnosť je prísna a body ležiace na kružnici samotnej nerovnici nevyhovujú, zostrojíme kružnicu bodkovanou čiarou.

Je ľahké skontrolovať, či súradnice stredu O kruhu nevyhovujú tejto nerovnosti. Výraz x 2 + 2x + y 2 - 4y + 1 mení svoje znamienko na zostrojenej kružnici. Potom je nerovnosť uspokojená bodmi umiestnenými mimo kruhu. Tieto body sú tieňované.

Príklad

Znázornime na súradnicovej rovine množinu riešení nerovnice

(y - x 2) (y - x - 3)< 0.

Najprv nakreslíme rovnicu (y - x 2) (y - x - 3) = 0. Sú to parabola y \u003d x 2 a priamka y \u003d x + 3. Zostavme tieto čiary a všimnime si, že zmena znamienka výrazu (y - x 2) (y - x - 3) nastáva len na týchto riadkoch. Pre bod A (0; 5) určíme znamienko tohto výrazu: (5-3) > 0 (t. j. táto nerovnosť nie je splnená). Teraz je ľahké označiť množinu bodov, pre ktoré je táto nerovnosť splnená (tieto oblasti sú tieňované).

Algoritmus na riešenie nerovností s dvoma premennými

1. Nerovnosť zredukujeme na tvar f (x; y)< 0 (f (х; у) >0; f (x; y) < 0; f (x; y) ≥ 0;)

2. Zapíšeme rovnosť f (x; y) = 0

3. Rozpoznajte grafy zaznamenané na ľavej strane.

4. Zostavíme tieto grafy. Ak je nerovnosť prísna (f (x; y)< 0 или f (х; у) >0), potom - s ťahmi, ak nerovnosť nie je striktná (f (x; y) ≤ 0 alebo f (x; y) ≥ 0), potom - s plnou čiarou.

5. Určte, koľko častí grafiky je rozdelených do súradnicovej roviny

6. Vyberte kontrolný bod v jednej z týchto častí. Určte znamienko výrazu f (x; y)

7. Značky usporiadame v iných častiach roviny, berúc do úvahy striedanie (ako pri metóde intervalov)

8. Vyberieme diely, ktoré potrebujeme podľa znamienka nerovnosti, ktorú riešime a aplikujeme šrafovanie

Nechať dané rovnica s dvoma premennými F(x; y). Už ste sa naučili analyticky riešiť takéto rovnice. Súbor riešení takýchto rovníc možno znázorniť aj vo forme grafu.

Graf rovnice F(x; y) je množina bodov súradnicovej roviny xOy, ktorých súradnice vyhovujú rovnici.

Ak chcete nakresliť rovnicu s dvoma premennými, najprv vyjadrite premennú y ako premennú x v rovnici.

Určite už viete, ako zostaviť rôzne grafy rovníc s dvoma premennými: ax + b \u003d c je priamka, yx \u003d k je hyperbola, (x - a) 2 + (y - b) 2 \u003d R 2 je kružnica, ktorej polomer je R a stred je v bode O(a; b).

Príklad 1

Nakreslite rovnicu x 2 - 9y 2 = 0.

Riešenie.

Rozložme ľavú stranu rovnice na faktor.

(x - 3y) (x+ 3y) = 0, t.j. y = x/3 alebo y = -x/3.

Odpoveď: obrázok 1.

Osobitné miesto zaujíma priraďovanie obrazcov v rovine rovnicami obsahujúcimi znamienko absolútna hodnota, ktorému sa budeme podrobne venovať. Zvážte fázy vykresľovania rovníc tvaru |y| = f(x) a |y| = |f(x)|.

Prvá rovnica je ekvivalentná systému

(f(x) ≥ 0,
(y = f(x) alebo y = -f(x).

To znamená, že jeho graf pozostáva z grafov dvoch funkcií: y = f(x) a y = -f(x), kde f(x) ≥ 0.

Na vykreslenie grafu druhej rovnice sa vynesú grafy dvoch funkcií: y = f(x) a y = -f(x).

Príklad 2

Nakreslite rovnicu |y| = 2 + x.

Riešenie.

Daná rovnica je ekvivalentná sústave

(x + 2 ≥ 0,
(y = x + 2 alebo y = -x - 2.

Vytvárame súbor bodov.

Odpoveď: obrázok 2.

Príklad 3

Nakreslite rovnicu |y – x| = 1.

Riešenie.

Ak y ≥ x, potom y = x + 1, ak y ≤ x, potom y = x - 1.

Odpoveď: obrázok 3.

Pri zostavovaní grafov rovníc obsahujúcich premennú pod znakom modulu je vhodné a racionálne použiť plošná metóda, založené na rozdelení súradnicovej roviny na časti, v ktorých si každý výraz podmodulu zachováva svoje znamienko.

Príklad 4

Nakreslite rovnicu x + |x| + y + |y| = 2.

Riešenie.

AT tento príklad znamienko každého výrazu podmodulu závisí od súradnicový štvrťrok.

1) V prvom súradnicovom kvadrante x ≥ 0 a y ≥ 0. Po rozšírení modulu daná rovnica bude vyzerať takto:

2x + 2y = 2 a po zjednodušení x + y = 1.

2) V druhom štvrťroku, kde x< 0, а y ≥ 0, уравнение будет иметь вид: 0 + 2y = 2 или y = 1.

3) V treťom štvrťroku x< 0, y < 0 будем иметь: x – x + y – y = 2. Перепишем этот результат в виде уравнения 0 · x + 0 · y = 2.

4) Vo štvrtom štvrťroku pre x ≥ 0 a y< 0 получим, что x = 1.

Rozvrh daná rovnica Budeme stavať po štvrtinách.

Odpoveď: obrázok 4.

Príklad 5

Nakreslite množinu bodov, ktorých súradnice spĺňajú rovnosť |x – 1| + |y – 1| = 1.

Riešenie.

Nuly výrazov submodulu x = 1 a y = 1 rozdeľujú rovinu súradníc na štyri oblasti. Rozdeľme moduly podľa regiónov. Uveďme to vo forme tabuľky.

región	Znak výrazu submodulu	Výsledná rovnica po rozšírení modulu
ja	x ≥ 1 a y ≥ 1	x + y = 3
II	X< 1 и y ≥ 1	-x+y=1
III	X< 1 и y < 1	x + y = 1
IV	x ≥ 1 a y< 1	x – y = 1

Odpoveď: obrázok 5.

Na rovine súradníc je možné špecifikovať čísla a nerovnosti.

Graf nerovností s dvoma premennými je množina všetkých bodov súradnicovej roviny, ktorých súradnice sú riešeniami tejto nerovnosti.

Zvážte algoritmus na zostavenie modelu na riešenie nerovnosti s dvoma premennými:

1. Napíšte rovnicu zodpovedajúcu nerovnosti.
2. Nakreslite rovnicu z kroku 1.
3. Vyberte si ľubovoľný bod v jednej z polrovín. Skontrolujte, či súradnice vybraného bodu vyhovujú danej nerovnosti.
4. Nakreslite graficky množinu všetkých riešení nerovnice.

Uvažujme najskôr nerovnosť ax + bx + c > 0. Rovnica ax + bx + c = 0 definuje priamku rozdeľujúcu rovinu na dve polroviny. V každom z nich funkcia f(x) = ax + bx + c zachováva znamienka. Na určenie tohto znamienka stačí zobrať ľubovoľný bod patriaci do polroviny a vypočítať hodnotu funkcie v tomto bode. Ak sa znamienko funkcie zhoduje so znamienkom nerovnice, tak táto polrovina bude riešením nerovnice.

Zvážte príklady grafických riešení najbežnejších nerovností s dvoma premennými.

1) ax + bx + c ≥ 0. Obrázok 6.

2) |x| ≤ a, a > 0. Obrázok 7.

3) x2 + y2 ≤ a, a > 0. Obrázok 8.

4) y ≥ x2. Obrázok 9

5) xy ≤ 1. Obrázok 10.

Ak máte otázky alebo si chcete precvičiť kreslenie na modelovej rovine, množiny všetkých riešení nerovníc v dvoch premenných pomocou matematické modelovanie, môžete minúť bezplatné 25-minútové sedenie s online lektor po registrácii. Pre ďalšiu prácu s učiteľom budete mať možnosť vybrať si tarifný plán, ktorý vám vyhovuje.

Máte nejaké otázky? Neviete, ako nakresliť obrazec v rovine súradníc?
Ak chcete získať pomoc tútora - zaregistrujte sa.
Prvá lekcia je zadarmo!

stránky, s úplným alebo čiastočným kopírovaním materiálu, je potrebný odkaz na zdroj.