უტოლობა არის ორი რიცხვი ან მათემატიკური გამონათქვამები, დაკავშირებულია ერთ-ერთი ნიშნით: > (მეტი, შემთხვევაში მკაცრი უთანასწორობები), < (меньше, в случае строгих неравенств), ≥ (больше или равно, в случае нестрогих неравенств), ≤ (меньше или равно, в случае нестрогих неравенств).

უთანასწორობა არის ხაზოვანიიგივე პირობებში, როგორც განტოლება: ის შეიცავს ცვლადებს მხოლოდ პირველ ხარისხში და არ შეიცავს ცვლადების პროდუქტებს.

გამოსავალი წრფივი უტოლობებიდა წრფივი უტოლობების სისტემები განუყოფლად არის დაკავშირებული მათთან გეომეტრიული გრძნობა: წრფივი უტოლობის ამონახსნი არის გარკვეული ნახევარსიბრტყე, რომელშიც მთელი სიბრტყე იყოფა სწორი წრფით, რომლის განტოლება მოცემულია წრფივი უტოლობით. ეს ნახევრად სიბრტყე და წრფივი უტოლობების სისტემის შემთხვევაში, სიბრტყის ნაწილი, რომელიც შემოსაზღვრულია რამდენიმე სწორი ხაზით, ნახაზში უნდა მოიძებნოს.

წრფივი უტოლობების სისტემების ამოხსნისთვის დიდი რიცხვიბევრი ცვლადი მცირდება ეკონომიკური ამოცანებიკერძოდ, ხაზოვანი პროგრამირების ამოცანები, რომლებშიც საჭიროა ფუნქციის მაქსიმუმის ან მინიმუმის პოვნა.

წრფივი უტოლობების სისტემების ამოხსნა ნებისმიერი რაოდენობის უცნობით

ჯერ გავაანალიზოთ წრფივი უტოლობა სიბრტყეში. განვიხილოთ ერთი უტოლობა ორი ცვლადით და:

,

სად არის ცვლადების კოეფიციენტები (ზოგიერთი რიცხვი), არის თავისუფალი წევრი (ასევე ზოგიერთი რიცხვი).

ერთ უტოლობას ორი უცნობით, ისევე როგორც განტოლებას, აქვს ამონახსნების უსასრულო რაოდენობა. ამ უტოლობის ამოხსნა არის რიცხვების წყვილი, რომელიც აკმაყოფილებს ამ უტოლობას. გეომეტრიულად, უტოლობის ამონახსნების სიმრავლე გამოსახულია, როგორც ნახევრად სიბრტყე, რომელიც შემოსაზღვრულია სწორი ხაზით.

,

რომელსაც დავარქმევთ სასაზღვრო ხაზს.

ნაბიჯი 1. ააგეთ სწორი ხაზი, რომელიც ზღუდავს წრფივი უტოლობის ამონახსნებს

ამისათვის თქვენ უნდა იცოდეთ ამ ხაზის ნებისმიერი ორი წერტილი. ვიპოვოთ გადაკვეთის წერტილები კოორდინატთა ღერძებთან. კვეთის ორდინატი აარის ნული (სურათი 1). ამ ფიგურაში მოცემული ღერძების რიცხვითი მნიშვნელობები ეხება მაგალითს 1, რომელსაც ჩვენ გავაანალიზებთ ამ თეორიული დიგრესიის შემდეგ.

აბსცისს ვპოულობთ ღერძის განტოლებასთან სწორი ხაზის განტოლების სისტემის სახით ამოხსნით.

ვიპოვოთ კვეთა ღერძთან:

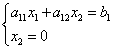
მნიშვნელობის პირველ განტოლებაში ჩანაცვლებით, მივიღებთ

სად .

ამრიგად, ჩვენ ვიპოვეთ წერტილის აბსცისა ა .

ვიპოვოთ ღერძთან გადაკვეთის წერტილის კოორდინატები.

აბსცისის წერტილი ბუდრის ნულს. მოდი ამოვხსნათ სასაზღვრო წრფის განტოლება კოორდინატთა ღერძის განტოლებით:

,

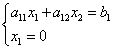
აქედან გამომდინარე წერტილის კოორდინატები ბ: .

ნაბიჯი 2. დახაზეთ ხაზი, რომელიც ზღუდავს ამონახსნების სიმრავლეს უტოლობასთან.ქულების ცოდნა ადა ბსასაზღვრო ხაზის გადაკვეთა კოორდინატთა ღერძებთან, შეგვიძლია დავხატოთ ეს ხაზი. სწორი ხაზი (ისევ სურათი 1) ყოფს მთელ სიბრტყეს ორ ნაწილად, რომლებიც მდებარეობს ამ სწორი ხაზის მარჯვნივ და მარცხნივ (ზემოთ და ქვემოთ).

ნაბიჯი 3. დაადგინეთ, რომელია ნახევრად სიბრტყეებიდან გამოსავალი ამ უტოლობაზე.ამისათვის ჩვენ უნდა ჩავანაცვლოთ კოორდინატების საწყისი (0; 0) ამ უტოლობით. თუ საწყისი კოორდინატები აკმაყოფილებს უტოლობას, მაშინ უტოლობის ამონახსნი არის ნახევარსიბრტყე, რომელშიც მდებარეობს საწყისი. თუ კოორდინატები არ აკმაყოფილებენ უტოლობას, მაშინ უტოლობის ამონახსნი არის ნახევრად სიბრტყე, რომელიც არ შეიცავს საწყისს. უტოლობის ამოხსნის ნახევრად სიბრტყე აღინიშნა ნახევრად სიბრტყის შიგნით სწორი ხაზის შტრიხებით, როგორც სურათზე 1.

თუ წრფივი უტოლობათა სისტემას მოვაგვარებთ, მაშინ თითოეული ნაბიჯი შესრულებულია სისტემის თითოეული უტოლობისთვის.

მაგალითი 1ამოხსენით უტოლობა

გამოსავალი. დავხატოთ სწორი ხაზი

სწორი ხაზის განტოლებაში ჩანაცვლებით ვიღებთ და ჩანაცვლებით ვიღებთ. მაშასადამე, ღერძებთან გადაკვეთის წერტილების კოორდინატები იქნება ა(3; 0) , ბ(0; 2) . დახაზეთ სწორი ხაზი ამ წერტილებში (ისევ, სურათი 1).

ჩვენ ვირჩევთ ამონახსნების ნახევარ სიბრტყეს უტოლობაზე. ამისათვის ჩვენ ვცვლით დასაწყისის კოორდინატებს (0; 0) უტოლობაში:

ვიღებთ, ანუ, საწყისი კოორდინატები აკმაყოფილებს ამ უთანასწორობას. შესაბამისად, უტოლობის გამოსავალი არის ნახევრად სიბრტყე, რომელიც შეიცავს საწყისს, ანუ მარცხენა (ან ქვედა) ნახევარ სიბრტყეს.

ეს უთანასწორობა რომ მკაცრი ყოფილიყო, ანუ ფორმა ექნებოდა

მაშინ სასაზღვრო ხაზის წერტილები არ იქნება გამოსავალი, რადგან ისინი არ აკმაყოფილებენ უთანასწორობას.

ახლა განვიხილოთ წრფივი უტოლობების სისტემა ორი უცნობით:

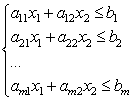
სიბრტყეზე ამ სისტემის თითოეული უტოლობა განსაზღვრავს ნახევრად სიბრტყეს. წრფივი უტოლობათა სისტემას ეწოდება თანმიმდევრული, თუ მას აქვს ერთი ამონახსნობა მაინც და არათანმიმდევრული, თუ მას არ აქვს ამონახსნები. წრფივი უტოლობების სისტემის ამონახსნი არის რიცხვების ნებისმიერი წყვილი () რომელიც აკმაყოფილებს ამ სისტემის ყველა უტოლობას.

გეომეტრიულად, წრფივი უტოლობების სისტემის ამონახსნი არის წერტილების ერთობლიობა, რომელიც აკმაყოფილებს სისტემის ყველა უტოლობას, ანუ მიღებული ნახევრად სიბრტყეების საერთო ნაწილს. ამიტომ, გეომეტრიულად ზოგადი შემთხვევაგამოსავალი შეიძლება იყოს გამოსახული როგორც გარკვეული მრავალკუთხედი, კონკრეტულ შემთხვევაში ეს შეიძლება იყოს წრფე, სეგმენტი და წერტილიც კი. თუ წრფივი უტოლობათა სისტემა არათანმიმდევრულია, მაშინ სიბრტყეზე არ არის არც ერთი წერტილი, რომელიც აკმაყოფილებს სისტემის ყველა უტოლობას.

მაგალითი 2

გამოსავალი. ასე რომ, საჭიროა ამ უტოლობათა სისტემის ამონახსნების პოლიგონის პოვნა. ავაშენოთ საზღვრის ხაზი პირველი უტოლობისთვის, ანუ წრფე და მეორე უტოლობისთვის, ანუ წრფე.

ჩვენ ამას ვაკეთებთ ეტაპობრივად, როგორც ეს ნაჩვენებია თეორიულ მითითებაში და მაგალით 1-ში, მით უმეტეს, რომ მაგალით 1-ში აშენდა სასაზღვრო ხაზი უტოლობისთვის, რომელიც პირველია ამ სისტემაში.

ამონახსნის ნახევრად სიბრტყეები, რომლებიც შეესაბამება ამ სისტემის უტოლობას, დაჩრდილულია 2-ში. საერთო ნაწილინახევრად სიბრტყე გადაწყვეტილებები არის ღია კუთხე ABC. ეს ნიშნავს, რომ სიბრტყეში წერტილების სიმრავლე, რომლებიც ქმნიან ღია კუთხეს ABC, არის ამონახსნები სისტემის როგორც პირველი, ასევე მეორე უტოლობების, ანუ არის ამონახსნი ორი წრფივი უტოლობის სისტემისა. სხვა სიტყვებით რომ ვთქვათ, ამ სიმრავლიდან ნებისმიერი წერტილის კოორდინატები აკმაყოფილებს სისტემის ორივე უტოლობას.

მაგალითი 3ამოხსენით წრფივი უტოლობების სისტემა

გამოსავალი. ავაშენოთ სისტემის უტოლობების შესაბამისი სასაზღვრო ხაზები. ჩვენ ამას ვაკეთებთ თითოეული უთანასწორობის თეორიულ ფონზე მოცემული ნაბიჯების მიხედვით. ახლა ჩვენ განვსაზღვრავთ ამონახსნების ნახევარ სიბრტყეებს თითოეული უტოლობისთვის (სურათი 3).

მოცემული სისტემის უტოლობების შესაბამისი ამონახსნის ნახევრად სიბრტყეები დაჩრდილულია შიგნით. ამონახსნების ნახევრად სიბრტყეების კვეთა გამოსახულია, როგორც სურათზეა ნაჩვენები, ოთხკუთხედის სახით. ABCE. ჩვენ აღმოვაჩინეთ, რომ ორი ცვლადის მქონე წრფივი უტოლობების სისტემის ამოხსნის მრავალკუთხედი არის ოთხკუთხედი. ABCE .

ყველაფერი, რაც ზემოთ იყო აღწერილი წრფივი უტოლობების სისტემების შესახებ ორი უცნობით, ასევე ეხება უტოლობათა სისტემას ნებისმიერი რაოდენობის უცნობით, იმ განსხვავებით, რომ უტოლობის ამოხსნა ნუცნობი იქნება მთლიანობა ნრიცხვები () რომლებიც აკმაყოფილებენ ყველა უტოლობას და სასაზღვრო ხაზის ნაცვლად იქნება სასაზღვრო ჰიპერპლანი ნ- განზომილებიანი სივრცე. გამოსავალი იქნება ხსნარის პოლიედონი (მარტივი), რომელიც შემოიფარგლება ჰიპერთვითმფრინავებით.

უტოლობის ამოხსნა ორი ცვლადით, და მით უმეტეს უტოლობების სისტემები ორი ცვლადით, როგორც ჩანს საკმაოდ გამოწვევაა. თუმცა, არსებობს მარტივი ალგორითმი, რომელიც ეხმარება მარტივად და მის გარეშე განსაკუთრებული ძალისხმევაგადაწყვიტე ერთი შეხედვით რთული ამოცანებიასეთი სახის. შევეცადოთ გავერკვეთ.

დავუშვათ, რომ გვაქვს უტოლობა ორი ცვლადთან ერთ-ერთი შემდეგი ტიპის:

y > f(x); y ≥ f(x); წ< f(x); y ≤ f(x).

ასეთი უტოლობის ამონახსნების სიმრავლის გამოსახვა საკოორდინაციო თვითმფრინავიგააგრძელეთ შემდეგნაირად:

1. ვაშენებთ y = f(x) ფუნქციის გრაფიკს, რომელიც სიბრტყეს ორ რეგიონად ყოფს.

2. ჩვენ ვირჩევთ რომელიმე მიღებულ სფეროს და განვიხილავთ მასში თვითნებური წერტილი. ჩვენ ვამოწმებთ თავდაპირველი უტოლობის დაკმაყოფილებას ამ წერტილისთვის. თუ ტესტის შედეგი სწორია რიცხვითი უტოლობა, შემდეგ დავასკვნით, რომ თავდაპირველი უტოლობა დაკმაყოფილებულია მთელ რეგიონში, რომელსაც ეკუთვნის შერჩეული წერტილი. ამრიგად, უტოლობის ამონახსნების სიმრავლე არის ტერიტორია, რომელსაც ეკუთვნის შერჩეული წერტილი. თუ შემოწმების შედეგად მიიღება არასწორი რიცხვითი უტოლობა, მაშინ უტოლობის ამონახსნების სიმრავლე იქნება მეორე რეგიონი, რომელსაც არ ეკუთვნის არჩეული წერტილი.

3. თუ უტოლობა მკაცრია, მაშინ რეგიონის საზღვრები, ანუ y = f(x) ფუნქციის გრაფიკის წერტილები არ შედის ამონახსნების სიმრავლეში და ზღვარი ნაჩვენებია წერტილოვანი ხაზის სახით. თუ უტოლობა არ არის მკაცრი, მაშინ რეგიონის საზღვრები, ანუ y = f (x) ფუნქციის გრაფიკის წერტილები შედის ამ უტოლობის ამონახსნების სიმრავლეში და საზღვარი ამ შემთხვევაში არის გამოსახული სქელი ხაზი.
ახლა მოდით შევხედოთ რამდენიმე პრობლემას ამ თემაზე.

დავალება 1.

რა ქულათა სიმრავლეა მოცემული x უტოლობით · y ≤ 4?

გამოსავალი.

1) ჩვენ ვაშენებთ განტოლების გრაფიკს x · y = 4. ამისათვის ჯერ მას გარდაქმნით. აშკარაა, რომ x in ამ საქმესარ გადადის 0-ზე, რადგან წინააღმდეგ შემთხვევაში გვექნებოდა 0 · y = 4, რაც არ არის მართალი. ასე რომ, ჩვენ შეგვიძლია გავყოთ ჩვენი განტოლება x-ზე. ვიღებთ: y = 4/x. ამ ფუნქციის გრაფიკი არის ჰიპერბოლა. ის მთელ სიბრტყეს ყოფს ორ რეგიონად: ჰიპერბოლის ორ შტოს შორის და მათ გარეთ.

2) ჩვენ ვირჩევთ თვითნებურ წერტილს პირველი რეგიონიდან, ეს იყოს წერტილი (4; 2).
უტოლობის შემოწმება: 4 2 ≤ 4 მცდარია.

ეს ნიშნავს, რომ ამ რეგიონის წერტილები არ აკმაყოფილებს თავდაპირველ უთანასწორობას. შემდეგ შეგვიძლია დავასკვნათ, რომ უტოლობის ამონახსნების სიმრავლე იქნება მეორე რეგიონი, რომელსაც არ მიეკუთვნება შერჩეული წერტილი.

3) ვინაიდან უტოლობა არ არის მკაცრი, საზღვრის წერტილებს, ანუ y = 4/x ფუნქციის გრაფიკის წერტილებს ვხატავთ მყარი ხაზით.

მოდით გავაფერადოთ წერტილების ნაკრები, რომელიც განსაზღვრავს თავდაპირველ უტოლობას, ყვითელი (ნახ. 1).

დავალება 2.

დახაზეთ სისტემის მიერ კოორდინატულ სიბრტყეზე განსაზღვრული ფართობი
( y > x 2 + 2;
(y + x > 1;
( x 2 + y 2 ≤ 9.

გამოსავალი.

გრაფიკის აშენება დასაწყებად შემდეგი ფუნქციები (ნახ. 2):

y \u003d x 2 + 2 - პარაბოლა,

y + x = 1 - სწორი ხაზი

x 2 + y 2 \u003d 9 არის წრე.

1) y > x 2 + 2.

ვიღებთ წერტილს (0; 5), რომელიც დევს ფუნქციის გრაფიკის ზემოთ.
უტოლობის შემოწმება: 5 > 0 2 + 2 სწორია.

მაშასადამე, მოცემულ პარაბოლაზე ზემოთ მდებარე ყველა წერტილი y = x 2 + 2 აკმაყოფილებს სისტემის პირველ უტოლობას. მოდით გავაფერადოთ ისინი ყვითლად.

2) y + x > 1.

ვიღებთ წერტილს (0; 3), რომელიც დევს ფუნქციის გრაფიკის ზემოთ.
უტოლობის შემოწმება: 3 + 0 > 1 სწორია.

მაშასადამე, y + x = 1 წრფის ზემოთ მდებარე ყველა წერტილი აკმაყოფილებს სისტემის მეორე უტოლობას. მოდით გავაფერადოთ ისინი მწვანეში.

3) x2 + y2 ≤ 9.

ჩვენ ვიღებთ წერტილს (0; -4), რომელიც მდებარეობს წრის გარეთ x 2 + y 2 = 9.
უტოლობის შემოწმება: 0 2 + (-4) 2 ≤ 9 არასწორია.

ამრიგად, ყველა წერტილი, რომელიც მდებარეობს წრის გარეთ x 2 + y 2 = 9, არ აკმაყოფილებდეს სისტემის მესამე უთანასწორობას. შემდეგ შეგვიძლია დავასკვნათ, რომ ყველა წერტილი, რომელიც მდებარეობს წრის შიგნით x 2 + y 2 = 9 აკმაყოფილებს სისტემის მესამე უტოლობას. მოდით დავხატოთ ისინი მეწამული ჩრდილით.

არ დაგავიწყდეთ, რომ თუ უტოლობა მკაცრია, მაშინ შესაბამისი სასაზღვრო ხაზი უნდა გაივლოს წერტილოვანი ხაზით. ჩვენ ვიღებთ შემდეგ სურათს (ნახ. 3).

(ნახ. 4).

დავალება 3.

დახაზეთ სისტემის მიერ კოორდინატულ სიბრტყეზე განსაზღვრული ფართობი:
(x 2 + y 2 ≤ 16;
(x ≥ -y;
(x 2 + y 2 ≥ 4.

გამოსავალი.

დასაწყისისთვის, ჩვენ ვაშენებთ შემდეგი ფუნქციების გრაფიკებს:

x 2 + y 2 \u003d 16 - წრე,

x \u003d -y - სწორი

x 2 + y 2 \u003d 4 - წრე (ნახ. 5).

ახლა ჩვენ განვიხილავთ თითოეულ უთანასწორობას ცალ-ცალკე.

1) x2 + y2 ≤ 16.

ჩვენ ვიღებთ წერტილს (0; 0), რომელიც დევს წრის შიგნით x 2 + y 2 = 16.
უტოლობის შემოწმება: 0 2 + (0) 2 ≤ 16 სწორია.

ამიტომ, ყველა წერტილი, რომელიც მდებარეობს წრის შიგნით x 2 + y 2 = 16, აკმაყოფილებს სისტემის პირველ უტოლობას.
მოდით გავაფერადოთ ისინი წითლად.

ვიღებთ წერტილს (1; 1), რომელიც დევს ფუნქციის გრაფიკის ზემოთ.
ჩვენ ვამოწმებთ უტოლობას: 1 ≥ -1 - მართალია.

მაშასადამე, x = -y წრფის ზემოთ მდებარე ყველა წერტილი აკმაყოფილებს სისტემის მეორე უტოლობას. მოდით გავაფერადოთ ისინი ლურჯად.

3) x2 + y2 ≥ 4.

ჩვენ ვიღებთ წერტილს (0; 5), რომელიც მდებარეობს წრის გარეთ x 2 + y 2 = 4.
ვამოწმებთ უტოლობას: 0 2 + 5 2 ≥ 4 სწორია.

ამიტომ, ყველა წერტილი წრის გარეთ x 2 + y 2 = 4 აკმაყოფილებს სისტემის მესამე უტოლობას. მოდით გავაფერადოთ ისინი ლურჯი.

ამ პრობლემაში ყველა უტოლობა არ არის მკაცრი, რაც ნიშნავს, რომ ყველა საზღვარს ვხატავთ მყარი ხაზით. ჩვენ ვიღებთ შემდეგ სურათს (ნახ. 6).

ინტერესის ზონა არის ტერიტორია, სადაც სამივე ფერადი უბანი კვეთს ერთმანეთს. (ნახ 7).

გაქვთ რაიმე შეკითხვები? არ იცით როგორ ამოხსნათ უტოლობათა სისტემა ორი ცვლადით?
დამრიგებლისგან დახმარების მისაღებად -.
პირველი გაკვეთილი უფასოა!

blog.site, მასალის სრული ან ნაწილობრივი კოპირებით, საჭიროა წყაროს ბმული.

ხშირად საჭიროა კოორდინატთა სიბრტყეზე გამოსახვა უტოლობის ამონახსნების სიმრავლე ორი ცვლადით. ორი ცვლადით უტოლობის ამოხსნა არის ამ ცვლადების მნიშვნელობების წყვილი, რომელიც მოცემულ უტოლობას აქცევს ნამდვილ რიცხვობრივ უტოლობად.

2 წ+ Zx< 6.

ჯერ გავავლოთ სწორი ხაზი. ამისათვის ჩვენ ვწერთ უტოლობას განტოლების სახით 2 წ+ Zx = 6 და გამოხატოს წ.ამრიგად, ჩვენ ვიღებთ: y=(6-3x)/2.

ეს ხაზი ყოფს კოორდინატთა სიბრტყის ყველა წერტილის სიმრავლეს მის ზემოთ და მის ქვემოთ წერტილებად.

აიღეთ მემი თითოეული რეგიონიდან საგუშაგო, მაგალითად A (1; 1) და B (1; 3)

A წერტილის კოორდინატები აკმაყოფილებს მოცემულ უტოლობას 2y + 3x< 6, т. е. 2 . 1 + 3 . 1 < 6.

B წერტილის კოორდინატები არადააკმაყოფილეთ ეს უტოლობა 2∙3 + 3∙1< 6.

ვინაიდან ამ უტოლობას შეუძლია შეცვალოს ნიშანი წრფეზე 2y + Zx = 6, მაშინ უტოლობა აკმაყოფილებს იმ უბნის წერტილთა სიმრავლეს, სადაც მდებარეობს A წერტილი. მოდით დავჩრდილოთ ეს ტერიტორია.

ამრიგად, ჩვენ გამოვსახეთ უთანასწორობის ამონახსნების ნაკრები 2y + Zx< 6.

მაგალითი

ჩვენ გამოვსახავთ ამონახსნების სიმრავლეს x 2 + 2x + y 2 - 4y + 1 > 0 უტოლობის კოორდინატულ სიბრტყეზე.

პირველი, ჩვენ ვაშენებთ განტოლების გრაფიკს x 2 + 2x + y 2 - 4y + 1 \u003d 0. ჩვენ ვყოფთ წრის განტოლებას ამ განტოლებაში: (x 2 + 2x + 1) + (y 2 - 4y + 4) \u003d 4, ან (x + 1) 2 + (y - 2) 2 \u003d 2 2.

ეს არის წრის განტოლება, რომელიც ორიენტირებულია 0 (-1; 2) წერტილზე და რადიუსზე R = 2. მოდით ავაშენოთ ეს წრე.

ვინაიდან ეს უტოლობა მკაცრია და თავად წრეზე მდებარე წერტილები არ აკმაყოფილებს უტოლობას, წრეს ვაშენებთ წერტილოვანი ხაზით.

ადვილია იმის შემოწმება, რომ წრის O ცენტრის კოორდინატები არ აკმაყოფილებდეს ამ უტოლობას. გამოხატულება x 2 + 2x + y 2 - 4y + 1 ცვლის თავის ნიშანს აგებულ წრეზე. მაშინ უტოლობა კმაყოფილდება წრის გარეთ მდებარე წერტილებით. ეს წერტილები დაჩრდილულია.

მაგალითი

კოორდინატულ სიბრტყეზე გამოვსახოთ უტოლობის ამონახსნების სიმრავლე

(y - x 2) (y - x - 3)< 0.

ჯერ გამოვსახოთ განტოლება (y - x 2) (y - x - 3) = 0. ეს არის პარაბოლა y \u003d x 2 და სწორი ხაზი y \u003d x + 3. ავაშენოთ ეს წრფეები და აღვნიშნოთ, რომ გამოხატვის (y - x 2) (y - x - 3) ნიშნის ცვლილება მხოლოდ ამ ხაზებზე ხდება. A წერტილისთვის (0; 5) განვსაზღვრავთ ამ გამოთქმის ნიშანს: (5-3) > 0 (ე.ი. ეს უტოლობა არ არის დაკმაყოფილებული). ახლა ადვილია იმ წერტილების სიმრავლის აღნიშვნა, რომლებისთვისაც ეს უთანასწორობა დაკმაყოფილებულია (ეს უბნები დაჩრდილულია).

უტოლობების ამოხსნის ალგორითმი ორი ცვლადით

1. უტოლობას ვამცირებთ f (x; y) ფორმამდე.< 0 (f (х; у) >0; f (x; y) ≤ 0; f (x; y) ≥ 0;)

2. ვწერთ ტოლობას f (x; y) = 0

3. მარცხენა მხარეს ჩაწერილი გრაფიკების ამოცნობა.

4. ჩვენ ვაშენებთ ამ გრაფიკებს. თუ უტოლობა მკაცრია (f (x; y)< 0 или f (х; у) >0), მაშინ - შტრიხებით, თუ უტოლობა არ არის მკაცრი (f (x; y) ≤ 0 ან f (x; y) ≥ 0), მაშინ - მყარი ხაზით.

5. დაადგინეთ, გრაფიკის რამდენი ნაწილია დაყოფილი კოორდინატულ სიბრტყეში

6. აირჩიეთ საკონტროლო წერტილი ერთ-ერთ ამ ნაწილში. განსაზღვრეთ გამოთქმის ნიშანი f (x; y)

7. ნიშანს ვაწყობთ სიბრტყის სხვა ნაწილებში მონაცვლეობის გათვალისწინებით (როგორც ინტერვალების მეთოდით)

8. ჩვენ ვირჩევთ ჩვენთვის საჭირო ნაწილებს იმ უთანასწორობის ნიშნის შესაბამისად, რომელსაც ვხსნით და ვიყენებთ გამოჩეკვას.

მიეცით განტოლება ორი ცვლადით F(x; y). თქვენ უკვე ისწავლეთ როგორ ამოხსნათ ასეთი განტოლებები ანალიტიკურად. ასეთი განტოლებების ამონახსნების სიმრავლე ასევე შეიძლება წარმოდგენილი იყოს გრაფიკის სახით.

F(x; y) განტოლების გრაფიკი არის xOy კოორდინატთა სიბრტყის წერტილების ერთობლიობა, რომელთა კოორდინატები აკმაყოფილებს განტოლებას.

ორცვლადიანი განტოლების გამოსათვლელად, ჯერ გამოთქვით y ცვლადი განტოლების x ცვლადის მიხედვით.

რა თქმა უნდა, თქვენ უკვე იცით, თუ როგორ უნდა ააწყოთ განტოლებების სხვადასხვა გრაფიკები ორი ცვლადით: ax + b \u003d c არის სწორი ხაზი, yx \u003d k არის ჰიპერბოლა, (x - a) 2 + (y - b) 2 \u003d R 2 არის წრე, რომლის რადიუსი არის R, ხოლო ცენტრი მდებარეობს O(a; b) წერტილში.

მაგალითი 1

დახაზეთ განტოლება x 2 - 9y 2 = 0.

გამოსავალი.

მოდით, განტოლების მარცხენა მხარე გავამრავლოთ.

(x - 3y) (x+ 3y) = 0, ანუ y = x/3 ან y = -x/3.

პასუხი: სურათი 1.

განსაკუთრებული ადგილი უჭირავს სიბრტყეზე ფიგურების მინიჭებას ნიშნის შემცველი განტოლებით აბსოლუტური მნიშვნელობა, რომელსაც დეტალურად განვიხილავთ. განვიხილოთ |y|-ის ფორმის განტოლებების გამოსახვის ეტაპები = f(x) და |y| = |f(x)|.

პირველი განტოლება სისტემის ტოლფასია

(f(x) ≥ 0,
(y = f(x) ან y = -f(x).

ანუ მისი გრაფიკი შედგება ორი ფუნქციის გრაფიკისაგან: y = f(x) და y = -f(x), სადაც f(x) ≥ 0.

მეორე განტოლების გრაფიკის გამოსათვლელად გამოსახულია ორი ფუნქციის გრაფიკები: y = f(x) და y = -f(x).

მაგალითი 2

დახაზეთ განტოლება |y| = 2 + x.

გამოსავალი.

მოცემული განტოლება სისტემის ტოლფასია

(x + 2 ≥ 0,
(y = x + 2 ან y = -x - 2.

ჩვენ ვაშენებთ ქულების კომპლექტს.

პასუხი: სურათი 2.

მაგალითი 3

დახაზეთ განტოლება |y – x| = 1.

გამოსავალი.

თუ y ≥ x, მაშინ y = x + 1, თუ y ≤ x, მაშინ y = x - 1.

პასუხი: სურათი 3.

მოდულის ნიშნის ქვეშ ცვლადის შემცველი განტოლებების გრაფიკების აგებისას მოსახერხებელი და რაციონალურია გამოყენება ფართობის მეთოდი, ეფუძნება კოორდინატთა სიბრტყის ნაწილებად დაყოფას, რომლებშიც თითოეული ქვემოდულის გამოხატულება ინარჩუნებს თავის ნიშანს.

მაგალითი 4

დახაზეთ განტოლება x + |x| + y + |y| = 2.

გამოსავალი.

AT ეს მაგალითითითოეული ქვემოდულის გამოხატვის ნიშანი დამოკიდებულია კოორდინატთა კვარტალი.

1) პირველ კოორდინატულ კვადრატში x ≥ 0 და y ≥ 0. მოდულის გაფართოების შემდეგ მოცემული განტოლებაასე გამოიყურება:

2x + 2y = 2 და გამარტივების შემდეგ x + y = 1.

2) მეორე კვარტალში, სადაც x< 0, а y ≥ 0, уравнение будет иметь вид: 0 + 2y = 2 или y = 1.

3) მესამე კვარტალში x< 0, y < 0 будем иметь: x – x + y – y = 2. Перепишем этот результат в виде уравнения 0 · x + 0 · y = 2.

4) მეოთხე კვარტალში, x ≥ 0 და y< 0 получим, что x = 1.

განრიგი მოცემული განტოლებავაშენებთ კვარტლებში.

პასუხი: სურათი 4.

მაგალითი 5

დახაზეთ წერტილების სიმრავლე, რომელთა კოორდინატები აკმაყოფილებს ტოლობას |x – 1| + |y – 1| = 1.

გამოსავალი.

ქვემოდულის გამონათქვამების ნულები x = 1 და y = 1 ყოფს კოორდინატთა სიბრტყეს ოთხ რეგიონად. მოდით დავყოთ მოდულები რეგიონების მიხედვით. დავდოთ ცხრილის სახით.

რეგიონი	სუბმოდულის გამოხატვის ნიშანი	მიღებული განტოლება მოდულის გაფართოების შემდეგ
მე	x ≥ 1 და y ≥ 1	x + y = 3
II	x< 1 и y ≥ 1	-x+y=1
III	x< 1 и y < 1	x + y = 1
IV	x ≥ 1 და y< 1	x – y = 1

პასუხი: ფიგურა 5.

კოორდინატთა სიბრტყეზე ფიგურები შეიძლება იყოს მითითებული და უთანასწორობები.

უტოლობის გრაფიკიორი ცვლადით არის კოორდინატთა სიბრტყის ყველა წერტილის სიმრავლე, რომელთა კოორდინატები არის ამ უტოლობის ამონახსნები.

განვიხილოთ ალგორითმი ორი ცვლადით უტოლობის ამოხსნის მოდელის ასაგებად:

1. ჩაწერეთ უტოლობის შესაბამისი განტოლება.
2. დახაზეთ განტოლება 1 საფეხურიდან.
3. აირჩიეთ თვითნებური წერტილი ერთ-ერთ ნახევრად სიბრტყეში. შეამოწმეთ, აკმაყოფილებს თუ არა შერჩეული წერტილის კოორდინატები მოცემულ უტოლობას.
4. გრაფიკულად დახაზეთ უტოლობის ყველა ამონახსნის სიმრავლე.

განვიხილოთ, უპირველეს ყოვლისა, უტოლობა ax + bx + c > 0. განტოლება ax + bx + c = 0 განსაზღვრავს სწორ ხაზს, რომელიც ყოფს სიბრტყეს ორ ნახევრად სიბრტყეზე. თითოეულ მათგანში ფუნქცია f(x) = ax + bx + c ნიშანთა დაცვაა. ამ ნიშნის დასადგენად საკმარისია აიღოთ ნახევრად სიბრტყის კუთვნილი ნებისმიერი წერტილი და გამოვთვალოთ ამ წერტილში ფუნქციის მნიშვნელობა. თუ ფუნქციის ნიშანი ემთხვევა უტოლობის ნიშანს, მაშინ ეს ნახევრად სიბრტყე იქნება უტოლობის ამოხსნა.

განვიხილოთ ყველაზე გავრცელებული უტოლობების გრაფიკული ამონახსნების მაგალითები ორი ცვლადით.

1) ცული + bx + c ≥ 0. სურათი 6.

2) |x| ≤ a, a > 0. სურათი 7.

3) x 2 + y 2 ≤ a, a > 0. Ფიგურა 8.

4) y ≥ x2. სურათი 9

5) xy ≤ 1. სურათი 10.

თუ თქვენ გაქვთ შეკითხვები ან გსურთ ივარჯიშოთ მოდელის სიბრტყეზე დახატვა უტოლობების ყველა ამონახსნის სიმრავლე ორ ცვლადში გამოყენებით მათემატიკური მოდელირება, შეგიძლიათ დახარჯოთ უფასო 25 წუთიანი სესია ონლაინ დამრიგებელი დარეგისტრირების შემდეგ. ამისთვის შემდგომი მუშაობამასწავლებელთან ერთად გექნებათ შესაძლებლობა აირჩიოთ თქვენთვის შესაფერისი სატარიფო გეგმა.

გაქვთ რაიმე შეკითხვები? არ იცით როგორ დავხატოთ ფიგურა კოორდინატულ სიბრტყეზე?
დამრიგებლის დახმარების მისაღებად - დარეგისტრირდით.
პირველი გაკვეთილი უფასოა!

საიტი, მასალის სრული ან ნაწილობრივი კოპირებით, საჭიროა წყაროს ბმული.