Pertidaksamaan adalah dua angka atau ekspresi matematika, dihubungkan oleh salah satu tanda: > (lebih, jika ketidaksetaraan yang ketat), < (меньше, в случае строгих неравенств), ≥ (больше или равно, в случае нестрогих неравенств), ≤ (меньше или равно, в случае нестрогих неравенств).

ketidaksetaraan adalah linier di bawah kondisi yang sama seperti persamaan: hanya berisi variabel tingkat pertama dan tidak mengandung produk variabel.

Larutan pertidaksamaan linier dan sistem pertidaksamaan linier terkait erat dengan pengertian geometris: solusi dari pertidaksamaan linier adalah setengah bidang tertentu, di mana seluruh bidang dibagi dengan garis lurus, yang persamaannya diberikan oleh pertidaksamaan linier. Setengah bidang ini, dan dalam kasus sistem pertidaksamaan linier, bagian dari bidang yang dibatasi oleh beberapa garis lurus, harus ditemukan dalam gambar.

Untuk solusi sistem pertidaksamaan linier dengan jumlah yang besar banyak variabel berkurang tugas ekonomi, khususnya, masalah pemrograman linier, di mana diperlukan untuk menemukan maksimum atau minimum dari suatu fungsi.

Memecahkan sistem pertidaksamaan linier dengan sejumlah yang tidak diketahui

Mari kita pertama menganalisis pertidaksamaan linier di pesawat. Pertimbangkan satu pertidaksamaan dengan dua variabel dan :

,

di mana adalah koefisien variabel (beberapa angka), adalah istilah bebas (juga beberapa angka).

Satu pertidaksamaan dengan dua yang tidak diketahui, seperti persamaan, memiliki jumlah solusi yang tak terbatas. Penyelesaian pertidaksamaan ini adalah sepasang bilangan yang memenuhi pertidaksamaan ini. Secara geometris, himpunan penyelesaian pertidaksamaan digambarkan sebagai setengah bidang yang dibatasi oleh garis lurus

,

yang akan kita sebut garis batas.

Langkah 1. Buat garis lurus yang membatasi himpunan solusi pertidaksamaan linier

Untuk melakukan ini, Anda perlu mengetahui dua titik dari garis ini. Mari kita cari titik potong dengan sumbu koordinat. Koordinat persimpangan SEBUAH adalah nol (Gambar 1). Nilai numerik pada sumbu pada gambar ini mengacu pada contoh 1, yang akan kami analisis segera setelah penyimpangan teoretis ini.

Kami menemukan absis dengan memecahkan sebagai sistem persamaan garis lurus dengan persamaan sumbu.

Mari kita cari persimpangan dengan sumbu:

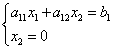
Substitusikan nilai ke persamaan pertama, kita dapatkan

Di mana .

Jadi, kami menemukan absis titik SEBUAH .

Mari kita cari koordinat titik potong dengan sumbu.

Titik absis B sama dengan nol. Selesaikan persamaan garis batas dengan persamaan sumbu koordinat:

,

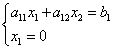
maka koordinat titik B: .

Langkah 2. Gambarlah garis yang membatasi himpunan solusi pertidaksamaan tersebut. Mengetahui poin SEBUAH dan B perpotongan garis batas dengan sumbu koordinat, kita dapat menggambar garis ini. Garis lurus (gambar 1 lagi) membagi seluruh bidang menjadi dua bagian yang terletak di sebelah kanan dan kiri (atas dan bawah) garis lurus ini.

Langkah 3. Tentukan yang mana dari setengah bidang yang merupakan solusi dari pertidaksamaan ini. Untuk melakukan ini, kita perlu mengganti titik asal koordinat (0; 0) ke dalam pertidaksamaan ini. Jika koordinat titik asal memenuhi pertidaksamaan, maka solusi pertidaksamaan adalah setengah bidang di mana titik asal berada. Jika koordinat tidak memenuhi pertidaksamaan, maka solusi pertidaksamaan tersebut adalah setengah bidang yang tidak memuat titik asal. Setengah bidang dari solusi pertidaksamaan akan dilambangkan dengan garis lurus di dalam setengah bidang, seperti pada Gambar 1.

Jika kita memecahkan sistem pertidaksamaan linier, maka setiap langkah dilakukan untuk setiap pertidaksamaan sistem.

Contoh 1 Selesaikan pertidaksamaan

Larutan. Mari menggambar garis lurus

Substitusikan garis lurus ke dalam persamaan, kita dapatkan, dan substitusikan, kita dapatkan. Oleh karena itu, koordinat titik-titik perpotongan dengan sumbu adalah SEBUAH(3; 0) , B(0; 2) . Gambarlah garis lurus melalui titik-titik ini (sekali lagi, Gambar 1).

Kami memilih setengah bidang solusi untuk pertidaksamaan. Untuk melakukan ini, kami mengganti koordinat awal (0; 0) ke dalam ketidaksetaraan:

kami memperoleh , yaitu, koordinat asal memenuhi ketidaksetaraan ini. Oleh karena itu, solusi pertidaksamaan adalah setengah bidang yang mengandung titik asal, yaitu, setengah bidang kiri (atau lebih rendah).

Jika ketidaksetaraan ini ketat, itu akan memiliki bentuk

maka titik-titik garis batas tidak akan menjadi solusi, karena tidak memenuhi pertidaksamaan.

Sekarang perhatikan sistem pertidaksamaan linier dengan dua yang tidak diketahui:

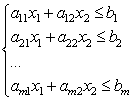
Setiap ketidaksetaraan sistem ini pada bidang mendefinisikan setengah bidang. Sistem pertidaksamaan linier disebut konsisten jika memiliki setidaknya satu solusi, dan tidak konsisten jika tidak memiliki solusi. Penyelesaian sistem pertidaksamaan linier adalah setiap pasangan bilangan () yang memenuhi semua pertidaksamaan sistem ini.

Secara geometris, solusi untuk sistem pertidaksamaan linier adalah himpunan titik-titik yang memenuhi semua pertidaksamaan sistem, yaitu bagian umum dari setengah bidang yang dihasilkan. Oleh karena itu, secara geometris kasus umum solusinya dapat digambarkan sebagai poligon tertentu, dalam kasus tertentu dapat berupa garis, segmen, dan bahkan titik. Jika sistem pertidaksamaan linier tidak konsisten, maka tidak ada satu titik pun pada bidang yang memenuhi semua pertidaksamaan sistem tersebut.

Contoh 2

Larutan. Jadi, diperlukan untuk menemukan poligon solusi dari sistem pertidaksamaan ini. Mari kita buat garis batas untuk pertidaksamaan pertama, yaitu garis, dan garis batas pertidaksamaan kedua, yaitu garis.

Kami melakukan ini langkah demi langkah, seperti yang ditunjukkan dalam referensi teoretis dan dalam contoh 1, terutama karena dalam contoh 1 garis batas dibuat untuk pertidaksamaan, yang merupakan yang pertama dalam sistem ini.

Solusi setengah bidang yang sesuai dengan pertidaksamaan sistem ini diarsir ke dalam pada Gambar 2. bagian umum solusi setengah bidang adalah sudut terbuka ABC. Ini berarti himpunan titik-titik pada bidang yang membentuk sudut terbuka ABC, adalah solusi untuk kedua pertidaksamaan pertama dan kedua dari sistem, yaitu, adalah solusi untuk sistem dua pertidaksamaan linier. Dengan kata lain, koordinat titik mana pun dari himpunan ini memenuhi kedua pertidaksamaan sistem.

Contoh 3 Memecahkan sistem pertidaksamaan linier

Larutan. Mari kita buat garis batas yang sesuai dengan pertidaksamaan sistem. Kami melakukan ini dengan mengikuti langkah-langkah yang diberikan di latar belakang teoritis untuk setiap ketidaksetaraan. Sekarang kita mendefinisikan setengah bidang solusi untuk setiap pertidaksamaan (Gambar 3).

Solusi setengah bidang yang sesuai dengan pertidaksamaan sistem yang diberikan diarsir ke dalam. Perpotongan setengah bidang solusi digambarkan, seperti yang ditunjukkan pada gambar, dalam bentuk segi empat ABCE. Kami telah menemukan bahwa poligon solusi dari sistem pertidaksamaan linier dengan dua variabel adalah segi empat ABCE .

Semua yang dijelaskan di atas tentang sistem pertidaksamaan linier dengan dua yang tidak diketahui juga berlaku untuk sistem pertidaksamaan dengan sejumlah yang tidak diketahui, dengan satu-satunya perbedaan bahwa solusi dari pertidaksamaan dengan n yang tidak diketahui akan menjadi totalitas n angka () memenuhi semua ketidaksetaraan, dan alih-alih garis batas akan ada hyperplane batas n-ruang dimensi Solusinya akan menjadi solusi polihedron (simpleks) yang dibatasi oleh hyperplanes.

Memecahkan Pertidaksamaan dengan Dua Variabel, dan terlebih lagi sistem pertidaksamaan dengan dua variabel, tampaknya cukup menantang. Namun, ada algoritma sederhana yang membantu dengan mudah dan tanpa upaya khusus memutuskan pada pandangan pertama tugas yang menantang semacam itu. Mari kita coba mencari tahu.

Misalkan kita memiliki pertidaksamaan dengan dua variabel dari salah satu jenis berikut:

y > f(x); y f(x); kamu< f(x); y ≤ f(x).

Untuk menggambarkan himpunan solusi dari pertidaksamaan seperti itu pada bidang koordinat lanjutkan sebagai berikut:

1. Kami membuat grafik fungsi y = f(x), yang membagi bidang menjadi dua daerah.

2. Kami memilih salah satu area yang diperoleh dan mempertimbangkan di dalamnya titik sewenang-wenang. Kami memeriksa kepuasan ketidaksetaraan asli untuk titik ini. Jika hasil tesnya benar ketidaksamaan numerik, maka kita menyimpulkan bahwa pertidaksamaan asli dipenuhi di seluruh wilayah tempat titik yang dipilih berada. Dengan demikian, himpunan solusi pertidaksamaan adalah area tempat titik yang dipilih berada. Jika sebagai hasil pemeriksaan diperoleh ketidaksetaraan numerik yang salah, maka himpunan solusi untuk pertidaksamaan akan menjadi wilayah kedua, di mana titik yang dipilih tidak termasuk.

3. Jika pertidaksamaan tegas, maka batas-batas wilayah, yaitu titik-titik dari grafik fungsi y = f(x), tidak termasuk dalam himpunan solusi dan batasnya ditampilkan sebagai garis putus-putus. Jika pertidaksamaan tidak tegas, maka batas-batas daerah, yaitu titik-titik grafik fungsi y = f (x), termasuk dalam himpunan solusi pertidaksamaan ini, dan batas dalam hal ini adalah digambarkan garis utuh.
Sekarang mari kita lihat beberapa masalah tentang topik ini.

Tugas 1.

Himpunan titik yang diberikan oleh pertidaksamaan x · y 4?

Larutan.

1) Kita buat grafik dari persamaan x · y = 4. Untuk melakukannya, kita ubah dulu. Jelas bahwa x dalam kasus ini tidak berubah menjadi 0, karena jika tidak, kita akan memiliki 0 · y = 4, yang tidak benar. Jadi kita bisa membagi persamaan kita dengan x. Kita peroleh: y = 4/x. Grafik fungsi ini adalah hiperbola. Ini membagi seluruh bidang menjadi dua wilayah: satu di antara dua cabang hiperbola dan yang di luarnya.

2) Kami memilih titik sewenang-wenang dari wilayah pertama, biarkan itu menjadi titik (4; 2).
Memeriksa pertidaksamaan: 4 2 4 salah.

Ini berarti bahwa titik-titik dari daerah ini tidak memenuhi pertidaksamaan asli. Kemudian kita dapat menyimpulkan bahwa himpunan solusi untuk pertidaksamaan akan menjadi wilayah kedua, di mana titik yang dipilih tidak termasuk.

3) Karena pertidaksamaan tidak tegas, kami menggambar titik batas, yaitu titik-titik grafik fungsi y = 4/x, dengan garis padat.

Mari kita warnai himpunan titik yang mendefinisikan pertidaksamaan asli, kuning (Gbr. 1).

Tugas 2.

Gambarlah luas yang didefinisikan pada bidang koordinat oleh sistem
( y > x 2 + 2;
(y + x > 1;
( x 2 + y 2 9.

Larutan.

Membangun grafik untuk memulai fungsi berikut: (Gbr. 2):

y \u003d x 2 + 2 - parabola,

y + x = 1 - garis lurus

x 2 + y 2 \u003d 9 adalah lingkaran.

1) y > x 2 + 2.

Kami mengambil titik (0; 5), yang terletak di atas grafik fungsi.
Memeriksa pertidaksamaan: 5 > 0 2 + 2 benar.

Oleh karena itu, semua titik yang terletak di atas parabola yang diberikan y = x 2 + 2 memenuhi pertidaksamaan pertama sistem. Mari kita warnai mereka dengan warna kuning.

2) y + x > 1.

Kami mengambil titik (0; 3), yang terletak di atas grafik fungsi.
Memeriksa pertidaksamaan: 3 + 0 > 1 benar.

Oleh karena itu, semua titik yang terletak di atas garis y + x = 1 memenuhi pertidaksamaan kedua dari sistem. Mari kita warnai mereka dengan warna hijau.

3) x2 + y2 9.

Kita ambil sebuah titik (0; -4), yang terletak di luar lingkaran x 2 + y 2 = 9.
Memeriksa pertidaksamaan: 0 2 + (-4) 2 9 salah.

Jadi, semua titik yang terletak di luar lingkaran x 2 + y 2 = 9, tidak memenuhi pertidaksamaan ketiga dari sistem. Kemudian kita dapat menyimpulkan bahwa semua titik yang terletak di dalam lingkaran x 2 + y 2 = 9 memenuhi pertidaksamaan ketiga dari sistem. Mari kita lukis mereka dengan bayangan ungu.

Jangan lupa bahwa jika pertidaksamaannya ketat, maka garis batas yang sesuai harus digambar dengan garis putus-putus. Kami mendapatkan gambar berikut: (Gbr. 3).

(Gbr. 4).

Tugas 3.

Gambarkan area yang didefinisikan pada bidang koordinat oleh sistem:
(x 2 + y 2 16;
(x -y;
(x 2 + y 2 4.

Larutan.

Untuk memulainya, kami membuat grafik dari fungsi-fungsi berikut:

x 2 + y 2 \u003d 16 - lingkaran,

x \u003d -y - lurus

x 2 + y 2 \u003d 4 - lingkaran (Gbr. 5).

Sekarang kita berurusan dengan setiap ketidaksetaraan secara terpisah.

1) x2 + y2 16.

Kita ambil titik (0;0) yang terletak di dalam lingkaran x 2 + y 2 = 16.
Memeriksa pertidaksamaan: 0 2 + (0) 2 16 benar.

Oleh karena itu, semua titik yang terletak di dalam lingkaran x 2 + y 2 = 16 memenuhi pertidaksamaan pertama sistem.
Mari kita warnai mereka dengan warna merah.

Kami mengambil titik (1; 1), yang terletak di atas grafik fungsi.
Kami memeriksa ketidaksetaraan: 1 -1 - benar.

Oleh karena itu, semua titik yang terletak di atas garis x = -y memenuhi pertidaksamaan kedua dari sistem. Mari kita warnai mereka dengan warna biru.

3) x2 + y2 4.

Kita ambil titik (0; 5), yang terletak di luar lingkaran x 2 + y 2 = 4.
Kami memeriksa ketidaksetaraan: 0 2 + 5 2 4 benar.

Oleh karena itu, semua titik di luar lingkaran x 2 + y 2 = 4 memenuhi pertidaksamaan ketiga dari sistem. Mari kita warnai mereka dengan warna biru.

Dalam masalah ini, semua ketidaksetaraan tidak ketat, yang berarti bahwa kita menggambar semua batas dengan garis yang solid. Kami mendapatkan gambar berikut: (Gbr. 6).

Area of ​​interest adalah area di mana ketiga area berwarna saling berpotongan. (gambar 7).

Apakah Anda memiliki pertanyaan? Tidak yakin bagaimana menyelesaikan sistem pertidaksamaan dengan dua variabel?
Untuk mendapatkan bantuan dari tutor -.
Pelajaran pertama gratis!

blog.site, dengan penyalinan materi secara penuh atau sebagian, diperlukan tautan ke sumbernya.

Seringkali perlu untuk menggambarkan pada bidang koordinat himpunan solusi untuk pertidaksamaan dengan dua variabel. Penyelesaian pertidaksamaan dengan dua variabel adalah pasangan nilai dari variabel-variabel tersebut yang mengubah pertidaksamaan yang diberikan menjadi pertidaksamaan numerik yang sebenarnya.

2 tahun+ Zx< 6.

Mari kita menggambar garis lurus terlebih dahulu. Untuk melakukan ini, kami menulis ketidaksetaraan sebagai persamaan 2 tahun+ Zx = 6 dan ekspresikan y. Dengan demikian, kita mendapatkan: y=(6-3x)/2.

Garis ini membagi himpunan semua titik bidang koordinat menjadi titik-titik di atasnya dan titik-titik di bawahnya.

Ambil meme dari masing-masing daerah pos pemeriksaan, misalnya A (1; 1) dan B (1; 3)

Koordinat titik A memenuhi pertidaksamaan yang diberikan 2y + 3x< 6, т. е. 2 . 1 + 3 . 1 < 6.

Koordinat titik B bukan memenuhi pertidaksamaan ini 2∙3 + 3∙1< 6.

Karena pertidaksamaan ini dapat mengubah tanda pada garis 2y + Zx = 6, maka pertidaksamaan tersebut memenuhi himpunan titik-titik daerah tempat titik A berada. Mari kita arsir daerah tersebut.

Jadi, kami telah menggambarkan himpunan solusi dari pertidaksamaan 2 tahun + Zx< 6.

Contoh

Kami menggambarkan himpunan solusi pertidaksamaan x 2 + 2x + y 2 - 4y + 1 > 0 pada bidang koordinat.

Pertama, kami membuat grafik persamaan x 2 + 2x + y 2 - 4y + 1 \u003d 0. Kami membagi persamaan lingkaran dalam persamaan ini: (x 2 + 2x + 1) + (y 2 - 4y + 4) \u003d 4, atau (x + 1) 2 + (y - 2) 2 \u003d 2 2.

Ini adalah persamaan lingkaran yang berpusat di titik 0 (-1; 2) dan jari-jari R = 2. Mari kita buat lingkaran ini.

Karena pertidaksamaan ini ketat dan titik-titik yang terletak pada lingkaran itu sendiri tidak memenuhi pertidaksamaan, kami membuat lingkaran dengan garis putus-putus.

Sangat mudah untuk memeriksa bahwa koordinat pusat O lingkaran tidak memenuhi pertidaksamaan ini. Ekspresi x 2 + 2x + y 2 - 4y + 1 berubah tandanya pada lingkaran yang dibangun. Kemudian pertidaksamaan dipenuhi oleh titik-titik yang terletak di luar lingkaran. Titik-titik ini diarsir.

Contoh

Mari kita gambarkan pada bidang koordinat himpunan solusi pertidaksamaan

(y - x 2) (y - x - 3)< 0.

Pertama, mari kita plot persamaan (y - x 2) (y - x - 3) = 0. Mereka adalah parabola y \u003d x 2 dan garis lurus y \u003d x + 3. Mari kita buat garis-garis ini dan perhatikan bahwa perubahan tanda dari ekspresi (y - x 2) (y - x - 3) hanya terjadi pada garis-garis ini. Untuk titik A (0; 5), kami menentukan tanda dari ekspresi ini: (5-3) > 0 (yaitu, pertidaksamaan ini tidak terpenuhi). Sekarang mudah untuk menandai himpunan titik-titik yang memenuhi ketidaksetaraan ini (area-area ini diarsir).

Algoritma untuk Memecahkan Pertidaksamaan dengan Dua Variabel

1. Kita kurangi pertidaksamaan menjadi bentuk f (x; y)< 0 (f (х; у) >0; f (x; y) 0; f (x; y) 0;)

2. Kita tulis persamaan f (x; y) = 0

3. Kenali grafik yang direkam di sisi kiri.

4. Kami membangun grafik ini. Jika pertidaksamaan tegas (f (x; y)< 0 или f (х; у) >0), lalu - dengan goresan, jika pertidaksamaan tidak tegas (f (x; y) 0 atau f (x; y) 0), maka - dengan garis padat.

5. Tentukan berapa banyak bagian grafik yang dibagi menjadi bidang koordinat

6. Pilih titik kontrol di salah satu bagian ini. Tentukan tanda dari ekspresi f (x; y)

7. Kami mengatur tanda-tanda di bagian lain dari pesawat, dengan mempertimbangkan pergantian (seperti dengan metode interval)

8. Kami memilih bagian yang kami butuhkan sesuai dengan tanda pertidaksamaan yang kami selesaikan, dan menerapkan penetasan

Biarkan diberikan persamaan dengan dua variabel F(x; y). Anda telah belajar bagaimana memecahkan persamaan tersebut secara analitis. Himpunan solusi persamaan tersebut juga dapat direpresentasikan dalam bentuk grafik.

Grafik persamaan F(x; y) adalah himpunan titik-titik pada bidang koordinat xOy yang koordinatnya memenuhi persamaan.

Untuk memplot persamaan dua variabel, pertama-tama nyatakan variabel y dalam bentuk variabel x dalam persamaan.

Tentunya Anda sudah tahu cara membuat berbagai grafik persamaan dengan dua variabel: ax + b \u003d c adalah garis lurus, yx \u003d k adalah hiperbola, (x - a) 2 + (y - b) 2 \u003d R 2 adalah lingkaran yang jari-jarinya R, dan pusatnya di titik O(a; b).

Contoh 1

Plot persamaan x 2 - 9y 2 = 0.

Larutan.

Mari kita memfaktorkan ruas kiri persamaan.

(x - 3y)(x+ 3y) = 0, yaitu y = x/3 atau y = -x/3.

Jawaban: gambar 1.

Tempat khusus ditempati oleh penetapan angka-angka di pesawat dengan persamaan yang mengandung tanda nilai mutlak, yang akan kita bahas secara rinci. Pertimbangkan tahapan memplot persamaan bentuk |y| = f(x) dan |y| = |f(x)|.

Persamaan pertama setara dengan sistem

(f(x) 0,
(y = f(x) atau y = -f(x).

Artinya, grafiknya terdiri dari grafik dua fungsi: y = f(x) dan y = -f(x), di mana f(x) 0.

Untuk plot grafik persamaan kedua, grafik dua fungsi diplot: y = f(x) dan y = -f(x).

Contoh 2

Gambarkan persamaan |y| = 2 + x.

Larutan.

Persamaan yang diberikan setara dengan sistem

(x + 2 0,
(y = x + 2 atau y = -x - 2.

Kami membangun satu set poin.

Jawaban: gambar 2.

Contoh 3

Gambarkan persamaan |y – x| = 1.

Larutan.

Jika y x, maka y = x + 1, jika y x, maka y = x - 1.

Jawaban: gambar 3.

Saat membuat grafik persamaan yang berisi variabel di bawah tanda modul, akan lebih mudah dan rasional untuk digunakan metode luas, berdasarkan pemisahan bidang koordinat menjadi bagian-bagian di mana setiap ekspresi submodul mempertahankan tandanya.

Contoh 4

Gambarkan persamaan x + |x| + y + |y| = 2.

Larutan.

PADA contoh ini tanda setiap ekspresi submodul bergantung pada koordinat kuartal.

1) Pada kuadran koordinat pertama x 0 dan y 0. Setelah modul diperluas persamaan yang diberikan akan terlihat seperti:

2x + 2y = 2, dan setelah disederhanakan x + y = 1.

2) Pada kuartal kedua, di mana x< 0, а y ≥ 0, уравнение будет иметь вид: 0 + 2y = 2 или y = 1.

3) Pada kuarter ketiga x< 0, y < 0 будем иметь: x – x + y – y = 2. Перепишем этот результат в виде уравнения 0 · x + 0 · y = 2.

4) Pada kuartal keempat, untuk x 0 dan y< 0 получим, что x = 1.

Jadwal persamaan yang diberikan Kami akan membangun di perempat.

Jawaban: gambar 4.

Contoh 5

Gambarlah himpunan titik-titik yang koordinatnya memenuhi persamaan |x – 1| + |y – 1| = 1.

Larutan.

Nol dari ekspresi submodul x = 1 dan y = 1 membagi bidang koordinat menjadi empat daerah. Mari kita uraikan modul berdasarkan wilayah. Mari kita letakkan ini dalam bentuk tabel.

Wilayah	Tanda ekspresi submodul	Persamaan yang dihasilkan setelah memperluas modul
Saya	x 1 dan y 1	x + y = 3
II	x< 1 и y ≥ 1	-x+y=1
AKU AKU AKU	x< 1 и y < 1	x + y = 1
IV	x 1 dan y< 1	x – y = 1

Jawaban: gambar 5.

Pada bidang koordinat, angka dapat ditentukan dan ketidaksetaraan.

Grafik pertidaksamaan dengan dua variabel adalah himpunan semua titik pada bidang koordinat yang koordinatnya merupakan solusi dari pertidaksamaan ini.

Mempertimbangkan algoritma untuk membangun model untuk memecahkan pertidaksamaan dengan dua variabel:

1. Tuliskan persamaan yang sesuai dengan pertidaksamaan tersebut.
2. Plot persamaan dari langkah 1.
3. Pilih titik sembarang di salah satu setengah bidang. Periksa apakah koordinat titik yang dipilih memenuhi pertidaksamaan yang diberikan.
4. Gambarkan secara grafis himpunan semua solusi pertidaksamaan tersebut.

Pertimbangkan, pertama-tama, pertidaksamaan ax + bx + c > 0. Persamaan ax + bx + c = 0 mendefinisikan garis lurus yang membagi bidang menjadi dua setengah bidang. Pada masing-masing dari mereka, fungsi f(x) = ax + bx + c adalah pelestarian tanda. Untuk menentukan tanda ini, cukup mengambil titik mana pun yang termasuk dalam setengah bidang dan menghitung nilai fungsi pada titik ini. Jika tanda fungsi bertepatan dengan tanda pertidaksamaan, maka setengah bidang ini akan menjadi solusi pertidaksamaan.

Pertimbangkan contoh solusi grafis untuk pertidaksamaan paling umum dengan dua variabel.

1) ax + bx + c 0. Gambar 6.

2) |x| a, a > 0. Gambar 7.

3) x 2 + y 2 a, a > 0. Angka 8.

4) y x2. Gambar 9

5) xy 1. Gambar 10.

Jika Anda memiliki pertanyaan atau ingin berlatih menggambar pada bidang model himpunan semua solusi pertidaksamaan dalam dua variabel menggunakan pemodelan matematika, Anda dapat menghabiskan sesi 25 menit gratis dengan guru online setelah Anda mendaftar. Untuk pekerjaan selanjutnya dengan seorang guru, Anda akan memiliki kesempatan untuk memilih paket tarif yang sesuai untuk Anda.

Apakah Anda memiliki pertanyaan? Tidak tahu cara menggambar angka di bidang koordinat?
Untuk mendapatkan bantuan tutor - daftar.
Pelajaran pertama gratis!

situs, dengan penyalinan materi secara penuh atau sebagian, tautan ke sumber diperlukan.