Virtatoiminto, sen ominaisuudet ja kaavio Demo materiaali Oppitunti-luento Toiminnan käsite. Toiminnan ominaisuudet. Tehofunktio, sen ominaisuudet ja kuvaaja. Arvosana 10 Kaikki oikeudet pidätetään. Tekijänoikeus ja tekijänoikeus

Oppitunnin eteneminen: toisto. Toiminto. Toiminnan ominaisuudet. Uuden materiaalin oppiminen. 1. Tehofunktion määritelmä Tehofunktion määritelmä. 2. Potenssifunktioiden ominaisuudet ja kuvaajat Potenssifunktioiden ominaisuudet ja kuvaajat. Tutkitun materiaalin konsolidointi. Sanallinen laskenta. Sanallinen laskenta. Yhteenveto oppitunnista. Kotitehtävät.

Toimintoalue ja funktion alue Kaikki riippumattoman muuttujan arvot muodostavat funktion toimialueen x y=f(x) f Toiminnon toimialue Funktioalue Kaikki arvot, jotka riippuvainen muuttuja ottaa, muodostavat funktion toimialueen Toiminto. Toiminnon ominaisuudet

Toiminnon kuvaaja Annetaan funktio, jossa xY y x.75 3 0.6 4 0.5 Funktion kuvaaja on joukko koordinaattitason kaikkia pisteitä, joiden abskissat ovat yhtä suuret kuin argumentin arvot, ja ordinaatit ovat yhtä suuria kuin funktion vastaavat arvot. Toiminto. Toiminnon ominaisuudet

Y x Määritelmäalue ja funktion alue 4 y=f(x) Funktioalue: Funktioalue: Funktio. Toiminnon ominaisuudet

Parillinen funktio y x y=f(x) Kuvaaja tasainen toiminto symmetrinen y-akselin suhteen Funktiota y=f(x) kutsutaan vaikka f(-x) = f(x) mille tahansa x:lle funktion toimialueesta. Toiminnon ominaisuudet

Pariton funktio y x y=f(x) Kuvaaja outo toiminto symmetrinen origon suhteen O(0;0) Funktiota y=f(x) kutsutaan parittomaksi, jos f(-x) = -f(x) mille tahansa x:lle funktion toimialueesta. Toiminnon ominaisuudet

Potenssifunktion määritelmä Funktiota, jossa p on annettu reaaliluku, kutsutaan potenssifunktioksi. p y \u003d x p P \u003d x y 0 Oppitunnin edistyminen

Potenssifunktio x y 1. Määritelmäalue ja potenssifunktioiden arvoalue muotoa, jossa n on luonnollinen luku, ovat kaikki todellisia lukuja. 2. Nämä funktiot ovat outoja. Niiden kaavio on symmetrinen origon suhteen. Tehofunktion ominaisuudet ja piirteet

Potenssifunktiot rationaalisella positiivisella eksponentilla Määritelmäalue - kaikki positiivisia lukuja ja luku 0. Tällaisella eksponentilla varustettujen funktioiden alue on myös kaikki positiiviset luvut ja luku 0. Nämä funktiot eivät ole parillisia eivätkä parittomia. y x Tehofunktion ominaisuudet ja kaaviot

Tehotoiminto rationaalisella negatiivinen indikaattori. Tällaisten funktioiden määritelmäalue ja alue ovat kaikki positiivisia lukuja. Funktiot eivät ole parillisia eivätkä parittomia. Tällaiset funktiot vähenevät koko määrittelyalueensa aikana. y x Tehofunktion ominaisuudet ja kaaviot Oppitunnin eteneminen

1. Tehofunktio, sen ominaisuudet ja graafi;

2. Muutokset:

Rinnakkaissiirto;

Symmetria koordinaattiakselien suhteen;

Symmetria alkuperästä;

Symmetria suoralla y = x;

Venyttely ja kutistuminen koordinaattiakseleita pitkin.

3. Eksponentiaalinen funktio, sen ominaisuudet ja graafi, vastaavat muunnokset;

4. Logaritminen funktio, sen ominaisuudet ja graafi;

5. Trigonometrinen funktio, sen ominaisuudet ja graafi, vastaavat muunnokset (y = sin x; y = cos x; y = tg x);

Funktio: y = x\n - sen ominaisuudet ja kaavio.

Tehofunktio, sen ominaisuudet ja kuvaaja

y \u003d x, y \u003d x 2, y \u003d x 3, y \u003d 1 / x jne. Kaikki nämä toiminnot ovat tehofunktion, eli funktion, erikoistapauksia y = xp, jossa p on annettu reaaliluku.
Potenssifunktion ominaisuudet ja kuvaaja riippuvat olennaisesti todellisen eksponentin potenssin ominaisuuksista ja erityisesti arvoista, joille x ja s käydä järkeen xp. Jatketaanpa samankaltaiseen pohdintaan. erilaisiin tilaisuuksiin riippuen
eksponentti s.

1. Indeksi p = 2n on parillinen luonnollinen luku.

y=x2n, missä n on luonnollinen luku ja sillä on seuraavat ominaisuudet:

• määritelmäalue on kaikki reaaliluvut, eli joukko R;
• arvosarja - ei-negatiiviset luvut eli y on suurempi tai yhtä suuri kuin 0;
• toiminto y=x2n jopa, koska x 2n = (-x) 2n
• toiminto pienenee aikavälillä x< 0 ja kasvaa välissä x > 0.

Funktiokaavio y=x2n on samassa muodossa kuin esimerkiksi funktion kuvaaja y=x4.

2. Ilmaisin p = 2n - 1- pariton luonnollinen luku

Tässä tapauksessa tehotoiminto y = x2n-1, jossa on luonnollinen luku, on seuraavat ominaisuudet:

• määritelmäalue - joukko R;
• arvojoukko - joukko R;
• toiminto y = x2n-1 outoa koska (- x) 2n-1= x 2n-1;
• funktio kasvaa koko reaaliakselilla.

Funktiokaavio y = x2n-1 y=x3.

3. Ilmaisin p = -2n, missä n- luonnollinen luku.

Tässä tapauksessa tehotoiminto y = x-2n = 1/x2n sillä on seuraavat ominaisuudet:

• arvojoukko - positiiviset luvut y>0;
• funktio y = 1/x2n jopa, koska 1/(-x) 2n= 1/x2n;
• funktio kasvaa välillä x0.

Funktion y kuvaaja = 1/x2n on samassa muodossa kuin esimerkiksi funktion y kuvaajalla = 1/x2.

4. Ilmaisin p = -(2n-1), missä n- luonnollinen luku.
Tässä tapauksessa tehotoiminto y=x-(2n-1) sillä on seuraavat ominaisuudet:

• määritelmäalue on joukko R, paitsi x = 0;
• arvojoukko - joukko R, paitsi y = 0;
• toiminto y=x-(2n-1) outoa koska (- x)-(2n-1) = -x-(2n-1);
• toiminto pienenee intervalleilla x< 0 ja x > 0.

Funktiokaavio y=x-(2n-1) on samassa muodossa kuin esimerkiksi funktion kuvaaja y = 1/x3.

The menetelmällinen materiaali on vain viitteellinen ja koskee monenlaisia aiheita. Artikkeli tarjoaa yleiskatsauksen tärkeimpien perusfunktioiden kaavioista ja tarkastelee niitä tärkein kysymys – kuinka rakentaa kaavio oikein ja NOPEASTI. Tutkimuksen aikana korkeampaa matematiikkaa perusfunktioiden kuvaajia tuntematta se on vaikeaa, joten on erittäin tärkeää muistaa, miltä paraabelin, hyperbelin, sinin, kosinin jne. kuvaajat näyttävät, muistaa joitain funktioarvoja. Puhumme myös joistakin päätoimintojen ominaisuuksista.

En väitä aineistojen täydellisyyttä ja tieteellistä perusteellisuutta, vaan painotetaan ennen kaikkea käytäntöä - niitä asioita, joilla täytyy kohdata kirjaimellisesti joka vaiheessa, missä tahansa korkeamman matematiikan aiheessa. Kaavioita nukkeille? Voit sanoa niin.

Tekijä: lukuisia pyyntöjä lukijat napsautettava sisällysluettelo:

Lisäksi aiheesta on erittäin lyhyt abstrakti
– hallitse 16 tyyppistä kaaviota tutkimalla KUUSI sivua!

Vakavasti, kuusi, jopa minä itse yllätyin. Tämä abstrakti sisältää parannetun grafiikan ja on saatavana nimellistä maksua vastaan, demoversio on katsottavissa. Tiedosto on kätevä tulostaa niin, että kaaviot ovat aina käsillä. Kiitos projektin tukemisesta!

Ja aloitamme heti:

Kuinka rakentaa koordinaattiakselit oikein?

Käytännössä opiskelijat laativat kokeet lähes aina erillisiin vihkoihin, jotka on vuorattu häkkiin. Miksi tarvitset ruudullisia merkintöjä? Loppujen lopuksi työ voidaan periaatteessa tehdä A4-arkeille. Ja häkki on tarpeellinen vain piirustusten laadukkaan ja tarkan suunnittelun vuoksi.

Mikä tahansa funktiokaavion piirustus alkaa koordinaattiakseleilla.

Piirustukset ovat kaksi- ja kolmiulotteisia.

Tarkastellaanpa ensin kaksiulotteista tapausta karteesinen suorakaiteen muotoinen järjestelmä koordinaatit:

1) Piirrämme koordinaattiakselit. Akseli on ns x-akseli , ja akseli y-akseli . Pyrimme aina piirtämään niitä siisti ja ei kiero. Nuolet eivät myöskään saa muistuttaa Papa Carlon partaa.

2) Allekirjoitamme akselit isot kirjaimet"x" ja "y". Älä unohda allekirjoittaa akseleita.

3) Aseta asteikko akseleita pitkin: piirrä nolla ja kaksi ykköstä. Piirustusta tehtäessä kätevin ja yleisin mittakaava on: 1 yksikkö = 2 solua (piirros vasemmalla) - pidä siitä kiinni, jos mahdollista. Ajoittain kuitenkin tapahtuu, että piirustus ei mahdu muistikirjan arkille - sitten pienennämme mittakaavaa: 1 yksikkö = 1 solu (piirros oikealla). Harvoin, mutta tapahtuu, että piirustuksen mittakaavaa on pienennettävä (tai lisättävä) vielä enemmän

ÄLÄ kirjoita konekiväärillä ... -5, -4, -3, -1, 0, 1, 2, 3, 4, 5, .... varten koordinaattitaso ei ole Descartesin muistomerkki, eikä opiskelija ole kyyhkynen. Laitamme nolla ja kaksi yksikköä akseleita pitkin. Joskus sijasta yksiköitä, on kätevää "tunnistaa" muita arvoja, esimerkiksi "kaksi" abskissa-akselilla ja "kolme" ordinaatta-akselilla - ja tämä järjestelmä (0, 2 ja 3) asettaa myös yksilöllisesti koordinaattiruudukon.

Piirustuksen arvioidut mitat on parempi arvioida ENNEN piirustuksen tekemistä.. Joten jos tehtävä edellyttää esimerkiksi kolmion piirtämistä, jonka kärjet ovat , , , niin on melko selvää, että suosittu mittakaava 1 yksikkö = 2 solua ei toimi. Miksi? Katsotaanpa asiaa - tässä sinun on mitattava viisitoista senttimetriä alaspäin, ja ilmeisesti piirustus ei mahdu (tai tuskin mahdu) muistikirjan arkille. Siksi valitsemme välittömästi pienemmän mittakaavan 1 yksikkö = 1 solu.

Muuten, noin senttimetrejä ja muistikirjan soluja. Onko totta, että 30 muistikirjan solussa on 15 senttimetriä? Mittaa viivaimella muistivihkosta kiinnostuksen kohteeksi 15 senttimetriä. Neuvostoliitossa tämä oli ehkä totta ... On mielenkiintoista huomata, että jos mittaat nämä samat senttimetrit vaaka- ja pystysuunnassa, tulokset (soluissa) ovat erilaisia! Tarkkaan ottaen nykyaikaiset muistikirjat eivät ole ruudullisia, vaan suorakaiteen muotoisia. Se voi tuntua hölmöltä, mutta esimerkiksi ympyrän piirtäminen kompassilla tällaisissa tilanteissa on erittäin hankalaa. Ollakseni rehellinen, sellaisina hetkinä alkaa miettiä toveri Stalinin oikeellisuutta, joka lähetettiin leireille hakkeroimaan tuotannossa, puhumattakaan kotimaisesta autoteollisuudesta, putoavista lentokoneista tai räjähtävistä voimalaitoksista.

Laadusta puheen ollen tai lyhyt suositus paperitavaroiden mukaan. Tähän mennessä useimmat muistikirjat ovat myynnissä, pahoja sanoja puhumattakaan, täyttä paskaa. Siitä syystä, että ne kastuvat, eikä vain geelikynistä, vaan myös kuulakärkikynistä! Säästä paperilla. Selvitystä varten ohjaus toimii Suosittelen käyttämään Arkangelin sellu- ja paperitehtaan muistikirjoja (18 arkkia, häkki) tai Pyaterochkan, vaikka se on kalliimpaa. On suositeltavaa valita geelikynä, halvinkin kiinalainen geelitäyttö on paljon parempi kuin kuulakärkikynä, joka joko tahraa tai repii paperia. Ainoa "kilpailukykyinen" kuulakärkikynä muistissani on "Erich Krause". Hän kirjoittaa selkeästi, kauniisti ja vakaasti - joko täydellä varrella tai melkein tyhjällä.

Lisäksi: suorakaiteen muotoisen koordinaattijärjestelmän näkeminen silmillä analyyttinen geometria artikkelissa käsitelty Vektorien lineaarinen (ei) riippuvuus. Vektoripohjalta, yksityiskohtainen tieto noin koordinoi neljännekset löytyy oppitunnin toisesta kappaleesta Lineaariset epäyhtälöt.

3D kotelo

Se on melkein sama täällä.

1) Piirrämme koordinaattiakselit. Vakio: soveltaa akselia – suunnattu ylöspäin, akseli – suunnattu oikealle, akseli – alaspäin vasemmalle tiukasti 45 asteen kulmassa.

2) Allekirjoitamme akselit.

3) Aseta asteikko akseleita pitkin. Mittakaava akselia pitkin - kaksi kertaa pienempi kuin asteikko muilla akseleilla. Huomaa myös, että oikeassa piirustuksessa käytin epästandardia "serifiä" akselilla (tämä mahdollisuus on jo mainittu edellä). Minun näkökulmastani se on tarkempi, nopeampi ja esteettisempi - sinun ei tarvitse etsiä kennon keskiosaa mikroskoopilla ja "veistää" yksikköä suoraan alkuperään asti.

Kun teet 3D-piirustuksen uudelleen - aseta mittakaava etusijalle
1 yksikkö = 2 solua (piirros vasemmalla).

Mitä varten nämä kaikki säännöt ovat? Säännöt on olemassa rikottavaksi. Mitä minä nyt teen. Tosiasia on, että artikkelin myöhemmät piirustukset teen Excelissä ja koordinaattiakselit näyttävät virheellisiltä oikea muotoilu. Voisin piirtää kaikki kaaviot käsin, mutta niiden piirtäminen on todella pelottavaa, koska Excel on haluton piirtämään niitä paljon tarkemmin.

Kuvaajat ja alkeisfunktioiden perusominaisuudet

Lineaarinen funktio saadaan yhtälöstä . Lineaarinen funktiokaavio on suoraan. Suoran rakentamiseksi riittää, että tietää kaksi pistettä.

Esimerkki 1

Piirrä funktio. Etsitään kaksi pistettä. On edullista valita nolla yhdeksi pisteeksi.

Jos sitten

Otamme toisen kohdan, esimerkiksi 1.

Jos sitten

Tehtäviä valmisteltaessa pisteiden koordinaatit kootaan yleensä taulukkoon:

Ja itse arvot lasketaan suullisesti tai luonnoksella, laskimella.

Kaksi pistettä löytyy, piirretään:

Piirustusta laadittaessa allekirjoitamme aina grafiikan.

Ei ole tarpeetonta muistaa lineaarisen funktion erikoistapauksia:

Huomaa, kuinka laitoin kuvatekstit, allekirjoitukset eivät saa olla moniselitteisiä piirustusta tutkittaessa. AT Tämä tapaus oli äärimmäisen epätoivottavaa laittaa allekirjoitusta viivojen leikkauspisteen viereen tai oikeaan alareunaan kaavioiden väliin.

1) Muodon () lineaarifunktiota kutsutaan suoraksi suhteelliseksi. Esimerkiksi, . Suoran verrannollisuuden graafi kulkee aina origon kautta. Siten suoran linjan rakentaminen yksinkertaistuu - riittää, että löytää vain yksi piste.

2) Muodollinen yhtälö määrittelee akselin suuntaisen suoran, erityisesti itse akseli on annettu yhtälöllä. Funktion kuvaaja rakennetaan välittömästi, ilman pisteitä. Toisin sanoen merkintä tulee ymmärtää seuraavasti: "y on aina yhtä suuri kuin -4, millä tahansa x:n arvolla."

3) Muotoinen yhtälö määrittelee akselin suuntaisen suoran, erityisesti itse akseli on yhtälöllä annettu. Myös funktion kuvaaja rakennetaan välittömästi. Merkintä tulee ymmärtää seuraavasti: "x on aina, millä tahansa y:n arvolla, yhtä suuri kuin 1."

Jotkut kysyvät, miksi muistaa 6. luokka?! Näin se ehkä onkin, vain harjoitteluvuosien aikana tapasin parikymmentä opiskelijaa, jotka olivat hämmentyneitä tehtävästä rakentaa graafi, kuten tai .

Suoran viivan piirtäminen on yleisin toimenpide piirustuksia tehtäessä.

Suoraa käsitellään yksityiskohtaisesti analyyttisen geometrian aikana, ja halukkaat voivat viitata artikkeliin Tason suoran yhtälö.

Neliöfunktiokaavio, kuutiofunktiograafi, polynomigraafi

Paraabeli. Ajoittaa neliöfunktio () on paraabeli. Harkitse kuuluisa tapaus:

Muistetaan joitain funktion ominaisuuksia.

Joten, ratkaisu yhtälöimme: - tässä pisteessä sijaitsee paraabelin kärki. Miksi näin on, voidaan oppia derivaatta käsittelevästä teoreettisesta artikkelista ja funktion ääripäistä. Sillä välin laskemme vastaavan y:n arvon:

Huippupiste on siis pisteessä

Nyt löydämme muita pisteitä, samalla kun käytämme röyhkeästi paraabelin symmetriaa. On huomattava, että toiminto – ei ole tasainen, mutta kukaan ei kuitenkaan kumonnut paraabelin symmetriaa.

Missä järjestyksessä jäljellä olevat pisteet löydetään, luulen, että se selviää finaalipöydästä:

Tämä algoritmi rakentamista voidaan kuvainnollisesti kutsua "sukkulaksi" tai "edestakaisin" -periaatteeksi Anfisa Chekhovan kanssa.

Tehdään piirustus:

Tarkastetuista kaavioista tulee mieleen toinen hyödyllinen ominaisuus:

Neliöfunktiolle () seuraava pitää paikkansa:

Jos , niin paraabelin haarat on suunnattu ylöspäin.

Jos , niin paraabelin haarat on suunnattu alaspäin.

Käyrästä saa syvällistä tietoa oppitunnilla Hyperbola ja parabola.

Kuutioparaabeli saadaan funktiolla . Tässä koulusta tuttu piirros:

Luettelemme funktion tärkeimmät ominaisuudet

Funktiokaavio

Se edustaa yhtä paraabelin haaroista. Tehdään piirustus:

Toiminnon tärkeimmät ominaisuudet:

Tässä tapauksessa akseli on vertikaalinen asymptootti hyperbolakaaviolle osoitteessa .

On SUURI virhe, jos annat kaavion leikkaamisen asymptootin kanssa huolimattomuudesta piirustusta tehdessäsi.

Myös yksipuoliset rajat, kerro meille, että hyperboli ei ole rajoitettu ylhäältä ja ei rajoitettu alhaalta.

Tutkitaan funktiota äärettömyydessä: eli jos alamme liikkua akselia pitkin vasemmalle (tai oikealle) äärettömään, niin "peleistä" tulee hoikka askel äärettömän lähellä lähestyy nollaa, ja vastaavasti hyperbelin haarat äärettömän lähellä lähestyä akselia.

Eli akseli on horisontaalinen asymptootti funktion kuvaajalle, jos "x" pyrkii plus tai miinus äärettömyyteen.

Toiminto on outo, mikä tarkoittaa, että hyperboli on symmetrinen origon suhteen. Tämä fakta on ilmeistä piirroksesta, lisäksi se voidaan helposti todentaa analyyttisesti: .

Muodon () funktion kuvaaja edustaa hyperbelin kahta haaraa.

Jos , Hyperbola sijaitsee ensimmäisessä ja kolmannessa koordinaattineljänneksessä(katso kuva yllä).

Jos , Hyperbola sijaitsee toisessa ja neljännessä koordinaattineljänneksessä.

Hyperbolin asuinpaikan määriteltyä säännöllisyyttä ei ole vaikea analysoida graafien geometristen muunnosten näkökulmasta.

Esimerkki 3

Muodosta hyperbelin oikea haara

Käytämme pistemäistä rakennusmenetelmää, mutta on edullista valita arvot siten, että ne jakautuvat kokonaan:

Tehdään piirustus:

Hyperbolan vasemman haaran rakentaminen ei ole vaikeaa, tässä funktion omituisuus vain auttaa. Karkeasti sanottuna, pisteviivaisessa rakennustaulukossa, lisää henkisesti miinus jokaiseen numeroon, laita vastaavat pisteet ja piirrä toinen haara.

Tarkat geometriset tiedot tarkasteltavasta viivasta löytyvät artikkelista Hyperbola ja parabola.

Kuvaaja eksponentiaalisesta funktiosta

AT tämä kohta Harkitsen välittömästi eksponentiaalista funktiota, koska korkeamman matematiikan ongelmissa 95% tapauksista esiintyy eksponenttia.

Muistutan, että tämä on irrationaalinen luku: , tätä vaaditaan rakennettaessa graafia, jonka itse asiassa rakennan ilman seremonioita. Kolme pistettä varmaan riittää:

Jätetään funktion kuvaaja toistaiseksi rauhaan, siitä myöhemmin.

Toiminnon tärkeimmät ominaisuudet:

Periaatteessa funktioiden kaaviot näyttävät samalta jne.

Minun on sanottava, että toinen tapaus on vähemmän yleinen käytännössä, mutta sitä esiintyy, joten katsoin tarpeelliseksi sisällyttää se tähän artikkeliin.

Logaritmisen funktion kuvaaja

Harkitse funktiota kanssa luonnollinen logaritmi.
Piirretään viiva:

Jos olet unohtanut mikä logaritmi on, katso koulun oppikirjoja.

Toiminnon tärkeimmät ominaisuudet:

Verkkotunnus:

Arvoalue: .

Toimintoa ei ole rajoitettu ylhäältä: , vaikkakin hitaasti, mutta logaritmin haara nousee äärettömyyteen.
Tarkastellaan oikealla lähellä nollaa olevan funktion käyttäytymistä: . Eli akseli on vertikaalinen asymptootti funktion kuvaajalle, jossa "x" pyrkii nollaan oikealla.

Muista tietää ja muistaa logaritmin tyypillinen arvo: .

Pohjimmiltaan logaritmin kaavio pohjassa näyttää samalta: , , ( desimaalilogaritmi pohjassa 10) jne. Samaan aikaan, kuin enemmän pohjaa, sitä litteämpi kaavio on.

Emme käsittele tapausta, en muista milloin viime kerta rakensi graafin sellaisella pohjalla. Kyllä, ja logaritmi näyttää olevan erittäin harvinainen vieras korkeamman matematiikan ongelmissa.

Kappaleen lopuksi sanon vielä yhden tosiasian: Eksponentti funktio ja logaritminen funktio ovat kaksi keskinäistä käänteiset funktiot . Jos katsot tarkasti logaritmin kuvaajaa, voit nähdä, että tämä on sama eksponentti, vain se sijaitsee hieman eri tavalla.

Trigonometristen funktioiden kuvaajat

Miten trigonometrinen piina alkaa koulussa? oikein. Sinistä

Piirretään funktio

Tämä rivi nimeltään sinusoidi.

Muistutan, että "pi" on irrationaalinen luku: ja trigonometriassa se häikäisee silmissä.

Toiminnon tärkeimmät ominaisuudet:

Tämä toiminto On kausijulkaisu jaksolla. Mitä se tarkoittaa? Katsotaanpa leikkausta. Sen vasemmalla ja oikealla puolella täsmälleen sama kaavion pala toistuu loputtomasti.

Verkkotunnus: , eli mille tahansa "x":n arvolle on siniarvo.

Arvoalue: . Toiminto on rajoitettu: , eli kaikki "pelit" ovat tiukasti segmentissä .
Tätä ei tapahdu: tai tarkemmin sanottuna tapahtuu, mutta näillä yhtälöillä ei ole ratkaisua.

Tehofunktion tarkastelun helpottamiseksi tarkastelemme neljää erillistä tapausta: tehofunktiota luonnollinen indikaattori, potenssifunktio kokonaislukueksponentilla, potenssifunktio kanssa järkevä indikaattori ja tehotoiminto irrationaalinen indikaattori.

Tehofunktio luonnollisella eksponentilla

Aluksi otamme käyttöön tutkinnon käsitteen luonnollisella eksponentilla.

Määritelmä 1

Luonnollisen eksponentin $n$ reaaliluvun $a$ potenssi on luku yhtä suuri kuin tuote$n$ tekijät, joista jokainen on yhtä suuri kuin luku $a$.

Kuva 1.

$a$ on tutkinnon perusta.

$n$ - eksponentti.

Tarkastellaan nyt potenssifunktiota, jolla on luonnollinen eksponentti, sen ominaisuuksia ja kuvaaja.

Määritelmä 2

$f\left(x\right)=x^n$ ($n\in N)$ kutsutaan potenssifunktioksi, jolla on luonnollinen eksponentti.

Lisämukavuuden vuoksi harkitse erikseen potenssifunktiota, jossa on parillinen eksponentti $f\left(x\right)=x^(2n)$ ja potenssifunktiota parittoman eksponentin kanssa $f\left(x\right)=x^(2n- 1)$ ($n\in N)$.

Luonnollisen parillisen eksponentin potenssifunktion ominaisuudet

$f\left(-x\right)=((-x))^(2n)=x^(2n)=f(x)$ on parillinen funktio.

Laajuus -- $ \

Funktio pienenee muodossa $x\in (-\infty ,0)$ ja kasvaa muodossa $x\in (0,+\infty)$.

$f("")\left(x\right)=(\left(2n\cdot x^(2n-1)\right))"=2n(2n-1)\cdot x^(2(n-1) ))\ge 0 $

Funktio on konveksi koko määritelmäalueella.

Käyttäytyminen laajuuden päissä:

\[(\mathop(lim)_(x\to -\infty ) x^(2n)\ )=+\infty \] \[(\mathop(lim)_(x\to +\infty ) x^( 2n)\ )=+\infty \]

Kaavio (kuva 2).

Kuva 2. Kuvaaja funktiosta $f\left(x\right)=x^(2n)$

Luonnollisen parittoman eksponentin potenssifunktion ominaisuudet

Määritelmäalue on kaikki reaaliluvut.

$f\left(-x\right)=((-x))^(2n-1)=(-x)^(2n)=-f(x)$ on pariton funktio.

$f(x)$ on jatkuva koko määritelmäalueella.

Alue on kaikki reaalilukuja.

$f"\left(x\right)=\left(x^(2n-1)\right)"=(2n-1)\cdot x^(2(n-1))\ge 0$

Funktio kasvaa koko määrittelyalueen yli.

$f\left(x\right)0$, $x\in (0,+\infty)$.

$f(""\left(x\right))=(\left(\left(2n-1\right)\cdot x^(2\left(n-1\right))\right))"=2 \left(2n-1\right)(n-1)\cdot x^(2n-3)$

\ \

Funktio on kovera arvolle $x\in (-\infty ,0)$ ja kupera arvolle $x\in (0,+\infty)$.

Kaavio (kuva 3).

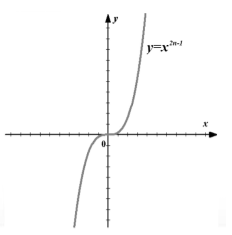
Kuva 3. Kuvaaja funktiosta $f\left(x\right)=x^(2n-1)$

Potenttifunktio kokonaislukueksponentilla

Aluksi otamme käyttöön asteen käsitteen kokonaislukueksponentilla.

Määritelmä 3

Tutkinto oikea numero$a$ kokonaislukuindeksillä $n$ määritetään kaavalla:

Kuva 4

Tarkastellaan nyt potenssifunktiota, jossa on kokonaislukueksponentti, sen ominaisuuksia ja kuvaajaa.

Määritelmä 4

$f\left(x\right)=x^n$ ($n\in Z)$ kutsutaan potenssifunktioksi, jossa on kokonaislukueksponentti.

Jos aste on suurempi kuin nolla, niin päästään luonnollisen eksponentin potenssifunktion tapaukseen. Olemme jo pohtineet sitä edellä. Saat $n=0$ lineaarinen funktio$y=1$. Jätämme sen pohdinnan lukijalle. On vielä tarkasteltava negatiivisen kokonaislukueksponentin potenssifunktion ominaisuuksia

Negatiivisen kokonaislukueksponentin potenssifunktion ominaisuudet

Alue on $\left(-\infty ,0\right)(0,+\infty)$.

Jos eksponentti on parillinen, funktio on parillinen, jos se on pariton, niin funktio on pariton.

$f(x)$ on jatkuva koko määritelmäalueella.

Arvoalue:

Jos eksponentti on parillinen, niin $(0,+\infty)$, jos pariton, niin $\left(-\infty ,0\right)(0,+\infty)$.

Jos eksponentti on pariton, funktio pienenee muodossa $x\in \left(-\infty ,0\right)(0,+\infty)$. Parillisen eksponentin kohdalla funktio pienenee muodossa $x\in (0,+\infty)$. ja kasvaa muodossa $x\in \left(-\infty ,0\right)$.

$f(x)\ge 0$ koko verkkotunnuksessa