Função liga-desliga, suas propriedades e gráfico Material de demonstração Aula-aula Conceito de função. Propriedades da função. Função potência, suas propriedades e gráfico. Grau 10 Todos os direitos reservados. Direitos autorais com Direitos autorais com

Progresso da lição: Repetição. Função. Propriedades da função. Aprendendo novos materiais. 1. Definição de função de potência Definição de função de potência. 2. Propriedades e gráficos de funções de potência Propriedades e gráficos de funções de potência. Consolidação do material estudado. Contagem verbal. Contagem verbal. Resumo da lição. Lição de casa.

Domínio e intervalo da função Todos os valores da variável independente formam o domínio da função x y=f(x) f Domínio da função Domínio da função Todos os valores que a variável dependente assume formam o domínio da função Função. Propriedades da função

Gráfico de uma função Seja uma função onde xY y x.75 3 0.6 4 0.5 O gráfico de uma função é o conjunto de todos os pontos do plano coordenado, cujas abcissas são iguais aos valores do argumento, e as ordenadas são iguais aos valores correspondentes da função. Função. Propriedades da função

Y x Domínio de definição e alcance da função 4 y=f(x) Domínio da função: Domínio da função: Função. Propriedades da função

Função par y x y=f(x) Gráfico função par simétrica em relação ao eixo y A função y=f(x) é chamada mesmo se f(-x) = f(x) para qualquer x do domínio da função Function. Propriedades da função

Função ímpar y x y=f(x) Gráfico Função estranha simétrica em relação à origem O(0;0) A função y=f(x) é chamada ímpar se f(-x) = -f(x) para qualquer x do domínio da função Function. Propriedades da função

Definição de uma função de potência Uma função, onde p é um dado número real, é chamada de função de potência. p y \u003d x p P \u003d x y 0 Progresso da lição

Função de potência x y 1. O domínio de definição e o intervalo de valores das funções de potência da forma, onde n é número natural, são todos números reais. 2. Essas funções são ímpares. Seu gráfico é simétrico em relação à origem. Propriedades e gráficos da função de potência

Funções de potência com expoente racional positivo Domínio de definição - todos números positivos e o número 0. O intervalo de funções com tal expoente é também todos os números positivos e o número 0. Essas funções não são nem pares nem ímpares. y x Propriedades e Gráficos da Função Potência

Função de potência com racional indicador negativo. O domínio de definição e alcance de tais funções são todos números positivos. As funções não são nem pares nem ímpares. Tais funções diminuem em todo o seu domínio de definição. y x Propriedades e gráficos da função potência Progresso da lição

1. Função potência, suas propriedades e gráfico;

2. Transformações:

Transferência paralela;

Simetria em torno dos eixos coordenados;

Simetria sobre a origem;

Simetria sobre a reta y = x;

Esticando e encolhendo ao longo dos eixos de coordenadas.

3. Uma função exponencial, suas propriedades e gráfico, transformações semelhantes;

4. Função logarítmica, suas propriedades e gráfico;

5. Função trigonométrica, suas propriedades e gráfico, transformações semelhantes (y = sin x; y = cos x; y = tg x);

Função: y = x\n - suas propriedades e gráfico.

Função potência, suas propriedades e gráfico

y \u003d x, y \u003d x 2, y \u003d x 3, y \u003d 1 / x etc. Todas essas funções são casos especiais da função de potência, ou seja, a função y = xp, onde p é um número real dado.
As propriedades e o gráfico de uma função de potência dependem essencialmente das propriedades de uma potência com um expoente real e, em particular, dos valores para os quais x e p faz sentido xp. Passemos a uma consideração semelhante. várias ocasiões dependendo do
expoente pág.

1. Índice p = 2né um número natural par.

y=x2n, Onde né um número natural e tem as seguintes propriedades:

• o domínio de definição são todos os números reais, ou seja, o conjunto R;
• conjunto de valores - números não negativos, ou seja, y é maior ou igual a 0;
• função y=x2n até porque x 2n = (-x) 2n
• a função é decrescente no intervalo x< 0 e aumentando no intervalo x > 0.

Gráfico de funções y=x2n tem a mesma forma que, por exemplo, o gráfico de uma função y=x4.

2. Indicador p = 2n - 1- número natural ímpar

Neste caso, a função de potência y=x2n-1, onde é um número natural, tem as seguintes propriedades:

• domínio de definição - conjunto R;
• conjunto de valores - conjunto R;
• função y=x2n-1 estranho porque (- x) 2n-1= x 2n-1;
• a função é crescente em todo o eixo real.

Gráfico de funções y=x2n-1 y=x3.

3. Indicador p=-2n, Onde n- número natural.

Neste caso, a função de potência y=x-2n=1/x2n tem as seguintes propriedades:

• conjunto de valores - números positivos y>0;
• função y = 1/x2n até porque 1/(-x) 2n= 1/x2n;
• a função é crescente no intervalo x0.

Gráfico da função y = 1/x2n tem a mesma forma que, por exemplo, o gráfico da função y = 1/x2.

4. Indicador p = -(2n-1), Onde n- número natural.
Neste caso, a função de potência y=x-(2n-1) tem as seguintes propriedades:

• o domínio de definição é o conjunto R, exceto para x = 0;
• conjunto de valores - conjunto R, exceto para y = 0;
• função y=x-(2n-1) estranho porque (- x)-(2n-1) = -x-(2n-1);
• a função é decrescente nos intervalos x< 0 e x > 0.

Gráfico de funções y=x-(2n-1) tem a mesma forma que, por exemplo, o gráfico da função y = 1/x3.

o material metódicoé apenas para referência e se aplica a uma grande variedade tópicos. O artigo fornece uma visão geral dos gráficos das principais funções elementares e considera a pergunta mais importante – como construir um gráfico corretamente e RÁPIDO. Durante o estudo matemática superior sem conhecer os gráficos das funções elementares básicas, será difícil, por isso é muito importante lembrar como são os gráficos de uma parábola, hipérbole, seno, cosseno, etc., lembre-se de alguns valores de função. Também falaremos sobre algumas propriedades das funções principais.

Não pretendo ser materiais completos e cientificamente completos, a ênfase será colocada, em primeiro lugar, na prática - aquelas coisas com as quais é preciso enfrentar literalmente a cada passo, em qualquer tópico de matemática superior. Gráficos para manequins? Você pode dizer assim.

Por inúmeros pedidos leitores índice clicável:

Além disso, há um resumo ultracurto sobre o tema
- domine 16 tipos de gráficos estudando SEIS páginas!

Sério, seis, até eu mesmo fiquei surpreso. Este resumo contém gráficos aprimorados e está disponível por uma taxa nominal, uma versão demo pode ser visualizada. É conveniente imprimir o arquivo para que os gráficos estejam sempre à mão. Obrigado por apoiar o projeto!

E começamos logo:

Como construir eixos coordenados corretamente?

Na prática, as provas são quase sempre elaboradas pelos alunos em cadernos separados, alinhados em uma gaiola. Por que você precisa de marcações quadriculadas? Afinal, o trabalho, em princípio, pode ser feito em folhas A4. E a gaiola é necessária apenas para o design preciso e de alta qualidade dos desenhos.

Qualquer desenho de um gráfico de função começa com eixos de coordenadas.

Os desenhos são bidimensionais e tridimensionais.

Consideremos primeiro o caso bidimensional cartesiano sistema retangular coordenadas:

1) Nós desenhamos eixos de coordenadas. O eixo é chamado eixo x , e o eixo eixo y . Nós sempre tentamos desenhá-los limpo e não torto. As flechas também não devem se parecer com a barba de Papa Carlo.

2) Assinamos os eixos letras maiúsculas"x" e "y". Não se esqueça de assinar os eixos.

3) Defina a escala ao longo dos eixos: desenhar zero e dois uns. Ao fazer um desenho, a escala mais conveniente e comum é: 1 unidade = 2 células (desenho à esquerda) - mantenha-a se possível. No entanto, de vez em quando acontece que o desenho não cabe em uma folha de caderno - então reduzimos a escala: 1 unidade = 1 célula (desenho à direita). Raramente, mas acontece que a escala do desenho tem que ser reduzida (ou aumentada) ainda mais

NÃO rabiscar de uma metralhadora ... -5, -4, -3, -1, 0, 1, 2, 3, 4, 5, .... Por plano de coordenadas não é um monumento a Descartes, e o estudante não é uma pomba. Nós colocamos zero e duas unidades ao longo dos eixos. As vezes ao invés de unidades, é conveniente “detectar” outros valores, por exemplo, “dois” no eixo das abcissas e “três” no eixo das ordenadas - e este sistema (0, 2 e 3) também definirá exclusivamente a grade de coordenadas.

É melhor estimar as dimensões estimadas do desenho ANTES do desenho ser desenhado.. Então, por exemplo, se a tarefa requer desenhar um triângulo com vértices , , , então é bastante claro que a escala popular 1 unidade = 2 células não funcionará. Por quê? Vejamos o ponto - aqui você tem que medir quinze centímetros para baixo e, obviamente, o desenho não caberá (ou mal caberá) em uma folha de caderno. Portanto, selecionamos imediatamente uma escala menor 1 unidade = 1 célula.

By the way, cerca de centímetros e células de notebook. É verdade que existem 15 centímetros em 30 células de notebook? Meça em um caderno para juros 15 centímetros com uma régua. Na URSS, talvez isso fosse verdade... É interessante notar que se você medir esses mesmos centímetros na horizontal e na vertical, os resultados (em células) serão diferentes! Estritamente falando, os notebooks modernos não são quadriculados, mas retangulares. Pode parecer bobagem, mas desenhar, por exemplo, um círculo com uma bússola em tais situações é muito inconveniente. Para ser honesto, nesses momentos você começa a pensar na correção do camarada Stalin, que foi enviado para campos de trabalho hacker na produção, sem mencionar a indústria automotiva doméstica, aviões caindo ou usinas elétricas explodindo.

Falando em qualidade, ou recomendação curta por papelaria. Até o momento, a maioria dos notebooks está à venda, palavrões para não mencionar, uma merda completa. Pelo motivo de ficarem molhadas, e não apenas de canetas de gel, mas também de canetas esferográficas! Economize no papel. Para liberação controle funciona Eu recomendo usar os cadernos do Arkhangelsk Pulp and Paper Mill (18 folhas, gaiola) ou Pyaterochka, embora seja mais caro. É aconselhável escolher uma caneta de gel, mesmo a recarga de gel chinesa mais barata é muito melhor do que uma caneta esferográfica, que mancha ou rasga o papel. O único "competitivo" caneta esferográfica na minha memória é "Erich Krause". Ela escreve com clareza, beleza e estabilidade - seja com uma haste cheia ou com uma quase vazia.

Adicionalmente: vendo um sistema de coordenadas retangulares com os olhos geometria analítica coberto no artigo (não) dependência linear de vetores. Base vetorial, informação detalhada cerca de coordenar quartos pode ser encontrado no segundo parágrafo da lição Desigualdades lineares.

caso 3D

Aqui é quase igual.

1) Desenhamos eixos coordenados. Padrão: aplicar eixo – direcionado para cima, eixo – direcionado para a direita, eixo – para baixo para a esquerda estritamente em um ângulo de 45 graus.

2) Assinamos os eixos.

3) Defina a escala ao longo dos eixos. Escala ao longo do eixo - duas vezes menor que a escala ao longo dos outros eixos. Observe também que no desenho certo, usei uma "serif" não padrão ao longo do eixo (esta possibilidade já foi mencionada acima). Do meu ponto de vista, é mais preciso, rápido e esteticamente mais agradável - você não precisa procurar o meio da célula sob um microscópio e “esculpir” a unidade até a origem.

Ao fazer um desenho 3D novamente - dê prioridade à escala
1 unidade = 2 células (desenho à esquerda).

Para que servem todas essas regras? As regras existem para serem quebradas. O que eu vou fazer agora. O fato é que os desenhos subsequentes do artigo serão feitos por mim no Excel, e os eixos de coordenadas parecerão incorretos do ponto de vista de projeto correto. Eu poderia desenhar todos os gráficos à mão, mas é realmente assustador desenhá-los, pois o Excel reluta em desenhá-los com muito mais precisão.

Gráficos e propriedades básicas de funções elementares

A função linear é dada pela equação . O gráfico da função linear é direto. Para construir uma reta, basta conhecer dois pontos.

Exemplo 1

Plote a função. Vamos encontrar dois pontos. É vantajoso escolher zero como um dos pontos.

Se então

Tomamos outro ponto, por exemplo, 1.

Se então

Ao preparar tarefas, as coordenadas dos pontos geralmente são resumidas em uma tabela:

E os próprios valores são calculados oralmente ou em um rascunho, calculadora.

Dois pontos são encontrados, vamos desenhar:

Ao elaborar um desenho, sempre assinamos os gráficos.

Não será supérfluo recordar casos especiais de uma função linear:

Observe como coloquei as legendas, assinaturas não devem ser ambíguas ao estudar o desenho. NO este caso era extremamente indesejável colocar uma assinatura próximo ao ponto de interseção das linhas, ou no canto inferior direito entre os gráficos.

1) Uma função linear da forma () é chamada de proporcionalidade direta. Por exemplo, . O gráfico de proporcionalidade direta sempre passa pela origem. Assim, a construção de uma linha reta é simplificada - basta encontrar apenas um ponto.

2) Uma equação da forma define uma linha reta paralela ao eixo, em particular, o próprio eixo é dado pela equação. O gráfico da função é construído imediatamente, sem encontrar nenhum ponto. Ou seja, a entrada deve ser entendida da seguinte forma: "y é sempre igual a -4, para qualquer valor de x."

3) Uma equação da forma define uma linha reta paralela ao eixo, em particular, o próprio eixo é dado pela equação. O gráfico da função também é construído imediatamente. A entrada deve ser entendida da seguinte forma: "x é sempre, para qualquer valor de y, igual a 1."

Alguns vão perguntar, bem, por que lembrar do 6º ano?! É assim, talvez seja, apenas durante os anos de prática conheci uma boa dúzia de alunos que ficaram perplexos com a tarefa de construir um gráfico como ou .

Desenhar uma linha reta é a ação mais comum ao fazer desenhos.

A linha reta é discutida em detalhes no curso de geometria analítica, e aqueles que desejarem podem consultar o artigo Equação de uma linha reta em um plano.

Gráfico de função quadrática, gráfico de função cúbica, gráfico polinomial

Parábola. Cronograma função quadrática () é uma parábola. Considerar caso famoso:

Vamos relembrar algumas propriedades da função.

Assim, a solução da nossa equação: - é neste ponto que se encontra o vértice da parábola. Por que isso é assim pode ser aprendido com o artigo teórico sobre a derivada e a lição sobre os extremos da função. Enquanto isso, calculamos o valor correspondente de "y":

Então o vértice está no ponto

Agora encontramos outros pontos, usando descaradamente a simetria da parábola. Vale lembrar que a função – não é mesmo, mas, no entanto, ninguém cancelou a simetria da parábola.

Em que ordem encontrar os pontos restantes, acho que ficará claro na mesa final:

Este algoritmo construção pode ser figurativamente chamada de "ônibus" ou o princípio de "vai e volta" com Anfisa Chekhova.

Vamos fazer um desenho:

Dos gráficos considerados, outro recurso útil vem à mente:

Para uma função quadrática () o seguinte é verdadeiro:

Se , então os ramos da parábola são direcionados para cima.

Se , então os ramos da parábola são direcionados para baixo.

O conhecimento aprofundado da curva pode ser obtido na lição Hipérbole e parábola.

A parábola cúbica é dada pela função . Aqui está um desenho familiar da escola:

Listamos as principais propriedades da função

Gráfico de funções

Representa um dos ramos da parábola. Vamos fazer um desenho:

As principais propriedades da função:

Neste caso, o eixo é assíntota vertical para o gráfico da hipérbole em .

Será um GRANDE erro se, ao fazer um desenho, por negligência, você permitir que o gráfico se cruze com a assíntota.

Também limites unilaterais, diga-nos que uma hipérbole não limitado de cima e não limitado a partir de baixo.

Vamos explorar a função no infinito: , ou seja, se começarmos a nos mover ao longo do eixo para a esquerda (ou direita) para o infinito, então os “jogos” serão um passo estreito infinitamente perto se aproximam de zero e, consequentemente, os ramos da hipérbole infinitamente perto aproximar do eixo.

Então o eixo é assíntota horizontal para o gráfico da função, se "x" tende a mais ou menos infinito.

A função é ímpar, o que significa que a hipérbole é simétrica em relação à origem. Este fatoé óbvio a partir do desenho, além disso, pode ser facilmente verificado analiticamente: .

O gráfico de uma função da forma () representa dois ramos de uma hipérbole.

Se , então a hipérbole está localizada no primeiro e terceiro quadrantes de coordenadas(veja a imagem acima).

Se , então a hipérbole está localizada no segundo e quarto quadrantes de coordenadas.

Não é difícil analisar a regularidade especificada do local de residência da hipérbole do ponto de vista das transformações geométricas dos gráficos.

Exemplo 3

Construir o ramo direito da hipérbole

Usamos o método de construção pontual, embora seja vantajoso selecionar os valores para que eles se dividam completamente:

Vamos fazer um desenho:

Não será difícil construir o ramo esquerdo da hipérbole, aqui a estranheza da função só ajudará. Grosso modo, na tabela de construção pontual, adicione mentalmente um menos a cada número, coloque os pontos correspondentes e desenhe o segundo ramo.

Informações geométricas detalhadas sobre a linha considerada podem ser encontradas no artigo Hyperbola and parabola.

Gráfico de uma função exponencial

NO este parágrafo Vou considerar imediatamente a função exponencial, pois nos problemas de matemática superior em 95% dos casos é o expoente que ocorre.

Lembro-lhe que este é Número irracional: , isso será necessário ao construir um gráfico, que, de fato, construirei sem cerimônia. Três pontos provavelmente o suficiente:

Vamos deixar o gráfico da função em paz por enquanto, sobre isso mais tarde.

As principais propriedades da função:

Fundamentalmente, os gráficos das funções parecem os mesmos, etc.

Devo dizer que o segundo caso é menos comum na prática, mas ocorre, então achei necessário incluí-lo neste artigo.

Gráfico de uma função logarítmica

Considere uma função com Logaritmo natural.
Vamos fazer um desenho de linha:

Se você esqueceu o que é um logaritmo, consulte os livros escolares.

As principais propriedades da função:

Domínio:

Faixa de valores: .

A função não é limitada a partir de cima: , embora lentamente, mas o ramo do logaritmo vai até o infinito.
Vamos examinar o comportamento da função perto de zero à direita: . Então o eixo é assíntota vertical para o gráfico da função com "x" tendendo a zero à direita.

Certifique-se de conhecer e lembrar o valor típico do logaritmo: .

Fundamentalmente, o gráfico do logaritmo na base parece o mesmo: , , ( logaritmo decimal na base 10), etc. Ao mesmo tempo, do que mais base, mais plano será o gráfico.

Não vamos considerar o caso, não me lembro quando última vez construiu um gráfico com essa base. Sim, e o logaritmo parece ser um convidado muito raro em problemas de matemática superior.

Para concluir o parágrafo, direi mais um fato: Função exponencial e função logarítmica são dois mútuos funções inversas . Se você observar atentamente o gráfico do logaritmo, poderá ver que este é o mesmo expoente, apenas localizado de forma um pouco diferente.

Gráficos de funções trigonométricas

Como o tormento trigonométrico começa na escola? Corretamente. Do seno

Vamos plotar a função

Está linha chamado sinusóide.

Relembro que “pi” é um número irracional: e em trigonometria deslumbra aos olhos.

As principais propriedades da função:

Esta funçãoé periódico com um período. O que isto significa? Vejamos o corte. À esquerda e à direita, exatamente a mesma parte do gráfico se repete infinitamente.

Domínio: , ou seja, para qualquer valor de "x" existe um valor de seno.

Faixa de valores: . A função é limitado: , ou seja, todos os “jogos” ficam estritamente no segmento .
Isso não acontece: ou, mais precisamente, acontece, mas essas equações não têm solução.

Para a conveniência de considerar uma função potência, consideraremos 4 casos separados: uma função potência com indicador natural, função potência com expoente inteiro, função potência com indicador racional e função de potência com indicador irracional.

Função de potência com expoente natural

Para começar, introduzimos o conceito de grau com um expoente natural.

Definição 1

A potência de um número real $a$ com expoente natural $n$ é o número igual ao produto$n$ fatores, cada um dos quais é igual ao número $a$.

Imagem 1.

$a$ é a base do grau.

$n$ - expoente.

Considere agora uma função potência com um expoente natural, suas propriedades e gráfico.

Definição 2

$f\left(x\right)=x^n$ ($n\in N)$ é chamada de função potência com expoente natural.

Para maior conveniência, considere separadamente a função potência com expoente par $f\left(x\right)=x^(2n)$ e a função potência com expoente ímpar $f\left(x\right)=x^(2n- 1)$ ($n\in N)$.

Propriedades de uma função potência com expoente par natural

$f\left(-x\right)=((-x))^(2n)=x^(2n)=f(x)$ é uma função par.

Escopo -- $ \

A função diminui conforme $x\in (-\infty ,0)$ e aumenta conforme $x\in (0,+\infty)$.

$f("")\left(x\right)=(\left(2n\cdot x^(2n-1)\right))"=2n(2n-1)\cdot x^(2(n-1) ))\ge 0$

A função é convexa em todo o domínio de definição.

Comportamento nas extremidades do escopo:

\[(\mathop(lim)_(x\to -\infty ) x^(2n)\ )=+\infty \] \[(\mathop(lim)_(x\to +\infty ) x^( 2n)\ )=+\infty\]

Gráfico (Fig. 2).

Figura 2. Gráfico da função $f\left(x\right)=x^(2n)$

Propriedades de uma função potência com expoente ímpar natural

O domínio de definição são todos os números reais.

$f\left(-x\right)=((-x))^(2n-1)=(-x)^(2n)=-f(x)$ é uma função ímpar.

$f(x)$ é contínua em todo o domínio de definição.

O intervalo são todos os números reais.

$f"\left(x\right)=\left(x^(2n-1)\right)"=(2n-1)\cdot x^(2(n-1))\ge 0$

A função aumenta em todo o domínio de definição.

$f\left(x\right)0$, para $x\in (0,+\infty)$.

$f(""\left(x\right))=(\left(\left(2n-1\right)\cdot x^(2\left(n-1\right))\right))"=2 \left(2n-1\right)(n-1)\cdot x^(2n-3)$

\ \

A função é côncava para $x\in (-\infty ,0)$ e convexa para $x\in (0,+\infty)$.

Gráfico (Fig. 3).

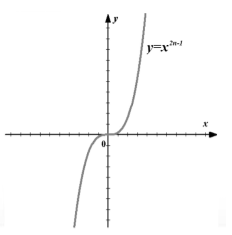
Figura 3. Gráfico da função $f\left(x\right)=x^(2n-1)$

Função de potência com expoente inteiro

Para começar, introduzimos o conceito de grau com um expoente inteiro.

Definição 3

Grau número real$a$ com índice inteiro $n$ é determinado pela fórmula:

Figura 4

Considere agora uma função potência com um expoente inteiro, suas propriedades e gráfico.

Definição 4

$f\left(x\right)=x^n$ ($n\in Z)$ é chamada de função potência com expoente inteiro.

Se o grau for maior que zero, chegamos ao caso de uma função potência com um expoente natural. Já discutimos isso acima. Para $n=0$ temos Função linear$y=1$. Deixamos sua consideração para o leitor. Resta considerar as propriedades de uma função de potência com um expoente inteiro negativo

Propriedades de uma função potência com um expoente inteiro negativo

O escopo é $\left(-\infty ,0\right)(0,+\infty)$.

Se o expoente for par, então a função é par; se for ímpar, então a função é ímpar.

$f(x)$ é contínua em todo o domínio de definição.

Faixa de valor:

Se o expoente for par, então $(0,+\infty)$, se for ímpar, então $\left(-\infty ,0\right)(0,+\infty)$.

Se o expoente for ímpar, a função diminui como $x\in \left(-\infty ,0\right)(0,+\infty)$. Para um expoente par, a função diminui como $x\in (0,+\infty)$. e aumenta como $x\in \left(-\infty ,0\right)$.

$f(x)\ge 0$ em todo o domínio