Seite 1

Der Schwingungsvorgang im Niederspannungskreis stoppt bereits während der ersten Periode hochfrequenter Schwingungen, da in der zweiten Hälfte der Periode dieser Schwingungen die Richtung des Stroms der Stromrichtung im Leistungskreis entgegengesetzt wird. Um die Helligkeit des Funkens im Generator zu erhöhen, ist es möglich, die Kapazität weiter zu erhöhen.

Schwingungsvorgänge umfassen ein breites Spektrum von Phänomenen, die durch die Wiederholung ihrer Charakteristika hindurch gekennzeichnet sind bestimmte Intervalle Zeit.

Ein Schwingungsvorgang tritt in einem System auf, wenn neben einer Kraft, die es aus dem Gleichgewicht bringt, auch eine rückstellende (zurückkehrende) Kraft vorhanden ist. Was passiert, wenn die Rückstellkraft mit konstanter Verzögerung auf das System einwirkt. Wenn darüber hinaus eine solche Instabilität, verbunden mit Verzögerungseffekten, schädlich für die Stabilisierungsmechanismen des Schiffs ist, dann ist sie bei der Entwicklung elektronischer Generatoren nützlich.

Die Schwingungsvorgänge, die die Größe der dynamischen Belastungen auf die Stäbe bestimmen, bestimmen wesentlich die Form der in der Nähe des polierten Stabes aufgenommenen Dynamogramme.

Der Schwingungsvorgang in der Schaltung findet unter Nicht-Null-Anfangsbedingungen statt. Der Anfangsstrom in der Induktivität x wird aus folgenden Überlegungen bestimmt. Schalter B unterbricht den Stromkreis, wenn der Strom tB - i0 - ic durch Null geht.

Auch in elektrischen Maschinen und anderen elektrischen Anlagen mit erheblicher Induktivität und rotierenden Massen können beim Ein-, Aus- und Einschalten schwingende Vorgänge auftreten. abrupte Änderungen Betriebsart. Unter bestimmten Bedingungen treten nicht gedämpfte, sondern schwingende Schwingungen auf. Solche Schwankungen können dazu führen schwerwiegende Verstöße Betrieb elektrischer Anlagen und sogar Unfälle verursachen. Daher müssen bei der Entwicklung von Steuerungen für elektrische Maschinen und andere Anlagen in manchen Fällen besondere Maßnahmen ergriffen werden, um schwingende Vorgänge möglichst schnell zu dämpfen (Widerstände in ihre Schaltkreise einführen usw.).

Oszillationsprozesse und Oszillationsgrenzen der Stabilität verschiedener nichtlineare Systeme kann oft bestimmt werden durch harmonische Linearisierung, dessen Konzept oben angegeben wurde. Es gibt auch andere Methoden. Am effektivsten sind hier die numerisch-grafischen Methoden zur Konstruktion transienter Vorgänge, sowie insbesondere die Methoden der elektrischen Simulation an mathematischen Maschinen kontinuierlicher und diskreter Wirkung.

Oszillatorische Prozesse und oszillatorische Stabilitätsgrenzen verschiedener nichtlinearer Systeme können oft durch die Methode der harmonischen Linearisierung bestimmt werden, deren Konzept oben angegeben wurde.

Schwingungsvorgänge sind in Natur und Technik weit verbreitet. Das Schwingen des Pendels einer Uhr, Wellen auf dem Wasser, elektrischer Wechselstrom, Licht, Ton sind Beispiele für die Schwingungen verschiedener physikalische Quantitäten. Wenn sich das Pendel bewegt, schwankt die Koordinate seines Schwerpunkts. Im Fall von Wechselstrom Spannung und Strom schwanken in der Schaltung. Diese beiden Verfahren sind in ihrer Qualität qualitativ völlig verschieden körperliche Natur. Die quantitativen Gesetzmäßigkeiten dieser Prozesse haben jedoch viele Gemeinsamkeiten.

Schwingungsvorgänge in den Stangen werden nicht nur durch den Betrieb von Oberflächengeräten verursacht, sondern auch durch die Bewegung des Kolbens. Hier sind synchrone Schwingungen wünschenswerter, da in dieser Fall sie verursachen keine Überlastung.

Schwingungsvorgänge sind in Natur und Technik weit verbreitet. Das Schwingen eines Pendels einer Uhr, Wellen auf Wasser, elektrischer Wechselstrom, Licht, Ton sind Beispiele für Schwingungen verschiedener physikalischer Größen. Wenn sich das Pendel bewegt, schwankt die Koordinate seines Schwerpunkts. Bei Wechselstrom schwanken Spannung und Strom im Stromkreis. Diese beiden Prozesse sind in ihrer physikalischen Natur qualitativ völlig verschieden. Die quantitativen Gesetzmäßigkeiten dieser Prozesse haben jedoch viele Gemeinsamkeiten.

Freischwingungen im Kreislauf.

Die in den vorherigen Abschnitten betrachteten Wechselstromkreise legen nahe, dass ein Paar Elemente - ein Kondensator und eine Induktivität - eine Art oszillierendes System bilden. Nun wollen wir zeigen, dass dies tatsächlich der Fall ist, in einem Kreislauf, der nur aus diesen Elementen besteht (Abb. 669), sind sogar freie Schwingungen möglich, also ohne externe Quelle EMF.

Reis. 669
Daher wird ein Stromkreis (oder Teil eines anderen Stromkreises) genannt, der aus einem Kondensator und einer Induktivität besteht Schwingkreis.
Der Kondensator sei auf eine Ladung qo aufgeladen und dann eine Induktivität daran angeschlossen. Ein solches Verfahren lässt sich leicht mit der Schaltung durchführen, deren Schema in Abb. 670: Zuerst wird der Schlüssel in Position geschlossen 1 , während der Kondensator auf eine Spannung gleich aufgeladen wird Quelle EMK, wonach der Schlüssel in Positionen geworfen wird 2 , wonach die Entladung des Kondensators durch die Spule beginnt.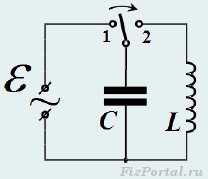

Reis. 670
Bestimmung der Abhängigkeit der Ladung des Kondensators von der Zeit q(t) Es gilt das Ohmsche Gesetz, wonach die Spannung am Kondensator ansteigt UC = q/C gleich EMF-Selbstinduktion, die in der Spule entstehen

hier bedeutet "Primzahl" zeitlich abgeleitet.
Damit erweist sich die Gleichung als gültig

Diese Gleichung enthält zwei unbekannte Funktionen - die Abhängigkeit von der Ladezeit q(t) und aktuell Es), kann also nicht gelöst werden. Die Stromstärke ist jedoch eine Ableitung der Ladung des Kondensators q / (t) = I(t), also ist die Ableitung der Stromstärke die zweite Ableitung der Ladung

Unter Berücksichtigung dieser Beziehung schreiben wir Gleichung (1) in die Form um

Überraschenderweise stimmt diese Gleichung vollständig mit der gut untersuchten Gleichung harmonischer Schwingungen überein (die zweite Ableitung der unbekannten Funktion ist proportional zu dieser Funktion selbst mit einem negativen Proportionalitätskoeffizienten). x // = -ω o 2 x)! Daher ist die Lösung dieser Gleichung die harmonische Funktion

mit Kreisfrequenz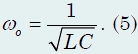

Diese Formel definiert Eigenfrequenz des Schwingkreises. Dementsprechend ist die Schwingungsdauer der Kondensatorladung (und der Stromstärke in der Schaltung) gleich

Der resultierende Ausdruck für die Schwingungsdauer wird aufgerufen Formel von J. Thompson.
Wie üblich, um beliebige Parameter zu definieren EIN, φ in gemeinsame Entscheidung(4) Es ist notwendig, die Anfangsbedingungen einzustellen - die Ladung und die Stromstärke Anfangsmoment Zeit. Insbesondere für das betrachtete Beispiel der Schaltung in Abb. 670 haben die Anfangsbedingungen die Form: at t = 0, q = qo, Ich=0, also wird die Abhängigkeit der Kondensatorladung von der Zeit durch die Funktion beschrieben

und die Stromstärke ändert sich mit der Zeit gemäß dem Gesetz

Die obige Betrachtung des Schwingkreises ist ungefähr - jeder reale Kreis hat einen aktiven Widerstand (Verbindungsdrähte und Spulenwicklungen).

Reis. 671
Daher sollte in Gleichung (1) der Spannungsabfall über diesem aktiven Widerstand berücksichtigt werden, damit diese Gleichung die Form annimmt

die unter Berücksichtigung des Verhältnisses zwischen Ladung und Stromstärke in die Form umgerechnet wird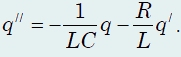

Auch diese Gleichung ist uns bekannt - das ist die Gleichung der gedämpften Schwingungen

und der Dämpfungskoeffizient ist wie erwartet proportional zum aktiven Widerstand der Schaltung β = R/L.
Die Prozesse, die in Schwingkreis, kann auch mit dem Energieerhaltungssatz beschrieben werden. Wenn wir den aktiven Widerstand des Stromkreises vernachlässigen, dann die Summe der Energien elektrisches Feld Kondensator u Magnetfeld Spule bleibt konstant, was durch die Gleichung ausgedrückt wird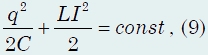

was auch eine Gleichung harmonischer Schwingungen mit einer durch Formel (5) bestimmten Frequenz ist. Diese Gleichung stimmt in ihrer Form auch mit den Gleichungen überein, die sich aus dem Energieerhaltungssatz bei mechanischen Schwingungen ergeben. Da die Gleichungen die Schwingungen beschreiben elektrische Ladung Kondensator sind ähnlich wie die Gleichungen beschreiben mechanische Schwingungen, dann können wir eine Analogie zwischen den Vorgängen im Schwingkreis und den Vorgängen in jedem ziehen Mechanisches System. Auf Abb. 672 eine solche Analogie wurde für Schwingungen gezogen mathematisches Pendel. In diesem Fall sind die Analoga "Kondensatorladung". q(t)− Pendelauslenkungswinkel φ(t)“ und „aktuell Ich (t) = q / (t)− Pendelgeschwindigkeit V(t)».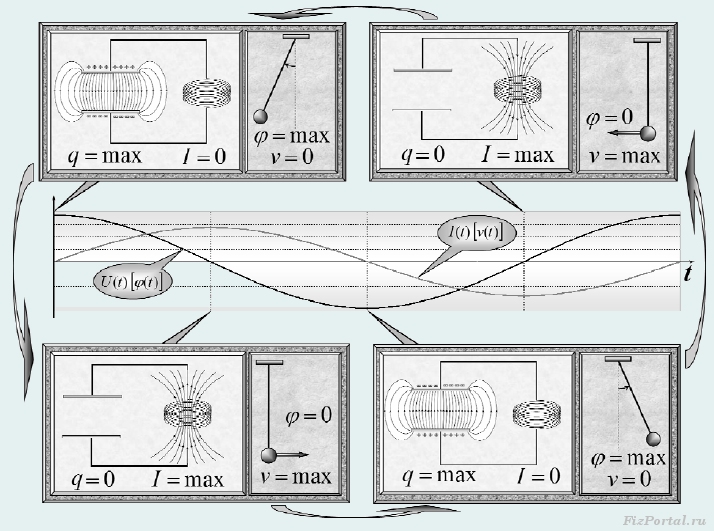



Reis. 672
Mit dieser Analogie beschreiben wir qualitativ den Prozess der Ladungsschwingungen und elektrischer Strom in Kontur. Im ersten Moment ist der Kondensator geladen, die Stärke des elektrischen Stroms ist Null, die gesamte Energie ist in der Energie des elektrischen Felds des Kondensators enthalten (was der maximalen Abweichung des Pendels vom Gleichgewicht entspricht). Position). Dann beginnt sich der Kondensator zu entladen, die Stromstärke nimmt zu, während in der Spule die Selbstinduktions-EMK auftritt, die verhindert, dass der Strom ansteigt; Die Energie des Kondensators nimmt ab und verwandelt sich in die Energie des Magnetfelds der Spule (eine Analogie - das Pendel bewegt sich in Richtung unterster Punkt mit zunehmender Geschwindigkeit). Wenn die Ladung auf dem Kondensator wird Null erreicht die Stromstärke ihren Maximalwert, während die gesamte Energie in die Energie des Magnetfeldes umgewandelt wird (das Pendel hat seinen tiefsten Punkt erreicht, seine Geschwindigkeit ist maximal). Dann beginnt das Magnetfeld abzunehmen, während die Selbstinduktions-EMK den Strom in der gleichen Richtung hält, während der Kondensator sich aufzuladen beginnt und die Vorzeichen der Ladungen auf den Kondensatorplatten der ursprünglichen Verteilung entgegengesetzt sind (analog - das Pendel bewegt sich auf die entgegengesetzte anfängliche maximale Abweichung). Dann hört der Strom in der Schaltung auf, während die Ladung des Kondensators wieder maximal wird, aber mit entgegengesetztem Vorzeichen (das Pendel hat seine maximale Abweichung erreicht), wonach der Vorgang in der entgegengesetzten Richtung wiederholt wird.

VORTRAG #8

Mechanik

Schwankungen

oszillierende Bewegung. Kinematische und dynamische Eigenschaften der Schwingbewegung. Mathematisches, physikalisches und Federpendel.

Wir leben in einer Welt, in der Schwingungsprozesse ein fester Bestandteil unserer Welt sind und überall zu finden sind.

Ein oszillatorischer Prozess oder eine Oszillation ist ein Prozess, der sich in dem einen oder anderen Wiederholungsgrad unterscheidet.

Wiederholt eine schwingende Größe ihre Werte in regelmäßigen Abständen, so nennt man solche Schwingungen periodisch und diese Zeiträume nennt man Schwingungsdauer.

Abhängig von der physikalischen Natur des Phänomens werden Schwingungen unterschieden: mechanisch, elektromechanisch, elektromagnetisch usw.

Schwankungen sind in Natur und Technik weit verbreitet. Oszillationsvorgänge liegen einigen Zweigen der Mechanik zugrunde. In dieser Vorlesung werden wir nur über mechanische Schwingungen sprechen.

Je nach Art der Einwirkung auf das schwingungsfähige System werden Schwingungen unterschieden: 1. Freie oder Eigenschwingungen, 2. Erzwungene Schwingungen, 3. Eigenschwingungen, 4. Parametrische Schwingungen.

Als freie Schwingungen bezeichnet man Schwingungen, die ohne äußere Einwirkung entstehen und durch den anfänglichen „Schub“ verursacht werden.

Erzwungene Schwingungen treten unter Einwirkung einer periodischen äußeren Kraft auf

Selbstschwingungen werden auch unter Einwirkung einer äußeren Kraft ausgeführt, aber der Moment der Krafteinwirkung auf das System wird durch das schwingungsfähige System selbst bestimmt.

Bei parametrischen Schwingungen durch äußere Einflüsse tritt eine periodische Änderung der Parameter des Systems auf, die diese Art von Schwingung verursacht.

Die einfachste Form ist harmonische Schwingungen

Harmonische Schwingungen sind gesetzmäßig auftretende SchwingungenSünde odercos . Ein Beispiel für harmonische Schwingungen ist die Schwingung eines mathematischen Pendels

Die maximale Abweichung einer schwingenden Größe im Schwingungsvorgang wird genannt Schwingungsamplitude(SONDERN) . Die Zeit, die benötigt wird, um eine vollständige Schwingung zu vollenden, wird genannt Periode der Schwingung(T) . Der Kehrwert der Schwingungsdauer wird genannt Oszillationsfrequenz(). Oft wird Schwankungen multipliziert mit 2 genannt zyklische Frequenz(). Somit werden harmonische Schwingungen durch den Ausdruck beschrieben

Hier ( t+  0 ) Schwingungsphase und  0 - Anfangsphase

Die einfachsten mechanischen Schwingungssysteme sind die sogenannten: mathematischen, Feder- und physikalischen Pendel. Schauen wir uns diese Pendel genauer an.

8.1. Mathematisches Pendel

Ein mathematisches Pendel ist ein schwingungsfähiges System, das aus einem massiven Punktkörper besteht, der an einem undehnbaren gewichtslosen Faden im Feld der Schwerkraft aufgehängt ist.

Am unteren Punkt hat das Pendel ein Minimum an potentieller Energie. Lassen Sie uns das Pendel in einem Winkel  auslenken. Der Schwerpunkt eines massiven Punktkörpers steigt auf eine Höhe an  h und in diesem Fall erhöht sich die potentielle Energie des Pendels um den Wert mg h. Außerdem wird das Gewicht in der ausgelenkten Position durch die Schwerkraft und die Spannung des Fadens beeinflusst. Die Wirkungslinien dieser Kräfte fallen nicht zusammen, und die resultierende Kraft wirkt auf die Last und neigt dazu, sie in die Gleichgewichtsposition zurückzuführen. Wenn die Last nicht gehalten wird, beginnt sie sich unter der Wirkung dieser Kraft in die anfängliche Gleichgewichtsposition zu bewegen, ihre kinetische Energie nimmt aufgrund einer Geschwindigkeitserhöhung zu, während die potenzielle Energie abnimmt. Wenn der Gleichgewichtspunkt erreicht ist, wirkt die resultierende Kraft nicht mehr auf den Körper (die Schwerkraft in diesem Punkt wird durch die Kraft der Fadenspannung kompensiert). Die potentielle Energie des Körpers wird an diesem Punkt minimal sein, und die kinetische Energie wird im Gegenteil ihre eigene haben höchster Wert. Der Körper, der sich durch Trägheit bewegt, passiert die Gleichgewichtsposition und beginnt sich von ihr zu entfernen, was zur Entstehung einer resultierenden Kraft (aus Spannung und Schwerkraft) führt, die gegen die Bewegung des Körpers gerichtet ist und ihn verlangsamt Nieder. Damit beginnt eine Abnahme kinetische Energie Fracht und ihre Zunahme potenzielle Energie. Dieser Prozess wird bis zur vollständigen Erschöpfung der kinetischen Energiereserven und ihrem Übergang in potentielle Energie fortgesetzt. In diesem Fall erreicht die Abweichung der Last von der Gleichgewichtslage einen Maximalwert und der Vorgang wiederholt sich. Wenn im System keine Reibung vorhanden ist, schwingt die Last unbegrenzt.

Schwingende mechanische Systeme zeichnen sich also dadurch aus, dass bei Abweichung von der Gleichgewichtslage eine Rückstellkraft im System entsteht, die das System in die Gleichgewichtslage zurückführen will. In diesem Fall treten Schwingungen auf, begleitet von einem periodischen Übergang der potentiellen Energie des Systems in seine kinetische Energie und umgekehrt.

Berechnung oszillierender Prozess. Moment der Kräfte M Einwirkung auf das Pendel ist offensichtlich gleich - mglsin Das Minuszeichen spiegelt die Tatsache wider, dass das Moment der Kräfte dazu neigt, die Last in ihre Gleichgewichtsposition zurückzubringen. Andererseits nach dem Grundgesetz Drehbewegung M=ICH WÜRDE 2  / dt 2 . Damit erhalten wir die Gleichheit

B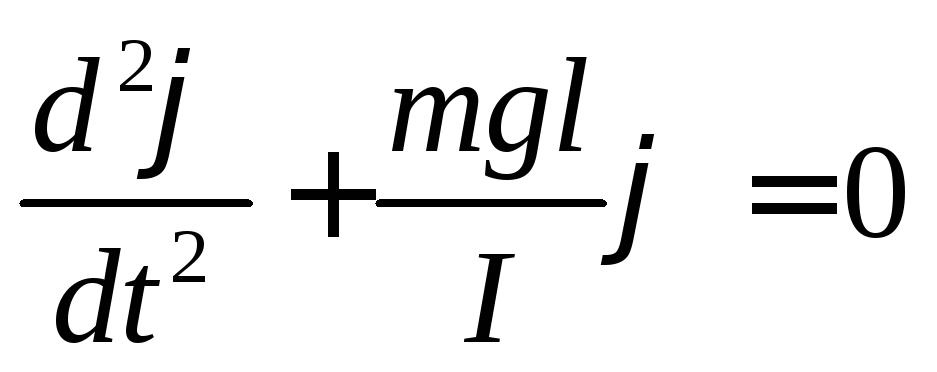

Betrachten wir nur kleine Abweichungswinkel des Pendels von der Gleichgewichtslage. Dann Sünde ≈  . Und unsere Gleichheit wird die Form annehmen:

D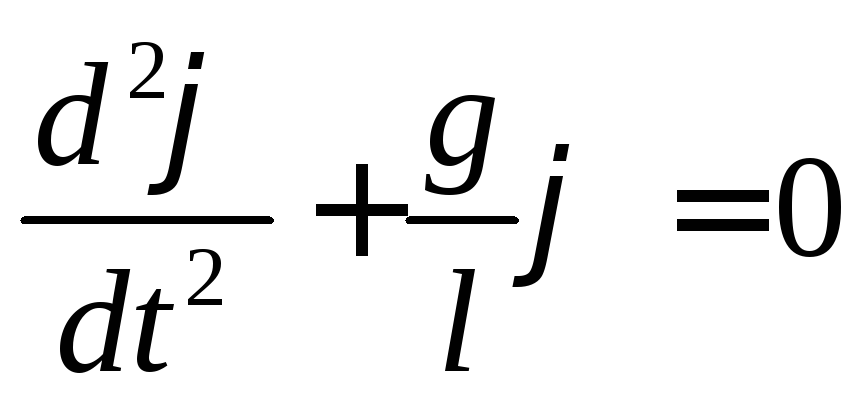

für ein mathematisches Pendel ist es wahr ich= ml 2 . Setzen wir diese Gleichheit in den resultierenden Ausdruck ein, erhalten wir eine Gleichung, die den Schwingungsvorgang eines mathematischen Pendels beschreibt:

Diese Differentialgleichung beschreibt einen Schwingungsvorgang. Die Lösung dieser Gleichung sind die harmonischen Funktionen Sünde( t+  0 ) oder cos ( t+  0 ) Tatsächlich setzen wir jede dieser Funktionen in die Gleichung ein und erhalten:  2 = g/ l. Wenn also diese Bedingung erfüllt ist, dann funktionieren die Sünde( t+  0 ) oder cos( t+  0 ) verwandeln die Differentialgleichung der Schwingungen in eine Identität.

Ö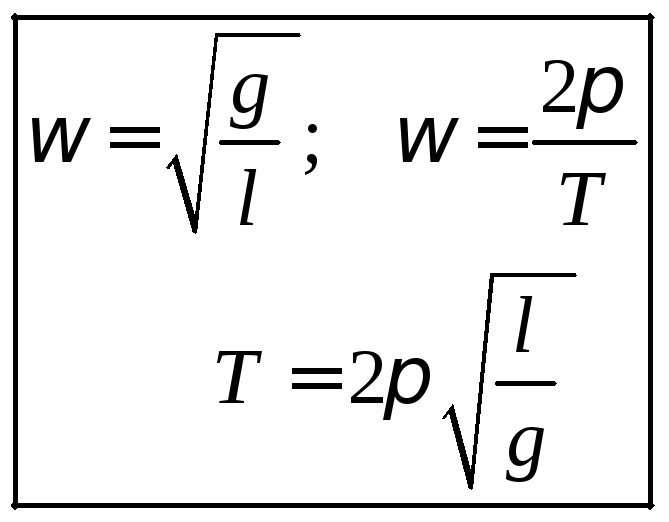

hier wird die zyklische Frequenz und Schwingungsdauer eines harmonischen Pendels ausgedrückt als:

Die Schwingungsamplitude wird aus den Anfangsbedingungen des Problems ermittelt.

Wie Sie sehen können, hängen Frequenz und Schwingungsdauer eines mathematischen Pendels nicht von der Masse der Last ab, sondern nur von der Erdbeschleunigung und der Länge des Aufhängungsfadens, wodurch das Pendel als einfaches verwendet werden kann aber sehr genaues Gerät zur Bestimmung der Erdbeschleunigung.

Eine andere Art von Pendel ist jeder physische Körper, der an einem beliebigen Punkt des Körpers aufgehängt ist und die Fähigkeit hat, oszillierende Bewegungen auszuführen.

8.2. physikalisches Pendel

BEIM Nehmen wir einen beliebigen Körper, durchbohren ihn irgendwann mit einer Achse, die nicht mit seinem Massenmittelpunkt zusammenfällt, um den sich der Körper frei drehen kann. Hängen Sie den Körper an dieser Achse auf und weichen Sie ihn um einen Winkel von der Gleichgewichtsposition ab  .

T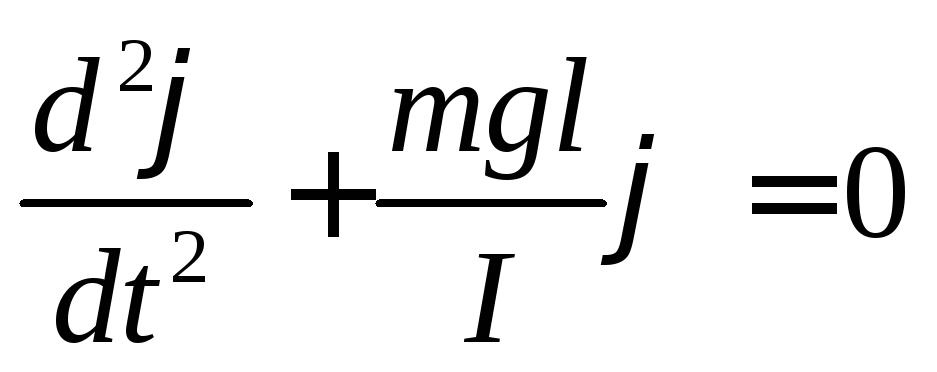

auf einem Körper mit einem Trägheitsmoment ich um die Achse Ö der Moment der Rückkehr in die Gleichgewichtsposition wirkt M = - mglsin und die Schwingungen eines physikalischen sowie eines mathematischen Pendels werden durch eine Differentialgleichung beschrieben:

Da das Trägheitsmoment für verschiedene physikalische Pendel unterschiedlich ausgedrückt wird, werden wir es nicht wie im Fall eines mathematischen Pendels beschreiben. Auch diese Gleichung hat die Form einer Schwingungsgleichung, deren Lösung Funktionen sind, die harmonische Schwingungen beschreiben. In diesem Fall die zyklische Frequenz ( ) , Schwingungsdauer (T) definiert als:

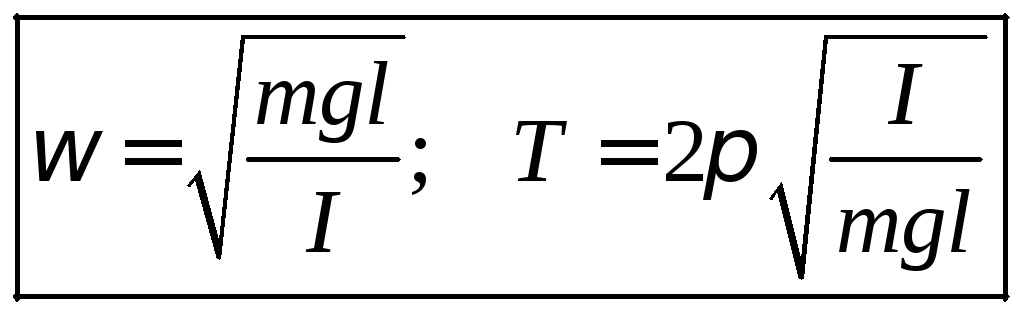
Wir sehen, dass bei einem physikalischen Pendel die Schwingungsdauer von der Geometrie des Pendelkörpers abhängt und nicht von seiner Masse wie bei einem mathematischen Pendel. Tatsächlich schließt der Ausdruck für das Trägheitsmoment die Masse des Pendels hoch 1 ein. Das Trägheitsmoment im Ausdruck für die Schwingungsdauer steht im Zähler, während die Masse des Pendels im Nenner und auch im ersten Grad enthalten ist. Also hebt sich die Masse im Zähler mit der Masse im Nenner auf.

Das physikalische Pendel hat noch eine Eigenschaft - die reduzierte Länge.

Die reduzierte Länge des physikalischen Pendels ist die Länge des mathematischen Pendels, dessen Periode mit der Periode des physikalischen Pendels zusammenfällt.

Diese Definition macht es einfach, einen Ausdruck für die reduzierte Länge zu definieren.

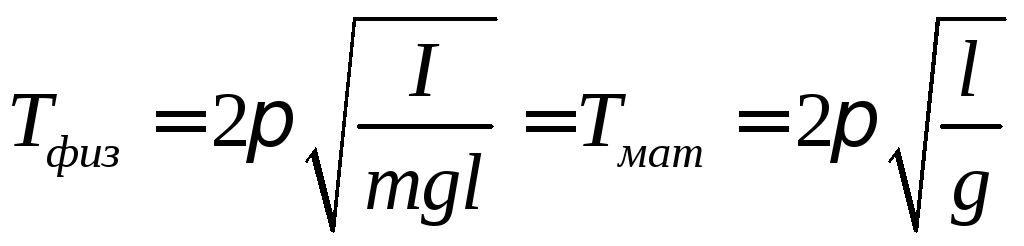
Wenn wir diese Ausdrücke vergleichen, erhalten wir

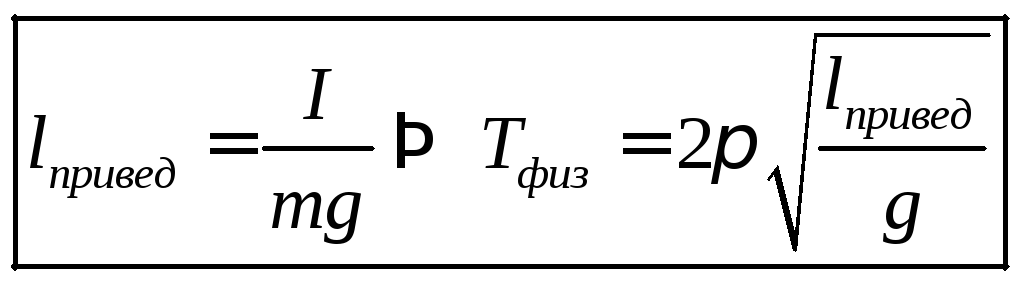
Wenn wir auf der Linie, die vom Aufhängungspunkt durch den Massenmittelpunkt des physikalischen Pendels gezogen wird, die reduzierte Länge des physikalischen Pendels einzeichnen (ausgehend vom Aufhängungspunkt), dann gibt es am Ende dieses Segments einen Punkt, der hat eine bemerkenswerte Eigenschaft. Wird an diesem Punkt ein physikalisches Pendel aufgehängt, so ist seine Schwingungsdauer dieselbe wie bei der Aufhängung des Pendels am vorherigen Aufhängepunkt. Diese Punkte werden die Schwingungszentren des physikalischen Pendels genannt.

Betrachten Sie ein anderes einfaches Schwingungssystem, das harmonische Schwingungen ausführt

8.3. Federpendel

P Stellen Sie sich das am Ende der Feder mit dem Steifigkeitskoeffizienten vor k Gewicht angebracht m.

Wenn wir die Last durch Spannen der Feder entlang der x-Achse bewegen, wirkt die Kraft, die in die Gleichgewichtsposition zurückkehrt, auf die Last F Rückkehr = - kx. Wenn die Last gelöst wird, bewirkt diese Kraft eine Beschleunigung d 2 x / dt 2 . Nach dem zweiten Newtonschen Gesetz erhalten wir:

md 2 x / dt 2 = - kx aus dieser Gleichung erhalten wir die Gleichung für die Schwingung einer Last an einer Feder in ihrer endgültigen Form: d 2 x / dt 2 + (k/ m) x = 0

E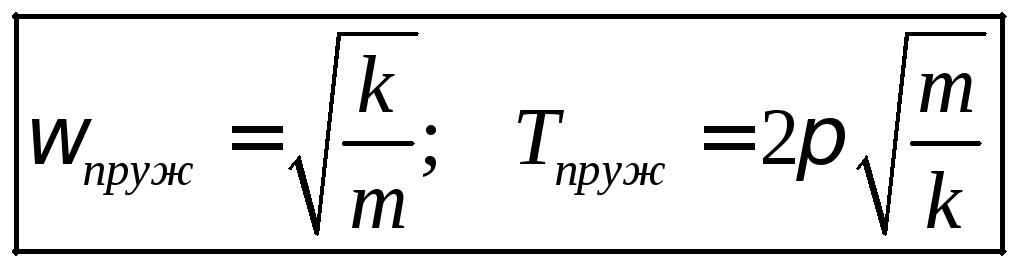

dann hat die Schwingungsgleichung die gleiche Form wie die Schwingungsgleichungen in den bereits betrachteten Fällen, was bedeutet, dass die Lösung dieser Gleichung die gleichen harmonischen Funktionen sein werden. Die Frequenz und Periode der Schwingungen sind jeweils gleich

Außerdem wirkt sich die Schwerkraft in keiner Weise auf die Schwingungen des Federpendels aus. Denn in diesem Fall handelt es sich um einen ständig wirkenden Faktor, der immer in eine Richtung wirkt und nichts mit der Rückstellkraft zu tun hat.

So wie wir den Schwingungsvorgang in einem mechanischen Schwingungssystem sehen, ist er in erster Linie durch die Anwesenheit im System gekennzeichnet Wiederherstellungskräfte auf das System einwirken, und die Schwingungen selbst sind gekennzeichnet durch: Amplitude der Schwankung durch ihre Periode, Frequenz und Phase der Schwankungen.