დენის ფუნქცია, მისი თვისებები და გრაფიკი დემო მასალაგაკვეთილი-ლექცია ფუნქციის ცნება. ფუნქციის თვისებები. სიმძლავრის ფუნქცია, მისი თვისებები და გრაფიკი. Grade 10 ყველა უფლება დაცულია. საავტორო უფლება საავტორო უფლებებით

გაკვეთილის მიმდინარეობა: გამეორება. ფუნქცია. ფუნქციის თვისებები. ახალი მასალის სწავლა. 1. სიმძლავრის ფუნქციის განმარტება სიმძლავრის ფუნქციის განსაზღვრა. 2. სიმძლავრის ფუნქციების თვისებები და გრაფიკები ძალაუფლების ფუნქციების თვისებები და გრაფიკები. შესწავლილი მასალის კონსოლიდაცია. ვერბალური დათვლა. ვერბალური დათვლა. გაკვეთილის შეჯამება. საშინაო დავალება.

ფუნქციის დომენი და დიაპაზონი დამოუკიდებელი ცვლადის ყველა მნიშვნელობა ქმნის ფუნქციის დომენს x y=f(x) f ფუნქციის დომენი ფუნქციის დომენი ყველა მნიშვნელობა, რომელსაც დამოკიდებული ცვლადი იღებს, ფუნქციის დომენს ქმნის. ფუნქცია. ფუნქციის თვისებები

ფუნქციის გრაფიკი მოცემული იყოს ფუნქცია, სადაც xY y x.75 3 0.6 4 0.5 ფუნქციის გრაფიკი არის კოორდინატთა სიბრტყის ყველა წერტილის სიმრავლე, რომელთა აბსციები უდრის არგუმენტის მნიშვნელობებს. და ორდინატები ტოლია ფუნქციის შესაბამისი მნიშვნელობების. ფუნქცია. ფუნქციის თვისებები

Y x ფუნქციის განსაზღვრის დომენი და დიაპაზონი 4 y=f(x) ფუნქციის დომენი: ფუნქციის დომენი: ფუნქცია. ფუნქციის თვისებები

ლუწი ფუნქცია y x y=f(x) გრაფიკი ფუნქციაც კისიმეტრიული y ღერძის მიმართ ფუნქცია y=f(x) იწოდება მაშინაც კი, თუ f(-x) = f(x) ფუნქციის დომენის ნებისმიერი x-ისთვის. ფუნქციის თვისებები

კენტი ფუნქცია y x y=f(x) გრაფიკი უცნაური ფუნქციასიმეტრიული საწყისის მიმართ O(0;0) y=f(x) ფუნქციას ეწოდება კენტი, თუ f(-x) = -f(x) ნებისმიერი x ფუნქციის დომენიდან. ფუნქციის თვისებები

სიმძლავრის ფუნქციის განმარტება ფუნქციას, სადაც p არის მოცემული რეალური რიცხვი, ეწოდება სიმძლავრის ფუნქციას. p y \u003d x p P \u003d x y 0 გაკვეთილის პროგრესი

სიმძლავრის ფუნქცია x y 1. ფორმის დეფინიციის დომენი და სიმძლავრის ფუნქციების მნიშვნელობების დიაპაზონი, სადაც n არის ბუნებრივი რიცხვი, ყველა რეალური რიცხვია. 2. ეს ფუნქციები კენტია. მათი გრაფიკი წარმოშობის მიმართ სიმეტრიულია. დენის ფუნქციის თვისებები და ნაკვეთები

სიმძლავრის ფუნქციები რაციონალური დადებითი მაჩვენებლით განსაზღვრების დომენი - ყველა დადებითი რიცხვებიდა რიცხვი 0. ფუნქციების დიაპაზონი ასეთი მაჩვენებლით არის ასევე ყველა დადებითი რიცხვი და რიცხვი 0. ეს ფუნქციები არც ლუწია და არც კენტი. y x დენის ფუნქციის თვისებები და გრაფიკები

დენის ფუნქცია რაციონალურად უარყოფითი მაჩვენებელი. ასეთი ფუნქციების განსაზღვრის სფერო და დიაპაზონი არის ყველა დადებითი რიცხვი. ფუნქციები არც ლუწია და არც კენტი. ასეთი ფუნქციები მცირდება მათი განმარტების მთელ დომენში. y x სიმძლავრის ფუნქციის თვისებები და გრაფიკები გაკვეთილის მიმდინარეობა

1. სიმძლავრის ფუნქცია, მისი თვისებები და გრაფიკი;

2. ტრანსფორმაციები:

პარალელური გადაცემა;

სიმეტრია კოორდინატთა ღერძების მიმართ;

სიმეტრია წარმოშობის შესახებ;

სიმეტრია y = x წრფის მიმართ;

გაჭიმვა და შემცირება კოორდინატთა ღერძების გასწვრივ.

3. ექსპონენციალური ფუნქცია, მისი თვისებები და გრაფიკი, მსგავსი გარდაქმნები;

4. ლოგარითმული ფუნქცია, მისი თვისებები და გრაფიკი;

5. ტრიგონომეტრიული ფუნქცია, მისი თვისებები და გრაფიკი, მსგავსი გარდაქმნები (y = sin x; y = cos x; y = tg x);

ფუნქცია: y = x\n - მისი თვისებები და გრაფიკი.

სიმძლავრის ფუნქცია, მისი თვისებები და გრაფიკი

y \u003d x, y \u003d x 2, y \u003d x 3, y \u003d 1 / xყველა ეს ფუნქცია არის დენის ფუნქციის განსაკუთრებული შემთხვევები, ანუ ფუნქცია y = xp, სადაც p არის მოცემული რეალური რიცხვი.
სიმძლავრის ფუნქციის თვისებები და გრაფიკი არსებითად დამოკიდებულია რეალური მაჩვენებლის მქონე სიმძლავრის თვისებებზე და განსაკუთრებით იმ მნიშვნელობებზე, რომელთათვისაც xდა გვმისცე მნიშვნელობა xp. მოდით გადავიდეთ მსგავს განხილვაზე. სხვადასხვა შემთხვევებიდამოკიდებულია
ექსპონენტი გვ.

1. ინდიკატორი p = 2nლუწი ნატურალური რიცხვია.

y=x2n, სად ნარის ნატურალური რიცხვი და აქვს შემდეგი თვისებები:

• განსაზღვრების დომენი არის ყველა რეალური რიცხვი, ე.ი. სიმრავლე R;
• ღირებულებების ნაკრები - არაუარყოფითი რიცხვები, ანუ y არის 0-ზე მეტი ან ტოლი;
• ფუნქცია y=x2nთუნდაც იმიტომ x 2n = (-x) 2n
• ფუნქცია მცირდება ინტერვალზე x< 0 და იზრდება ინტერვალით x > 0.

ფუნქციის გრაფიკი y=x2nაქვს იგივე ფორმა, რაც, მაგალითად, ფუნქციის გრაფიკს y=x4.

2. ინდიკატორი p = 2n - 1- კენტი ნატურალური რიცხვი

ამ შემთხვევაში, დენის ფუნქცია y=x2n-1სადაც არის ნატურალური რიცხვი, აქვს შემდეგი თვისებები:

• განსაზღვრების დომენი - ნაკრები R;
• მნიშვნელობების ნაკრები - ნაკრები R;
• ფუნქცია y=x2n-1უცნაურია, რადგან (- x) 2n-1= x 2n-1;
• ფუნქცია იზრდება მთელ რეალურ ღერძზე.

ფუნქციის გრაფიკი y=x2n-1 y=x3.

3. ინდიკატორი p=-2n, სად n-ბუნებრივი რიცხვი.

ამ შემთხვევაში, დენის ფუნქცია y=x-2n=1/x2nაქვს შემდეგი თვისებები:

• მნიშვნელობების ნაკრები - დადებითი რიცხვები y>0;
• ფუნქცია y = 1/x2nთუნდაც იმიტომ 1/(-x) 2n= 1/x2n;
• ფუნქცია იზრდება x0 ინტერვალზე.

y ფუნქციის გრაფიკი = 1/x2nაქვს იგივე ფორმა, როგორც, მაგალითად, y ფუნქციის გრაფიკი = 1/x2.

4. ინდიკატორი p = -(2n-1), სად ნ- ნატურალური რიცხვი.
ამ შემთხვევაში, დენის ფუნქცია y=x-(2n-1)აქვს შემდეგი თვისებები:

• განმარტების დომენი არის ნაკრები R, გარდა x = 0;
• მნიშვნელობების ნაკრები - ნაკრები R, გარდა y = 0;
• ფუნქცია y=x-(2n-1)უცნაურია, რადგან (- x)-(2n-1) = -x-(2n-1);
• ფუნქცია მცირდება ინტერვალებით x< 0 და x > 0.

ფუნქციის გრაფიკი y=x-(2n-1)აქვს იგივე ფორმა, როგორც, მაგალითად, ფუნქციის გრაფიკი y = 1/x3.

The მეთოდური მასალაარის მხოლოდ მითითებისთვის და ვრცელდება ფართო სპექტრითემები. სტატიაში მოცემულია ძირითადი ელემენტარული ფუნქციების გრაფიკების მიმოხილვა და განიხილება ყველაზე მნიშვნელოვანი კითხვა – როგორ სწორად და სწრაფად ავაშენოთ გრაფიკი. სწავლის დროს უმაღლესი მათემატიკაძირითადი ელემენტარული ფუნქციების გრაფიკების ცოდნის გარეშე, რთული იქნება, ამიტომ ძალიან მნიშვნელოვანია გვახსოვდეს, როგორ გამოიყურება პარაბოლის, ჰიპერბოლის, სინუსის, კოსინუსის და ა.შ. გრაფიკები, დაიმახსოვრეთ ზოგიერთი ფუნქციის მნიშვნელობა. ჩვენ ასევე ვისაუბრებთ ძირითადი ფუნქციების ზოგიერთ თვისებებზე.

მე არ ვაპირებ პრეტენზიას მასალების სისრულესა და მეცნიერულ სიზუსტეზე, აქცენტი გაკეთდება, პირველ რიგში, პრაქტიკაზე - იმ საკითხებზე, რაც პირისპირ უნდა შეხვდე სიტყვასიტყვით ყოველ ნაბიჯზე, უმაღლესი მათემატიკის ნებისმიერ თემაზე. დუმების სქემები? შეგიძლიათ ასე თქვათ.

ავტორი უამრავი მოთხოვნამკითხველებს დაწკაპუნებადი სარჩევი:

გარდა ამისა, არის ულტრამოკლე რეფერატი ამ თემაზე
- დაეუფლეთ 16 ტიპის სქემებს ექვსი გვერდის შესწავლით!

სერიოზულად, ექვსი, მეც კი გამიკვირდა. ეს აბსტრაქტიშეიცავს გაუმჯობესებულ გრაფიკას და ხელმისაწვდომია ნომინალური გადასახადით, შეგიძლიათ ნახოთ დემო ვერსია. მოსახერხებელია ფაილის დაბეჭდვა ისე, რომ გრაფიკები ყოველთვის ხელთ იყოს. მადლობა პროექტის მხარდაჭერისთვის!

და ჩვენ მაშინვე ვიწყებთ:

როგორ ავაშენოთ კოორდინატთა ღერძები სწორად?

პრაქტიკაში ტესტებს სტუდენტები თითქმის ყოველთვის ადგენენ ცალკეულ რვეულებში, გალიაში ჩასმული. რატომ გჭირდებათ მონიშნული ნიშნები? ყოველივე ამის შემდეგ, სამუშაო, პრინციპში, შეიძლება გაკეთდეს A4 ფურცლებზე. და გალია აუცილებელია მხოლოდ ნახატების მაღალი ხარისხის და ზუსტი დიზაინისთვის.

ფუნქციის გრაფიკის ნებისმიერი ნახაზი იწყება კოორდინატთა ღერძებით.

ნახატები არის ორგანზომილებიანი და სამგანზომილებიანი.

ჯერ განვიხილოთ ორგანზომილებიანი შემთხვევა დეკარტიანი მართკუთხა სისტემაკოორდინატები:

1) ჩვენ ვხატავთ კოორდინატთა ღერძები. ღერძი ე.წ x-ღერძი და ღერძი y-ღერძი . ჩვენ ყოველთვის ვცდილობთ დავხატოთ ისინი სისუფთავე და არა მრუდე. ისრები ასევე არ უნდა ჰგავდეს პაპა კარლოს წვერს.

2) ვაწერთ ცულებს დიდი ასოები"x" და "y". არ დაგავიწყდეთ ცულების ხელმოწერა.

3) დააყენეთ მასშტაბი ღერძების გასწვრივ: დახაზეთ ნული და ორი ერთი. ნახატის გაკეთებისას ყველაზე მოსახერხებელი და გავრცელებული მასშტაბია: 1 ერთეული = 2 უჯრედი (ნახატი მარცხნივ) - თუ შესაძლებელია, მიჰყევით მას. თუმცა, დროდადრო ხდება ისე, რომ ნახატი არ ჯდება ნოუთბუქის ფურცელზე - შემდეგ ვამცირებთ მასშტაბს: 1 ერთეული = 1 უჯრედი (ნახატი მარჯვნივ). იშვიათად, მაგრამ ხდება ისე, რომ ნახატის მასშტაბი კიდევ უფრო უნდა შემცირდეს (ან გაიზარდოს).

არ დაწეროთ ავტომატიდან ... -5, -4, -3, -1, 0, 1, 2, 3, 4, 5, ....ამისთვის საკოორდინაციო თვითმფრინავიარ არის დეკარტის ძეგლი და სტუდენტი არ არის მტრედი. Ჩვენ ვდებთ ნულიდა ორი ერთეული ღერძების გასწვრივ. ხანდახან იმის მაგივრადერთეულები, მოსახერხებელია სხვა მნიშვნელობების „გამოვლენა“, მაგალითად, „ორი“ აბსცისის ღერძზე და „სამი“ ორდინატთა ღერძზე - და ეს სისტემა (0, 2 და 3) ასევე ცალსახად დააყენებს კოორდინატთა ბადეს.

ნახატის დახატამდე უკეთესია ნახატის სავარაუდო ზომების შეფასება.. მაგალითად, თუ დავალება მოითხოვს სამკუთხედის დახატვას წვეროებით , , მაშინ სრულიად გასაგებია, რომ პოპულარული მასშტაბი 1 ერთეული = 2 უჯრედი არ იმუშავებს. რატომ? მოდით შევხედოთ საკითხს - აქ თქვენ უნდა გაზომოთ თხუთმეტი სანტიმეტრი ქვემოთ და, ცხადია, ნახატი არ ჯდება (ან ძლივს ჯდება) ნოუთბუქის ფურცელზე. ამიტომ, ჩვენ დაუყოვნებლივ ვირჩევთ უფრო მცირე მასშტაბს 1 ერთეული = 1 უჯრედი.

სხვათა შორის, დაახლოებით სანტიმეტრი და ნოუთბუქის უჯრედები. მართალია, რომ 30 ბლოკნოტის უჯრედში 15 სანტიმეტრია? გაზომეთ რვეულში ინტერესისთვის 15 სანტიმეტრი სახაზავთან ერთად. სსრკ-ში, ალბათ, ეს ასეც იყო... საინტერესოა აღინიშნოს, რომ თუ თქვენ გაზომავთ იმავე სანტიმეტრებს ჰორიზონტალურად და ვერტიკალურად, მაშინ შედეგები (უჯრედებში) განსხვავებული იქნება! მკაცრად რომ ვთქვათ, თანამედროვე ნოუთბუქები არ არის ჩექმიანი, არამედ მართკუთხა. შეიძლება სისულელედ მოგეჩვენოთ, მაგრამ ასეთ სიტუაციებში, მაგალითად, კომპასით წრის დახატვა ძალიან მოუხერხებელია. მართალი გითხრათ, ასეთ მომენტებში იწყებ ფიქრს ამხანაგი სტალინის სისწორეზე, რომელიც გაგზავნეს ბანაკებში წარმოებაში ჰაკერული სამუშაოსთვის, რომ აღარაფერი ვთქვათ შიდა საავტომობილო ინდუსტრიაზე, თვითმფრინავების დაცემაზე ან ელექტროსადგურების აფეთქებაზე.

ხარისხზეა საუბარი, ან მოკლე რეკომენდაციასაკანცელარიო ნივთებით. დღემდე, ნოუთბუქების უმეტესობა იყიდება, ცუდი სიტყვებირომ აღარაფერი ვთქვათ, სრული სიგიჟე. იმ მიზეზით, რომ ისინი სველდებიან და არა მხოლოდ გელის კალმებიდან, არამედ ბურთულიანი კალმებიდანაც! შეინახეთ ქაღალდზე. განბაჟებისთვის საკონტროლო სამუშაოებიგირჩევთ გამოიყენოთ არხანგელსკის რბილობი და ქაღალდის წისქვილის რვეულები (18 ფურცელი, გალია) ან პიატეროჩკა, თუმცა ეს უფრო ძვირია. მიზანშეწონილია აირჩიოთ გელის კალამი, ყველაზე იაფი ჩინური გელის შემავსებელიც კი ბევრად უკეთესია ბურთულიანი კალმისა, რომელიც ან ნაცხის ან ამსხვრევს ქაღალდს. ერთადერთი "კონკურენტი" ბურთულიანი კალამიჩემს მეხსიერებაში არის "ერიხ კრაუზე". ის წერს მკაფიოდ, ლამაზად და სტაბილურად - ან სავსე ფუძით, ან თითქმის ცარიელი.

დამატებით: თვალებით მართკუთხა კოორდინატთა სისტემის დანახვა ანალიტიკური გეომეტრიასტატიაში გაშუქებული ვექტორების წრფივი (არა) დამოკიდებულება. ვექტორული საფუძველი, დეტალური ინფორმაციაშესახებ საკოორდინაციო კვარტლებიშეგიძლიათ იხილოთ გაკვეთილის მეორე აბზაცში წრფივი უტოლობა.

3D ქეისი

აქაც თითქმის იგივეა.

1) ვხატავთ კოორდინატთა ღერძებს. სტანდარტული: აპლიკაციის ღერძი – მიმართული ზემოთ, ღერძი – მიმართული მარჯვნივ, ღერძი – ქვევით მარცხნივ მკაცრად 45 გრადუსიანი კუთხით.

2) ვაწერთ ცულებს.

3) დააყენეთ სასწორი ღერძების გასწვრივ. მასშტაბი ღერძის გასწვრივ - ორჯერ უფრო მცირე ვიდრე მასშტაბი სხვა ღერძების გასწვრივ. ასევე გაითვალისწინეთ, რომ სწორ ნახაზში მე გამოვიყენე არასტანდარტული "სერიფი" ღერძის გასწვრივ (ეს შესაძლებლობა უკვე აღინიშნა ზემოთ). ჩემი გადმოსახედიდან, ეს უფრო ზუსტი, სწრაფი და ესთეტიურად სასიამოვნოა - თქვენ არ გჭირდებათ მიკროსკოპის ქვეშ მოძებნოთ უჯრედის შუა ნაწილი და „გამოძერწოთ“ ერთეული საწყისამდე.

როდესაც კვლავ აკეთებთ 3D ნახატს - უპირატესობა მიანიჭეთ მასშტაბებს
1 ერთეული = 2 უჯრედი (ნახაზი მარცხნივ).

რისთვის არის ყველა ეს წესი? წესები არსებობს იმისთვის, რომ დაირღვეს. რას ვაპირებ ახლა. ფაქტია, რომ სტატიის შემდგომ ნახატებს ჩემი გავაკეთებ Excel-ში და კოორდინატთა ღერძები არასწორად გამოიყურება. სწორი დიზაინი. მე შემეძლო ყველა გრაფიკის ხელით დახატვა, მაგრამ მათი დახატვა ნამდვილად საშინელებაა, რადგან Excel-ს არ სურს უფრო ზუსტად დახატოს ისინი.

ელემენტარული ფუნქციების გრაფიკები და ძირითადი თვისებები

წრფივი ფუნქცია მოცემულია განტოლებით. ხაზოვანი ფუნქციის გრაფიკი არის პირდაპირი. სწორი ხაზის ასაგებად საკმარისია ორი წერტილის ცოდნა.

მაგალითი 1

დახაზეთ ფუნქცია. მოდი ვიპოვოთ ორი წერტილი. ხელსაყრელია ნულის არჩევა ერთ-ერთ პუნქტად.

თუ, მაშინ

ჩვენ ვიღებთ სხვა პუნქტს, მაგალითად, 1.

თუ, მაშინ

დავალებების მომზადებისას, ქულების კოორდინატები ჩვეულებრივ შეჯამებულია ცხრილში:

და თავად მნიშვნელობები გამოითვლება ზეპირად ან მონახაზზე, კალკულატორზე.

ნაპოვნია ორი წერტილი, დავხატოთ:

ნახატის შედგენისას ყოველთვის ვაწერთ ხელს გრაფიკას.

ზედმეტი არ იქნება წრფივი ფუნქციის განსაკუთრებული შემთხვევების გახსენება:

დააკვირდით, როგორ დავდე წარწერები, ნახატის შესწავლისას ხელმოწერები არ უნდა იყოს ორაზროვანი. AT ამ საქმესუკიდურესად არასასურველი იყო ხელმოწერის დადება ხაზების გადაკვეთის წერტილის გვერდით, ან ქვედა მარჯვენა კუთხეში გრაფიკებს შორის.

1) () ფორმის წრფივ ფუნქციას პირდაპირი პროპორციულობა ეწოდება. Მაგალითად, . პირდაპირი პროპორციულობის გრაფიკი ყოველთვის გადის საწყისზე. ამრიგად, სწორი ხაზის აგება გამარტივებულია - საკმარისია მხოლოდ ერთი წერტილის პოვნა.

2) ფორმის განტოლება განსაზღვრავს ღერძის პარალელურ სწორ ხაზს, კერძოდ, განტოლებით მოცემულია თავად ღერძი. ფუნქციის გრაფიკი აგებულია დაუყოვნებლივ, წერტილების პოვნის გარეშე. ანუ, ჩანაწერი უნდა გავიგოთ შემდეგნაირად: "y ყოველთვის უდრის -4, x-ის ნებისმიერი მნიშვნელობისთვის."

3) ფორმის განტოლება განსაზღვრავს ღერძის პარალელურ სწორ ხაზს, კერძოდ, თავად ღერძი მოცემულია განტოლებით. ფუნქციის გრაფიკი ასევე აგებულია დაუყოვნებლივ. ჩანაწერი უნდა გავიგოთ შემდეგნაირად: "x ყოველთვის, y-ის ნებისმიერი მნიშვნელობისთვის, უდრის 1-ს."

ზოგი იკითხავს, ​​აბა, რატომ გახსოვს მე-6 კლასიო?! ასეა, შეიძლება ასეც არის, მხოლოდ პრაქტიკის წლების განმავლობაში შევხვდი ათეულ სტუდენტს, რომლებიც გაოგნებული იყვნენ გრაფიკის მსგავსი ან .

სწორი ხაზის დახატვა ყველაზე გავრცელებული მოქმედებაა ნახატების გაკეთებისას.

სწორი ხაზი დეტალურად განიხილება ანალიტიკური გეომეტრიის კურსში და მსურველებს შეუძლიათ მიმართონ სტატიას სიბრტყეზე სწორი ხაზის განტოლება.

კვადრატული ფუნქციის გრაფიკი, კუბური ფუნქციის გრაფიკი, პოლინომიური გრაფიკი

პარაბოლა. განრიგი კვადრატული ფუნქცია () არის პარაბოლა. განიხილეთ ცნობილი შემთხვევა:

გავიხსენოთ ფუნქციის ზოგიერთი თვისება.

ასე რომ, ჩვენი განტოლების ამონახსნი: - სწორედ ამ წერტილში მდებარეობს პარაბოლის წვერო. რატომ არის ეს ასე, შეიძლება გავიგოთ წარმოებულის თეორიული სტატიიდან და ფუნქციის ექსტრემის შესახებ გაკვეთილიდან. იმავდროულად, ჩვენ ვიანგარიშებთ "y"-ის შესაბამის მნიშვნელობას:

ასე რომ, წვერო არის წერტილში

ახლა ჩვენ ვპოულობთ სხვა წერტილებს პარაბოლის სიმეტრიის თავხედურად გამოყენებისას. უნდა აღინიშნოს, რომ ფუნქცია – არც კი არის, მაგრამ, მიუხედავად ამისა, არავინ გააუქმა პარაბოლას სიმეტრია.

რა მიზნით ვიპოვოთ დარჩენილი ქულები, ვფიქრობ, საბოლოო ცხრილიდან გაირკვევა:

ეს ალგორითმიკონსტრუქციას გადატანითი მნიშვნელობით შეიძლება ვუწოდოთ „შატლი“ ან „წინ და უკან“ პრინციპი ანფისა ჩეხოვასთან.

მოდით დავხატოთ ნახატი:

განხილული გრაფიკებიდან მახსენდება კიდევ ერთი სასარგებლო თვისება:

კვადრატული ფუნქციისთვის () შემდეგი მართალია:

თუ , მაშინ პარაბოლას ტოტები მიმართულია ზემოთ.

თუ , მაშინ პარაბოლას ტოტები მიმართულია ქვევით.

მრუდის სიღრმისეული ცოდნა შეიძლება მივიღოთ გაკვეთილზე ჰიპერბოლა და პარაბოლა.

კუბური პარაბოლა მოცემულია ფუნქციით. აქ არის სკოლიდან ნაცნობი ნახატი:

ჩვენ ჩამოვთვლით ფუნქციის ძირითად თვისებებს

ფუნქციის გრაფიკი

იგი წარმოადგენს პარაბოლას ერთ-ერთ ტოტს. მოდით დავხატოთ ნახატი:

ფუნქციის ძირითადი თვისებები:

ამ შემთხვევაში, ღერძი არის ვერტიკალური ასიმპტოტი ჰიპერბოლის გრაფიკისთვის ზე.

დიდი შეცდომა იქნება, თუ ნახატის შედგენისას, დაუდევრობით, ნებას დართავთ გრაფიკს გადაკვეთოს ასიმპტოტთან.

ასევე ცალმხრივი საზღვრები, გვითხარით, რომ ჰიპერბოლა არ შემოიფარგლება ზემოდანდა არ შემოიფარგლება ქვემოდან.

მოდით გამოვიკვლიოთ ფუნქცია უსასრულობაში: ანუ, თუ ღერძის გასწვრივ დავიწყებთ მოძრაობას მარცხნივ (ან მარჯვნივ) უსასრულობამდე, მაშინ "თამაშები" იქნება წვრილი ნაბიჯი. უსასრულოდ ახლოსმიუახლოვდით ნულს და, შესაბამისად, ჰიპერბოლის ტოტებს უსასრულოდ ახლოსმიუახლოვდით ღერძს.

ასე რომ, ღერძი არის ჰორიზონტალური ასიმპტოტი ფუნქციის გრაფიკისთვის, თუ "x" მიდრეკილია პლუს-მინუს უსასრულობისკენ.

ფუნქცია არის კენტი, რაც ნიშნავს, რომ ჰიპერბოლა სიმეტრიულია საწყისის მიმართ. Ეს ფაქტინახატიდან აშკარაა, უფრო მეტიც, მისი ადვილად გადამოწმება შესაძლებელია ანალიტიკურად: .

() ფორმის ფუნქციის გრაფიკი წარმოადგენს ჰიპერბოლის ორ ტოტს.

თუ , მაშინ ჰიპერბოლა მდებარეობს პირველ და მესამე კოორდინატთა კვადრატში(იხ. სურათი ზემოთ).

თუ , მაშინ ჰიპერბოლა მდებარეობს მეორე და მეოთხე კოორდინატთა კვადრატში.

არ არის რთული ჰიპერბოლის საცხოვრებელი ადგილის განსაზღვრული კანონზომიერების ანალიზი გრაფიკების გეომეტრიული გარდაქმნების თვალსაზრისით.

მაგალითი 3

ააგეთ ჰიპერბოლის მარჯვენა ტოტი

ჩვენ ვიყენებთ წერტილოვანი კონსტრუქციის მეთოდს, ხოლო ხელსაყრელია მნიშვნელობების შერჩევა ისე, რომ ისინი მთლიანად იყოფა:

მოდით დავხატოთ ნახატი:

ჰიპერბოლის მარცხენა განშტოების აგება რთული არ იქნება, აქ ფუნქციის უცნაურობა უბრალოდ დაგეხმარებათ. უხეშად რომ ვთქვათ, წერტილოვანი კონსტრუქციის ცხრილში გონებრივად დაუმატეთ თითოეულ რიცხვს მინუსი, ჩასვით შესაბამისი წერტილები და დახაზეთ მეორე ტოტი.

დეტალური გეომეტრიული ინფორმაცია განხილული ხაზის შესახებ შეგიძლიათ იხილოთ სტატიაში ჰიპერბოლა და პარაბოლა.

ექსპონენციალური ფუნქციის გრაფიკი

AT ამ პუნქტსმე დაუყოვნებლივ განვიხილავ ექსპონენციალურ ფუნქციას, რადგან უმაღლესი მათემატიკის ამოცანებში 95% შემთხვევაში ეს არის ექსპონენტი.

შეგახსენებთ, რომ ეს არის ირაციონალური რიცხვი: , ეს საჭირო იქნება გრაფიკის აგებისას, რომელსაც, ფაქტობრივად, ცერემონიის გარეშე ავაშენებ. სამი ქულაალბათ საკმარისია:

მოდით, ფუნქციის გრაფიკი მარტო დავტოვოთ, ამის შესახებ მოგვიანებით.

ფუნქციის ძირითადი თვისებები:

პრინციპში, ფუნქციების გრაფიკები ერთნაირად გამოიყურება და ა.შ.

უნდა ვთქვა, რომ მეორე შემთხვევა პრაქტიკაში ნაკლებად გავრცელებულია, მაგრამ ხდება, ამიტომ საჭიროდ მივიჩნიე ამ სტატიაში მისი ჩართვა.

ლოგარითმული ფუნქციის გრაფიკი

განვიხილოთ ფუნქცია ბუნებრივი ლოგარითმი.
მოდით გავაკეთოთ ხაზის ნახაზი:

თუ დაგავიწყდათ რა არის ლოგარითმი, მიმართეთ სასკოლო სახელმძღვანელოებს.

ფუნქციის ძირითადი თვისებები:

დომენი:

მნიშვნელობების დიაპაზონი: .

ფუნქცია არ არის შეზღუდული ზემოდან: თუმცა ნელა, მაგრამ ლოგარითმის განშტოება უსასრულობამდე მიდის.
მოდით განვიხილოთ ფუნქციის ქცევა ნულთან ახლოს მარჯვნივ: . ასე რომ, ღერძი არის ვერტიკალური ასიმპტოტი ფუნქციის გრაფიკისთვის, რომელსაც აქვს "x" ნულისკენ მარჯვნივ.

დარწმუნდით, რომ იცოდეთ და გახსოვდეთ ლოგარითმის ტიპიური მნიშვნელობა: .

პრინციპში, ლოგარითმის დიაგრამა ბაზაზე ერთნაირად გამოიყურება: , , ( ათობითი ლოგარითმიბაზაში 10) და ა.შ. ამავე დროს, ვიდრე მეტი ბაზა, მით უფრო ბრტყელი იქნება გრაფიკი.

საქმეს არ განვიხილავთ, არ მახსოვს როდის ბოლოჯერააგო გრაფიკი ასეთი საფუძვლით. დიახ, და ლოგარითმი, როგორც ჩანს, ძალიან იშვიათი სტუმარია უმაღლესი მათემატიკის ამოცანებში.

აბზაცის დასასრულს კიდევ ერთ ფაქტს გეტყვით: ექსპონენციალური ფუნქციადა ლოგარითმული ფუნქცია არის ორი ერთმანეთის შებრუნებული ფუნქციები . თუ ყურადღებით დააკვირდებით ლოგარითმის გრაფიკს, ხედავთ, რომ ეს არის იგივე მაჩვენებელი, უბრალოდ ის მდებარეობს ოდნავ განსხვავებულად.

ტრიგონომეტრიული ფუნქციების გრაფიკები

როგორ იწყება ტრიგონომეტრიული ტანჯვა სკოლაში? სწორად. სინუსიდან

მოდით დავხატოთ ფუნქცია

ეს ხაზიდაურეკა სინუსოიდი.

შეგახსენებთ, რომ "პი" არის ირაციონალური რიცხვი: და ტრიგონომეტრიაში ის თვალებში ანათებს.

ფუნქციის ძირითადი თვისებები:

ეს ფუნქციაარის პერიოდულიპერიოდით. Რას ნიშნავს? მოდით შევხედოთ ჭრილს. მისგან მარცხნივ და მარჯვნივ, გრაფიკის ზუსტად ერთი და იგივე ნაწილი უსასრულოდ მეორდება.

დომენი: , ანუ "x"-ის ნებისმიერი მნიშვნელობისთვის არის სინუსური მნიშვნელობა.

მნიშვნელობების დიაპაზონი: . ფუნქცია არის შეზღუდული: ანუ ყველა "თამაში" მკაცრად ზის სეგმენტში.
ეს არ ხდება: ან, უფრო ზუსტად, ხდება, მაგრამ ამ განტოლებებს არ აქვთ გამოსავალი.

სიმძლავრის ფუნქციის განხილვის მოხერხებულობისთვის განვიხილავთ 4 ცალკეულ შემთხვევას: სიმძლავრის ფუნქციასთან ბუნებრივი მაჩვენებელი, სიმძლავრის ფუნქცია მთელი რიცხვის მაჩვენებლით, სიმძლავრის ფუნქცია ერთად რაციონალური მაჩვენებელიდა დენის ფუნქცია ირაციონალური მაჩვენებელი.

დენის ფუნქცია ბუნებრივი მაჩვენებლით

დასაწყისისთვის, ჩვენ წარმოგიდგენთ ხარისხის ცნებას ბუნებრივი მაჩვენებლით.

განმარტება 1

რეალური რიცხვის სიმძლავრე $a$ ბუნებრივი მაჩვენებლით $n$ არის რიცხვი პროდუქტის ტოლი$n$ ფაქტორები, რომელთაგან თითოეული უდრის რიცხვს $a$.

სურათი 1.

$a$ არის ხარისხის საფუძველი.

$n$ - მაჩვენებელი.

ახლა განვიხილოთ სიმძლავრის ფუნქცია ბუნებრივი მაჩვენებლით, მისი თვისებებით და გრაფიკით.

განმარტება 2

$f\left(x\right)=x^n$ ($n\in N)$ ეწოდება სიმძლავრის ფუნქციას ბუნებრივი მაჩვენებლით.

დამატებითი მოხერხებულობისთვის განიხილეთ ცალ-ცალკე სიმძლავრის ფუნქცია ლუწი მაჩვენებლით $f\left(x\right)=x^(2n)$ და სიმძლავრის ფუნქცია კენტი მაჩვენებლით $f\left(x\right)=x^(2n- 1)$ ($n\ N)$.

სიმძლავრის ფუნქციის თვისებები ბუნებრივი ლუწი მაჩვენებლით

$f\left(-x\right)=((-x))^(2n)=x^(2n)=f(x)$ არის ლუწი ფუნქცია.

ფარგლები -- $ \

ფუნქცია მცირდება როგორც $x\in (-\infty ,0)$ და იზრდება $x\in (0,+\infty)$.

$f("")\left(x\right)=(\left(2n\cdot x^(2n-1)\right))"=2n(2n-1)\cdot x^(2(n-1 ))\ge 0$

ფუნქცია ამოზნექილია განსაზღვრების მთელ დომენზე.

ქცევა სფეროს ბოლოებში:

\[(\mathop(lim)_(x\to -\infty) x^(2n)\ )=+\infty \] \[(\mathop(lim)_(x\to +\infty) x^( 2n)\ )=+\infty \]

გრაფიკი (ნახ. 2).

სურათი 2. $f\left(x\right)=x^(2n)$ ფუნქციის გრაფიკი

სიმძლავრის ფუნქციის თვისებები ბუნებრივი კენტი მაჩვენებლით

განმარტების დომენი არის ყველა რეალური რიცხვი.

$f\left(-x\right)=((-x))^(2n-1)=(-x)^(2n)=-f(x)$ არის კენტი ფუნქცია.

$f(x)$ არის უწყვეტი განსაზღვრების მთელ დომენზე.

დიაპაზონი არის ყველა რეალური რიცხვი.

$f"\left(x\right)=\left(x^(2n-1)\right)"=(2n-1)\cdot x^(2(n-1))\ge 0$

ფუნქცია იზრდება განმარტების მთელ დომენზე.

$f\left(x\right)0$, $x\in (0,+\infty)$.

$f(""\მარცხნივ(x\მარჯვნივ))=(\მარცხნივ(\მარცხნივ(2n-1\მარჯვნივ)\cdot x^(2\მარცხნივ(n-1\მარჯვნივ))\მარჯვნივ)"=2 \მარცხნივ(2n-1\მარჯვნივ)(n-1)\cdot x^(2n-3)$

\ \

ფუნქცია არის ჩაზნექილი $x\in (-\infty ,0)$-სთვის და ამოზნექილი $x\in (0,+\infty)$-ისთვის.

გრაფიკი (სურ. 3).

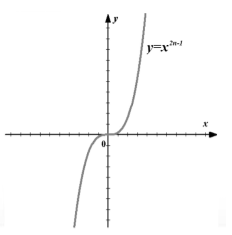
სურათი 3. $f\left(x\right)=x^(2n-1)$ ფუნქციის გრაფიკი

სიმძლავრის ფუნქცია მთელი რიცხვის მაჩვენებლით

დასაწყისისთვის, ჩვენ წარმოგიდგენთ ხარისხის ცნებას მთელი რიცხვის მაჩვენებლით.

განმარტება 3

ხარისხი ნამდვილი რიცხვი$a$ მთელი ინდექსით $n$ განისაზღვრება ფორმულით:

სურათი 4

ახლა განვიხილოთ ძალაუფლების ფუნქცია მთელი რიცხვის მაჩვენებლით, მისი თვისებებით და გრაფიკით.

განმარტება 4

$f\left(x\right)=x^n$ ($n\in Z)$ ეწოდება სიმძლავრის ფუნქციას მთელი რიცხვის მაჩვენებლით.

თუ ხარისხი ნულზე მეტია, მაშინ მივდივართ ბუნებრივი მაჩვენებლის მქონე სიმძლავრის ფუნქციის შემთხვევამდე. ზემოთ უკვე განვიხილეთ. $n=0$-ად ვიღებთ ხაზოვანი ფუნქცია$y=1$. მის განხილვას მკითხველს ვუტოვებთ. რჩება უარყოფითი მთელი რიცხვის მაჩვენებლით დენის ფუნქციის თვისებების გათვალისწინება

დენის ფუნქციის თვისებები უარყოფითი მთელი რიცხვის მაჩვენებლით

ფარგლები არის $\left(-\infty,0\right)(0,+\infty)$.

თუ მაჩვენებელი ლუწია, მაშინ ფუნქცია ლუწია; თუ ის კენტია, მაშინ ფუნქცია კენტია.

$f(x)$ არის უწყვეტი განსაზღვრების მთელ დომენზე.

ღირებულების დიაპაზონი:

თუ მაჩვენებელი ლუწია, მაშინ $(0,+\infty)$, თუ კენტი, მაშინ $\left(-\infty ,0\right)(0,+\infty)$.

თუ მაჩვენებელი კენტია, ფუნქცია მცირდება $x\in \left(-\infty ,0\right)(0,+\infty)$. ლუწი მაჩვენებლისთვის ფუნქცია მცირდება $x\in (0,+\infty)$. და იზრდება $x\in \left(-\infty,0\right)$.

$f(x)\ge 0$ მთელ დომენზე