Fungsi daya, sifat dan grafiknya Materi Demo Pelajaran-kuliah Konsep fungsi. Properti fungsi. Fungsi daya, sifat dan grafiknya. Kelas 10 Hak cipta dilindungi undang-undang. Hak Cipta dengan Hak Cipta dengan

Kemajuan pelajaran: Pengulangan. Fungsi. Properti fungsi. Mempelajari materi baru. 1. Definisi fungsi daya Definisi fungsi daya. 2. Sifat dan grafik fungsi daya Sifat dan grafik fungsi daya. Konsolidasi materi yang dipelajari. Penghitungan lisan. Penghitungan lisan. Ringkasan pelajaran. Pekerjaan rumah.



Domain dan range fungsi Semua nilai variabel bebas membentuk domain fungsi x y=f(x) f Domain fungsi Domain fungsi Semua nilai variabel dependen membentuk domain fungsi Fungsi. Properti Fungsi

Grafik suatu fungsi Misalkan suatu fungsi diberikan di mana xY y x.75 3 0,6 4 0,5 Grafik suatu fungsi adalah himpunan semua titik pada bidang koordinat, yang absisnya sama dengan nilai argumen, dan ordinatnya sama dengan nilai fungsi yang sesuai. Fungsi. Properti Fungsi

Y x Domain definisi dan jangkauan fungsi 4 y=f(x) Domain fungsi: Domain fungsi: Fungsi. Properti Fungsi

Fungsi Genap y x y=f(x) Grafik fungsi genap simetris terhadap sumbu y Fungsi y=f(x) disebut genap jika f(-x) = f(x) untuk sembarang x dari domain fungsi Fungsi. Properti Fungsi

Fungsi ganjil y x y=f(x) Grafik fungsi ganjil simetris terhadap asal O(0;0) Fungsi y=f(x) disebut ganjil jika f(-x) = -f(x) untuk sembarang x dari domain fungsi Fungsi. Properti Fungsi

Definisi fungsi daya Fungsi, di mana p adalah bilangan real tertentu, disebut fungsi daya. p y \u003d x p P \u003d x y 0 Kemajuan pelajaran




Fungsi pangkat x y 1. Domain definisi dan rentang nilai fungsi daya dari bentuk, di mana n adalah bilangan asli, semua bilangan real. 2. Fungsi-fungsi ini ganjil. Grafik mereka simetris sehubungan dengan asal. Properti dan Plot Fungsi Daya


Fungsi pangkat dengan eksponen positif rasional Domain definisi - semua bilangan positif dan bilangan 0. Jangkauan fungsi dengan eksponen seperti itu juga semua bilangan positif dan bilangan 0. Fungsi-fungsi ini bukan genap maupun ganjil. y x Properti dan Grafik Fungsi Daya

Fungsi daya dengan rasional indikator negatif. Domain definisi dan jangkauan fungsi tersebut semuanya bilangan positif. Fungsinya tidak genap maupun ganjil. Fungsi-fungsi tersebut menurun di seluruh domain definisi mereka. y x Properti dan grafik fungsi daya Kemajuan pelajaran

1. Fungsi daya, sifat dan grafiknya;
2. Transformasi:
Pemindahan paralel;
Simetri tentang sumbu koordinat;
Simetri tentang asal;
Simetri terhadap garis y = x;
Peregangan dan penyusutan sepanjang sumbu koordinat.
3. Fungsi eksponensial, sifat dan grafiknya, transformasi serupa;
4. Fungsi logaritma, sifat dan grafiknya;
5. Fungsi trigonometri, sifat dan grafiknya, transformasi sejenis (y = sin x; y = cos x; y = tg x);
Fungsi: y = x\n - sifat dan grafiknya.
Fungsi daya, sifat dan grafiknya
y \u003d x, y \u003d x 2, y \u003d x 3, y \u003d 1 / x dll. Semua fungsi ini adalah kasus khusus dari fungsi daya, yaitu fungsi y = xp, di mana p adalah bilangan real tertentu.
Sifat dan grafik fungsi daya pada dasarnya bergantung pada sifat-sifat pangkat dengan eksponen nyata, dan khususnya pada nilai-nilai yang x dan p masuk akal xp. Mari beralih ke pertimbangan serupa. berbagai kesempatan tergantung pada
eksponen p.
- Indikator p = 2n adalah bilangan asli genap.
y=x2n, di mana n adalah bilangan asli dan memiliki sifat-sifat berikut:
- domain definisi adalah semua bilangan real, yaitu himpunan R;
- kumpulan nilai- bilangan non-negatif, yaitu y lebih besar dari atau sama dengan 0;
- fungsi y=x2n bahkan, karena x 2n = (-x) 2n
- fungsi menurun pada interval x< 0 dan meningkat pada interval x > 0.
Grafik Fungsi y=x2n memiliki bentuk yang sama seperti, misalnya, grafik fungsi y=x4.
2. Indikator p = 2n - 1- bilangan asli ganjil
Dalam hal ini, fungsi daya y=x2n-1, di mana adalah bilangan asli, memiliki sifat-sifat berikut:
- domain definisi - atur R;
- set nilai - set R;
- fungsi y=x2n-1 aneh karena (- x) 2n-1= x 2n-1 ;
- fungsi meningkat pada seluruh sumbu nyata.
Grafik Fungsi y=x2n-1 y=x3.

3. Indikator p=-2n, di mana n- bilangan asli.
Dalam hal ini, fungsi daya y=x-2n=1/x2n memiliki sifat-sifat berikut:
- set nilai - angka positif y>0;
- fungsi y = 1/x2n bahkan, karena 1/(-x) 2n= 1/x2n;
- fungsi meningkat pada interval x0.
Grafik fungsi y = 1/x2n memiliki bentuk yang sama seperti, misalnya, grafik fungsi y = 1/x2.

4. Indikator p = -(2n-1), di mana n- bilangan asli.
Dalam hal ini, fungsi daya y=x-(2n-1) memiliki sifat-sifat berikut:
- domain definisi adalah himpunan R, kecuali untuk x = 0;
- set nilai - set R, kecuali untuk y = 0;
- fungsi y=x-(2n-1) aneh karena (- x)-(2n-1) = -x-(2n-1);
- fungsi menurun pada interval x< 0 dan x > 0.
Grafik Fungsi y=x-(2n-1) memiliki bentuk yang sama seperti, misalnya, grafik fungsi y = 1/x3.

Itu bahan metodis hanya untuk referensi dan berlaku untuk jarak yang lebar topik. Artikel ini memberikan gambaran umum tentang grafik fungsi dasar utama dan mempertimbangkan pertanyaan yang paling penting – cara membuat grafik yang benar dan CEPAT. Selama studi matematika yang lebih tinggi tanpa mengetahui grafik fungsi dasar dasar, itu akan sulit, jadi sangat penting untuk mengingat seperti apa grafik parabola, hiperbola, sinus, kosinus, dll., ingat beberapa nilai fungsi. Kami juga akan berbicara tentang beberapa properti dari fungsi utama.
Saya tidak berpura-pura untuk kelengkapan dan ketelitian ilmiah dari materi, penekanan akan ditempatkan, pertama-tama, pada praktik - hal-hal yang dengannya seseorang harus menghadapi secara harfiah di setiap langkah, dalam topik matematika yang lebih tinggi. Grafik untuk boneka? Anda bisa mengatakan demikian.
Oleh banyak permintaan pembaca daftar isi yang dapat diklik:
Selain itu, ada abstrak ultra-pendek tentang topik ini
– kuasai 16 jenis grafik dengan mempelajari ENAM halaman!
Serius, enam, bahkan saya sendiri terkejut. abstrak ini berisi grafik yang ditingkatkan dan tersedia dengan biaya nominal, versi demo dapat dilihat. Lebih mudah untuk mencetak file sehingga grafik selalu ada. Terima kasih telah mendukung proyek ini!
Dan kita mulai segera:
Bagaimana cara membangun sumbu koordinat dengan benar?
Dalam praktiknya, tes hampir selalu dibuat oleh siswa di buku catatan terpisah, berjajar di dalam sangkar. Mengapa Anda membutuhkan tanda kotak-kotak? Bagaimanapun, pekerjaan itu, pada prinsipnya, dapat dilakukan pada lembar A4. Dan sangkar diperlukan hanya untuk desain gambar yang berkualitas tinggi dan akurat.
Setiap gambar grafik fungsi dimulai dengan sumbu koordinat.
Gambar adalah dua dimensi dan tiga dimensi.
Mari kita pertimbangkan kasus dua dimensi terlebih dahulu Kartesius sistem persegi panjang koordinat:

1) Kami menggambar sumbu koordinat. Sumbu disebut sumbu x , dan sumbu sumbu y . Kami selalu mencoba menggambar mereka rapi dan tidak bengkok. Anak panah juga tidak boleh menyerupai janggut Papa Carlo.
2) Kami menandatangani kapak huruf kapital"x" dan "y". Jangan lupa untuk menandatangani kapak.
3) Atur skala di sepanjang sumbu: menggambar nol dan dua satu. Saat membuat gambar, skala yang paling nyaman dan umum adalah: 1 unit = 2 sel (menggambar di sebelah kiri) - tempel jika memungkinkan. Namun, dari waktu ke waktu terjadi bahwa gambar tidak muat pada lembar buku catatan - maka kami mengurangi skala: 1 unit = 1 sel (gambar di sebelah kanan). Jarang, tetapi kebetulan skala gambar harus dikurangi (atau ditingkatkan) bahkan lebih
JANGAN mencoret-coret dari senapan mesin ... -5, -4, -3, -1, 0, 1, 2, 3, 4, 5, .... Untuk bidang koordinat bukanlah monumen bagi Descartes, dan siswa bukanlah seekor merpati. Kami meletakkan nol dan dua unit di sepanjang sumbu. Kadang-kadang alih-alih unit, akan lebih mudah untuk "mendeteksi" nilai lain, misalnya, "dua" pada sumbu absis dan "tiga" pada sumbu ordinat - dan sistem ini (0, 2 dan 3) juga akan mengatur kisi koordinat secara unik.
Lebih baik memperkirakan perkiraan dimensi gambar SEBELUM gambar digambar.. Jadi, misalnya, jika tugas mengharuskan menggambar segitiga dengan simpul , , , maka cukup jelas bahwa skala populer 1 unit = 2 sel tidak akan berfungsi. Mengapa? Mari kita lihat intinya - di sini Anda harus mengukur lima belas sentimeter ke bawah, dan, jelas, gambarnya tidak akan muat (atau hampir tidak muat) pada lembar buku catatan. Oleh karena itu, kami segera memilih skala yang lebih kecil 1 unit = 1 sel.
By the way, sekitar sentimeter dan sel notebook. Benarkah ada 15 sentimeter dalam 30 sel notebook? Ukur dalam buku catatan untuk bunga 15 sentimeter dengan penggaris. Di Uni Soviet, mungkin ini benar ... Sangat menarik untuk dicatat bahwa jika Anda mengukur sentimeter yang sama ini secara horizontal dan vertikal, maka hasilnya (dalam sel) akan berbeda! Sebenarnya, notebook modern tidak kotak-kotak, tetapi persegi panjang. Ini mungkin tampak seperti omong kosong, tetapi menggambar, misalnya, lingkaran dengan kompas dalam situasi seperti itu sangat merepotkan. Sejujurnya, pada saat-saat seperti itu Anda mulai berpikir tentang kebenaran Kamerad Stalin, yang dikirim ke kamp untuk pekerjaan peretasan dalam produksi, belum lagi industri otomotif dalam negeri, pesawat jatuh atau pembangkit listrik yang meledak.
Berbicara tentang kualitas, atau rekomendasi singkat oleh alat tulis. Sampai saat ini, sebagian besar notebook sedang dijual, kata-kata buruk belum lagi, omong kosong. Karena mereka basah, dan tidak hanya dari pena gel, tetapi juga dari pulpen! Hemat di atas kertas. Untuk izin pekerjaan kontrol Saya sarankan menggunakan notebook dari Arkhangelsk Pulp and Paper Mill (18 lembar, sangkar) atau Pyaterochka, meskipun lebih mahal. Dianjurkan untuk memilih pena gel, bahkan isi ulang gel Cina termurah jauh lebih baik daripada bolpoin, yang mengolesi atau merobek kertas. Satu-satunya "kompetitif" pulpen dalam ingatan saya adalah "Erich Krause". Dia menulis dengan jelas, indah dan stabil - baik dengan batang penuh, atau dengan batang yang hampir kosong.
Selain itu: melihat sistem koordinat persegi panjang dengan mata geometri analitik tercakup dalam artikel Linear (non) ketergantungan vektor. Dasar vektor, Informasi rinci tentang koordinat perempat dapat ditemukan di paragraf kedua pelajaran Pertidaksamaan linier.
kasus 3D

Ini hampir sama di sini.
1) Kami menggambar sumbu koordinat. Standar: menerapkan sumbu – diarahkan ke atas, sumbu – diarahkan ke kanan, sumbu – ke bawah ke kiri dengan ketat pada sudut 45 derajat.
2) Kami menandatangani kapak.
3) Atur skala di sepanjang sumbu. Skala di sepanjang sumbu - dua kali lebih kecil dari skala di sepanjang sumbu lainnya. Perhatikan juga bahwa pada gambar yang benar, saya menggunakan "serif" non-standar di sepanjang sumbu (kemungkinan ini telah disebutkan di atas). Dari sudut pandang saya, ini lebih akurat, lebih cepat, dan lebih estetis - Anda tidak perlu mencari bagian tengah sel di bawah mikroskop dan "memahat" unit sampai ke asalnya.
Saat melakukan gambar 3D lagi - prioritaskan skala
1 unit = 2 sel (menggambar di sebelah kiri).
Untuk apa semua aturan ini? Aturan ada untuk dilanggar. Apa yang akan saya lakukan sekarang. Faktanya adalah bahwa gambar artikel selanjutnya akan dibuat oleh saya di Excel, dan sumbu koordinat akan terlihat salah dari sudut pandang desain yang benar. Saya dapat menggambar semua grafik dengan tangan, tetapi menggambarnya sangat menakutkan, karena Excel enggan menggambarnya dengan lebih akurat.
Grafik dan sifat dasar fungsi dasar
Fungsi linier diberikan oleh persamaan . Grafik fungsi linier adalah langsung. Untuk membuat garis lurus, cukup mengetahui dua titik.
Contoh 1
Gambarkan fungsinya. Mari kita temukan dua poin. Adalah menguntungkan untuk memilih nol sebagai salah satu poin.
Jika kemudian
Kami mengambil beberapa poin lain, misalnya, 1.
Jika kemudian
Saat menyiapkan tugas, koordinat titik biasanya diringkas dalam tabel:

Dan nilai-nilai itu sendiri dihitung secara lisan atau pada konsep, kalkulator.
Dua poin ditemukan, mari kita menggambar:

Saat menggambar, kami selalu menandatangani grafik.
Tidak akan berlebihan untuk mengingat kasus khusus dari fungsi linier:

Perhatikan bagaimana saya menempatkan teks, tanda tangan tidak boleh ambigu saat mempelajari gambar. PADA kasus ini sangat tidak diinginkan untuk membubuhkan tanda tangan di sebelah titik perpotongan garis, atau di kanan bawah di antara grafik.
1) Fungsi linier dari bentuk () disebut proporsionalitas langsung. Sebagai contoh, . Grafik proporsionalitas langsung selalu melalui titik asal. Dengan demikian, konstruksi garis lurus disederhanakan - cukup untuk menemukan hanya satu titik.
2) Persamaan bentuk mendefinisikan garis lurus yang sejajar dengan sumbu, khususnya sumbu itu sendiri diberikan oleh persamaan. Grafik fungsi dibangun segera, tanpa menemukan titik. Artinya, entri harus dipahami sebagai berikut: "y selalu sama dengan -4, untuk setiap nilai x."
3) Persamaan bentuk mendefinisikan garis lurus yang sejajar dengan sumbu, khususnya sumbu itu sendiri diberikan oleh persamaan. Grafik fungsi juga segera dibangun. Entrinya harus dipahami sebagai berikut: "x selalu, untuk setiap nilai y, sama dengan 1."
Beberapa akan bertanya, nah, mengapa ingat kelas 6?! Begitulah, mungkin begitu, hanya selama bertahun-tahun latihan saya bertemu selusin siswa yang bingung dengan tugas membuat grafik seperti atau .
Menggambar garis lurus adalah tindakan yang paling umum saat membuat gambar.
Garis lurus dibahas secara rinci dalam kursus geometri analitik, dan mereka yang ingin dapat merujuk ke artikel Persamaan garis lurus pada bidang.
Grafik fungsi kuadrat, grafik fungsi kubik, grafik polinomial
Parabola. Jadwal fungsi kuadrat ![]() () adalah parabola. Mempertimbangkan kasus terkenal:
() adalah parabola. Mempertimbangkan kasus terkenal:

Mari kita mengingat kembali beberapa properti dari fungsi tersebut.
Jadi, solusi untuk persamaan kita: - pada titik inilah titik parabola berada. Mengapa demikian dapat dipelajari dari artikel teoretis tentang turunan dan pelajaran tentang ekstrem dari fungsi. Sementara itu, kami menghitung nilai "y" yang sesuai:
Jadi simpulnya berada di titik
Sekarang kita menemukan titik lain, sambil dengan berani menggunakan simetri parabola. Perlu diperhatikan bahwa fungsi ![]() – tidak genap, tetapi, bagaimanapun, tidak ada yang membatalkan simetri parabola.
– tidak genap, tetapi, bagaimanapun, tidak ada yang membatalkan simetri parabola.
Dalam urutan apa untuk menemukan poin yang tersisa, saya pikir itu akan menjadi jelas dari tabel final:
Algoritma ini konstruksi dapat secara kiasan disebut "shuttle" atau prinsip "bolak-balik" dengan Anfisa Chekhova.
Mari kita membuat gambar:

Dari grafik yang dipertimbangkan, fitur lain yang berguna muncul dalam pikiran:
Untuk fungsi kuadrat ![]() () berikut ini benar:
() berikut ini benar:
Jika , maka cabang-cabang parabola diarahkan ke atas.
Jika , maka cabang-cabang parabola diarahkan ke bawah.
Pengetahuan mendalam tentang kurva dapat diperoleh dalam pelajaran Hiperbola dan parabola.
Parabola kubik diberikan oleh fungsi . Berikut adalah gambar yang familiar dari sekolah:

Kami mencantumkan properti utama dari fungsi
Grafik Fungsi
Ini mewakili salah satu cabang parabola. Mari kita membuat gambar:

Sifat utama dari fungsi:
Dalam hal ini, sumbunya adalah asimtot vertikal untuk grafik hiperbola di .
Akan menjadi kesalahan BESAR jika, saat menggambar, karena kelalaian, Anda membiarkan grafik berpotongan dengan asimtot.
Juga batas satu sisi, beri tahu kami bahwa hiperbola tidak terbatas dari atas dan tidak terbatas dari bawah.
Mari kita telusuri fungsinya di tak terhingga: , yaitu, jika kita mulai bergerak sepanjang sumbu ke kiri (atau kanan) hingga tak terhingga, maka "permainan" akan menjadi langkah ramping sangat dekat mendekati nol, dan, karenanya, cabang-cabang hiperbola sangat dekat mendekati sumbu.
Jadi sumbunya adalah asimtot horizontal untuk grafik fungsi, jika "x" cenderung plus atau minus tak terhingga.
Fungsinya adalah aneh, yang berarti hiperbola simetris terhadap titik asal. Fakta ini jelas dari gambar, apalagi, dapat dengan mudah diverifikasi secara analitis: ![]() .
.
Grafik fungsi bentuk () mewakili dua cabang hiperbola.
Jika , maka hiperbola terletak pada kuadran koordinat pertama dan ketiga(lihat gambar di atas).
Jika , maka hiperbola terletak pada kuadran koordinat kedua dan keempat.
Tidak sulit untuk menganalisis keteraturan yang ditentukan dari tempat tinggal hiperbola dari sudut pandang transformasi geometris grafik.
Contoh 3
Bangun cabang kanan hiperbola
Kami menggunakan metode konstruksi pointwise, sementara itu menguntungkan untuk memilih nilai sehingga mereka membagi sepenuhnya:
![]()
Mari kita membuat gambar:

Tidak akan sulit untuk membangun cabang kiri hiperbola, di sini keanehan fungsi hanya akan membantu. Secara kasar, dalam tabel konstruksi pointwise, secara mental tambahkan minus ke setiap angka, letakkan titik yang sesuai dan gambar cabang kedua.
Informasi geometris terperinci tentang garis yang dipertimbangkan dapat ditemukan di artikel Hiperbola dan parabola.
Grafik fungsi eksponensial
PADA paragraf ini Saya akan segera mempertimbangkan fungsi eksponensial, karena dalam masalah matematika tingkat tinggi dalam 95% kasus eksponenlah yang muncul.
Saya mengingatkan Anda bahwa ini adalah bilangan irasional: , ini akan diperlukan saat membuat grafik, yang sebenarnya akan saya bangun tanpa upacara. Tiga poin mungkin cukup:
![]()

Mari kita tinggalkan grafik fungsinya untuk saat ini, tentangnya nanti.
Sifat utama dari fungsi:
Pada dasarnya, grafik fungsi terlihat sama, dll.
Saya harus mengatakan bahwa kasus kedua kurang umum dalam praktiknya, tetapi itu memang terjadi, jadi saya merasa perlu untuk memasukkannya ke dalam artikel ini.
Grafik fungsi logaritma
Pertimbangkan fungsi dengan logaritma natural.
Mari kita menggambar garis:
Jika Anda lupa apa itu logaritma, silakan merujuk ke buku teks sekolah.

Sifat utama dari fungsi:
Domain: ![]()
Jarak nilai: .
Fungsinya tidak terbatas dari atas: ![]() , meskipun lambat, tetapi cabang logaritma naik hingga tak terhingga.
, meskipun lambat, tetapi cabang logaritma naik hingga tak terhingga.
Mari kita periksa perilaku fungsi mendekati nol di sebelah kanan: ![]() . Jadi sumbunya adalah asimtot vertikal
untuk grafik fungsi dengan "x" cenderung nol di sebelah kanan.
. Jadi sumbunya adalah asimtot vertikal
untuk grafik fungsi dengan "x" cenderung nol di sebelah kanan.
Pastikan untuk mengetahui dan mengingat nilai khas logaritma: .
Pada dasarnya, grafik logaritma di pangkalan terlihat sama: , , ( logaritma desimal di basis 10), dll. Pada saat yang sama, dari lebih dasar, semakin datar grafiknya.
Kami tidak akan mempertimbangkan kasusnya, saya tidak ingat kapan terakhir kali membangun grafik dengan dasar seperti itu. Ya, dan logaritma tampaknya menjadi tamu yang sangat jarang dalam masalah matematika yang lebih tinggi.
Sebagai penutup paragraf, saya akan mengatakan satu fakta lagi: Fungsi eksponensial dan fungsi logaritma adalah dua saling fungsi terbalik . Jika Anda melihat lebih dekat pada grafik logaritma, Anda dapat melihat bahwa ini adalah eksponen yang sama, hanya terletak sedikit berbeda.
Grafik fungsi trigonometri
Bagaimana siksaan trigonometri dimulai di sekolah? Benar. Dari sinus
Mari kita plot fungsinya

Garis ini ditelepon sinusoida.
Saya mengingatkan Anda bahwa "pi" adalah bilangan irasional :, dan dalam trigonometri itu mempesona di mata.
Sifat utama dari fungsi:
Fungsi ini adalah berkala dengan suatu periode. Apa artinya? Mari kita lihat potongannya. Di kiri dan kanannya, potongan grafik yang sama berulang tanpa henti.
Domain: , yaitu, untuk setiap nilai "x" ada nilai sinus.
Jarak nilai: . Fungsinya adalah terbatas: , yaitu, semua "permainan" duduk dengan ketat di segmen tersebut .
Ini tidak terjadi: atau, lebih tepatnya, itu terjadi, tetapi persamaan ini tidak memiliki solusi.
Untuk kenyamanan mempertimbangkan fungsi daya, kami akan mempertimbangkan 4 kasus terpisah: fungsi daya dengan indikator alami, fungsi daya dengan eksponen bilangan bulat, fungsi daya dengan indikator rasional dan fungsi daya dengan indikator irasional.
Fungsi daya dengan eksponen alami
Untuk memulainya, kami memperkenalkan konsep gelar dengan eksponen alami.
Definisi 1
Perpangkatan bilangan real $a$ dengan eksponen natural $n$ adalah bilangannya sama dengan produk$n$ faktor, yang masing-masing sama dengan angka $a$.
Gambar 1.
$a$ adalah dasar dari derajat.
$n$ - eksponen.
Pertimbangkan sekarang fungsi pangkat dengan eksponen alami, sifat dan grafiknya.
Definisi 2
$f\left(x\right)=x^n$ ($n\in N)$ disebut fungsi pangkat dengan eksponen natural.
Untuk kenyamanan lebih lanjut, pertimbangkan secara terpisah fungsi pangkat dengan eksponen genap $f\left(x\right)=x^(2n)$ dan fungsi daya dengan eksponen ganjil $f\left(x\right)=x^(2n- 1)$ ($n\dalam N)$.
Sifat-sifat fungsi pangkat dengan eksponen genap alami
$f\left(-x\right)=((-x))^(2n)=x^(2n)=f(x)$ adalah fungsi genap.
Cakupan -- $ \
Fungsi berkurang sebagai $x\in (-\infty ,0)$ dan meningkat sebagai $x\in (0,+\infty)$.
$f("")\left(x\kanan)=(\left(2n\cdot x^(2n-1)\right))"=2n(2n-1)\cdot x^(2(n-1 ))\ge 0$
Fungsinya cembung pada seluruh domain definisi.
Perilaku di ujung ruang lingkup:
\[(\mathop(lim)_(x\to -\infty ) x^(2n)\ )=+\infty \] \[(\mathop(lim)_(x\to +\infty ) x^( 2n)\ )=+\infty \]
Grafik (Gbr. 2).

Gambar 2. Grafik fungsi $f\left(x\right)=x^(2n)$
Sifat-sifat fungsi pangkat dengan eksponen ganjil alami
Domain definisi adalah semua bilangan real.
$f\left(-x\right)=((-x))^(2n-1)=(-x)^(2n)=-f(x)$ adalah fungsi ganjil.
$f(x)$ kontinu pada seluruh domain definisi.
Rentangnya adalah semua bilangan real.
$f"\left(x\right)=\left(x^(2n-1)\right)"=(2n-1)\cdot x^(2(n-1))\ge 0$
Fungsi meningkat di seluruh domain definisi.
$f\kiri(x\kanan)0$, untuk $x\in (0,+\infty)$.
$f(""\kiri(x\kanan))=(\kiri(\kiri(2n-1\kanan)\cdot x^(2\kiri(n-1\kanan))\kanan))"=2 \left(2n-1\right)(n-1)\cdot x^(2n-3)$
\ \
Fungsinya cekung untuk $x\in (-\infty ,0)$ dan cembung untuk $x\in (0,+\infty)$.
Grafik (Gbr. 3).
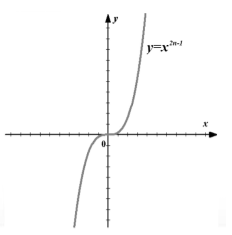
Gambar 3. Grafik fungsi $f\left(x\right)=x^(2n-1)$
Fungsi daya dengan eksponen bilangan bulat
Untuk memulainya, kami memperkenalkan konsep derajat dengan eksponen bilangan bulat.
Definisi 3
Derajat bilangan asli$a$ dengan indeks bilangan bulat $n$ ditentukan oleh rumus:

Gambar 4
Pertimbangkan sekarang fungsi pangkat dengan eksponen bilangan bulat, properti dan grafiknya.
Definisi 4
$f\left(x\right)=x^n$ ($n\in Z)$ disebut fungsi pangkat dengan eksponen bilangan bulat.
Jika derajat lebih besar dari nol, maka kita sampai pada kasus fungsi pangkat dengan eksponen alami. Kami sudah mempertimbangkannya di atas. Untuk $n=0$ kita mendapatkan fungsi linear$y=1$. Kami menyerahkan pertimbangannya kepada pembaca. Tetap mempertimbangkan sifat-sifat fungsi pangkat dengan eksponen bilangan bulat negatif
Sifat-sifat fungsi pangkat dengan eksponen bilangan bulat negatif
Cakupannya adalah $\left(-\infty ,0\right)(0,+\infty)$.
Jika pangkatnya genap, maka fungsinya genap; jika eksponennya genap, maka fungsinya ganjil.
$f(x)$ kontinu pada seluruh domain definisi.
Rentang nilai:
Jika pangkatnya genap, maka $(0,+\infty)$, jika ganjil, maka $\left(-\infty ,0\right)(0,+\infty)$.
Jika eksponen ganjil, fungsi berkurang sebagai $x\in \left(-\infty ,0\right)(0,+\infty)$. Untuk eksponen genap, fungsi berkurang sebagai $x\in (0,+\infty)$. dan meningkat sebagai $x\in \left(-\infty ,0\right)$.
$f(x)\ge 0$ di seluruh domain
