មុខងារថាមពល, លក្ខណៈសម្បត្តិ និងក្រាហ្វរបស់វា។ សម្ភារៈសាកល្បងមេរៀនមេរៀន គំនិតនៃមុខងារ។ មុខងារមុខងារ។ មុខងារថាមពល លក្ខណៈសម្បត្តិ និងក្រាហ្វរបស់វា។ ថ្នាក់ទី១០ រក្សាសិទ្ធិគ្រប់យ៉ាង។ រក្សាសិទ្ធិដោយរក្សាសិទ្ធិជាមួយ

វឌ្ឍនភាពនៃមេរៀន៖ ពាក្យដដែលៗ។ មុខងារ។ មុខងារមុខងារ។ រៀនសម្ភារៈថ្មី។ 1. និយមន័យនៃអនុគមន៍ថាមពល និយមន័យនៃអនុគមន៍ថាមពលមួយ។ 2. លក្ខណៈសម្បត្តិ និងក្រាហ្វនៃអនុគមន៍ថាមពល លក្ខណៈសម្បត្តិ និងក្រាហ្វនៃអនុគមន៍ថាមពល។ ការបង្រួបបង្រួមនៃសម្ភារៈសិក្សា។ ការរាប់ពាក្យសំដី។ ការរាប់ពាក្យសំដី។ សេចក្តីសង្ខេបនៃមេរៀន។ កិច្ចការផ្ទះ។

ដែន និងជួរនៃអនុគមន៍ តម្លៃទាំងអស់នៃអថេរឯករាជ្យបង្កើតបានជាដែននៃអនុគមន៍ x y=f(x) f ដែននៃអនុគមន៍ ដែននៃអនុគមន៍ តម្លៃទាំងអស់ដែលអថេរអាស្រ័យបង្កើតបានជាដែននៃអនុគមន៍ មុខងារ។ មុខងារមុខងារ

ក្រាហ្វនៃអនុគមន៍ អនុញ្ញាតឱ្យអនុគមន៍មួយត្រូវបានផ្តល់ឱ្យដែល xY y x.75 3 0.6 4 0.5 ក្រាហ្វនៃអនុគមន៍មួយគឺជាសំណុំនៃចំណុចទាំងអស់នៃប្លង់កូអរដោនេ ដែលជា abscissas ដែលស្មើនឹងតម្លៃនៃអាគុយម៉ង់។ ហើយការចាត់តាំងគឺស្មើនឹងតម្លៃដែលត្រូវគ្នានៃមុខងារ។ មុខងារ។ មុខងារមុខងារ

Y x Domain នៃនិយមន័យ និងជួរនៃអនុគមន៍ 4 y=f(x) Domain of the function: Domain of the function: Function. មុខងារមុខងារ

អនុគមន៍ y x y = f(x) ក្រាហ្វ មុខងារសូម្បីតែស៊ីមេទ្រីអំពីអ័ក្ស y អនុគមន៍ y=f(x) ត្រូវបានហៅទោះបីជា f(-x) = f(x) សម្រាប់ x ណាមួយពីដែននៃអនុគមន៍។ មុខងារមុខងារ

មុខងារសេស y x y = f(x) ក្រាហ្វ មុខងារសេសស៊ីមេទ្រីទាក់ទងនឹងប្រភពដើម O(0;0) អនុគមន៍ y=f(x) ត្រូវបានគេហៅថាសេស ប្រសិនបើ f(-x) = -f(x) សម្រាប់ x ណាមួយពីដែននៃអនុគមន៍។ មុខងារមុខងារ

និយមន័យនៃអនុគមន៍ថាមពល អនុគមន៍ A ដែល p ជាចំនួនពិតដែលបានផ្តល់ឱ្យ ត្រូវបានគេហៅថាអនុគមន៍ថាមពល។ p y \u003d x p P \u003d x y 0 វឌ្ឍនភាពមេរៀន

អនុគមន៍​ថាមពល x y 1. ដែន​នៃ​និយមន័យ និង​ជួរ​តម្លៃ​នៃ​អនុគមន៍​ថាមពល​នៃ​ទម្រង់ ដែល n គឺ លេខធម្មជាតិគឺជាចំនួនពិតទាំងអស់។ 2. មុខងារទាំងនេះគឺសេស។ ក្រាហ្វរបស់ពួកគេគឺស៊ីមេទ្រីទាក់ទងនឹងប្រភពដើម។ មុខងារមុខងារថាមពល និងដីឡូតិ៍

អនុគមន៍ថាមពលជាមួយនឹងនិទស្សន្តវិជ្ជមានសមហេតុផល ដែននៃនិយមន័យ - ទាំងអស់។ លេខវិជ្ជមាននិងលេខ 0. ជួរនៃអនុគមន៍ដែលមាននិទស្សន្តបែបនេះក៏ជាលេខវិជ្ជមានទាំងអស់ និងលេខ 0។ អនុគមន៍ទាំងនេះមិនសូម្បីតែឬសេស។ y x លក្ខណៈសម្បត្តិ និងក្រាហ្វនៃអនុគមន៍ថាមពល

អនុគមន៍​អំណាច​ដោយ​សនិទានភាព សូចនាករអវិជ្ជមាន. ដែននៃនិយមន័យ និងជួរនៃអនុគមន៍ទាំងនោះគឺជាលេខវិជ្ជមានទាំងអស់។ មុខងារគឺមិនសូម្បីតែឬសេស។ មុខងារបែបនេះថយចុះនៅលើដែននិយមន័យទាំងមូលរបស់វា។ y x លក្ខណៈសម្បត្តិ និងក្រាហ្វនៃអនុគមន៍ថាមពល ដំណើរការមេរៀន

1. មុខងារថាមពល លក្ខណៈសម្បត្តិ និងក្រាហ្វរបស់វា;

2. ការផ្លាស់ប្តូរ៖

ការផ្ទេរប៉ារ៉ាឡែល;

ស៊ីមេទ្រីអំពីអ័ក្សកូអរដោនេ;

ស៊ីមេទ្រីអំពីប្រភពដើម;

ស៊ីមេទ្រីអំពីបន្ទាត់ y = x;

ពង្រីក និងបង្រួមតាមអ័ក្សកូអរដោនេ។

3. អនុគមន៍អិចស្ប៉ូណង់ស្យែល លក្ខណៈសម្បត្តិ និងក្រាហ្វរបស់វា ការបំប្លែងស្រដៀងគ្នា។

4. អនុគមន៍លោការីត លក្ខណៈសម្បត្តិ និងក្រាហ្វរបស់វា;

5. អនុគមន៍ត្រីកោណមាត្រ លក្ខណៈសម្បត្តិ និងក្រាហ្វរបស់វា ការបំប្លែងស្រដៀងគ្នា (y = sin x; y = cos x; y = tg x);

មុខងារ៖ y = x\n - លក្ខណៈសម្បត្តិ និងក្រាហ្វរបស់វា។

មុខងារថាមពល លក្ខណៈសម្បត្តិ និងក្រាហ្វរបស់វា។

y \u003d x, y \u003d x 2, y \u003d x 3, y \u003d 1 / xល មុខងារទាំងអស់នេះគឺជាករណីពិសេសនៃអនុគមន៍ថាមពល ពោលគឺមុខងារ y = xpដែល p គឺជាចំនួនពិតដែលបានផ្តល់ឱ្យ។
លក្ខណសម្បត្តិ និងក្រាហ្វនៃអនុគមន៍ថាមពល អាស្រ័យទៅលើលក្ខណៈសម្បត្តិនៃថាមពលដែលមាននិទស្សន្តពិតប្រាកដ ហើយជាពិសេសទៅលើតម្លៃដែល xនិង ទំធ្វើអោយ​យល់​ច្បាស់ xp. ចូរបន្តទៅការពិចារណាស្រដៀងគ្នា។ ឱកាសផ្សេងៗអាស្រ័យលើ
និទស្សន្ត ទំ។

1. សន្ទស្សន៍ p = 2nគឺជាលេខធម្មជាតិ។

y=x2nកន្លែងណា នជាលេខធម្មជាតិ និងមានលក្ខណៈសម្បត្តិដូចខាងក្រោមៈ

• ដែននៃនិយមន័យគឺជាចំនួនពិតទាំងអស់ ពោលគឺសំណុំ R;
• សំណុំ​នៃ​តម្លៃ - លេខមិនអវិជ្ជមានពោលគឺ y ធំជាង ឬស្មើ 0;
• មុខងារ y=x2nសូម្បីតែ, ដោយសារតែ x 2n = (-x) 2n
• មុខងារកំពុងថយចុះនៅចន្លោះពេល x< 0 និងកើនឡើងនៅចន្លោះពេល x > 0 ។

ក្រាហ្វមុខងារ y=x2nមានទម្រង់ដូចគ្នានឹងឧទាហរណ៍ក្រាហ្វនៃអនុគមន៍ y=x4.

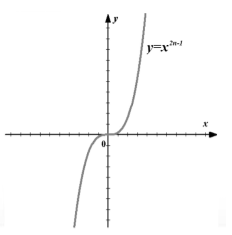
2. សូចនាករ p = 2n − 1- លេខសេសធម្មជាតិ

ក្នុងករណីនេះមុខងារថាមពល y=x2n-1ដែលជាលេខធម្មជាតិ មានលក្ខណៈសម្បត្តិដូចខាងក្រោម៖

• ដែននៃនិយមន័យ - កំណត់ R;
• សំណុំនៃតម្លៃ - កំណត់ R;
• មុខងារ y=x2n-1ប្លែកព្រោះ (- x) 2n-1= x 2n-1 ;
• មុខងារកំពុងកើនឡើងនៅលើអ័ក្សពិតទាំងមូល។

ក្រាហ្វមុខងារ y=x2n-1 y=x3.

3. សូចនាករ p=-2nកន្លែងណា n-លេខធម្មជាតិ។

ក្នុងករណីនេះមុខងារថាមពល y=x-2n=1/x2nមានលក្ខណៈសម្បត្តិដូចខាងក្រោមៈ

• សំណុំនៃតម្លៃ - លេខវិជ្ជមាន y> 0;
• មុខងារ y = 1/x2nសូម្បីតែ, ដោយសារតែ 1/(-x) 2 ន= 1/x2n;
• មុខងារកំពុងកើនឡើងនៅលើចន្លោះ x0 ។

ក្រាហ្វនៃអនុគមន៍ y = 1/x2nមានទម្រង់ដូចគ្នានឹងឧទាហរណ៍ក្រាហ្វនៃអនុគមន៍ y = 1/x2.

4. សូចនាករ p = -(2n-1)កន្លែងណា ន- លេខធម្មជាតិ។
ក្នុងករណីនេះមុខងារថាមពល y=x-(2n-1)មានលក្ខណៈសម្បត្តិដូចខាងក្រោមៈ

• ដែននៃនិយមន័យគឺជាសំណុំ R លើកលែងតែ x = 0;
• សំណុំនៃតម្លៃ - កំណត់ R លើកលែងតែ y = 0;
• មុខងារ y=x-(2n-1)ប្លែកព្រោះ (- x)-(2n-1) = -x-(2n-1);
• មុខងារកំពុងថយចុះតាមចន្លោះពេល x< 0 និង x > 0.

ក្រាហ្វមុខងារ y=x-(2n-1)មានទម្រង់ដូចគ្នានឹងឧទាហរណ៍ក្រាហ្វនៃអនុគមន៍ y = 1/x3.

នេះ។ សម្ភារៈវិធីសាស្រ្តគឺសម្រាប់ជាឯកសារយោងតែប៉ុណ្ណោះ ហើយអនុវត្តចំពោះ ជួរធំទូលាយមួយ។ប្រធានបទ។ អត្ថបទផ្តល់នូវទិដ្ឋភាពទូទៅនៃក្រាហ្វនៃមុខងារបឋមសំខាន់ៗ និងពិចារណា សំណួរសំខាន់បំផុត – របៀបបង្កើតក្រាហ្វយ៉ាងត្រឹមត្រូវ និងរហ័ស. ក្នុងអំឡុងពេលសិក្សា គណិតវិទ្យាខ្ពស់ជាងដោយមិនដឹងពីក្រាហ្វនៃអនុគមន៍បឋម វានឹងពិបាក ដូច្នេះវាពិតជាសំខាន់ណាស់ក្នុងការចងចាំពីរបៀបដែលក្រាហ្វនៃប៉ារ៉ាបូឡា អ៊ីពែបូឡា ស៊ីនុស កូស៊ីនុស ជាដើម។ ដើម្បីចងចាំតម្លៃមុខងារមួយចំនួន។ យើងក៏នឹងនិយាយអំពីលក្ខណៈសម្បត្តិមួយចំនួននៃមុខងារសំខាន់ៗផងដែរ។

ខ្ញុំ​មិន​ធ្វើ​ពុត​ជា​នឹង​ភាព​ពេញលេញ​និង​ភាព​ហ្មត់ចត់​ផ្នែក​វិទ្យាសាស្ត្រ​នៃ​សម្ភារៈ​នោះ​ទេ ការ​សង្កត់​ធ្ងន់​នឹង​ត្រូវ​បាន​ដាក់​ជា​ដំបូង​នៃ​ការ​អនុវត្ត - រឿង​ទាំង​នោះ​ជាមួយ​នឹង មនុស្សម្នាក់ត្រូវតែប្រឈមមុខនឹងព្យញ្ជនៈនៅគ្រប់ជំហានក្នុងប្រធានបទណាមួយនៃគណិតវិទ្យាខ្ពស់។. តារាងសម្រាប់អត់ចេះសោះ? អ្នកអាចនិយាយដូច្នេះ។

ដោយ សំណើជាច្រើន។អ្នកអាន តារាងមាតិកាដែលអាចចុចបាន។:

លើសពីនេះ មានអរូបីខ្លីបំផុតលើប្រធានបទ
- ធ្វើជាម្ចាស់នៃគំនូសតាង 16 ប្រភេទដោយសិក្សាប្រាំមួយទំព័រ!

ធ្ងន់ធ្ងរ ប្រាំមួយ សូម្បីតែខ្ញុំខ្លួនឯងក៏ភ្ញាក់ផ្អើលដែរ។ អរូបីនេះ។មានក្រាហ្វិចដែលប្រសើរឡើង ហើយអាចរកបានសម្រាប់ថ្លៃដើម កំណែសាកល្បងអាចមើលបាន។ វាងាយស្រួលក្នុងការបោះពុម្ពឯកសារ ដូច្នេះក្រាហ្វនៅនឹងដៃជានិច្ច។ អរគុណសម្រាប់ការគាំទ្រគម្រោង!

ហើយយើងចាប់ផ្តើមភ្លាមៗ៖

តើធ្វើដូចម្តេចដើម្បីកសាងអ័ក្សកូអរដោនេឱ្យបានត្រឹមត្រូវ?

នៅក្នុងការអនុវត្ត ការធ្វើតេស្តស្ទើរតែតែងតែត្រូវបានគូរឡើងដោយសិស្សនៅក្នុងសៀវភៅកត់ត្រាដាច់ដោយឡែក តម្រង់ជួរនៅក្នុងទ្រុងមួយ។ ហេតុអ្វីបានជាអ្នកត្រូវការសញ្ញាធីក? យ៉ាងណាមិញការងារជាគោលការណ៍អាចត្រូវបានធ្វើនៅលើសន្លឹក A4 ។ ហើយទ្រុងគឺចាំបាច់សម្រាប់តែការរចនាដែលមានគុណភាពខ្ពស់ និងត្រឹមត្រូវនៃគំនូរ។

គំនូរណាមួយនៃក្រាហ្វមុខងារចាប់ផ្តើមដោយអ័ក្សកូអរដោនេ.

គំនូរមានពីរវិមាត្រនិងបីវិមាត្រ។

ចូរយើងពិចារណាករណីពីរវិមាត្រជាមុនសិន ខាតេសៀន ប្រព័ន្ធចតុកោណកូអរដោនេ:

1) យើងគូរ សំរបសំរួលអ័ក្ស. អ័ក្សត្រូវបានគេហៅថា អ័ក្ស x , និងអ័ក្ស អ័ក្ស y . យើងតែងតែព្យាយាមគូរពួកគេ។ ស្អាតហើយមិនកោង. ព្រួញក៏មិនគួរស្រដៀងនឹងពុកចង្ការរបស់ Papa Carlo ដែរ។

2) យើងចុះហត្ថលេខាលើអ័ក្ស អក្សរ​ធំ"x" និង "y" ។ កុំភ្លេចចុះហត្ថលេខាលើអ័ក្ស.

៣) កំណត់មាត្រដ្ឋានតាមអ័ក្ស៖ គូរលេខសូន្យ និងពីរ. នៅពេលបង្កើតគំនូរ មាត្រដ្ឋានដែលងាយស្រួល និងសាមញ្ញបំផុតគឺ៖ 1 ឯកតា = 2 ក្រឡា (គំនូរនៅខាងឆ្វេង) - បិទវាប្រសិនបើអាចធ្វើទៅបាន។ ទោះយ៉ាងណាក៏ដោយពីពេលមួយទៅពេលមួយវាកើតឡើងថាគំនូរមិនសមនឹងសន្លឹកសៀវភៅកត់ត្រា - បន្ទាប់មកយើងកាត់បន្ថយមាត្រដ្ឋាន: 1 ឯកតា = 1 ក្រឡា (គំនូរនៅខាងស្តាំ) ។ កម្រណាស់ ប៉ុន្តែវាកើតឡើងដែលទំហំគំនូរត្រូវកាត់បន្ថយ (ឬកើនឡើង) កាន់តែច្រើន

កុំសរសេរពីកាំភ្លើងយន្ត ... -៥, -៤, -៣, -១, ០, ១, ២, ៣, ៤, ៥, ...។សម្រាប់ សំរបសំរួលយន្តហោះមិនមែនជាវិមានសម្រាប់ Descartes ទេ ហើយសិស្សក៏មិនមែនជាសត្វព្រាបដែរ។ យើងដាក់ សូន្យនិង ពីរគ្រឿងតាមអ័ក្ស. ពេលខ្លះ ជំនួស​អោយឯកតាវាងាយស្រួលក្នុងការ "រកឃើញ" តម្លៃផ្សេងទៀតឧទាហរណ៍ "ពីរ" នៅលើអ័ក្ស abscissa និង "បី" នៅលើអ័ក្សតម្រៀប - ហើយប្រព័ន្ធនេះ (0, 2 និង 3) ក៏នឹងកំណត់ក្រឡាចត្រង្គកូអរដោនេផងដែរ។

វាជាការប្រសើរក្នុងការប៉ាន់ប្រមាណវិមាត្រប៉ាន់ស្មាននៃគំនូរ មុនពេលគំនូរត្រូវបានគូរ។. ដូច្នេះ ជាឧទាហរណ៍ ប្រសិនបើកិច្ចការតម្រូវឱ្យគូរត្រីកោណជាមួយចំនុចកំពូល , , , នោះវាច្បាស់ណាស់ថាមាត្រដ្ឋានពេញនិយម 1 ឯកតា = 2 ក្រឡានឹងមិនដំណើរការទេ។ ហេតុអ្វី? សូមក្រឡេកមើលចំណុច - នៅទីនេះអ្នកត្រូវវាស់ដប់ប្រាំសង់ទីម៉ែត្រចុះក្រោម ហើយជាក់ស្តែង គំនូរនឹងមិនសម (ឬស្ទើរតែសម) នៅលើសន្លឹកសៀវភៅកត់ត្រាទេ។ ដូច្នេះហើយ យើងជ្រើសរើសមាត្រដ្ឋានតូចជាង 1 ឯកតា = 1 ក្រឡា។

ដោយវិធីនេះប្រហែលសង់ទីម៉ែត្រនិងកោសិកាសៀវភៅកត់ត្រា។ តើ​វា​ជា​ការ​ពិត​ទេ​ដែល​មាន 15 សង់ទីម៉ែត្រ​នៅ​ក្នុង 30 កោសិកា notebook? វាស់ក្នុងសៀវភៅកត់ត្រាសម្រាប់ការប្រាក់ 15 សង់ទីម៉ែត្រជាមួយបន្ទាត់។ នៅសហភាពសូវៀត ប្រហែលជានេះជាការពិត ... វាគួរឱ្យចាប់អារម្មណ៍ក្នុងការកត់សម្គាល់ថា ប្រសិនបើអ្នកវាស់សង់ទីម៉ែត្រដូចគ្នាទាំងនេះ ផ្ដេក និងបញ្ឈរ នោះលទ្ធផល (ជាកោសិកា) នឹងខុសគ្នា! និយាយយ៉ាងតឹងរឹង សៀវភៅកត់ត្រាទំនើបមិនត្រូវបានគូសទេ ប៉ុន្តែមានរាងចតុកោណ។ វាអាចហាក់ដូចជាមិនសមហេតុសមផល ប៉ុន្តែឧទាហរណ៍ ការគូររង្វង់ដែលមានត្រីវិស័យក្នុងស្ថានភាពបែបនេះគឺមានការរអាក់រអួលខ្លាំងណាស់។ និយាយឱ្យត្រង់ទៅ នៅពេលនេះ អ្នកចាប់ផ្តើមគិតអំពីភាពត្រឹមត្រូវរបស់សមមិត្តស្តាលីន ដែលត្រូវបានបញ្ជូនទៅជំរុំសម្រាប់ការងារ hack នៅក្នុងផលិតកម្ម ដោយមិននិយាយអំពីឧស្សាហកម្មរថយន្តក្នុងស្រុក យន្តហោះធ្លាក់ ឬផ្ទុះរោងចក្រថាមពល។

និយាយពីគុណភាព ឬ អនុសាសន៍ខ្លីដោយសម្ភារៈការិយាល័យ។ មក​ដល់​ពេល​នេះ កុំព្យូទ័រ​យួរ​ដៃ​ភាគ​ច្រើន​មាន​លក់ ពាក្យអាក្រក់មិន​មែន​និយាយ​ទេ​រឿង​ពេញលេញ​។ សម្រាប់ហេតុផលដែលពួកគេសើមហើយមិនត្រឹមតែមកពីប៊ិចជែលប៉ុណ្ណោះទេថែមទាំងពីប៊ិចប៊ិចផងដែរ! រក្សាទុកនៅលើក្រដាស។ សម្រាប់ការបោសសំអាត ការងារត្រួតពិនិត្យខ្ញុំសូមណែនាំឱ្យប្រើសៀវភៅកត់ត្រារបស់ Arkhangelsk Pulp និង Paper Mill (18 សន្លឹកទ្រុង) ឬ Pyaterochka ទោះបីជាវាមានតម្លៃថ្លៃជាងក៏ដោយ។ គួរតែជ្រើសរើសប៊ិចជែល សូម្បីតែជែលជ័រចិនថោកបំផុតក៏ល្អជាងប៊ិចប៊ិចដែលលាប ឬក្រដាសជូតទឹកភ្នែកដែរ។ "ប្រកួតប្រជែង" តែមួយគត់ ប៊ិចប៊ិចនៅក្នុងការចងចាំរបស់ខ្ញុំគឺ "Erich Krause" ។ នាងសរសេរយ៉ាងច្បាស់ ស្អាត និងមានស្ថេរភាព - ទាំងដើមពេញ ឬស្ទើរតែទទេ។

បន្ថែម៖ មើលឃើញប្រព័ន្ធកូអរដោណេចតុកោណដោយភ្នែក ធរណីមាត្រវិភាគគ្របដណ្តប់នៅក្នុងអត្ថបទ លីនេអ៊ែរ (មិន) ការពឹងផ្អែកនៃវ៉ិចទ័រ។ មូលដ្ឋានវ៉ិចទ័រ, ព​ត៌​មាន​លំអិតអំពី សំរបសំរួលត្រីមាសអាចរកបាននៅក្នុងកថាខណ្ឌទីពីរនៃមេរៀន វិសមភាពលីនេអ៊ែរ.

ករណី 3D

វាស្ទើរតែដូចគ្នានៅទីនេះ។

1) យើងគូរអ័ក្សកូអរដោនេ។ ស្តង់ដារ៖ អនុវត្តអ័ក្ស - តម្រង់ឡើងលើ, អ័ក្ស - តម្រង់ទៅខាងស្តាំ, អ័ក្ស - ចុះក្រោមទៅខាងឆ្វេង យ៉ាងតឹងរ៉ឹងនៅមុំ 45 ដឺក្រេ។

2) យើងចុះហត្ថលេខាលើអ័ក្ស។

3) កំណត់មាត្រដ្ឋានតាមអ័ក្ស។ ធ្វើមាត្រដ្ឋានតាមអ័ក្ស - ពីរដងតូចជាងមាត្រដ្ឋានតាមបណ្តោយអ័ក្សផ្សេងទៀត។. សូមចំណាំផងដែរថានៅក្នុងគំនូរត្រឹមត្រូវខ្ញុំបានប្រើ "serif" ដែលមិនមានស្តង់ដារតាមអ័ក្ស (លទ្ធភាពនេះត្រូវបានរៀបរាប់ខាងលើរួចហើយ). តាមទស្សនៈរបស់ខ្ញុំ វាកាន់តែត្រឹមត្រូវ លឿនជាងមុន និងកាន់តែមានសោភ័ណភាព - អ្នកមិនចាំបាច់ស្វែងរកផ្នែកកណ្តាលនៃកោសិកាក្រោមមីក្រូទស្សន៍ និង "ឆ្លាក់" អង្គភាពរហូតដល់ប្រភពដើមនោះទេ។

នៅពេលធ្វើគំនូរ 3D ម្តងទៀត - ផ្តល់អាទិភាពដល់មាត្រដ្ឋាន
1 ឯកតា = 2 ក្រឡា (គូរនៅខាងឆ្វេង) ។

តើច្បាប់ទាំងអស់នេះសម្រាប់អ្វី? ច្បាប់​ត្រូវ​តែ​ខូច។ តើខ្ញុំនឹងធ្វើអ្វីឥឡូវនេះ។ ការពិតគឺថាគំនូរជាបន្តបន្ទាប់នៃអត្ថបទនឹងត្រូវបានធ្វើឡើងដោយខ្ញុំនៅក្នុង Excel ហើយអ័ក្សកូអរដោនេនឹងមើលទៅមិនត្រឹមត្រូវតាមទស្សនៈ។ ការរចនាត្រឹមត្រូវ។. ខ្ញុំអាចគូរក្រាហ្វទាំងអស់ដោយដៃ ប៉ុន្តែវាពិតជាគួរឱ្យខ្លាចក្នុងការគូរវា ដោយសារ Excel មានការស្ទាក់ស្ទើរក្នុងការគូរវាឱ្យកាន់តែត្រឹមត្រូវ។

ក្រាហ្វនិងលក្ខណៈសម្បត្តិមូលដ្ឋាននៃអនុគមន៍បឋម

អនុគមន៍លីនេអ៊ែរត្រូវបានផ្តល់ដោយសមីការ។ ក្រាហ្វមុខងារលីនេអ៊ែរគឺ ផ្ទាល់. ដើម្បីបង្កើតបន្ទាត់ត្រង់វាគ្រប់គ្រាន់ដើម្បីដឹងពីរចំណុច។

ឧទាហរណ៍ ១

គ្រោងមុខងារ។ ចូរយើងស្វែងរកចំណុចពីរ។ វាជាគុណសម្បត្តិក្នុងការជ្រើសរើសលេខសូន្យជាចំនុចមួយ។

បើអញ្ចឹង

យើងលើកយកចំណុចផ្សេងទៀត ឧទាហរណ៍ ១.

បើអញ្ចឹង

នៅពេលរៀបចំកិច្ចការ កូអរដោនេនៃចំណុចជាធម្មតាត្រូវបានសង្ខេបនៅក្នុងតារាង៖

ហើយ​តម្លៃ​ខ្លួន​គេ​ត្រូវ​បាន​គណនា​ផ្ទាល់​មាត់​ឬ​លើ​សេចក្តី​ព្រាង​ម៉ាស៊ីន​គិតលេខ។

រកឃើញពីរចំណុច តោះគូរ៖

នៅពេលគូរគំនូរយើងតែងតែចុះហត្ថលេខាលើក្រាហ្វិក.

វានឹងមិនត្រូវបាននាំអោយក្នុងការរំលឹកករណីពិសេសនៃមុខងារលីនេអ៊ែរទេ៖

កត់សម្គាល់ពីរបៀបដែលខ្ញុំដាក់ចំណងជើង, ហត្ថលេខាមិនគួរមានភាពមិនច្បាស់លាស់នៅពេលសិក្សាគំនូរ. អេ ករណីនេះវាជាការមិនចង់បានខ្លាំងណាស់ក្នុងការដាក់ហត្ថលេខានៅជាប់នឹងចំនុចប្រសព្វនៃបន្ទាត់ ឬនៅខាងក្រោមខាងស្តាំរវាងក្រាហ្វ។

1) អនុគមន៍លីនេអ៊ែរនៃទម្រង់ () ត្រូវបានគេហៅថាសមាមាត្រដោយផ្ទាល់។ ឧទាហរណ៍, ។ ក្រាហ្វសមាមាត្រដោយផ្ទាល់តែងតែឆ្លងកាត់ប្រភពដើម។ ដូច្នេះការសាងសង់បន្ទាត់ត្រង់ត្រូវបានធ្វើឱ្យសាមញ្ញ - វាគ្រប់គ្រាន់ដើម្បីស្វែងរកចំណុចតែមួយគត់។

2) សមីការនៃទម្រង់កំណត់បន្ទាត់ត្រង់ស្របទៅនឹងអ័ក្ស ជាពិសេសអ័ក្សខ្លួនវាត្រូវបានផ្តល់ដោយសមីការ។ ក្រាហ្វនៃមុខងារត្រូវបានបង្កើតឡើងភ្លាមៗដោយមិនស្វែងរកចំណុចណាមួយឡើយ។ នោះគឺធាតុគួរតែត្រូវបានយល់ដូចខាងក្រោម: "y គឺតែងតែស្មើនឹង -4 សម្រាប់តម្លៃណាមួយនៃ x" ។

3) សមីការនៃទម្រង់កំណត់បន្ទាត់ត្រង់ស្របទៅនឹងអ័ក្ស ជាពិសេសអ័ក្សខ្លួនវាត្រូវបានផ្តល់ដោយសមីការ។ ក្រាហ្វនៃមុខងារក៏ត្រូវបានសាងសង់ភ្លាមៗផងដែរ។ ធាតុគួរតែត្រូវបានយល់ដូចខាងក្រោម: "x គឺតែងតែសម្រាប់តម្លៃណាមួយនៃ y ស្មើនឹង 1 ។"

អ្នកខ្លះសួរថា ម៉េចចាំថ្នាក់ទី៦?! នោះហើយជារបៀបដែលវាគឺដូច្នេះ មានតែក្នុងអំឡុងពេលប៉ុន្មានឆ្នាំនៃការអនុវត្តប៉ុណ្ណោះ ដែលខ្ញុំបានជួបសិស្សល្អរាប់សិបនាក់ ដែលមានការងឿងឆ្ងល់ពីភារកិច្ចនៃការសាងសង់ក្រាហ្វដូច ឬ .

ការគូរបន្ទាត់ត្រង់គឺជាសកម្មភាពទូទៅបំផុតនៅពេលបង្កើតគំនូរ។

បន្ទាត់ត្រង់ត្រូវបានពិភាក្សាយ៉ាងលម្អិតនៅក្នុងវគ្គសិក្សានៃធរណីមាត្រវិភាគ ហើយអ្នកដែលប្រាថ្នាអាចយោងទៅលើអត្ថបទ សមីការនៃបន្ទាត់ត្រង់នៅលើយន្តហោះ.

ក្រាហ្វអនុគមន៍បួនជ្រុង ក្រាហ្វអនុគមន៍គូប ក្រាហ្វពហុនាម

ប៉ារ៉ាបូឡា។ កាលវិភាគ មុខងារបួនជ្រុង () គឺជាប៉ារ៉ាបូឡា។ ពិចារណា ករណីដ៏ល្បីល្បាញ:

ចូរយើងរំលឹកឡើងវិញនូវលក្ខណៈសម្បត្តិមួយចំនួននៃមុខងារ។

ដូច្នេះដំណោះស្រាយចំពោះសមីការរបស់យើង៖ - វាស្ថិតនៅត្រង់ចំណុចនេះដែលចំនុចកំពូលនៃប៉ារ៉ាបូឡាស្ថិតនៅ។ ហេតុអ្វី​បាន​ជា​ដូច្នេះ​អាច​ត្រូវ​បាន​រៀន​ពី​អត្ថបទ​ទ្រឹស្ដី​ស្តី​ពី​និស្សន្ទវត្ថុ និង​មេរៀន​អំពី​មុខងារ​ខ្លាំង​ក្លា។ ក្នុងពេលនេះ យើងគណនាតម្លៃដែលត្រូវគ្នានៃ "y"៖

ដូច្នេះចំនុចកំពូលគឺនៅចំណុច

ឥឡូវនេះយើងរកឃើញចំណុចផ្សេងទៀតខណៈពេលដែល brazenly ប្រើស៊ីមេទ្រីនៃ parabola នេះ។ គួរកត់សំគាល់ថាមុខងារ – គឺមិនមែនសូម្បីតែប៉ុន្តែយ៉ាងណាក៏ដោយ គ្មាននរណាម្នាក់លុបចោលភាពស៊ីមេទ្រីនៃប៉ារ៉ាបូឡានោះទេ។

ដើម្បីស្វែងរកពិន្ទុដែលនៅសល់ ខ្ញុំគិតថាវានឹងច្បាស់ពីតារាងចុងក្រោយ៖

ក្បួនដោះស្រាយនេះ។ការសាងសង់អាចត្រូវបានគេហៅថាជា "shuttle" ឬគោលការណ៍នៃ "ត្រឡប់មកវិញ" ជាមួយ Anfisa Chekhova ។

តោះធ្វើគំនូរ៖

ពីក្រាហ្វដែលបានពិចារណា មុខងារមានប្រយោជន៍មួយទៀតមកក្នុងគំនិត៖

សម្រាប់មុខងារបួនជ្រុង () ខាងក្រោមនេះជាការពិត៖

ប្រសិនបើ នោះសាខារបស់ប៉ារ៉ាបូឡាត្រូវបានតម្រង់ទៅខាងលើ.

ប្រសិនបើ នោះមែករបស់ប៉ារ៉ាបូឡាត្រូវបានតម្រង់ចុះក្រោម.

ចំណេះដឹងស៊ីជម្រៅនៃខ្សែកោងអាចទទួលបាននៅក្នុងមេរៀន Hyperbola និង parabola ។

ប៉ារ៉ាបូឡាគូបត្រូវបានផ្តល់ដោយមុខងារ។ នេះជាគំនូរដែលធ្លាប់ស្គាល់ពីសាលា៖

យើងរាយបញ្ជីលក្ខណៈសម្បត្តិសំខាន់ៗនៃមុខងារ

ក្រាហ្វមុខងារ

វាតំណាងឱ្យសាខាមួយនៃប៉ារ៉ាបូឡា។ តោះធ្វើគំនូរ៖

លក្ខណៈសំខាន់ៗនៃមុខងារ៖

ក្នុងករណីនេះអ័ក្សគឺ asymptote បញ្ឈរ សម្រាប់ក្រាហ្វអ៊ីពែបូឡានៅ .

វានឹងក្លាយជាកំហុសធំមួយ ប្រសិនបើនៅពេលគូរគំនូរដោយការធ្វេសប្រហែស អ្នកអនុញ្ញាតឱ្យក្រាហ្វប្រសព្វជាមួយ asymptote ។

ដែនកំណត់មួយចំហៀងផងដែរ ប្រាប់យើងថា hyperbole មួយ។ មិនកំណត់ពីខាងលើនិង មិនកំណត់ពីខាងក្រោម.

ចូរយើងស្វែងយល់ពីមុខងារនៅភាពគ្មានកំណត់៖ ពោលគឺប្រសិនបើយើងចាប់ផ្តើមផ្លាស់ទីតាមអ័ក្សទៅឆ្វេង (ឬស្តាំ) ទៅគ្មានកំណត់ នោះ "ហ្គេម" នឹងក្លាយជាជំហានដ៏ស្តើង។ ជិតស្និទ្ធគ្មានកំណត់ចូលទៅជិតសូន្យ ហើយតាមនោះ សាខានៃអ៊ីពែបូឡា ជិតស្និទ្ធគ្មានកំណត់ខិតទៅជិតអ័ក្ស។

ដូច្នេះអ័ក្សគឺ asymptote ផ្ដេក សម្រាប់ក្រាហ្វនៃអនុគមន៍ ប្រសិនបើ "x" ទំនោរទៅបូកឬដកគ្មានដែនកំណត់។

មុខងារគឺ សេសដែលមានន័យថាអ៊ីពែបូឡាមានភាពស៊ីមេទ្រីទាក់ទងនឹងប្រភពដើម។ ការពិតនេះ។ជាក់ស្តែងពីគំនូរ លើសពីនេះ វាអាចត្រូវបានផ្ទៀងផ្ទាត់យ៉ាងងាយស្រួលតាមការវិភាគ៖ .

ក្រាហ្វនៃអនុគមន៍នៃទម្រង់ () តំណាងឱ្យសាខាពីរនៃអ៊ីពែបូឡា.

ប្រសិនបើ នោះអ៊ីពែបូឡាមានទីតាំងនៅក្នុងបួនជ្រុងកូអរដោនេទីមួយ និងទីបី(សូមមើលរូបភាពខាងលើ)។

ប្រសិនបើ នោះអ៊ីពែបូឡាមានទីតាំងនៅក្នុងបួនជ្រុងកូអរដោនេទីពីរ និងទីបួន.

វាមិនពិបាកក្នុងការវិភាគភាពទៀងទាត់នៃទីកន្លែងរស់នៅរបស់អ៊ីពែបូឡាពីចំណុចនៃទិដ្ឋភាពនៃការបំប្លែងធរណីមាត្រនៃក្រាហ្វនោះទេ។

ឧទាហរណ៍ ៣

បង្កើតសាខាខាងស្តាំនៃអ៊ីពែបូឡា

យើងប្រើវិធីសាស្ត្រសាងសង់តាមចំនុច ខណៈពេលដែលវាមានអត្ថប្រយោជន៍ក្នុងការជ្រើសរើសតម្លៃដើម្បីឱ្យពួកគេបែងចែកទាំងស្រុង៖

តោះធ្វើគំនូរ៖

វានឹងមិនពិបាកក្នុងការសាងសង់សាខាខាងឆ្វេងនៃអ៊ីពែបូឡាទេ នៅទីនេះភាពចម្លែកនៃមុខងារនឹងជួយ។ និយាយដោយប្រយោល នៅក្នុងតារាងសំណង់ដោយគិតគូរ បន្ថែមដកទៅលេខនីមួយៗ ដាក់ចំនុចដែលត្រូវគ្នា ហើយគូរសាខាទីពីរ។

ព័ត៌មានធរណីមាត្រលម្អិតអំពីបន្ទាត់ដែលបានពិចារណាអាចរកបាននៅក្នុងអត្ថបទ Hyperbola និង parabola ។

ក្រាហ្វនៃអនុគមន៍អិចស្ប៉ូណង់ស្យែល

អេ កថាខណ្ឌនេះ។ខ្ញុំនឹងពិចារណាភ្លាមៗអំពីអនុគមន៍អិចស្ប៉ូណង់ស្យែល ដោយហេតុថានៅក្នុងបញ្ហានៃគណិតវិទ្យាខ្ពស់ក្នុង 95% នៃករណីវាគឺជានិទស្សន្តដែលកើតឡើង។

ខ្ញុំរំលឹកអ្នកថានេះគឺជា លេខមិនសមហេតុផល: , វានឹងត្រូវបានទាមទារនៅពេលសាងសង់ក្រាហ្វ ដែលតាមពិត ខ្ញុំនឹងសាងសង់ដោយគ្មានពិធី។ បីពិន្ទុប្រហែលជាគ្រប់គ្រាន់ហើយ៖

សូមទុកក្រាហ្វនៃមុខងារតែម្នាក់ឯងសម្រាប់ពេលនេះ អំពីវានៅពេលក្រោយ។

លក្ខណៈសំខាន់ៗនៃមុខងារ៖

ជាមូលដ្ឋាន ក្រាហ្វនៃមុខងារមើលទៅដូចគ្នា ។ល។

ខ្ញុំត្រូវតែនិយាយថាករណីទី 2 គឺមិនសូវមានក្នុងការអនុវត្តទេ ប៉ុន្តែវាកើតឡើង ដូច្នេះខ្ញុំមានអារម្មណ៍ថាវាចាំបាច់ក្នុងការបញ្ចូលវានៅក្នុងអត្ថបទនេះ។

ក្រាហ្វនៃអនុគមន៍លោការីត

ពិចារណាមុខងារជាមួយ លោការីតធម្មជាតិ.
តោះគូរបន្ទាត់៖

ប្រសិនបើអ្នកភ្លេចថាលោការីតជាអ្វី សូមយោងទៅសៀវភៅសិក្សារបស់សាលា។

លក្ខណៈសំខាន់ៗនៃមុខងារ៖

ដែន:

ជួរនៃតម្លៃ: .

មុខងារមិនត្រូវបានកំណត់ពីខាងលើទេ៖ ទោះបីជាយឺតក៏ដោយ ប៉ុន្តែសាខានៃលោការីតឡើងដល់គ្មានកំណត់។
អនុញ្ញាតឱ្យយើងពិនិត្យមើលឥរិយាបថនៃមុខងារនៅជិតសូន្យនៅខាងស្តាំ៖ . ដូច្នេះអ័ក្សគឺ asymptote បញ្ឈរ សម្រាប់ក្រាហ្វនៃអនុគមន៍ដែលមាន "x" ទំនោរទៅសូន្យនៅខាងស្តាំ។

ត្រូវប្រាកដថាដឹង និងចងចាំតម្លៃធម្មតានៃលោការីត: .

ជាមូលដ្ឋាន ក្រាហ្វលោការីតនៅមូលដ្ឋានមើលទៅដូចគ្នា៖ , , ( លោការីតទសភាគនៅក្នុងមូលដ្ឋាន 10) ។ល។ ទន្ទឹមនឹងនេះដែរ, ជាង មូលដ្ឋានបន្ថែមទៀតក្រាហ្វនឹងមានភាពទាក់ទាញ។

យើង​នឹង​មិន​ពិចារណា​ករណី​នេះ​ទេ ខ្ញុំ​មិន​ចាំ​ថា​ពេល​ណា​ទេ។ ពេលមុនបានបង្កើតក្រាហ្វជាមួយនឹងមូលដ្ឋានបែបនេះ។ បាទ/ចាស ហើយលោការីតហាក់ដូចជាភ្ញៀវដ៏កម្រនៅក្នុងបញ្ហាគណិតវិទ្យាខ្ពស់។

សរុបសេចក្តីនៃកថាខណ្ឌ ខ្ញុំនឹងនិយាយការពិតមួយទៀត៖ អនុគមន៍អិចស្ប៉ូណង់ស្យែលនិង មុខងារលោការីត គឺពីរទៅវិញទៅមក មុខងារបញ្ច្រាស . ប្រសិនបើអ្នកក្រឡេកមើលក្រាហ្វនៃលោការីត នោះអ្នកអាចមើលឃើញថានេះគឺជានិទស្សន្តដូចគ្នា គ្រាន់តែវាស្ថិតនៅខុសគ្នាបន្តិច។

ក្រាហ្វនៃអនុគមន៍ត្រីកោណមាត្រ

តើការធ្វើទារុណកម្មត្រីកោណមាត្រចាប់ផ្តើមនៅសាលារៀនយ៉ាងដូចម្តេច? ត្រឹមត្រូវ។ ពីស៊ីនុស

ចូរយើងរៀបចំផែនការមុខងារ

បន្ទាត់នេះ។ហៅ sinusoid.

ខ្ញុំរំលឹកអ្នកថា "pi" គឺជាចំនួនមិនសមហេតុផល៖ ហើយនៅក្នុងត្រីកោណមាត្រវាងក់ភ្នែកក្នុងភ្នែក។

លក្ខណៈសំខាន់ៗនៃមុខងារ៖

មុខងារនេះ។គឺ តាមកាលកំណត់ជាមួយនឹងរយៈពេលមួយ។ តើ​វា​មានន័យ​យ៉ាង​ដូចម្តេច? តោះមើលការកាត់។ នៅខាងឆ្វេង និងខាងស្ដាំរបស់វា បំណែកដូចគ្នានៃក្រាហ្វនេះធ្វើឡើងវិញដោយគ្មានទីបញ្ចប់។

ដែន: មានន័យថាសម្រាប់តម្លៃណាមួយនៃ "x" មានតម្លៃស៊ីនុស។

ជួរនៃតម្លៃ: . មុខងារគឺ មានកំណត់: នោះគឺ "ហ្គេម" ទាំងអស់អង្គុយយ៉ាងតឹងរ៉ឹងនៅក្នុងផ្នែក។
វាមិនកើតឡើងទេ៖ ឬច្បាស់ជាងនេះទៅទៀត វាកើតឡើង ប៉ុន្តែសមីការទាំងនេះមិនមានដំណោះស្រាយទេ។

សម្រាប់ភាពងាយស្រួលនៃការពិចារណាមុខងារថាមពលយើងនឹងពិចារណាករណី 4 ដាច់ដោយឡែកពីគ្នា: មុខងារថាមពលជាមួយ សូចនាករធម្មជាតិ, អនុគមន៍ថាមពលជាមួយនិទស្សន្តចំនួនគត់, អនុគមន៍ថាមពលជាមួយ សូចនាករសមហេតុផលនិងមុខងារថាមពលជាមួយ សូចនាករមិនសមហេតុផល.

មុខងារថាមពលជាមួយនិទស្សន្តធម្មជាតិ

ដើម្បីចាប់ផ្តើមជាមួយ យើងណែនាំគោលគំនិតនៃសញ្ញាប័ត្រដែលមាននិទស្សន្តធម្មជាតិ។

និយមន័យ ១

អំណាចនៃចំនួនពិត $a$ ជាមួយនឹងនិទស្សន្តធម្មជាតិ $n$ គឺជាលេខ ស្មើនឹងផលិតផលកត្តា $n$ ដែលនីមួយៗស្មើនឹងចំនួន $a$ ។

រូបភាពទី 1 ។

$a$ គឺជាមូលដ្ឋាននៃសញ្ញាបត្រ។

$n$ - និទស្សន្ត។

ឥឡូវនេះ សូមពិចារណាមុខងារថាមពលដែលមាននិទស្សន្តធម្មជាតិ លក្ខណៈសម្បត្តិ និងក្រាហ្វរបស់វា។

និយមន័យ ២

$f\left(x\right)=x^n$ ($n\in N)$ ត្រូវបានគេហៅថាអនុគមន៍ថាមពលដែលមាននិទស្សន្តធម្មជាតិ។

ដើម្បីភាពងាយស្រួលបន្ថែមទៀត សូមពិចារណាដោយឡែកពីគ្នានូវអនុគមន៍ថាមពលជាមួយនឹងនិទស្សន្ត $f\left(x\right)=x^(2n)$ និងអនុគមន៍ថាមពលដែលមាននិទស្សន្តសេស $f\left(x\right)=x^(2n- 1)$ ($n\in N)$។

លក្ខណៈសម្បត្តិនៃមុខងារថាមពលជាមួយនិទស្សន្តធម្មជាតិ

$f\left(-x\right)=((-x))^(2n)=x^(2n)=f(x)$ គឺជាមុខងារគូ។

វិសាលភាព -- $ \

មុខងារថយចុះជា $x\in (-\infty ,0)$ និងកើនឡើងជា $x\in (0,+\infty)$ ។

$f("")\left(x\right)=(\left(2n\cdot x^(2n-1)\right))"=2n(2n-1)\cdot x^(2(n-1) ))\ge 0$

មុខងារគឺប៉ោងនៅលើដែនទាំងមូលនៃនិយមន័យ។

ឥរិយាបថនៅចុងបញ្ចប់នៃវិសាលភាព៖

\[(\mathop(lim)_(x\to -\infty) x^(2n)\)=+\infty \] \[(\mathop(lim)_(x\to +\infty) x^( 2n)\)=+\infty \]

ក្រាហ្វ (រូបភាពទី 2) ។

រូបភាពទី 2. ក្រាហ្វនៃអនុគមន៍ $f\left(x\right)=x^(2n)$

លក្ខណៈសម្បត្តិនៃអនុគមន៍ថាមពលដែលមាននិទស្សន្តសេសធម្មជាតិ

ដែននៃនិយមន័យគឺជាចំនួនពិតទាំងអស់។

$f\left(-x\right)=((-x))^(2n-1)=(-x)^(2n)=-f(x)$ គឺជាមុខងារសេស។

$f(x)$ គឺបន្តនៅលើដែនទាំងមូលនៃនិយមន័យ។

ជួរគឺជាចំនួនពិតទាំងអស់។

$f"\left(x\right)=\left(x^(2n-1)\right)"=(2n-1)\cdot x^(2(n-1))\ge 0$

មុខងារកើនឡើងលើដែនទាំងមូលនៃនិយមន័យ។

$f\left(x\right)0$, សម្រាប់ $x\in (0,+\infty)$។

$f(""\left(x\right))=(\left(\left(2n-1\right)\cdot x^(2\left(n-1\right))\right))"=2 \left(2n-1\right)(n-1)\cdot x^(2n-3)$

\ \

មុខងារគឺប៉ោងសម្រាប់ $x\in (-\infty ,0)$ និងប៉ោងសម្រាប់ $x\in (0,+\infty)$ ។

ក្រាហ្វ (រូបភាពទី 3) ។

រូបភាពទី 3. ក្រាហ្វនៃអនុគមន៍ $f\left(x\right)=x^(2n-1)$

អនុគមន៍ថាមពលជាមួយលេខនិទស្សន្ត

ដើម្បីចាប់ផ្តើមជាមួយ យើងណែនាំគោលគំនិតនៃសញ្ញាប័ត្រដែលមាននិទស្សន្តចំនួនគត់។

និយមន័យ ៣

សញ្ញាបត្រ ចំនួនពិត$a$ ជាមួយចំនួនគត់លិបិក្រម $n$ ត្រូវបានកំណត់ដោយរូបមន្ត៖

រូបភាពទី 4

ឥឡូវនេះ សូមពិចារណាមុខងារថាមពលដែលមាននិទស្សន្តចំនួនគត់ លក្ខណៈសម្បត្តិ និងក្រាហ្វរបស់វា។

និយមន័យ ៤

$f\left(x\right)=x^n$ ($n\in Z)$ ត្រូវបានគេហៅថាអនុគមន៍ថាមពលដែលមាននិទស្សន្តចំនួនគត់។

ប្រសិនបើដឺក្រេធំជាងសូន្យ នោះយើងមកករណីនៃអនុគមន៍ថាមពលដែលមាននិទស្សន្តធម្មជាតិ។ យើងបានពិភាក្សារួចហើយខាងលើ។ សម្រាប់ $n=0$ យើងទទួលបាន មុខងារលីនេអ៊ែរ$y=1$។ យើងទុកការពិចារណារបស់វាដល់អ្នកអាន។ វានៅសល់ដើម្បីពិចារណាលក្ខណៈសម្បត្តិនៃអនុគមន៍ថាមពលដែលមាននិទស្សន្តចំនួនគត់អវិជ្ជមាន

លក្ខណៈសម្បត្តិនៃអនុគមន៍ថាមពលដែលមាននិទស្សន្តចំនួនគត់អវិជ្ជមាន

វិសាលភាពគឺ $\left(-\infty,0\right)(0,+\infty)$។

ប្រសិនបើនិទស្សន្តគឺស្មើ នោះអនុគមន៍គឺស្មើ ប្រសិនបើវាសេស នោះអនុគមន៍គឺសេស។

$f(x)$ គឺបន្តនៅលើដែនទាំងមូលនៃនិយមន័យ។

ជួរតម្លៃ៖

ប្រសិនបើនិទស្សន្តស្មើ នោះ $(0,+\infty)$ ប្រសិនបើសេស បន្ទាប់មក $\left(-\infty,0\right)(0,+\infty)$ ។

ប្រសិនបើនិទស្សន្តគឺសេស មុខងារថយចុះជា $x\in \left(-\infty ,0\right)(0,+\infty)$។ សម្រាប់និទស្សន្តមួយ អនុគមន៍ថយចុះជា $x\in (0,+\infty)$ ។ និងបង្កើនជា $x\in \left(-\infty,0\right)$។

$f(x)\ge 0$ លើដែនទាំងមូល