Definição de logaritmo

O logaritmo de b na base a é o expoente ao qual a deve ser elevado para obter b.

Número e em matemática, costuma-se denotar o limite ao qual uma expressão se esforça

Número eé Número irracional - um número incomensurável com um, não pode ser expresso com precisão como um número inteiro ou uma fração racional número.

Carta e- primeira carta palavra latina expor- para se exibir, daí o nome em matemática exponencial- função exponencial.

Número e amplamente utilizado em matemática e em todas as ciências que de uma forma ou de outra utilizam cálculos matemáticos para suas necessidades.

Logaritmos. Propriedades dos logaritmos

Definição: O logaritmo de um número positivo b em sua base é o expoente c ao qual o número a deve ser elevado para obter o número b.

Identidade logarítmica básica:

7) Fórmula para mudança para uma nova base:

lna = log e a, e ≈ 2,718…

Problemas e testes sobre o tema “Logaritmos. Propriedades dos logaritmos"

• Logaritmos - Tópicos importantes para revisão do Exame Estadual Unificado em matemática

Para implementação bem sucedida Para tarefas sobre este tópico, você deve conhecer a definição de logaritmo, as propriedades dos logaritmos, a identidade logarítmica básica, as definições de logaritmos decimais e naturais. Os principais tipos de problemas deste tema são problemas que envolvem cálculo e transformação de expressões logarítmicas. Vamos considerar a solução deles usando os exemplos a seguir.

Solução: Usando as propriedades dos logaritmos, obtemos

Solução: Usando as propriedades dos graus, obtemos

1) (2 2) log 2 5 =(2 log 2 5) 2 =5 2 =25

Propriedades de logaritmos, formulações e provas.

Os logaritmos têm vários propriedades características. Neste artigo veremos os principais propriedades dos logaritmos. Aqui daremos suas formulações, anotaremos as propriedades dos logaritmos na forma de fórmulas, mostraremos exemplos de sua aplicação e também forneceremos provas das propriedades dos logaritmos.

Navegação na página.

Propriedades básicas de logaritmos, fórmulas

Para facilitar a lembrança e o uso, vamos imaginar propriedades básicas de logaritmos na forma de uma lista de fórmulas. EM próximo ponto Daremos suas formulações, evidências, exemplos de uso e explicações necessárias.

Propriedade do logaritmo da unidade: log a 1=0 para qualquer a>0, a≠1.

Logaritmo de um número, igual à base: log a a=1 para a>0, a≠1.

Propriedade do logaritmo da potência da base: log a a p =p, onde a>0, a≠1 e p – qualquer número real.

Logaritmo do produto de dois números positivos: log a (x y)=log a x+log a y , a>0 , a≠1 , x>0 , y>0 ,
e a propriedade do logaritmo do produto de n números positivos: log a (x 1 · x 2 ·…·x n)= log a x 1 +log a x 2 +…+log a x n , a>0 , a≠1 , x 1 >0, x 2 >0, …, x n >0 .

Propriedade do logaritmo de um quociente: , onde a>0, a≠1, x>0, y>0.

Logaritmo da potência de um número: log a b p =p·log a |b| , onde a>0, a≠1, b e p são números tais que o grau b p faz sentido e b p >0.

Consequência: , onde a>0, a≠1, n – número natural, maior que um, b>0.

Corolário 1: , a>0 , a≠1 , b>0 , b≠1 .

Corolário 2: , a>0 , a≠1 , b>0 , p e q são números reais, q≠0 , em particular para b=a temos .

Formulações e provas de propriedades

Prosseguimos com a formulação e prova das propriedades escritas dos logaritmos. Todas as propriedades dos logaritmos são provadas com base na definição do logaritmo e no princípio básico que dele segue identidade logarítmica, bem como propriedades de grau.

Vamos começar com propriedades do logaritmo de um. Sua formulação é a seguinte: logaritmo da unidade igual a zero, aquilo é, registrar um 1=0 para qualquer a>0, a≠1. A prova não é difícil: como a 0 =1 para qualquer a que satisfaça as condições acima a>0 e a≠1, então o log de igualdade a 1=0 a ser provado segue imediatamente da definição do logaritmo.

Vamos dar exemplos de aplicação da propriedade considerada: log 3 1=0, log1=0 e .

Vamos passar para a próxima propriedade: logaritmo de um número igual à base igual a um , aquilo é, registrar uma a = 1 para a>0, a≠1. Na verdade, como a 1 =a para qualquer a, então, por definição do logaritmo, log a a=1.

Exemplos de uso desta propriedade de logaritmos são as igualdades log 5 5=1, log 5,6 5,6 e lne=1.

Logaritmo de uma potência de um número igual à base do logaritmo, igual ao indicador graus. Esta propriedade do logaritmo corresponde a uma fórmula da forma log a a p =p, onde a>0, a≠1 e p – qualquer número real. Esta propriedade decorre diretamente da definição do logaritmo. Observe que permite indicar imediatamente o valor do logaritmo, caso seja possível representar o número sob o sinal do logaritmo como uma potência da base; falaremos mais sobre isso no artigo cálculo de logaritmos.

Por exemplo, log 2 2 7 =7, log10 -4 =-4 e .

Logaritmo do produto de dois números positivos x e y igual ao produto logaritmos desses números: log a (x y) = log a x + log a y, uma>0 , uma≠1 . Vamos provar a propriedade do logaritmo de um produto. Devido às propriedades do grau a log a x+log a y =a log a x ·a log a y, e como pela identidade logarítmica principal um log a x =x e um log a y =y, então um log a x ·a log a y =x·y. Assim, um log a x+log a y =x·y, do qual, pela definição de logaritmo, segue a igualdade que está sendo provada.

Vamos mostrar exemplos de uso da propriedade do logaritmo de um produto: log 5 (2 3)=log 5 2+log 5 3 e .

A propriedade do logaritmo de um produto pode ser generalizada para o produto de um número finito n de números positivos x 1 , x 2 , …, x n como log a (x 1 · x 2 ·…·x n)= log a x 1 +log a x 2 +…+log a x n. Esta igualdade pode ser provada sem problemas usando o método de indução matemática.

Por exemplo, o logaritmo natural do produto pode ser substituído pela soma de três logaritmos naturais dos números 4, e, e.

Logaritmo do quociente de dois números positivos xey é igual à diferença entre os logaritmos desses números. A propriedade do logaritmo de um quociente corresponde a uma fórmula da forma , onde a>0, a≠1, x e y são alguns números positivos. A validade desta fórmula é comprovada assim como a fórmula do logaritmo de um produto: desde , então por definição do logaritmo .

Aqui está um exemplo de uso desta propriedade do logaritmo: .

Vamos passar para propriedade do logaritmo da potência. O logaritmo de um grau é igual ao produto do expoente pelo logaritmo do módulo da base deste grau. Vamos escrever esta propriedade do logaritmo de uma potência como uma fórmula: log a b p =p·log a |b|, onde a>0, a≠1, b e p são números tais que o grau b p faz sentido e b p >0.

Primeiro provamos esta propriedade para b positivo. A identidade logarítmica básica nos permite representar o número b como a log a b , então b p =(a log a b) p , e a expressão resultante, devido à propriedade de potência, é igual a a p·log a b . Chegamos então à igualdade b p =a p·log a b, da qual, pela definição de logaritmo, concluímos que log a b p =p·log a b.

Resta provar esta propriedade para b negativo. Aqui notamos que a expressão log a b p para b negativo só faz sentido para expoentes pares p (já que o valor do grau b p deve ser maior que zero, caso contrário o logaritmo não fará sentido), e neste caso b p =|b| pág. Então bp =|b| p =(a log a |b|) p =a p·log a |b| , de onde log a b p =p·log a |b| .

Por exemplo, e ln(-3) 4 =4·ln|-3|=4·ln3 .

Segue da propriedade anterior propriedade do logaritmo da raiz: o logaritmo da enésima raiz é igual ao produto da fração 1/n e o logaritmo expressão radical, isto é, , onde a>0, a≠1, n é um número natural maior que um, b>0.

A prova é baseada na igualdade (ver definição de grau com indicador fracionário), que é válido para qualquer b positivo, e a propriedade do logaritmo da potência: .

Aqui está um exemplo de uso desta propriedade: .

Agora vamos provar fórmula para mudar para uma nova base logarítmica tipo . Para isso, basta provar a validade do log de igualdade c b=log a b·log c a. A identidade logarítmica básica nos permite representar o número b como a log a b , então log c b=log c a log a b . Resta usar a propriedade do logaritmo do grau: log c a log a b =log a b·log c a . Isso prova a igualdade log c b=log a b·log c a, o que significa que a fórmula para transição para uma nova base do logaritmo também está provada .

Vamos mostrar alguns exemplos de uso desta propriedade dos logaritmos: e .

A fórmula para passar para uma nova base permite que você passe a trabalhar com logaritmos que possuem uma base “conveniente”. Por exemplo, pode ser usado para alterar logaritmos naturais ou decimais para que você possa calcular o valor de um logaritmo a partir de uma tabela de logaritmos. A fórmula para mudar para uma nova base logarítmica também permite encontrar o valor em alguns casos dado logaritmo, quando são conhecidos os valores de alguns logaritmos com outras bases.

Usado com frequência caso especial fórmulas para transição para uma nova base do logaritmo com c=b da forma. Isso mostra que log a b e log b a são números mutuamente inversos. Por exemplo, .

A fórmula também é frequentemente usada, o que é conveniente para encontrar os valores dos logaritmos. Para confirmar nossas palavras, mostraremos como ele pode ser usado para calcular o valor de um logaritmo da forma . Nós temos . Para provar a fórmula, basta usar a fórmula de mudança para uma nova base do logaritmo a: .

Resta provar as propriedades de comparação de logaritmos.

Vamos usar o método oposto. Suponha que para a 1 >1, a 2 >1 e a 1 2 e para 0 1, log a 1 b≤log a 2 b seja verdadeiro. Com base nas propriedades dos logaritmos, essas desigualdades podem ser reescritas como E respectivamente, e deles segue que log b a 1 ≤log b a 2 e log b a 1 ≥log b a 2, respectivamente. Então, pelas propriedades das potências com pelos mesmos motivos as igualdades b log b a 1 ≥b log b a 2 e b log b a 1 ≥b log b a 2 devem ser satisfeitas, ou seja, a 1 ≥a 2 . Então chegamos a uma contradição com a condição a 1 2. Isso completa a prova.

Propriedades básicas dos logaritmos

• Materiais para a aula
• Baixe todas as fórmulas

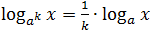
Os logaritmos, como qualquer número, podem ser somados, subtraídos e transformados de todas as maneiras. Mas como os logaritmos não são exatamente números comuns, existem regras aqui, que são chamadas propriedades principais.

Definitivamente, você precisa conhecer essas regras - sem elas, nenhum problema logarítmico sério pode ser resolvido. Além disso, são poucos - você pode aprender tudo em um dia. Então vamos começar.

Adição e subtração de logaritmos

Considere dois logaritmos com as mesmas bases: log a x e log a y. Então eles podem ser adicionados e subtraídos e:

Assim, a soma dos logaritmos é igual ao logaritmo do produto, e a diferença é igual ao logaritmo do quociente. Observação: momento chave Aqui - motivos idênticos. Se os motivos forem diferentes, estas regras não funcionam!

Essas fórmulas ajudarão você a calcular expressão logarítmica mesmo quando suas partes individuais não são contadas (veja a lição “O que é um logaritmo”). Dê uma olhada nos exemplos e veja:

Tarefa. Encontre o valor da expressão: log 6 4 + log 6 9.

Como os logaritmos têm as mesmas bases, usamos a fórmula da soma:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.

Tarefa. Encontre o valor da expressão: log 2 48 − log 2 3.

As bases são iguais, usamos a fórmula da diferença:
log 2 48 - log 2 3 = log 2 (48: 3) = log 2 16 = 4.

Tarefa. Encontre o valor da expressão: log 3 135 − log 3 5.

Novamente as bases são iguais, então temos:
log 3 135 - log 3 5 = log 3 (135: 5) = log 3 27 = 3.

Como você pode ver, as expressões originais são compostas de logaritmos “ruins”, que não são calculados separadamente. Mas após as transformações, são obtidos números completamente normais. Muitos são construídos sobre este fato papéis de teste. E os controles? expressões semelhantes com toda a seriedade (às vezes praticamente sem alterações) são oferecidos no Exame de Estado Unificado.

Extraindo o expoente do logaritmo

Agora vamos complicar um pouco a tarefa. E se a base ou argumento de um logaritmo for uma potência? Então o expoente deste grau pode ser retirado do sinal do logaritmo de acordo com as seguintes regras:

• log a x n = n · log a x ;
• 
• 

É fácil perceber isso última regra segue os dois primeiros. Mas é melhor lembrar disso de qualquer maneira - em alguns casos, isso reduzirá significativamente a quantidade de cálculos.

Claro, todas essas regras fazem sentido se o ODZ do logaritmo for observado: a > 0, a ≠ 1, x > 0. E mais uma coisa: aprenda a aplicar todas as fórmulas não só da esquerda para a direita, mas também vice-versa , ou seja Você pode inserir os números antes do sinal do logaritmo no próprio logaritmo. Isto é o que é mais frequentemente necessário.

Tarefa. Encontre o valor da expressão: log 7 49 6 .

Vamos nos livrar do grau no argumento usando a primeira fórmula:
log 7 49 6 = 6 log 7 49 = 6 2 = 12

Tarefa. Encontre o significado da expressão:

[Legenda da foto]

Observe que o denominador contém um logaritmo, cuja base e argumento são potências exatas: 16 = 2 4 ; 49 = 7 2. Nós temos:

[Legenda da foto]

eu acho que último exemplo esclarecimento necessário. Para onde foram os logaritmos? Até o muito último momento trabalhamos apenas com o denominador. Apresentamos a base e o argumento do logaritmo ali na forma de potências e retiramos os expoentes - obtivemos uma fração de “três andares”.

Agora vamos dar uma olhada na fração principal. O numerador e o denominador contêm o mesmo número: log 2 7. Como log 2 7 ≠ 0, podemos reduzir a fração - 2/4 permanecerá no denominador. Pelas regras da aritmética, o quatro pode ser transferido para o numerador, e foi isso que foi feito. O resultado foi a resposta: 2.

Transição para uma nova fundação

Falando sobre as regras de adição e subtração de logaritmos, enfatizei especificamente que elas só funcionam com as mesmas bases. E se os motivos forem diferentes? E se não forem potências exatas do mesmo número?

As fórmulas para a transição para uma nova base vêm em socorro. Vamos formulá-los na forma de um teorema:

Seja dado o logaritmo log a x. Então, para qualquer número c tal que c > 0 e c ≠ 1, a igualdade é verdadeira:

[Legenda da foto]

Em particular, se definirmos c = x, obteremos:

[Legenda da foto]

Da segunda fórmula segue-se que a base e o argumento do logaritmo podem ser trocados, mas neste caso toda a expressão é “invertida”, ou seja, o logaritmo aparece no denominador.

Estas fórmulas raramente são encontradas em expressões numéricas. Só é possível avaliar o quão convenientes eles são decidindo equações logarítmicas e desigualdades.

No entanto, existem problemas que não podem ser resolvidos de forma alguma, exceto com a mudança para uma nova fundação. Vejamos alguns deles:

Tarefa. Encontre o valor da expressão: log 5 16 log 2 25.

Observe que os argumentos de ambos os logaritmos contêm potências exatas. Vamos retirar os indicadores: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2 log 2 5;

Agora vamos “inverter” o segundo logaritmo:

[Legenda da foto]

Como o produto não muda quando os fatores são reorganizados, multiplicamos calmamente quatro por dois e depois tratamos dos logaritmos.

Tarefa. Encontre o valor da expressão: log 9 100 lg 3.

A base e o argumento do primeiro logaritmo são potências exatas. Vamos anotar isso e nos livrar dos indicadores:

[Legenda da foto]

Agora vamos nos livrar do logaritmo decimal passando para uma nova base:

[Legenda da foto]

Identidade logarítmica básica

Muitas vezes no processo de solução é necessário representar um número como um logaritmo para uma determinada base. Neste caso, as seguintes fórmulas nos ajudarão:

1. n = log a a n

2. No primeiro caso, o número n torna-se o expoente do argumento. O número n pode ser absolutamente qualquer coisa, porque é apenas um valor logarítmico.

   A segunda fórmula é na verdade uma definição parafraseada. É assim que se chama: a identidade logarítmica básica.

   Na verdade, o que acontece se o número b for elevado a tal potência que o número b elevado a esta potência dê o número a? Isso mesmo: o resultado é o mesmo número a. Leia este parágrafo com atenção novamente - muitas pessoas ficam presas nele.

   Tal como as fórmulas para passar para uma nova base, a identidade logarítmica básica é por vezes a única solução possível.

   [Legenda da foto]

   Observe que log 25 64 = log 5 8 - simplesmente pegamos o quadrado da base e o argumento do logaritmo. Levando em consideração as regras de multiplicação de potências com a mesma base, obtemos:

   [Legenda da foto]

   Se alguém não sabe, esta foi uma tarefa real do Exame Estadual Unificado :)

   Unidade logarítmica e zero logarítmico

   Concluindo, darei duas identidades que dificilmente podem ser chamadas de propriedades - antes, são consequências da definição do logaritmo. Eles aparecem constantemente em problemas e, surpreendentemente, criam problemas até mesmo para alunos “avançados”.

   1. log a a = 1 é uma unidade logarítmica. Lembre-se de uma vez por todas: o logaritmo para qualquer base a dessa base é igual a um.
   2. log a 1 = 0 é zero logarítmico. A base a pode ser qualquer coisa, mas se o argumento contiver um, o logaritmo será igual a zero! Porque 0 = 1 é uma consequência direta da definição.

   Essas são todas as propriedades. Certifique-se de praticar colocá-los em prática! Baixe a folha de dicas no início da lição, imprima-a e resolva os problemas.

   Logaritmo. Propriedades do logaritmo (adição e subtração).

   Propriedades do logaritmo segue de sua definição. E então o logaritmo do número b baseado em Aé definido como o expoente ao qual um número deve ser elevado a para obter o número b(logaritmo existe apenas para números positivos).

   Desta formulação segue-se que o cálculo x = log a b, é equivalente a resolver a equação uma x = b. Por exemplo, log 2 8 = 3 porque 8 = 2 3 . A formulação do logaritmo permite justificar que se b=uma c, então o logaritmo do número b baseado em aé igual a Com. Também está claro que o tema dos logaritmos está intimamente relacionado ao tema das potências.

   Com logaritmos, como com qualquer número, você pode fazer operações de adição, subtração e transformar de todas as maneiras possíveis. Mas devido ao fato de que os logaritmos não são números inteiramente comuns, suas próprias regras especiais se aplicam aqui, que são chamadas propriedades principais.

   Adição e subtração de logaritmos.

   Tomemos dois logaritmos com as mesmas bases: registrar um x E registrar um ano. Então é possível realizar operações de adição e subtração:

   Como vemos, soma dos logaritmosé igual ao logaritmo do produto, e diferença logaritmos- logaritmo do quociente. Além disso, isso é verdade se os números A, X E no positivo e uma ≠ 1.

   É importante notar que o aspecto principal nestas fórmulas são as mesmas bases. Se os motivos forem diferentes, estas regras não se aplicam!

   As regras para somar e subtrair logaritmos com as mesmas bases são lidas não apenas da esquerda para a direita, mas também vice-versa. Como resultado, temos os teoremas do logaritmo do produto e do logaritmo do quociente.

   Logaritmo do produto dois números positivos igual à soma seus logaritmos ; reformulando este teorema, obtemos o seguinte se os números A, x E no positivo e uma ≠ 1, Que:

   Logaritmo do quociente dois números positivos é igual à diferença entre os logaritmos do dividendo e do divisor. Dito de outra forma, se os números A, X E no positivo e uma ≠ 1, Que:

   Vamos aplicar os teoremas acima para resolver exemplos:

   Se os números x E no são negativos, então fórmula do logaritmo do produto torna-se sem sentido. Assim, é proibido escrever:

   já que as expressões log 2 (-8) e log 2 (-4) não estão definidas ( função logarítmica no= registro 2 X definido apenas para valores positivos argumento X).

   Teorema do produto aplicável não apenas para dois, mas também para um número ilimitado de fatores. Isto significa que para cada natural k e quaisquer números positivos x 1 , x 2 , . . . ,x n existe uma identidade:

   De teorema do quociente logaritmo Mais uma propriedade do logaritmo pode ser obtida. É de conhecimento geral que o log a 1= 0, portanto

   Isso significa que existe uma igualdade:

   Logaritmos de dois mutuamente números recíprocos pela mesma razão, diferirão entre si apenas pelo sinal. Então:

   Logaritmo. Propriedades dos logaritmos

   Logaritmo. Propriedades dos logaritmos

   Vamos considerar a igualdade. Deixe-nos saber os valores de e e queremos encontrar o valor de .

   Ou seja, estamos procurando o expoente pelo qual precisamos ajustá-lo para obter .

   Deixar uma variável pode assumir qualquer valor real, então as seguintes restrições são impostas às variáveis: o" title="a>o"/> , 1″ title="a1″/>, 0″ title="b>0″ />

   Se conhecemos os valores de e e nos deparamos com a tarefa de encontrar a incógnita, então, para esse propósito, introduzimos Operação matematica que é chamado logaritmo.

   Para encontrar o valor, tomamos logaritmo de um número Por base :

   O logaritmo de um número à sua base é o expoente ao qual ele deve ser elevado para obter .

   Aquilo é identidade logarítmica básica:

   o» título=»a>o»/> , 1″ título=»a1″/>, 0″ título=»b>0″/>

   é essencialmente notação matemática definições de logaritmo.

   A operação matemática do logaritmo é o inverso da operação de exponenciação, então propriedades dos logaritmos estão intimamente relacionados às propriedades do grau.

   Vamos listar os principais propriedades dos logaritmos:

   (o" title="a>o"/> , 1″ title=»a1″/>, 0″ title=»b>0″/>, 0,

   d>0″/>, 1″ título=”d1″/>

   4.

   5.

   O seguinte grupo de propriedades permite representar o expoente de uma expressão sob o sinal do logaritmo, ou na base do logaritmo na forma de um coeficiente na frente do sinal do logaritmo:

   6.

   7.

   8.

   9.

   O próximo grupo de fórmulas permite passar de um logaritmo com uma determinada base para um logaritmo com uma base arbitrária e é chamado fórmulas para transição para uma nova base:

   10.

   12. (corolário da propriedade 11)

   

   As três propriedades a seguir não são bem conhecidas, mas são frequentemente usadas na resolução de equações logarítmicas ou na simplificação de expressões contendo logaritmos:

   13.

   14.

   15.

   Casos especiais:

   — logaritmo decimal

   — Logaritmo natural

   Ao simplificar expressões contendo logaritmos, é usada uma abordagem geral:

   1. Apresentando decimais na forma de comuns.

   2. Números mistos representados como frações impróprias.

   3. Decompomos os números na base do logaritmo e sob o sinal do logaritmo em fatores simples.

   4. Tentamos reduzir todos os logaritmos à mesma base.

   5. Aplique as propriedades dos logaritmos.

   Vejamos exemplos de expressões simplificadas contendo logaritmos.

   Exemplo 1.

   Calcular:

   Vamos simplificar todos os expoentes: nossa tarefa é reduzi-los a logaritmos, cuja base é o mesmo número que a base do expoente.

   ==(pela propriedade 7)=(pela propriedade 6) =

   Vamos substituir os indicadores que obtivemos na expressão original. Nós temos:

   Resposta: 5,25

   Exemplo 2. Calcule:

   

   Vamos reduzir todos os logaritmos para a base 6 (neste caso, os logaritmos do denominador da fração irão “migrar” para o numerador):

   Vamos decompor os números sob o sinal do logaritmo em fatores simples:

   Vamos aplicar as propriedades 4 e 6:

   Vamos apresentar a substituição

   Nós temos:

   Resposta 1

   Logaritmo . Identidade logarítmica básica.

   Propriedades dos logaritmos. Logaritmo decimal. Logaritmo natural.

   Logaritmo número positivo N para base (b > 0, b 1) é o expoente x ao qual b deve ser elevado para obter N .

   Esta entrada é equivalente ao seguinte: b x = N .

   Exemplos: log 3 81 = 4, já que 3 4 = 81;

   registro 1/3 27 = – 3, já que (1/3) - 3 = 3 3 = 27.

   A definição de logaritmo acima pode ser escrita como uma identidade:

   

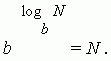
   Propriedades básicas dos logaritmos.

   2) log 1 = 0, pois b 0 = 1 .

   3) O logaritmo do produto é igual à soma dos logaritmos dos fatores:

   4) O logaritmo do quociente é igual à diferença entre os logaritmos do dividendo e do divisor:

   5) O logaritmo de uma potência é igual ao produto do expoente pelo logaritmo de sua base:

   A consequência desta propriedade é a seguinte: logaritmo da raiz igual ao logaritmo número radical dividido pela potência da raiz:

   

   6) Se a base do logaritmo for um grau, então o valor o inverso do expoente pode ser obtido como uma rima logarítmica:

   

   As duas últimas propriedades podem ser combinadas em uma:

   

   7) Fórmula do módulo de transição (ou seja, transição de uma base logarítmica para outra base):

   

   No caso especial quando N = uma Nós temos:

   

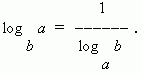
   Logaritmo decimal chamado logaritmo básico 10. É denotado lg, ou seja, registro 10 N= registro N. Logaritmos dos números 10, 100, 1000, . p são 1, 2, 3,…, respectivamente, ou seja, tem tantos positivos

   unidades, quantos zeros existem em um número logarítmico após um. Logaritmos dos números 0,1, 0,01, 0,001, . p são respectivamente –1, –2, –3,…, ou seja, tem tantos negativos quantos zeros no número logarítmico antes de um (incluindo zero inteiros). Os logaritmos de outros números têm uma parte fracionária chamada mantissa. Parte inteira o logaritmo é chamado característica. Para uso prático, os logaritmos decimais são mais convenientes.

   Logaritmo natural chamado logaritmo básico e. É denotado por ln, ou seja, registro e N= registro N. Número eé irracional, seu valor aproximado é 2,718281828. É o limite para o qual tende o número (1 + 1 / n) n com aumento ilimitado n(cm. primeiro limite maravilhoso na página "Limites" sequências numéricas»).
   Por mais estranho que pareça, os logaritmos naturais revelaram-se muito convenientes na realização de vários tipos de operações relacionadas com a análise de funções. Calculando logaritmos para base e realizado muito mais rápido do que por qualquer outro motivo.

• O que é necessário hoje para adotar uma criança na Rússia? A adoção na Rússia, além de uma decisão pessoal responsável, envolve uma série de procedimentos para verificação estatal dos candidatos. Seleção difícil para fase preparatória contribui para mais […]
• Informações gratuitas por TIN ou PSRN do registro fiscal de toda a Rússia - online em Portal único Os serviços fiscais podem obter informações sobre registro estadual entidades legais, empreendedores individuais, […]
• Punição por dirigir sem documentos (carteira de habilitação, seguro, STS) Às vezes, por esquecimento, o motorista fica ao volante sem carteira e recebe multa por dirigir sem documento. Lembramos que o entusiasta do carro dirige com seu obrigatório […]
• Flores para homens. Que flores você pode dar a um homem? Que flores você pode dar a um homem? Não existem muitas flores “masculinas”, mas existem algumas que são dadas aos homens. Uma pequena lista de flores à sua frente: Crisântemos. Rosas. Cravos. […]
• Memorando de serviço- Esse formulário especial documento usado em ambiente interno empresas e serve para solução rápida atual problemas de produção. Normalmente este documento é elaborado com o propósito de apresentar alguns […]
• Quando e como receber a parte capitalizada da sua pensão do Sberbank? O Sberbank é um banco parceiro do fundo de pensão estatal. Com base nisso, os cidadãos que se inscreveram para uma pensão por capitalização poderiam transferir a parte capitalizada […]
• Benefícios para crianças em Ulyanovsk e Região de Ulyanovsk em 2018 Além disso, todas as disciplinas operam programas aprovados pela legislação federal. Vejamos quem pode contar com quais benefícios. Como as autoridades regionais […]
• Guia detalhado sobre como lavrar procuração para representação de interesses Individual em juízo Em uma ação cível ou arbitral, em um processo administrativo ou criminal, os interesses tanto do autor quanto do réu podem ser representados por um advogado: […]

propriedades principais.

1. logax + logay = loga(x y);
2. logax - logay = loga (x: y).

motivos idênticos

Log6 4 + log6 9.

Agora vamos complicar um pouco a tarefa.

Exemplos de resolução de logaritmos

E se a base ou argumento de um logaritmo for uma potência? Então o expoente deste grau pode ser retirado do sinal do logaritmo de acordo com as seguintes regras:

É claro que todas essas regras fazem sentido se a ODZ do logaritmo for observada: a > 0, a ≠ 1, x >

Tarefa. Encontre o significado da expressão:

Transição para uma nova fundação

Seja dado o logaritmo logax. Então, para qualquer número c tal que c > 0 e c ≠ 1, a igualdade é verdadeira:

Tarefa. Encontre o significado da expressão:

Veja também:

Propriedades básicas do logaritmo

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.

O expoente é 2,718281828…. Para lembrar o expoente, você pode estudar a regra: o expoente é igual a 2,7 e duas vezes o ano de nascimento de Leo Nikolaevich Tolstoy.

Propriedades básicas dos logaritmos

Conhecendo esta regra, você saberá e valor exato expositores e a data de nascimento de Leo Tolstoy.

Exemplos para logaritmos

Expressões logarítmicas

Exemplo 1.
A). x=10ac^2 (a>0,c>0).

Usando as propriedades 3.5 calculamos

2.

3.

4. Onde .

Exemplo 2. Encontre x se

Exemplo 3. Seja dado o valor dos logaritmos

Calcule log(x) se

Propriedades básicas dos logaritmos

Os logaritmos, como qualquer número, podem ser somados, subtraídos e transformados de todas as maneiras. Mas como os logaritmos não são exatamente números comuns, existem regras aqui, que são chamadas propriedades principais.

Definitivamente, você precisa conhecer essas regras - sem elas, nenhum problema logarítmico sério pode ser resolvido. Além disso, são poucos - você pode aprender tudo em um dia. Então vamos começar.

Adição e subtração de logaritmos

Considere dois logaritmos com as mesmas bases: logax e logay. Então eles podem ser adicionados e subtraídos e:

1. logax + logay = loga(x y);
2. logax - logay = loga (x: y).

Assim, a soma dos logaritmos é igual ao logaritmo do produto, e a diferença é igual ao logaritmo do quociente. Atenção: o ponto chave aqui é motivos idênticos. Se os motivos forem diferentes, estas regras não funcionam!

Estas fórmulas irão ajudá-lo a calcular uma expressão logarítmica mesmo quando suas partes individuais não são consideradas (veja a lição “O que é um logaritmo”). Dê uma olhada nos exemplos e veja:

Como os logaritmos têm as mesmas bases, usamos a fórmula da soma:
log6 4 + log6 9 = log6 (4 9) = log6 36 = 2.

Tarefa. Encontre o valor da expressão: log2 48 − log2 3.

As bases são iguais, usamos a fórmula da diferença:
log2 48 - log2 3 = log2 (48: 3) = log2 16 = 4.

Tarefa. Encontre o valor da expressão: log3 135 − log3 5.

Novamente as bases são iguais, então temos:
log3 135 − log3 5 = log3 (135: 5) = log3 27 = 3.

Como você pode ver, as expressões originais são compostas de logaritmos “ruins”, que não são calculados separadamente. Mas após as transformações, são obtidos números completamente normais. Muitos testes são baseados neste fato. Sim, expressões semelhantes a testes são oferecidas com toda a seriedade (às vezes praticamente sem alterações) no Exame de Estado Unificado.

Extraindo o expoente do logaritmo

É fácil perceber que a última regra segue as duas primeiras. Mas é melhor lembrar disso de qualquer maneira - em alguns casos, isso reduzirá significativamente a quantidade de cálculos.

Claro, todas essas regras fazem sentido se o ODZ do logaritmo for observado: a > 0, a ≠ 1, x > 0. E mais uma coisa: aprenda a aplicar todas as fórmulas não só da esquerda para a direita, mas também vice-versa , ou seja Você pode inserir os números antes do sinal do logaritmo no próprio logaritmo. Isto é o que é mais frequentemente necessário.

Tarefa. Encontre o valor da expressão: log7 496.

Vamos nos livrar do grau no argumento usando a primeira fórmula:
log7 496 = 6 log7 49 = 6 2 = 12

Tarefa. Encontre o significado da expressão:

Observe que o denominador contém um logaritmo, cuja base e argumento são potências exatas: 16 = 24; 49 = 72. Temos:

Acho que o último exemplo requer alguns esclarecimentos. Para onde foram os logaritmos? Até o último momento trabalhamos apenas com o denominador.

Fórmulas de logaritmo. Soluções de exemplos de logaritmos.

Apresentamos a base e o argumento do logaritmo ali na forma de potências e retiramos os expoentes - obtivemos uma fração de “três andares”.

Agora vamos dar uma olhada na fração principal. O numerador e o denominador contêm o mesmo número: log2 7. Como log2 7 ≠ 0, podemos reduzir a fração - 2/4 permanecerá no denominador. Pelas regras da aritmética, o quatro pode ser transferido para o numerador, e foi isso que foi feito. O resultado foi a resposta: 2.

Transição para uma nova fundação

Falando sobre as regras de adição e subtração de logaritmos, enfatizei especificamente que elas só funcionam com as mesmas bases. E se os motivos forem diferentes? E se não forem potências exatas do mesmo número?

As fórmulas para a transição para uma nova base vêm em socorro. Vamos formulá-los na forma de um teorema:

Seja dado o logaritmo logax. Então, para qualquer número c tal que c > 0 e c ≠ 1, a igualdade é verdadeira:

Em particular, se definirmos c = x, obteremos:

Da segunda fórmula segue-se que a base e o argumento do logaritmo podem ser trocados, mas neste caso toda a expressão é “invertida”, ou seja, o logaritmo aparece no denominador.

Essas fórmulas raramente são encontradas em expressões numéricas comuns. É possível avaliar o quão convenientes eles são apenas na resolução de equações e desigualdades logarítmicas.

No entanto, existem problemas que não podem ser resolvidos de forma alguma, exceto com a mudança para uma nova fundação. Vejamos alguns deles:

Tarefa. Encontre o valor da expressão: log5 16 log2 25.

Observe que os argumentos de ambos os logaritmos contêm potências exatas. Vamos retirar os indicadores: log5 16 = log5 24 = 4log5 2; log2 25 = log2 52 = 2log2 5;

Agora vamos “inverter” o segundo logaritmo:

Como o produto não muda quando os fatores são reorganizados, multiplicamos calmamente quatro por dois e depois tratamos dos logaritmos.

Tarefa. Encontre o valor da expressão: log9 100 lg 3.

A base e o argumento do primeiro logaritmo são potências exatas. Vamos anotar isso e nos livrar dos indicadores:

Agora vamos nos livrar do logaritmo decimal passando para uma nova base:

Identidade logarítmica básica

Muitas vezes no processo de solução é necessário representar um número como um logaritmo para uma determinada base. Neste caso, as seguintes fórmulas nos ajudarão:

No primeiro caso, o número n torna-se o expoente do argumento. O número n pode ser absolutamente qualquer coisa, porque é apenas um valor logarítmico.

A segunda fórmula é na verdade uma definição parafraseada. É assim que se chama: .

Na verdade, o que acontece se o número b for elevado a tal potência que o número b elevado a esta potência dê o número a? Isso mesmo: o resultado é o mesmo número a. Leia este parágrafo com atenção novamente - muitas pessoas ficam presas nele.

Tal como as fórmulas para passar para uma nova base, a identidade logarítmica básica é por vezes a única solução possível.

Tarefa. Encontre o significado da expressão:

Observe que log25 64 = log5 8 - simplesmente tirou o quadrado da base e do argumento do logaritmo. Levando em consideração as regras de multiplicação de potências com a mesma base, obtemos:

Se alguém não sabe, esta foi uma tarefa real do Exame Estadual Unificado :)

Unidade logarítmica e zero logarítmico

Concluindo, darei duas identidades que dificilmente podem ser chamadas de propriedades - antes, são consequências da definição do logaritmo. Eles aparecem constantemente em problemas e, surpreendentemente, criam problemas até mesmo para alunos “avançados”.

1. logaa = 1 é. Lembre-se de uma vez por todas: o logaritmo para qualquer base a dessa base é igual a um.
2. loga 1 = 0 é. A base a pode ser qualquer coisa, mas se o argumento contiver um, o logaritmo será igual a zero! Porque a0 = 1 é uma consequência direta da definição.

Essas são todas as propriedades. Certifique-se de praticar colocá-los em prática! Baixe a folha de dicas no início da lição, imprima-a e resolva os problemas.

Veja também:

O logaritmo de b na base a denota a expressão. Calcular o logaritmo significa encontrar uma potência x () na qual a igualdade é satisfeita

Propriedades básicas do logaritmo

É necessário conhecer as propriedades acima, pois quase todos os problemas e exemplos relacionados aos logaritmos são resolvidos com base nelas. O resto das propriedades exóticas podem ser derivadas através de manipulações matemáticas com estas fórmulas

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.

Ao calcular a fórmula para a soma e diferença dos logaritmos (3.4), você se depara com bastante frequência. Os demais são um tanto complexos, mas em diversas tarefas são indispensáveis ​​para simplificar expressões complexas e calcular seus valores.

Casos comuns de logaritmos

Alguns dos logaritmos comuns são aqueles em que a base é igual a dez, exponencial ou dois.
O logaritmo na base dez é geralmente chamado de logaritmo decimal e é simplesmente denotado por lg(x).

Fica claro na gravação que o básico não está escrito na gravação. Por exemplo

Um logaritmo natural é um logaritmo cuja base é um expoente (denotado por ln(x)).

O expoente é 2,718281828…. Para lembrar o expoente, você pode estudar a regra: o expoente é igual a 2,7 e duas vezes o ano de nascimento de Leo Nikolaevich Tolstoy. Conhecendo esta regra, você saberá o valor exato do expoente e a data de nascimento de Leão Tolstói.

E outro logaritmo importante para a base dois é denotado por

A derivada do logaritmo de uma função é igual a um dividido pela variável

O logaritmo integral ou antiderivado é determinado pela relação

O material fornecido é suficiente para você resolver uma ampla classe de problemas relacionados a logaritmos e logaritmos. Para ajudá-lo a entender o material, darei apenas alguns exemplos comuns de currículo escolar e universidades.

Exemplos para logaritmos

Expressões logarítmicas

Exemplo 1.
A). x=10ac^2 (a>0,c>0).

Usando as propriedades 3.5 calculamos

2.
Pela propriedade da diferença de logaritmos temos

3.
Usando as propriedades 3.5 encontramos

4. Onde .

Pelo olhar expressão complexa usando uma série de regras é simplificado para formar

Encontrando valores de logaritmo

Exemplo 2. Encontre x se

Solução. Para cálculo, aplicamos ao último termo 5 e 13 propriedades

Nós registramos e lamentamos

Como as bases são iguais, igualamos as expressões

Logaritmos. Primeiro nível.

Deixe o valor dos logaritmos ser dado

Calcule log(x) se

Solução: vamos pegar um logaritmo da variável para escrever o logaritmo através da soma de seus termos

Este é apenas o começo de nosso conhecimento dos logaritmos e suas propriedades. Pratique cálculos, enriqueça suas habilidades práticas - em breve você precisará do conhecimento adquirido para resolver equações logarítmicas. Tendo estudado os métodos básicos para resolver tais equações, expandiremos seu conhecimento para outro não menos tópico importante- desigualdades logarítmicas...

Propriedades básicas dos logaritmos

Os logaritmos, como qualquer número, podem ser somados, subtraídos e transformados de todas as maneiras. Mas como os logaritmos não são exatamente números comuns, existem regras aqui, que são chamadas propriedades principais.

Definitivamente, você precisa conhecer essas regras - sem elas, nenhum problema logarítmico sério pode ser resolvido. Além disso, são poucos - você pode aprender tudo em um dia. Então vamos começar.

Adição e subtração de logaritmos

Considere dois logaritmos com as mesmas bases: logax e logay. Então eles podem ser adicionados e subtraídos e:

1. logax + logay = loga(x y);
2. logax - logay = loga (x: y).

Assim, a soma dos logaritmos é igual ao logaritmo do produto, e a diferença é igual ao logaritmo do quociente. Atenção: o ponto chave aqui é motivos idênticos. Se os motivos forem diferentes, estas regras não funcionam!

Estas fórmulas irão ajudá-lo a calcular uma expressão logarítmica mesmo quando suas partes individuais não são consideradas (veja a lição “O que é um logaritmo”). Dê uma olhada nos exemplos e veja:

Tarefa. Encontre o valor da expressão: log6 4 + log6 9.

Como os logaritmos têm as mesmas bases, usamos a fórmula da soma:
log6 4 + log6 9 = log6 (4 9) = log6 36 = 2.

Tarefa. Encontre o valor da expressão: log2 48 − log2 3.

As bases são iguais, usamos a fórmula da diferença:
log2 48 - log2 3 = log2 (48: 3) = log2 16 = 4.

Tarefa. Encontre o valor da expressão: log3 135 − log3 5.

Novamente as bases são iguais, então temos:
log3 135 − log3 5 = log3 (135: 5) = log3 27 = 3.

Como você pode ver, as expressões originais são compostas de logaritmos “ruins”, que não são calculados separadamente. Mas após as transformações, são obtidos números completamente normais. Muitos testes são baseados neste fato. Sim, expressões semelhantes a testes são oferecidas com toda a seriedade (às vezes praticamente sem alterações) no Exame de Estado Unificado.

Extraindo o expoente do logaritmo

Agora vamos complicar um pouco a tarefa. E se a base ou argumento de um logaritmo for uma potência? Então o expoente deste grau pode ser retirado do sinal do logaritmo de acordo com as seguintes regras:

É fácil perceber que a última regra segue as duas primeiras. Mas é melhor lembrar disso de qualquer maneira - em alguns casos, isso reduzirá significativamente a quantidade de cálculos.

Claro, todas essas regras fazem sentido se o ODZ do logaritmo for observado: a > 0, a ≠ 1, x > 0. E mais uma coisa: aprenda a aplicar todas as fórmulas não só da esquerda para a direita, mas também vice-versa , ou seja Você pode inserir os números antes do sinal do logaritmo no próprio logaritmo.

Como resolver logaritmos

Isto é o que é mais frequentemente necessário.

Tarefa. Encontre o valor da expressão: log7 496.

Vamos nos livrar do grau no argumento usando a primeira fórmula:
log7 496 = 6 log7 49 = 6 2 = 12

Tarefa. Encontre o significado da expressão:

Observe que o denominador contém um logaritmo, cuja base e argumento são potências exatas: 16 = 24; 49 = 72. Temos:

Acho que o último exemplo requer alguns esclarecimentos. Para onde foram os logaritmos? Até o último momento trabalhamos apenas com o denominador. Apresentamos a base e o argumento do logaritmo ali na forma de potências e retiramos os expoentes - obtivemos uma fração de “três andares”.

Agora vamos dar uma olhada na fração principal. O numerador e o denominador contêm o mesmo número: log2 7. Como log2 7 ≠ 0, podemos reduzir a fração - 2/4 permanecerá no denominador. Pelas regras da aritmética, o quatro pode ser transferido para o numerador, e foi isso que foi feito. O resultado foi a resposta: 2.

Transição para uma nova fundação

Falando sobre as regras de adição e subtração de logaritmos, enfatizei especificamente que elas só funcionam com as mesmas bases. E se os motivos forem diferentes? E se não forem potências exatas do mesmo número?

As fórmulas para a transição para uma nova base vêm em socorro. Vamos formulá-los na forma de um teorema:

Seja dado o logaritmo logax. Então, para qualquer número c tal que c > 0 e c ≠ 1, a igualdade é verdadeira:

Em particular, se definirmos c = x, obteremos:

Da segunda fórmula segue-se que a base e o argumento do logaritmo podem ser trocados, mas neste caso toda a expressão é “invertida”, ou seja, o logaritmo aparece no denominador.

Essas fórmulas raramente são encontradas em expressões numéricas comuns. É possível avaliar o quão convenientes eles são apenas na resolução de equações e desigualdades logarítmicas.

No entanto, existem problemas que não podem ser resolvidos de forma alguma, exceto com a mudança para uma nova fundação. Vejamos alguns deles:

Tarefa. Encontre o valor da expressão: log5 16 log2 25.

Observe que os argumentos de ambos os logaritmos contêm potências exatas. Vamos retirar os indicadores: log5 16 = log5 24 = 4log5 2; log2 25 = log2 52 = 2log2 5;

Agora vamos “inverter” o segundo logaritmo:

Como o produto não muda quando os fatores são reorganizados, multiplicamos calmamente quatro por dois e depois tratamos dos logaritmos.

Tarefa. Encontre o valor da expressão: log9 100 lg 3.

A base e o argumento do primeiro logaritmo são potências exatas. Vamos anotar isso e nos livrar dos indicadores:

Agora vamos nos livrar do logaritmo decimal passando para uma nova base:

Identidade logarítmica básica

Muitas vezes no processo de solução é necessário representar um número como um logaritmo para uma determinada base. Neste caso, as seguintes fórmulas nos ajudarão:

No primeiro caso, o número n torna-se o expoente do argumento. O número n pode ser absolutamente qualquer coisa, porque é apenas um valor logarítmico.

A segunda fórmula é na verdade uma definição parafraseada. É assim que se chama: .

Na verdade, o que acontece se o número b for elevado a tal potência que o número b elevado a esta potência dê o número a? Isso mesmo: o resultado é o mesmo número a. Leia este parágrafo com atenção novamente - muitas pessoas ficam presas nele.

Tal como as fórmulas para passar para uma nova base, a identidade logarítmica básica é por vezes a única solução possível.

Tarefa. Encontre o significado da expressão:

Observe que log25 64 = log5 8 - simplesmente tirou o quadrado da base e do argumento do logaritmo. Levando em consideração as regras de multiplicação de potências com a mesma base, obtemos:

Se alguém não sabe, esta foi uma tarefa real do Exame Estadual Unificado :)

Unidade logarítmica e zero logarítmico

Concluindo, darei duas identidades que dificilmente podem ser chamadas de propriedades - antes, são consequências da definição do logaritmo. Eles aparecem constantemente em problemas e, surpreendentemente, criam problemas até mesmo para alunos “avançados”.

1. logaa = 1 é. Lembre-se de uma vez por todas: o logaritmo para qualquer base a dessa base é igual a um.
2. loga 1 = 0 é. A base a pode ser qualquer coisa, mas se o argumento contiver um, o logaritmo será igual a zero! Porque a0 = 1 é uma consequência direta da definição.

Essas são todas as propriedades. Certifique-se de praticar colocá-los em prática! Baixe a folha de dicas no início da lição, imprima-a e resolva os problemas.

Um dos elementos da álgebra de nível primitivo é o logaritmo. O nome vem de língua grega da palavra “número” ou “potência” e significa o grau em que o número na base deve ser elevado para encontrar o número final.

Tipos de logaritmos

• log a b – logaritmo do número b na base a (a > 0, a ≠ 1, b > 0);
• log b – logaritmo decimal (logaritmo na base 10, a = 10);
• ln b – logaritmo natural (logaritmo na base e, a = e).

Como resolver logaritmos?

O logaritmo de b na base a é um expoente que requer que b seja elevado à base a. O resultado obtido é pronunciado assim: “logaritmo de b na base a”. Solução problemas logarítmicosé que você precisa determinar um determinado grau por números de acordo com os números indicados. Existem algumas regras básicas para determinar ou resolver o logaritmo, bem como converter a própria notação. Usando-os, equações logarítmicas são resolvidas, derivadas são encontradas, integrais são resolvidas e muitas outras operações são realizadas. Basicamente, a solução para o logaritmo em si é a sua notação simplificada. Abaixo estão fórmulas básicas e propriedades:

Para qualquer um; uma > 0; a ≠ 1 e para qualquer x ; y > 0.

• a log a b = b – identidade logarítmica básica
• registrar a 1 = 0
• loga a = 1
• log a (x y) = log a x + log a y
• log a x/ y = log a x – log a y
• log a 1/x = -log a x
• log a x p = p log a x
• log a k x = 1/k log a x , para k ≠ 0
• log a x = log a c x c
• log a x = log b x/ log b a – fórmula para mover para uma nova base
• log a x = 1/log x a

Como resolver logaritmos - instruções passo a passo para resolver

• Primeiro, anote a equação necessária.

Observação: se o logaritmo base for 10, a entrada será abreviada, resultando em um logaritmo decimal. Se houver um número natural e, então o anotamos, reduzindo-o a um logaritmo natural. Isso significa que o resultado de todos os logaritmos é a potência à qual o número base é elevado para obter o número b.

Diretamente, a solução está no cálculo desse grau. Antes de resolver uma expressão com logaritmo, ela deve ser simplificada conforme a regra, ou seja, por meio de fórmulas. Você pode encontrar as principais identidades voltando um pouco no artigo.

Adição e subtração de logaritmos com dois números diferentes, mas com as mesmas bases, substitua por um logaritmo pelo produto ou divisão dos números b e c, respectivamente. Neste caso, você pode aplicar a fórmula de mudança para outra base (veja acima).

Se você usar expressões para simplificar um logaritmo, há algumas limitações a serem consideradas. E isto é: a base do logaritmo a é apenas número positivo, mas não igual a um. O número b, assim como a, deve ser maior que zero.

Há casos em que, ao simplificar uma expressão, não será possível calcular o logaritmo em forma numérica. Acontece que tal expressão não faz sentido, porque muitas potências são números irracionais. Nessa condição, deixe a potência do número como logaritmo.

O logaritmo de um número positivo b na base a (a>0, a não é igual a 1) é um número c tal que a c = b: log a b = c ⇔ a c = b (a > 0, a ≠ 1, b > 0)       

Observe que o logaritmo de um número não positivo é indefinido. Além disso, a base do logaritmo deve ser um número positivo que não seja igual a 1. Por exemplo, se elevarmos ao quadrado -2, obteremos o número 4, mas isso não significa que o logaritmo na base -2 de 4 é igual a 2.

Identidade logarítmica básica

um log a b = b (a > 0, a ≠ 1) (2)

É importante que o âmbito de definição dos lados direito e esquerdo desta fórmula seja diferente. O lado esquerdo é definido apenas para b>0, a>0 e a ≠ 1. Parte direitaé definido para qualquer b, mas não depende de a. Assim, a aplicação da “identidade” logarítmica básica na resolução de equações e desigualdades pode levar a uma mudança no DO.

Duas consequências óbvias da definição de logaritmo

log a a = 1 (a > 0, a ≠ 1) (3)
log a 1 = 0 (a > 0, a ≠ 1) (4)

Na verdade, ao elevar o número a à primeira potência, obtemos o mesmo número, e ao elevá-lo à primeira potência grau zero- um.

Logaritmo do produto e logaritmo do quociente

log a (b c) = log a b + log a c (a > 0, a ≠ 1, b > 0, c > 0) (5)

Log a b c = log a b - log a c (a > 0, a ≠ 1, b > 0, c > 0) (6)

Gostaria de alertar os alunos contra o uso impensado dessas fórmulas ao resolver equações logarítmicas e desigualdades. Ao usá-los “da esquerda para a direita”, o ODZ se estreita, e ao passar da soma ou diferença dos logaritmos para o logaritmo do produto ou quociente, o ODZ se expande.

Na verdade, a expressão log a (f (x) g (x)) é definida em dois casos: quando ambas as funções são estritamente positivas ou quando f(x) e g(x) são ambas menores que zero.

Transformando esta expressão na soma log a f (x) + log a g (x) , somos forçados a nos limitar apenas ao caso em que f(x)>0 e g(x)>0. Há um estreitamento da área valores aceitáveis, e isso é categoricamente inaceitável, pois pode levar à perda de soluções. Problema semelhante existe para a fórmula (6).

O grau pode ser retirado do sinal do logaritmo

log a b p = p log a b (a > 0, a ≠ 1, b > 0) (7)

E mais uma vez gostaria de apelar à precisão. Considere o seguinte exemplo:

Log a (f (x) 2 = 2 log a f (x)

O lado esquerdo da igualdade é obviamente definido para todos os valores de f(x), exceto zero. O lado direito é apenas para f(x)>0! Ao retirar o grau do logaritmo, estreitamos novamente a ODZ. O procedimento inverso leva a uma expansão da faixa de valores aceitáveis. Todas estas observações aplicam-se não apenas à potência 2, mas também a qualquer potência par.

Fórmula para mudar para uma nova fundação

log a b = log c b log c a (a > 0, a ≠ 1, b > 0, c > 0, c ≠ 1) (8)

Que caso raro, quando a ODZ não muda durante a transformação. Se você escolheu a base c com sabedoria (positiva e diferente de 1), a fórmula para mudar para uma nova base é completamente segura.

Se escolhermos o número b como nova base c, obteremos um importante caso especial da fórmula (8):

Log a b = 1 log b a (a > 0, a ≠ 1, b > 0, b ≠ 1) (9)

Alguns exemplos simples com logaritmos

Exemplo 1. Calcule: log2 + log50.
Solução. log2 + log50 = log100 = 2. Utilizamos a fórmula da soma dos logaritmos (5) e a definição do logaritmo decimal.

Exemplo 2. Calcule: lg125/lg5.
Solução. log125/log5 = log 5 125 = 3. Usamos a fórmula para passar para uma nova base (8).

Tabela de fórmulas relacionadas a logaritmos

um log a b = b (a > 0, a ≠ 1)

log a a = 1 (a > 0, a ≠ 1)

log a 1 = 0 (a > 0, a ≠ 1)

log a (b c) = log a b + log a c (a > 0, a ≠ 1, b > 0, c > 0)

log a b c = log a b - log a c (a > 0, a ≠ 1, b > 0, c > 0)

log a b p = p log a b (a > 0, a ≠ 1, b > 0)

log a b = log c b log c a (a > 0, a ≠ 1, b > 0, c > 0, c ≠ 1)

log a b = 1 log b a (a > 0, a ≠ 1, b > 0, b ≠ 1)